1.   引言

当前，随着光学技术和采集设备的快速发展，面向计算机视觉和模式识别领域的应用范围已逐步从大气环境向水下环境进行拓展^[1,2]。然而，由于水下作业环境的复杂多变，获取到的图像数据一方面呈现出高维形态(属于图像类数据的共性)，另一方面存在可用样本数量受限且易伴随噪声干扰等现象的出现(属于水下应用环境的特有属性)。因此，如何找到一种有效方法去提升水下光视觉图像数据的识别精度变得十分重要。近二三十年来，子空间学习技术因其模型结构简单、可解释性强以及泛化能力好等特点，已在小样本图像数据的特征描述中获得成功应用，并逐步成为图像识别的主流技术之一。在面向其研究的方法中，PCA(Principal Component Analysis)^[3]，LDA(Linear Discriminant Analysis)^[4]，LPP(Locality Preserving Projection)^[5]是3种最为经典的方法。PCA用于提取图像数据中最具表现力的特征信息，LDA寻找嵌入在图像数据中最具辨别力的特征信息，LPP试图挖掘图像数据之间的局部几何结构信息。

应用上述方法对图像进行描述之前，需要预先将2维(2D)图像矩阵转化为一维(1D)向量数据，此操作不仅会增大投影向量的计算代价而且易丢失隐藏于像素之间的空间结构信息。为了克服这个困难，Yang等人^[6]提出了经典的2DPCA方法，受到2DPCA在图像特征提取方面获得成功的启发，一系列基于矩阵的子空间学习方法得以相继提出，包括2DLDA^[7]，2DLPP^[8]等。尽管上述方法利用2维矩阵信息能够直接提取图像的主要特征，但其均使用欧氏距离的平方作为数据之间相似性的度量。众所周知，大距离度量对噪声干扰不具有鲁棒性，会导致实际投影方向与期望解存在明显偏差。因此，面向2维子空间学习方法的鲁棒性展开研究变得十分重要。

目前，采取鲁棒范数度量策略认为是有效提升2维子空间学习方法性能的重要技术手段，且大多考虑在经典的2DPCA中率先进行应用。例如Wang等人^[9]利用${l_1}$范数提出基于非贪婪算法的2DPCA-L1方法。Wang等人^[10]在2DPCA-L1鲁棒性的基础上，引入稀疏诱导回归策略，进而提出具有稀疏约束的2DPCA-L1-S方法。Wang等人^[11]考虑将${l_1}$范数的使用广度进行延拓，提出使用${l_p}$范数度量的广义2DPCA方法(G-2DPCA)。然而，在上述方法中，其距离度量机制选用的是非欧氏空间范数度量(${l_1}$范数)，由于其不具有旋转不变性，导致获取到的解与保护数据几何结构的协方差矩阵无关^[12]。为了解决该问题，许多选用欧氏空间的鲁棒范数度量方法得以相继发展，比较经典的有Li等人^[13]在目标函数中使用F范数替代F范数的平方策略提出的F-norm 2DPCA, Gao等人^[14]提出${R_1}$-2-DPCA用于提取图像关键特征，考虑通过${R_1}$范数最大化投影数据的方差。Zhao等人^[15]提出面向四元数框架下的2DPCA方法(2DQPCA)，其利用标签和颜色信息连续在两个投影子空间中完成特征提取，实现了小样本数据识别精度的提升。Zhou等人^[16]将中心化权重矩阵作用到投影数据中提出广义中心化2DPCA(GC-2DPCA)，有效保护了数据的结构信息。尽管这些方法的度量机制比${l_1}$范数更具优势，但其在结构上无法同时满足最小化重构误差和最大化方差的双重诉求。因此，合理化体系建设将进一步提升方法的鲁棒性。

自然地，学者会将重构误差与方差之间可能存在的关联纳入到考虑范围之内，得到更具鲁棒性的体系结构，如Gao等人^[17]利用二者夹角正切值提出的角度2DPCA(Angle-2DPCA)，Wang等人^[18]在此基础之上通过使用可调参数提出的余弦2DPCA(Cos-2DPCA)，其本质均是基于直角三角形体系结构，找到了可同时满足最小化重构误差和最大化方差的最优解。然而，这些方法在取得自身结构优势的前提下，间接制约了对于更具鲁棒性度量模式的可匹配性，在一定程度上削弱了噪声环境中对于主要特征准确描述的能力。为了改善此种困扰，Zhang等人^[19]提出联合2范数和l_p范数度量机制的2DPCA(2DPCA-2-L_P)，其可通过p值变化提升度量模式多样性的选择，但同时也会在p不为2时丢失2DPCA模型固有的旋转不变性。此外，2DPCA-2-L_P考虑以平等对待每个样本数据为主导思想，忽略了噪声数据和正常样本在重构误差贡献上形成的差异。因此，现存具有鲁棒属性的2DPCA方法没能最大程度在易受噪声干扰的应用场景中对光视觉观测数据的重要特征进行准确描述。

鉴于上述改进方法在整体鲁棒表现力方面存在的不足，本文以前人研究方法为根基并提出了新颖的双灵活度量自适应加权2DPCA方法(Dual Flexible Metric Adaptive Weighted two-Dimensional Principal Component Analysis, DFMAW-2DPCA)，并将其在具有高维小样本属性且易受噪声干扰的水下图像识别中进行应用。该方法的主要贡献包括如下几个方面：

(1)DFMAW-2DPCA在同时考虑重构误差和方差之间关系的前提下，决定选用l_2,p范数作为衡量数据之间相似性的策略，不仅成功突破了双层结构模型度量机制不灵活的局限性，而且保留了欧氏范数测度自身所固有的优势(如旋转不变性)，有效提升了模型在噪声环境中的特征提取能力。

(2)DFMAW-2DPCA构造了一个自适应加权学习框架，该框架结构简单且不需要人工干预，能够为每个样本数据合理分配不同的权重，既增大形成重构误差较小的样本作用又减少产生重构误差较大的样本影响，进一步实现模型鲁棒性的提升。

(3)面向DFMAW-2DPCA的优化求解过程，该文设计了一个有效的非贪婪迭代算法，其在每次迭代过程中均能获取到具有封闭形式的解，并最终快速收敛到局部最优解。

在此基础上，3个水下图像数据库中的大量实验结果也有力佐证了该文提出方法的卓越性能。综上所述，该文提出的方法具备良好的理论研究意义和实际应用价值。

2.   问题提出

2.1   相关工作

假设有$N$幅$m \times n$维的训练样本图像数据集合${{\boldsymbol{A}}_i} \in {R ^{m \times n}}\left( {i = 1,2, \cdots ,N} \right)$，${{\boldsymbol{A}}_i}$表示第$i$个训练样本。通常来说，预先需要完成对于输入数据的中心化处理，即$\displaystyle\sum\nolimits_{i = 1}^N {\left( {{{\boldsymbol{A}}_i} - {\boldsymbol{m}}} \right)} = {{{\textit{0}}}}$，其中${\boldsymbol{m}} = {1 \mathord{\left/ {\vphantom {1 N}} \right. } N}\displaystyle\sum\nolimits_{i = 1}^N {{{\boldsymbol{A}}_i}}$是所有训练样本的均值数据。基于Angle-2DPCA^[17]思想本质上是通过求解以下优化模型来找到最优投影矩阵

其中，${\left\|\cdot\right\|}_{\text{F}}$和${{\boldsymbol{I}}_k} \in {{{R}}^{k \times k}}$分别指出一个矩阵的F范数运算和$k$维单位矩阵。

在整体结构建立以及距离度量方式的使用方面，Angle-2DPCA表现出良好的鲁棒性。然而，其在一定程度上仍具有明显的局限性。首先，Angle-2DPCA在建立重构误差和方差关系的基础时，所选用的距离度量模式欠缺一定的灵活性，没能最大程度对噪声干扰实行有效抑制。此外，针对Angle-2DPCA提出的优化求解算法并未在理论上给出明确的收敛性证明，导致无法确保获取到的投影矩阵为最优解。最后，Angle-2DPCA在求解过程中涉及较多的中间变量和除法运算，这增加了对存储空间的需求。

2.2   动机与目标函数

正如2.1节分析所述，目标函数(1)合理兼顾了重构误差与方差之间的双层关系，其能够匹配到的鲁棒距离度量策略通常以F范数为主，而该度量模式在结构选择方面缺乏一定的灵活性，并不能充分且有效地抑制噪声信息的干扰。为了解决这个问题，该文希望保留目标函数(1)中双层关系所具备优势的同时，选择以输入图像的每一行作为新的样本数据，此时可寻找到${l_2}$范数作为距离度量策略。在此基础上，针对优化模型结构使用$p\left( {0 < p < 2} \right)$次方进行缩放比例调节，进而形成更具鲁棒性的${l_{2,p}}$范数度量模式，其不仅能够根据$p$值的变化提升自身的灵活性而且同时保留了欧氏距离度量所特有的旋转不变性。此外，考虑到现存鲁棒2DPCA方法普遍选择平等地处理每个样本数据，忽略了噪声干扰相对于正常样本具有更大重构误差的事实，很大程度上影响了实际应用的有效性。从进一步改善模型鲁棒性的角度出发，该文引入一个自适应加权学习框架，目的是在不需人为干预的情况下，合理为每个数据分配与其相适的权重，真正在噪声环境中实现重构误差与方差之间距离加权和最小化的诉求。最后，该文希望模型的最优解能与保护数据几何结构的协方差矩阵有着紧密的关联，这会对识别精度产生积极的推进作用。综上所述，该文提出了新颖的双灵活度量自适应加权2维主成分分析方法(Dual Flexible Metric Adaptive Weighted 2DPCA, DFMAW-2DPCA)，其目标函数为

其中，$0 \le {l_{ij}} \le 1$表示为分配给第$ij$个投影数据方差与重构误差之间距离项的权重且满足$\displaystyle\sum\nolimits_{i = 1}^N {\displaystyle\sum\nolimits_{j = 1}^m {{l_{ij}}} } = 1$，${\boldsymbol{l}} = {\left( {{l_{11}}, {l_{12}} , \cdots , {l_{Nm}}} \right)^{\mathrm{T}}}$代表由每一个${l_{ij}}$组成的权重向量，${{\boldsymbol{A}}_i}\left( {j,:} \right)$代表矩阵${{\boldsymbol{A}}_i}$的第$j$行元素。

目标函数(2)的建立一方面在结构上突破了兼顾方差和重构误差关系2DPCA模型体系的局限性，能够获取到更为灵活的鲁棒距离度量模式，另一方面改善了在噪声干扰环境下平等对待每个样本所带来的不利影响，其可以根据样本固有属性自适应分配权重占比，全面提升对于关键特征信息的有效刻画能力。此外，针对提出模型的求解问题，该文设计了一个快速的非贪婪迭代算法，使其在每次迭代过程中都能获得封闭形式的解。最后，相比于同类算法，在确保识别精度提升的基础上，并没有增加时间复杂度。

3.   算法求解

本节给出DFMAW-2DPCA获取最优投影矩阵${\boldsymbol{V}}$的求解过程。根据参考文献[19]传递的信息可知，假设${{\boldsymbol{B}}_v}$与${{\boldsymbol{H}}_v}$均与${\boldsymbol{V}}$有关，则式(3)最优解

能通过迭代求解式(4)

其中${\alpha _v}$可定义为

此时，考虑令${{\boldsymbol{B}}_{ij}}\left( {\boldsymbol{V}} \right) = {{\boldsymbol{A}}_i}\left( {j,:} \right) - {{\boldsymbol{A}}_i}\left( {j,:} \right){\boldsymbol{V}}{{\boldsymbol{V}}^{\mathrm{T}}}$以及${{\boldsymbol{H}}_{ij}}\left( {\boldsymbol{V}} \right) = {{\boldsymbol{A}}_i}\left( {j,:} \right){\boldsymbol{V}}$。受式(4)表现形式的启发，目标函数(2)能够变为

其中，$0 \le {\alpha _{ij}} \le 1$，且与${{\boldsymbol{M}}_{ij}}\left( {\boldsymbol{V}} \right)$以及${{\boldsymbol{H}}_{ij}}\left( {\boldsymbol{V}} \right)$有关，其表达式为

通过相应的代数运算，可得

其中，${\mathrm{tr}}\left( \cdot \right)$为矩阵的迹，${s_{ij}} = 1 / \left\| {{\boldsymbol{A}}_i}\left( {j,:} \right) - {{\boldsymbol{A}}_i}\left( {j,:} \right){\boldsymbol{V}}{{\boldsymbol{V}}^{\mathrm{T}}} \right\|_2^{2 - p}$以及${g_{ij}} = {1 / {\left\| {{{\boldsymbol{A}}_i}\left( {j,:} \right){\boldsymbol{V}}} \right\|_2^{2 - p}}}$。在实际应用中，输入数据${{\boldsymbol{A}}_i}\left( {j,:} \right)$存在为零向量的可能。因此，为了防止分母为0的现象出现，需要考虑对${s_{ij}}$和${g_{ij}}$的表达式进行重新定义，具体为

将式(8)代入到目标函数(6)中，进行合理的整合，可得

通过观察目标函数(11)，不难发现其内部共包含5个未知变量${\alpha _{ij}}$, ${g_{ij}}$, ${s_{ij}}$, ${l_{ij}}$和${\boldsymbol{V}}$，且${\alpha _{ij}}$, ${g_{ij}}$, ${s_{ij}}$和${l_{ij}}$的值均与投影矩阵${\boldsymbol{V}}$存在着紧密的关联。因此，其不存在封闭形式的解并且想要直接求解目标函数(11)将会变得十分困难。针对这个问题，该文考虑采用交替求解和块坐标下降的优化策略来求解最优投影矩阵。具体来说，解决过程可以分为以下3个步骤

步骤1　固定${\boldsymbol{V}}$，完成${\alpha _{ij}}$, ${s_{ij}}$和${g_{ij}}$的更新。

利用式(7)，式(9)以及式(10)，可分别完成对于${\alpha _{ij}}$, ${s_{ij}}$和${g_{ij}}$的更新操作。

步骤2　固定${\alpha _{ij}}$, ${s_{ij}}$, ${g_{ij}}$和${\boldsymbol{V}}$，完成${l_{ij}}$的更新。

基于${\alpha _{ij}}$, ${g_{ij}}$, ${s_{ij}}$和${\boldsymbol{V}}$均已视为固定值的事实，即可考虑令${r_{ij}} = {\mathrm{tr}}\left( {{\boldsymbol{A}}_i}{{\left( {j,:} \right)}^{\mathrm{T}}}{{\boldsymbol{A}}_i}\left( {j,:} \right) - {{\boldsymbol{V}}^{\mathrm{T}}}{{\boldsymbol{A}}_i}{{\left( {j,:} \right)}^{\mathrm{T}}} {{\boldsymbol{A}}_i}\left( {j,:} \right){\boldsymbol{V}} \right){s_{ij}}$$- {\alpha _{ij}}{\mathrm{tr}}\left( {{{\boldsymbol{V}}^{\mathrm{T}}}{{\boldsymbol{A}}_i}{{\left( {j,:} \right)}^{\mathrm{T}}}{{\boldsymbol{A}}_i}\left( {j,:} \right){\boldsymbol{V}}} \right){{{g}}_{ij}}$，此时的目标函数(11)可变为

结合拉格朗日乘子法，优化问题式(12)的拉格朗日函数能够定义为

其中，$\lambda$和${\mu _{ij}}$为拉格朗日乘子。式(13)所对应的KKT(Karush-Kuhn-Tucker)条件陈列为

通过整合式(14)并进行相应的代数运算，最终可获得${l_{ij}}$的最优解，其表达式为

步骤3　固定${\alpha _{ij}}$, ${s_{ij}}$, ${g_{ij}}$和${l_{ij}}$，完成${\boldsymbol{V}}$的更新。

考虑将${\alpha _{ij}}$, ${s_{ij}}$, ${g_{ij}}$和${l_{ij}}$共4个变量固定时，目标函数(12)中的${\mathrm{tr}}\left( {{{\boldsymbol{A}}_i}{{\left( {j,:} \right)}^{\mathrm{T}}}{{\boldsymbol{A}}_i}\left( {j,:} \right){s_{ij}}} \right)$能够视为一个常数项。因此，目标函数(12)可进一步转化为

其中，${\boldsymbol{A}} = [{{\boldsymbol{A}}_1}{\left( {1,:} \right)^{\mathrm{T}}},{{\boldsymbol{A}}_1}{\left( {2,:} \right)^{\mathrm{T}}}, \cdots ,{{\boldsymbol{A}}_N}{\left( {1,:} \right)^{\mathrm{T}}}, {{\boldsymbol{A}}_N} {\left( {m,:} \right)^{\mathrm{T}}}]^{\mathrm{T}} \in {{{R}}^{mN \times n}}$是由输入数据${{\boldsymbol{A}}_i}\left( {j,:} \right)$所组成的样本增广矩阵。${\boldsymbol{S}}$, ${\boldsymbol{D }}$, ${\boldsymbol{G}}$, ${\boldsymbol{L}}$和${\boldsymbol{U}} = {\boldsymbol{L}}\left( {{\boldsymbol{S}} + {\boldsymbol{DG}}} \right)$分别是由对角元素${s_{ij}}$, ${\alpha _{ij}}$, ${g_{ij}}$, ${1 \mathord{\left/ {\vphantom {1 {{l_{ij}}}}} \right. } {{l_{ij}}}}$和${u_{ij}} = {1 \mathord{\left/ {\vphantom {1 {{l_{ij}}}}} \right. } {{l_{ij}}}} \left( {{s_{ij}} + {\alpha _{ij}}{g_{ij}}} \right)$构成的对角矩阵。根据拉格朗日乘子法可知，目标函数(16)的解${\boldsymbol{V}}$由矩阵${{\boldsymbol{A}}^{\mathrm{T}}}{\boldsymbol{UA}}$前$k$个最大特征值所对应特征向量所组成。在此基础上，利用已求取的当前时刻${\boldsymbol{V}}$完成对于${s_{ij}}$, ${\alpha _{ij}}$和${g_{ij}}$的更新操作，同时根据上述更新的信息，开展面向${l_{ij}}$的计算。最后，反复执行上述迭代过程直至发现满足收敛条件的最优投影矩阵${\boldsymbol{V }}$，具体求解过程详见算法1。

表 1  DFMAW-2DPCA优化求解算法

输入：样本增广矩阵${\boldsymbol{A}} \in {R ^{mN \times n}}$，特征维度$k$和$p \in \left( {0,2} \right)$，其中样本数据${{\boldsymbol{A}}_i}$已完成数据中心化处理。
初始化：${{\boldsymbol{V}}^{\left( {t - 1} \right)}} \in {{{R}}^{n \times k}}$，其满足${{\boldsymbol{V}}^{\mathrm{T}}}{\boldsymbol{V}} = {{\boldsymbol{I}}_k}$，$t = 1$，$\delta = 0.01$。
当 不收敛时 执行
1：分别利用式(7)、式(10)和式(11)计算对角矩阵${{\boldsymbol{D}}^{\left( {t - 1} \right)}}$，${{\boldsymbol{S}}^{\left( {t - 1} \right)}}$和${{\boldsymbol{G}}^{\left( {t - 1} \right)}}$的对角元素$\alpha _{ij}^{\left( {t - 1} \right)}$，$s_{ij}^{\left( {t - 1} \right)}$和$g_{ij}^{\left( {t - 1} \right)}$。
2：利用式(16)计算$l_{ij}^{\left( {t - 1} \right)}$，并同时构建由对角元素${1 \mathord{\left/ {\vphantom {1 {l_{ij}^{\left( {t - 1} \right)}}}} \right. } {l_{ij}^{\left( {t - 1} \right)}}}$所组成的对角矩阵${{\boldsymbol{L}}^{\left( {t - 1} \right)}}$。
3：计算对角矩阵${{\boldsymbol{U}}^{\left( {t - 1} \right)}}$的对角元素$u_{ij}^{\left( {t - 1} \right)}$，其中$u_{ij}^{\left( {t - 1} \right)} = {1 \mathord{\left/ {\vphantom {1 {l_{ij}^{\left( {t - 1} \right)}}}} \right. } {l_{ij}^{\left( {t - 1} \right)}}}\left( {s_{ij}^{\left( {t - 1} \right)} + \alpha _{ij}^{\left( {t - 1} \right)}g_{ij}^{\left( {t - 1} \right)}} \right)$。
4：计算加权协方差矩阵${{\boldsymbol{A}}^{\mathrm{T}}}{{\boldsymbol{U}}^{\left( {t - 1} \right)}}{\boldsymbol{A}}$。
5：求解目标函数式(8)的最优投影矩阵${{\boldsymbol{V}}^{\left( t \right)}}$，${{\boldsymbol{V}}^{\left( t \right)}}$是由${{\boldsymbol{A}}^{\mathrm{T}}}{{\boldsymbol{U}}^{\left( {t - 1} \right)}}{\boldsymbol{A}}$的前$k$个最大特征值所对应特征向量组成。
6：检验收敛条件$J({{\boldsymbol{V}}^{\left( t \right)}}) - J({{\boldsymbol{V}}^{\left( {t - 1} \right)}}) \le \delta$满足；如果满足，结束循环；否则执行步骤7。
7：通过获取到的${{\boldsymbol{V}}^{\left( t \right)}}$完成对角矩阵${{\boldsymbol{D}}^{\left( t \right)}}$，${{\boldsymbol{S}}^{\left( t \right)}}$和${{\boldsymbol{G}}^{\left( t \right)}}$中的每个对角元素$\alpha _{ij}^{\left( t \right)}$，$s_{ij}^{\left( t \right)}$和$g_{ij}^{\left( t \right)}$的计算。
8：根据${{\boldsymbol{V}}^{\left( t \right)}}$，$\alpha _{ij}^{\left( t \right)}$，$s_{ij}^{\left( t \right)}$和$g_{ij}^{\left( t \right)}$执行对于对角矩阵${{\boldsymbol{L}}^{\left( t \right)}}$中每个对角元素${1 \mathord{\left/ {\vphantom {1 {l_{ij}^{\left( t \right)}}}} \right. } {l_{ij}^{\left( t \right)}}}$的计算。
9：完成对角矩阵${{\boldsymbol{U}}^{\left( t \right)}}$中每个对角元素$u_{ij}^{\left( t \right)}$的计算。
10：$t \leftarrow t + 1$。
结束循环
输出：${{\boldsymbol{V}}^{\left( t \right)}} \in {{{R}}^{n \times k}}$。

下载: 导出CSV 

| 显示表格

4.   实验结果与分析

该文选用NF, JEDI和EPIDHEU共3组水下图像数据库作为验证平台，将所提方法与现存主要具有鲁棒特性的2DPCA模型2DPCA-L1^[10], F-2DPCA^[13], Angle-2DPCA^[17], GC-2DPCA^[16], Cos-2DPCA^[18]和2DPCA-2-L_P^[19]进行了对比。此外，针对3组数据库中的实验，该文考虑通过改变特征维数(变化范围设定为0～200)的策略实现对方法识别精度以及重构性能的验证，其中识别精度可利用最近邻(1-Nearest Neighbor, 1NN)分类器的结果进行判断，而重构误差(Reconstruction Error, RE)可使用式(17)获知

其中，$M$为无噪声样本的数量，${\boldsymbol{A}}_i^{{\mathrm{clean}}}$为第$i$个无噪声样本数据。最后，为了最大限度避免实验结果存在偶然性的现象，本章决定将每个数据库中的实验过程重复10次。

4.1   实验数据

NF数据库^[20]包含超过50000个与海洋生物相关的视频数据，其中可用的水下生物视频数据不低于8000个。基于这些视频，挑选出具有不同类别和物理变化的45种鱼类视频作为研究基础，并进一步截取每个视频中具有不同姿态的40帧图像数据用于实验分析。在实验中，统一将每个图像样本的尺寸裁剪成30×50像素的同时，考虑从每个水下生物包含的40帧图像中任意选取12帧并放置椒盐噪声，噪声强度的变化区间设定为0.005～0.050且为随机分布。接下来，随机选取每个水下生物的24帧图像用于训练(包括16帧干净图像和8帧噪声图像)，余下图像全部用于测试，图1陈列了NF数据库中的一些图像样本。

图 1  NF数据库中一些图像样本

下载: 全尺寸图片 幻灯片

JEDI数据库^[21]是由日本国立海洋研究机构所建立的。该数据库的构成包含了超过250类水下生物体的视频数据，其中每个视频数据中生物体的姿态、背景以及光强存在区别。在实验中，该文决定选取35个具有代表性的生物体视频并从中随机采集28帧图像数据，将获取到的每一帧图像数据执行灰度化处理以及尺寸裁剪任务(30×50像素)。与此同时，从每个生物体的28帧图像中任意选取7帧引入高斯噪声，噪声分布状态与强度变化范围与NF数据库保持一致。此后，随机选取每类生物体的17帧图像用于训练(包括11帧干净图像和6帧噪声图像)，剩余的图像用于测试。图2陈列了JEDI数据库中一些图像样本。

图 2  JEDI数据库中一些图像样本

下载: 全尺寸图片 幻灯片

EPIDHEU数据库^[22]是一个用于验证水下图像识别方法性能的非开源数据集，共包含30类水下物体的600张光学图像，其中每类物体拥有20幅具有不同状态的图像，且存在微小的光照变化。在实验过程中，每幅图像的尺寸标准化到44×36像素。根据水下图像常面临遮挡与椒盐噪声同时出现的事实，考虑从每类物体的样本数据中随机选取7幅图像并引入混合噪声，其中遮挡占比为图像目标区域的5%～25%，噪声的波动强度则设定为在0.005～0.035任意变化，二者均呈随机分布，图3展示了EPIDHEU数据库中部分图像样本。该文随机选取每个物体的8幅干净图像和4幅噪声图像用于训练，其余图像用于测试。

图 3  EPIDHEU数据库中一些图像样本

下载: 全尺寸图片 幻灯片

4.2   图像识别与重构实验

为了直观且充分说明DFMAW-2DPCA的表现力，本小节考虑将其与6种同类型对比方法2DPCA-L1^[10], F-2DPCA^[13], Angle-2DPCA^[17], GC-2DPCA^[16], Cos-2DPCA^[18]和2DPCA-2-L_P^[19]在识别精度和重构结果等方面进行对比和验证。表1陈列了NF数据库中每种方法的平均最优识别准确率(%)和平均最小重构误差及其所对应的标准差。表2陈列了JEDI数据库中每种方法的平均最优识别准确率(%)和平均最小重构误差及其所对应的标准差。表3陈列了EPIDHEU数据库中每种方法的平均最优识别准确率(%)和平均最小重构误差及其所对应的标准差。表4陈列了EPIDHEU数据库中部分样本的可视化识别结果。表5分别列出了3个水下图像数据库中7种对比方法的平均运行时间(s)和所对应的标准差(SD)。图4分别展示了3个水下图像数据库中所有对比方法在不同特征维度下的识别准确率以及10组实验下的最小重构误差。针对上述实验结果进行观测和分析，可以总结得出如下有价值的结论：

表 1  NF数据库中每种方法的平均最优识别准确率(%)和平均最小重构误差及其所对应的标准差

	2DPCA-L1	F-2DPCA	Angle-2DPCA	GC-2DPCA	Cos-2DPCA	2DPCA-2-LP	DFMAW-2DPCA
							p =0.5	p = 1	p =1.5
识别精度	80.25±0.76	85.77±0.69	87.16±0.82	87.50±0.85	88.27±0.66	88.64±0.65	89.85±0.60	88.42±0.68	89.38±0.64
重构误差	462.47±2.14	415.86±1.92	391.25±2.01	382.04±1.97	364.59±1.88	356.78±1.90	326.14±1.81	357.51±1.92	338.92±1.86

下载: 导出CSV 

| 显示表格

表 2  JEDI数据库中每种方法的平均最优识别准确率(%)和平均最小重构误差及其所对应的标准差

	2DPCA-L1	F-2DPCA	Angle-2DPCA	GC-2DPCA	Cos-2DPCA	2DPCA-2-LP	DFMAW-2DPCA
							p =0.5	p = 1	p =1.5
识别精度	68.70±0.64	73.15±0.72	73.77±0.73	74.29±0.67	75.06±0.58	75.63±0.61	76.67±0.56	75.30±0.58	76.07±0.53
重构误差	226.59±1.75	210.36±1.68	193.42±1.84	178.90±1.65	155.81±1.60	146.04±1.57	121.53±1.62	149.64±1.67	133.42±1.63

下载: 导出CSV 

| 显示表格

表 3  EPIDHEU数据库中每种方法的平均最优识别准确率(%)和平均最小重构误差及其所对应的标准差

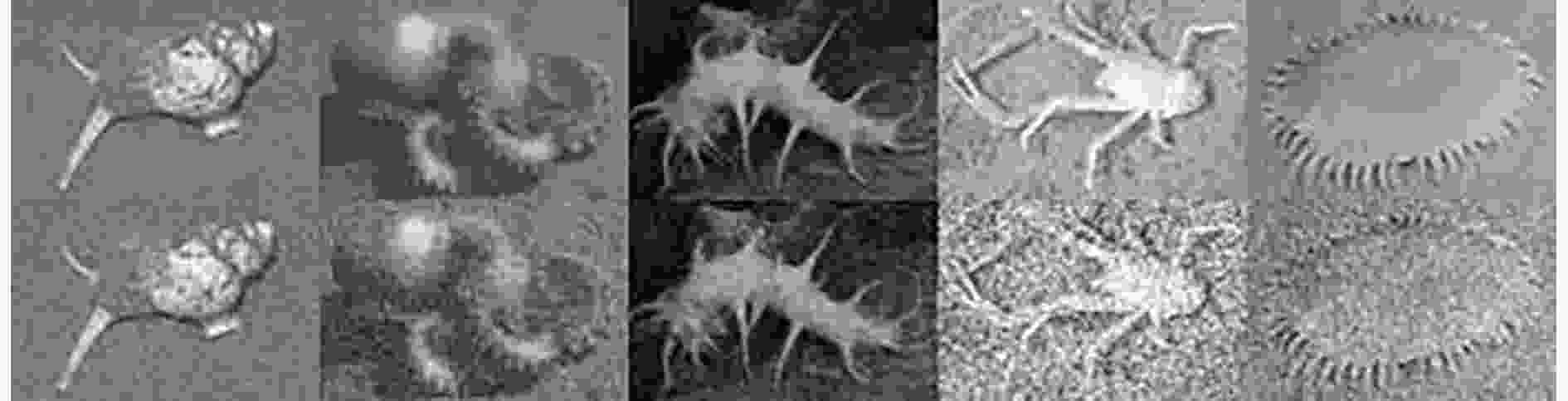
	2DPCA-L1	F-2DPCA	Angle-2DPCA	GC-2DPCA	Cos-2DPCA	2DPCA-2-LP	DFMAW-2DPCA
							p =0.5	p = 1	p =1.5
识别精度	77.38±1.57	82.79±1.81	83.71±1.73	84.25±1.59	84.96±1.55	85.50±1.52	86.04±1.54	85.25±1.50	86.54±1.56
重构误差	300.47±3.21	279.80±3.08	268.92±3.03	261.76±3.10	245.28±2.93	236.04±2.97	232.42±2.90	240.53±2.89	227.34±2.92

下载: 导出CSV 

| 显示表格

表 4  EPIDHEU数据库中部分示例样本的可视化识别结果

下载: 导出CSV 

| 显示表格

表 5  3个水下图像数据库中每种方法的平均运行时间与对应的标准差(s)

	2DPCA-L1	F-2DPCA	Angle-2DPCA	GC-2DPCA	Cos-2DPCA	2DPCA-2-LP	DFMAW-2DPCA
NF	11.26±0.58	2.13±0.15	5.60±0.44	4.79±0.37	3.08±0.30	3.15±0.34	3.19±0.25
JEDI	7.53±0.46	1.84±0.12	3.37±0.49	2.68±0.34	2.26±0.32	2.31±0.28	2.37±0.21
EPIDHEU	6.24±0.77	1.52±0.18	2.64±0.61	2.21±0.40	1.80±0.39	1.83±0.36	1.88±0.32

下载: 导出CSV 

| 显示表格

图 4  3个水下图像数据库中所有对比方法在不同特征维度下的识别准确率曲线以及10组实验下的最小重构误差

下载: 全尺寸图片 幻灯片

(1)根据表1–表3以及图4中所呈现出的内容，能够清晰地知道DFMAW-2DPCA在所有图像数据库上的识别精度和重构误差都明显优于其他6种对比方法，其中一个主要原因是DFMAW-2DPCA在同时最小化重构误差和最大化方差双层关系的基础上，成功匹配到更具灵活性的${l_{2,p}}$范数作为距离度量，此度量策略可通过p值的合理选取实现基于2DPCA方法在噪声环境中鲁棒性的提升。另一个重要原因是所提方法构建了自适应加权学习框架，即在不需要人为干预的情况下，能够根据每个输入样本数据状态自动分配与之相适应的权重，合理改善了模型在噪声环境中的特征提取能力。与此同时，表4所陈列的可视化结果充分的表明，本文所提出的方法对于水下目标识别具有杰出的表现力。

(2)进一步深入观察表1–表3以及图4所反映出的实验结果可知，尽管2DPCA-L1选用了具有鲁棒特性的${l_1}$范数作为距离度量标准，但其整体性能却逊色于其他对比方法，出现此结果可能主要包含两点原因，其一是2DPCA-L1在优化模型中采用最大化方差的策略，而最大化方差并不是基于2DPCA方法的本质诉求。其二是${l_1}$范数的度量模式是在丢失了诸如旋转不变性等一些宝贵性质的前提下实现了鲁棒性的提升，此种改变并没有达到预期目标。

(3)图4中的实验结果表明，当特征维数处于相对较低的某个阶段时，2DPCA-L1的识别率曲线存在明显下降趋势，可能是因为该方法前$k$个特征维度主要描述的是噪声数据特征信息，形成类内样本之间差异大于类间样本差异的现象发生，导致识别精度结果变差。然而，与2DPCA-L1表现不同，F-2DPCA, Angle-2DPCA, GC-2DPCA, Cos-2DPCA以及2DPCA-2-Lp均采用非贪婪算法进行最优解的捕获，且这个最优解与保护数据几何结构的协方差矩阵有着密切的关联，因此能够很大程度上降低水下噪声干扰。

4.3   计算效率实验

本小节主要面向两个方面检验所提模型DFMAW-2DPCA的计算效率，其一是考察DFMAW-2DPCA自身的计算复杂度，其二是检验所有对比方法在3个水下图像数据库中的运行时间，相关描述如下所示。

(1)在算法1执行每一次迭代更新任务过程中，DFMAW-2DPCA的计算复杂度主要体现在对于投影矩阵${\boldsymbol{V}} \in {{{R}}^{n \times k}}$的求解，而${\boldsymbol{V}}$的获取方式为协方差矩阵${{\boldsymbol{A}}^{\mathrm{T}}}{\boldsymbol{UA}}$的特征值分解操作，故其计算复杂度不会超过$O({n^3})$，这与经典的2DPCA方法保持一致。综上分析可知，DFMAW-2DPCA经过算法1每一次迭代后的整体计算复杂度最大限度为$O({n^3})$，若共需$t$次迭代完成收敛，那么最终的计算复杂度便为$O(t{n^3})$。

(2)算法1收敛速度的快慢会直接影响到DFMAW-2DPCA在执行特征提取任务过程中的效率。为了将迭代变化的结果进行更加直观展示，本文最终通过图5明确刻画了DFMAW-2DPCA在经过算法1每次迭代时所获取到的目标函数值。根据图5的实验结果可知，随着迭代次数的逐渐增加，DFMAW-2DPCA在3个数据库中的目标函数值也都呈现出单调递减的趋势，且均在10次以内趋于平稳。这说明了算法1拥有较快的收敛速度，从另一个角度展现了其在性能上的杰出表现力。将迭代变化的结果进行更加直观展示，该文最终通过图5明确刻画了DFMAW-2DPCA在经过算法1每次迭代时所获取到的目标函数值。根据图5的实验结果可知，随着迭代次数的逐渐增加，DFMAW-2DPCA在3个数据库中的目标函数值也都呈现出单调递减的趋势，且均在10次以内趋于平稳。这说明了算法1拥有较快的收敛速度，从另一个角度展现了其在性能上的杰出表现力。

图 5  3个水下图像数据库中DFMAW-2DPCA的收敛曲线

下载: 全尺寸图片 幻灯片

(3)呈现在表5中的实验结果表明，在所有具有迭代特性的算法中，DFMAW-2DPCA的运行时间接近于F-2DPCA, Cos-2DPCA和2DPCA-2-Lp，因为针对其模型结构所设计的求解算法求解更为便捷；比Angle-2DPCA和GC-2DPCA略快，原因是Angle-2DPCA在同时兼顾投影数据方差和重构误差的前提下，需每次迭代过程中使用奇异值分解操作，GC-2DPCA要引入较多的中间变量去获取保护模型几何结构的权重矩阵；明显优于2DPCA-L1，出现此结果是因为2DPCA-L1中基于${l_1}$范数的非贪婪求解算法较为复杂，从而在计算过程中增大了存储空间需求和时间损耗。因此，综合DFMAW-2DPCA在噪声环境中的识别结果可知，其在对比方法中拥有最为出色的整体性能。

5.   结束语

该文提出一种双灵活度量自适应加权2DPCA (DFMAW-2DPCA)方法并将其应用于水下光视觉图像识别的研究，该方法在同时建立最大化方差与最小化重构误差双层诉求的基础上，合理选用了灵活的${l_{2,p}}$范数作为距离度量模式，不仅成功保留了欧氏范数的旋转不变性而且有效改善了大距离测度对于水下噪声干扰的敏感度。此外，DFMAW-2DPCA采用自适应加权学习策略成功为每个样本数据分配了与之相匹配的权重，进一步提升了模型在水下复杂观测环境中的整体表现力。最后，DFMAW-2DPCA的解与加权协方差矩阵有着紧密关联，实现了对于识别结果有着重要影响的数据几何结构保护。针对DFMAW-2DPCA的求解问题，该文设计了一个具有快速收敛特性的非贪婪迭代算法。在NF, JEDI和EPIDHEU全部3个水下图像数据库上的实验结果表明，DFMAW-2DPCA较同类方法展现出了更为卓越的识别性能。