静态与动态域先验增强的两阶段视频压缩感知重构网络

杨春玲; 梁梓文

doi:10.11999/JEIT240295

静态与动态域先验增强的两阶段视频压缩感知重构网络

doi: 10.11999/JEIT240295

杨春玲^,,
梁梓文

华南理工大学电子与信息学院广州 510000

基金项目: 广东省自然科学基金(2019A1515011949)

详细信息

作者简介:
杨春玲：女，教授，研究方向为图像/视频压缩编码、图像质量评价

梁梓文：男，硕士生，研究方向为图像/视频压缩感知

通讯作者:
杨春玲　eeclyang@scut.edu.cn

中图分类号: TN919.8; TN911.7
计量
- 文章访问数: 116
- HTML全文浏览量: 93
- PDF下载量: 13
- 被引次数: 0
出版历程
- 收稿日期: 2024-04-19
- 修回日期: 2024-09-19
- 网络出版日期: 2024-10-08
- 刊出日期: 2024-11-10

Static and Dynamic-domain Prior Enhancement Two-stage Video Compressed Sensing Reconstruction Network

YANG Chunling^,,
LIANG Ziwen

School of Electronic and Information, South China University of Technology, Guangzhou 510000, China

Funds: The Natural Science Foundation of Guangdong Province (2019A1515011949)

摘要

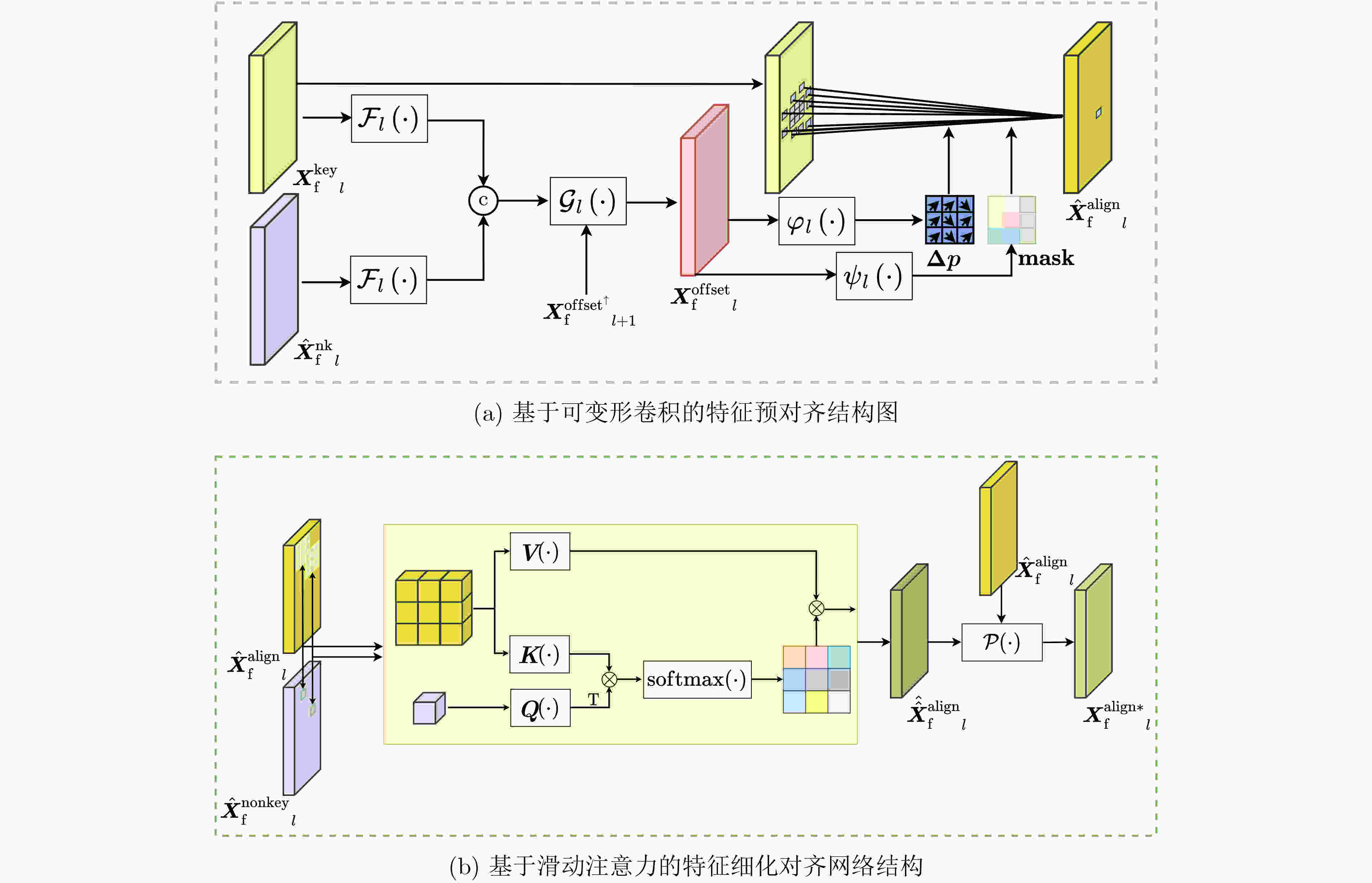
摘要: 视频压缩感知重构属于高度欠定问题，初始重构质量低与运动估计方式单一限制了帧间相关性的有效建模。为改善视频重构性能，该文提出静态与动态域先验增强两阶段重构网络(SDPETs-Net)。首先，提出利用参考帧测量值重构2阶静态域残差的策略，并设计相应的静态域先验增强网络(SPE-Net)，为动态域先验建模提供可靠基础。其次，设计塔式可变形卷积联合注意力搜索网络(PDCA-Net)，通过结合可变形卷积与注意力机制的优势，并构建塔式级联结构，有效地建模并利用动态域先验知识。最后，多特征融合残差重构网络(MFRR-Net)从多尺度提取并融合各特征的关键信息以重构残差，缓解两阶段耦合导致不稳定的模型训练，并抑制特征的退化。实验结果表明，在UCF101测试集下，与具有代表性的两阶段网络JDR-TAFA-Net相比，峰值信噪比(PSNR)平均提升3.34 dB，与近期的多阶段网络DMIGAN相比，平均提升0.79 dB。
- 视频压缩感知 /
- 帧间相关性建模 /
- 两阶段重构 /
- 特征对齐
Abstract: Video compressed sensing reconstruction is a highly underdetermined problem, where the low-quality of initial reconstructed and the single-motion estimation approach limit the effective modeling of inter-frames correlations. To improve video reconstruction performance, the Static and Dynamic-domain Prior Enhancement Two-stage reconstruction Network (SDPETs-Net) is proposed. Firstly, a strategy of reconstructing second-order static-domain residuals using reference frame measurements is proposed, and a corresponding Static-domain Prior Enhancement Network (SPE-Net) is designed to provide a reliable basis for dynamic-domain prior modeling. Secondly, the Pyramid Deformable-convolution Combined with Attention-search Network (PDCA-Net) is designed, which combines the advantages of deformable-convolution and attention mechanisms, and a pyramid cascade structure is constructed to effectively model and utilize dynamic-domain prior knowledge. Lastly, the Multi-Feature Fusion Residual Reconstruction Network (MFRR-Net) extracts and fuses key information of each feature from multiple scales to reconstruct residues, alleviating the instability of model training caused by the coupling of the two stages and suppressing feature degradation. Simulation results show that the Peak Signal-to-Noise Ratio (PSNR) is improved by an average of 3.34 dB compared to the representative two-stage network JDR-TAFA-Net under the UCF101 test set, and by an average of 0.79 dB compared to the recent multi-stage network DMIGAN.
- Video Compressed Sensing (VCS) /
- Inter-frame correlation modeling /
- Two-stage reconstruction /
- Feature alignment

HTML全文

1. 引言

视频压缩感知技术^[1]通过欠采样方法同时完成信号采集和压缩，突破了奈奎斯特采样定理限制，缓解了编码端设备的计算负担。然而，重构问题高度欠定，如何高精度地恢复原始信号是视频压缩感知(Video Compressed Sensing, VCS)重构任务的一大挑战。

在早期，为高效地采集视频信号，分布式视频压缩感知(Distributed Video Compressed Sensing, DVCS)框架^[2]被提出，在此框架下，视频帧按图像组(Group of Pictures, GOP)划分，组内独立地以不同采样率完成视频帧采样。基于该框架，传统迭代优化驱动的VCS重构算法构造视频帧的多假设预测集合^[3,4]或者相似块组的稀疏表示^[5,6]，并利用相应的迭代优化算法重构视频帧。然而，人工设置参数与复杂的迭代过程，限制了该类型算法的泛化能力与推理速度，难以在实际中应用。

近年来，深度学习驱动的VCS重构网络因其快速推理和高精度重构性能备受关注。根据帧间建模方式，该方法可分为两大类：帧间隐式关联网络^[7–12]与显式关联网络^[13–20]。前者通过学习视频帧空间和时间特征的提取来隐式建模帧间相关性，例如，文献[11]提出分层信息交互的VCS网络，该网络将视频帧编码为多尺度特征，并通过融合交互策略实现信息的隐式补偿，文献[12]提出基于生成对抗的VCS网络，将参考帧作为生成网络的输入，完成非关键帧的隐式重构。后者着重于帧间位移关系的建立，并根据位移矢量采取运动补偿与帧融合策略重构出高质量的视频帧，一般情况下，该类网络具有更优的恢复效果。

运动估计与补偿是帧间显式关联网络的核心，根据运动估计方式不同，其可细分为3类：基于光流、可变形卷积与注意力机制对齐的VCS网络。第1类网络^[14–19]通过光流模型^[21]和插值实现运动补偿，然而，精确光流场的估计难度较大，并且额外训练的光流网络对于VCS任务不一定是最优解^[22]。第2类网络^[13]利用可变形卷积自适应地估计特征偏移量，在偏移多样性的条件下能够改善对齐质量，但在低采样率下，非关键帧的恢复质量限制了偏移估计的准确性，导致对齐帧中存在伪影。第3类网络^[20]采用注意力机制建模远距离位置的相关性，能有效地处理大位移运动，但其通常需要执行大范围的搜索，计算复杂度较高。

重构低信息量的非关键帧属于病态问题，由于非关键帧质量差，直接建模复杂运动关系会降低准确性并产生伪影。部分网络^[13–15]尝试利用非关键帧的先验知识改善重构质量，但由于极低的信息量，恢复效果不理想。此外，现有方法运动建模方式单一，难以充分地利用帧间相关性。根据位移特点，帧间关系可分为静态(静止与极小位移)与动态两种，其中静态域先验更易建模，且其信息的恢复能降低建模动态域先验的难度。因此，本文提出静态与动态域先验增强的两阶段重构网络(Static and Dynamic-domain Prior Enhancement Two-stage Network, SDPETs-Net)。在静态域先验增强阶段，提出利用参考帧测量值建模静态域先验知识，以辅助非关键恢复的策略，并设计静态域先验增强网络(Static-domain Prior Enhancement Network, SPE-Net)实现该策略。在动态域先验增强阶段，提出塔式可变形卷积联合注意力搜索网络(Pyramid Deformable-convolution Combined with Attention-search Network, PDCA-Net)建模动态域先验，并设计多特征融合残差重构网络(Multi-Features Residual Reconstruction Network, MFRR-Net)将动态域先验增强的信息作为静态域先验增强阶段输出的补充。

通过将视频帧重构分解为静态与动态域的先验建模与增强，本文设计充分考虑了帧间关系的特点，具体贡献如下：(1)提出了静态与动态域先验增强的两阶段视频重构网络(SDPETs-Net)，实现了一种由静态到动态的帧间相关性建模策略。(2)提出静态域先验增强网络(SPE-Net)，通过建模帧间静态域先验知识，显著地改善了初始恢复质量，为动态关系的建模奠定了有利基础。(3)动态域先验增强阶段实现了可变形卷积与注意力机制的结合，增强了运动估计结果的鲁棒性，并缓解了单一运动估计方式的建模难度。(4)与现有先进的模型相比，SDPETs-Net在保持实时性的同时，参数量更少、重构精度更优。

2. 静态与动态域先验增强的两阶段视频重构网络

2.1 SDPETs-Net整体框

静态与动态域先验增强的两阶段视频重构网络(SDPETs-Net)采用了分布式视频压缩感知^[2]的采样方式，以缓解信号采集对硬件的负担。网络结构如图1所示，在采集端，视频帧被划分为多个GOP, GOP第1帧为关键帧，采用高采样率采样，其余帧为非关键帧，采用低采样率采样。

图 1 SDPETs-Net整体架构

下载: 全尺寸图片幻灯片

在解码端，模型重点求解非关键帧的重构问题，网络以最近的两个重构关键帧为参考，并将关键帧测量值 ${\boldsymbol{y}}_{1}$ 作为补充信息源，首先利用静态域先验增强网络(SPE-Net)完成帧信号的高质量初始恢复。动态域先验增强阶段由塔式可变形卷积联合注意力搜索网络(PDCA-Net)与多特征融合残差重构网络(MFRR-Net)组成。与过去VCS算法在图像域实现运动补偿不同，PDCA-Net在特征域上实现运动估计与补偿，得到补偿特征 ${\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{n}}$ 后，MFRR-Net从多帧特征中提取关键信息，并以残差的形式补充到SPE-Net输出图像 ${\hat{\boldsymbol{x}}}^{*}$ 。接下来，以一个参考帧实现的非关键帧重构过程为例进行算法思想与相应网络设计的描述。

2.2 参考帧测量值引导的静态域先验增强阶段

在模型初始阶段，相比于动态域先验，帧间静态域先验更易建模。为充分地利用帧间相关性及为建模动态域先验提供可靠基础，本文利用静态域先验知识重构非关键帧的残差，重构过程表示如

${\hat{\hat{\boldsymbol{x}}}}_{\mathrm{n}\mathrm{k}}={\hat{\boldsymbol{x}}}_{\mathrm{n}\mathrm{k}}+\mathcal{R}\left({\hat{\boldsymbol{x}}}_{\mathrm{k}\mathrm{e}\mathrm{y}}-{\hat{\boldsymbol{x}}}_{\mathrm{n}\mathrm{k}},{\hat{\boldsymbol{x}}}_{\mathrm{n}\mathrm{k}}\right)$

(1)

式中， ${\hat{\boldsymbol{x}}}_{\mathrm{n}\mathrm{k}}$ 表示重构非关键帧； ${\boldsymbol{x}}_{\mathrm{k}\mathrm{e}\mathrm{y}}$ 表示重构关键帧；为能感知并利用静态域先验知识，残差生成网络 $\mathcal{R}\left(\cdot \right)$ 在 ${\hat{\boldsymbol{x}}}_{\mathrm{n}\mathrm{k}}$ 上下文信息的引导下提取静态域残差。然而，引入重构参考帧会增加串行计算，影响重构速度。因此，本文利用参考帧测量值实现静态域先验的建模，在此条件下，重构静态域残差过程可转化为

$\begin{split} {\hat{\hat{\boldsymbol{x}}}}_{\mathrm{n}\mathrm{k}}\;& ={\hat{\boldsymbol{x}}}_{\mathrm{n}\mathrm{k}}+\mathcal{R}\left({\boldsymbol{\varPhi }}_{1}^{\mathrm{T}}{\boldsymbol{\varPhi }}_{1}\left({\boldsymbol{x}}_{\mathrm{k}\mathrm{e}\mathrm{y}}-{\hat{\boldsymbol{x}}}_{\mathrm{n}\mathrm{k}}\right),{\hat{\boldsymbol{x}}}_{\mathrm{n}\mathrm{k}}\right)\\ & ={\hat{\boldsymbol{x}}}_{\mathrm{n}\mathrm{k}}+\mathcal{R}\left({\boldsymbol{\varPhi }}_{1}^{\mathrm{T}}\left({\boldsymbol{y}}_{1}-{\boldsymbol{\varPhi }}_{1}{\hat{\boldsymbol{x}}}_{\mathrm{n}\mathrm{k}}\right),{\hat{\boldsymbol{x}}}_{\mathrm{n}\mathrm{k}}\right) \end{split}$

(2)

式中， ${\boldsymbol{\varPhi }}_{1}$ 为参考帧测量矩阵； ${\boldsymbol{y}}_{1}$ 为参考帧测量值。由于非关键帧自身测量值先验与参考帧测量值的静态域先验知识有重合。因此，可进一步将静态域残差作为自身测量值信息的补充，式(2)转化为

$\begin{split} {\hat{\hat{\boldsymbol{x}}}}_{\mathrm{n}\mathrm{k}}=\;& {\hat{\boldsymbol{x}}}_{\mathrm{n}\mathrm{k}}+{\boldsymbol{\varPhi }}_{2}^{\mathrm{T}}\left({\boldsymbol{y}}_{2}-{\boldsymbol{\varPhi }}_{2}{\hat{\boldsymbol{x}}}_{{\mathrm{nk}}}\right)\\ & +\mathcal{R}\left({\boldsymbol{\varPhi }}_{1}^{\mathrm{T}}\left({\boldsymbol{y}}_{1}-{\boldsymbol{\varPhi }}_{1}{\hat{\boldsymbol{x}}}_{\mathrm{n}\mathrm{k}}\right),{\boldsymbol{\varPhi }}_{2}^{\mathrm{T}}\left({\boldsymbol{y}}_{2}-{\boldsymbol{\varPhi }}_{2}{\hat{\boldsymbol{x}}}_{\mathrm{n}\mathrm{k}}\right)\right) \end{split}$

(3)

式中， ${\boldsymbol{\varPhi }}_{2}$ 为非关键帧测量矩阵； ${\boldsymbol{y}}_{2}$ 为非关键帧测量值。式(3)过程可视为在利用自身测量值实现残差重构的基础上，引入参考帧测量值静态域先验知识，在1阶残差引导下，生成2阶残差，实现两级残差补充。

为了有效地建模和利用参考帧测量值的静态域先验知识，本文设计了静态域先验增强网络(SPE-Net)。SPE-Net基于特征域近端高维梯度下降图像重构网络^[23]，并结合式(3)，引入参考帧测量值计算多维假设梯度，以及通过1阶残差的引导生成2阶残差，2阶残差作为1阶残差的补充信息，增强后的1阶残差用以更新重构特征。两级残差补充不仅抑制了参考帧中冗余信息的引入，还避免了1阶残差与重构特征的退化。此外，在每次更新过程中均计算多维真实与假设梯度，充分挖掘了测量值信息。SPE-Net由K个两级多维残差补充阶段组成，第 $k$ 阶段如图2所示，过程依次进行特征逆变换、梯度计算、2阶残差生成和特征更新，最终经过去噪得到输出特征，对应数学表示如

图 2 两级多维残差补充阶段实现细节

下载: 全尺寸图片幻灯片

$\quad{\boldsymbol{X}}_{\mathrm{i}}^{\left(k\right)}={\tilde{F}}^{\left(k\right)}\left({\boldsymbol{X}}_{\mathrm{f}}^{\left(k-1\right)}\right)$

(4)

$\begin{split} \quad \left[{\boldsymbol{\varDelta }}_{\mathrm{i}1}^{\left(k\right)},{\boldsymbol{\varDelta }}_{\mathrm{i}2}^{\left(k\right)}\right]=\,&\left[{S}_{{\boldsymbol{\varPhi }}_{1}^{\mathrm{T}}}\left({S}_{{\boldsymbol{\varPhi }}_{1}}\left({\boldsymbol{X}}_{\mathrm{i}}^{\left(k\right)}\right)-{\boldsymbol{Y}}_{1}\right),\right.\\ & \left.{S}_{{\boldsymbol{\varPhi }}_{2}^{\mathrm{T}}}\left({S}_{{\boldsymbol{\varPhi }}_{2}}\left({\boldsymbol{X}}_{\mathrm{i}}^{\left(k\right)}\right)-{\boldsymbol{Y}}_{2}\right)\right] \end{split}$

(5)

$\quad {\boldsymbol{\varDelta }}_{\mathrm{i}}^{\left(k\right)}={\boldsymbol{\varDelta }}_{\mathrm{i}1}^{\left(k\right)}+{\mathcal{R}}^{\left(k\right)}\left({\mathcal{C}}^{\left(k\right)}\left({\boldsymbol{\varDelta }}_{\mathrm{i}1}^{\left(k\right)}\right),{\boldsymbol{\varDelta }}_{\mathrm{i}2}^{\left(k\right)}\right)$

(6)

$\quad{\boldsymbol{U}}^{\left(k\right)}={\boldsymbol{X}}_{\mathrm{f}}^{\left(k-1\right)}+{F}^{\left(k\right)}\left({\boldsymbol{\varDelta }}_{\mathrm{i}}^{\left(k\right)}\right)$

(7)

$\quad{\boldsymbol{X}}_{\mathrm{f}}^{\left(k\right)}={\mathcal{D}}^{\left(k\right)}\left({\boldsymbol{U}}^{\left(k\right)}\right)$

(8)

其中，下标i表示图像域， ${\boldsymbol{X}}_{\mathrm{f}}^{\left(k-1\right)}$ 为重构非关键帧特征， ${\boldsymbol{Y}}_{1}$ 与 ${\boldsymbol{Y}}_{2}$ 分别由关键帧与非关键帧测量值 ${\boldsymbol{y}}_{1}$ , ${\boldsymbol{y}}_{2}$ 重复拓展得到，算子 ${\mathcal{C}}^{\left(k\right)}\left(\cdot \right)$ 与 ${\mathcal{R}}^{\left(k\right)}\left(\cdot \right)$ 分别由卷积网络实现去噪及残差生成，测量算子( ${S}_{{\boldsymbol{\varPhi }}_{1}}$ , ${S}_{{\boldsymbol{\varPhi }}_{2}}$ )及其转置( ${S}_{{\boldsymbol{\varPhi }}_{1}^{\mathrm{T}}}$ , ${S}_{{\boldsymbol{\varPhi }}_{2}^{\mathrm{T}}}$ )、特征变换( ${\tilde{F}}^{\left(k\right)}$ )及其逆变换( ${\tilde{F}}^{\left(k\right)}$ )和去噪网络( ${\mathcal{D}}^{\left(k\right)}$ )的结构与文献[23]一致。与现有两阶段算法的独立重构阶段^[13–15,20]相比，SPE-Net通过多维梯度计算、利用静态域先验知识生成2阶残差，并在特征域实现信息更新，有效地改善了信息挖掘与优化等过程，能实现更高精度的初始恢复。

2.3 塔式可变形卷积联合注意力搜索的动态域先验增强阶段

静态域先验增强阶段为建模动态域先验知识提供了有利基础，动态域先验增强阶段进一步建模非关键帧与参考帧之间复杂的帧间相关先验知识，以改善非关键帧恢复质量，该阶段由塔式可变形卷积联合注意力搜索网络(PDCA-Net)与多特征融合残差重构网络(MFRR-Net)构成。过程首先采用PDCA-Net在特征层级上实现参考帧特征到非关键帧特征的运动补偿。随后，MFRR-Net提取并融合多帧特征的关键信息，重构静态域先验增强阶段输出与真实图像之间的残差。接下来，将详细描述动态域先验增强阶段核心设计。

2.3.1 PDCA-Net实现思想及结构设计

运动估计准确性的限制主要在于非关键帧质量和算法设计。为改善对齐质量，动态域先验增强阶段构建了特征域帧间对齐网络PDCA-Net，结构如图3所示，其核心设计包括：基于可变形卷积的特征预对齐、基于滑动注意力的特征细化对齐以及塔式级联结构。一方面，可变形卷积与滑动注意力的结合可以降低单一模型建模难度，并提高对齐的鲁棒性。另一方面，塔式级联结构不仅利用前一层已对齐特征改善当前层非关键特征质量，还实现整体到局部的特征对齐方式，提高模型对粗粒度与大位移运动的建模能力。

图 3 PDCA-Net网络结构

下载: 全尺寸图片幻灯片

(1)塔式级联结构与PDCA-Net整体实现

在塔式级联结构中，首先对参考帧特征与非关键帧特征逐级下采样形成多尺度特征空间。经过静态域先验增强阶段后，非关键帧质量得到大程度改善，但与关键帧相比，其质量仍然较差。为了提高运动估计结果的准确性，在塔式级联结构中采用时域空间内积注意力融合前一层级的对齐特征，利用动态域先验知识自适应地细化非关键帧特征，以第 $l$ 层为例，该过程数学表示如

${\bf{m}\bf{a}\bf{p}}_{l}=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{m}\mathrm{o}\mathrm{i}\mathrm{d}\left(\left\langle{{\theta }_{l}\left({{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{n}\mathrm{k}}}_{l}\right),{\phi }_{l}\left({{{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{n}}}^{\uparrow }}_{l+1}\right)}\right\rangle\right)$

(9)

${{{\hat{\boldsymbol{X}}}_{\mathrm{f}}^{\mathrm{n}\mathrm{k}}}}{}_{l}= {\mathcal{D}}_{l}\left({{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{n}\mathrm{k}}}_{l}+{\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{e}}_{l}\left({{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{n}\mathrm{k}}}_{l},{{{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{n} }}}_{l+1}^{\uparrow} \odot {\bf{map}}_{l}\right)\right)$

(10)

式中， ${{{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{n}}}^{\uparrow }}_{l+1}$ 表示第 $l+1$ 层对齐特征的上采样结果； ${\theta }_{l}$ 与 ${\phi }_{l}$ 由 $1\times 1$ 卷积实现； $< \cdot ,\cdot >$ 表示特征向量的内积运算； $\odot$ 表示对 ${\bf{m}\bf{a}\bf{p}}_{l}$ 进行广播后的哈达玛积运算； ${\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{e}}_{l}\left(\cdot \right)$ 由3个带有整流线性单元(ReLU)的卷积层构成； ${\mathcal{D}}_{l}\left(\cdot \right)$ 由两个残差块构成，用以去除过程引入的噪声。在得到每个尺度空间的对齐特征后，塔式级联结构自底向上地级联对齐特征，并融合粗粒度与细粒度的运动估计，该过程可描述为

$\begin{split} {{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{n}}}_{l}=\;& {\mathrm{M}\mathrm{S}\mathrm{F}}_{l}({{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{n}*}}_{l},{\mathrm{M}\mathrm{S}\mathrm{F}}_{l+1} \\ & \left.\left({{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{n}*}}_{l+1},{{{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{n}}}^{\uparrow }}_{l+2}\right)^{\uparrow }\right) \end{split}$

(11)

式中， ${{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{n}*}}_{l}$ 表示第 $l$ 层融合前的对齐特征， ${\mathrm{M}\mathrm{S}\mathrm{F}}_{l}\left(\cdot \right)$ 由一个卷积层与一个残差块构成。

为抑制最终对齐特征的噪声与无关信息，在塔式级联结构的输出端引入非关键帧测量值进行校正，该后处理过程与图2类似，但不包含参考帧测量值支路，并仅使用少量优化阶段处理，以平衡模型的性能与计算量。接下来，将详细描述PDCA-Net塔式级联结构中特征域运动估计与补偿过程的实现。

(2)基于可变形卷积的特征预对齐

可变形卷积对齐算法通过计算时域特征偏移量，实现采样位置的动态调整并完成相应特征向量的聚合。为提高算法的有效性，本文进行以下设计优化实现过程：(a)计算时域偏移特征前，利用非线性变换将当前帧与参考帧特征映射至适合偏移估计的特征空间。(b)计算时域偏移特征时，引入前一层时域偏移特征作为先验知识。(c)在特征聚合过程，估计采样位置的掩模^[24]，灵活地调整支撑区域，实现特征动态聚合。

强化后算法实现如所示，分为3个步骤：(a)生成时域偏移特征：利用非线性变换 ${\mathcal{F}}_{l}\left(\cdot \right)$ 将参考帧与非关键帧特征变换到合适的特征空间，并结合前一层时域偏移特征 ${{\boldsymbol{X}}_{\mathrm{f}}^{{\mathrm{o}\mathrm{f}\mathrm{f}\mathrm{s}\mathrm{e}\mathrm{t}}^{\uparrow }}}_{l+1}$ ，利用卷积神经网络 ${\mathcal{G}}_{l}\left(\cdot \right)$ 生成当前偏移特征 ${{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{o}\mathrm{f}\mathrm{f}\mathrm{s}\mathrm{e}\mathrm{t}}}_{l}$ 。(b)生成偏移与掩模估计：基于 ${{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{o}\mathrm{f}\mathrm{f}\mathrm{s}\mathrm{e}\mathrm{t}}}_{l}$ ，利用卷积网络 ${\varphi }_{l}\left(\cdot \right)$ 与 ${\psi }_{l}\left(\cdot \right)$ 计算采样位置的偏移与掩模。(c)动态聚合特征：基于偏移与掩模估计，在参考帧特征图上完成插值、采样与聚合过程

图 4 预对齐与细化对齐

下载: 全尺寸图片幻灯片

${{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{o}\mathrm{f}\mathrm{f}\mathrm{s}\mathrm{e}\mathrm{t}}}_{l}={\mathcal{G}}_{l}\left({\mathcal{F}}_{l}\left({{\hat{\boldsymbol{X}}}_{\mathrm{f}}^{\mathrm{n}\mathrm{k}}}{}_{l}\right),{\mathcal{F}}_{l}\left({{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{k}\mathrm{e}\mathrm{y}}}_{l}\right),{{\boldsymbol{X}}_{\mathrm{f}}^{{\mathrm{o}\mathrm{f}\mathrm{f}\mathrm{s}\mathrm{e}\mathrm{t}}^{\uparrow }}}_{l+1}\right)$

(12)

$\left[\Delta \boldsymbol{p},\bf{m}\bf{a}\bf{s}\bf{k}\right]=\left[{\varphi }_{l}\left({{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{o}\mathrm{f}\mathrm{f}\mathrm{s}\mathrm{e}\mathrm{t}}}_{l}\right),{\psi }_{l}\left({{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{o}\mathrm{f}\mathrm{f}\mathrm{s}\mathrm{e}\mathrm{t}}}_{l}\right)\right]$

(13)

$\begin{split} {{\hat{\boldsymbol{X}}}_{\mathrm{f}}^{\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{n}}}{}_{l}\left({p}_{i}\right)=\,& \underset{m=-\varepsilon }{\sum ^{\varepsilon }}\underset{n=-\varepsilon }{\sum ^{\varepsilon }}{\boldsymbol{w}}_{lmn}\cdot {{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{k}\mathrm{e}\mathrm{y}}}_{l}\\ & \left({p}_{i}+{\boldsymbol{p}}_{imn}+{\Delta \boldsymbol{p}}_{imn}\right)\cdot {\bf{m}\bf{a}\bf{s}\bf{k}}_{imn} \end{split}$

(14)

式中， ${\mathcal{F}}_{l}\left(\cdot \right)$ 表示特征变换， ${\mathcal{G}}_{l}\left(\cdot \right)$ 表示偏移特征生成函数， ${\phi }_{l}\left(\cdot \right)$ 表示偏移生成函数， ${\psi }_{l}\left(\cdot \right)$ 表示掩模生成函数，均由卷积网络实现， $\left(2\varepsilon +1\right)\times \left(2\varepsilon +1\right)$ 表示多假设偏移数量； ${p}_{i}$ 表示采样的中心位置； ${\boldsymbol{p}}_{imn}$ 表示相对于中心位置的预定义偏移，其与标准卷积的采样位置一致； $\Delta \boldsymbol{p}$ 表示偏移集合； $\bf{m}\bf{a}\bf{s}\bf{k}$ 表示掩模估计集合。

(3)基于滑动注意力的特征细化对齐

非关键帧质量欠佳，可变形卷积难以精确定位，影响对齐的准确性。为了增强对齐特征的鲁棒性，PDCA-Net引入注意力机制在预对齐结果基础上进行相关信息的搜索与聚合。由于模糊效应，预对齐容易将相关信息聚合到目标位置附近，因此注意力机制仅需专注于建模局部区域关系，从而改善对齐特征质量。与非重叠分窗的注意力机制不同^[25]，本文采用步长1滑动局部窗口以缓解边界块效应并避免非对称搜索。

基于滑动注意力的特征细化对齐如所示。实现中，将非关键帧特征向量作为注意力网络 “查询”，预对齐特征图中以相应特征向量为中心 $\left(2s+1\right)\times \left(2s+1\right)$ 区域内的预对齐特征向量作为 “键”与“值”。通过计算“查询”和“键”的相似度，并利用指数归一化得到的权重，聚合“值”向量，实现搜索与聚合。为了避免对齐特征退化，输出端利用前馈神经网络融合两次对齐特征。上述过程数学表示如下

${\boldsymbol{A}}_{\left(ij\right)\left(op\right)}=\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left({{\boldsymbol{Q}}\left({\left({{\hat{\boldsymbol{X}}}_{\mathrm{f}}^{\mathrm{n}\mathrm{k}}}{}_{l}\right)}_{ij}\right)}^{\mathrm{T}}\cdot {\boldsymbol{K}}\left({\left({{\hat{\boldsymbol{X}}}_{\mathrm{f}}^{\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{n}}}{}_{l}\right)}_{\left(i+o\right)\left(j+p\right)}\right)\right)}{{\displaystyle\sum ^{s}_{m=-s}}\; {\displaystyle\sum ^{s}_{n=-s}}\mathrm{e}\mathrm{x}\mathrm{p}\left({{\boldsymbol{Q}}\left({\left({{\hat{\boldsymbol{X}}}_{\mathrm{f}}^{\mathrm{n}\mathrm{k}}}{}_{l}\right)}_{ij}\right)}^{T}\cdot {\boldsymbol{K}}\left({\left({{\hat{\boldsymbol{X}}}_{\mathrm{f}}^{\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{n}}}{}_{l}\right)}_{\left(i+m\right)\left(j+n\right)}\right)\right)}$

(15)

$\begin{split} \qquad\; {\left({{\hat{\hat{\boldsymbol{X}}}}_{\mathrm{f}}^{\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{n}}}{}_{l}\right)}_{ij}=\;& { {\sum ^{s}_{m=-s}} \;{\sum ^{s}_{n=-s}}\boldsymbol{A}}_{\left(ij\right)\left(mn\right)}\\ & {\boldsymbol{V}}\left({\left({{\hat{\boldsymbol{X}}}_{\mathrm{f}}^{\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{n}}}{}_{l}\right)}_{\left(i+m\right)\left(j+n\right)}\right) \end{split}$

(16)

${{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{n}*}}_{l}=\mathcal{P}\left({{\hat{\boldsymbol{X}}}_{\mathrm{f}}^{\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{n}}}{}_{l},{{\hat{\hat{\boldsymbol{X}}}}_{\mathrm{f}}^{\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{n}}}{}_{l}\right)$

(17)

式中， $o,p\in \left[-s,\cdots ,0,\cdots s\right]$ ； ${\boldsymbol{Q}}\left(\cdot \right)$ 、 ${\boldsymbol{K}}\left(\cdot \right)$ 与 ${\boldsymbol{V}}\left(\cdot \right)$ 均由 $1\times 1$ 卷积实现；前馈网络 $\mathcal{P}\left(\cdot \right)$ 由两个残差块实现。预对齐特征图为缩小注意力机制搜索范围创造有利条件，较全图搜索复杂度 $O\left({\left(HW\right)}^{2}C\right)$ ，设计模块注意力计算复杂度为 $O\left({\left(2s+1\right)}^{2}HWC\right)$ ， ${\left(2s+1\right)}^{2}\ll HW$ 。总的来说，PDCA-Net结合可变形卷积与注意力对齐方式的优势，一定程度缓解各自独立使用存在的不足。

2.3.2 多特征融合残差重构网络

通过重构残差，PDCA-Net增强后的信息可作为SPE-Net输出的修正与补充，有助于缓解两阶段耦合导致不稳定的模型训练，梯度的反向传播能够直接作用在静态域先验增强阶段，有效地抑制重构特征退化。

MFRR-Net被设计用于准确地重构出静态域先验增强阶段输出图像 ${\hat{x}}^{*}$ 关于真实图像的残差，多特征融合过程采用轻量级UNet^[26]实现，与将图像作为融合网络输入^{[13–15,17–20]}相比，网络输入为特征集合 $\left[{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{k}\mathrm{e}\mathrm{y}},{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{n}\mathrm{k}},{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{n}}\right]$ ，充分利用了特征的强表示能力，更灵活地在不同尺度层上提取并融合关键信息。在得到丰富的信息后，由两个残差块组成的卷积网络 $\mathrm{R}\mathrm{R}\left(\cdot \right)$ 被用于重构残差特征。最终，残差特征经过特征逆变换 $\tilde{{\boldsymbol{f}}}\left(\cdot \right)$ 输出残差图像 ${\hat{\boldsymbol{x}}}^{\mathrm{r}\mathrm{e}\mathrm{s}}$ ， ${\hat{\boldsymbol{x}}}^{\mathrm{r}\mathrm{e}\mathrm{s}}$ 与 ${\hat{\boldsymbol{x}}}^{*}$ 相加，获得重构非关键帧。上述过程表示为

$\hat{\boldsymbol{x}}={\hat{\boldsymbol{x}}}^{*}+\tilde{{\boldsymbol{f}}}\left(\mathrm{R}\mathrm{R}\left(\mathrm{U}\mathrm{N}\mathrm{e}\mathrm{t}\left(\left[{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{k}\mathrm{e}\mathrm{y}},{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{n}\mathrm{k}},{\boldsymbol{X}}_{\mathrm{f}}^{\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{n}}\right]\right)\right)\right)$

(18)

2.4 关键帧重构网络与损失函数

为权衡重构速度和精度，关键帧重构使用深度展开阶段数量为8的FPHGD-Net^[23]实现。考虑到SPE-Net需要从参考帧测量值获取多维假设梯度，因此SDPETs-Net由关键帧采样与重构、非关键帧采样与重构整体联合训练得到。假设输入GOP长度为 $\lambda$ ，GOP第1帧为关键帧，其余为非关键帧，使用两个最近的重构关键帧作为参考帧，辅助非关键帧恢复。模型训练分别约束重构关键帧、SPE-Net输出非关键帧以及最终重构非关键帧，此外对采样矩阵采取正交性约束作为辅助损失函数，具体训练损失函数如

$\begin{split} \quad\; {L\left({\boldsymbol{\varPhi }}_{1},{\boldsymbol{\varPhi }}_{2},\boldsymbol{\varTheta }\right)}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}}=\;& \sum _{s=1}^{\lambda +1}{\left\|{\boldsymbol{x}}_{s}-{\hat{\boldsymbol{x}}}_{s}\right\|}_{{\mathrm{F}}}^{2}\\ & +\beta \sum _{s=2}^{\lambda }{\left\|{\boldsymbol{x}}_{s}-{{\hat{\boldsymbol{x}}}_{s}}^{\mathrm{*}}\right\|}_{{\mathrm{F}}}^{2} \end{split}$

(19)

$\quad {L\left({\boldsymbol{\varPhi }}_{1},{\boldsymbol{\varPhi }}_{2}\right)}_{\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{h}}=\sum _{i=1}^{2}{\left\|{\boldsymbol{\varPhi }}_{i}{{\boldsymbol{\varPhi }}_{i}}^{\mathrm{T}}-\boldsymbol{I}\right\|}_{{\mathrm{F}}}^{2}$

(20)

$\begin{split} \quad {L\left({\boldsymbol{\varPhi }}_{1},{\boldsymbol{\varPhi }}_{2},\boldsymbol{\varTheta }\right)}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}=\;& {L\left({\boldsymbol{\varPhi }}_{1},{\boldsymbol{\varPhi }}_{2},\boldsymbol{\varTheta }\right)}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}}\\ & +{\gamma L\left({\boldsymbol{\varPhi }}_{1},{\boldsymbol{\varPhi }}_{2}\right)}_{\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{h}} \end{split}$

(21)

式中，s是视频帧的序号， ${\boldsymbol{\varPhi }}_{1}$ , ${\boldsymbol{\varPhi }}_{2}$ 为采集端测量矩阵； $\boldsymbol{\varTheta }$ 为解码端网络参数； ${\boldsymbol{x}}_{s}$ 为原始图像； ${{\hat{\boldsymbol{x}}}_{s}}^{*}$ 为SPE-Net输出图像； ${\hat{\boldsymbol{x}}}_{s}$ 为最终重构输出图像； $\beta ,\;\gamma$ 为权重因子，实验中分别设置为1, 0.2。

3. 实验仿真与分析

3.1 模型实现

(1)数据集。为了缓解训练过程不稳定，采用BSD500数据集^[27]预训练关键帧重构网络。模型整体训练采用UCF101数据集^[28]，训练、测试与验证集划分比例为8:1:1。模型评估采用UCF101测试集( $320\times 240$ )、6个QCIF序列( $176\times 144$ )以及REDS4序列^[29]( $1280\times 720$ )，评价指标为峰值信噪比(PSNR)与结构相似度(SSIM)。

(2)模型设置。采集端分块大小为32；解码端SPE-Net子阶段数量为8；常规卷积核大小为 $3\times 3$ ，特征通道数为32；考虑到模型复杂度与感受野，PDCA-Net注意力窗口大小由前向后为3, 3, 5，后处理子阶段数为3。

(3)训练细节。训练图像按中心裁剪为 $160\times 160$ 并提取亮度分量；首先预训练关键帧重构网络，随后对整体执行联合训练。联合训练采用权重衰减量为 $1\times {10}^{-4}$ 的AdamW优化器，epoch数量为100，每个epoch迭代3次数据，batch size为6；训练的初始学习率为 $1\times {10}^{-4}$ ，并采用余弦退火学习率策略衰减至 $1\times {10}^{-6}$ ；实验均在NVIDIA GTX2080ti GPU的Pytorch平台上实现。

3.2 实验结果与分析

本节对SDPETs-Net性能进行分析，包括与现有模型重构精度、高分辨率序列泛化性能、视觉效果与模型空间与运行时间。对比方法包括：2种迭代优化驱动的VCS算法：RRS^[5], SSIM-InterF-GSR^[6]；7种深度学习驱动的VCS网络：CSVideoNet^[9], ImrNet^[14], STM-Net^[15], JDR-TAFA-Net^[20], VCSNet-2^[8], DUMHAN^[18]与DMIGAN^[17]。前4种深度学习方法为两阶段模型，VCSNet—2为单阶段模型，最后2种为多阶段模型。文献[5,6,8,14,15,17,18,20]测试结果根据原文献并结合开源模型得到，其余测试结果从原文献引用得到。

3.2.1 与现有算法及网络模型重构精度对比与分析

(1)UCF101测试序列对比与分析

在UCF101测试集对比实验中，由于视频序列数量庞大，迭代优化驱动算法计算复杂度高且重构时间长，因此，该实验仅与深度学习方法比较。UCF101测试集对比实验设置如下：关键帧采样率 ${r}_{\mathrm{k}}=0.2$ ，GOP为10，3种非关键帧采样率分别设置为 ${r}_{\mathrm{n}\mathrm{k}}=0.037$ , ${r}_{\mathrm{n}\mathrm{k}}=0.018$ , ${r}_{\mathrm{n}\mathrm{k}}=0.009$ 。

如表1所示，SDPETs-Net 在不同设置下均取得最优的重构精度。与多阶段模型DMIGAN相比， PSNR平均提升0.79 dB，与近期由独立与联合重构组成的两阶段模型JDR-TAFA-Net相比，平均PSNR/SSIM提升3.34 dB/0.04。采样率越低，SDPETs-Net的提升越显著，表明所设计模型能够更有效地挖掘并利用帧内与帧间的相关信息，实现更高精度的恢复效果。

表 1 UCF101测试集重构性能对比PSNR(dB)/SSIM

${r}_{\mathrm{n}\mathrm{k}}$	CSVideoNet	STM-Net	Imr-Net	JDRTAFA-Net	DUMHAN	DMIGAN	本文 SDPETs-Net
$0.037$	26.87/0.81	32.50/0.93	33.40/—	33.14/0.94	35.37/—	35.86/—	36.36/0.96
$0.018$	25.09/0.77	31.14/0.91	31.90/—	31.63/0.91	33.70/—	34.23/—	35.01/0.95
$0.009$	24.23/0.74	29.98/0.89	30.51/—	30.33/0.89	32.11/—	32.65/—	33.75/0.94
平均值	25.40/0.77	31.21/0.91	31.94/—	31.70/0.91	33.73/—	34.25/—	35.04/0.95

下载: 导出CSV

| 显示表格

(2)QCIF序列实验对比与分析

为进一步评估模型对不同运动类型序列的恢复性能，本小节选取6个QCIF序列(前96帧)进行对比，其中包括背景静止前景慢速运动序列(Silent)、背景静止前景快速运动序列(Ice)、背景慢速运动前景快速运动序列(Foreman)与背景快速运动前景快速运动序列(Coastguard, Soccer, Mobile)。实验设置为：关键帧采样率 ${r}_{\mathrm{k}}=0.5$ ，GOP为8，非关键帧采样率分别设置为 ${r}_{\mathrm{n}\mathrm{k}}=0.01$ , ${r}_{\mathrm{n}\mathrm{k}}=0.05$ , ${r}_{\mathrm{n}\mathrm{k}}=0.1$ 。

如表2所示，深度学习驱动的VCS网络在各种运动序列上的性能优于传统算法，表明数据驱动的深度学习模型能够得到更优解。SDPETs-Net在不同运动序列下均表现最佳，与ImrNet相比，均有大于3 dB平均性能的提升，与DUMHAN相比，平均提升1.05 dB。在0.01采样率下，SDPETs-Net仍能高精度恢复背景静止与慢速序列，并显著改善快速序列的重构质量，验证了其对帧间相关先验知识建模的有效性。

表 2 QCIF序列重构性能对比PSNR(dB)(

${r}_{\mathrm{k}}=0.5$ ，

$\mathrm{G}\mathrm{O}\mathrm{P}=8$ )

${r}_{\mathrm{n}\mathrm{k}}$	算法 (网络)	视频序列						平均值
${r}_{\mathrm{n}\mathrm{k}}$	算法 (网络)	Silent	Ice	Foreman	Coastguard	Soccer	Mobile	平均值
0.01	RRS	21.25	20.72	18.51	21.16	21.42	15.24	19.72
	SSIM-InterF-GSR	24.77	24.65	26.86	25.08	23.39	21.92	24.45
	VCSNet-2	31.94	25.77	26.07	25.66	24.62	21.42	25.91
	ImrNet	35.30	29.25	31.58	28.94	27.10	25.02	29.53
	DUMHAN	37.25	31.69	34.46	31.63	28.37	29.28	32.11
	本文SDPETs-Net	38.05	32.92	36.05	32.76	29.50	30.35	33.27
0.05	RRS	25.76	26.15	26.84	22.66	26.80	16.68	24.15
	SSIM-InterF-GSR	33.68	28.81	33.18	28.09	27.65	22.99	29.07
	VCSNet-2	34.52	29.51	29.75	27.01	28.62	22.79	28.70
	ImrNet	38.07	33.76	36.03	30.80	31.81	27.55	33.00
	DUMHAN	40.42	36.58	39.44	33.63	33.74	31.61	35.90
	本文SDPETs-Net	41.09	37.98	40.82	34.31	34.85	32.36	36.90
0.1	RRS	33.95	31.09	35.17	27.34	29.74	20.00	29.55
	SSIM-InterF-GSR	35.09	31.73	35.75	30.24	30.31	24.35	31.25
	VCSNet-2	34.92	30.95	31.14	28.01	30.51	23.62	29.86
	ImrNet	39.17	35.90	37.37	31.44	34.24	28.19	34.39
	DUMHAN	41.73	38.66	41.68	34.73	36.40	32.48	37.61
	本文SDPETs-Net	42.71	40.10	42.97	35.22	37.52	33.07	38.60

下载: 导出CSV

| 显示表格

3.2.2 模型泛化性能测试与分析

本小节选取REDS4数据集验证模型的泛化性能以及对高清视频序列的恢复效果。对比模型均为深度学习驱动的VCS网络，这两种非关键帧采样率下进行测试，具体为：关键帧采样率 ${r}_{\mathrm{k}}=0.5$ ，GOP为8，非关键帧采样率分别设置为 ${r}_{\mathrm{n}\mathrm{k}}=0.01$ , ${r}_{\mathrm{n}\mathrm{k}}=0.1$ 。

各模型重构REDS4结果的PSNR/SSIM如表3所示。从表格数据可以看出，在两种采样率设置下，SDPETs-Net对4个高清视频序列均能取得最高精度的重构结果，与基于光流网络的两阶段模型STM-Net相比，PSNR/SSIM分别平均提升1.71 dB/0.06与1.79 dB/0.03；与多阶段模型DUMHAN相比，PSNR/SSIM分别平均提升1.35 dB/0.05与0.98 dB/0.02。本章提出网络取得优越重构性能的原因在于构造了从静态域到动态域的帧间相关先验知识建模网络，实现更准确、更充分的信息挖掘与利用。该测试结果充分验证了SDPETs-Net对不同类型与分布的视频序列具有更好的泛化能力，进一步证明设计的有效性。

表 3 REDS4序列重构性能对比PSNR(dB)/SSIM

${r}_{\mathrm{n}\mathrm{k}}$	序列	VCSNet-2	ImrNet	STM-Net	DUMHAN	本文SDPETs-Net
0.01	000	23.24/—	25.71/0.67	26.45/0.73	27.74/0.77	29.44/0.85
	011	24.19/—	25.93/0.66	26.89/0.71	26.72/0.70	27.77/0.74
	015	26.85/—	30.01/0.81	30.67/0.84	31.02/0.85	32.66/0.89
	020	23.34/—	25.15/0.66	25.98/0.71	25.97/0.70	26.99/0.75
0.1	000	27.55/—	29.09/0.85	30.69/0.90	31.80/0.91	32.82/0.94
	011	29.65/—	32.29/0.89	32.82/0.90	33.52/0.90	34.36/0.92
	015	32.34/—	36.33/0.94	37.06/0.95	38.00/0.95	39.07/0.96
	020	28.88/—	31.23/0.90	31.65/0.91	32.17/0.91	33.16/0.93

下载: 导出CSV

| 显示表格

3.2.3 重构视觉效果对比与分析

在本小节中，进一步对比与分析不同模型的重构视觉效果。测试实验分别在Soccer(快速运动)序列的第12帧(0.5关键帧采样率，0.05非关键帧采样率，GOP为8)与REDS4-000(高清)序列的第36帧(0.5关键帧采样率，0.01非关键帧采样率，GOP为8)下进行，重构结果结合色度分量展示。

如图5所示，传统算法RRS由于过度依赖稀疏性先验，前景(如人和足球)区域破坏了图像的结构和细节，而深度学习方法能更清晰地恢复图像的轮廓及细节。显式建模方法ImrNet比隐式方法VCSNet-2能取得更优的重构效果，但由于独立重构阶段较差的恢复质量，以及运动建模方式单一，导致重构图像模糊、细节丢失，SDPETs-Net能够在前景与背景上取得最精细的恢复效果。图6重构结果显示，在极低采样率(0.01)下，与两阶段模型ImrNet和STMNet相比，SDPETs-Net能更有效地抑制模糊并更清晰地恢复细节，如车牌号清晰可见，该实验验证了本文设计在提升重构视觉效果方面的有效性。

图 5 不同算法及模型重构视觉效果对比(Soccer序列第12帧)

下载: 全尺寸图片幻灯片

图 6 不同模型重构视觉效果对比(REDS4-000序列第36帧)

下载: 全尺寸图片幻灯片

3.2.4 模型空间及运行时间的对比与分析

本小节比较了模型的参数量与GPU上单帧推理时间。实验在关键帧采样率0.5、非关键帧采样率0.1、GOP为8的条件下进行，平均单帧推理时间基于6个QCIF序列，结果如表4所示。最右侧展示了在不同设置下重构UCF101测试序列的PSNR/SSIM。可以看出，SDPETs-Net参数量最少，比JDR-TAFA-Net减少了约40%的参数量；结合并行计算平台，具备实时的重构速度，在单帧计算上，模型采用了可变形联合注意力的搜索机制，重构速度稍慢于ImrNet，在GOP并行计算条件下，平均重构速度为50 Frame/s，并且相比于其他模型，重构精度显著提高。综合表明SDPETs-Net能取得优于其他模型的性能，验证了其有效性。

表 4 不同模型的空间与重构时间(GPU)与重构精度(PSNR(dB)/SSIM)对比

模型	参数量(M)	平均单帧重构时间(GPU)(s)	平均重构精度(PSNR(dB)/SSIM)
ImrNet	8.69	0.03	31.94/—
STM-Net	9.20	0.03	31.21/0.91
JDR-TAFA-Net	12.41	0.04	31.70/0.91
本文SDPETs-Net	7.44	0.04	35.04/0.95
本文SDPETs-Net	7.44	0.02(GOP并行)	35.04/0.95

下载: 导出CSV

| 显示表格

3.2.5 模型消融实验与分析

本节将对所提网络展开分析。SDPETs-Net由静态与动态域先验增强阶段构成。在两个阶段分别设计了静态域先验增强网络(SPE-Net)、特征域塔式可变形卷积联合注意力搜索网络(PDCA-Net)与多特征融合残差重构网络(MFRR-Net)，本小节对模型设计进行研究，以验证不同策略对重构性能的影响。

(1)静态域先验增强阶段的消融分析

静态域先验增强网络(SPE-Net)的核心思想包括：引入参考帧测量值重构2阶残差(Second-order Reconstruction, SR)，多维梯度重构(Multi-dimensional Gradients Reconstruction, MR)。为了更清晰地探究网络组件对SPE-Net性能的影响，该实验将SPE-Net作为消融的基础。实验结果在关键帧采样率为0.5、非关键帧采样率为0.01、GOP为8的条件下，重构3.2.1节的6个QCIF序列得到。具体设置如表5所示，表中模型2可视为，与以往两阶段模型^[12–14,17]一致，仅利用非关键帧自身先验知识完成初始独立重构。

表 5 静态域先验增强阶段的消融研究(PSNR(dB)/SSIM)

模型	设置		QCIF序列						平均值
模型	SR	MG	Silent	Ice	Foreman	Coastguard	Soccer	Mobile	平均值
基础	√	√	36.71/0.97	31.42/0.94	34.04/0.94	31.19/0.88	28.20/0.76	27.82/0.92	31.56/0.90
1	√	×	36.32/0.96	31.09/0.94	33.14/0.92	30.14/0.85	27.99/0.74	26.78/0.90	30.91/0.89
2	×	×	26.65/0.61	26.21/0.80	24.90/0.63	24.06/0.51	26.77/0.67	19.42/0.35	24.67/0.60

下载: 导出CSV

| 显示表格

表5不同设置下结果的PSNR/SSIM表明：去除多维残差计算(模型1)，PSNR平均下降0.65 dB，复杂运动序列下降更明显，说明多维残差有助于挖掘帧间相关信息并提升视频恢复性能。缺乏参考帧测量值作为重构的先验知识(模型2)导致性能急剧下降，尤其在静态域信息丰富的序列(Silent)中，验证了引入参考帧测量值的有效性。综上，引入参考帧测量值和多维梯度估计显著提高了初始恢复质量，相比于依赖自身先验知识的独立重构，模型的静态域先验增强阶段表现更佳，为后续动态建模奠定更可靠的基础。

(2)动态域先验增强阶段消融分析

在动态域先验增强阶段， PDCA-Net通过建模动态域先验知识实现运动估计与补偿。该网络的组件包括：特征预对齐(Pre-Alignment, PA)、对齐特征后处理(Post-Processing, PP)、特征细化对齐(Refined-Alignment, RA)、塔式级联(Pyramid-Cascade, PC)、细化非关键帧特征(Refined-Features, RF)。将SDPETs-Net作为基础模型，通过删减组件以探究其对性能的影响。实验结果在关键帧采样率为0.5、非关键帧采样率为0.05、GOP为8的条件下，重构REDS4序列得到，具体设置如表6所示。

表 6 PDCA-Net消融实验对比(PSNR(dB)/SSIM)

模型	设置					REDS4序列				平均值
模型	PA	PP	RA	PC	RF	000	011	015	020	平均值
基础	√	√	√	√	√	31.74/0.91	32.17/0.87	36.99/0.95	31.00/0.89	32.98/0.90
1	√	√	√	√	×	31.56/0.91	31.92/0.87	36.78/0.94	30.81/0.88	32.77/0.90
2	√	√	√	×	×	30.38/0.88	31.04/0.85	35.94/0.93	29.82/0.86	31.80/0.88
3	√	√	×	×	×	30.32/0.87	30.96/0.85	35.87/0.93	29.79/0.86	31.73/0.88
4	√	×	×	×	×	30.08/0.87	30.80/0.84	35.65/0.93	29.67/0.86	31.55/0.87
5	×	×	×	×	×	29.38/0.84	30.55/0.84	35.19/0.92	29.40/0.85	31.13/0.86

下载: 导出CSV

| 显示表格

表6显示不同设置下的重构结果。去除RF(模型1)导致重构精度下降，表明利用已对齐特征能提高非关键帧特征质量。去除PC(模型2)使PSNR下降0.97 dB，表明扩大帧间运动建模范围有助于捕捉粗粒度和大位移运动。去除RA(模型3)降低整体精度，表明注意力机制提高了对齐结果的鲁棒性。去除PP(模型4)进一步下降0.18 dB，强调非关键帧测量值校正的重要性。去除PA(模型5) 下降0.42 dB，证明静态和动态域先验增强的结合对性能提升至关重要。上述结果验证了PDCA-Net在视频帧运动估计和对动态域先验知识利用的有效性，整体设计对性能的提升明显，结构的有效性得到充分验证。

4. 结束语

本文提出由静态与动态域先验增强组成的两阶段视频压缩感知重构模型SDPETs-Net。在静态域先验增强阶段，提出了静态域先验增强网络(SPE-Net)，改善了信息挖掘、利用与优化等过程，初始重构精度显著提高；在动态域先验增强阶段，提出了特征域塔式可变形卷积联合注意力搜索网络(PDCA-Net)，有效地结合可变形卷积与注意力机制的优势，缓解各自独立使用下的限制与不足，并通过构造塔式级联结构，实现更准确的运动估计与补偿。仿真实验结果表明，与现有模型相比，SDPETs-Net在较少的参数量下取得了最优的重构精度，并具备出色的细节恢复能力，消融实验也充分验证了设计模型的有效性。

图 1 SDPETs-Net整体架构

下载: 全尺寸图片幻灯片

图 2 两级多维残差补充阶段实现细节

下载: 全尺寸图片幻灯片

图 3 PDCA-Net网络结构

下载: 全尺寸图片幻灯片

图 4 预对齐与细化对齐

下载: 全尺寸图片幻灯片

图 5 不同算法及模型重构视觉效果对比(Soccer序列第12帧)

下载: 全尺寸图片幻灯片

图 6 不同模型重构视觉效果对比(REDS4-000序列第36帧)

下载: 全尺寸图片幻灯片

表 1 UCF101测试集重构性能对比PSNR(dB)/SSIM

${r}_{\mathrm{n}\mathrm{k}}$	CSVideoNet	STM-Net	Imr-Net	JDRTAFA-Net	DUMHAN	DMIGAN	本文 SDPETs-Net
$0.037$	26.87/0.81	32.50/0.93	33.40/—	33.14/0.94	35.37/—	35.86/—	36.36/0.96
$0.018$	25.09/0.77	31.14/0.91	31.90/—	31.63/0.91	33.70/—	34.23/—	35.01/0.95
$0.009$	24.23/0.74	29.98/0.89	30.51/—	30.33/0.89	32.11/—	32.65/—	33.75/0.94
平均值	25.40/0.77	31.21/0.91	31.94/—	31.70/0.91	33.73/—	34.25/—	35.04/0.95

下载: 导出CSV

QCIF序列重构性能对比PSNR(dB)( ${r}_{\mathrm{k}}=0.5$ ， $\mathrm{G}\mathrm{O}\mathrm{P}=8$ )

${r}_{\mathrm{n}\mathrm{k}}$	算法 (网络)	视频序列						平均值
${r}_{\mathrm{n}\mathrm{k}}$	算法 (网络)	Silent	Ice	Foreman	Coastguard	Soccer	Mobile	平均值
0.01	RRS	21.25	20.72	18.51	21.16	21.42	15.24	19.72
	SSIM-InterF-GSR	24.77	24.65	26.86	25.08	23.39	21.92	24.45
	VCSNet-2	31.94	25.77	26.07	25.66	24.62	21.42	25.91
	ImrNet	35.30	29.25	31.58	28.94	27.10	25.02	29.53
	DUMHAN	37.25	31.69	34.46	31.63	28.37	29.28	32.11
	本文SDPETs-Net	38.05	32.92	36.05	32.76	29.50	30.35	33.27
0.05	RRS	25.76	26.15	26.84	22.66	26.80	16.68	24.15
	SSIM-InterF-GSR	33.68	28.81	33.18	28.09	27.65	22.99	29.07
	VCSNet-2	34.52	29.51	29.75	27.01	28.62	22.79	28.70
	ImrNet	38.07	33.76	36.03	30.80	31.81	27.55	33.00
	DUMHAN	40.42	36.58	39.44	33.63	33.74	31.61	35.90
	本文SDPETs-Net	41.09	37.98	40.82	34.31	34.85	32.36	36.90
0.1	RRS	33.95	31.09	35.17	27.34	29.74	20.00	29.55
	SSIM-InterF-GSR	35.09	31.73	35.75	30.24	30.31	24.35	31.25
	VCSNet-2	34.92	30.95	31.14	28.01	30.51	23.62	29.86
	ImrNet	39.17	35.90	37.37	31.44	34.24	28.19	34.39
	DUMHAN	41.73	38.66	41.68	34.73	36.40	32.48	37.61
	本文SDPETs-Net	42.71	40.10	42.97	35.22	37.52	33.07	38.60

下载: 导出CSV

表 3 REDS4序列重构性能对比PSNR(dB)/SSIM

${r}_{\mathrm{n}\mathrm{k}}$	序列	VCSNet-2	ImrNet	STM-Net	DUMHAN	本文SDPETs-Net
0.01	000	23.24/—	25.71/0.67	26.45/0.73	27.74/0.77	29.44/0.85
	011	24.19/—	25.93/0.66	26.89/0.71	26.72/0.70	27.77/0.74
	015	26.85/—	30.01/0.81	30.67/0.84	31.02/0.85	32.66/0.89
	020	23.34/—	25.15/0.66	25.98/0.71	25.97/0.70	26.99/0.75
0.1	000	27.55/—	29.09/0.85	30.69/0.90	31.80/0.91	32.82/0.94
	011	29.65/—	32.29/0.89	32.82/0.90	33.52/0.90	34.36/0.92
	015	32.34/—	36.33/0.94	37.06/0.95	38.00/0.95	39.07/0.96
	020	28.88/—	31.23/0.90	31.65/0.91	32.17/0.91	33.16/0.93

下载: 导出CSV

表 4 不同模型的空间与重构时间(GPU)与重构精度(PSNR(dB)/SSIM)对比

模型	参数量(M)	平均单帧重构时间(GPU)(s)	平均重构精度(PSNR(dB)/SSIM)
ImrNet	8.69	0.03	31.94/—
STM-Net	9.20	0.03	31.21/0.91
JDR-TAFA-Net	12.41	0.04	31.70/0.91
本文SDPETs-Net	7.44	0.04	35.04/0.95
本文SDPETs-Net	7.44	0.02(GOP并行)	35.04/0.95

下载: 导出CSV

表 5 静态域先验增强阶段的消融研究(PSNR(dB)/SSIM)

模型	设置		QCIF序列						平均值
模型	SR	MG	Silent	Ice	Foreman	Coastguard	Soccer	Mobile	平均值
基础	√	√	36.71/0.97	31.42/0.94	34.04/0.94	31.19/0.88	28.20/0.76	27.82/0.92	31.56/0.90
1	√	×	36.32/0.96	31.09/0.94	33.14/0.92	30.14/0.85	27.99/0.74	26.78/0.90	30.91/0.89
2	×	×	26.65/0.61	26.21/0.80	24.90/0.63	24.06/0.51	26.77/0.67	19.42/0.35	24.67/0.60

下载: 导出CSV

表 6 PDCA-Net消融实验对比(PSNR(dB)/SSIM)

模型	设置					REDS4序列				平均值
模型	PA	PP	RA	PC	RF	000	011	015	020	平均值
基础	√	√	√	√	√	31.74/0.91	32.17/0.87	36.99/0.95	31.00/0.89	32.98/0.90
1	√	√	√	√	×	31.56/0.91	31.92/0.87	36.78/0.94	30.81/0.88	32.77/0.90
2	√	√	√	×	×	30.38/0.88	31.04/0.85	35.94/0.93	29.82/0.86	31.80/0.88
3	√	√	×	×	×	30.32/0.87	30.96/0.85	35.87/0.93	29.79/0.86	31.73/0.88
4	√	×	×	×	×	30.08/0.87	30.80/0.84	35.65/0.93	29.67/0.86	31.55/0.87
5	×	×	×	×	×	29.38/0.84	30.55/0.84	35.19/0.92	29.40/0.85	31.13/0.86

下载: 导出CSV

参考文献(29)

[1]	DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582.
[2]	DO T T, CHEN Yi, NGUYEN D T, et al. Distributed compressed video sensing[C]. 2009 16th IEEE International Conference on Image Processing (ICIP), Cairo, Egypt, 2009: 1393–1396. doi: 10.1109/ICIP.2009.5414631.
[3]	KUO Yonghong, WU Kai, and CHEN Jian. A scheme for distributed compressed video sensing based on hypothesis set optimization techniques[J]. Multidimensional Systems and Signal Processing, 2017, 28(1): 129–148. doi: 10.1007/s11045-015-0337-4.
[4]	OU Weifeng, YANG Chunling, LI Wenhao, et al. A two-stage multi-hypothesis reconstruction scheme in compressed video sensing[C]. 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, USA, 2016: 2494–2498. doi: 10.1109/ICIP.2016.7532808.
[5]	ZHAO Chen, MA Siwei, ZHANG Jian, et al. Video compressive sensing reconstruction via reweighted residual sparsity[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2017, 27(6): 1182–1195. doi: 10.1109/TCSVT.2016.2527181.
[6]	和志杰, 杨春玲, 汤瑞东. 视频压缩感知中基于结构相似的帧间组稀疏表示重构算法研究[J]. 电子学报, 2018, 46(3): 544–553. doi: 10.3969/j.issn.0372-2112.2018.03.005. HE Zhijie, YANG Chunling, and TANG Ruidong. Research on structural similarity based inter-frame group sparse representation for compressed video sensing[J]. Acta Electronica Sinica, 2018, 46(3): 544–553. doi: 10.3969/j.issn.0372-2112.2018.03.005.
[7]	CHEN Can, WU Yutong, ZHOU Chao, et al. JsrNet: A joint sampling–reconstruction framework for distributed compressive video sensing[J]. Sensors, 2019, 20(1): 206. doi: 10.3390/s20010206.
[8]	SHI Wuzhen, LIU Shaohui, JIANG Feng, et al. Video compressed sensing using a convolutional neural network[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2021, 31(2): 425–438. doi: 10.1109/TCSVT.2020.2978703.
[9]	XU Kai and REN Fengbo. CSVideoNet: A real-time end-to-end learning framework for high-frame-rate video compressive sensing[C]. 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, USA, 2018: 1680–1688. doi: 10.1109/WACV.2018.00187.
[10]	XIA Kaiguo, PAN Zhisong, and MAO Pengqiang. Video compressive sensing reconstruction using unfolded LSTM[J]. Sensors, 2022, 22(19): 7172. doi: 10.3390/s22197172.
[11]	ZHANG Tong, CUI Wenxue, HUI Chen, et al. Hierarchical interactive reconstruction network for video compressive sensing[C]. 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 2023: 1–5. doi: 10.1109/ICASSP49357.2023.10095587.
[12]	NEZHAD V A, AZGHANI M, and MARVASTI F. Compressed video sensing based on deep generative adversarial network[J]. Circuits, Systems, and Signal Processing, 2024, 43(8): 5048–5064. doi: 10.1007/s00034-024-02672-8.
[13]	LING Xi, YANG Chunling, and PEI Hanqi. Compressed video sensing network based on alignment prediction and residual reconstruction[C]. 2020 IEEE International Conference on Multimedia and Expo (ICME), London, UK, 2020: 1–6. doi: 10.1109/ICME46284.2020.9102723.
[14]	YANG Xin and YANG Chunling. Imrnet: An iterative motion compensation and residual reconstruction network for video compressed sensing[C]. 2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, Canada, 2021: 2350–2354. doi: 10.1109/ICASSP39728.2021.9414534.
[15]	WEI Zhichao, YANG Chunling, and XUAN Yunyi. Efficient video compressed sensing reconstruction via exploiting spatial-temporal correlation with measurement constraint[C]. 2021 IEEE International Conference on Multimedia and Expo (ICME), Shenzhen, China, 2021: 1–6. doi: 10.1109/ICME51207.2021.9428203.
[16]	ZHOU Chao, CHEN Can, and ZHANG Dengyin. Deep video compressive sensing with attention-aware bidirectional propagation network[C]. 2022 15th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Beijing, China, 2022: 1–5. doi: 10.1109/CISP-BMEI56279.2022.9980235.
[17]	杨鑫, 杨春玲. 基于MAP的多信息流梯度更新与聚合视频压缩感知重构算法[J]. 电子学报, 2023, 51(11): 3320–3330. doi: 10.12263/DZXB.20220958. YANG Xin and YANG Chunling. MAP-based multi-information flow gradient update and aggregation for video compressed sensing reconstruction[J]. Acta Electronica Sinica, 2023, 51(11): 3320–3330. doi: 10.12263/DZXB.20220958.
[18]	YANG Xin and YANG Chunling. MAP-inspired deep unfolding network for distributed compressive video sensing[J]. IEEE Signal Processing Letters, 2023, 30: 309–313. doi: 10.1109/LSP.2023.3260707.
[19]	GU Zhenfei, ZHOU Chao, and LIN Guofeng. A temporal shift reconstruction network for compressive video sensing[J]. IET Computer Vision, 2024, 18(4): 448–457. doi: 10.1049/cvi2.12234.
[20]	魏志超, 杨春玲. 时域注意力特征对齐的视频压缩感知重构网络[J]. 电子学报, 2022, 50(11): 2584–2592. doi: 10.12263/DZXB.20220041. WEI Zhichao and YANG Chunling. Video compressed sensing reconstruction network based on temporal-attention feature alignment[J]. Acta Electronica Sinica, 2022, 50(11): 2584–2592. doi: 10.12263/DZXB.20220041.
[21]	RANJAN A and BLACK M J. Optical flow estimation using a spatial pyramid network[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, USA, 2017: 2720–2729. doi: 10.1109/CVPR.2017.291.
[22]	CHAN K C K, WANG Xintao, YU Ke, et al. Understanding deformable alignment in video super-resolution[C]. 2021 35th AAAI Conference on Artificial Intelligence, 2021: 973–981. doi: 10.1609/aaai.v35i2.16181.
[23]	LIANG Ziwen and YANG Chunling. Feature-domain proximal high-dimensional gradient descent network for image compressed sensing[C]. 2023 IEEE International Conference on Image Processing (ICIP), Kuala Lumpur, Malaysia, 2023: 1475–1479. doi: 10.1109/ICIP49359.2023.10222347.
[24]	ZHU Xizhou, HU Han, LIN S, et al. Deformable ConvNets v2: More deformable, better results[C]. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, USA, 2019: 9300–9308. doi: 10.1109/CVPR.2019.00953.
[25]	LIU Ze, HU Han, LIN Yutong, et al. Swin transformer V2: Scaling up capacity and resolution[C]. 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, USA, 2022: 11999–12009. doi: 10.1109/CVPR52688.2022.01170.
[26]	HUANG Cong, LI Jiahao, LI Bin, et al. Neural compression-based feature learning for video restoration[C]. 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, USA, 2022: 5862–5871. doi: 10.1109/CVPR52688.2022.00578.
[27]	ARBELÁEZ P, MAIRE M, FOWLKES C, et al. Contour detection and hierarchical image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(5): 898–916. doi: 10.1109/TPAMI.2010.161.
[28]	SOOMRO K, ZAMIR A R, and SHAH M. UCF101: A dataset of 101 human actions classes from videos in the wild[EB/OL]. https://arxiv.org/abs/1212.0402, 2012.
[29]	NAH S, BAIK S, HONG S, et al. NTIRE 2019 challenge on video deblurring and super-resolution: Dataset and study[C]. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Long Beach, USA, 2019: 1996–2005. doi: 10.1109/CVPRW.2019.00251.

施引文献

资源附件(0)

访问统计

图(6) / 表(6)

计量

文章访问数: 116
HTML全文浏览量: 93
PDF下载量: 13
被引次数: 0

1. 引言
2. 静态与动态域先验增强的两阶段视频重构网络
2.1 SDPETs-Net整体框
2.2 参考帧测量值引导的静态域先验增强阶段
2.3 塔式可变形卷积联合注意力搜索的动态域先验增强阶段
2.4 关键帧重构网络与损失函数
3. 实验仿真与分析
3.1 模型实现
3.2 实验结果与分析
4. 结束语

1. 引言
2. 静态与动态域先验增强的两阶段视频重构网络
2.1 SDPETs-Net整体框
2.2 参考帧测量值引导的静态域先验增强阶段
2.3 塔式可变形卷积联合注意力搜索的动态域先验增强阶段
2.4 关键帧重构网络与损失函数
3. 实验仿真与分析
3.1 模型实现
3.2 实验结果与分析
4. 结束语

参考文献(29)

施引文献

资源附件(0)

访问统计

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

静态与动态域先验增强的两阶段视频压缩感知重构网络

doi: 10.11999/JEIT240295

作者简介:
杨春玲：女，教授，研究方向为图像/视频压缩编码、图像质量评价

梁梓文：男，硕士生，研究方向为图像/视频压缩感知

通讯作者:
杨春玲　eeclyang@scut.edu.cn

计量

Static and Dynamic-domain Prior Enhancement Two-stage Video Compressed Sensing Reconstruction Network

1. 引言

2. 静态与动态域先验增强的两阶段视频重构网络

2.1 SDPETs-Net整体框

2.2 参考帧测量值引导的静态域先验增强阶段

2.3 塔式可变形卷积联合注意力搜索的动态域先验增强阶段

2.3.1 PDCA-Net实现思想及结构设计

2.3.2 多特征融合残差重构网络

2.4 关键帧重构网络与损失函数

3. 实验仿真与分析

3.1 模型实现

3.2 实验结果与分析

3.2.1 与现有算法及网络模型重构精度对比与分析

3.2.2 模型泛化性能测试与分析

3.2.3 重构视觉效果对比与分析

3.2.4 模型空间及运行时间的对比与分析

3.2.5 模型消融实验与分析

4. 结束语

计量

目录

1. 引言

2. 静态与动态域先验增强的两阶段视频重构网络

2.1 SDPETs-Net整体框

2.2 参考帧测量值引导的静态域先验增强阶段

2.3 塔式可变形卷积联合注意力搜索的动态域先验增强阶段

2.4 关键帧重构网络与损失函数

3. 实验仿真与分析

3.1 模型实现

3.2 实验结果与分析

4. 结束语

留言板

静态与动态域先验增强的两阶段视频压缩感知重构网络

doi: 10.11999/JEIT240295

作者简介: 杨春玲：女，教授，研究方向为图像/视频压缩编码、图像质量评价 梁梓文：男，硕士生，研究方向为图像/视频压缩感知

通讯作者: 杨春玲 eeclyang@scut.edu.cn

计量

出版历程

Static and Dynamic-domain Prior Enhancement Two-stage Video Compressed Sensing Reconstruction Network

1. 引言

2. 静态与动态域先验增强的两阶段视频重构网络

2.1 SDPETs-Net整体框

2.2 参考帧测量值引导的静态域先验增强阶段

2.3 塔式可变形卷积联合注意力搜索的动态域先验增强阶段

2.3.1 PDCA-Net实现思想及结构设计

2.3.2 多特征融合残差重构网络

2.4 关键帧重构网络与损失函数

3. 实验仿真与分析

3.1 模型实现

3.2 实验结果与分析

3.2.1 与现有算法及网络模型重构精度对比与分析

3.2.2 模型泛化性能测试与分析

3.2.3 重构视觉效果对比与分析

3.2.4 模型空间及运行时间的对比与分析

3.2.5 模型消融实验与分析

4. 结束语

计量

出版历程

目录

1. 引言

2. 静态与动态域先验增强的两阶段视频重构网络

2.1 SDPETs-Net整体框

2.2 参考帧测量值引导的静态域先验增强阶段

2.3 塔式可变形卷积联合注意力搜索的动态域先验增强阶段

2.4 关键帧重构网络与损失函数

3. 实验仿真与分析

3.1 模型实现

3.2 实验结果与分析

4. 结束语

作者简介:
杨春玲：女，教授，研究方向为图像/视频压缩编码、图像质量评价

梁梓文：男，硕士生，研究方向为图像/视频压缩感知

通讯作者:
杨春玲　eeclyang@scut.edu.cn