SMCA: A Framework for Scaling Chiplet-Based Computing-in-Memory Accelerators
-
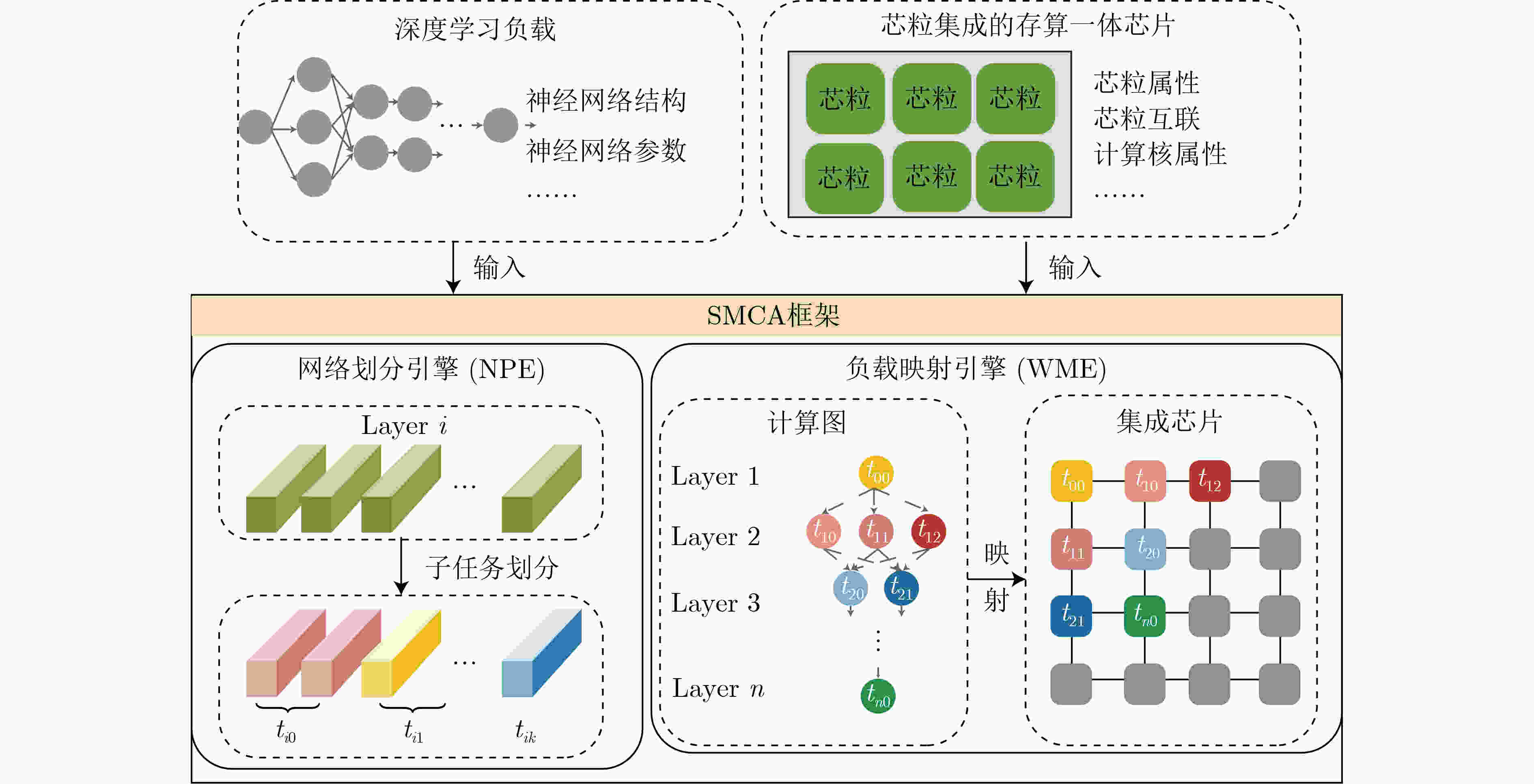
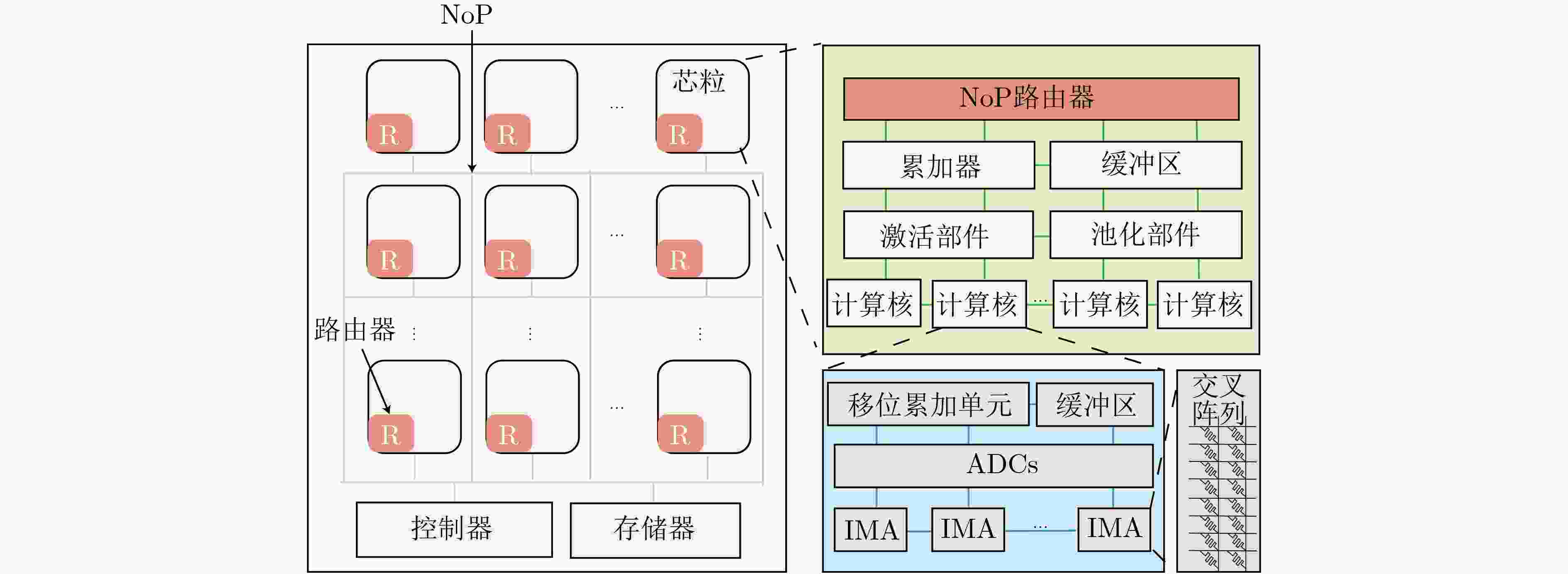
摘要: 基于可变电阻式随机存取存储器(ReRAM)的存算一体芯片已经成为加速深度学习应用的一种高效解决方案。随着智能化应用的不断发展,规模越来越大的深度学习模型对处理平台的计算和存储资源提出了更高的要求。然而,由于ReRAM器件的非理想性,基于ReRAM的大规模计算芯片面临着低良率与低可靠性的严峻挑战。多芯粒集成的芯片架构通过将多个小芯粒封装到单个芯片中,提高了芯片良率、降低了芯片制造成本,已经成为芯片设计的主要发展趋势。然而,相比于单片式芯片数据的片上传输,芯粒间的昂贵通信成为多芯粒集成芯片的性能瓶颈,限制了集成芯片的算力扩展。因此,该文提出一种基于芯粒集成的存算一体加速器扩展框架—SMCA。该框架通过对深度学习计算任务的自适应划分和基于可满足性模理论(SMT)的自动化任务部署,在芯粒集成的深度学习加速器上生成高能效、低传输开销的工作负载调度方案,实现系统性能与能效的有效提升。实验结果表明,与现有策略相比,SMCA为深度学习任务在集成芯片上自动生成的调度优化方案可以降低35%的芯粒间通信能耗。Abstract: Computing-in-Memory (CiM) architectures based on Resistive Random Access Memory (ReRAM) have been recognized as a promising solution to accelerate deep learning applications. As intelligent applications continue to evolve, deep learning models become larger and larger, which imposes higher demands on the computational and storage resources on processing platforms. However, due to the non-idealism of ReRAM, large-scale ReRAM-based computing systems face severe challenges of low yield and reliability. Chiplet-based architectures assemble multiple small chiplets into a single package, providing higher fabrication yield and lower manufacturing costs, which has become a primary trend in chip design. However, compared to on-chip wiring, the expensive inter-chiplet communication becomes a performance bottleneck for chiplet-based systems which limits the chip’s scalability. As the countermeasure, a novel scaling framework for chiplet-based CiM accelerators, SMCA (SMT-based CiM chiplet Acceleration) is proposed in this paper. This framework comprises an adaptive deep learning task partition strategy and an automated SMT-based workload deployment to generate the most energy-efficient DNN workload scheduling strategy with the minimum data transmission on chiplet-based deep learning accelerators, achieving effective improvement in system performance and efficiency. Experimental results show that compared to existing strategies, the SMCA-generated automatically schedule strategy can reduce the energy costs of inter-chiplet communication by 35%.
-
Key words:
- Chiplet /
- Deep learning processor /
- Computing-in-Memory (CiM) /
- Task dispatching
-
1 自适应层级网络划分策略
1: 输入:单个芯粒的固定算力M;网络$l({l_0},{l_1}, \cdots,{l_{L - 1}}) $的算力
需求$w({w_0},{w_1}, \cdots ,{w_{L - 1}}) $。2: 输出:网络划分策略bestP。 3: ${C_{{\text{idle}}}}{{ = M}} $; /*初始化${C_{{\text{idle}}}} $*/ 4: for $i = 0,1, \cdots ,L - 1 $ 5: if ${C_{{\text{idle}}}} \ge {w_i} $ then 6: ${\text{bestP}} \leftarrow {\text{NoPartition}}(i{\text{,}}{w_i}) $; 7: else if $\left\lceil {\dfrac{{{w_i}}}{{{M}}} = = \dfrac{{{w_i} - {C_{{\text{idle}}}}}}{{{M}}}} \right\rceil $ then 8: ${\text{bestP}} \leftarrow {\text{CMP}}(i{\text{,}}{w_i}) $; 9: else 10: ${\text{bestP}} \leftarrow {\text{CAP}}(i{\text{,}}{w_i}) $; 11: Update(${C_{{\text{idle}}}} $) 表 1 SMT约束中的符号表示
符号 含义 $ {T},{E},{C} $ 计算任务集合,计算图中边的集合以及
芯片封装的芯粒集合$ t,c $ 计算任务$ t $,芯粒$ c $ $ {e}_{i,j} $ 计算图中,任务$ i $到任务$ j $的有向边 $ {x}^{c},\;{y}^{c} $ 芯粒$ c $在芯片上的$ \left(x,y\right) $坐标 $ {w}^{t} $ 任务$ t $的计算需求 $ {o}^{t} $ 任务$ t $计算产生的中间数据量 $ {s}^{t} $ 任务$ t $的开始执行时间 $ {d}^{t} $ 完成任务t所有前置任务所需的芯粒间最小数据传输开销 $ {\tau }^{t} $ 任务$ t $的执行时间 $ \mathrm{s}{\mathrm{w}}^{c} $ 芯粒$ c $所在的波前编号 $ \mathrm{d}\mathrm{i}\mathrm{s}({c}_{i},{c}_{j}) $ 芯粒$ i $到芯粒$ j $的距离 表 2 系统配置
架构层次 属性 参数 封装 频率 1.8 GHz 芯粒间互联网络带宽 100 Gb/s 芯粒间通信能耗 1.75 p/bit 芯粒 工艺制程 16 nm 单个芯粒包含的计算核个数 16 单个计算核包含的ReRAM交叉
阵列个数16 计算核
ReRAM交叉阵列大小 128$ \times $128 ADC 1 bit DAC 8 bit 一个ReRAM单元存储的位数 2 权重精度 8 bit 数据流 权重固定型 -
[1] THOMPSON N C, GREENEWALD K, LEE K, et al. The computational limits of deep learning[EB/OL]. https://arxiv.org/abs/2007.05558, 2022. [2] HAN Yinhe, XU Haobo, LU Meixuan, et al. The big chip: Challenge, model and architecture[J]. Fundamental Research, 2023. doi: 10.1016/j.fmre.2023.10.020. [3] FENG Yinxiao and MA Kaisheng. Chiplet actuary: A quantitative cost model and multi-chiplet architecture exploration[C]. The 59th ACM/IEEE Design Automation Conference, San Francisco, USA, 2022: 121–126. doi: 10.1145/3489517.35304. [4] SHAFIEE A, NAG A, MURALIMANOHAR N, et al. ISAAC: A convolutional neural network accelerator with in-situ analog arithmetic in crossbars[C]. 2016 ACM/IEEE 43rd Annual International Symposium on Computer Architecture, Seoul, the Republic of Korea, 2016: 14–26. doi: 10.1109/ISCA.2016.12. [5] KRISHNAN G, GOKSOY A A, MANDAL S K, et al. Big-little chiplets for in-memory acceleration of DNNs: A scalable heterogeneous architecture[C]. 2022 IEEE/ACM International Conference on Computer Aided Design, San Diego, USA, 2022: 1–9. [6] LI Wen, WANG Ying, LI Huawei, et al. RRAMedy: Protecting ReRAM-based neural network from permanent and soft faults during its lifetime[C]. 2019 IEEE 37th International Conference on Computer Design (ICCD), Abu Dhabi, United Arab Emirates, 2019: 91–99. doi: 10.1109/ICCD46524.2019.00020. [7] AKINAGA H and SHIMA H. ReRAM technology; challenges and prospects[J]. IEICE Electronics Express, 2012, 9(8): 795–807. doi: 10.1587/elex.9.795. [8] IYER S S. Heterogeneous integration for performance and scaling[J]. IEEE Transactions on Components, Packaging and Manufacturing Technology, 2016, 6(7): 973–982. doi: 10.1109/TCPMT.2015.2511626. [9] SABAN K. Xilinx stacked silicon interconnect technology delivers breakthrough FPGA capacity, bandwidth, and power efficiency[R]. Virtex-7 FPGAs, 2011. [10] WADE M, ANDERSON E, ARDALAN S, et al. TeraPHY: A chiplet technology for low-power, high-bandwidth in-package optical I/O[J]. IEEE Micro, 2020, 40(2): 63–71. doi: 10.1109/MM.2020.2976067. [11] 王梦迪, 王颖, 刘成, 等. Puzzle: 面向深度学习集成芯片的可扩展框架[J]. 计算机研究与发展, 2023, 60(6): 1216–1231. doi: 10.7544/issn1000-1239.202330059.WANG Mengdi, WANG Ying, LIU Cheng, et al. Puzzle: A scalable framework for deep learning integrated chips[J]. Journal of Computer Research and Development, 2023, 60(6): 1216–1231. doi: 10.7544/issn1000-1239.202330059. [12] KRISHNAN G, MANDAL S K, PANNALA M, et al. SIAM: Chiplet-based scalable in-memory acceleration with mesh for deep neural networks[J]. ACM Transactions on Embedded Computing Systems (TECS), 2021, 20(5s): 68. doi: 10.1145/3476999. [13] SHAO Y S, CEMONS J, VENKATESAN R, et al. Simba: Scaling deep-learning inference with chiplet-based architecture[J]. Communications of the ACM, 2021, 64(6): 107–116. doi: 10.1145/3460227. [14] TAN Zhanhong, CAI Hongyu, DONG Runpei, et al. NN-Baton: DNN workload orchestration and chiplet granularity exploration for multichip accelerators[C]. 2021 ACM/IEEE 48th Annual International Symposium on Computer Architecture (ISCA), Valencia, Spain, 2021: 1013–1026. doi: 10.1109/ISCA52012.2021.00083. [15] LI Wanqian, HAN Yinhe, and CHEN Xiaoming. Mathematical framework for optimizing crossbar allocation for ReRAM-based CNN accelerators[J]. ACM Transactions on Design Automation of Electronic Systems, 2024, 29(1): 21. doi: 10.1145/3631523. [16] GOMES W, KOKER A, STOVER P, et al. Ponte vecchio: A multi-tile 3D stacked processor for exascale computing[C]. 2022 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, USA, 2022: 42–44, doi: 10.1109/ISSCC42614.2022.9731673. [17] ZHU Haozhe, JIAO Bo, ZHANG Jinshan, et al. COMB-MCM: Computing-on-memory-boundary NN processor with bipolar bitwise sparsity optimization for scalable multi-chiplet-module edge machine learning[C]. 2022 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, USA, 2022: 1–3. doi: 10.1109/ISSCC42614.2022.9731657. [18] HWANG R, KIM T, KWON Y, et al. Centaur: A chiplet-based, hybrid sparse-dense accelerator for personalized recommendations[C]. 2020 ACM/IEEE 47th Annual International Symposium on Computer Architecture (ISCA), Valencia, Spain, 2020: 968–981. doi: 10.1109/ISCA45697.2020.00083. [19] SHARMA H, MANDAL S K, DOPPA J R, et al. SWAP: A server-scale communication-aware chiplet-based manycore PIM accelerator[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2022, 41(11): 4145–4156. doi: 10.1109/TCAD.2022.3197500. [20] 何斯琪, 穆琛, 陈迟晓. 基于存算一体集成芯片的大语言模型专用硬件架构[J]. 中兴通讯技术, 2024, 30(2): 37–42. doi: 10.12142/ZTETJ.202402006.HE Siqi, MU Chen, and CHEN Chixiao. Large language model specific hardware architecture based on integrated compute-in-memory chips[J]. ZTE Technology Journal, 2024, 30(2): 37–42. doi: 10.12142/ZTETJ.202402006. [21] CHEN Yiran, XIE Yuan, SONG Linghao, et al. A survey of accelerator architectures for deep neural networks[J]. Engineering, 2020, 6(3): 264–274. doi: 10.1016/j.eng.2020.01.007. [22] SONG Linghao, CHEN Fan, ZHUO Youwei, et al. AccPar: Tensor partitioning for heterogeneous deep learning accelerators[C]. 2020 IEEE International Symposium on High Performance Computer Architecture (HPCA), San Diego, USA, 2020: 342–355. doi: 10.1109/HPCA47549.2020.00036. [23] DE MOURA L and BJØRNER N. Z3: An efficient SMT solver[C]. The 14th International Conference on Tools and Algorithms for the Construction and Analysis of Systems, Budapest, Hungary, 2008: 337–340. doi: 10.1007/978-3-540-78800-3_24. [24] PAPAIOANNOU G I, KOZIRI M, LOUKOPOULOS T, et al. On combining wavefront and tile parallelism with a novel GPU-friendly fast search[J]. Electronics, 2023, 12(10): 2223. doi: 10.3390/electronics12102223. -






 下载:
下载:







 下载:
下载:
