Time-varying Sea Surface Temperature Reconstruction Leveraging Low Rank and Joint Smoothness Constraints
-
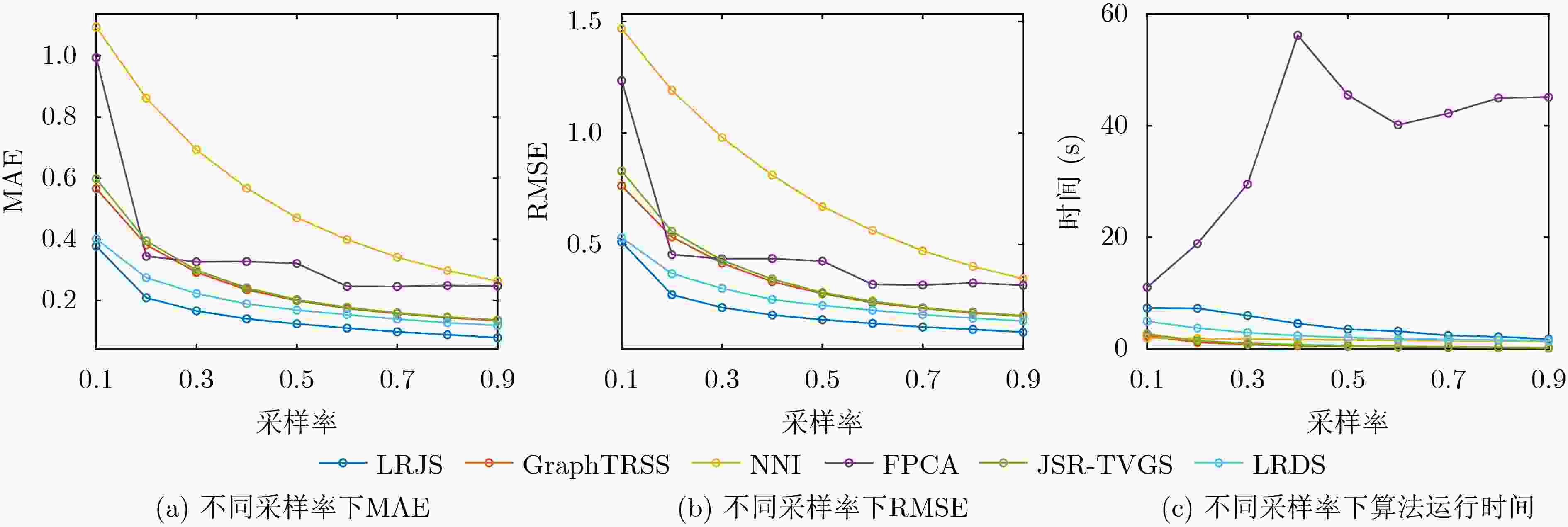
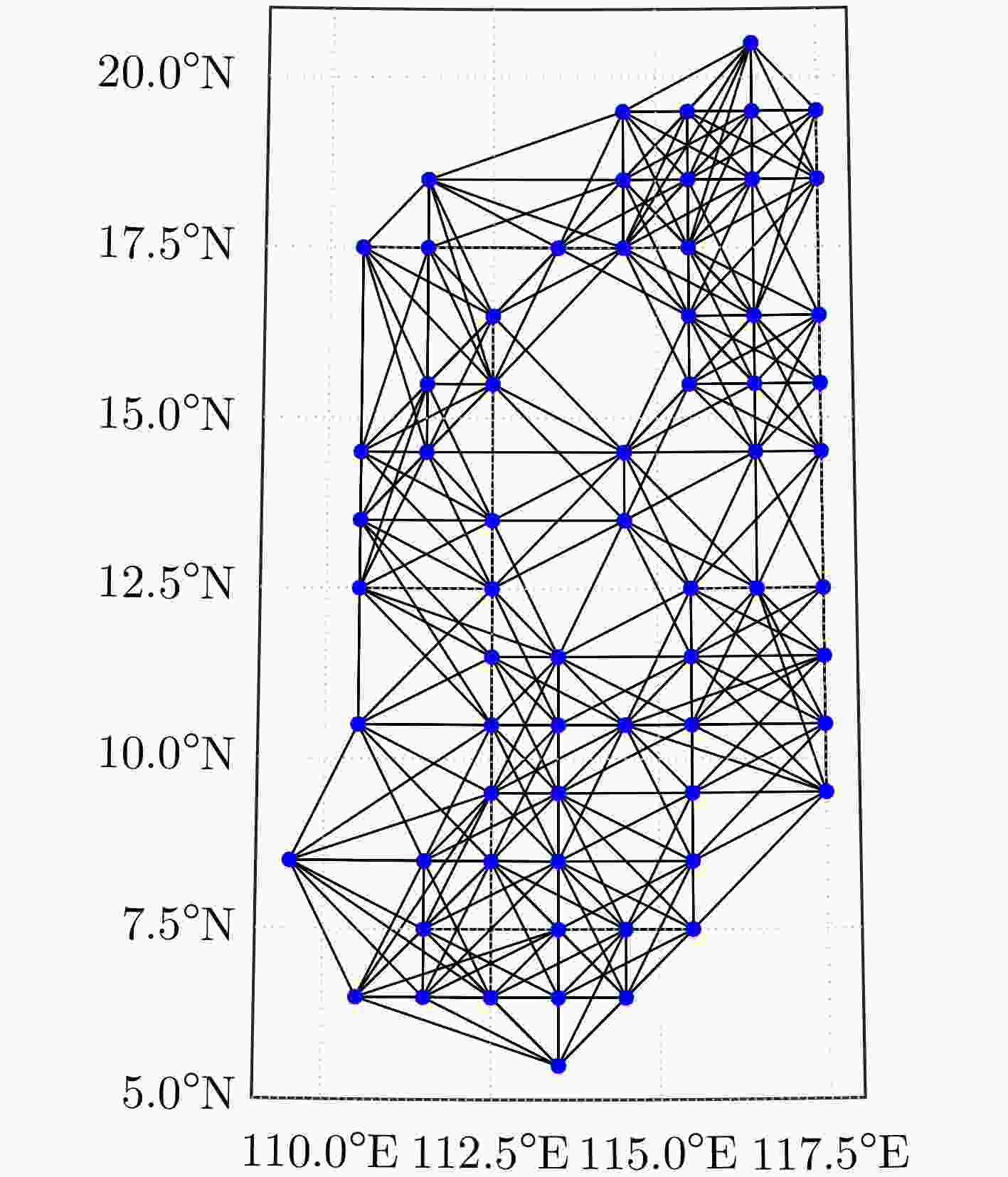
摘要: 海表面温度对于海洋动力过程及海气相互作用等具有重要意义,是海洋环境关键要素之一。浮标是海表面温度观测的常用手段,但由于浮标在空间的分布不规则,浮标采集的海表面温度数据也呈现非规则性。另外,浮标在实际工作中难免存在故障,致使采集的海表面温度数据存在缺失。因此对存在缺失的非规则海表面温度数据进行重构具有重要意义。该文通过将海表面温度数据建立为时变图信号,利用图信号处理方法解决海表面温度缺失数据重构问题。首先,利用数据的低秩性和时域-图域联合变差特性构建海表面温度重构模型;其次,基于交替方向乘子法框架提出一种求解该优化模型的基于低秩和联合平滑性(LRJS)的时变图信号重构方法,并分析该方法的计算复杂度和估计误差的理论极限;最后,采用南海和太平洋海域海表温度数据对方法的有效性进行了评估,结果表明,与现有缺失数据重构方法相比,该文所提LRJS方法有更高的重建精度。Abstract: Sea surface temperature is one of the key elements of the marine environment, which is of great significance to the marine dynamic process and air-sea interaction. Buoy is a commonly used method of sea surface temperature observation. However, due to the irregular distribution of buoys in space, the sea surface temperature data collected by buoys also show irregularity. In addition, it is inevitable that sometimes the buoy is out of order, so that the sea surface temperature data collected is incomplete. Therefore, it is of great significance to reconstruct the incomplete irregular sea surface temperature data. In this paper, the sea surface temperature data is established as a time-varying graph signal, and the graph signal processing method is used to solve the problem of missing data reconstruction of sea surface temperature. Firstly, the sea surface temperature reconstruction model is constructed by using the low rank data and the joint variation characteristics of time-domain and graph-domain. Secondly, a time-varying graph signal reconstruction method based on Low Rank and Joint Smoothness (LRJS) constraints is proposed to solve the optimization problem by using the framework of alternating direction multiplier method, and the computational complexity and the theoretical limit of the estimation error of the method are analyzed. Finally, the sea surface temperature data of the South China Sea and the Pacific Ocean are used to evaluate the effectiveness of the method. The results show that the LRJS method proposed in this paper can improve the reconstruction accuracy compared with the existing missing data reconstruction methods.
-
1 共轭梯度法
输入:$ {\boldsymbol{Y}},{\boldsymbol{J}},{{\boldsymbol{L}}_{\rm{G}}},{{\boldsymbol{L}}_T},{{\boldsymbol{Z}}^k},{{\boldsymbol{P}}^k},{\boldsymbol{D}},\alpha ,\beta ,\rho $,终止迭代阈值$ \varepsilon $,最
大迭代次数$ K $输出:重构信号时变图信号$ {{\boldsymbol{X}}_{^i}} $ 初始化设置:$ {{\boldsymbol{X}}_i} = 0,\Delta {{\boldsymbol{X}}_i} = 0,i = 0 $ 迭代: (1) 确定步长:
$ \tau = - \dfrac{{\left\langle {\Delta {{\boldsymbol{X}}_i},\nabla f({{\boldsymbol{X}}_i})} \right\rangle }}{{\left\langle {\Delta {{\boldsymbol{X}}_i},\nabla f({{\boldsymbol{X}}_i}) + {\boldsymbol{Y}} + \rho {{\boldsymbol{Z}}_i} - {{\boldsymbol{P}}_i}} \right\rangle }} $其中,$ \Delta {{\boldsymbol{X}}_i} $为第$ i $步的搜索方向,$ \tau $为第$ i $步的最优步长,其由
线性最小化步长准则$ \mathop {\min }\limits_\tau f({{\boldsymbol{X}}_i} + \tau \Delta {{\boldsymbol{X}}_i}) $决定。确定步长: (2) 更新搜索方向: $ \begin{aligned} & {{\boldsymbol{X}}_{i + 1}} = {{\boldsymbol{X}}_i} + \tau \Delta {{\boldsymbol{X}}_i}; \xi {\text{ = }}\frac{{||\nabla f({{\boldsymbol{X}}_{i + 1}})||_{{\mathrm{F}}} ^2}}{{||\nabla f({{\boldsymbol{X}}_{i + 1}})||_{{\mathrm{F}}} ^2}};\\& \Delta {{\boldsymbol{X}}_{i + 1}} = - \nabla f({{\boldsymbol{X}}_{i + 1}}) + \xi \Delta {{\boldsymbol{X}}_i}\end{aligned}$ 终止条件:如果$ i = K $或者$ {\text{||}}\Delta {{\boldsymbol{X}}_i}|{|_{\mathrm{F}}} \le \varepsilon $,则停止迭代;否则令$ i = i + 1 $,继续迭代,直至满足终止条件。 2 LRJS算法求解步骤
输入:$ {\boldsymbol{Y}},{\boldsymbol{J}},{{\boldsymbol{L}}_{{\mathrm{G}}} },{{\boldsymbol{L}}_{{{T}}} },{{\boldsymbol{Z}}^k},{{\boldsymbol{P}}^k},{\boldsymbol{D}},\alpha ,\beta ,\rho ,\mu $,终止迭代阈值$ \varepsilon $,
最大迭代次数$ K $输出:重构海表面温度数据$ {{\boldsymbol{X}}^k} $ 初始化设置:$ {{\boldsymbol{X}}^0} = {{\boldsymbol{Z}}^0} = {\boldsymbol{Y}},{{\boldsymbol{P}}^0} = 0,k = 0 $ 迭代: (1) 更新${{\boldsymbol{X}}^{k + 1}}$:利用算法1的共轭梯度法; (2) 更新${{\boldsymbol{Z}}^{k + 1}}$:利用式(21); (3) 更新${{\boldsymbol{P}}^{k + 1}}$:利用式(17); 终止条件:如果$ k = K $或者${\text{||}}\Delta {{\boldsymbol{X}}^k}|{|_{{\mathrm{F}}} } \le \varepsilon $,则停止迭代;否则
令$k = k + 1$,继续迭代,直至满足终止条件。 -
[1] DONEY S C, RUCKELSHAUS M, EMMETT DUFFY J, et al. Climate change impacts on marine ecosystems[J]. Annual Review of Marine Science, 2012, 4: 11–37. doi: 10.1146/annurev-marine-041911-111611. [2] LODER J W, VAN DER BAAREN A, and YASHAYAEV I. Climate comparisons and change projections for the Northwest Atlantic from six CMIP5 models[J]. Atmosphere-Ocean, 2015, 53(5): 529–555. doi: 10.1080/07055900.2015.1087836. [3] BARREIRO M, CHANG Ping, and SARAVANAN R. Variability of the South Atlantic convergence zone simulated by an atmospheric general circulation model[J]. Journal of Climate, 2002, 15(7): 745–763. doi: 10.1175/1520-0442(2002)015<0745:VOTSAC>2.0.CO;2. [4] 王奎民. 主要海洋环境因素对水下航行器航行影响分析[J]. 智能系统学报, 2015, 10(2): 316–323. doi: 10.3969/j.issn.1673-4785.201503006.WANG Kuimin. Influence of main ocean environments on the navigation of underwater vehicles[J]. CAAI Transactions on Intelligent Systems, 2015, 10(2): 316–323. doi: 10.3969/j.issn.1673-4785.201503006. [5] SHUMAN D I, NARANG S K, FROSSARD P, et al. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains[J]. IEEE Signal Processing Magazine, 2013, 30(3): 83–98. doi: 10.1109/MSP.2012.2235192. [6] LIU Jinling, JIANG Junzheng, LIN Jiming, et al. Generalized Newton methods for graph signal matrix completion[J]. Digital Signal Processing, 2021, 112: 103009. doi: 10.1016/j.dsp.2021.103009. [7] 张彦海, 蒋俊正. 基于笛卡尔乘积图上Sobolev平滑的时变图信号分布式批量重构[J]. 电子与信息学报, 2023, 45(5): 1585–1592. doi: 10.11999/JEIT221194.ZHANG Yanhai and JIANG Junzheng. Distributed batch reconstruction of time-varying graph signals via Sobolev smoothness on Cartesian product graph[J]. Journal of Electronics & Information Technology, 2023, 45(5): 1585–1592. doi: 10.11999/JEIT221194. [8] QIU Kai, MAO Xianghui, SHEN Xinyue, et al. Time-varying graph signal reconstruction[J]. IEEE Journal of Selected Topics in Signal Processing, 2017, 11(6): 870–883. doi: 10.1109/JSTSP.2017.2726969. [9] MAO Xianghui, QIU Kai, LI Tiejian, et al. Spatio-temporal signal recovery based on low rank and differential smoothness[J]. IEEE Transactions on Signal Processing, 2018, 66(23): 6281–6296. doi: 10.1109/TSP.2018.2875886. [10] GIRALDO J H, MAHMOOD A, GARCIA-GARCIA B, et al. Reconstruction of time-varying graph signals via Sobolev smoothness[J]. IEEE Transactions on Signal and Information Processing over Networks, 2022, 8: 201–214. doi: 10.1109/TSIPN.2022.3156886. [11] 索秋月, 林基明, 王俊义. 利用联合平滑性的时变图信号重构算法[J]. 计算机应用与软件, 2022, 39(4): 275–280. doi: 10.3969/j.issn.1000-386x.2022.04.043.SUO Qiuyue, LIN Jiming, and WANG Junyi. A time-varying graph signal reconstruction algorithm based on joint smoothness[J]. Computer Applications and Software, 2022, 39(4): 275–280. doi: 10.3969/j.issn.1000-386x.2022.04.043. [12] ZHAI Shiyu, LI Guobing, ZHANG Guomei, et al. Spatio-temporal signal recovery under diffusion-induced smoothness and temporal correlation priors[J]. IET Signal Processing, 2022, 16(2): 157–169. doi: 10.1049/sil2.12082. [13] LIU Jinling, LIN Jiming, QIU Hongbing, et al. Time-varying signal recovery based on low rank and graph-time smoothness[J]. Digital Signal Processing, 2023, 133: 103821. doi: 10.1016/j.dsp.2022.103821. [14] QI Zefeng, LIAO Xuewen, LI Ang, et al. Signal recovery for incomplete ocean data via graph signal processing[C]. GLOBECOM 2022-2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 2022: 4274–4279. doi: 10.1109/GLOBECOM48099.2022.10000902. [15] LI Siyuan, CHENG Lei, ZHANG Ting, et al. Graph-guided Bayesian matrix completion for ocean sound speed field reconstruction[J]. The Journal of the Acoustical Society of America, 2023, 153(1): 689–710. doi: 10.1121/10.0017064. [16] CHEN Yangge, CHENG Lei, and WU Y C. Bayesian low-rank matrix completion with dual-graph embedding: Prior analysis and tuning-free inference[J]. Signal Processing, 2023, 204: 108826. doi: 10.1016/j.sigpro.2022.108826. [17] LOUKAS A and FOUCARD D. Frequency analysis of time-varying graph signals[C]. 2016 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Washington, USA, 2016: 346–350. doi: 10.1109/GlobalSIP.2016.7905861. [18] GRASSI F, LOUKAS A, PERRAUDIN N, et al. A time-vertex signal processing framework: Scalable processing and meaningful representations for time-series on graphs[J]. IEEE Transactions on Signal Processing, 2018, 66(3): 817–829. doi: 10.1109/TSP.2017.2775589. [19] HACKBUSCH W. Iterative Solution of Large Sparse Systems of Equations[M]. New York, USA: Springer, 1994: 248–295. doi: 10.1007/978-1-4612-4288-8. [20] BELL H E. Gershgorin’s theorem and the zeros of polynomials[J]. The American Mathematical Monthly, 1965, 72(3): 292–295. doi: 10.2307/2313703. [21] MA Shiqian, GOLDFARB D, and CHEN Lifeng. Fixed point and Bregman iterative methods for matrix rank minimization[J]. Mathematical Programming, 2011, 128(1/2): 321–353. doi: 10.1007/s10107-009-0306-5. [22] SIBSON R. A brief description of natural neighbour interpolation[M]. BARNETT V. Interpreting Multivariate Data. Hoboken: Wiley, 1981. [23] PERRAUDIN N, PARATTE J, SHUMAN D, et al. GSPBOX: A toolbox for signal processing on graphs[J]. Eprint Arxiv, 2016, 61(7): 1644–1656. [24] Physical Sciences Division, Earth System Research Laboratory, National Oceanic and Atmospheric Administration. Sea surface temperature (SST) V2[EB/OL]. http://www.esrl.noaa.gov/psd/data/gridded/data.noaa.oisst.v2.html, 2023. [25] China Argo Real-Time Data Center. Argo real-time data[EB/OL]. ftp: //data. argo. org. cn/pub/ARGO/, 2023. -






 下载:
下载:



 下载:
下载:
