SDL PUF: A High Reliability Self-Adaption Deviation Locking PUF
-
摘要: 物理不可克隆函数(Physical Unclonable Function, PUF)作为一种新的硬件安全原语，通过提取工艺偏差产生唯一的响应序列为计算系统提供可信根。然而现有基于现场可编辑门阵列(Field Programmable Gate Array, FPGA)的PUF难以在较宽的温度和电压范围内实现高可靠性。该文提出一种基于自定时环(Self-Timed Ring，STR)的自适应偏差锁定PUF(Self-adaption Deviation Locking PUF, SDL PUF)，首先利用STR延迟引起的振荡频率差产生PUF响应；然后通过在初始化阶段自适应配置，有效扩大STR环内的事件到达时间偏差，从而显著提高PUF的可靠性；最后进一步提出一种对比混淆策略，通过提取工艺偏差自动生成随机比特配置并混淆比较器，以抵抗侧信道攻击。在Xilinx Virtex-6 FPGA上实验结果表明， SDL PUF在0～80°C的温度范围和0.85～1.15V的电压范围内误码率为0， 唯一性和均匀性分别为49.29%和49.84%。Abstract: As a novel hardware security primitive, Physical Unclonable Function (PUF) extracts process deviations to generate a unique response sequence, providing a root of trust for computing systems. However, existing PUFs based on Field Programmable Gate Arrays (FPGAs) cannot maintain high reliability over a wide range of temperatures and voltages. In this work, we propose a Self-Timed Ring (STR) based Self-adaption Deviation Locking PUF (SDL PUF). Firstly, the PUF response is generated utilizing the oscillation frequency difference caused by the STR delay. Secondly, the adaptive configuration in the initialization stage can effectively expand the deviation of the event arrival time in the STR, substantially enhancing the reliability of PUF. Finally, a comparator obfuscation strategy is proposed, automatically configuring the comparator by extracting the process deviation to resist the side-channel attack. The proposed structure is implemented on a Xilinx Virtex-6 FPGA. Experimental results show that the proposed SDL PUF achieves 0 bit error rate in the temperature range of 0°C～80°C and the voltage range of 0.85～1.15V, and ensures 49.29% uniqueness and 49.84% uniformity while maintaining high reliability.
-
Key words:
- Physical unclonable function /
- Self-timed ring /
- FPGA /
- Reliability
-
[1] 福布斯: 2016年物联网预测和市场估算总结[EB/OL]. http://tech.163.com/16/1130/07/C73Q381P00097U7R.html, 2016. [2] Grand View Research, Inc. IoT security market size worth $9.88 billion By 2025 | CAGR: 29.7%[EB/OL]. https://www.grandviewresearch.com/press-release/global-internet-of-things-iot-security-market, 2018. [3] 杨庚, 许建, 陈伟, 等. 物联网安全特征与关键技术[J]. 南京邮电大学学报: 自然科学版, 2010, 30(4): 20–29. doi: 10.3969/j.issn.1673-5439.2010.04.004.YANG Geng, XU Jian, CHEN Wei, et al. Security characteristic and technology in the internet of things[J]. Journal of Nanjing University of Posts and Telecommunications: Natural Science, 2010, 30(4): 20–29. doi: 10.3969/j.issn.1673-5439.2010.04.004. [4] XU Chongyao, ZHANG Jieyun, LAW M K, et al. Transfer-path-based hardware-reuse strong PUF achieving modeling attack resilience with200 million training CRPs[J]. IEEE Transactions on Information Forensics and Security, 2023, 18: 2188–2203. doi: 10.1109/TIFS.2023.3263621. [5] 汪鹏君, 连佳娜, 陈博. 基于序列密码的强PUF抗机器学习攻击方法[J]. 电子与信息学报, 2021, 43(9): 2474–2481. doi: 10.11999/JEIT210726.WANG Pengjun, LIAN Jiana, and CHEN Bo. Sequence cipher based machine learning-attack resistance method for strong-PUF[J]. Journal of Electronics & Information Technology, 2021, 43(9): 2474–2481. doi: 10.11999/JEIT210726. [6] ZHANG Jiliang, SHEN Chaoqun, GUO Zhiyang, et al. CT PUF: Configurable tristate PUF against machine learning attacks for IoT security[J]. IEEE Internet of Things Journal, 2022, 9(16): 14452–14462. doi: 10.1109/JIOT.2021.3090475. [7] ZHANG Jiliang, DING Lin, CHEN Zhuojun, et al. DA PUF: Dual-state analog PUF[C]. The 59th ACM/IEEE Design Automation Conference (DAC), San Francisco, USA, 2022: 73–78. doi: 10.1145/3489517.3530412. [8] DELLA SALA R and SCOTTI G. A novel FPGA implementation of the NAND-PUF with minimal resource usage and high reliability[J]. Cryptography, 2023, 7(2): 18. doi: 10.3390/cryptography7020018. [9] GAN Jiayan, ZHOU Jun, and WANG Ning. A FPGA-based RO PUF with LUT-based self-compare structure and adaptive counter time period tuning[C]. 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 2018: 1–5. doi: 10.1109/ISCAS.2018.8351014. [10] DELLA SALA R, BELLIZIA D, and SCOTTI G. A lightweight FPGA compatible weak-PUF primitive based on XOR gates[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2022, 69(6): 2972–2976. doi: 10.1109/TCSII.2022.3156788. [11] STREIT F J, KRÜGER P, BECHER A, et al. Design and evaluation of a tunable PUF architecture for FPGAs[J]. ACM Transactions on Reconfigurable Technology and Systems, 2022, 15(1): 7. doi: 10.1145/3491237. [12] DUBROVA E. A reconfigurable arbiter PUF with 4 x 4 switch blocks[C]. 2018 IEEE 48th International Symposium on Multiple-Valued Logic (ISMVL), Linz, Austria, 2018: 31–37. doi: 10.1109/ISMVL.2018.00014. [13] SINGH S, BODAPATI S, PATKAR S, et al. PA-PUF: A novel priority arbiter PUF[C]. 2022 IFIP/IEEE 30th International Conference on Very Large Scale Integration (VLSI-SoC), Patras, Greece, 2022: 1–6. doi: 10.1109/VLSI-SoC54400.2022.9939642. [14] NI Li, WANG Pengjun, ZHANG Yuejun, et al. SI PUF: An SRAM and inverter-based PUF with a bit error rate of 0.0053% and 0.073/0.042 pJ/bit[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2024, 71(4): 2339–2343. doi: 10.1109/TCSII.2023.3339296. [15] YAO Liang, LIANG Huaguo, HUANG Zhengfeng, et al. A lightweight configurable XOR RO-PUF design based on Xilinx FPGA[C]. Proceedings of 2021 IEEE 4th International Conference on Electronics Technology (ICET), Chengdu, China, 2021: 83–88. doi: 10.1109/ICET51757.2021.9451016. [16] RIZK D, RIZK R, RIZK F, et al. An economic uniqueness-improved reliable reconfigurable RO PUF for IoT security[C]. 2022 IEEE International Symposium on Circuits and Systems (ISCAS), Austin, USA, 2022: 1680–1684. doi: 10.1109/ISCAS48785.2022.9937931. [17] LU Yingchun, WANG Xinyu, WANG Yanjie, et al. Pure digital scalable mixed entropy separation structure for physical unclonable function and true random number generator[J]. IEEE Transactions on Very Large scale Integration (VLSI) Systems, 2021, 29(11): 1922–1929. doi: 10.1109/TVLSI.2021.3116104. [18] LV Shenglai, HUANG Yangbo, CHEN Lei, et al. RO PUF design in FPGAs with frequency-offsetting strategies[C]. 2021 IEEE 2nd International Conference on Information Technology, Big Data and Artificial Intelligence (ICIBA), Chongqing, China, 2021: 558–562. doi: 10.1109/ICIBA52610.2021.9688287. [19] WINSTANLEY A and GREENSTREET M. Temporal properties of self-timed rings[C]. Proceedings of the 11th IFIP WG 10.5 Advanced Research Working Conference on Correct Hardware Design and Verification Methods, Scotland, UK, 2001: 140–154. doi: 10.1007/3-540-44798-9_12. [20] CHERKAOUI A, FISCHER V, AUBERT A, et al. Comparison of self-timed ring and inverter ring oscillators as entropy sources in FPGAS[C]. 2012 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 2012: 1325–1330. doi: 10.1109/DATE.2012.6176697. [21] HUANG Zhengfeng, BIAN Jingchang, LIN Yankun, et al. Design guidelines and feedback structure of ring oscillator PUF for performance improvement[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2024, 43(1): 71–84. doi: 10.1109/TCAD.2023.3301386. [22] BOKE A K, NAKHATE S, and RAJAWAT A. FPGA implementation of PUF based key generator for secure communication in IoT[J]. Integration, 2023, 89: 241–247. doi: 10.1016/j.vlsi.2022.12.006. -
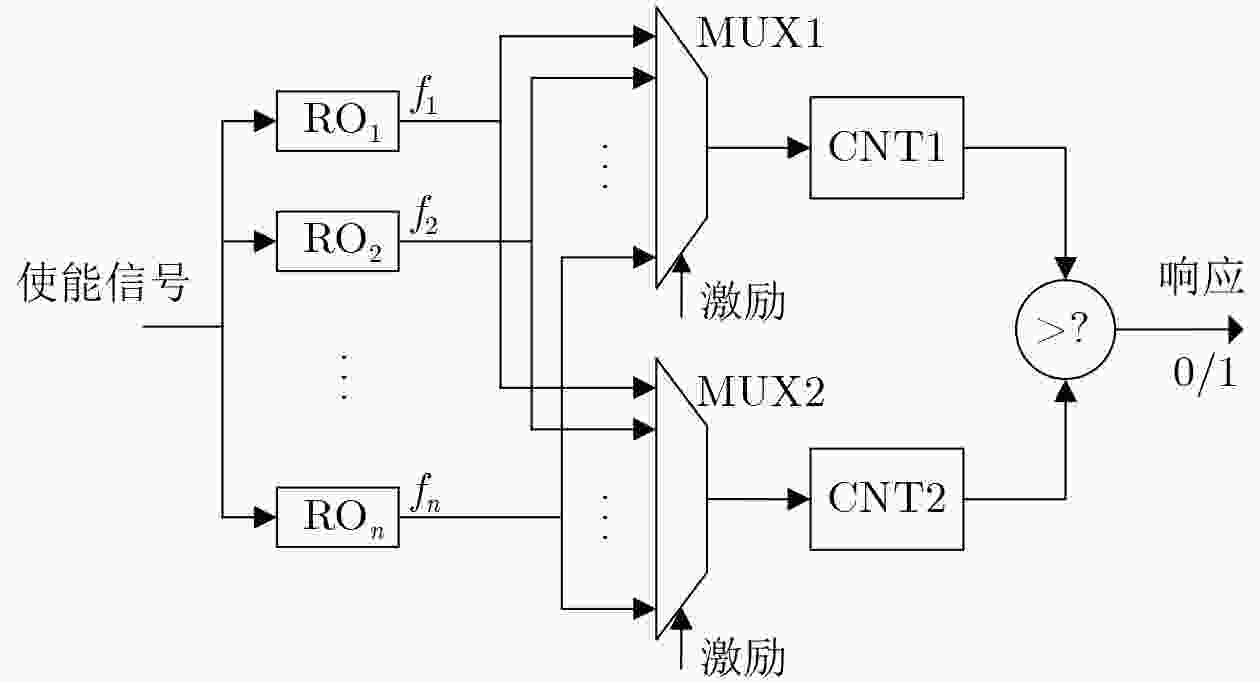
下载:
图(9) / 表(1)
计量
- 文章访问数: 287
- HTML全文浏览量: 162
- PDF下载量: 33
- 被引次数: 0
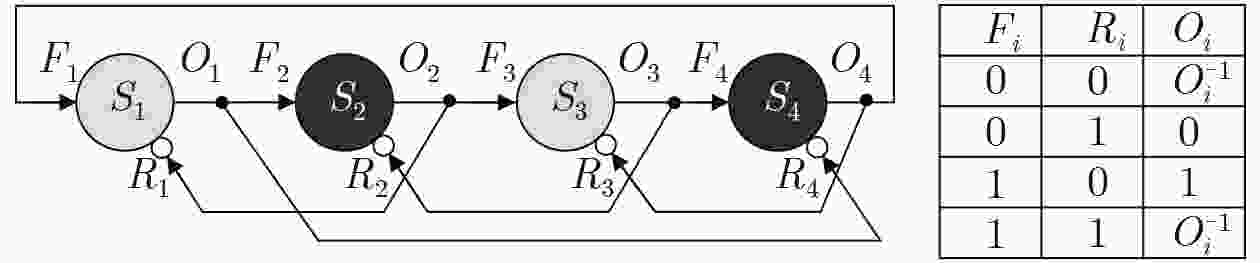
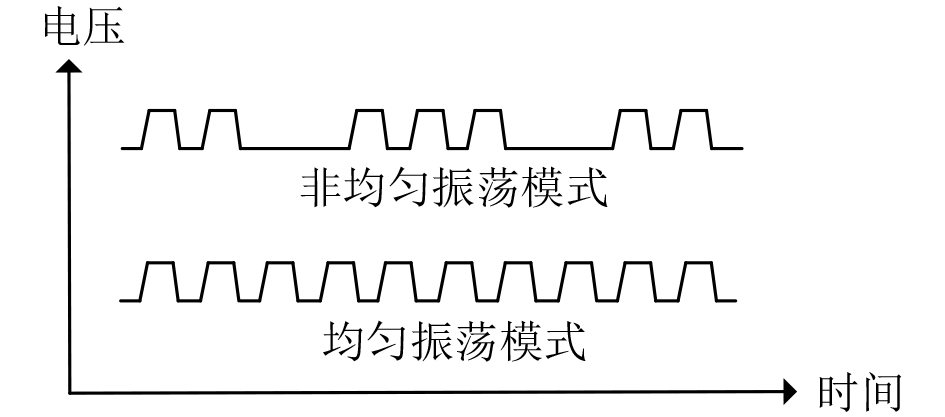
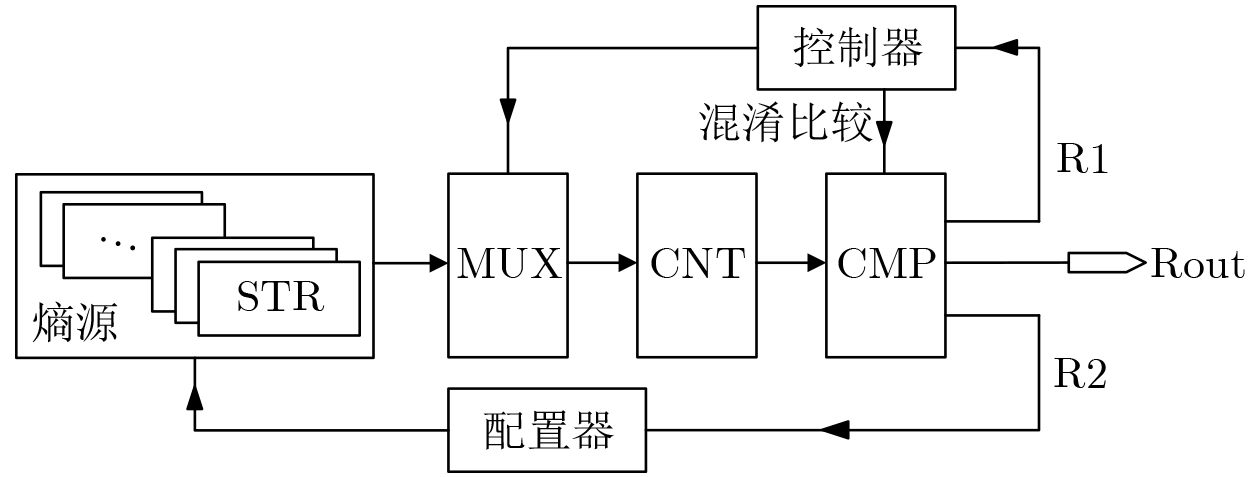
下载:
