面向自旋存内计算架构的图算法优化设计

王雪岩; 陈序航; 贾小涛; 杨建磊; 屈钢; 赵巍胜

doi:10.11999/JEIT230371

面向自旋存内计算架构的图算法优化设计

doi: 10.11999/JEIT230371

1.
北京航空航天大学集成电路科学与工程学院北京 100191
2.
北京航空航天大学计算机学院北京 100191
3.
马里兰大学帕克分校电子与计算机工程系马里兰州 20742

基金项目: 国家自然科学基金(62004011, 62006011, U20A20204, 62072019)

详细信息

作者简介:
王雪岩：女，助理教授，研究方向为存算一体架构、图计算、芯片安全

陈序航：男，硕士，研究方向为存算一体架构、图计算

贾小涛：男，副教授，研究方向为贝叶斯神经网络、EDA算法设计

杨建磊：男，副教授，研究方向为智能计算系统与芯片设计

屈钢：男，教授，研究方向为硬件安全、低功耗设计

赵巍胜：男，教授，研究方向为自旋电子芯片

通讯作者:
赵巍胜　weisheng.zhao@buaa.edu.cn

中图分类号: TN402
计量
- 文章访问数: 505
- HTML全文浏览量: 235
- PDF下载量: 95
- 被引次数: 0
出版历程
- 收稿日期: 2023-05-04
- 修回日期: 2023-07-19
- 网络出版日期: 2023-07-25
- 刊出日期: 2023-09-27

Graph Algorithm Optimization for Spintronics-based In-memory Computing Architecture

1.
School of Integrated Circuit Science and Engineering, Beihang University, Beijing 100191, China
2.
School of Computer Science and Engineering, Beihang University, Beijing 100191, China
3.
Department of Electrical and Computer Engineering, University of Maryland, College Park, Maryland 20742, USA

Funds: The National Natural Science Foundation of China (62004011, 62006011, U20A20204, 62072019)

摘要

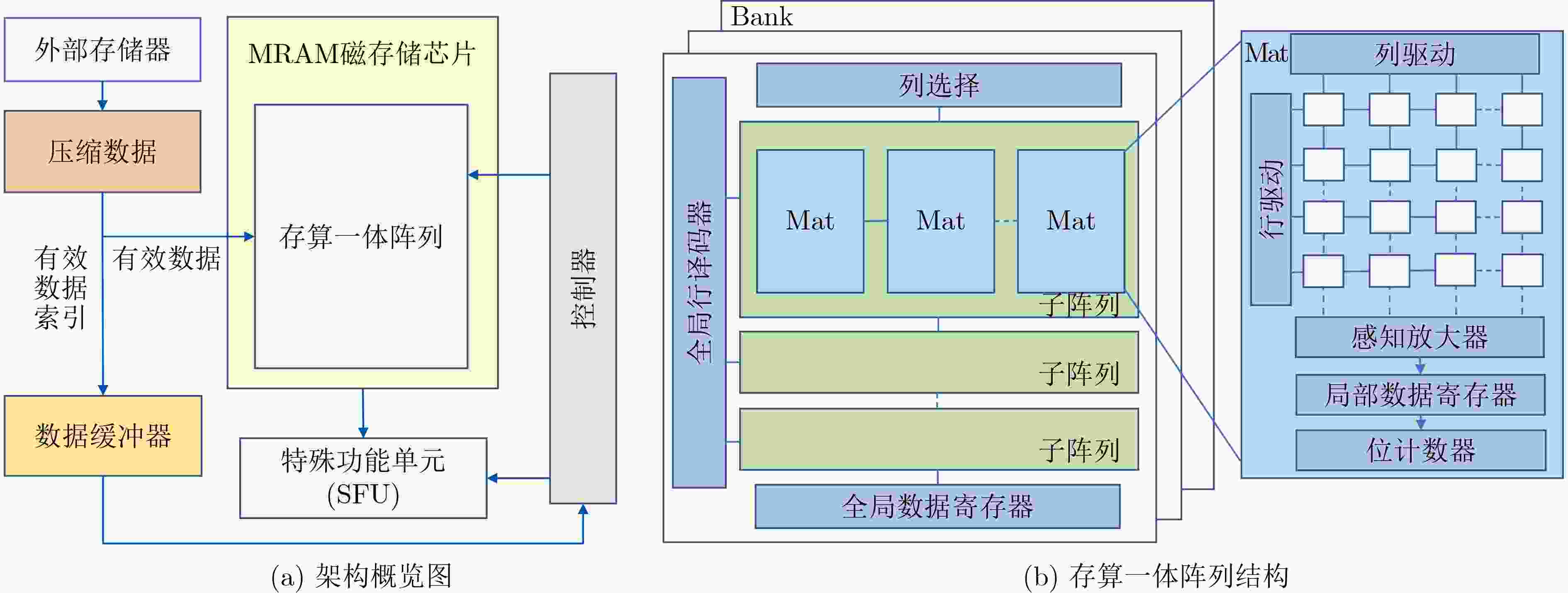
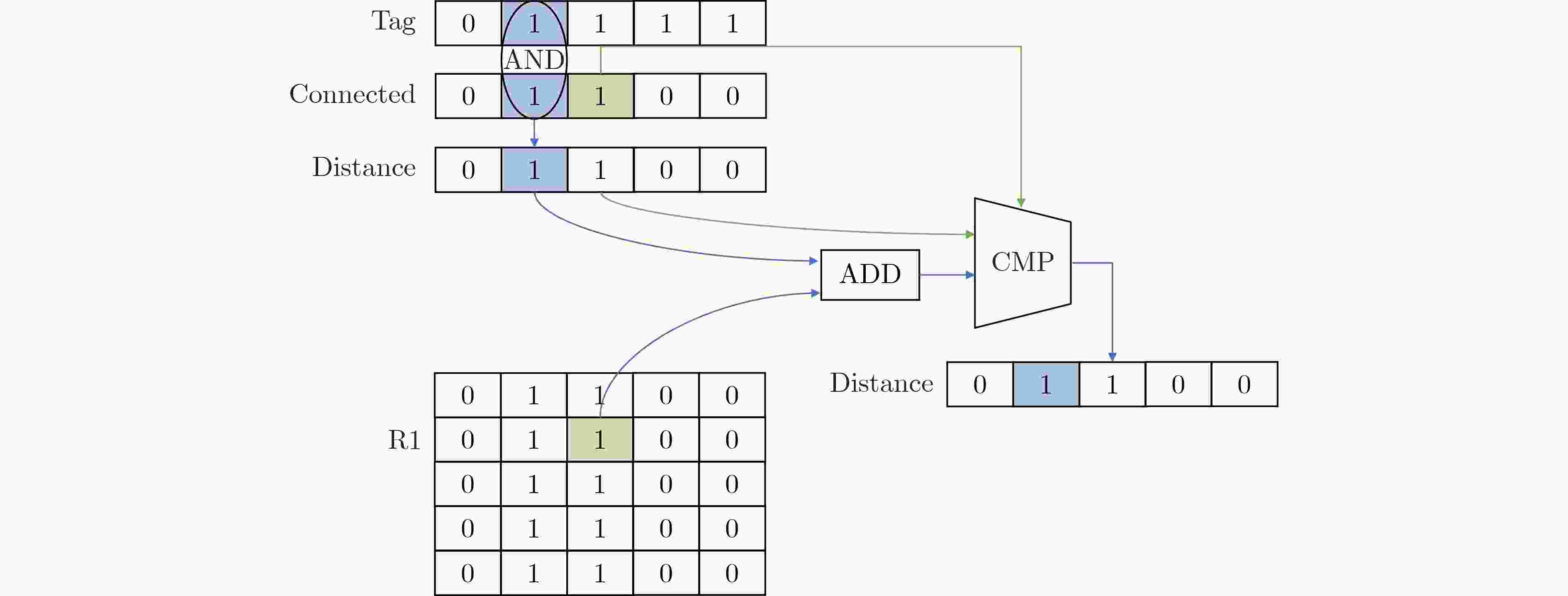
摘要: 图计算广泛应用于社交网络分析、推荐系统等诸多关键领域，然而，传统的大规模图计算系统面临冯诺依曼架构下访存带来的性能瓶颈。新型存内计算架构成为加速大规模图计算非常有前景的方案，尤其是非易失自旋磁存储器(MRAM)具备超高耐擦写性和超快写入等优点，可使图计算的存内实现更为高效。实现这种潜力的关键挑战之一是如何优化存内计算架构下的图算法设计。该文的前期工作表明，三角形计数算法和图连通分量计算算法可以通过按位运算实现，从而高效地部署在自旋存内处理核中加速。该文探索了更多图算法的优化实现，例如单源最短路径、K-core、链路预测，并提出了面向新型存内计算架构的图算法优化设计模型。该研究对于突破冯诺依曼架构下大规模图计算的内存访问瓶颈具有关键意义。
- 图计算 /
- 存内计算架构 /
- 位逻辑运算 /
- 自旋磁存储器
Abstract: Graph computing has been widely applied to emerging fields such as social network analysis and recommendation systems. However, large-scale graph computing under the traditional Von-Neumann architecture faces the memory access bottleneck. The newly developed in-memory computing architecture becomes a promising alternative for accelerating graph computing. Due to its ultra-high endurance and ultra-fast writing speed, non-volatile Magnetoresistive Random Access Memory (MRAM) has the potential in building efficient in-memory accelerators. One of the key challenges to achieve such potential is how to optimize the graph algorithm design under the in-memory computing architecture. Our previous work shows that the triangle counting algorithms and graph connected component computing algorithms can be implemented with bitwise operations, which enables efficient spintronics in-memory computations. In this paper, the optimized implementation of more graph algorithms is explored such as single-source shortest path, K-core and link prediction, and an optimized design model of graph algorithms for the new in-memory computing architecture based is proposed. This research is of key significance for the breakthrough of solving the memory access bottleneck in large-scale graph computing under the Von Neumann architecture.
- Graph computing /
- In memory computing architecture /
- Bitwise logical operation /
- Magnetoresistive Random Access Memory (MRAM)

HTML全文

1. 引言

20世纪90年代，混沌同步现象首次被发现存在于两个耦合的系统中，这一突破性的发现为混沌理论应用于通信领域奠定了基础。此后，国内外众多学者开始研究混沌理论在通信领域的应用，混沌通信技术成为非线性动力学系统中的一个重要应用分支。混沌信号产生方式简单，具有初始条件极度敏感性、优良的频谱特性、高度随机性、非周期性以及良好的自(互)相关性等特性^[1,2]，在保密通信中具有较大应用价值^[3-6]。

Kolumban等人于1996年提出第1种非相干混沌数字解调技术—差分混沌移位键控(Differential Chaos Shift Keying, DCSK)技术；后又针对DCSK中发送信号比特能量不恒定的问题，提出调频DCSK(Frequency Modulated DCSK, FM-DCSK)技术。DCSK和FM-DCSK都采用传输参考(Transmitted-Reference, T-R)模式，分时隙发送参考信号和信息信号，因此具有较好的误码性能，但也造成了系统的传输速率极低^[7,8]。针对传输速率低的缺点，文献[9-12]以DCSK和FM-DCSK为基础提出改进方案，虽提高了传输速率，但也增加了系统复杂度。文献[13]以高效差分混沌移位键控(High Efficiency Differential Chaos Shift Keying, HE-DCSK)系统为基础进行改进，提出VHE-DCSK(Very High Efficiency Differential Chaos Shift Keying)系统，将信息信号延迟不同时间从而实现多用户传输。文献[14]提出多载波差分混沌移位键控(MultiCarrier Differential Chaos Shift Keying, MC-DCSK)系统，通过使用多个不同中心频率的载波来实现信息比特的并行传输。文献[15]提出短参倍速差分混沌键控(Short Reference Multifold Rate Differential Chaos Shift Keying, SRMR-DCSK)系统，增加单个信息时隙内传输的比特数用于提升系统的传输速率。

Walsh码具有良好的正交特性和产生方式简单等优点，且Walsh码的引入不会过多地增加系统复杂度。为有效提升传输速率和能量效率，本文结合Walsh码的优良特性，提出一种OMU-SR-DCSK系统，将参考时隙缩短为信息时隙的 ${1 / P}$ ，并在参考时隙后增加两路连续的信息时隙，使得系统发送一帧共可传输 $2N\,{\rm{bit}}$ 用户信息，Walsh码保证用户间完全正交，完全消除了相关运算时产生的用户间干扰，改善了系统误码性能。

2. OMU-SR-DCSK系统原理

Hadamard矩阵中只包含“+1”和“–1”两种元素，Walsh函数码是一组同步正交码，故可由 ${2^n}$ 阶Hadamard矩阵产生，码序列构造为^[16]

${{{W}}_{{2^n}}} = \left[ {\begin{array}{*{20}{c}} {{{{W}}_{{2^{(n - 1)}}}}}&{{{{W}}_{{2^{(n - 1)}}}}} \\ {{{{W}}_{{2^{(n - 1)}}}}}&{ - {{{W}}_{{2^{(n - 1)}}}}} \end{array}} \right]$

(1)

式(1)中， $n = 0,1, ···$ , ${{{W}}_{{2^0}}} = [1]$ 。矩阵的每行代表一个长度P 的Walsh码序列， $P = {2^n}$ 。

图1为DCSK和OMU-SR-DCSK系统第k帧结构对比图。相比于DCSK系统，OMU-SR-DCSK系统将参考信号长度缩短为 $R(R = {\beta / P})$ ，有效节省了时间和能量，其中，将扩频因子 $\beta$ 定义为比特周期 ${T_s}$ 和码片周期 ${T_c}$ 的比值，为便于后文理论公式的推导，取 ${T_c} = 1$ ；此外，还将信息时隙由1路扩展为2路，每个信息时隙内，用户之间乘以不同的Walsh码 ${w_{i,j}}$ 加以区分，使得系统发送1帧共可传输 $2N\,{\rm{bit}}$ 用户信息，从而提高了传输速率和能量效率，Walsh码的引入消除了用户间干扰项，改善了系统误码性能。

图 1 OMU-SR-DCSK和DCSK系统第k帧结构对比图

下载: 全尺寸图片幻灯片

图2为OMU-SR-DCSK系统的发送机结构。首先由混沌信号发生器产生一段R长度的混沌序列 ${x_{i,k}}$ ，经重复 $P$ 次后，其长度变为 $\beta$ 。然后将这段长度为 $\beta$ 的混沌序列延迟R，用于传输前N个用户的信息比特，每个用户分别与 ${w_{i,j}}(\,\,\,\,j = 1,2, ··· ,N)$ 相乘，后由加法器将前N个用户信息加和在第1个信息时隙内传输；同理，将这段长度为 $\beta$ 的混沌序列延迟 $(P + 1)R$ ，用于传输后N个用户的信息比特，为每个用户分配一段Walsh码序列 ${w_{i,j}}$ ，后将这N个用户信息加和在第2个信息时隙内传输。则第k帧的发送信号 ${s_{i,k}}$ 表达式为

图 2 OMU-SR-DCSK系统发送机结构

下载: 全尺寸图片幻灯片

${s_{i,k}} =\,\,\left\{ \begin{aligned} & {x_{i,k\,}}\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, 0 < i \le R\,\,\,\\ & \sum\limits_{j = 1}^N {{w_{i,j}}{b_j}{x_{i - R,k}},\,\,\, R < i \le (P + 1)R} \\ & \sum\limits_{j = 1}^N {w_{i,j}}{b_{N + j}}{x_{i - (P + 1)R,k}}\,,\\ & \qquad\qquad\qquad\quad\ \ (P + 1)R < i \le (2P + 1)R \\ & {x_{i - R,k}} \equiv {x_{0,k}}\,,\,\,\,\,\,\,\,\, od (R) \end{aligned} \right.$

(2)

式(2)中， ${w_{i,j}}$ 为第j和第N+j个用户所乘的Walsh码序列， $b{}_j$ 和 $b{}_{N + j}$ 分别为第j和第N+j个用户的信息比特，由 ${s_{i,k}}$ 表达式计算平均比特能量 ${E_{{\rm{b,OMU - SR - DCSK}}}}$ 为

${E_{{\rm{b,OMU - SR - DCSK}}}} = {{(1 + 2NP)R{T_c}{\rm{E}}(x_{i,k}^2)} / {(2N)}}$

(3)

图3为OMU-SR-DCSK的接收机结构。解调端将接收信号 ${r_{i,k}}$ 延迟R，用于分离出前N个用户信息的参考信号；同理，延迟 $(P + 1)R$ 用于分离出后N个用户信息的参考信号；若要解调出信息比特 ${b_u}$ ( ${b_{N + u}}$ )，需将接收信号 ${r_{i,k}}$ 与对应的Walsh码 ${w_{i,u}}$ 相乘，再与参考信号进行P次相关运算，则第k帧第 $u(u = 1,2, ··· ,N)$ 个用户和第N+u个用户的相关器输出值 ${Z_u}$ 和 ${Z_{N + u}}$ 表示为

图 3 OMU-SR-DCSK系统接收机结构

下载: 全尺寸图片幻灯片

${Z_u} = \sum\limits_{p = 1}^P {\sum\limits_{i = 1}^R {{r_{i,k}}} } {r_{i - R,k}}{w_{i,u}}$

(4)

${Z_{N + u}} = \sum\limits_{p = 1}^P {\sum\limits_{i = 1}^R {{r_{i,k}}} } {r_{i - (P + 1)R,k}}{w_{i,u}}$

(5)

相关运算值 ${Z_u}$ ( ${Z_{N + u}}$ )经相关器输出后，再送入门限判决器进行判决，根据式(6)的判决准则，最终可恢复出信息信号 ${b_u}$ ( ${b_{N + u}}$ )。

${b_u} = \left\{ \begin{aligned} & + 1\,\,,\,\,\,\, {Z_u} \ge 0 \\ & - 1\,\,,\,\,\,\,\, {Z_u} < 0 \\ \end{aligned} \right., \,\,{b_{N + u}} = \left\{ \begin{aligned} & + 1\,,\,\,\,\,\,\, {Z_{N + u}} \ge 0 \\ & - 1\,,\,\,\,\,\, {Z_{N + u}} < 0 \end{aligned} \right.$

(6)

3. OMU-SR-DCSK系统性能分析

2阶Chebyshev映射作为最常用的产生混沌序列的混沌映射方程之一，且利用该映射产生的混沌序列拥有良好的数学统计特性。因此，OMU-SR-DCSK系统采用2阶Chebyshev映射产生混沌序列 ${x_{i,k}}$ ，并将其归一化。归一化后的混沌序列其均值为0，方差为1。

多径Rayleigh衰落信道更接近于实际应用中的传输信道，因此采用两径Rayleigh衰落信道模型作为OMU-SR-DCSK系统信道模型，两径Rayleigh衰落信道模型如图4所示。

图 4 两径Rayleigh衰落信道模型

下载: 全尺寸图片幻灯片

其中， ${n_{i,k}}$ 是均值为0，方差为 ${{{N_0}} / 2}$ 的加性高斯白噪声， $\tau$ 是两个独立信道之间的延迟， ${\alpha _1}$ 和 ${\alpha _2}$ 代表两个独立的、服从Rayleigh分布的信道随机变量，其概率密度函数表示为

$f(\alpha |\sigma ) = (\alpha /{\sigma ^2}){{\rm{e}}^{ - {\alpha ^2}/(2{\sigma ^2})}}\,\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\alpha > 0$

(7)

经图4中Rayleigh信道传输后，接收信号 ${r_{i,k}}$ 的表达式可表示为

${r_{i,k}} = {\alpha _1}{s_{i,k}} + {\alpha _2}{s_{i - \tau }}_{,k} + {n_{i,k}}$

(8)

由于第k帧第 $u$ 个和第 $N + u$ 个用户的解调方式相同，故以解调第k帧第 $u$ 个用户的信息比特为例，分析OMU-SR-DCSK系统理论BER公式的推导过程。则相关运算值 ${Z_u}$ 的表达式可进一步表示为

$\begin{split} {Z_u} =\,& \sum\limits_{p = 1}^P {\sum\limits_{i = 1}^R {({r_{i,k}}{r_{i - R,k}}{w_{i,u}})} } \\ =\,& \sum\limits_{p = 1}^P \sum\limits_{i = 1}^R (({\alpha _1}\sum\limits_{j = 1}^N {w_{i,j}}{b_j}{x_{i - R,k}} \\ & + {\alpha _2}\sum\limits_{j = 1}^N {{w_{i,j}}{b_j}{x_{i - R - \tau ,k}}} + {n_{i,P,k}})\\ & \cdot ({\alpha _1}{x_{i - R,k}} + {\alpha _2}{x_{i - R - \tau ,k}} + {n_{i - R,k}}){w_{i,u}} ) \\ =\,& A + B + C \end{split}$

(9)

$A = \sum\limits_{p = 1}^P {\sum\limits_{i = 1}^R {(\alpha _1^2{b_u}x_{i - R,k}^2 + \alpha _2^2{b_u}x_{i - R - \tau ,k}^2)} }$

(10)

$B = \sum\limits_{p = 1}^P {\sum\limits_{i = 1}^R {({n_{i,P,k}}{n_{i - R,k}}{w_{i,u}})} }$

(11)

$\begin{split} \; C =\,&\sum\limits_{p = 1}^P {\sum\limits_{i = 1}^R {({\alpha _1}{x_{i - R,k}}{n_{i,P,k}} } }\\ & +\alpha _1^2\sum\limits_{j = 1,j \ne u}^N {{w_{i,j}}{b_j}{x_{i - R,k}}{x_{i - R,k}}{w_{i,u}}} \\ &+ \alpha _2^2\sum\limits_{j = 1,j \ne u}^N {{w_{i,j}}{b_j}{x_{i - R - \tau ,k}}{x_{i - R - \tau ,k}}{w_{i,u}}} \\ & +{\alpha _2}{x_{i - R - \tau ,k}}{n_{i,P,k}} + {\alpha _1}{\alpha _2}\\ & \cdot \sum\limits_{j = 1,j \ne u}^N {{w_{i,j}}{b_j}{x_{i - R,k}}{x_{i - R - \tau ,k}}{w_{i,u}}}\\ &+ {\alpha _1}\sum\limits_{j = 1}^N {{w_{i,j}}{b_j}{x_{i - R,k}}{n_{i - R,k}}{w_{i,u}}} \\ & +{\alpha _2}\sum\limits_{j = 1}^N {{w_{i,j}}{b_j}{x_{i - R - \tau ,k}}{n_{i - R,k}}{w_{i,u}}}\\ &+ 2\,{\alpha _1}{\alpha _2}{b_u}{x_{i - R,k}}{x_{i - R - \tau ,k}}\\ & +{\alpha _1}{\alpha _2}\sum\limits_{j = 1,j \ne u}^N \!\!\!{{w_{i,j}}{b_j}{x_{i - R - \tau ,k}}{x_{i - R,k}}{w_{i,u}}} ) \!\! \end{split}$

(12)

假设Rayleigh衰落信道的延迟 $\tau$ 远远小于符号间隔，忽略不计 $\tau$ 的影响，有 $\displaystyle\sum\nolimits_{i = 1}^R {{x_{i,k}}{x_{i - \tau ,k}} \approx 0}$ ; ${n_{i,k}}$ 和 ${n_{i,p,k}}$ 具有相同的统计特性，都是均值为0、方差为 ${{{N_0}} / 2}$ 的高斯白噪声，其瞬时值服从高斯分布； ${n_{i,k}}$ 和 ${x_{i,k}}$ 之间相互独立，且当 $i \ne j$ 时， ${n_{i,k}}$ 和 ${n_{j,k}}$ 之间也相互独立；系统等概率发送二进制信息“+1”和“–1”。

基于以上假设，当扩频因子足够大时， ${Z_u}$ 近似服从高斯分布，故采用高斯近似法推导OMU-SR-DCSK在Rayleigh衰落信道和AWGN信道下的理论BER公式，对式(9)计算均值和方差得

${\rm{E}}[{Z_u}] = {\rm{E}}[A] + {\rm{E}}[B] + {\rm{E}}[C] = (\alpha _1^2 + \alpha _2^2)PR$

(13)

$\begin{split} \;{\rm{Var}} [{Z_u}] \,& = {\rm{Var}} [A] + {\rm{Var}} [B] + {\rm{Var}} [C] \\ & = \frac{1}{2}(\alpha _1^2 + \alpha _2^2)(NP + 1)PRN{}_0 + \frac{1}{4}PRN_0^2 \end{split}$

(14)

$\begin{split} \;{\rm{BER[}}{Z_u}{\rm{]}} =\,& \frac{1}{2}\Pr ({Z_u} < 0|{b_u} = + 1) \\ & + \frac{1}{2}\Pr ({Z_u} \ge 0|{b_u} = - 1) \\ =\,& \frac{1}{2}{\rm{erfc}} \left( {\frac{{\left| {{\rm{E}}[{Z_u}]} \right|}}{{\sqrt {2{\rm{Var}} [{Z_u}]} }}} \right) \end{split}$

(15)

其中， ${\rm{E}}[\centerdot ]$ 表示数学期望运算， ${\rm{Var}}[\centerdot ]$ 表示方差运算， ${\rm{erfc}}(x) = {{2\displaystyle\int_x^\infty {{{\rm{e}}^{ - {\mu ^2}}}} {\rm{d}}\mu } / {\sqrt{ \pi } }}$ 为互补误差函数。将式(13)和式(14)代入式(15)，计算第k帧第u个用户的BER公式为

$\begin{split} {\rm{BER}}({Z_u}) = \,& \frac{1}{2}{\rm{erfc}} \left( {\left[ {\frac{{\left| {{\rm{E}}[{Z_u}]} \right|}}{{\sqrt {2{\rm{Var}} [{Z_u}]} }}} \right]} \right)\,\,\\ =\,& \frac{1}{2}{\rm{erfc}} \left( \left[ \frac{{(NP + 1)(2NP + 1)}}{{2NP(\alpha _1^2 + \alpha _2^2)}}{{\left( {\frac{{{E_{\rm{b}}}}}{{{N_0}}}} \right)}^{ - 1}}\right.\right. \\ & \left.\left.+ \frac{{{{(2NP + 1)}^2}R}}{{8P{N^2}{{(\alpha _1^2 + \alpha _2^2)}^2}}}{{\left( {\frac{{{E_{\rm{b}}}}}{{{N_0}}}} \right)}^{ - 2}} \right]^{ - \frac{1}{2}} \right)\\[-20pt] \end{split}$

(16)

从而可得到OMU-SR-DCSK系统的瞬时BER公式为

$\begin{split} {\rm{BER}}({\alpha _1},{\alpha _2}) =\,& \frac{1}{2}{\rm{erfc}} \left( {\left[ {\frac{{\left| {{\rm{E}}[{Z_j}]} \right|}}{{\sqrt {2{\rm{Var}} [{Z_j}]} }}} \right]} \right)\,\,\\ =\,& \frac{1}{2}{\rm{erfc}} \left( \left[ \frac{{(NP + 1)(2NP + 1)}}{{2NP(\alpha _1^2 + \alpha _2^2)}}{{\left( {\frac{{{E_{\rm{b}}}}}{{{N_0}}}} \right)}^{ - 1}}\right.\right. \\ & \left.\left. + \frac{{{{(2NP + 1)}^2}R}}{{8P{N^2}{{(\alpha _1^2 + \alpha _2^2)}^2}}}{{\left( {\frac{{{E_{\rm{b}}}}}{{{N_0}}}} \right)}^{ - 2}} \right]^{ - \frac{1}{2}} \right) \end{split}$

(17)

令 ${\gamma _1} \!=\! \alpha _1^2({{{E_{\rm{b}}}} / {{N_0}}}),{\gamma _2} \!=\! \alpha _2^2({{{E_{\rm{b}}}} / {{N_0}}}),{\gamma _{\rm{b}}} \!=\! {\gamma _1} \!+ \! {\gamma _2}$ ，则式(17)可进一步化简为

$\begin{split} {\rm{BER}}({\gamma _{\rm{b}}}) =\,& \frac{1}{2}{\rm{erfc}}\Biggr( \Biggr[ \frac{{(NP + 1)(2NP + 1)}}{{2NP}}{{\left( {{\gamma _{\rm{b}}}} \right)}^{ - 1}} \\ & + \frac{{{{(2NP + 1)}^2}R}}{{8P{N^2}}}{{\left( {{\gamma _{\rm{b}}}} \right)}^{ - 2}} \Biggr]^{ - \frac{1}{2}} \Biggr)\\[-21pt] \end{split}$

(18)

令 ${\bar \gamma _1} \!=\! {\rm{E}}\left[ {{\gamma _1}} \right] \!=\! ({{{E_{\rm{b}}}} / {{N_0}}}){\rm{E}}\left[ {\alpha _1^2} \right],{\bar \gamma _2} \!=\! {\rm{E}}\left[ {{\gamma _2}} \right] \!=\! ({{E_{\rm{b}}}} / {{N_0}}){\rm{E}} \left[ {\alpha _2^2} \right]$ , ${\bar \gamma _1}$ 和 ${\bar \gamma _2}$ 服从式(19)的卡方分布

$f(\gamma )={{{{\rm{e}}}^{-{\gamma }/{{\bar{\gamma }}}\,}}}/{{\bar{\gamma }}}\,,\gamma \ge 0$

(19)

因此 ${\gamma _{\rm{b}}} = {\gamma _1} + {\gamma _2}$ 服从式(20)的卡方分布

$f({\gamma _{\rm{b}}}) = \left\{ \begin{aligned} & (\,{{{{\rm{e}}^{ - {{{\gamma _{\rm{b}}}} / {{{\bar \gamma }_1}}}}}{\gamma _{\rm{b}}})} / {\bar \gamma _1^2}}\,\,,\\ &\qquad {\rm{E}}[\alpha _1^2] = {\rm{E}}[\alpha _2^2] \\ & {{({{\rm{e}}^{ - {{{\gamma _{\rm{b}}}} / {{{\bar \gamma }_1}}}}} - {{\rm{e}}^{ - {{{\gamma _{\rm{b}}}} / {{{\bar \gamma }_2}}}}})\,\,} / {({{\bar \gamma }_1} - {\gamma _2})}}\\ &\qquad{\rm{E}}[\alpha _1^2] \ne {\rm{E}}[\alpha _2^2] \end{aligned} \right.$

(20)

由于信道参数是持续变化的，因此采用式(21)得到OMU-SR-DCSK在Rayleigh衰落信道下的BER公式为

$\begin{split} {\rm{BER}} =\,& \int_0^\infty {{\rm{BER}} \left( {{\gamma _{\rm{b}}}} \right)f({\gamma _{\rm{b}}}){\rm{d}}{\gamma _{\rm{b}}}\,} \\ =\,& \int_0^\infty \frac{1}{2}{\rm{erfc}} \left( \left[ \frac{{(NP + 1)(2NP + 1)}}{{2NP}}{{\left( {{\gamma _{\rm{b}}}} \right)}^{ - 1}} \right.\right.\\ & \left.\left. + \frac{{{{(2NP + 1)}^2}R}}{{8P{N^2}}}{{\left( {{\gamma _{\rm{b}}}} \right)}^{ - 2}} \right]^{ - \frac{1}{2}} \right)f({\gamma _{\rm{b}}}){\rm{d}}{\gamma _{\rm{b}}}\\[-21pt] \end{split}$

(21)

令式(17)中 ${\alpha _1}{\rm{ = }}1,\;{\alpha _2}{\rm{ = 0}}$ ，得到AWGN信道下的BER公式为

$\begin{split} {\rm{BER}} =\,& \frac{1}{2}{\rm{erfc}} \left( \left[ \frac{{(NP + 1)(2NP + 1)}}{{2NP}}{{\left( {\frac{{{E_{\rm{b}}}}}{{{N_0}}}} \right)}^{ - 1}} \right.\right.\\ & \left.\left.+ \frac{{{{(2NP + 1)}^2}R}}{{8P{N^2}}}{{\left( {\frac{{{E_{\rm{b}}}}}{{{N_0}}}} \right)}^{ - 2}} \right]^{ - \frac{1}{2}} \right)\\[-20pt] \end{split}$

(22)

4. OMU-SR-DCSK系统传输速率、能量效率和安全性分析

计算OMU-SR-DCSK和DCSK的传输速率 ${R_{{\rm{OMU \;-\; SR \;-\; DCSK}}}} \,=\, {{2N} / {((R \;+\; 2\beta )}}{T_{\rm{c}}})$ 和 ${R_{{\rm{DCSK}}}} = 1 / {(2\beta {T_{\rm{c}}})}$ ，平均比特能量 ${E_{{\rm{b,OMU - SR - DCSK}}}} = (1 + 2NP) {{R{T_{\rm{c}}}{\rm{E}}(x_{i,k}^2)} / {(2N)}}$ 和 ${E_{{\rm{b,DCSK}}}} = 2\beta {T_{\rm{c}}}{\rm{E}}(x_{i,k}^2)$ ，并分别将其代入式(23)和式(24)，得到OMU-SR-DCSK相比于DCSK的传输速率提升百分比 ${R_d}$ 和节省比特能量的百分比 ${E_B}$ 。

$\begin{split} {R_d}\,& = \frac{{{R_{{\rm{OMU - SR - DCSK}}}} - {R_{{\rm{DCSK}}}}}}{{{R_{{\rm{DCSK}}}}}} \times 100\%\\ & = \frac{{4N\beta - (2\beta + R)}}{{2\beta + R}} \times 100\% \end{split}$

(23)

$\begin{split} {E_B} \,& = \frac{{{E_{{\rm{b}},{\rm{DCSK}}}} - {E_{{\rm{b,OMU {\text{-}} SR {\text{-}} DCSK}}}}}}{{{E_{{\rm{b,DCSK}}}}}} \times 100\% \\ & = \frac{{4N\beta - (1 + 2NP)}R}{{4N\beta}} \times 100\% \end{split}$

(24)

图5和图6中分别分析了 $[P,N] = [4,2],[4,4]$ 时， ${R_d}$ 和 ${E_B}$ 的曲线。曲线表明：OMU-SR-DCSK相比于DCSK，极大程度上提升了传输速率，节约了比特能量。从式(23)和式(24)可以看出：当 $R = \beta$ 时，传输速率提高百分比 ${R_d}$ 只与用户数2N有关，比特能量节约百分比 ${E_B}$ 只与用户数2N和重复次数P有关。

图 5 传输速率提升百分比

${R_d}$

下载: 全尺寸图片幻灯片

图 6 比特能量节省百分比

${E_B}$

下载: 全尺寸图片幻灯片

图7和图8分别为DCSK和OMU-SR-DCSK的平方幅度谱。图7中，在归一化的比特频率为奇数时，DCSK的平方幅度为零，这是由于DCSK的信息信号只与参考信号同相或反相，从而导致了DCSK的安全性很低。而OMU-SR-DCSK的信息信号是N个信号的加和，且其参考时隙和信息时隙不等长，从图8中也可以发现，OMU-SR-DCSK的平方幅度谱具有类噪声性，证实了OMU-SR-DCSK的安全性很高。

图 7 DCSK的平方幅度谱

下载: 全尺寸图片幻灯片

图 8 OMU-SR-DCSK的平方幅度谱

下载: 全尺寸图片幻灯片

5. 系统仿真结果及分析

本节将在AWGN信道和两径Rayleigh衰落信道下对OMU-SR-DCSK系统进行仿真，验证理论BER公式推导的正确性，为确保仿真结果的准确性，仿真值均是在 ${10^6}$ 次仿真结果取平均值的前提下得到的。

5.1 AWGN信道下的误码性能分析

图9为各项参数取值 $[R,N,P] = [64,2,2], [128,2,2],[256,2,2]$ 时，系统BER随 ${{{E_{\rm{b}}}} / {{N_0}}}$ 变化的曲线，理论值和仿真值的良好契合验证了理论BER公式推导的准确无误性。图中显示 $R{\rm{ = }}64$ 时系统BER明显优于 $R{\rm{ = }}128$ 时的BER，这是由于R的增加导致信号间干扰增多，从而导致系统误码性能恶化。

图 9 R不同时BER随

${{{E_{\rm{b}}}} / {{N_0}}}$ 变化的曲线

下载: 全尺寸图片幻灯片

图10为 $[R,N,P] = [128,1,4], [128,2,4], [128,4,4]$ 时，系统BER随 ${{{E_{\rm{b}}}} / {{N_0}}}$ 变化的曲线。R和 $P$ 一定，在 ${{{E_{\rm{b}}}} / {{N_0}}} \le 10{\rm{dB}}$ 的情况下，不同N值对应的BER值基本吻合，而当 ${{{E_{\rm{b}}}} / {{N_0}}} > 12{\rm{dB}}$ 时，BER随着N的增加而增加。据此可见： ${{{E_{\rm{b}}}} / {{N_0}}}$ 较低的情况下，用户数变化不足以影响BER，此时扩频因子和重复次数为主要决定因素，而 ${{{E_{\rm{b}}}} / {{N_0}}}$ 较高的情况下，用户数成为误码性能恶化的主要影响因素。

图 10 N不同时BER随

${{{E_{\rm{b}}}} / {{N_0}}}$ 变化的曲线

下载: 全尺寸图片幻灯片

图11为 $[R,N,P] = [128,4,1], [128,4,2], [128,4,4]$ 时，系统BER随 ${{{E_{\rm{b}}}} / {{N_0}}}$ 变化的曲线。R和N一定，当 ${{{E_{\rm{b}}}} / {{N_0}}} \le 6{\rm{dB}}$ 时，不同 $P$ 值对应的BER值基本吻合，而当 ${{{E_{\rm{b}}}} / {{N_0}}} > 7{\rm{dB}}$ 时，BER随着 $P$ 的增加而增加。与N变化对BER的影响类似，在 ${{{E_{\rm{b}}}} / {{N_0}}}$ 较低的情况下， $P$ 值变化对误码性能的影响微乎其微，扩频因子和用户数为主要决定因素，而在 ${{{E_{\rm{b}}}} / {{N_0}}}$ 大于某个定值时，误码性能随着 $P$ 值的增加呈现恶化的趋势。区别于N值变化对系统误码性能影响的是：重复次数的变化对系统误码性能的影响更为显著。

图 11 P不同时BER随

${{{E_{\rm{b}}}} / {{N_0}}}$ 变化的曲线

下载: 全尺寸图片幻灯片

图12和图13为 ${{{{E_{\rm{b}}}} / N}_0} = 10\,\,\,{\rm{dB}},14\,\,\,{\rm{dB}}$ , N和 $P$ 取不同数值时，系统BER随R变化的曲线。根据图中曲线可以发现： ${{{E_{\rm{b}}}} / {{N_0}}}$ 越大误码性能越佳，且当 ${{{E_{\rm{b}}}} / {{N_0}}}$ 一定时，系统误码性能随着R的增加呈现恶化的趋势，最后趋于一个定值，而P值变化会影响这一定值，N值变化却不会影响这一定值。

图 12

${{{E_{\rm{b}}}} / {{N_0}}},P$ 不同时BER随R变化的曲线

下载: 全尺寸图片幻灯片

图 13

${{{E_{\rm{b}}}} / {{N_0}}},N$ 不同时BER随R变化的曲线

下载: 全尺寸图片幻灯片

表1中对比了OMU-SR-DCSK, SRMR-DCSK, VHE-DCSK和MC-DCSK系统的传输速率和能量效率，假设这几种系统的 $\beta$ 都相等。与长参考系统VHE-DCSK和短参考系统SRMR-DCSK相比，OMU-SR-DCSK的能量效率和传输速率都较优，而与多用户并行传输系统MC-DCSK相比，OMU-SR-DCSK采用多用户串行传输的方法，其能量效率虽优于MC-DCSK，但传输速率却远低于MC-DCSK。

表 1 OMU-SR-DCSK, SRMR-DCSK, VHE-DCSK和MC-DCSK系统的能量效率及传输速率

系统名称	传输速率( ${R_B}$ )	能量效率( ${E_\eta }$ )
OMU-SR-DCSK	${{2N} / {(R + 2\beta )}}$	${{2N\beta } / {(R + 2N\beta )}}$
SRMR-DCSK	${N / {(R + \beta )}}$	${{N\beta } / {(R + N\beta )}}$
VHE-DCSK	${N / {(2\beta }})$	${N / {(1 + N)}}$
MC-DCSK	${N / \beta }$	${N / {(1 + N)}}$

下载: 导出CSV

| 显示表格

为进一步分析表1中对比的几种系统的误码性能，图14中对比了AWGN信道下这几种系统的BER曲线。假设所有系统传输的信息比特数都相等，且 $\beta$ 也相等。观察图中BER曲线，当 ${{{E_{\rm{b}}}} / {{N_0}}} \le 11\;{\rm{dB}}$ 时，OMU-SR-DCSK, MC-DCSK和SRMR-DCSK的误码率基本相等，且都优于VHE-DCSK的误码率。但当 ${{{E_{\rm{b}}}} / {{N_0}}} > 11{\rm{dB}}$ 时，MC-DCSK的误码性能最优，其次是OMU-SR-DCSK。虽然OMU-SR-DCSK的误码性能差于多用户并行传输系统，但是相比于其他两种多用户串行传输系统，其误码性能较优。

图 14 AWNG信道下不同系统间误码性能对比

下载: 全尺寸图片幻灯片

5.2 两径Rayleigh衰落信道下的误码性能分析

本小节将在两径Rayleigh衰落信道下分析了OMU-SR-DCSK的误码性能。图15为R不同时，两种不同增益情况下的OMU-SR-DCSK系统BER曲线，其中，情况1为等增益情况，平均信道增益取值为： ${\rm{E}}\left[ {|{\alpha _1}{|^2}} \right] = {\rm{E}}\left[ {|{\alpha _2}{|^2}} \right] = {1 / 2}$ ，情况2为非等增益的情况，平均信道增益取值为： ${\rm{E}}\left[ {|{\alpha _1}{|^2}} \right] = {1 / 5}, {\rm{E}}\left[ {|{\alpha _2}{|^2}} \right] = {4 / 5}$ 。与AWGN信道下仿真类似，BER随着R增大而增大，且等增益情况下系统误码性能总是优于非等增益情况下的误码性能。

图 15 OMU-SR-DCSK系统在两种增益下的性能比较

下载: 全尺寸图片幻灯片

图16中对比了表1中几种系统的误码性能。当 ${{{E_{\rm{b}}}} / {{N_0}}}$ 较小时，OMU-SR-DCSK和SRMR-DCSK的误码率基本相等，都略优于MC-DCSK。但随着信噪比的增加，MC-DCSK的误码率逐渐降低，最后都优于其他几种系统，与AWGN信道下的对比结果一致，相比于其他两种多用户串行传输系统，OMU-SR-DCSK的误码性能最优。

图 16 不同系统在等增益情况下的性能比较

下载: 全尺寸图片幻灯片

6. 结束语

本文提出的OMU-SR-DCSK缩短了参考信号的长度，虽然会造成信噪比降低，从而影响系统的误码性能，但同时也提升了系统的传输速率、能量效率和安全性。此外，通过引入构造简单的Walsh码消除了用户间干扰，改善了OMU-SR-DCSK的误码性能，弥补了信噪比降低对系统误码性能造成的影响。通过仿真验证了OMU-SR-DCSK在传输速率和能量效率方面的优势，从而为其应用于多用户串行传输系统提供了理论依据。本文只分析了两路延迟线的情况，后续可扩展为M条延迟线，更大程度上提升系统的传输速率和能量效率；此外，将OMU-SR-DCSK与多载波技术结合，实现多用户并行传输也是后续需要研究的内容。

图 1 基于MRAM的图计算存内加速架构

下载: 全尺寸图片幻灯片

图 2 基于位逻辑运算优化实现单源最短路径

下载: 全尺寸图片幻灯片

图 3 基于位逻辑运算优化实现链路预测算法

下载: 全尺寸图片幻灯片

图 4 图计算存内加速架构实现与CPU实现的能耗标准化结果对比

下载: 全尺寸图片幻灯片

表 1 图算法存内计算优化模型

图计算步骤	边计算		社区发现		结构预测
图计算步骤	连通分量计算^[15]	单源最短路径	三角形计数^[12]	K-core	链路预测
目标定位	逻辑操作(AND)	逻辑操作(AND)	Scan(A[i][j]=1)	Scan(每行)	行选择
属性汇聚	逻辑操作(OR)	加法	逻辑操作(AND)	位计数(Bitcount)	逻辑操作(AND/OR)
计算更新	Bitcount比较	比较	Bitcount	比较删除顶点	Bitcount除法

下载: 导出CSV

表 2 MTJ关键参数

参数	值	参数	值
磁性隧道结表面长度	40 nm	隧道磁电阻	100%
磁性隧道结表面宽度	40 nm	饱和场	10⁶ A/m
自旋霍尔角	0.3	吉尔伯特阻尼常数	0.03
磁性隧道结电阻面积乘积	10^–12 Ω·m²	垂直磁各向异性	4.5×10⁵ A/m
氧化物阻挡层厚度	0.82 nm	温度	300 K

下载: 导出CSV

表 3 图计算存内加速架构实现与CPU实现速度对比(s)

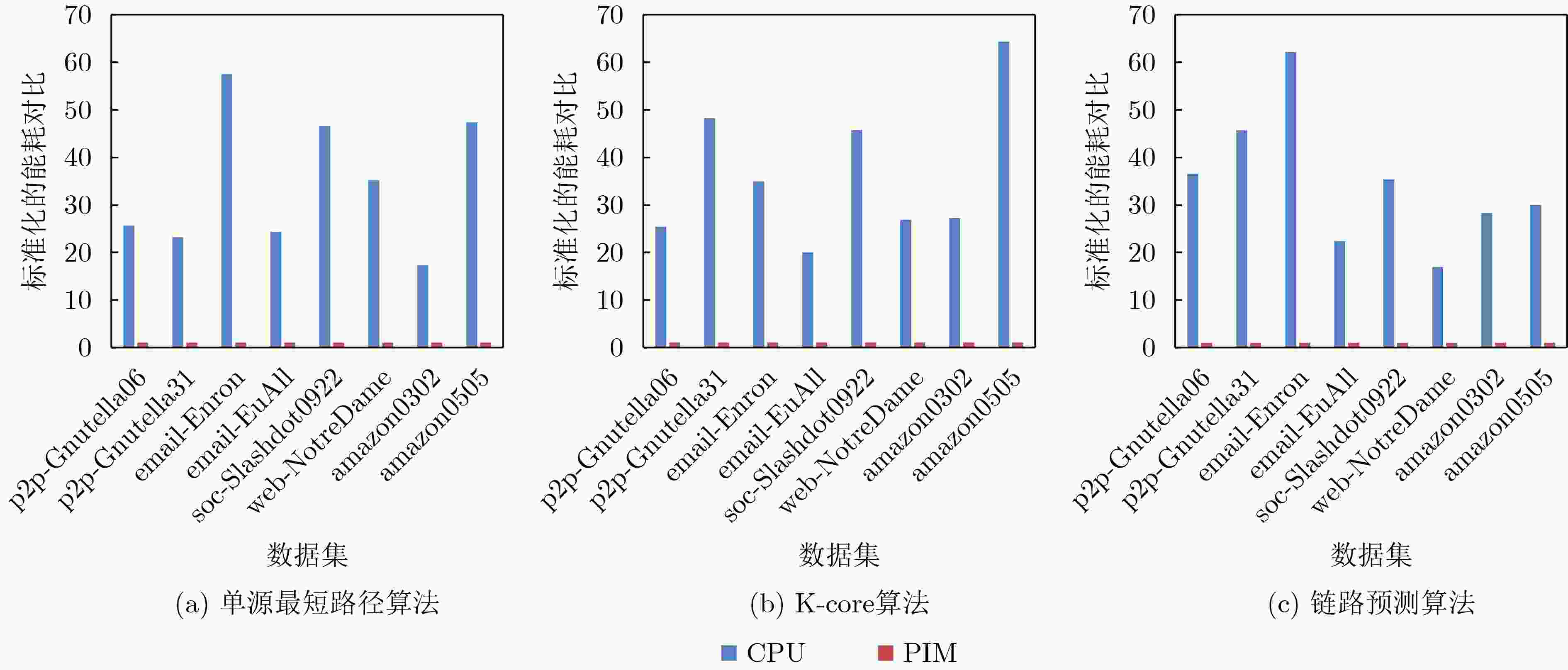
图数据集	单源最短路径		K-core		链路预测
图数据集	CPU	PIM	CPU	PIM	CPU	PIM
p2p-Gnutella06	0.063	0.0014	0.187	0.006	0.001	0.00012
p2p-Gnutella31	1.187	0.021	1.084	0.031	0.002	0.00016
email-Enron	2.972	0.071	1.383	0.056	0.001	0.00010
email-EuAll	2.826	0.081	3.832	0.193	0.003	0.00041
soc-Slashdot0922	10.989	0.203	10.137	0.241	0.002	0.00017
web-NotreDame	12.567	0.184	43.975	0.754	0.005	0.00037
amazon0302	17.837	0.329	14.392	0.381	0.002	0.00013
amazon0505	38.608	0.565	50.632	1.649	0.003	0.00043

下载: 导出CSV

参考文献(17)

[1]	CHI Ping, LI Shuangchen, XU Cong, et al. PRIME: A novel processing-in-memory architecture for neural network computation in ReRAM-based main memory[J]. ACM SIGARCH Computer Architecture News, 2016, 44(3): 27–39. doi: 10.1145/3007787.3001140
[2]	OZDAL M M, YESIL S, KIM T, et al. Energy efficient architecture for graph analytics accelerators[J]. ACM SIGARCH Computer Architecture News, 2016, 44(3): 166–177. doi: 10.1145/3007787.3001155
[3]	HAM T J, WU Lisa, SUNDARAM N, et al. Graphicionado: A high-performance and energy-efficient accelerator for graph analytics[C]. 2016 49th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO), Taipei, China, 2016: 1–13.
[4]	KYROLA A, BLELLOCH G, and GUESTRIN C. GraphChi: Large-scale graph computation on just a PC[C]. Proceedings of the 10th USENIX conference on Operating Systems Design and Implementation, Hollywood, USA, 2012: 31–46.
[5]	LIANG Shengwen, WANG Ying, LIU Cheng, et al. EnGN: A high-throughput and energy-efficient accelerator for large graph neural networks[J]. IEEE Transactions on Computers, 2021, 70(9): 1511–1525. doi: 10.1109/TC.2020.3014632
[6]	DAI Guohao, HUANG Tianhao, CHI Yuze, et al. GraphH: A processing-in-memory architecture for large-scale graph processing[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2018, 38(4): 640–653. doi: 10.1109/TCAD.2018.2821565
[7]	BEAMER S, ASANOVIC K, and PATTERSON D. Locality exists in graph processing: Workload characterization on an ivy bridge server[C]. 2015 IEEE International Symposium on Workload Characterization, Atlanta, USA, 2015: 56–65.
[8]	WANG Mengxing, CAI Wenlong, ZHU Daoqian, et al. Field-free switching of a perpendicular magnetic tunnel junction through the interplay of spin-orbit and spin-transfer torques[J]. Nature Electronics, 2018, 1(11): 582–588. doi: 10.1038/s41928-018-0160-7
[9]	GUO Zongxia, YIN Jialiang, BAI Yue, et al. Spintronics for energy-efficient computing: An overview and outlook[J]. Proceedings of the IEEE, 2021, 109(8): 1398–1417. doi: 10.1109/JPROC.2021.3084997
[10]	JAIN S, RANJAN A, ROY K, et al. Computing in memory with spin-transfer torque magnetic RAM[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2018, 26(3): 470–483. doi: 10.1109/TVLSI.2017.2776954
[11]	ANGIZI S, SUN Jiao, ZHANG Wei, et al. GraphS: A graph processing accelerator leveraging SOT-MRAM[C]. 2019 Design, Automation & Test in Europe Conference & Exhibition (DATE), Florence, Italy, 2019: 378–383.
[12]	WANG Xueyan, YANG Jianlei, ZHAO Yinglin, et al. Triangle counting accelerations: From algorithm to in-memory computing architecture[J]. IEEE Transactions on Computers, 2022, 71(10): 2462–2472. doi: 10.1109/TC.2021.3131049
[13]	LI Shuangchen, XU Cong, ZOU Qiaosha, et al. Pinatubo: A processing-in-memory architecture for bulk bitwise operations in emerging non-volatile memories[C]. The 53rd ACM/EDAC/IEEE Design Automation Conference, Austin, USA, 2016: 1–6.
[14]	HAN Lei, SHEN Zhaoyan, LIU Duo, et al. A novel ReRAM-based processing-in-memory architecture for graph traversal[J]. ACM Transactions on Storage, 2018, 14(1): 9. doi: 10.1145/3177916
[15]	CHEN Xuhang, WANG Xueyan, JIA Xiaotao, et al. Accelerating graph-connected component computation with emerging processing-in-memory architecture[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2022, 41(12): 5333–5342. doi: 10.1109/TCAD.2022.3163628
[16]	PEROZZI B, AL-RFOU R, and SKIENA S. DeepWalk: Online learning of social representations[C]. The 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, USA, 2014: 701–710.
[17]	LESKOVEC J and KREVL A. SNAP Datasets: Stanford large network dataset collection[EB/OL]. http://snap.stanford.edu/data, 2014.

施引文献

资源附件(0)

访问统计

图(4) / 表(3)

计量

文章访问数: 505
HTML全文浏览量: 235
PDF下载量: 95
被引次数: 0

1. 引言
2. OMU-SR-DCSK系统原理
3. OMU-SR-DCSK系统性能分析
4. OMU-SR-DCSK系统传输速率、能量效率和安全性分析
5. 系统仿真结果及分析
5.1 AWGN信道下的误码性能分析
5.2 两径Rayleigh衰落信道下的误码性能分析
6. 结束语

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

面向自旋存内计算架构的图算法优化设计

doi: 10.11999/JEIT230371

通讯作者:
赵巍胜　weisheng.zhao@buaa.edu.cn

计量

Graph Algorithm Optimization for Spintronics-based In-memory Computing Architecture

1. 引言

2. OMU-SR-DCSK系统原理

3. OMU-SR-DCSK系统性能分析

4. OMU-SR-DCSK系统传输速率、能量效率和安全性分析

5. 系统仿真结果及分析

5.1 AWGN信道下的误码性能分析

5.2 两径Rayleigh衰落信道下的误码性能分析

6. 结束语

计量

目录

1. 引言

2. OMU-SR-DCSK系统原理

3. OMU-SR-DCSK系统性能分析

4. OMU-SR-DCSK系统传输速率、能量效率和安全性分析

5. 系统仿真结果及分析

5.1 AWGN信道下的误码性能分析

5.2 两径Rayleigh衰落信道下的误码性能分析

6. 结束语

留言板

面向自旋存内计算架构的图算法优化设计

doi: 10.11999/JEIT230371

通讯作者: 赵巍胜 weisheng.zhao@buaa.edu.cn

计量

出版历程

Graph Algorithm Optimization for Spintronics-based In-memory Computing Architecture

1. 引言

2. OMU-SR-DCSK系统原理

3. OMU-SR-DCSK系统性能分析

4. OMU-SR-DCSK系统传输速率、能量效率和安全性分析

5. 系统仿真结果及分析

5.1 AWGN信道下的误码性能分析

5.2 两径Rayleigh衰落信道下的误码性能分析

6. 结束语

计量

出版历程

目录

1. 引言

2. OMU-SR-DCSK系统原理

3. OMU-SR-DCSK系统性能分析

4. OMU-SR-DCSK系统传输速率、能量效率和安全性分析

5. 系统仿真结果及分析

5.1 AWGN信道下的误码性能分析

5.2 两径Rayleigh衰落信道下的误码性能分析

6. 结束语

通讯作者:
赵巍胜　weisheng.zhao@buaa.edu.cn