M2PI: Processing-in-Memory Modular Computing Accelerator for Full Homomorphic Encryption
-
摘要: 全同态加密(FHE)由于其可以实现隐私数据的计算，大大提高了数据的安全性而在医疗诊断、云计算、机器学习等领域取得了广泛的关注。但是全同态密码高昂的计算代价阻碍了其广泛应用。即使经过算法和软件设计优化，FHE全同态加密中一个整数明文的密文数据规模可以达到56 MByte，端侧生成的密钥最大都会达到11 k Byte。密文以及密钥数据规模过大引起严重的计算和访存瓶颈。存内计算(PIM)是一个解决该问题的有效方案，其完全消除了内存墙的延迟和功耗问题，在端侧计算大规模数据时更具优势。利用存内计算加速全同态计算的工作已经被广泛研究，但是全同态加密端侧的执行过程由于耗时的模运算也面临着执行时间的瓶颈。该文分析了BFV方案加密、解密、密钥生成操作中各个关键算子的计算开销，发现模计算的计算开销平均占比达到了41%，延迟占比中访存占97%，因此，该文提出一个名为魔方派(M2PI)的基于静态随机存取存储器(SRAM)存内计算的模运算加速器设计。实验结果表明，该文所提加速器相比CPU中模计算有1.77倍的计算速度提升以及32.76倍能量的节省。Abstract: Fully Homomorphic Encryption (FHE) attracts emerging interests from the fields of medical diagnosis, cloud computing, machine learning, etc. because it can realize the calculation on encrypted data and improve significantly the security of private data in the cloud computing scenarios. However, the expensive computational cost of FHE prevents its wide application. Even after algorithm and software design optimization, the ciphertext data size of an integer plaintext in FHE reaches 56 MByte, and the secret key data size reaches 11 k Byte. The large size of ciphertext and key causes serious bottlenecks in computation and memory access. Processing-In-Memory (PIM) is an effective solution to this problem, which eliminates completely the efficiency and power problem of the memory wall, and enables the deployment of data-intensive of application to the edge side. The application of processing-in memory to accelerate fully homomorphic computing has been widely studied, but the execution of homomorphic encryption still faces the execution time bottleneck induced by time-consuming modular computing. The computational costs of various key operators in BFV encryption, decryption, and key generation operations are analyzed in this paper, and found that the average computational cost of modular computing reached 41%, with memory access accounting for 97%. A modular accelerator called Processing-In-Memory Modular(M2PI) based on Static Random-Access Memory(SRAM) array is proposed to optimize modular computing in full-homomorphic encryption. The experimental results show that the proposed work achieves 1.77 times speedup and 32.76 times energy saving compared to CPU.
-
算法 1 巴雷特模算法 计算：$r = c{\text{ mod }}q$ (q为n 位数，2n) 准备：模数q, 被模数c (1) $mu = {2^{2n}}/q$ (2) ${t_1} = c > > n - 1$ (3) ${t_2} = {t_1} \times mu$ (4) ${t_3} = {t_2} > > n + 1$ (5) $ {r_1} = c{\text{ }}\% {\text{ }}{2^{n + 1}} $ (6) ${r_2} = ({t_3} \times q){\text{ \% }}{{\text{2}}^{n + 1}}$ (7) $r = {r_1} - {r_2}$ 判断：$r > q/2?(r - q):r$ 返回 r 
下载: 导出CSV
算法 2 PIM中执行巴雷特模算法 计算：$r = c{\text{ mod }}q$ (q为n bit数) (1) $x = c > > n - 1$ (2) $a = x < < n - 1$ (3) $r = c - a$ 判断：$r > q/2?(r - q):r$ 返回 r
下载: 导出CSV
算法 3 PIM 中实现减法 输入：c(被减数)，$na$(${{a}}$对应的补码) 输出：${\text{Sub}}$(为最终减法结果) (1) $t = (((c + na)' + c)' + ((c + na)' + na)')'$ (2) $b = ((t + b)' + (c + na)')'$ (3) ${\text{Sub}} = ((t + (t + b)')' + (b + (t + b)')')'$
下载: 导出CSV
-
[1] RIVEST R L, SHAMIR A, and ADLEMAN L. A method for obtaining digital signatures and public-key cryptosystems[J]. Communications of the ACM, 1978, 21(2): 120–126. doi: 10.1145/359340.359342 [2] GENTRY C. Fully homomorphic encryption using ideal lattices[C]. The Forty-First Annual ACM Symposium on Theory of Computing, Bethesda, USA, 2009: 169–178. [3] FAN Junfeng and VERCAUTEREN F. Somewhat practical fully homomorphic encryption[R]. Paper 2012/144, 2012. [4] MARCOLLA C, SUCASAS V, MANZANO M, et al. Survey on fully homomorphic encryption, theory, and applications[J]. Proceedings of the IEEE, 2022, 110(10): 1572–1609. doi: 10.1109/JPROC.2022.3205665 [5] KIM S, KIM J, KIM M J, et al. BTS: An accelerator for bootstrappable fully homomorphic encryption[C]. The 49th Annual International Symposium on Computer Architecture, New York, USA, 2022: 711–725. [6] NEJATOLLAHI H, GUPTA S, IMANI M, et al. CryptoPIM: In-memory acceleration for lattice-based cryptographic hardware[C]. 2020 57th ACM/IEEE Design Automation Conference (DAC), San Francisco, USA, 2020: 1–6. [7] SAMARDZIC N, FELDMANN A, KRASTEV A, et al. F1: A fast and programmable accelerator for fully homomorphic encryption[C/OL]. MICRO-54: 54th Annual IEEE/ACM International Symposium on Microarchitecture, Greece, 2021: 238–252. [8] AHN J, HONG S, YOO S, et al. A scalable processing-in-memory accelerator for parallel graph processing[C]. The 42nd Annual International Symposium on Computer Architecture, Portland, USA, 2015: 105–117. [9] AGA S, JELOKA S, SUBRAMANIYAN A, et al. Compute caches[C]. 2017 IEEE International Symposium on High Performance Computer Architecture (HPCA), Austin, USA, 2017: 481–492. [10] CAO Zhengjun, WEI Ruizhong, and LIN Xiaodong. A fast modular reduction method[R]. Paper 2014/040, 2014. [11] CHEN Paiyu, PENG Xiaochen, and YU Shimeng. NeuroSim+: An integrated device-to-algorithm framework for benchmarking synaptic devices and array architectures[C]. 2017 IEEE International Electron Devices Meeting (IEDM), San Francisco, USA, 2017: 6.1. 1–6.1. 4. [12] HE Yuquan, QU Songyun, LIN Gangliang, et al. Processing-in-SRAM acceleration for ultra-low power visual 3D perception[C]. The 59th ACM/IEEE Design Automation Conference, San Francisco, USA, 2022: 295–300. [13] LI Dai, PAKALA A, and YANG Kaiyuan. MeNTT: A compact and efficient processing-in-memory number theoretic transform (NTT) accelerator[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2022, 30(5): 579–588. doi: 10.1109/TVLSI.2022.3151321 [14] REIS D, TAKESHITA J, JUNG T, et al. Computing-in-memory for performance and energy-efficient homomorphic encryption[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2020, 28(11): 2300–2313. doi: 10.1109/TVLSI.2020.3017595 [15] GUPTA S, CAMMAROTA R, and ROSING T Š. MemFHE: End-to-end computing with fully homomorphic encryption in memory[J]. ACM Transactions on Embedded Computing Systems, 2022, 30(5): 579−588. [16] Sarojaerabelli. py-FHE - A python library for fully homomorphic encryption[EB/OL]. https://github.com/sarojaerabelli/py-fhe, 2022. [17] ALBRECHT M, CHASE M, CHEN Hao, et al. Homomorphic encryption standard[M]. LAUTER K, DAI Wei, and LAINE K. Protecting Privacy Through Homomorphic Encryption. Cham: Springer, 2021: 31–62. [18] AKYEL K C, CHARLES H P, MOTTIN J, et al. DRC2: Dynamically reconfigurable computing circuit based on memory architecture[C]. 2016 IEEE International Conference on Rebooting Computing (ICRC), San Diego, USA, 2016: 1–8. [19] HASAN M, SAHA U K, HOSSAIN M S, et al. Low power design of a two bit mangitude comparator for high speed operation[C]. 2019 International Conference on Computer Communication and Informatics (ICCCI), Coimbatore, India, 2019: 1–4. [20] TALATI N, GUPTA S, MANE P, et al. Logic design within memristive memories using memristor-aided loGIC (MAGIC)[J]. IEEE Transactions on Nanotechnology, 2016, 15(4): 635–650. doi: 10.1109/TNANO.2016.2570248 [21] YANG Y, JEONG H, SONG S C, et al. Single bit-line 7T SRAM cell for near-threshold voltage operation with enhanced performance and energy in 14 nm FinFET technology[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2016, 63(7): 1023–1032. doi: 10.1109/TCSI.2016.2556118 -
图(11) / 表(4)
计量
- 文章访问数: 662
- HTML全文浏览量: 259
- PDF下载量: 119
- 被引次数: 0
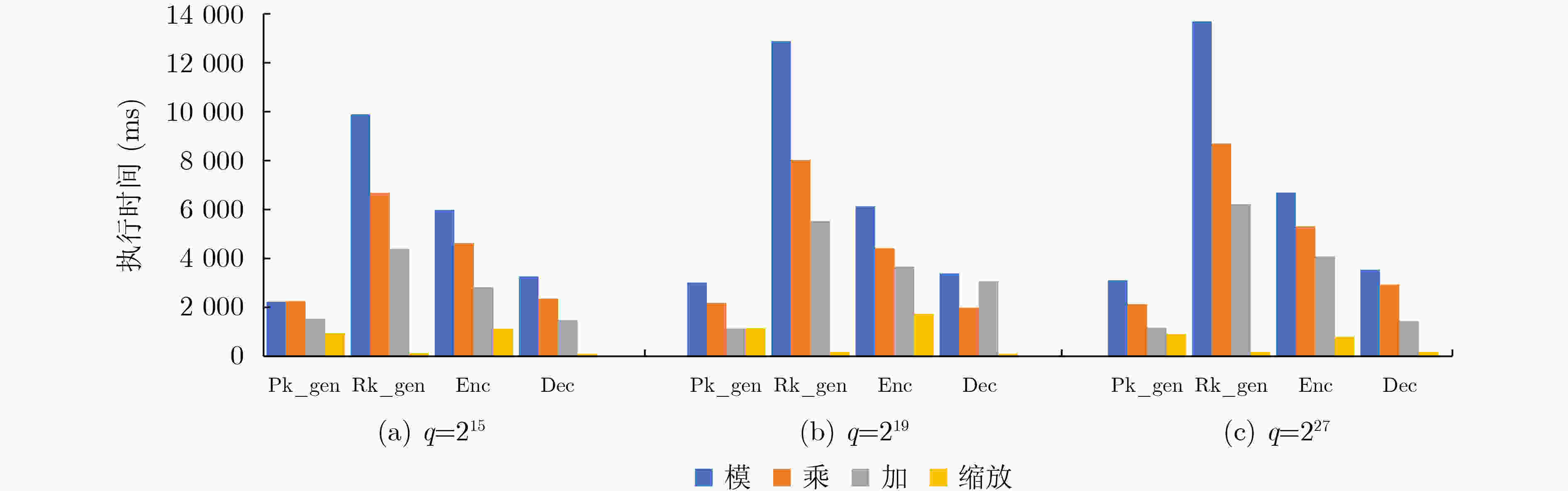
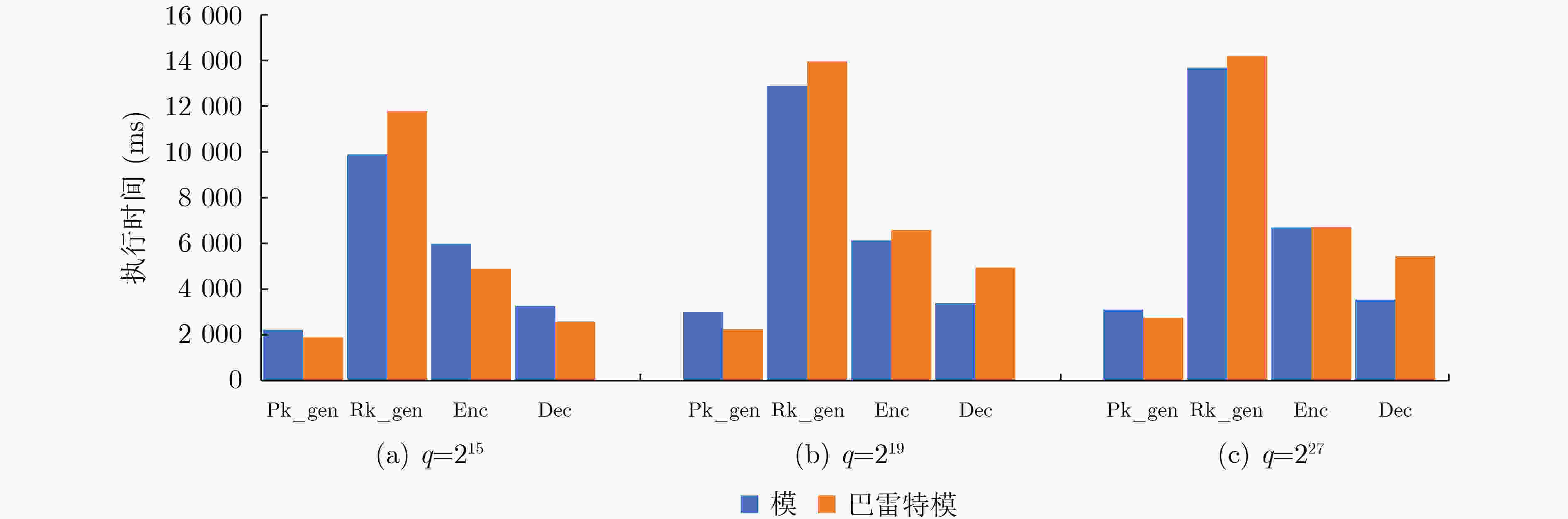
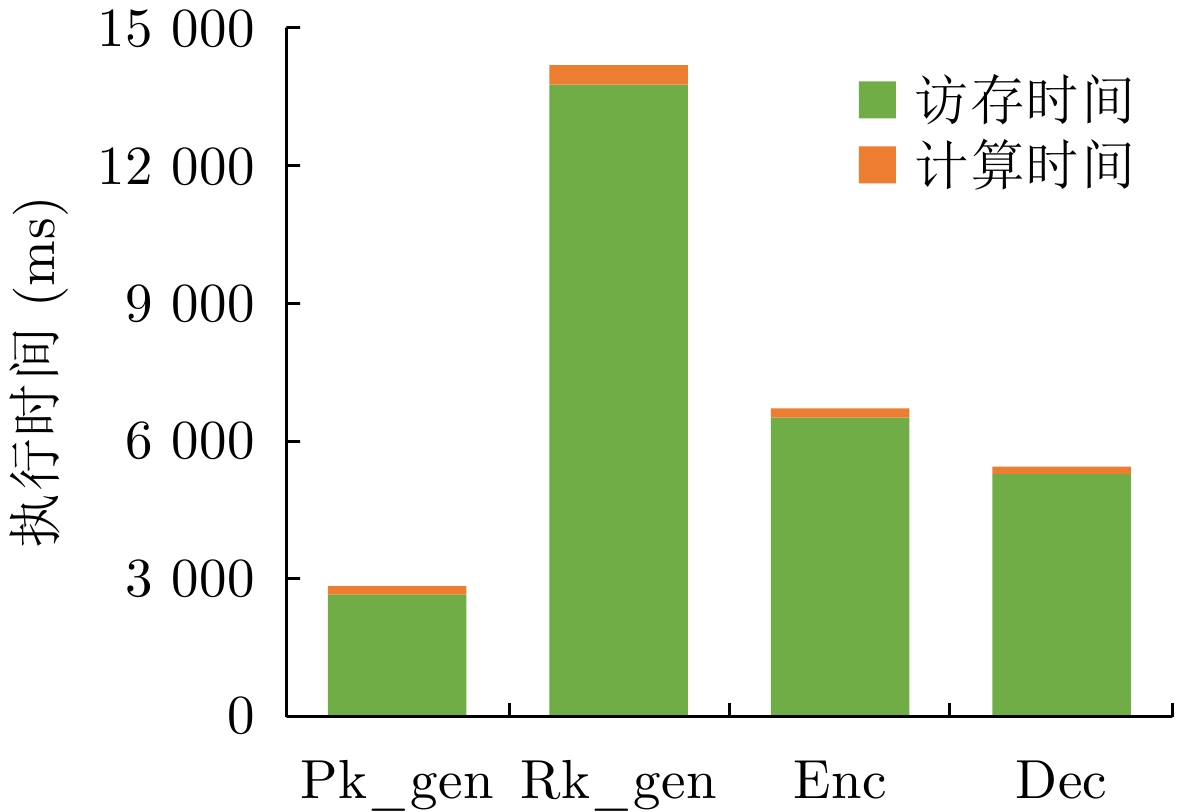
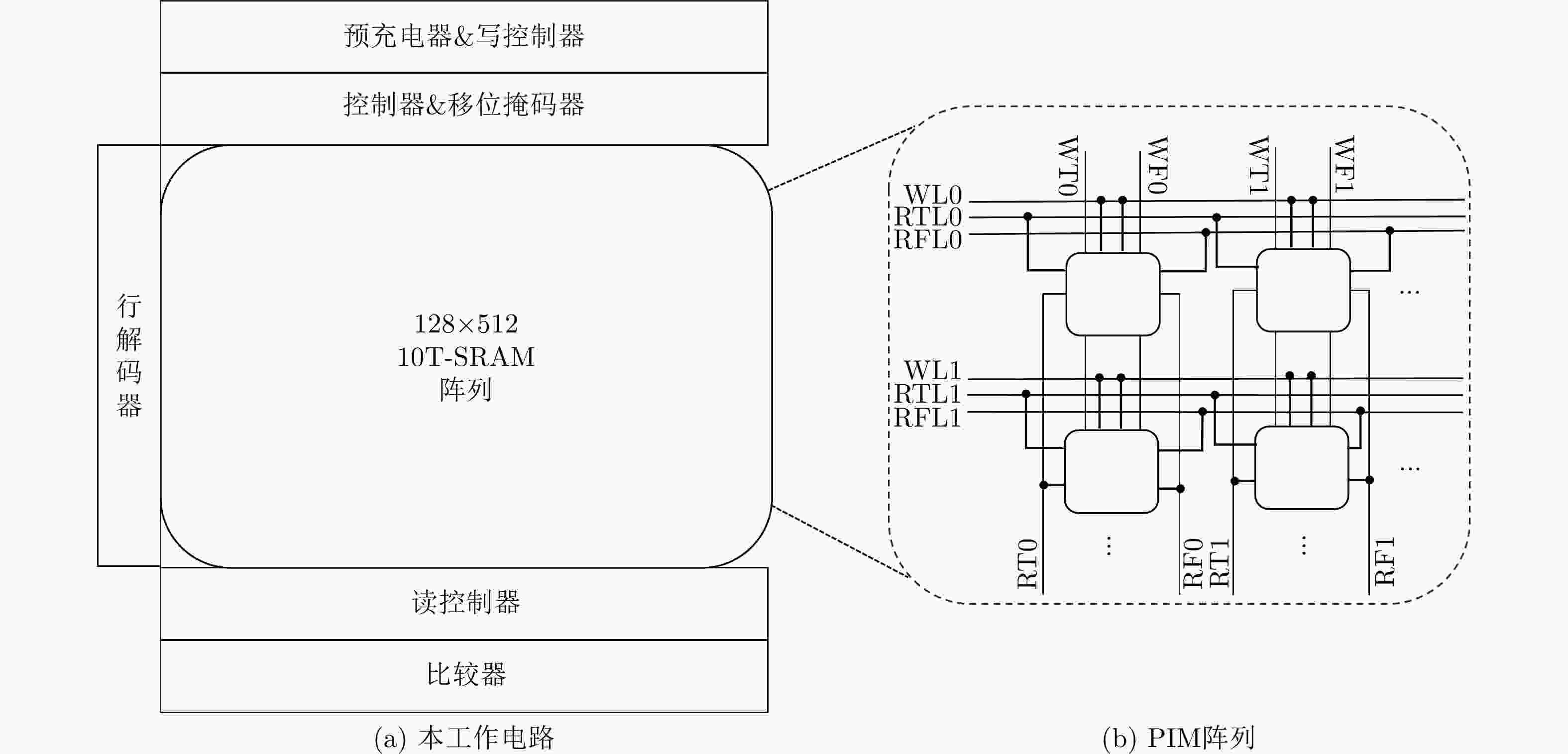
下载:
