Stereo Array Positioning Algorithm Based on Vector Projection
-
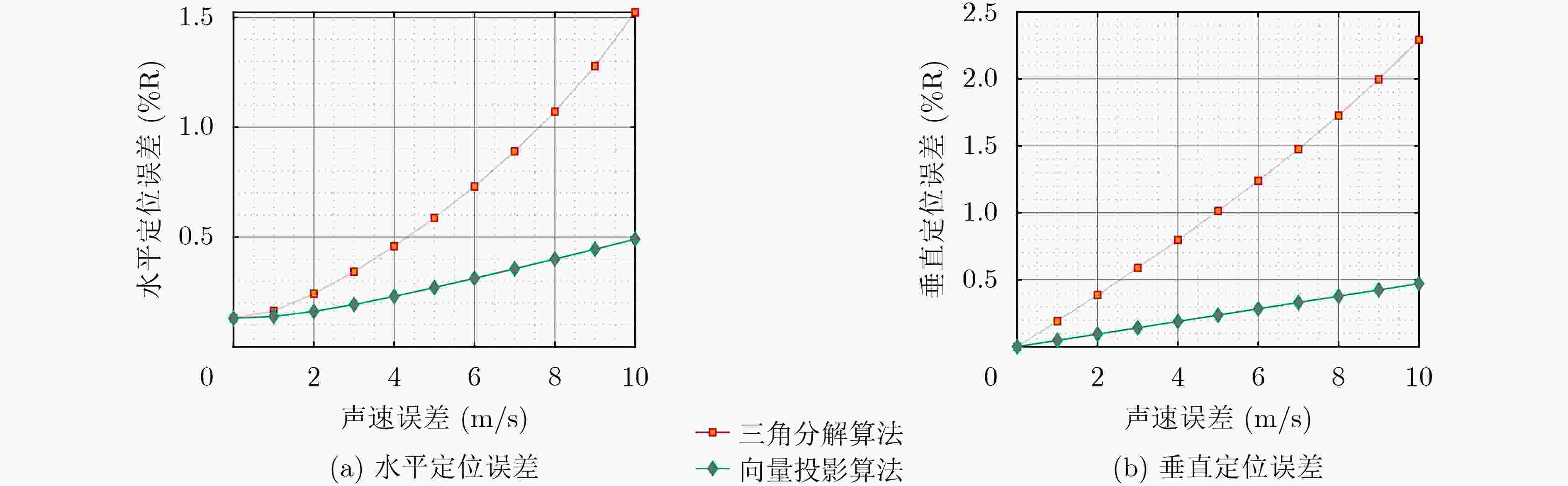
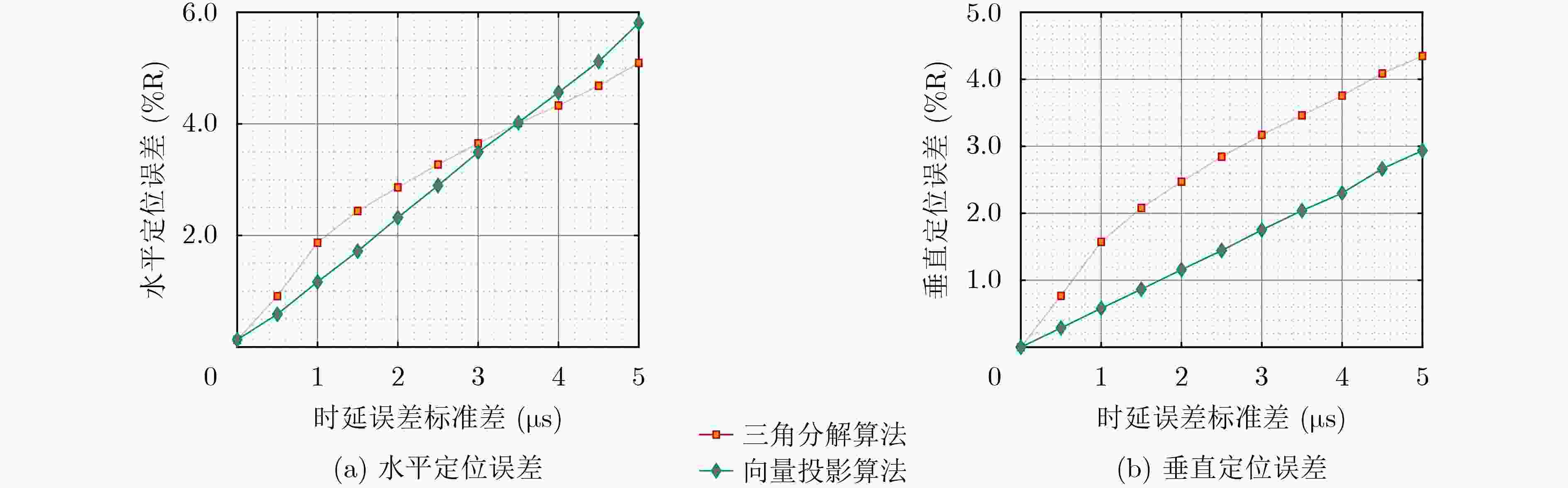
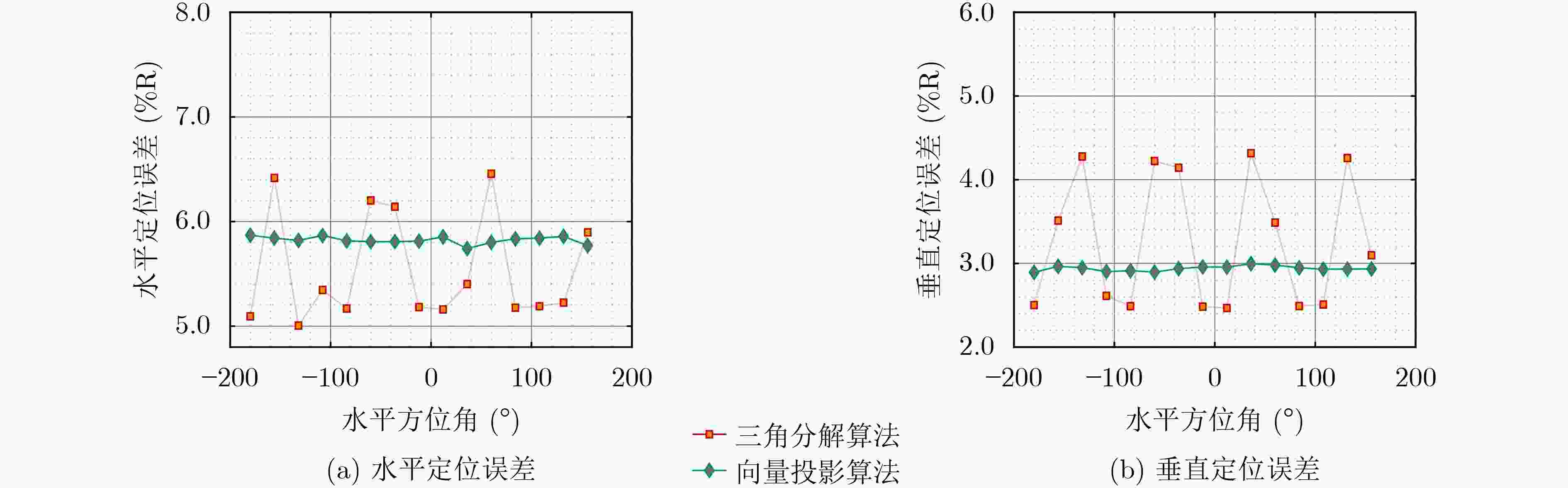
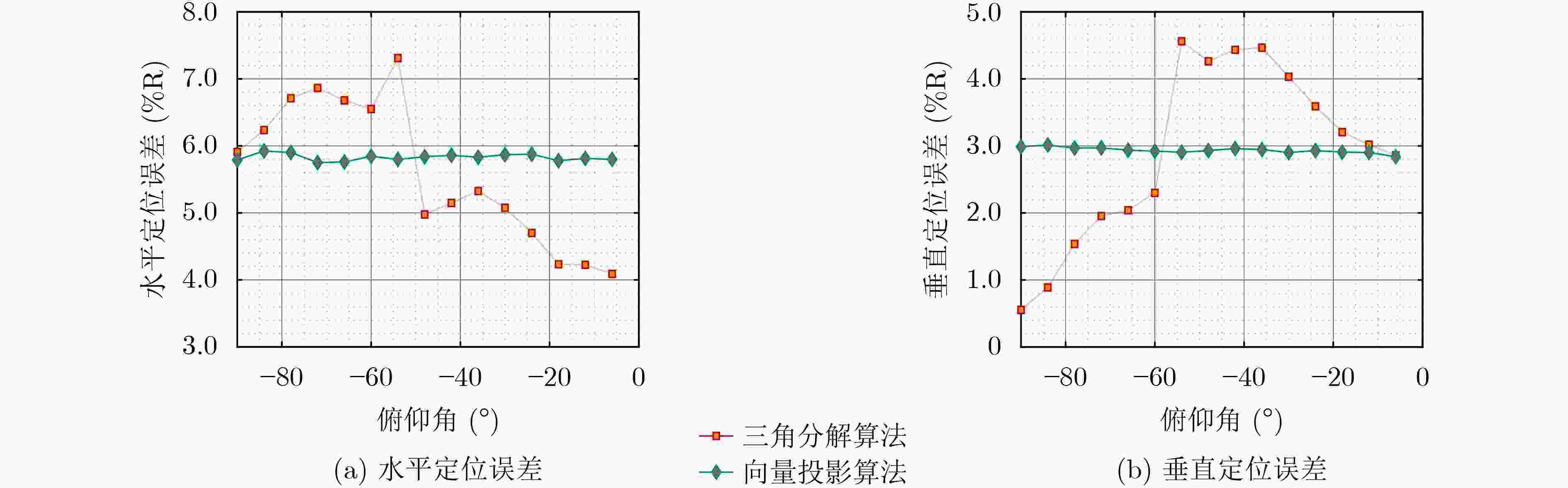
摘要: 传统适配立体阵型的超短基线定位算法计算量大、定位误差难以通过解析式精确表征。针对这些问题,该文提出基于向量投影的立体阵定位算法,从向量投影的角度构建立体阵中各基线向量与目标方位之间的观测方程,实现对传统算法定位模型的简化。该文算法通过求解线性方程组即可实现对目标方位的估计,时间复杂度远小于传统算法。此外,基于该文算法简洁的观测方程,给出了适配立体阵的定位误差精确解析表征。仿真结果表明,该文算法消耗的运算时间远小于传统算法,且定位误差变化规律与基于理论解析式得到的结论相符。湖试试验结果表明,该文算法的定位精度与传统算法几乎一致,且计算效率更高。Abstract: The traditional ultra-short baseline positioning algorithm for stereo arrays exhibits high computational complexity and struggles to accurately represent the positioning error through an explicit formula. To address these challenges, a stereo array positioning algorithm based on vector projection is proposed. The observation equations between the baseline vectors in the stereo array and the target bearing were constructed based on the vector projection theorem, simplifying the positioning model of the traditional algorithm. In the proposed algorithm, the target bearing is obtained by solving a system of linear equations, which results in lower time complexity. Additionally, an accurate analytical representation of the positioning error applicable to the stereo array is provided based on the concise observation equations of the proposed algorithm. The simulation results show that the computational time required by the proposed algorithm is significantly lower compared to the traditional algorithm, and the variation pattern of the positioning error is consistent with the conclusion drawn from the theoretical analysis. The experimental results further indicate that the proposed algorithm achieves almost the same positioning accuracy but higher computation efficiency comparable to the traditional algorithm.
-
Key words:
- Ultra-short baseline positioning /
- Stereo array /
- Vector projection
-
表 1 算法均方根误差及运行时间统计结果
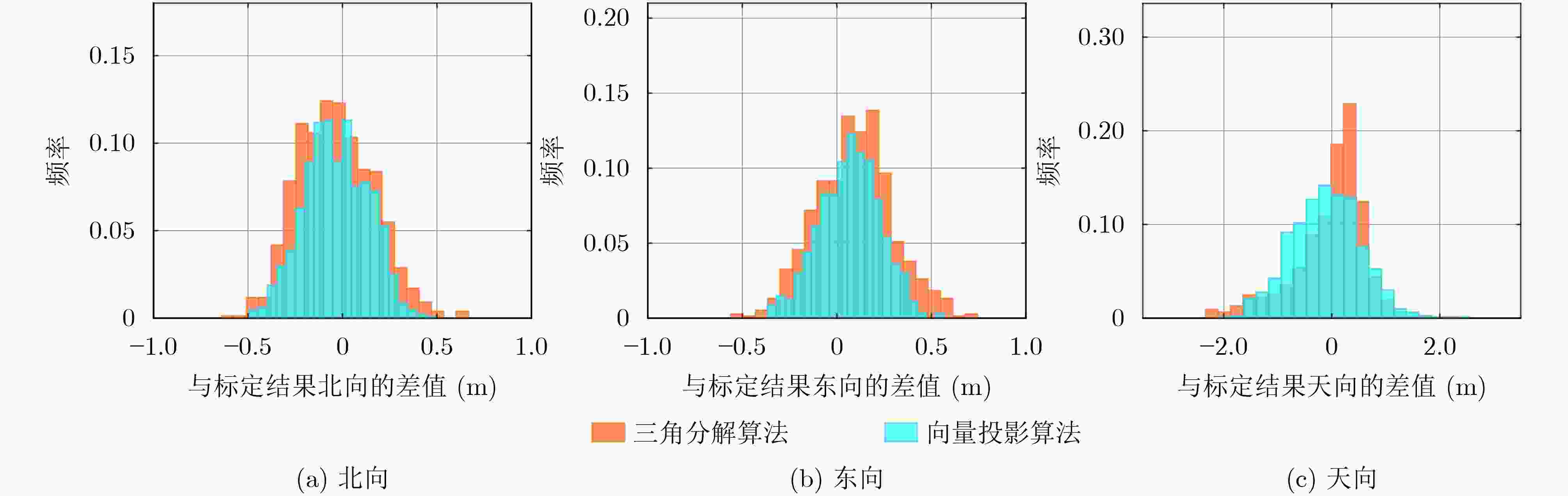
算法名称 北向均方根误差(m) 东向均方根误差(m) 天向均方根误差(m) 运行时间(s) 三角分解算法 0.2048 0.2244 0.6600 0.1225 向量投影算法 0.1714 0.1752 0.6561 0.0131 -
[1] 孙大军, 郑翠娥, 张居成, 等. 水声定位导航技术的发展与展望[J]. 中国科学院院刊, 2019, 34(3): 331–338. doi: 10.16418/j.issn.1000-3045.2019.03.011SUN Dajun, ZHENG Cuie, ZHANG Jucheng, et al. Development and prospect for underwater acoustic positioning and navigation technology[J]. Bulletin of Chinese Academy of Sciences, 2019, 34(3): 331–338. doi: 10.16418/j.issn.1000-3045.2019.03.011 [2] 张涛, 夏茂栋, 张佳宇, 等. 水下导航定位技术综述[J]. 全球定位系统, 2022, 47(4): 1–16. doi: 10.12265/j.gnss.2022094ZHANG Tao, XIA Maodong, ZHANG Jiayu, et al. Review of underwater navigation and positioning technology[J]. GNSS World of China, 2022, 47(4): 1–16. doi: 10.12265/j.gnss.2022094 [3] 郭晓明, 田甜. 基于四元阵的超短基线便携式定位设备定向算法[J]. 水下无人系统学报, 2022, 30(6): 794–800. doi: 10.11993/j.issn.2096-3920.2022-0006GUO Xiaoming and TIAN Tian. Ultra short baseline direction-finding algorithm based on quaternion stereo array for portable positioning equipment[J]. Journal of Unmanned Undersea Systems, 2022, 30(6): 794–800. doi: 10.11993/j.issn.2096-3920.2022-0006 [4] 张晓飞, 辛明真, 隋海琛, 等. 基于交互式多模型卡尔曼滤波的AUV超短基线跟踪算法[J]. 水下无人系统学报, 2022, 30(1): 29–36. doi: 10.11993/j.issn.2096-3920.2022.01.004ZHANG Xiaofei, XIN Mingzhen, SUI Haichen, et al. AUV ultra-short baseline tracking algorithm based on interactive multi-model Kalman filter[J]. Journal of Unmanned Undersea Systems, 2022, 30(1): 29–36. doi: 10.11993/j.issn.2096-3920.2022.01.004 [5] 李璇, 解禹. 水下定位导航系统展望[J]. 无人系统技术, 2022, 5(3): 79–86. doi: 10.19942/j.issn.2096-5915.2022.3.029LI Xuan and XIE Yu. Envision to the development of underwater position and navigation systems[J]. Unmanned Systems Technology, 2022, 5(3): 79–86. doi: 10.19942/j.issn.2096-5915.2022.3.029 [6] iXblue. USBL solution[EB/OL]. https://www.ixblue.com/maritime/subsea-positioning/usbl-solutions/, 2023. [7] Sonardyne. HPT 5000/7000[EB/OL]. https://www.sonardyne.com/products/hpt-5000-and-7000-usbl-positioning-transceiver/, 2023. [8] Kongsberg. CPAP - ROV positioning in long base line transponder array[EB/OL]. https://www.kongsberg.com/maritime/products/Acoustics-Positioning-and-Communication/transponders/cPAP, 2023. [9] 刘德铸, 郭晓明, 朱琳, 等. 一种微小型等边三元阵的超短基线定位方法[J]. 电声技术, 2022, 46(2): 93–97,106. doi: 10.16311/j.audioe.2022.02.023LIU Dezhu, GUO Xiaoming, ZHU Lin, et al. An ultra-short baseline location method based on miniature equilateral ternary array[J]. Audio Engineering, 2022, 46(2): 93–97,106. doi: 10.16311/j.audioe.2022.02.023 [10] 李伟嘉, 王振杰, 孙振, 等. 基于深度约束的超短基线声速改正方法[J]. 导航定位学报, 2022, 10(5): 40–45. doi: 10.3969/j.issn.2095-4999.2022.05.006LI Weijia, WANG Zhenjie, SUN Zhen, et al. An USBL sound velocity correction method based on depth constraint[J]. Journal of Navigation and Positioning, 2022, 10(5): 40–45. doi: 10.3969/j.issn.2095-4999.2022.05.006 [11] LI Xiang, LIU Xin, QU Long, et al. Three-dimensional ultra-short base line based underwater acoustical localization utilizing modified newton algorithm[J]. IEEE Access, 2021, 9: 80671–80681. doi: 10.1109/ACCESS.2021.3085304 [12] 郑恩明, 陈新华, 孙长瑜, 等. 一种四元超短基线阵实现高精度定位[J]. 应用声学, 2013, 32(1): 15–22. doi: 10.11684/j.issn.1000-310X.2013.01.003ZHENG Enming, CHEN Xinhua, SUN Changyu, et al. An innovation four-element array to achieve high-precision positioning of the Ultra-short baseline[J]. Journal of Applied Acoustics, 2013, 32(1): 15–22. doi: 10.11684/j.issn.1000-310X.2013.01.003 [13] 郑翠娥, 李琪, 孙大军, 等. 一种超短基线定位系统阵型的改进方法[J]. 中国海洋大学学报, 2009, 39(3): 505–508. doi: 10.3969/j.issn.1672-5174.2009.03.030ZHENG Cuie, LI Qi, SUN Dajun, et al. An improved measurement method for array design of USBL[J]. Periodical of Ocean University of China, 2009, 39(3): 505–508. doi: 10.3969/j.issn.1672-5174.2009.03.030 [14] DING Jie, SUN Dajun, and ZHENG Cuie. Underwater acoustic localization approach to an arbitrary distributed multi-element array[C]. OCEANS 2015 - MTS/IEEE Washington, USA, 2015: 1–5. [15] WANG Wei, ZHU Min, and YANG Bo. Positioning combination method of USBL using four-element stereo array[J]. Sensors, 2021, 21(22): 7722. doi: 10.3390/s21227722 [16] ARKHIPOV M. Utilizing Johnson solids for designing multielement USBL systems[J]. IEEE Journal of Oceanic Engineering, 2016, 41(4): 783–793. doi: 10.1109/JOE.2016.2540758 [17] 田坦. 声呐技术[M]. 2版. 哈尔滨: 哈尔滨工程大学出版社, 2010: 46–48.TIAN Tan. Sonar Technology[M]. 2nd ed. Harbin: Harbin Engineering University Press, 2010: 46–48. [18] CORMEN T H, LEISERSON C E, RIVEST R L, et al. Introduction to Algorithms[M]. 3rd ed. Cambridge: The MIT Press, 2009: 813–832. [19] SUN Dajun, DING Jie, ZHENG Cuie, et al. Array geometry calibration for underwater compact arrays[J]. Applied Acoustics, 2019, 145: 374–384. doi: 10.1016/j.apacoust.2018.10.004 [20] LIU Yixu, LU Xiushan, XUE Shuqiang, et al. A new underwater positioning model based on average sound speed[J]. The Journal of Navigation, 2021, 74(5): 1009–1025. doi: 10.1017/S0373463321000400 -





 下载:
下载:


 下载:
下载:
