脉冲神经网络权重量化方法与对抗鲁棒性分析

李莹; 李艳杰; 崔小欣; 倪庆龙; 周崟灏

doi:10.11999/JEIT230300

脉冲神经网络权重量化方法与对抗鲁棒性分析

doi: 10.11999/JEIT230300

李莹¹,
李艳杰^{1, 2},
崔小欣³,
倪庆龙^{1, 2},
周崟灏^1, ,

1.
中国科学院微电子研究所北京 100029
2.
中国科学院大学集成电路学院北京 100049
3.
北京大学集成电路学院北京 100087

基金项目: 科技创新2030重大项目(2022ZD0208700)

详细信息

作者简介:
李莹：女，博士，副研究员，研究方向为集成电路设计与验证、硬件安全

李艳杰：女，硕士生，研究方向为神经网络算法与安全

崔小欣：女，博士，研究员，研究方向为类脑芯片、信息处理、硬件安全

倪庆龙：男，硕士生，研究方向为神经网络算法与电路设计

周崟灏：男，硕士，高级工程师，研究方向为集成电路设计、硬件安全

通讯作者:
周崟灏　zhouyinhao@ime.ac.cn

中图分类号: TN918; TP183
计量
- 文章访问数: 525
- HTML全文浏览量: 312
- PDF下载量: 84
- 被引次数: 0
出版历程
- 收稿日期: 2023-04-19
- 修回日期: 2023-08-17
- 网络出版日期: 2023-08-23
- 刊出日期: 2023-09-27

Weight Quantization Method for Spiking Neural Networks and Analysis of Adversarial Robustness

LI Ying¹,
LI Yanjie^{1, 2},
CUI Xiaoxin³,
NI Qinglong^{1, 2},
ZHOU Yinhao^{1
, ,}

1.
Institute of Microelectronics, Chinese Academy of Sciences, Beijing 100029, China
2.
School of Integrated Circuits, University of Chinese Academy of Sciences, Beijing 100049, China
3.
School of Integrated Circuits, Peking University, Beijing 100087, China

Funds: STI 2030-Major Projects (2022ZD0208700)

摘要

摘要: 类脑芯片中的脉冲神经网络(SNNs)具有高稀疏性和低功耗的特点，在视觉分类任务中存在应用优势，但仍面临对抗攻击的威胁。现有研究缺乏对网络部署到硬件的量化过程中鲁棒性损失的度量方法。该文研究硬件映射阶段的SNN权重量化方法及其对抗鲁棒性。建立基于反向传播和替代梯度的监督训练算法，并在CIFAR-10数据集上生成快速梯度符号法(FGSM)对抗攻击样本。创新性地提出一种感知量化的权重量化方法，并建立与对抗攻击的训练与推理相融合的评估框架。实验结果表明，在VGG9网络下，直接编码对抗鲁棒性最差。在权重量化前后，4种编码和4种结构参数组合方式下，推理精度损失差与层间脉冲活动的平均变化幅度分别增大73.23%和51.5%。该文指出稀疏性因素对鲁棒性的影响相关度为：阈值增加大于权重量化bit降低大于稀疏编码，所提对抗鲁棒性分析框架与权重量化方法在PIcore类脑芯片中得到了硬件验证。
- 脉冲神经网络 /
- 权重量化 /
- 对抗鲁棒性 /
- 稀疏性 /
- 对抗攻击
Abstract: Spiking Neural Networks (SNNs) in neuromorphic chips have the advantages of high sparsity and low power consumption, which make them suitable for visual classification tasks. However, they are still vulnerable to adversarial attacks. Existing studies lack robustness metrics for the quantization process when deploying the network into hardware. The weight quantization method of SNNs during hardware mapping is studied and the adversarial robustness is analyzed in this paper. A supervised training algorithm based on backpropagation and alternative gradients is proposed, and one types of adversarial attack samples, Fast Gradient Sign Method (FGSM), on the CIFAR-10 dataset are generated. A perception quantization method and an evaluation framework that integrates adversarial training and inference are provided innovatively. Experimental results show that direct encoding leads to the worst adversarial robustness in the VGG9 network. The difference between the accuracy loss and inter-layer pulse activity change before and after weight quantization increases by 73.23% and 51.5%, respectively, for four encoding and four structural parameter combinations. The impact of sparsity factors on robustness is: threshold increase more than bit reduction in weight quantization more than sparse coding. The proposed analysis framework and weight quantization method have been proved on the PIcore neuromorphic chip.
- Spiking Neural Network (SNN) /
- Weight quantization /
- Adversarial robustness /
- Sparsity /
- Adversarial attack

HTML全文

图 1 链式求导法则在时间和空间上展开后的求导原理

下载: 全尺寸图片幻灯片

图 2 FGSM攻击原理

下载: 全尺寸图片幻灯片

图 3 量化前后不同组合方式下的脉冲活动

下载: 全尺寸图片幻灯片

图 4 量化后不同编码方式下的脉冲NSR

下载: 全尺寸图片幻灯片

图 5 PKU-NC64C 芯片

下载: 全尺寸图片幻灯片

算法1　加入感知量化算法的训练框架
(1) 输入：数据集T，epoch，攻击强度参数($\varepsilon $,k)Timestep，权重　　量化比特K，编码式，网络架构，攻击类型
(2) 加载：感知训练好的模型.pt文件
(3) 初始化：网络初始化，参数初始化，攻击模型初始化，量化　　初始化
(4) 损失函数，优化器选择
(5) 执行量化函数
(6) for T do:
(7) 　　采样 batch (x, y)
(8) 　目标模型的对抗攻击前向传播
(9) 　累计adv_loss
(10) 　攻击模型的对抗攻击前向传播
(11) 累计adv_loss
(12)restore函数
(13)计算最终的adv_loss

下载: 导出CSV

算法2　感知量化与对抗攻击融合的推理框架
(1) 输入：数据集训练集D，测试集T, epoch, Timestep，权重量　　化比特K，编码式，网络架构
(2) 初始化：网络初始化，参数初始化，量化初始化
(3) 损失函数，优化器选择
(4) for epoch do
(5) for D do:
(6) 　执行量化函数
(7) 　从D中采样 batch (x, y)
(8) 　网络前向传播
(9)　求单轮loss
(10) 训练loss更新
(11) 网络反向传播
(12) restore函数
(13) 调整学习率
(14) 执行量化函数
(15) for T do:
(16) 从T中采样 batch (x, y)
(17) 网络前向传播
(18) restore函数
(19) 测量推理精度
(20) 保存训练模型到pt文件

下载: 导出CSV

表 1 VGG5量化前后不同攻击强度下的推理精度损失(%)

组合参数		直接编码			速率编码			相位编码			延迟编码
组合参数		I	II	III	I	II	III	I	II	III	I	II	III
0.4,1.0,0.5	Q₁	7.41	13,42	34,52	3.21	8.04	13,81	2.32	5.56	16.33	1.82	7.81	25.88
0.4,1.0,0.5	Q₂	6.37	11.65	22.44	0.89	3.24	5.37	0.89	3.24	5.37	1.73	7.74	22.10

下载: 导出CSV

表 2 VGG9量化前后不同攻击强度下的推理精度损失(%)

组合参数		直接编码			速率编码			相位编码			延迟编码
组合参数		I	II	III	I	II	III	I	II	III	I	II	III
0.4,1.0,0.5	Q₁	5.84	21.61	46.63	2.08	6.3	12.16	1.71	7.48	16.10	0.77	8.07	26.71
0.4,1.0,0.5	Q₂	3.76	7.46	23.21	0.41	2.92	6.94	0.62	4.70	12.73	0.44	5.27	19.59
0.6,1.0,0.5	Q₁	5.24	19.31	41.23	2.38	8.43	12.01	2.1	7.71	16.75	2	7.23	24.8
0.6,1.0,0.5	Q₂	5.41	11.31	26.69	1.94	7.81	16.28	1.07	5.93	13.94	0.72	3.27	12.32
0.8,1.0,0.5	Q₁	5.56	19.07	38.87	2.13	7.93	11.44	2.7	8.15	15.61	1.89	6.21	19.55
0.8,1.0,0.5	Q₂	4.45	13.41	42.92	2.42	6.96	13.07	2.08	7.87	17.67	1.80	7.43	21.72
1,0,1.0,0.5	Q₁	5.03	17.14	30.14	3.01	8.23	12.75	1.86	7.05	15.15	–	–	–
1,0,1.0,0.5	Q₂	4.60	13.37	44.31	1.96	6.09	12.44	2.08	7.86	17.26	1.06	5.43	17.63
Q₁变化幅度		0.81	4.47	16.49	0.93	2.13	1.31	0.99	1.10	1.60	1.23	1.86	7.16
Q₂变化幅度		1.65	5.95	21.10	2.01	4.89	9.34	1.46	3.17	4.94	1.36	4.16	9.40

下载: 导出CSV

表 3 量化前后不同攻击强度下的层间脉冲活动均值

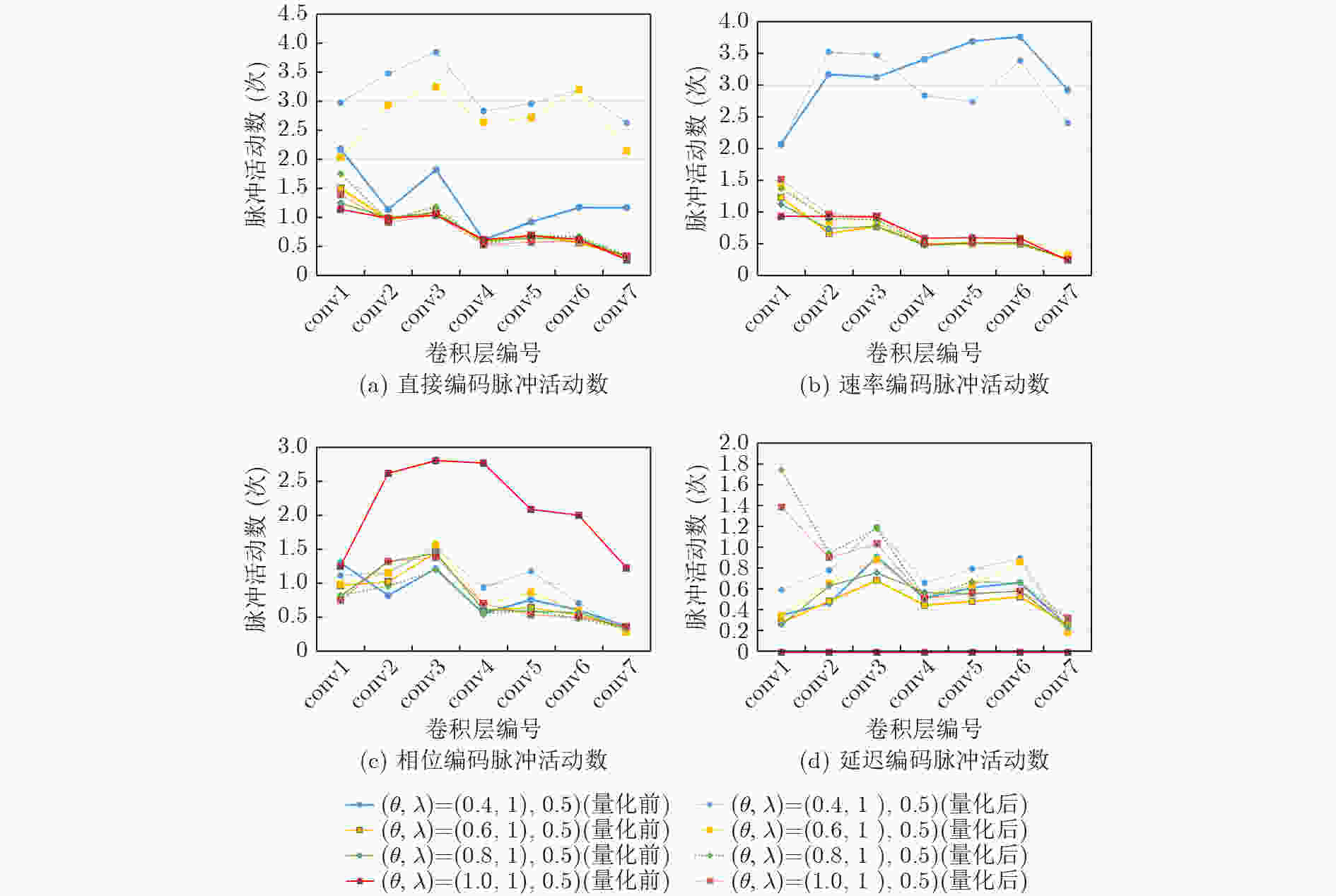
组合参数		直接编码	速率编码	相位编码	延迟编码
0.4,1.0,0.5	Q₁	1.2758	3.1738	–	0.5347
0.4,1.0,0.5	Q₂	3.1236	2.8196	0.9885	0.7321
0.6,1.0,0.5	Q₁	0.8081	0.6398	0.7925	0.4854
0.6,1.0,0.5	Q₂	2.6948	0.7227	0.8795	0.5869
0.8,1.0,0.5	Q₁	0.7804	0.6343	0.8082	0.5144
0.8,1.0,0.5	Q₂	0.8659	0.7018	0.7042	0.4158
1,0,1.0,0.5	Q₁	0.7578	0.6913	2.1092	–
1,0,1.0,0.5	Q₂	0.7585	0.7463	0.7939	0.4784
Q₁变化幅度		0.5180	2.5395	0.1752	0.0493
Q₂变化幅度		2.3651	2.1178	0.2843	0.3162

下载: 导出CSV

表 4 NSR数量级差异

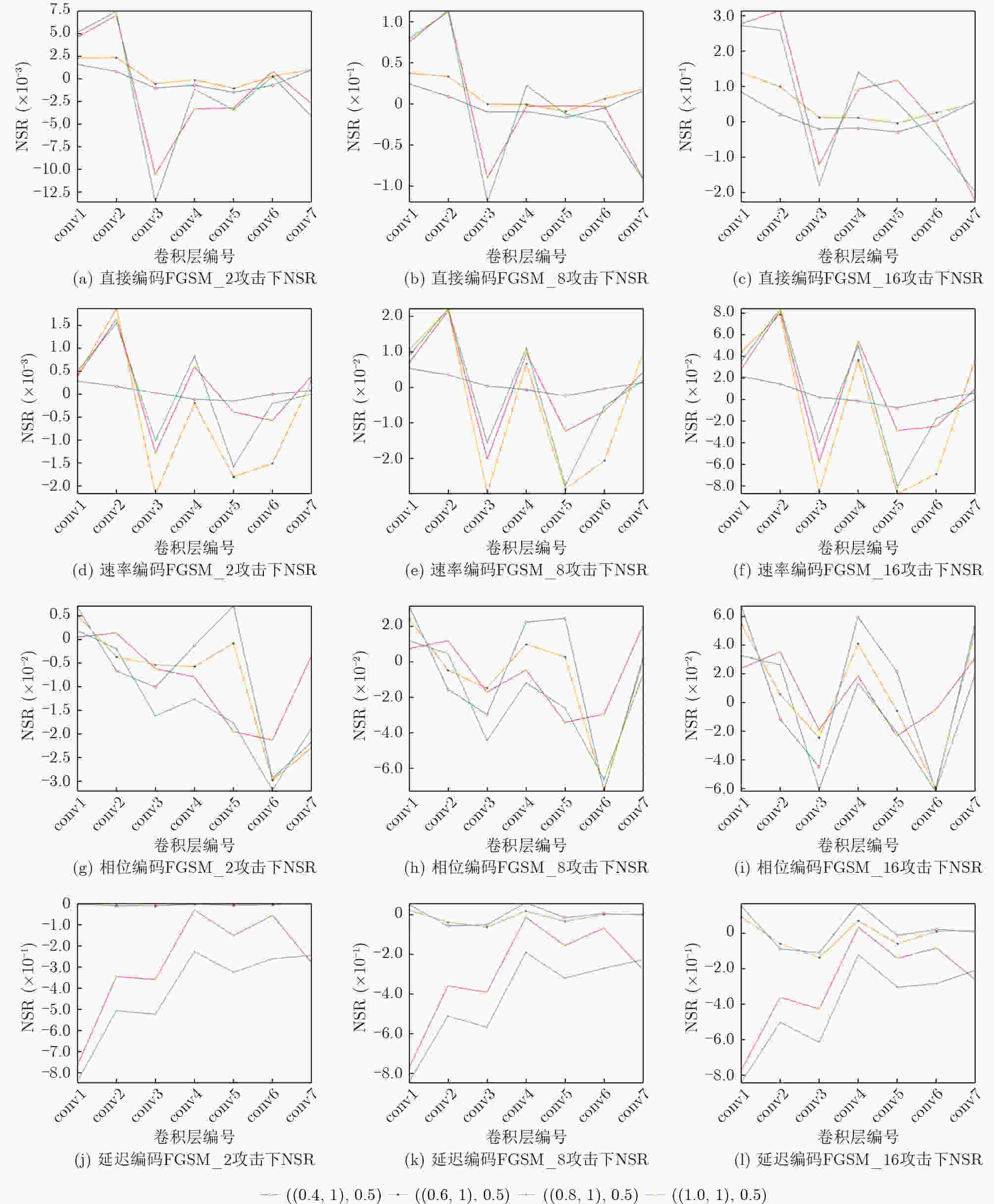
	直接编码	速率编码	相位编码	延迟编码
低强度攻击	0.001	0.0001	0.001	1
中强度攻击	0.01	0.01	0.01	1
高强度攻击	0.1	0.001	0.01	1

下载: 导出CSV

表 5 软件和PKU-NC64C硬件映射adv_loss对比(%)

验证类型	FGSM_2	FGSM_8	FGSM_16
算法级	5.42	12	23.27
硬件级	7.02	10.0	24.52

下载: 导出CSV

参考文献(19)

[1]	谭铁牛: 人工智能的历史、现状和未来[EB/OL]. https://www.cas.cn/zjs/201902/t20190218_4679625.shtml, 2019. Tan Tieniu. The historyk, present and future of artificial intelligence. Chinese Academy of Sciences[EB/OL]. https://www.cas.cn/zjs/201902/t20190218_4679625.shtml, 2019.
[2]	LIU Aishan, LIU Xianglong, FAN Jiaxin, et al. Perceptual-sensitive GAN for generating adversarial patches[C]. The 33rd AAAI Conference on Artificial Intelligence and Thirty-First Innovative Applications of Artificial Intelligence Conference and Ninth AAAI Symposium on Educational Advances in Artificial Intelligence, Honolulu, USA, 2019: 127.
[3]	ZHANG Guoming, YAN Chen, JI Xiaoyu, et al. DolphinAttack: Inaudible voice commands[C]. The 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, USA, 2017: 103–117.
[4]	WARREN T. Microsoft’s Outlook spam email filters are broken for many right now[EB/OL]. https://www.theverge.com/2023/2/20/23607056/microsoft-outlook-spam-email-filters-not-working-broken, 2023.
[5]	董庆宽, 何浚霖. 基于信息瓶颈的深度学习模型鲁棒性增强方法[J]. 电子与信息学报, 2023, 45(6): 2197–2204. doi: 10.11999/JEIT220603 DONG Qingkuan and HE Junlin. Robustness enhancement method of deep learning model based on information bottleneck[J]. Journal of Electronics &Information Technology, 2023, 45(6): 2197–2204. doi: 10.11999/JEIT220603
[6]	WEI Mingliang, YAYLA M, HO S Y, et al. Binarized SNNs: Efficient and error-resilient spiking neural networks through binarization[C]. 2021 IEEE/ACM International Conference on Computer Aided Design, Munich, Germany, 2021: 1–9.
[7]	EL-ALLAMI R, MARCHISIO A, SHAFIQUE M, et al. Securing deep spiking neural networks against adversarial attacks through inherent structural parameters[C]. 2021 Design, Automation & Test in Europe Conference & Exhibition, Grenoble, France, 2021: 774–779.
[8]	SHARMIN S, RATHI N, PANDA P, et al. Inherent adversarial robustness of deep spiking neural networks: Effects of discrete input encoding and non-linear activations[C]. The 16th European Conference, Glasgow, UK, 2020: 399–414.
[9]	KUNDU S, PEDRAM M, and BEEREL P A. HIRE-SNN: Harnessing the inherent robustness of energy-efficient deep spiking neural networks by training with crafted input noise[C]. 2021 IEEE/CVF International Conference on Computer Vision, Montreal, Canada, 2021: 5209–5218.
[10]	KIM Y, PARK H, MOITRA A, et al. Rate coding or direct coding: Which one is better for accurate, robust, and energy-efficient spiking neural networks?[C]. 2022 IEEE International Conference on Acoustics, Speech and Signal Processing, Singapore, 2022: 71–75.
[11]	O'CONNOR P and WELLING M. Deep spiking networks[J]. arXiv preprint arXiv: 1602.08323, 2016.
[12]	RATHI N, SRINIVASAN G, PANDA P, et al. Enabling deep spiking neural networks with hybrid conversion and spike timing dependent backpropagation[C]. The 8th International Conference on Learning Representations, Addis Ababa, Ethiopia, 2020.
[13]	TAVANAEI A and MAIDA A. BP-STDP: Approximating backpropagation using spike timing dependent plasticity[J]. Neurocomputing, 2019, 330: 39–47. doi: 10.1016/j.neucom.2018.11.014
[14]	SZEGEDY C, ZAREMBA W, SUTSKEVER I, et al. Intriguing properties of neural networks[C]. The 2nd International Conference on Learning Representations, Banff, Canada, 2014.
[15]	GOODFELLOW I J, SHLENS J, and SZEGEDY C. Explaining and harnessing adversarial examples[C]. The 3rd International Conference on Learning Representations, San Diego, USA, 2015.
[16]	SHAFAHI A, NAJIBI M, GHIASI A, et al. Adversarial training for free![C]. The 32nd International Conference on Neural Information Processing Systems, Vancouver, Canada, 2019.
[17]	MADRY A, MAKELOV A, SCHMIDT L, et al. Towards deep learning models resistant to adversarial attacks[C]. The 6th International Conference on Learning Representations, Vancouver, Canada, 2018.
[18]	LI Yanjie, CUI Xiaoxin, ZHOU Yihao, et al. A comparative study on the performance and security evaluation of spiking neural networks[J]. IEEE Access, 2022, 10: 117572–117581. doi: 10.1109/ACCESS.2022.3220367
[19]	KUANG Yisong, CUI Xiaoxin, ZHONG Yi, et al. A 64K-neuron 64M-1b-synapse 2.64 pJ/SOP neuromorphic chip with all memory on chip for spike-based models in 65nm CMOS[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2021, 68(7): 2655–2659. doi: 10.1109/TCSII.2021.3052172