Multicast Service Function Tree Embedding Algorithm Based on Delay and Jitter Awareness
-
摘要: 针对软件定义网络/网络功能虚拟化(SDN/NFV)架构中，多播请求流(MRs)需满足严格时延和抖动约束下遍历由多个虚拟网络功能(VNFs)依序组成的服务功能树(SFT)问题。该文提出一种基于最优链路选择函数进行深度优先搜索构建SFT的路由算法。首先，提出网络资源相对成本函数，以保证网络负载自动均衡。其次，联合考虑网络资源、VNF动态放置及多播流延迟和抖动约束，构建SFT动态嵌入问题的整数线性规划模型(ILP)。最后，针对该NP难问题，设计辅助边权图和最优链路选择函数进行路由路径选择，并以最小化资源消耗成本为目标提出具有延迟和抖动感知的SFT嵌入算法(SFT-EA)。仿真结果表明，SFT-EA在吞吐量，流接受率和网络负载均衡方面具有更好的性能。Abstract: To solve the problem that Multicast Request flows (MRs) need to traverse sequentially a Service Function Tree (SFT) consisting of Virtual Network Functions (VNFs) as well as ensuring stringent delay and jitter constraints of SFT in Network Function Virtualization (NFV)-enabled Software-Defined Networks (SDNs), a routing algorithm for constructing a multicast SFT based on depth-first search with an optimal link selection function is proposed. Firstly, the relative cost functions of network resources are proposed to guarantee the automatic load balancing of the network. Secondly, an Integer Linear Programming model (ILP) for the SFT dynamic embedding is constructed by jointly considering network resources, VNF dynamic placement and delay and jitter constraints of a multicast flow. Finally, for this NP-hard problem, an auxiliary edge-weight graph and optimal link selection function are designed for routing path selection, and a delay and jitter-aware SFT Embedding Algorithm (SFT-EA) is proposed with the objective of minimizing the resource consumption cost. Simulation results demonstrate the SFT-EA has better performance in terms of throughput, traffic acceptance rate, and network load balance.
-
算法1 SFT-EA算法 输入： $ G(N,L) $，流请求$ {\text{M}}{{\text{R}}_i} $，资源容量，资源剩余率，最大迭
代次数$ K $。输出：多播树$ T $。 1. 根据2.4.1枚举$ G $中功能节点上所有可能的VNFs 2. 根据3.1构造$ G_i^\prime $ 3. 基于$ G_i^\prime $构造$ {\hat G_i} $ 4. 求最小时延树$ {T_{{\text{LDT}}}}\leftarrow $KruskalMST($ {\hat G_i} $) 5. if${D_{ {\text{max} } } }\;{\rm{in}}\;{T_{ {\text{LDT} } } } > R_i^{ {\text{delay} } }$则算法结束 6. else 7. while$ (({\Delta _T} \in [\max \left\{ {{D_{\max }},R_i^{{\text{jitter}}}} \right\},R_i^{{\text{delay}}}]) $且$k \le K$)//算法最多迭代$ K $次 8. $ {T_i} \leftarrow s;V[\hat u] = 0;L[\hat u][\hat v] = 0;V[s] = 1 $，//数组$ V $和$ L $分别用于记录节点和链路是否已被访问 ${{Pre} }({{s} }) = \emptyset ;\hat u = {\text{s} };{\Delta _T} = \max \left\{ { {D_{\max } },R_i^{ {\text{jitter} } } } \right\}$//$ pre() $函数表示一个节点的前驱 9. while $ L[\hat u][\hat v] \ne 1 $ 10. if $ \hat v \notin {D_i} \cup \{ s\} $ and $ D(\hat u) + d(\hat u,\hat v) \leqslant {\Delta _T} $ 11. $ N = N \cup \{ \hat v\} $//$ N $记录候选节点 12. else if $ \hat v \in {D_i} $且${\Delta _T} - R_i^{ {\text{Jitter} } } \le D(\hat u) + d(\hat u,\hat v) \le {\Delta _T}$ 13. $ N = N \cup \{ \hat v\} $ 14. end if 15. if $ N \ne \emptyset $ 16. for each $ \hat v \in N $ 17. if $ D(\hat u) + d(\hat u,\hat v) = = {\Delta _T} $ 18. if $ \hat v \in {D_i} $ 19. $ V[\hat v] = 1;L[\hat u][\hat v] = 1;{T_i} = {T_i} \cup \{ \hat v\} $ 20. else $ L[\hat u][\hat v] = 1 $ 21. end if 22. else if $ D(\hat u) + d(\hat u,\hat v) < {\Delta _T} $ 23. 选择$ f(\hat u,\hat v) $中最小的节点$ \hat v $ 24. $ {T_i} = {T_i} \cup \{ \hat v\} ;V[\hat v] = 1;L[\hat u][\hat v] = 1;Pre(\hat v) = \hat u$;
$\hat u = \hat v;L[\hat u][\hat v] = 0; $25. end if 26. end for 27. else 将$ L[\hat u][\hat v] $为0的链路设置为1，$ \hat u = pre(\hat u) $ 28. end if 29. end while 30. for each $ \hat v \in {D_i} $ 31. if 所有$ V[\hat v] = = 1 $ 则转到36 32. else $ {\Delta _T} + + ;k + + $;break; 33. end if 34. end for 35. end while 36. if $ {T_i} $包含$ {D_i} $中的所有目的节点 37. 通过将$ {T_i} $中的每条边替换为其在$ G $中对应的路径来映射多播
树$ T $，并更新$r_{i,{\rm{uv}}}^{ {\text{bw} } }\;,r_{i,u}^{ {\text{ft} } }\;,r_{i,u}^{ {\text{cpu} } }$和$ r_{i,m}^{{\text{cpu}}} $38. else 路由失败，$ {\text{M}}{{\text{R}}_i} $请求被拒绝，Return 39. end if 40. end if 
下载: 导出CSV
-
[1] 唐伦, 吴婷, 周鑫隆, 等. 一种基于联邦学习资源需求预测的虚拟网络功能迁移算法[J]. 电子与信息学报, 2022, 44(10): 3532–3540. doi: 10.11999/JEIT210743TANG Lun, WU Ting, ZHOU Xinlong, et al. A virtual network function migration algorithm based on federated learning prediction of resource requirements[J]. Journal of Electronics &Information Technology, 2022, 44(10): 3532–3540. doi: 10.11999/JEIT210743 [2] LIU Liang, GUO Songtao, LIU Guiyan, et al. Joint dynamical VNF placement and SFC routing in NFV-enabled SDNs[J]. IEEE Transactions on Network and Service Management, 2021, 18(4): 4263–4276. doi: 10.1109/TNSM.2021.3091424 [3] 徐勇军, 谷博文, 谢豪, 等. 全双工中继协作下的移动边缘计算系统能耗优化算法[J]. 电子与信息学报, 2021, 43(12): 3621–3628. doi: 10.11999/JEIT200937XU Yongjun, GU Bowen, XIE Hao, et al. Energy consumption optimization algorithm for full-duplex relay-assisted mobile edge computing systems[J]. Journal of Electronics &Information Technology, 2021, 43(12): 3621–3628. doi: 10.11999/JEIT200937 [4] MALI R, ZHANG Xijun, and QIAO Chunming. Benefits of multicasting in all-optical networks[C]. SPIE 3531, All-Optical Networking: Architecture, Control, and Management Issues. Boston, United States, 1998: 209–220. [5] Grand View Research. Video streaming market size, share & trends analysis report by streaming type, by solution, by platform, by service, by revenue model, by deployment type, by user, by region, and segment forecasts, 2023 – 2030[EB/OL].https://www.grandviewresearch.com/industry-analysis/video-streaming-market, 2023. [6] XIE Yanghao, HUANG Lin, KONG Yuyang, et al. Virtualized network function forwarding graph placing in SDN and NFV-Enabled IoT networks: A graph neural network assisted deep reinforcement learning method[J]. IEEE Transactions on Network and Service Management, 2022, 19(1): 524–537. doi: 10.1109/TNSM.2021.3123460 [7] XU Zichuan, LIANG Weifa, HUANG Meitian, et al. Approximation and online algorithms for NFV-enabled multicasting in SDNs[C]. 2017 IEEE 37th International Conference on Distributed Computing Systems (ICDCS), Atlanta, USA, 2017: 625–634. [8] MUHAMMAD A, SORKHOH I, QU Long, et al. Delay-sensitive multi-source multicast resource optimization in NFV-enabled networks: A column generation approach[J]. IEEE Transactions on Network and Service Management, 2021, 18(1): 286–300. doi: 10.1109/TNSM.2021.3049718 [9] 孔紫璇, 李航, 向万, 等. 用户动态接入下的多播业务链部署和调整方法[J]. 北京邮电大学学报, 2022, 45(6): 53–59. doi: 10.13190/j.jbupt.2022-116KONG Zixuan, LI Hang, XIANG Wan, et al. Multicast service chain deployment and adjustment method under user dynamic access[J]. Journal of Beijing University of Posts and Telecommunications, 2022, 45(6): 53–59. doi: 10.13190/j.jbupt.2022-116 [10] WANG Xinhan, XING Huanlai, SONG Fuhong, et al. Dynamic multicast-oriented virtual network function placement with SFC request prediction[C]. 2022 14th International Conference on Communication Software and Networks (ICCSN), Chongqing, China, 2022: 81–88. [11] JIA Mike, LIANG Weifa, HUANG Meitian, et al. Routing cost minimization and throughput maximization of NFV-enabled unicasting in software-defined networks[J]. IEEE Transactions on Network and Service Management, 2018, 15(2): 732–745. doi: 10.1109/TNSM.2018.2810817 [12] XU Zichuan, LIANG Weifa, HUANG Meitian, et al. Efficient NFV-enabled multicasting in SDNs[J]. IEEE Transactions on Communications, 2019, 67(3): 2052–2070. doi: 10.1109/TCOMM.2018.2881438 [13] REN Bangbang, GUO Deke, SHEN Yulong, et al. Embedding service function tree with minimum cost for NFV-enabled multicast[J]. IEEE Journal on Selected Areas in Communications, 2019, 37(5): 1085–1097. doi: 10.1109/JSAC.2019.2906764 [14] ASGARIAN M, MIRJALILY G, and LUO Zhiquan. Trade-off between efficiency and complexity in multi-stage embedding of multicast VNF service chains[J]. IEEE Communications Letters, 2022, 26(2): 429–433. doi: 10.1109/LCOMM.2021.3132134 [15] REN Haozhe, XU Zichuan, LIANG Weifa, et al. Efficient algorithms for delay-aware NFV-enabled multicasting in mobile edge clouds with resource sharing[J]. IEEE Transactions on Parallel and Distributed Systems, 2020, 31(9): 2050–2066. doi: 10.1109/TPDS.2020.2983918 [16] ALHUSSEIN O, DO P T, YE Qiang, et al. A virtual network customization framework for multicast services in NFV-enabled core networks[J]. IEEE Journal on Selected Areas in Communications, 2020, 38(6): 1025–1039. doi: 10.1109/JSAC.2020.2986591 [17] REN Cheng, CHEN Xuxiang, XIANG Haiyun, et al. On efficient delay-aware multisource multicasting in NFV-Enabled softwarized networks[J]. IEEE Transactions on Network and Service Management, 2022, 19(3): 3371–3386. doi: 10.1109/TNSM.2022.3188777 [18] LI Hang, WANG Luhan, ZHU Zhenghe, et al. Multicast service function chain orchestration in SDN/NFV-Enabled networks: Embedding, readjustment, and expanding[J]. IEEE Transactions on Network and Service Management, 2023. [19] MIRJALILY G, ASGARIAN M, and LUO Zhiquan. Interference-aware NFV-enabled multicast service in resource-constrained wireless mesh networks[J]. IEEE Transactions on Network and Service Management, 2022, 19(1): 424–436. doi: 10.1109/TNSM.2021.3083798 [20] Python Community. Networkx 3.1[EB/OL]. https://pypi.org/project/networkx/, 2023. [21] Internet topology[EB/OL]. http://topology-zoo.org/maps/, 2022. [22] CHENG Yulun and YANG Longxiang. VNF deployment and routing for NFV-enabled multicast: A Steiner tree-based approach[C]. 2017 9th International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 2017: 1–4. -
图(12) / 表(1)
计量
- 文章访问数: 370
- HTML全文浏览量: 135
- PDF下载量: 48
- 被引次数: 0
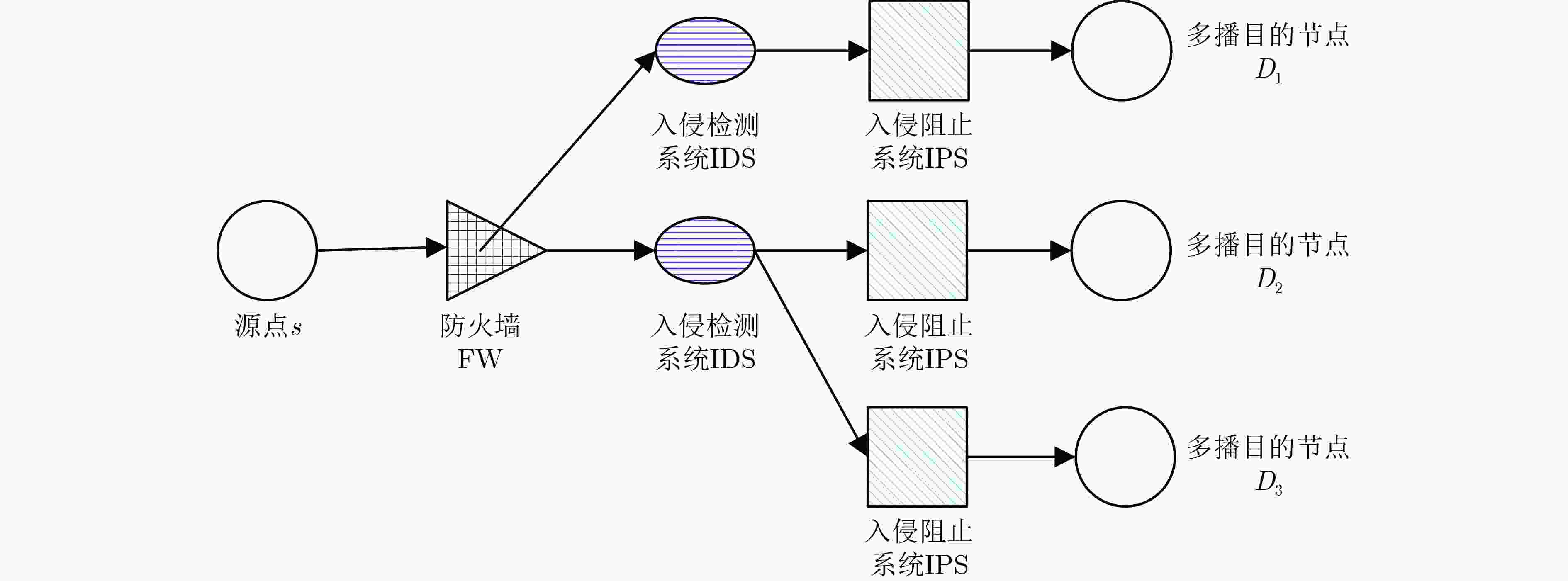
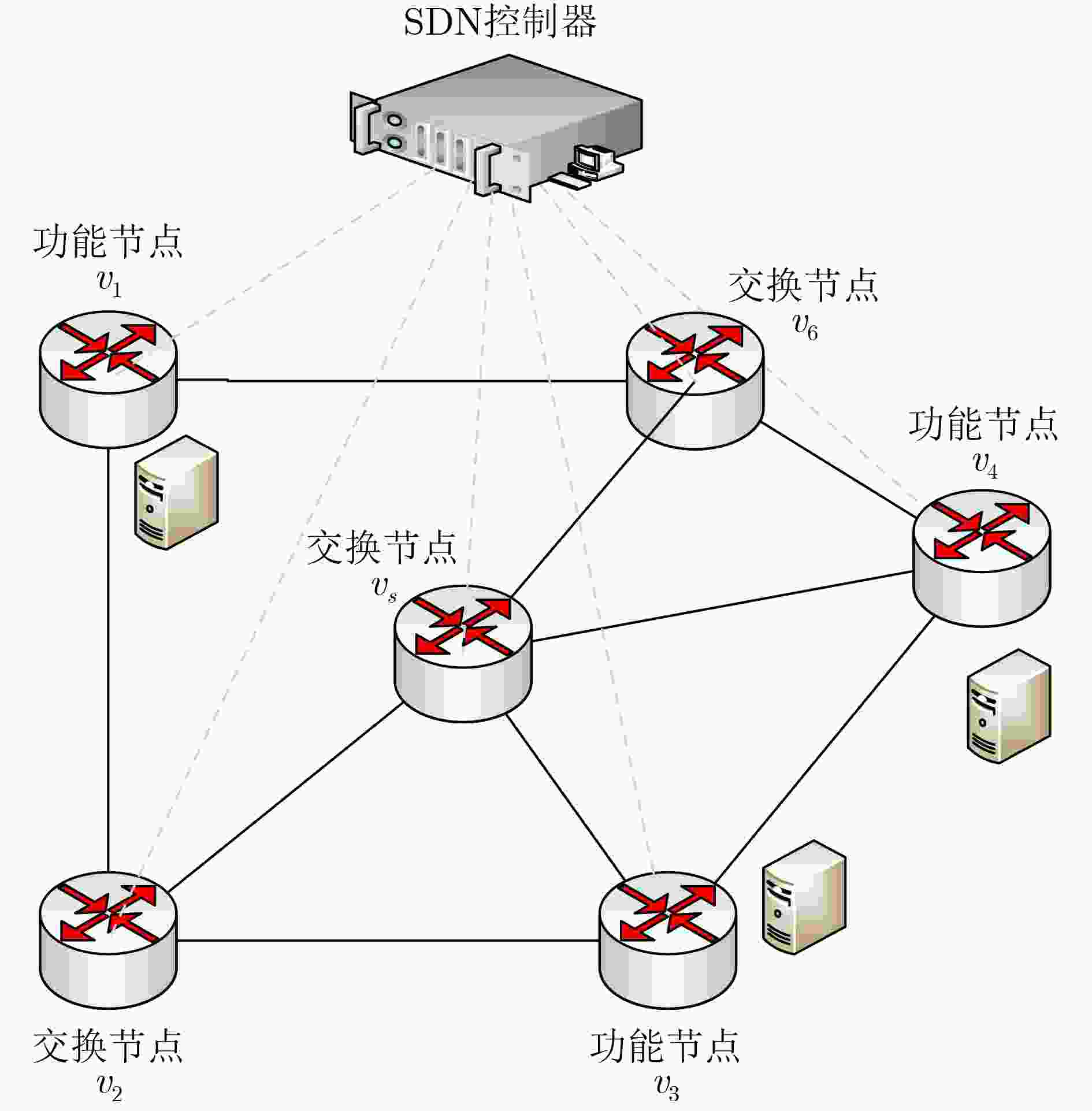
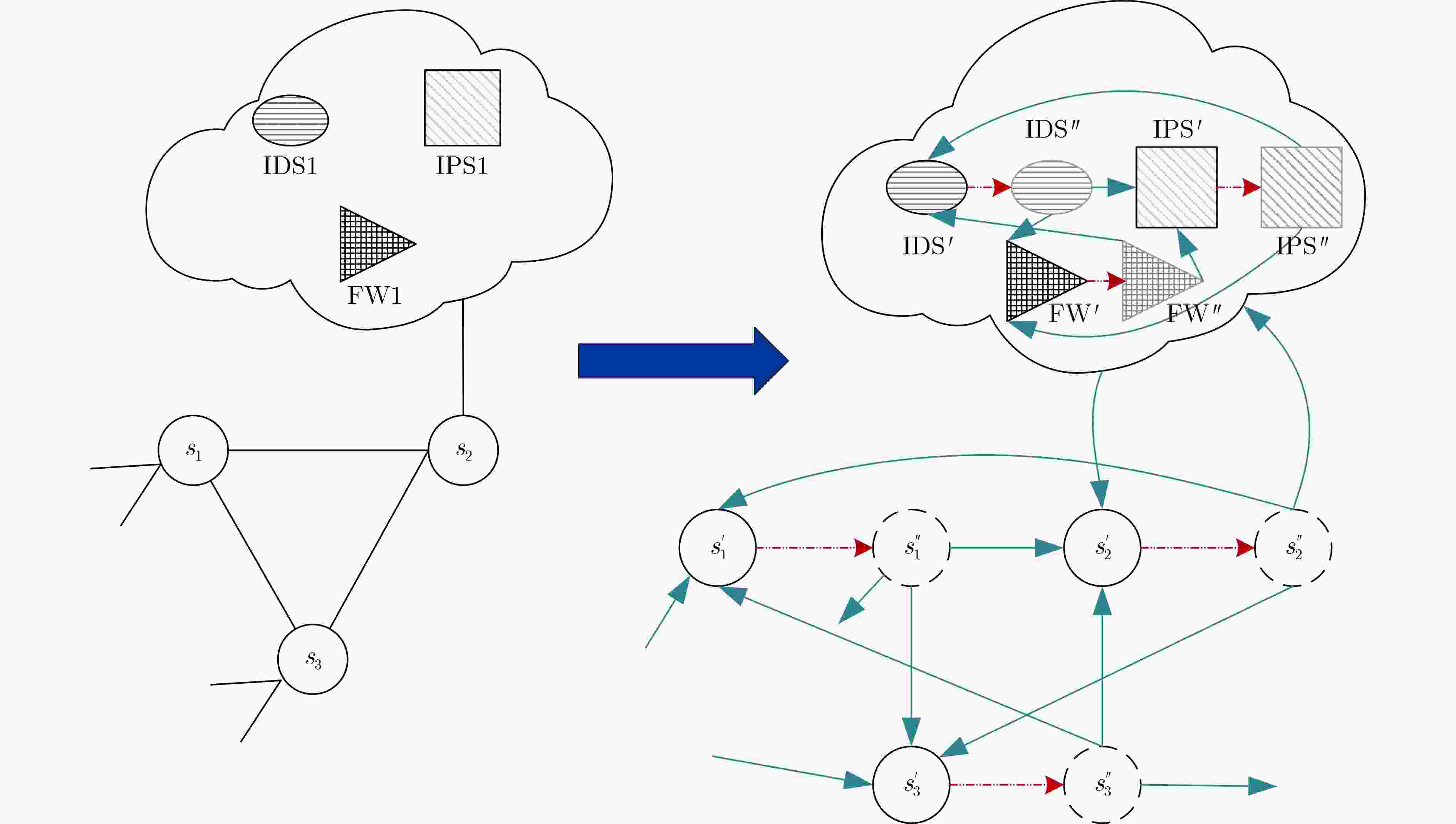
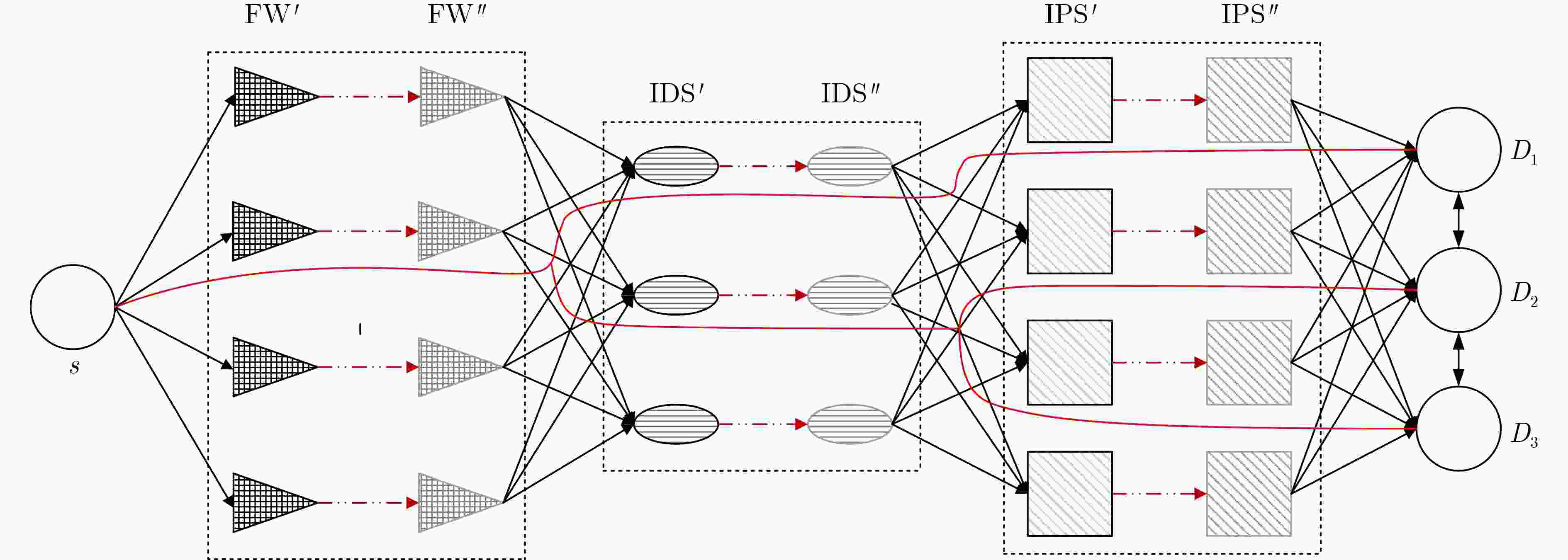
下载:
