Meet-in-the-middle Attack on RAIN-128
-
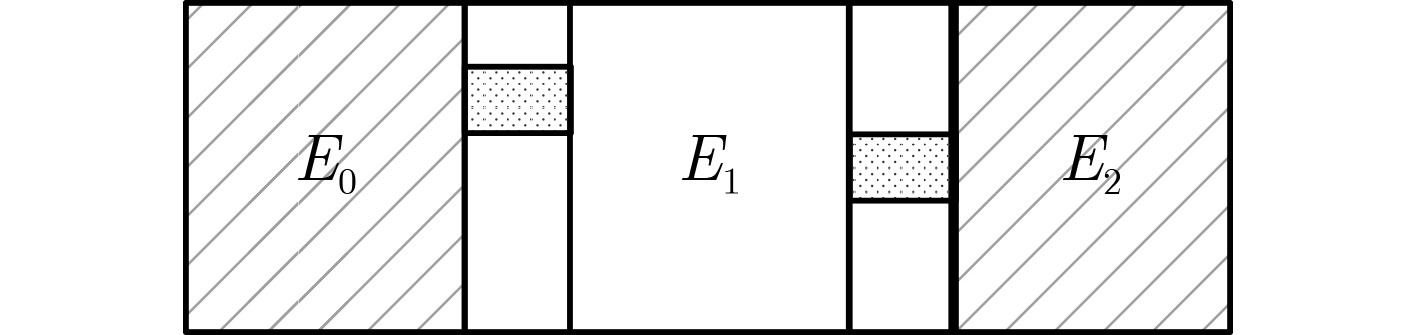
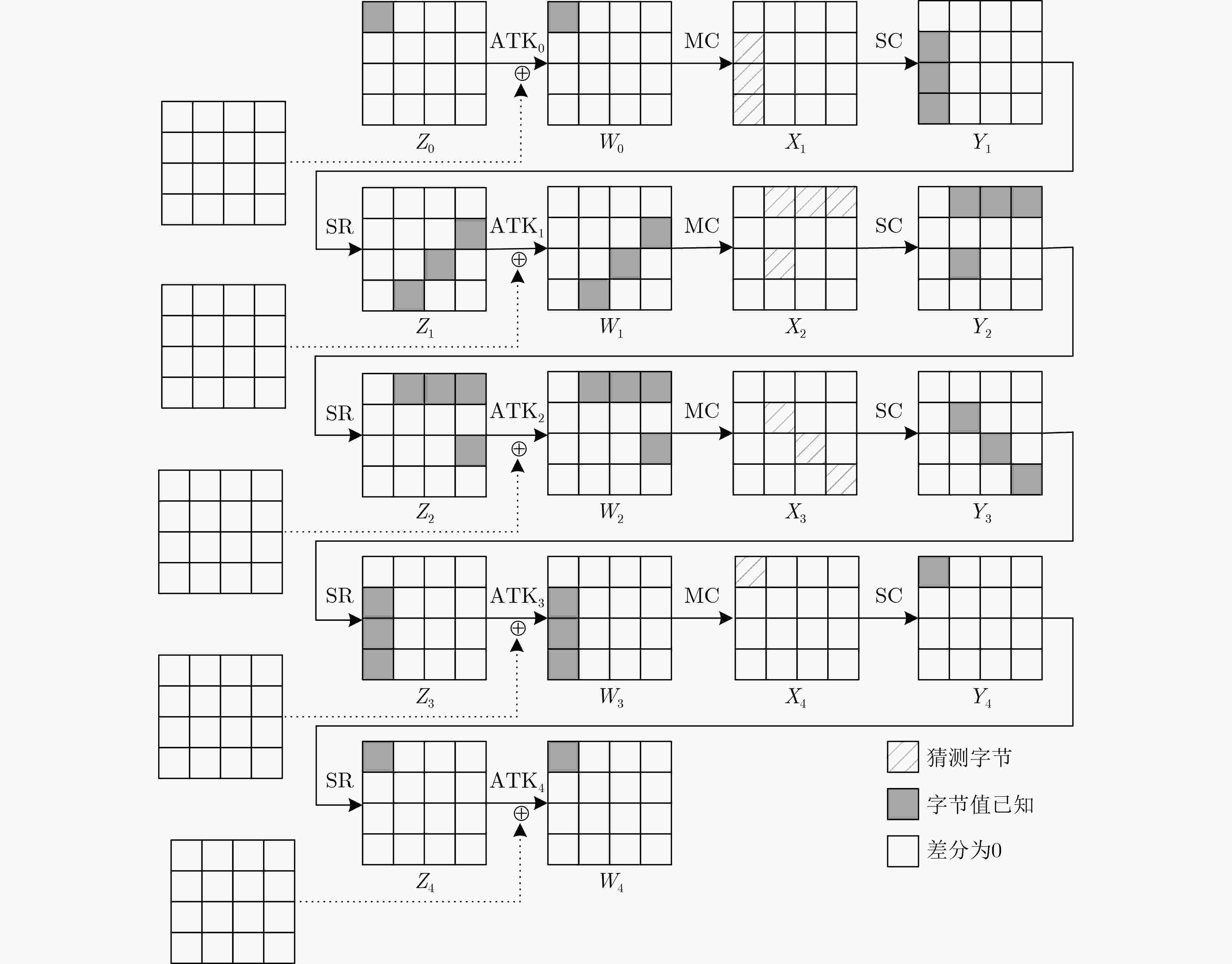
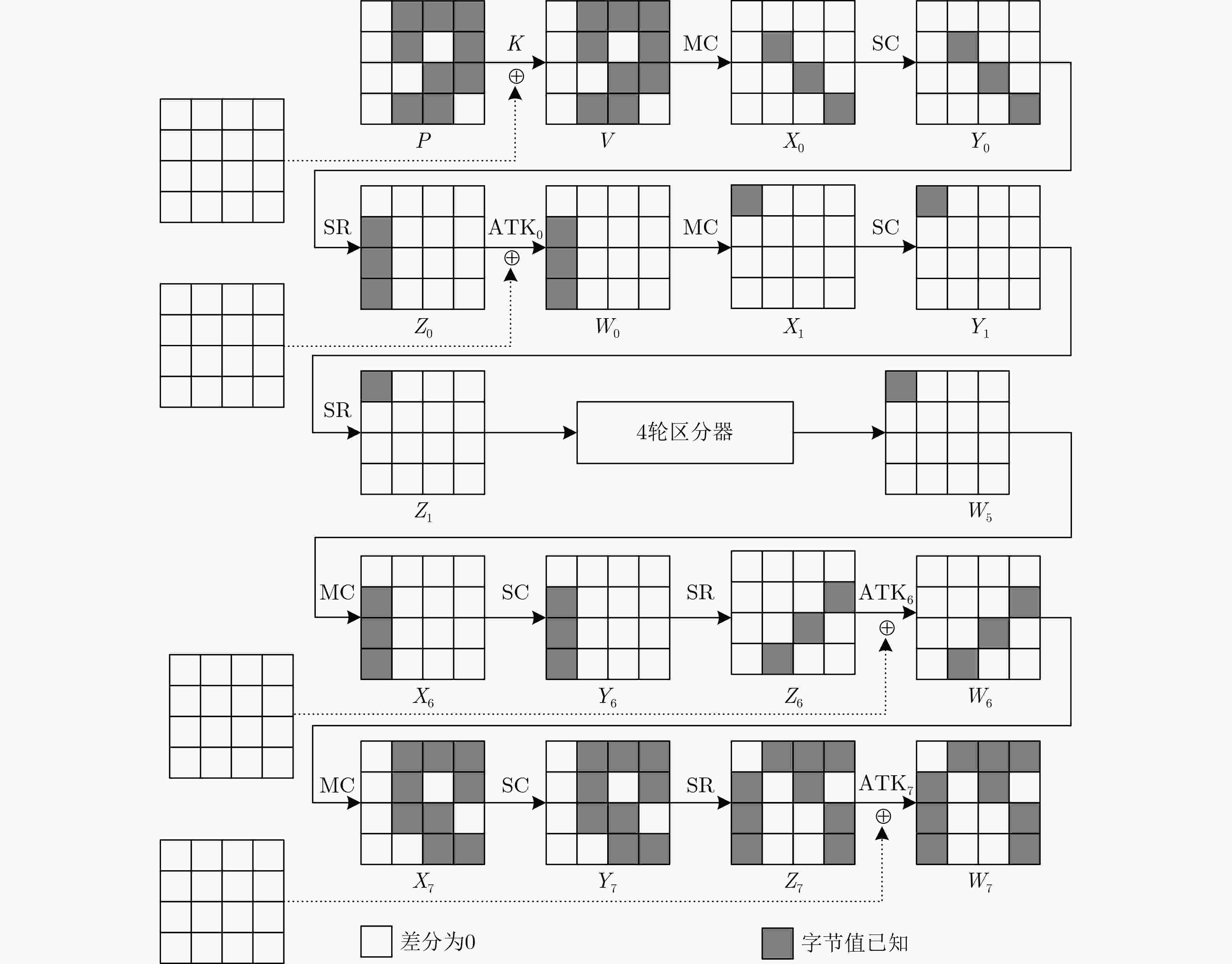
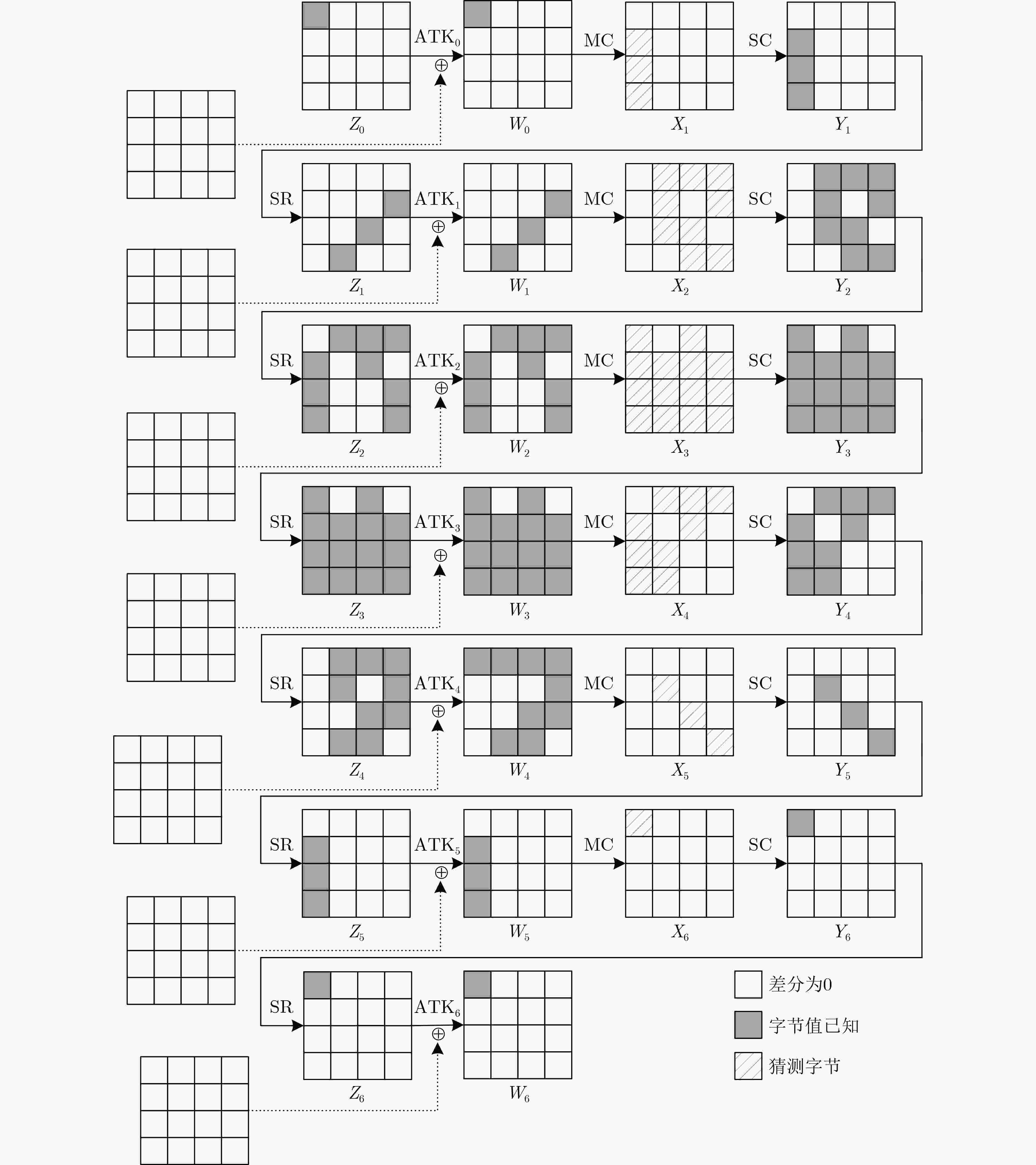
摘要: RAIN是一族SPN结构的轻量级分组密码算法,该算法具有软硬件实现效率高、安全性强等特点。中间相遇攻击被广泛应用于分组密码算法的安全性分析中。该文通过分析RAIN-128的结构特性和截断差分特征,利用差分枚举技术分别构造了4轮和6轮中间相遇区分器,给出了8轮及10轮的中间相遇攻击。当攻击轮数为8轮时,预计算阶段的时间复杂度为$ {2^{68}} $次8轮RAIN-128加密,存储复杂度为$ {2^{75}} $ bit,在线攻击阶段的时间复杂度为$ {2^{109}} $次8轮加密,数据复杂度是$ {2^{72}} $个选择明文;当攻击轮数为10轮时,预计算阶段的时间复杂度为$ {2^{214}} $次10轮加密,存储复杂度为$ {2^{219}} $ bit,在线攻击阶段的时间复杂度为$ {2^{109}} $次10轮加密,数据复杂度是$ {2^{72}} $个选择明文,分析结果显示,RAIN-128可以抵抗中间相遇攻击,并具有较高的安全冗余。Abstract: RAIN is a lightweight block cipher with SPN structure, which not only has strong security, but also possesses high software and hardware implementation efficiency. Meet-in-the-middle attacks are widely used in the security analysis of block ciphers algorithms. In this paper, the meet-in-the-middle attack on RAIN is researched. By examining the structural characteristics and the properties of truncated differential of RAIN-128, both 4-round and 6-round meet-in-the-middle distinguishers are first constructed by using differential enumeration technique, and meet-in-the-middle attacks on 8-round and 10-round RAIN-128 are presented, respectively. For 8-round attack, in the preprocessing, the time complexity is $ {2^{68}} $ 8-round encryptions, and the memory complexity is $ {2^{75}} $ bit, in the online, the time complexity is $ {2^{109}} $ 8-round encryptions, and the data complexity is $ {2^{72}} $ chosen plaintexts. For 10-round attack, in the preprocessing, the time complexity is $ {2^{214}} $ 10-round encryptions, and the memory complexity is $ {2^{219}} $ bit, in the online, the time complexity is $ {2^{109}} $ 10-round encryptions, and the data complexity is $ {2^{72}} $ chosen plaintexts. The result shows that RAIN-128 can be against meet-in-the-middle attack and has high security redundancy.
-
Key words:
- Block ciphers /
- RAIN-128 /
- Meet-in-the-middle attack /
- Differential enumeration technique
-
表 1 RAIN算法的8/10轮中间相遇攻击复杂度
轮数(r) 时间(预计算) 时间(在线) 数据 存储(bit) 8 $ {2^{68}} $ $ {2^{109}} $ $ {2^{72}} $ $ {2^{75}} $ 10 $ {2^{214}} $ $ {2^{109}} $ $ {2^{72}} $ $ {2^{219}} $ -
[1] DIFFIE W and HELLMAN M E. Special feature exhaustive cryptanalysis of the NBS data encryption standard[J]. Computer, 1977, 10(6): 74–84. doi: 10.1109/C-M.1977.217750 [2] National Institute of Standards and Technology. FIPS 46–3 Data encryption standard (DES)[S]. National Institute of Standards and Technology, 1999. [3] DEMIRCI H and SELÇUK A A. A meet-in-the-middle attack on 8-round AES[C]. Proceedings of the 15th International Workshop on Fast Software Encryption, Lausanne, Switzerland, 2008: 116–126. [4] DAEMEN J and RIJMEN V. The Design of Rijndael: AES -The Advanced Encryption Standard[M]. Berlin: Springer, 2002: 137–139. [5] DUNKELMAN O, KELLER N, and SHAMIR A. Improved single-key attacks on 8-round AES-192 and AES-256[J]. Journal of Cryptology, 2015, 28(3): 397–422. doi: 10.1007/s00145-013-9159-4 [6] DERBEZ P and FOUQUE P A. Exhausting Demirci-Selçuk meet-in-the-middle attacks against reduced-round AES[C]. Proceedings of the 20th International Workshop on Fast Software Encryption, Singapore, 2013: 541–560. [7] SHI Danping, SUN Siwei, DERBEZ P, et al. Programming the Demirci-Selçuk meet-in-the-middle attack with constraints[C]. Proceedings of the 24th International Conference on the Theory and Application of Cryptology and Information Security, Brisbane, Australia, 2018: 3–34. [8] BEIERLE C, JEAN J, KÖLBL S, et al. The SKINNY family of block ciphers and its low-latency variant MANTIS[C]. Proceedings of the 36th Annual International Cryptology Conference, Santa Barbara, USA, 2016: 123–153. [9] CHEN Qiu, SHI Danping, SUN Siwei, et al. Automatic Demirci-Selçuk meet-in-the-middle attack on SKINNY with key-bridging[C]. Proceedings of the 21st International Conference on Information and Communications Security, Beijing, China, 2020: 233–247. [10] 肖钰汾, 田甜. 减轮SKINNY-128-384算法的中间相遇攻击[J]. 密码学报, 2021, 8(2): 338–351. doi: 10.13868/j.cnki.jcr.000442XIAO Yufen and TIAN Tian. Meet-in-the-Middle attack on round-reduced SKINNY-128-384[J]. Journal of Cryptologic Research, 2021, 8(2): 338–351. doi: 10.13868/j.cnki.jcr.000442 [11] SUGITA M, KOBARA K, and IMAI H. Security of reduced version of the block cipher Camellia against truncated and impossible differential cryptanalysis[C]. Proceedings of the 7th International Conference on the Theory and Application of Cryptology and Information Security, Gold Coast, Australia, 2001: 193–207. [12] BIHAM E. Cryptanalysis of Patarin’s 2-round public key system with S boxes (2R)[C]. Proceedings of 2000 International Conference on the Theory and Applications of Cryptographic Techniques, Bruges, Belgium, 2000: 408–416. [13] 曹梅春, 张文英, 陈彦琴, 等. RAIN: 一种面向软硬件和门限实现的轻量分组密码算法[J]. 计算机研究与发展, 2021, 58(5): 1045–1055. doi: 10.7544/issn1000-1239.2021.20200933CAO Meichun, ZHANG Wenying, CHEN Yanqin, et al. RAIN: A lightweight block cipher towards software, hardware and threshold implementations[J]. Journal of Computer Research and Development, 2021, 58(5): 1045–1055. doi: 10.7544/issn1000-1239.2021.20200933 [14] AVANZI R. The QARMA block cipher family. Almost MDS matrices over rings with Zero Divisors, Nearly Symmetric Even-mansour constructions with Non-involutory central rounds, and search heuristics for low-latency S-Boxes[J]. IACR Transactions on Symmetric Cryptology, 2017, 2017(1): 4–44. doi: 10.13154/tosc.v2017.i1.4-44 [15] BEIERLE C, LEANDER G, MORADI A, et al. CRAFT: Lightweight tweakable block cipher with efficient protection against DFA attacks[J]. IACR Transactions on Symmetric Cryptology, 2019, 2019(1): 5–45. doi: 10.13154/tosc.v2019.i1.5-45 [16] 蒋梓龙, 金晨辉. Saturnin算法的不可能差分分析[J]. 通信学报, 2022, 43(3): 53–62. doi: 10.11959/j.issn.1000-436x.2022045JIANG Zilong and JIN Chenhui. Impossible differential cryptanalysis of Saturnin algorithm[J]. Journal on Communications, 2022, 43(3): 53–62. doi: 10.11959/j.issn.1000-436x.2022045 [17] 叶涛, 韦永壮, 李灵琛. ACE密码算法的积分分析[J]. 电子与信息学报, 2021, 43(4): 908–914. doi: 10.11999/JEIT200234YE Tao, WEI Yongzhuang, and LI Lingchen. Integral cryptanalysis of ACE encryption algorithm[J]. Journal of Electronics &Information Technology, 2021, 43(4): 908–914. doi: 10.11999/JEIT200234 [18] LEANDER G, ABDELRAHEEM M A, ALKHZAIMI H, et al. A cryptanalysis of PRINTCIPHER: The invariant subspace attack[C]. Proceedings of the 31st Annual Cryptology Conference, Santa Barbara, USA, 2011: 206–221. -






 下载:
下载:



 下载:
下载:
