Multi-Stage Co-Optimization FPGA Routing for Time-Division Multiplexing Technique
-
摘要: 时分复用(Time-Division Multiplexing, TDM)技术被广泛地运用于解决IO瓶颈问题,以提高现场可编程门阵列(Field Programmable Gate Array, FPGA)系统的可布线性,但TDM比率的增大会导致系统时延的显著增加。因此,为了优化FPGA系统时延以及可布线性,该文提出一种用于时分复用技术的多阶段协同优化FPGA布线(Multi-Stage Co-Optimization FPGA Routing, MSCOFRouting)方法。首先,设计自适应布线算法,以减少布线拥塞情况,提高可布线性,解决FPGA间的布线优化问题,为后续的TDM比率分配提供高质量的布线结果。其次,为了避免因大规模线网组的TDM比率过大而导致系统时延劣化的情况,提出基于拉格朗日松弛(Lagrangian Relaxation, LR)的TDM比率分配算法,为布线图的边分配系统时延更小的初始TDM比率。此外,为了进一步减小最大线网组的TDM比率,通过一种多层次的TDM比率优化算法,缩减线网组和FPGA连接对的TDM比率。同时,为了提高MSCOFRouter的运行效率,在上述3个算法中使用多线程并行化方法,有效缩减运行时间。实验结果表明,MSCOFRouting可以获得满足TDM比率约束的结果,取得同类工作中最佳的布线优化结果和TDM比率分配结果。Abstract: Time-Division Multiplexing (TDM) technology is widely applied to solving the IO limitation problem to improve the routability of FPGA system. However, the increase of the TDM ratio leads to a significant increase in system delay. Therefore, a Multi-Stage Co-Optimization FPGA routing (MSCOFRouting) for Time-Division Multiplexing is proposed in this paper to optimize the system delay and the routability of FPGA system. First, an adaptive routing algorithm is proposed to reduce routing congestion, improve the routability, solve the routing optimization problem between FPGAs, and provide high-quality routing results for subsequent TDM ratio assignment. Second, to avoid the delay degradation caused by excessive TDM ratio of large-scale net groups, a TDM ratio assignment algorithm based on Lagrangian relaxation is utilized to assign the initial TDM ratio with a smaller delay to the edge distribution system of the routing graph. In addition, a multi-level TDM ratio optimization algorithm is used to reduce the TDM ratios of the net group with maximum TDM ratios. The TDM ratio reduction is employed for the net group and the FPGA connection pair. Meanwhile, a multi-thread parallelization method is integrated into the three algorithms above to improve further the efficiency of MSCOFRouter. Experiments show that MSCOFRouting can obtain the results satisfying the TDM ratio constraint, and achieve the best routing optimization results and TDM ratio assignment results.
-
Key words:
- FPGA systems /
- Logic verification /
- Time-division multiplexing /
- Routing /
- Lagrangian relaxation
-
表 1 常用符号
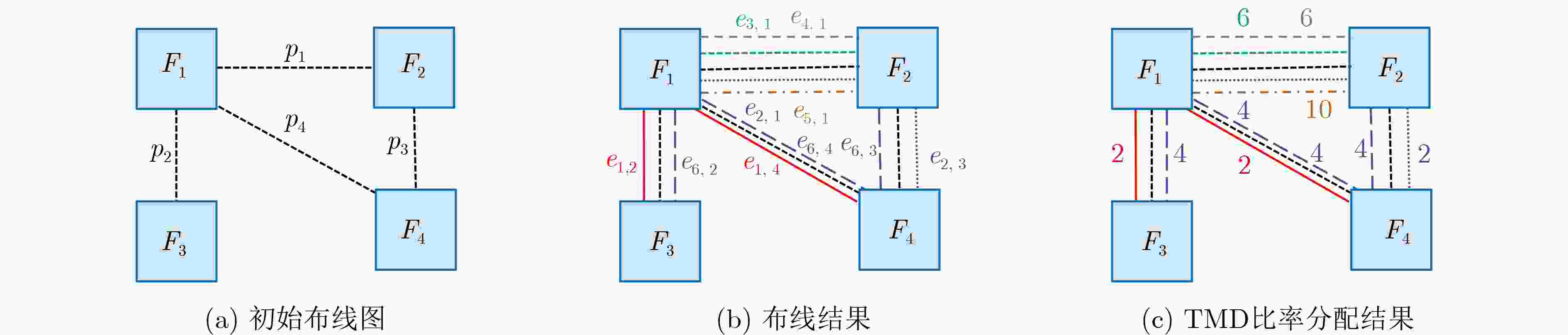
符号 含义 NG 所有线网组 N 所有线网 P 所有FPGA连接对 E 所有线网的边 Ne 经过边e的所有线网 ngi NG中第i个线网组 nj N中第j个线网 pk P中第k个FPGA连接对 nglj 包含nj的线网组,nglj ⊆NG ngj,m nglj中的第m个线网组 ej,k nj中使用pk的边 elk pk的边 elj nj的边 nli ngi的线网 α 线网组的数量 mngj nglj中带有最大TDM比率的线网组 表 2 线网组信息
线网组 线网 FPGA 示例 NG1 N1 F3, F4 
N2 F1, F4 
NG2 N3 F1, F2 
N4 F1, F2 
NG3 N1 F3, F4 
NG4 N5 F1, F2 
NG5 N6 F2, F3 
表 3 测试用例信息
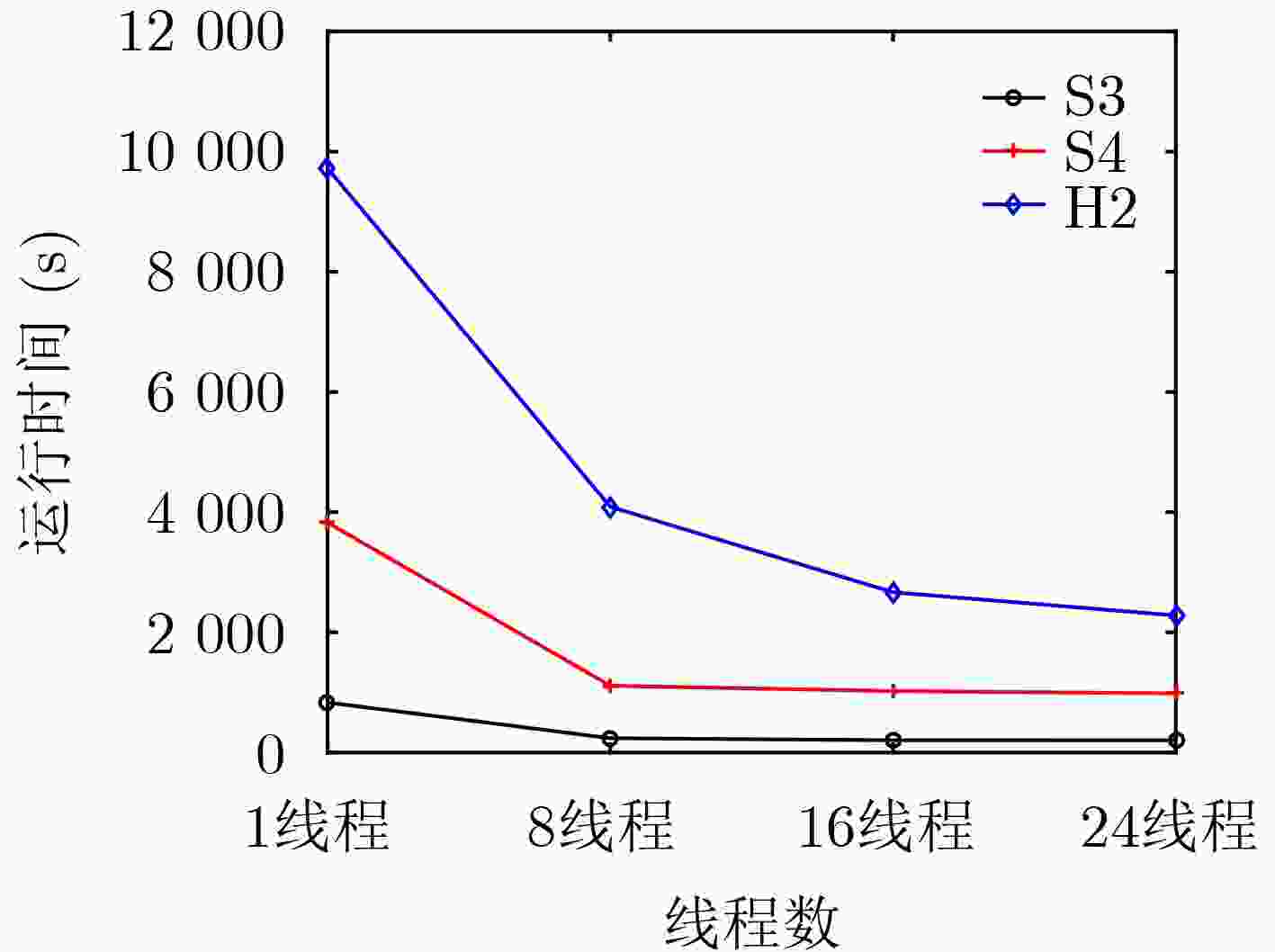
测试用例 #FPGA #Net #NG #Edge S1 43 68456 40552 214 S2 56 35155 56308 157 S3 114 302956 334652 350 S4 229 551956 464867 1087 S5 301 881480 879145 2153 S6 410 785539 910739 1852 H1 73 54310 50417 289 H2 157 610675 501594 803 H3 487 720520 886720 2720 表 4 本文算法与ALIFRouter及MSFRoute的实验比较(TR为TDM Ratio)
测试用例 MSFRoute ALIFRouter 本文算法 TR(103) RT sco TR(103) RT sco TR(103) RT sco S1 39 34.32 39 38 24.88 38 37 30.58 37 S2 32097 20.51 32097 31736 19.58 31730 31671 20.86 31673 S3 129396 289.91 129375 127826 304.50 127832 127046 300.99 127046 S4 7301 642.51 7301 6466 641.62 6466 6312 619.88 6311 S5 5370 1673.51 5371 4766 1558.48 4766 4618 1570.51 4618 S6 15759857 4536.33 15757896 15751307 4668.18 15751307 15747236 4845.90 15749791 H1 409654 76.86 409661 409026 76.54 409026 408487 66.81 408246 H2 45947775 1322.96 45947798 45942757 1322.81 45942757 45934257 1217.81 45917758 H3 4871917 5283.91 4868324 4866484 6593.58 4867575 4861401 6261.79 4861401 sum – – 62289539 – – 62273922 – – 62245480 Normalized 1.0457 1.0208 – 1.0105 1.0044 – 1.0000 1.0000 – 表 5 自适应布线算法有效性验证
测试用例 采用(te=1, to=1) 采用(te=0.21, to=1.79) 采用(te=0.2, to=1.8) 采用(te=0.19, to=1.81) 采用(te=0.18, to=1.82) △TR(103) Ratio △TR(103) Ratio △TR(103) Ratio △TR(103) Ratio △TR(104) Ratio S1 1 1.0000 1 1.0000 1 1.0000 2 2.0000 1 1.0000 S2 375 1.0000 417 1.1120 423 1.1280 428 1.1413 412 1.0987 S3 1841 1.0000 1864 1.0125 1948 1.0581 1986 1.0788 1941 1.0543 S4 832 1.0000 857 1.0300 931 1.1190 950 1.1418 927 1.1142 S5 604 1.0000 627 1.0381 697 1.1540 717 1.1871 687 1.1374 S6 11574 1.0000 13614 1.1763 12001 1.0369 12009 1.0376 12004 1.0372 H1 798 1.0000 801 1.0038 807 1.0113 812 1.0175 808 1.0125 H2 7742 1.0000 7785 1.0056 7795 1.0068 7821 1.0102 7801 1.0076 H3 6214 1.0000 6245 1.0050 9521 1.5322 10098 1.6250 9457 1.5219 平均 – 1.0000 – 1.0426 – 1.1163 – 1.2488 – 1.1093 表 6 LR分配算法(即TDM比率分配算法)和TDM比率优化算法有效性验证
测试用例 ALIFRouter 只使用LR分配算法 只使用TDM比率优化算法 △TR(103) Ratio △TR(103) Ratio △TR(103) Ratio S1 1 1.0000 1 1.0000 1 1.0000 S2 384 1.0000 421 1.0964 419 1.1607 S3 1877 1.0000 1960 1.0442 2155 1.3726 S4 848 1.0000 889 1.0483 937 1.1222 S5 621 1.0000 635 1.0225 690 1.1424 S6 11994 1.0000 18550 1.5466 11989 1.4022 H1 799 1.0000 804 1.0063 804 0.0022 H2 7775 1.0000 7776 1.0001 7776 1.5496 H3 6220 1.0000 6419 1.0320 6429 1.1833 平均 – 1.0000 – 1.0885 – 1.1039 -
[1] TURKI M, MARRAKCHI Z, MEHREZ H, et al. Signal multiplexing approach to improve inter-FPGA bandwidth of prototyping platform[J]. Design Automation for Embedded Systems, 2015, 19(3): 223–242. doi: 10.1007/s10617-014-9155-4 [2] LING A and ANDERSON J. The role of FPGAs in deep learning[C]. Proceedings of the 2017 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, USA, 2017: 3. [3] CHIU G R, LING A C, CAPALIJA D, et al. Flexibility: FPGAs and cad in deep learning acceleration[C]. Proceedings of the 2018 International Symposium on Physical Design, Monterey, USA, 2018: 34–41. [4] HUNG W N N and SUN R. Challenges in large FPGA-based logic emulation systems[C]. Proceedings of the 2018 International Symposium on Physical Design, Monterey, USA, 2018: 26–33. [5] HAUCK S. The roles of FPGAs in reprogrammable systems[J]. Proceedings of the IEEE, 1998, 86(4): 615–638. doi: 10.1109/5.663540 [6] CHEN S C, SUN R, and CHANG Yaowen. Simultaneous partitioning and signals grouping for time-division multiplexing in 2.5D FPGA-based systems[C]. 2018 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Diego, USA, 2018: 1–7. [7] TURKI M, MARRAKCHI Z, MEHREZ H, et al. Iterative routing algorithm of inter-FPGA signals for multi-FPGA prototyping platform[C]. The 9th International Symposium on Reconfigurable Computing: Architectures, Tools and Applications, Los Angeles, USA, 2013: 210–217. [8] FAROOQ U, CHOTIN-AVOT R, AZEEM M, et al. Inter-FPGA routing environment for performance exploration of multi-FPGA systems[C]. 2016 International Symposium on Rapid System Prototyping (RSP), Pittsburgh, USA, 2016: 1–7. [9] PUI C W and YOUNG E F Y. Lagrangian relaxation-based time-division multiplexing optimization for multi-FPGA systems[J]. ACM Transactions on Design Automation of Electronic Systems, 2020, 25(2): 21. doi: 10.1145/3377551 [10] INAGI M, TAKASHIMA Y, and NAKAMURA Y. Globally optimal time-multiplexing in inter-FPGA connections for accelerating multi-FPGA systems[C]. 2009 International Conference on Field Programmable Logic and Applications, Prague, Czech Republic, 2009: 212–217. [11] ZHUANG Zhen, HUANG Xing, LIU Genggeng, et al. ALIFRouter: A practical architecture-level inter-FPGA router for logic verification[C]. 2021 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 2021: 1570–1573. [12] SU Y H, SUN R, and HO P H. 2019 CAD contest: System-level FPGA routing with timing division multiplexing technique[C]. 2019 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), Westminster, USA, 2019: 1–2. [13] FRESCHI V and LATTANZI E. A prim–Dijkstra algorithm for Multihop calibration of networked embedded systems[J]. IEEE Internet of Things Journal, 2021, 8(14): 11320–11328. doi: 10.1109/JIOT.2021.3051270 [14] CHEN Xiaohua, ZHOU Ruping, LIU Genggeng, et al. Timing-driven X-architecture Steiner minimum tree construction based on social learning multi-objective particle swarm optimization[C]. Companion Proceedings of the Web Conference, Ljubljana, Slovenia, 2021: 77–84. [15] KULIK A, SHACHNAI H, and TAMIR G. On Lagrangian relaxation for constrained maximization and reoptimization problems[J]. Discrete Applied Mathematics, 2021, 296: 164–178. doi: 10.1016/j.dam.2020.10.001 [16] SHARMA A, CHINNERY D, DHAMDHERE S, et al. Rapid gate sizing with fewer iterations of Lagrangian relaxation[C]. 2017 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), Irvine, USA, 2017: 337–343. [17] MANGIRAS D, STEFANIDIS A, SEITANIDIS I, et al. Timing-driven placement optimization facilitated by timing-compatibility flip-flop clustering[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2020, 39(10): 2835–2848. doi: 10.1109/TCAD.2019.2942001 [18] ZHUANG Zhen, LIU Genggeng, HUANG Xing, et al. MSFRoute: Multi-stage FPGA routing for timing division multiplexing technique[C/OL]. Proceedings of the 2020 on Great Lakes Symposium on VLSI, 2020: 107–112. -





 下载:
下载:



 下载:
下载:
