Efficiency Optimized Design of Active Neutral Point Clamped Inverter Based on Deep Reinforcement Learning
-
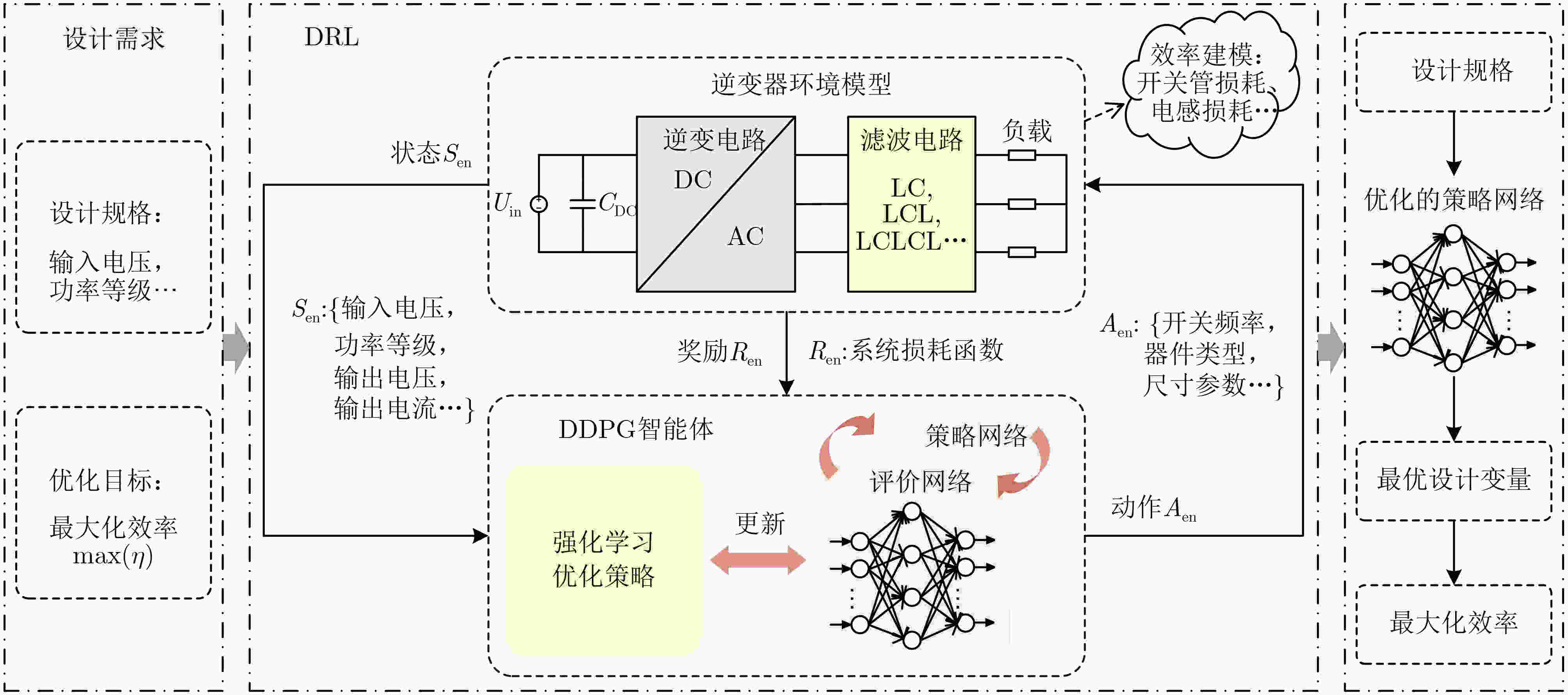
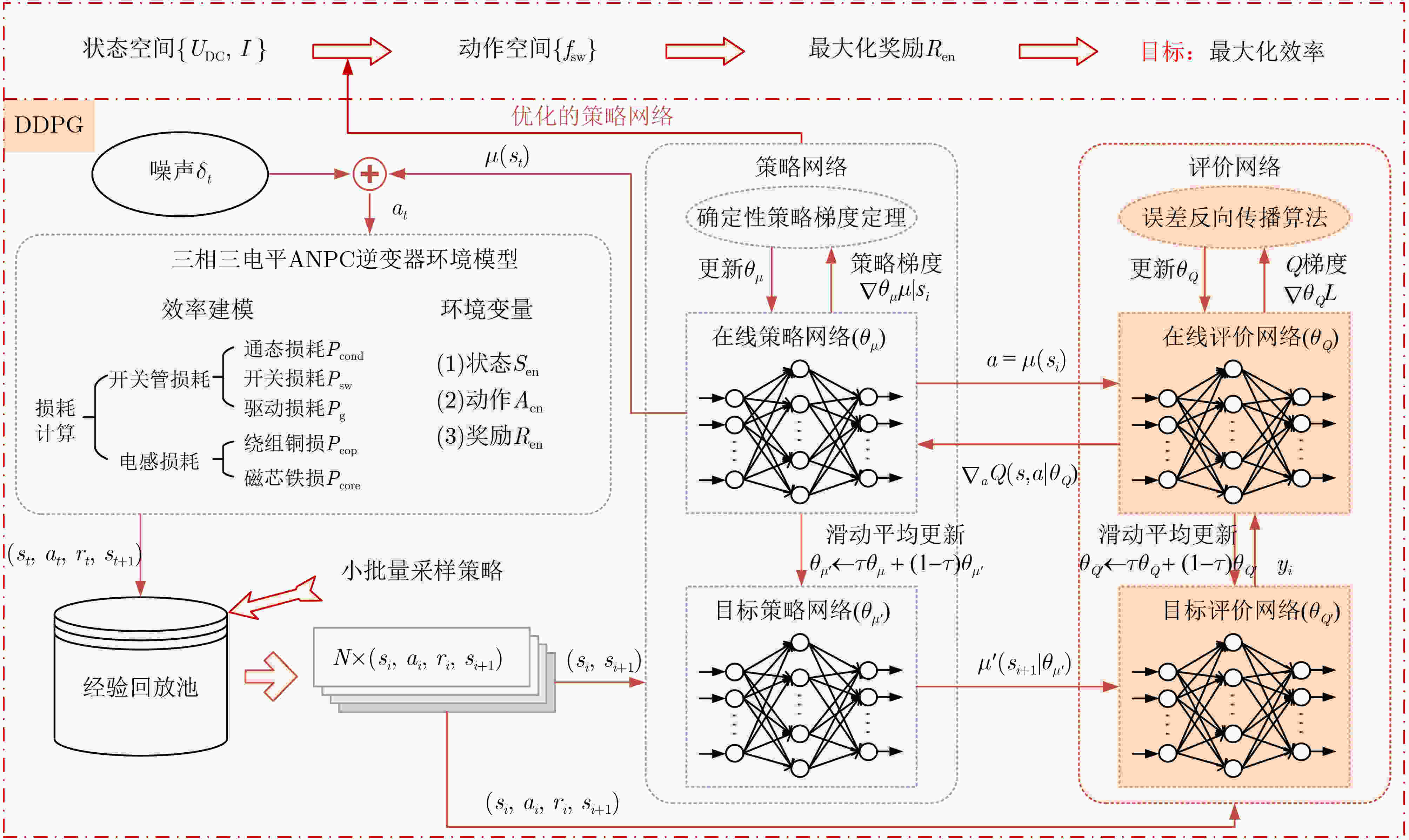
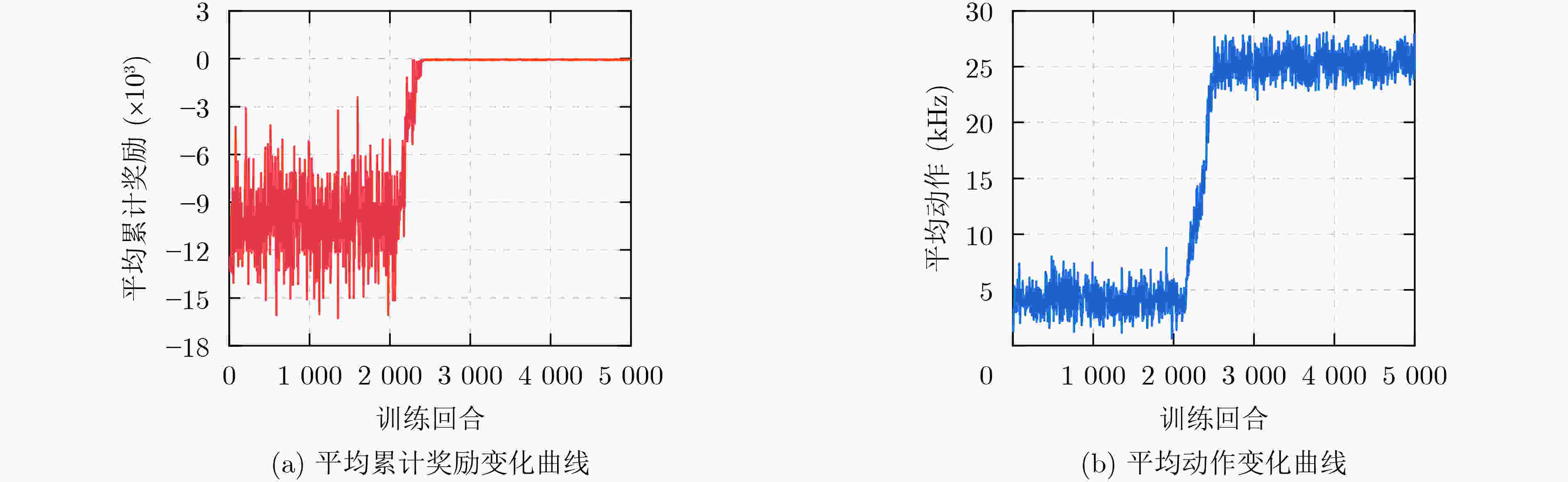
摘要: 传统电力电子变换器设计多采用顺序设计法,依赖人工经验。近年来,电力电子自动化设计可通过计算机快速优化设计电力电子系统而备受关注。该文以有源中点钳位(ANPC)逆变器的效率优化设计为例,提出一种基于深度强化学习(DRL)的电力电子自动化设计方法,可实现在变换器设计需求变化时,根据设计目标快速得到最优的设计参数。首先介绍了基于DRL的逆变器效率优化整体框架;然后建立了逆变器的效率模型;接着通过深度确定性策略梯度(DDPG)算法的自学习不断训练智能体,获得了最小化功率损耗的优化策略,该策略能够快速响应设计规格变化提供最大化效率的设计变量;最后,搭建了140 kW的实验样机,实验结果验证了所提方法的有效性,相比于遗传算法和强化学习(RL),实测效率分别提高了0.025 %和0.025 %。Abstract: The traditional power electronic converter design adopts mostly the sequential design method, which relies on manual experience. In recent years, power electronics automation design has attracted much attention by optimizing rapidly the design of power electronic systems with computers. Taking the efficiency optimized design of Active Neutral Point Clamped (ANPC) inverter as an example, a power electronics automation design method based on Deep Reinforcement Learning (DRL) is proposed, which can realize quickly to obtain the optimal design parameters according to the design objectives when the design requirements of converter change. Firstly, the overall framework of inverter efficiency optimization based on DRL is introduced; Then the efficiency model of the inverter is established; After that the agent is continuously trained through the self-learning of the Deep Deterministic Policy Gradient (DDPG) algorithm, and an optimization strategy that minimizes power loss is obtained; The strategy can quickly respond to design specification changes and provide design variables that maximize efficiency; Finally, a 140 kW experimental prototype is built, and the effectiveness of the proposed method is verified by the experimental results, which demonstrates efficiency improvements of 0.025 % and 0.025 % respectively compared to genetic algorithm and Reinforcement Learning (RL).
-
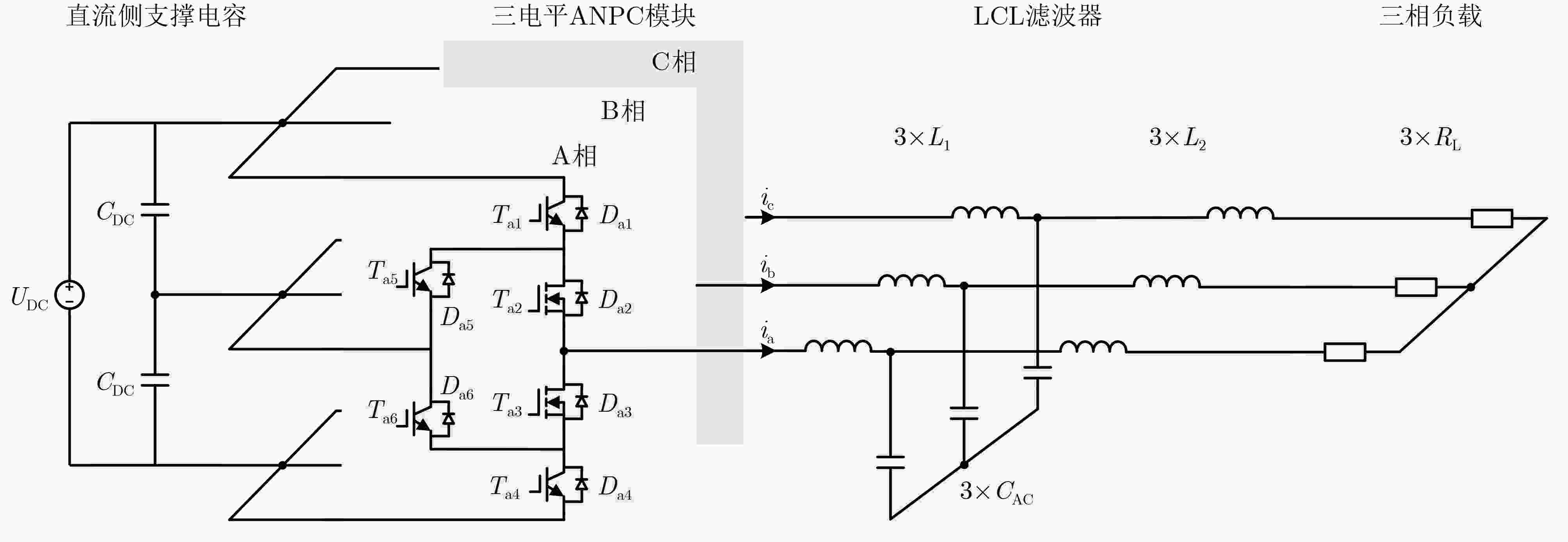
表 1 三相三电平ANPC逆变器的系统规格
参数 数值 额定功率Prated(kW) 140 直流侧输入电压UDC(V) 1 200 直流侧支撑电容CDC(μF) 20 滤波电容CAC(μF) 3 调制度m 0.9 功率因数λ 1 表 2 DDPG算法的关键参数
变量 取值 超参数 数值 UDC(V) 1000~1200 奖励系数ϕ 1 I(A) 100~120 经验回放池容量 40000 fsw(kHz) 10~100 小批量数目N 32 表 3 不同状态下的开关频率优化结果对比
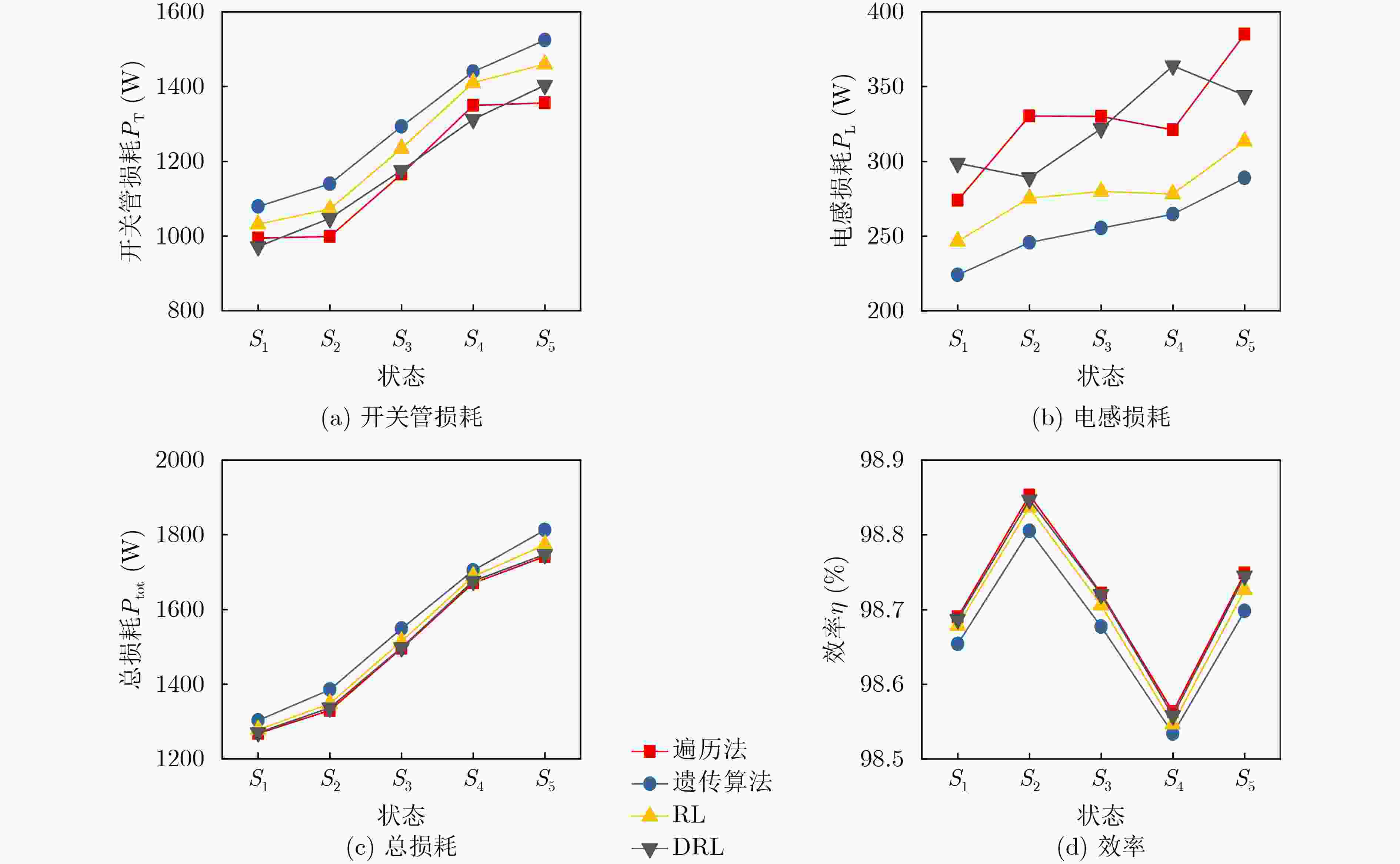
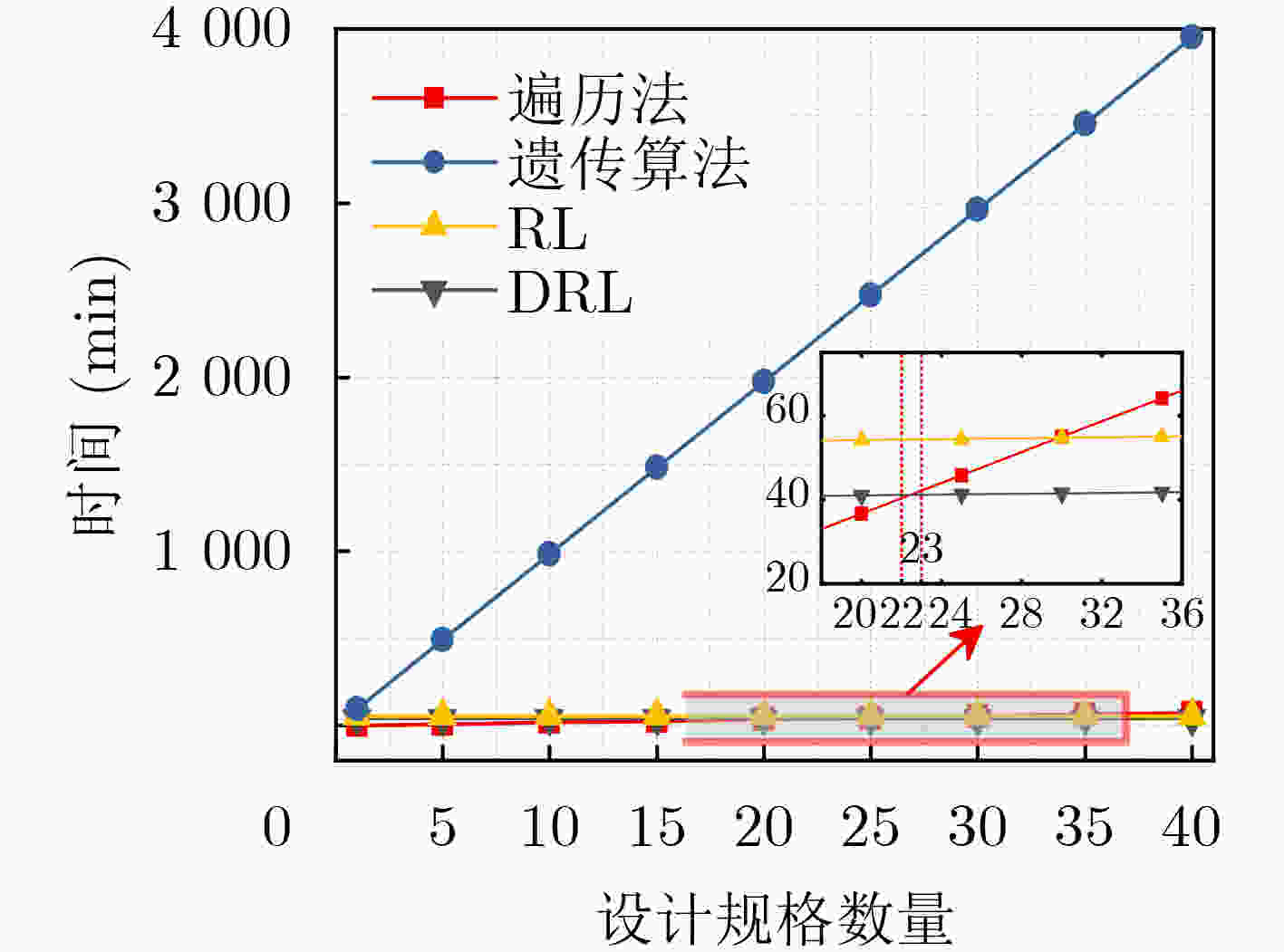
状态 UDC(V) I(A) fsw(kHz) 遍历法 遗传算法 RL DRL S1 1000 100 25.7 36.5 30.5 22.9 S2 1200 100 22.0 37.0 29.8 27.1 S3 1100 110 24.1 37.6 31.4 25.2 S4 1000 120 27.2 36.8 33.7 23.2 S5 1200 120 23.3 38.2 32.5 27.5 表 4 I = 30 A时,相比于遍历法,其他优化方法的各部分功率损耗对比
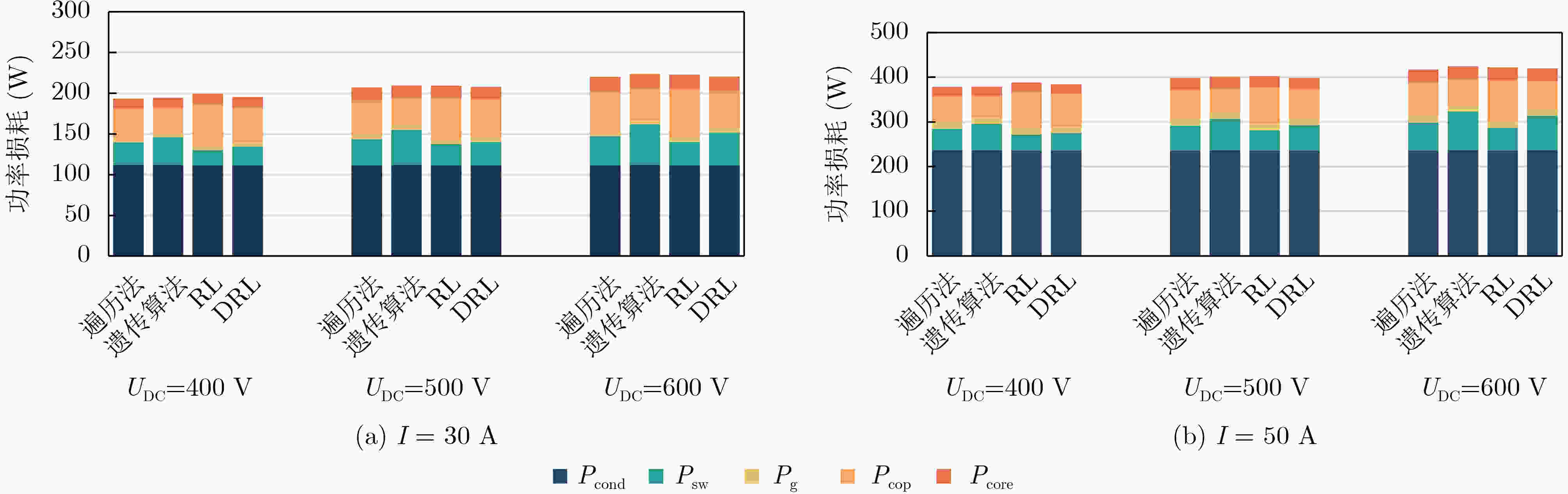
UDC(V) 方法 Pcond(W) Psw(W) Pg(W) Pcop(W) Pcore(W) 误差百分比平均值(%) 400 遍历法 111.73 27.98 4.95 36.35 12.44 – 遗传算法 111.89 33.97 4.92 31.22 12.45 7.27 RL 111.47 18.81 4.99 51.31 12.70 15.41 DRL 111.58 22.76 4.97 43.34 12.47 7.73 500 遍历法 111.66 32.17 4.96 42.78 15.35 – 遗传算法 111.91 43.05 4.92 34.49 15.15 11.11 RL 111.52 25.97 4.98 51.60 15.05 8.47 DRL 111.58 28.57 4.97 47.63 15.09 4.90 600 遍历法 111.60 35.52 4.97 50.24 17.80 – 遗传算法 111.88 50.12 4.92 38.75 17.97 13.24 RL 111.48 28.92 4.99 59.64 17.68 7.70 DRL 111.69 39.93 4.95 46.14 17.73 4.29 表 5 实验样机的测试条件
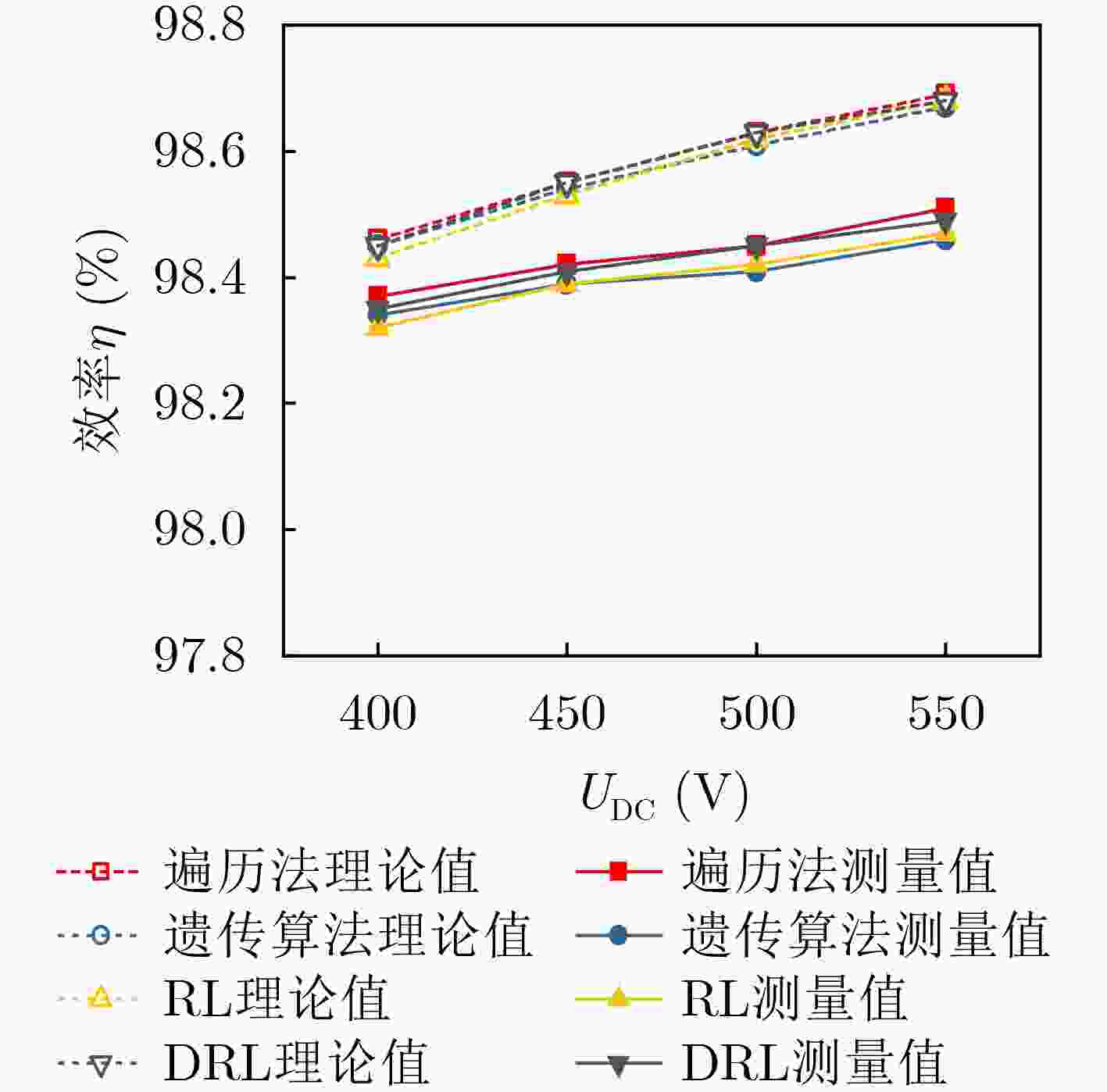
测试条件 输入功率
Pin(kW)直流侧输入电压
UDC(V)负载电阻
RL(Ω)开关频率fsw(kHz) 遍历法 遗传算法 RL DRL P1 7.0 400 6.5 30.6 35.2 21.8 25.0 P2 8.8 450 6.5 29.6 36.3 22.5 27.1 P3 11.0 500 6.5 28.1 36.7 23.1 29.2 P4 13.1 550 6.5 26.8 36.4 22.4 31.3 -
[1] BURKART R M and KOLAR J W. Comparative η-ρ-σ Pareto optimization of Si and SiC multilevel dual-active-bridge topologies with wide input voltage range[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5258–5270. doi: 10.1109/TPEL.2016.2614139 [2] YU Ruiyang, PONG B M H, LING B W K, et al. Two-stage optimization method for efficient power converter design including light load operation[J]. IEEE Transactions on Power Electronics, 2012, 27(3): 1327–1337. doi: 10.1109/TPEL.2011.2114676 [3] BUSQUETS-MONGE S, SOREMEKUN G, HEFIZ E, et al. Power converter design optimization[J]. IEEE Industry Applications Magazine, 2004, 10(1): 32–38. doi: 10.1109/MIA.2004.1256250 [4] 袁立强, 陆子贤, 戴宇轩, 等. 高性能电力电子设计自动化求解器关键因素与解决方法[J]. 中国电机工程学报, 2021, 41(20): 7055–7068. doi: 10.13334/j.0258-8013.pcsee.202413YUAN Liqiang, LU Zixian, DAI Yuxuan, et al. Key factors and methodology of high-performance design automation solver for power electronics[J]. Proceedings of the CSEE, 2021, 41(20): 7055–7068. doi: 10.13334/j.0258-8013.pcsee.202413 [5] DE LEÓN-ALDACO S E, CALLEJA H, and AGUAYO ALQUICIRA J. Metaheuristic optimization methods applied to power converters: A review[J]. IEEE Transactions on Power Electronics, 2015, 30(12): 6791–6803. doi: 10.1109/TPEL.2015.2397311 [6] BIELA J, KOLAR J W, STUPAR A, et al. Towards virtual prototyping and comprehensive multi-objective optimisation in power electronics[C]. The Power Conversion and Intelligent Motion Conference Europe, Nuremberg, Germany, 2010: 515–538. [7] BURKART R M and KOLAR J W. Comparative life cycle cost analysis of Si and SiC PV converter systems based on advanced η-ρ-σ multiobjective optimization techniques[J]. IEEE Transactions on Power Electronics, 2017, 32(6): 4344–4358. doi: 10.1109/TPEL.2016.2599818 [8] 赵斌, 王刚, 宋婧妍, 等. 基于粒子群算法的LCLC谐振变换器优化设计[J]. 电子与信息学报, 2021, 43(6): 1622–1629. doi: 10.11999/JEIT190337ZHAO Bin, WANG Gang, SONG Jingyan, et al. Optimal design method of the LCLC resonant converter based on particle-swarm-optimization algorithm[J]. Journal of Electronics &Information Technology, 2021, 43(6): 1622–1629. doi: 10.11999/JEIT190337 [9] LI Xinze, ZHANG Xin, LIN Fanfan, et al. Artificial-intelligence-based design for circuit parameters of power converters[J]. IEEE Transactions on Industrial Electronics, 2022, 69(11): 11144–11155. doi: 10.1109/TIE.2021.3088377 [10] CHEN Xin, QU Guannan, TANG Yujie, et al. Reinforcement learning for selective key applications in power systems: Recent advances and future challenges[J]. IEEE Transactions on Smart Grid, 2022, 13(4): 2935–2958. doi: 10.1109/TSG.2022.3154718 [11] 陈学松, 杨宜民. 强化学习研究综述[J]. 计算机应用研究, 2010, 27(8): 2834–2838,2844. doi: 10.3969/j.issn.1001-3695.2010.08.006CHEN Xuesong and YANG Yimin. Reinforcement learning: Survey of recent work[J]. Application Research of Computers, 2010, 27(8): 2834–2838,2844. doi: 10.3969/j.issn.1001-3695.2010.08.006 [12] LILLICRAP T P, HUNT J J, PRITZEL A, et al. Continuous control with deep reinforcement learning[C]. The 4th International Conference on Learning Representations, San Diego, America, 2016. [13] 乔骥, 王新迎, 张擎, 等. 基于柔性行动器–评判器深度强化学习的电–气综合能源系统优化调度[J]. 中国电机工程学报, 2021, 41(3): 819–832. doi: 10.13334/j.0258-8013.pcsee.201704QIAO Ji, WANG Xinying, ZHANG Qing, et al. Optimal dispatch of integrated electricity-gas system with soft actor-critic deep reinforcement learning[J]. Proceedings of the CSEE, 2021, 41(3): 819–832. doi: 10.13334/j.0258-8013.pcsee.201704 [14] TANG Yuanhong, HU Weihao, CAO Di, et al. Artificial intelligence-aided minimum reactive power control for the DAB converter based on harmonic analysis method[J]. IEEE Transactions on Power Electronics, 2021, 36(9): 9704–9710. doi: 10.1109/TPEL.2021.3059750 [15] TANG Yuanhong, HU Weihao, ZHANG Bin, et al. Deep reinforcement learning-aided efficiency optimized dual active bridge converter for the distributed generation system[J]. IEEE Transactions on Energy Conversion, 2022, 37(2): 1251–1262. doi: 10.1109/TEC.2021.3126754 [16] SUTTON R S and BARTO A G. Reinforcement Learning: An Introduction[M]. 2nd ed. Cambridge: MIT Press, 2018: 47–50. [17] JIAO Yang and LEE F C. LCL filter design and inductor current ripple analysis for a three-level NPC grid interface converter[J]. IEEE Transactions on Power Electronics, 2015, 30(9): 4659–4668. doi: 10.1109/TPEL.2014.2361907 [18] WANG Jianing, XUN Yuanwu, LIU Xiaohui, et al. Soft switching circuit of high-frequency active neutral point clamped inverter based on SiC/Si hybrid device[J]. Journal of Power Electronics, 2021, 21(1): 71–84. doi: 10.1007/s43236-020-00166-9 [19] ELIZONDO D, BARRIOS E L, URSÚA A, et al. Analytical modeling of high-frequency winding loss in round-wire toroidal inductors[J]. IEEE Transactions on Industrial Electronics, 2023, 70(6): 5581–5591. doi: 10.1109/TIE.2022.3192689 [20] SHIMIZU T and IYASU S. A practical iron loss calculation for AC filter inductors used in PWM inverters[J]. IEEE Transactions on Industrial Electronics, 2009, 56(7): 2600–2609. doi: 10.1109/TIE.2009.2018436 -





 下载:
下载:



 下载:
下载:
