Secure Computation of Two-party Multisets with Rational Numbers
-
摘要: 集合的安全多方计算(SMC)在联合数据分析、敏感数据安全查询、数据可信交换等场景有着广泛的应用。该文基于有理数的几何编码,结合保密内积协议,首次提出了有理数域上两方多重集交集和并集的保密计算协议。应用模拟范例证明了协议在半诚实模型下的安全性,分别通过理论分析和仿真测试验证了协议的高效性。与现有协议相比,所设计协议无需给定包含所有集合元素的全集,可以保护集合势的隐私性,且在协议执行过程主要使用乘法运算,达到了信息论安全。Abstract: Secure Multiparty Computation (SMC) of sets has wide applications in joint data analysis, secure search over sensitive data, data security exchange. Based on geometric coding of rational numbers and the scalar product protocol, two secure computation protocols for computing the intersection and the union of two multisets with private rational numbers are proposed for the first time. The simulation paradigm is used to prove the privacy- preserving properties of proposed protocols in the semi-honest model, and the protocols’ efficiency is verified by theoretical analysis and programming test. Compared with existing protocols, the proposed protocols do not need to specify a universal set, which can protect the privacy of set potential. Moreover, the multiplication operation is mainly used in the implementation of the protocols, which achieves the security of information theory.
-
Key words:
- Secure computation /
- Multiset /
- Set operation /
- Scalar product protocol
-
算法1 保密内积协议 输入:Alice和Bob分别输入私密向量${\boldsymbol{X}} = {({x_1},{x_2}, \cdots ,{x_n})^{\text{T}}}$和
$ {\boldsymbol{Y}} = {({y_1},{y_2}, \cdots ,{y_n})^{\text{T}}} $。输出:Alice输出内积$ {\boldsymbol{X}} \cdot {\boldsymbol{Y}} = \displaystyle\sum\nolimits_{i = 1}^n {{x_i}{y_i}} $。 (1)Alice和Bob共同生成一个$ n \times 1 $阶的矩阵$ {\boldsymbol{P}} $。 (2)Alice进行如下操作: (a)随机生成一个1维向量$ {\boldsymbol{R}}{\text{ = (}}r{\text{)}} $。 (b)计算$ n \times 1 $阶矩阵${\boldsymbol{X'}}$:${\boldsymbol{X'}} = {\boldsymbol{PR}}$。 (c)计算${\boldsymbol{X''}} = {\boldsymbol{X'}} + {\boldsymbol{X}}$,并将$ {\boldsymbol{X''}} $发送给Bob。 (3)Bob进行如下操作:
(a)计算内积$Z'$:$Z' = {\boldsymbol{X''} } \cdot {\boldsymbol{Y} } = \displaystyle\sum\nolimits_{i = 1}^n { { x''_i} } {y_i}$。(b)计算1阶矩阵${\boldsymbol{Y'}}$:${\boldsymbol{Y'}} = {{\boldsymbol{P}}^{\text{T}}}{\boldsymbol{Y}}$。 (c)将$Z'$和${\boldsymbol{Y'}}$发送给Alice。 (4)Alice进行如下操作:
(a)计算减法因子$Z''$:$ Z'' = {\boldsymbol{R}} \cdot {\boldsymbol{Y'}} = r\displaystyle\sum\nolimits_{i = 1}^n {{p_i}{y_i}} $。(b)计算内积$Z$:$Z = Z' - Z''$。最后输出内积$ Z{\boldsymbol{ = X}} \cdot {\boldsymbol{Y}} $。 协议1 有理数域上两方多重集交集的保密计算 输入:Alice和Bob分别输入有理数多重集$U = \{ < {u_{11}},{u_{21}} > , < {u_{12}},{u_{22}} > , \cdots , < {u_{1n}},{u_{2n}} > \} $和$V = \{ < {v_{11} },{v_{21} } > , < {v_{12} },{v_{22} } > , \cdots ,$
$< {v_{1m} } \cdot {v_{2m} } > \}$。输出:交集$ U \cap V $。 准备:Alice和Bob根据计算原理1构造标准集${U_1},{V_1}$,并协商正整数$ l $,合作生成$ (l + 1) \times 1 $阶矩阵${{\boldsymbol{P}}_1}$。Alice将$ {U_1} $中元素转化为对应直线上
的整数点,保证每个元素至少对应1个整数点,设共得到$ l $个整数点,根据式(7)构造标准集$ {U_1} $对应的向量${\boldsymbol{C} }{\text{ = } }{({c_l},{c_{l - 1} }, \cdots ,{c_1},{c_0})^{\text{T} } }$。Bob
将$ {v_{1j}} $$ (j{\text{ = }}1,2, \cdots ,m) $转化为对应直线上的任意两个整数点,构造$ {v_{1j}} $对应的向量$ {{\boldsymbol{A}}_j}{\text{ = }}{({a_j}^l,{a_j}^{l - 1}{b_j}, \cdots ,{a_j}{b_j}^{l - 1},{b_j}^l)^{\text{T}}} $。对$ j{\text{ = }}1,2, \cdots ,l $,Alice和Bob执行如下步骤: (1)Alice进行如下操作: (a)随机生成1维向量$ {{\boldsymbol{R}}_j}{\text{ = (}}{r_j}{\text{)}} $。 (b)生成对应的$ (l + 1) \times 1 $阶矩阵${ {\boldsymbol{C} }'_j}$:${ {\boldsymbol{C} }'_j} = { {\boldsymbol{P} }_1}{ {\boldsymbol{R} }_j}$。 (c)计算${ {\boldsymbol{C} }''_j} = { {\boldsymbol{C} }'_j} + {\boldsymbol{C} }$,并将所有的$ {{\boldsymbol{C}}''_j} $发送给Bob。 (2)Bob进行如下操作: (a)对$j{\text{ = }}1,2, \cdots ,m$计算内积${Z'_j}$:${Z'_j} = {{\boldsymbol{A}}_j} \cdot {{\boldsymbol{C}}''_j}$;对$j{\text{ = }}m + 1,m + 2, \cdots ,l$随机生成$l + 1$维向量${{\boldsymbol{A}}_j}$,并计算内积${Z'_j} = {{\boldsymbol{A}}_j} \cdot {{\boldsymbol{C}}''_j}$。 (b)生成对应的1阶矩阵${ {\boldsymbol{A} }'_j}$:${ {\boldsymbol{A} }'_j} = {\boldsymbol{P} }_1^{\text{T} }{ {\boldsymbol{A} }_j}$。 (c)将${Z'_j}$和${ {\boldsymbol{A} }'_j}$发送给Alice。 (3)Alice进行如下操作: (a)生成减法因子${Z''_j}$:${Z''_j} = { {\boldsymbol{R} }_j} \cdot { {\boldsymbol{A} }'_j}$。 (b)计算内积$ {Z_j} $:$ {Z_j} = {Z'_j} - {Z''_j} = {{\boldsymbol{A}}_j} \cdot {\boldsymbol{C}} $。如果$ {Z_j} = 0 $,令${e_j} = 1$;否则${e_j} = 0$,得到向量${\boldsymbol{E}} = ({e_1},{e_2}, \cdots ,{e_l})$,将向量${\boldsymbol{E}}$发送给Bob。 (4)Bob选取向量${\boldsymbol{E}}$中前$ m $个分量中1所在位置对应的元素$ {v_{1j}} $构成集合$ {X_1} $,将集合$ {X_1} $中的元素进行随机置换后输出集合${X_1}{\text{ = }}{U_1} \cap {V_1} = $
$ \{ {x_{11}},{x_{12}}, \cdots ,{x_{1k}}\} $。(5)Alice和Bob按照计算原理1根据${x_{1i}}$$(i = 1,2, \cdots ,k)$在$U,V$中的重数${p_i},{q_i}$构造$d$维向量${{\boldsymbol{S}}_i} = {({s_{i1}},{s_{i2}}, \cdots ,{s_{id}})^{\text{T}}}$和${{\boldsymbol{T}}_i} = {({t_{i1}},{t_{i2}}, \cdots ,{t_{id}})^{\text{T}}}$,
两人分别随机生成$d$维向量${\boldsymbol{S}}_i^1,{\boldsymbol{T}}_i^1$,计算${\boldsymbol{S}}_i^2$和${\boldsymbol{T}}_i^2$,其中,${\boldsymbol{S}}_i^2 = {{\boldsymbol{S}}_i} - {\boldsymbol{S}}_i^1$,${\boldsymbol{T}}_i^2 = {{\boldsymbol{T}}_i} - {\boldsymbol{T}}_i^1$,并合作生成$ d \times 1 $阶矩阵${{\boldsymbol{P}}_2}$。对$i = 1,2, \cdots ,k$,Alice和Bob执行如下步骤: (6)Alice进行如下操作: (a)生成4个1维向量${\boldsymbol{R}}_i^{ab} = ({r_i}^{ab})$,$a = 1,2$,$b = 1,2$。 (b)对应计算$d \times 1$阶矩阵${\boldsymbol{S}}'^{ab}_i = { {\boldsymbol{P} }_2}{\boldsymbol{R} }_i^{ab}$。 (c)计算${\boldsymbol{S} }''^{ab}_i = {\boldsymbol{S} }'^{ab}_i + {\boldsymbol{S} }_i^a$,并将所有的${\boldsymbol{S} }''^{ab}_i$发送给Bob。 (7)Bob进行如下操作: (a)计算内积$W{'}_i^{ab} = {\boldsymbol{S} }''^{ab}_i \cdot {\boldsymbol{T} }_i^b$。 (b)计算1阶矩阵${\boldsymbol{T} }'^{ab}_i = {\boldsymbol{P} }_2^{\text{T} }{\boldsymbol{T} }_i^b$。 (c)将$ {W{'}}_i^{ab} $和$ {\boldsymbol{T'}}_i^{ab} $发送给Alice。 (8)Alice进行如下操作: (a)计算$W''^{ab}_i = {\boldsymbol{T} }'^{ab}_i \cdot {\boldsymbol{R} }_i^{ab}$。 (b)计算内积$W_i^{ab} = W'{ab}_i^ - W''^{ab}_i = {\boldsymbol{S} }_i^a \cdot {\boldsymbol{T} }_i^b$。 (c)令${x_{2i}} = {W_i} = W_i^{11} + W_i^{12} + W_i^{21} + W_i^{22} = {{\boldsymbol{S}}_i} \cdot {{\boldsymbol{T}}_i}$,得到集合${X_2} = \{ {x_{21}},{x_{22}}, \cdots ,{x_{2k}}\} $。 (9)输出两方多重集交集$X = U \cap V = \{ < {x_{11}},{x_{21}} > , < {x_{12}},{x_{22}} > , \cdots , < {x_{1k}},{x_{2k}} > \} $。 协议2 有理数域上两方多重集并集的保密计算 协议2保持协议1中第(1)和第(2)步不变,对后续步骤做如下修改,输出有理数域上两方多重集并集$U \cup V$。 (3)Alice进行如下操作: (a)生成减法因子${Z''_j}$:${Z''_j} = { {\boldsymbol{R} }_j} \cdot { {\boldsymbol{A} }'_j}$。 (b)计算内积$ {Z_j} $:$ {Z_j} = {Z'_j} - {Z''_j} = {{\boldsymbol{A}}_j} \cdot {\boldsymbol{C}} $。如果${Z_j} = 0$,令${e_j} = 1$;否则${e_j} = 0$,得到$l$维向量${\boldsymbol{E}} = ({e_1},{e_2}, \cdots ,{e_l})$。 (c)随机选取整数$ r $,满足$ 0 \le r < \displaystyle\sum\nolimits_{i = 1}^l {{e_i}} $,在$ {\boldsymbol{E}} $的分量中选取$ r $个1变为0,得到新的向量$ {\boldsymbol{E'}} $,把$ {\boldsymbol{E'}} $发送给Bob。 (4)Bob选取$ {\boldsymbol{E'}} $中的前$ m $个分量中0所在位置对应的$ {v_{1j}} $构成集合$ H $,将$ H $中元素随机置换后发送给Alice。 (5)Alice输出${Y_1} = {U_1} \cup H = {U_1} \cup {V_1} = \{ {y_{11}},{y_{12}}, \cdots ,{y_{1h}}\} $。 (6)Alice和Bob根据计算原理2 构造${y_{1i}}$$(i = 1, 2,\cdots ,h)$在$U,V$中的重数${p_i},{q_i}$对应的向量${{\boldsymbol{S}}_i} = {({s_{i1}},{s_{i2}}, \cdots ,{s_{id}})^{\text{T}}}$和${{\boldsymbol{T}}_i} = {({t_{i1}},{t_{i2}}, \cdots ,{t_{id}})^{\text{T}}}$,根
据协议2的后续步骤构造${\boldsymbol{S}}_i^1$,${\boldsymbol{S}}_i^2$和${\boldsymbol{T}}_i^1$,${\boldsymbol{T}}_i^2$,满足${{\boldsymbol{S}}_i} = {\boldsymbol{S}}_i^1 + {\boldsymbol{S}}_i^2$,${{\boldsymbol{T}}_i} = {\boldsymbol{T}}_i^1 + {\boldsymbol{T}}_i^2$,计算内积${{\boldsymbol{S}}_i} \cdot {{\boldsymbol{T}}_i} = {\boldsymbol{S}}_i^1 \cdot {\boldsymbol{T}}_i^1 + {\boldsymbol{S}}_i^1 \cdot {\boldsymbol{T}}_i^2 + {\boldsymbol{S}}_i^2 \cdot {\boldsymbol{T}}_i^1 + {\boldsymbol{S}}_i^2 \cdot {\boldsymbol{T}}_i^2$,
则${y_{1i}}$的重数${y_{2i}} = d - {{\boldsymbol{S}}_i} \cdot {{\boldsymbol{T}}_i} = \max \{ {p_i},{q_i}\} $。(7)输出两方多重集并集$Y = U \cup V = \{ < {y_{11}},{y_{21}} > , < {y_{12}},{y_{22}} > , \cdots , < {y_{1h}},{y_{2h}} > \} $。 表 1 协议的效率分析和适用性范围比较
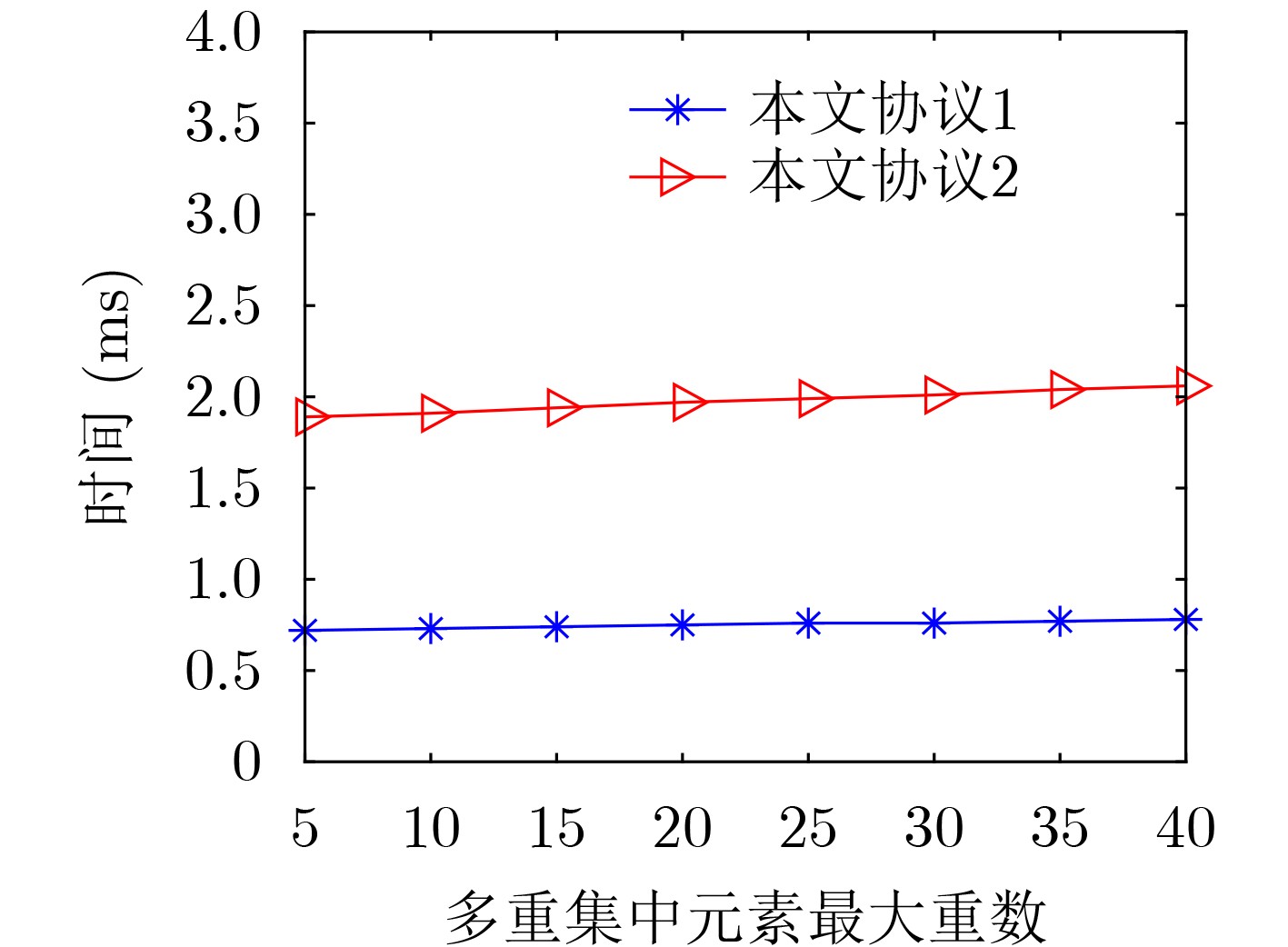
表 2 实验结果分析(ms)
协议 数据预处理耗时 交互计算耗时 实验总耗时 协议1 38.31 0.73 39.04 协议2 38.65 1.91 40.56 -
[1] YAO A C. Protocols for secure computations[C]. The 23rd Annual Symposium on Foundations of Computer Science, Chicago, USA, 1982: 160–164. [2] TANG Chunming, SHI Guihua, and YAO Zhengan. Secure multi-party computation protocol for sequencing problem[J]. Science China Information Sciences, 2011, 54(8): 1654–1662. doi: 10.1007/s11432-011-4272-1 [3] TOFT T. Sub-linear, secure comparison with two non-colluding parties[C]. The 14th International Conference on Practice and Theory in Public Key Cryptography, Taormina, Italy, 2011: 174–191. [4] LI Shundong, WU Chunying, WANG Daoshun, et al. Secure multiparty computation of solid geometric problems and their applications[J]. Information Sciences, 2014, 282: 401–413. doi: 10.1016/j.ins.2014.04.004 [5] 郭奕旻, 周素芳, 窦家维, 等. 高效的区间保密计算及应用[J]. 计算机学报, 2017, 40(7): 1664–1679. doi: 10.11897/SP.J.1016.2017.01664GUO Yimin, ZHOU Sufang, DOU Jiawei, et al. Efficient privacy-preserving interval computation and its applications[J]. Chinese Journal of Computers, 2017, 40(7): 1664–1679. doi: 10.11897/SP.J.1016.2017.01664 [6] 张卫国, 孙嫚, 陈振华, 等. 空间位置关系的安全多方计算及其应用[J]. 电子与信息学报, 2016, 38(9): 2294–2300. doi: 10.11999/JEIT160102ZHANG Weiguo, SUN Man, CHEN Zhenhua, et al. Secure multi-party computation of spatial relationship and its application[J]. Journal of Electronics &Information Technology, 2016, 38(9): 2294–2300. doi: 10.11999/JEIT160102 [7] NIKSEFAT S, SADEGHIYAN B, MOHASSEL P, et al. ZIDS: A privacy-preserving intrusion detection system using secure two-party computation protocols[J]. The Computer Journal, 2014, 57(4): 494–509. doi: 10.1093/comjnl/bxt019 [8] GRIGORIEV D and SHPILRAIN V. Yao’s millionaires’ problem and decoy-based public key encryption by classical physics[J]. International Journal of Foundations of Computer Science, 2014, 25(4): 409–417. doi: 10.1142/S0129054114400036 [9] LI Shundong, WANG Daoshun, and DAI Yiqi. Symmetric cryptographic protocols for extended millionaires’ problem[J]. Science in China Series F:Information Sciences, 2009, 52(6): 974–982. doi: 10.1007/s11432-009-0109-6 [10] FREEDMAN M J, NISSIM K, and PINKAS B. Efficient private matching and set intersection[C]. International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2004: 1–19. [11] 陈振华, 李顺东, 黄琼, 等. 非加密方法安全计算两种集合关系[J]. 软件学报, 2018, 29(2): 473–482. doi: 10.13328/j.cnki.jos.005262CHEN Zhenhua, LI Shundong, HUANG Qiong, et al. Secure computation of two set-relationships with the unencrypted method[J]. Journal of Software, 2018, 29(2): 473–482. doi: 10.13328/j.cnki.jos.005262 [12] SEO J H, CHEON J H, and KATZ J. Constant-round multi-party private set union using reversed Laurent series[C]. The 15th International Conference on Practice and Theory in Public Key Cryptography, Darmstadt, Germany, 2012: 398–412. [13] CHUN Jiyong, HONG D, JEONG I R, et al. Privacy-preserving disjunctive normal form operations on distributed sets[J]. Information Sciences, 2013, 231: 113–122. doi: 10.1016/j.ins.2011.07.003 [14] KISSNER L and SONG D. Privacy-preserving set operations[C]. The 25th Annual International Cryptology Conference on Advances in Cryptology, Santa Barbara, USA, 2005: 241–257. [15] BLANTON M and AGUIAR E. Private and oblivious set and multiset operations[J]. International Journal of Information Security, 2016, 15(5): 493–518. doi: 10.1007/s10207-015-0301-1 [16] 窦家维, 陈明艳. 多重集的保密计算及应用[J]. 电子学报, 2020, 48(1): 204–208. doi: 10.3969/j.issn.0372-2112.2020.01.025DOU Jiawei and CHEN Mingyan. Secure multiset operations and their applications[J]. Acta Electronica Sinica, 2020, 48(1): 204–208. doi: 10.3969/j.issn.0372-2112.2020.01.025 [17] CHUNG H and KIM M. Encoding of rational numbers and their homomorphic computations for FHE-based applications[J]. International Journal of Foundations of Computer Science, 2018, 29(6): 1023–1044. doi: 10.1142/S0129054118500193 [18] 李顺东, 杜润萌, 杨颜璟, 等. 有理数相等的保密判定[J]. 电子学报, 2020, 48(10): 1933–1937. doi: 10.3969/j.issn.0372-2112.2020.10.009LI Shundong, DU Runmeng, YANG Yanjing, et al. Privately determining equality of rational numbers[J]. Acta Electronica Sinica, 2020, 48(10): 1933–1937. doi: 10.3969/j.issn.0372-2112.2020.10.009 [19] 窦家维, 刘旭红, 王文丽. 有理数域上两方集合的高效保密计算[J]. 计算机学报, 2020, 43(8): 1397–1413. doi: 10.11897/SP.J.1016.2020.01397DOU Jiawei, LIU Xuhong, and WANG Wenli. Privacy preserving two-party rational set computation[J]. Chinese Journal of Computers, 2020, 43(8): 1397–1413. doi: 10.11897/SP.J.1016.2020.01397 [20] GOLDREICH O. Foundations of Cryptography Volume 2: Basic Applications[M]. Cambridge: Cambridge University Press, 2004. [21] REIMER B, FRIED R, MEHLER B, et al. Brief report: Examining driving behavior in young adults with high functioning autism spectrum disorders: A pilot study using a driving simulation paradigm[J]. Journal of Autism and Developmental Disorders, 2013, 43(9): 2211–2217. doi: 10.1007/s10803-013-1764-4 [22] CLIFTON C, KANTARCIOGLU M, VAIDYA J, et al. Tools for privacy preserving distributed data mining[J]. ACM SIGKDD Explorations Newsletter, 2002, 4(2): 28–34. doi: 10.1145/772862.772867 -





 下载:
下载:


 下载:
下载:
