A Fast Signal Parameter Estimation Algorithm for Linear Frequency Modulation Signal under Low Signal-to-Noise Ratio Based on Fractional Fourier Transform
-
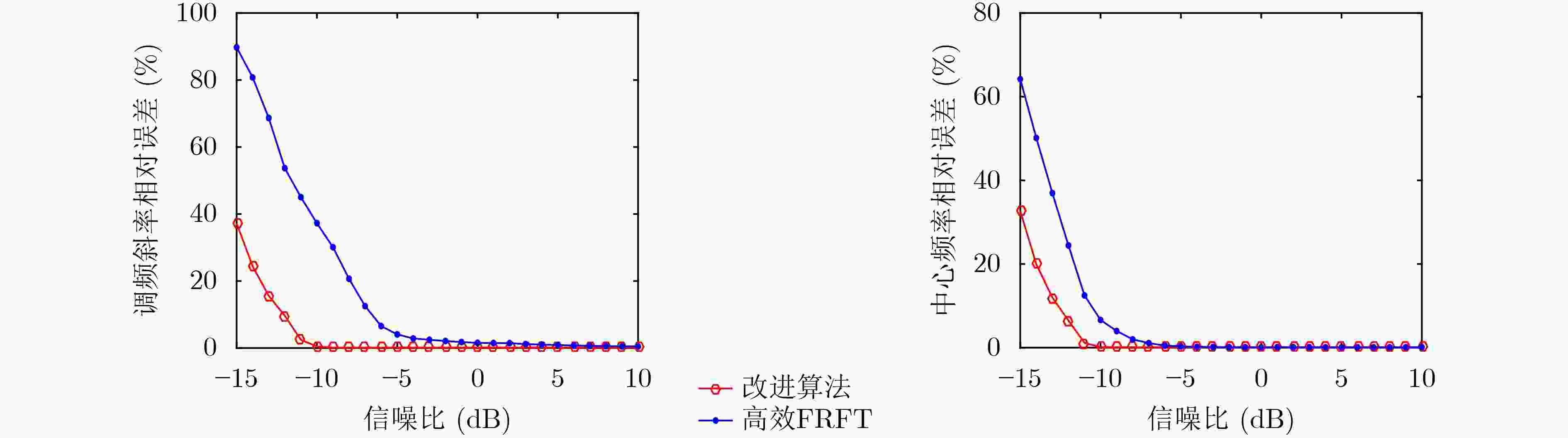
摘要: 针对低信噪比线性调频信号参数估计精度低且运算量大的问题,该文提出一种基于高效分数阶傅里叶变换(FRFT)和分数阶频谱4阶原点矩的快速估计算法。该算法通过判断调频斜率的正负,以确定旋转阶次所在初始区间;进而应用高效FRFT获得初始旋转阶次;最终利用分数阶频谱4阶原点矩,进一步确定搜索区间和步长,实现精准搜索,从而满足参数精度的要求。实验结果表明,该算法尤其适合用于低信噪比情况下的线性调频(LFM)信号检测与参数的准确估计,而且运算量较低。
-
关键词:
- 线性调频信号 /
- 高效分数阶傅里叶变换 /
- 分数阶频谱4阶原点矩 /
- 低信噪比
Abstract: An algorithm based on high-efficiency FRactional Fourier Transform (FRFT) and fourth-order origin moments in the fractional-domain spectrum is proposed to estimate quickly the chirp signal at low signal-to-noise ratio. Firstly, the initial interval of the rotation order is determined by the sign of the FM slope. Then, the rotation order is estimated roughly by the efficient FRFT algorithm. Finally, the search interval and step size are determined according to the fourth-order origin moments of the spectrum in the fractional-domain. The simulation results show that the Linear Frequency Modulation (LFM) signal can be detected under low signal-to-noise ratio and the parameters of the signal can be estimated accurately using this algorithm, and the signal can be detected with a small amount of calculation. -
表 1 3种算法对比仿真结果
估计方法 允许阶次误差 $\hat k\left({\rm{Hz /t}} \right)$ $\hat f\left( {{\rm{Hz}}} \right)$ ${k_{{{\rm{error}}}}}\left( \% \right)$ ${f_{{{\rm{error}}}}}\left( \% \right)$ FRFT运算次数 高效FRFT算法 – 1537.2000 1580.3 53.7244 5.3565 3 FRFT 2维搜索 <0.0100 1104.0000 1511.1 10.4010 0.7417 201 FRFT 2维搜索 <0.0010 1024.6000 1501.8 2.4580 0.1214 2001 FRFT 2维搜索 <0.0001 1003.9000 1501.5 0.3950 0.1007 20001 改进搜索算法 <0.0100 940.2061 1510.2 5.9794 0.6800 7 改进搜索算法 <0.0010 993.1624 1501.1 0.6838 0.0754 20 改进搜索算法 <0.0001 1002.3000 1500.8 0.2281 0.0531 43 -
[1] DUAN Yu, WANG Jinzhen, SU Shaoying, et al. Detection of LFM signals in low SNR based on STFT and wavelet denoising[C]. 2014 International Conference on Audio, Language and Image Processing, Shanghai, China, 2014: 921–925. [2] YIN Qingbo, SHEN Liran, LU Mingyu, et al. Selection of optimal window length using STFT for quantitative SNR analysis of LFM signal[J]. Journal of Systems Engineering and Electronics, 2013, 24(1): 26–35. doi: 10.1109/JSEE.2013.00004 [3] XU Fenfei, BAO Qinglong, CHEN Zengping, et al. Parameter estimation of multi-component LFM signals based on STFT+Hough transform and fractional fourier transform[C]. The 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 2018: 839–842. [4] ZHANG Zhichao. Linear canonical Wigner distribution based noisy LFM signals detection through the output SNR improvement analysis[J]. IEEE Transactions on Signal Processing, 2019, 67(21): 5527–5542. doi: 10.1109/TSP.2019.2941071 [5] WU Yushuang and LI Xiukun. Elimination of cross-terms in the Wigner–Ville distribution of multi-component LFM signals[J]. IET Signal Processing, 2017, 11(6): 657–662. doi: 10.1049/iet-spr.2016.0358 [6] ZHANG Zhichao. The optimal linear canonical Wigner distribution of noisy linear frequency-modulated signals[J]. IEEE Signal Processing Letters, 2019, 26(8): 1127–1131. doi: 10.1109/LSP.2019.2922510 [7] HUANG Xiang, ZHANG Linrang, ZHANG Juan, et al. Efficient angular chirp-Fourier transform and its application to high-speed target detection[J]. Signal Processing, 2019, 164: 234–248. doi: 10.1016/j.sigpro.2019.06.011 [8] YANG Tiantian, SHAO Jie, CHEN Yongliang, et al. Parameter estimation of multi component LFM signals based on nonlinear mode decomposition and FRFT[C]. The 10th International Conference on Advanced Computational Intelligence (ICACI), Xiamen, China, 2018: 204–209. [9] MIAO Hongxia, ZHANG Feng, and TAO Ran. Fractional Fourier analysis using the Möbius inversion formula[J]. IEEE Transactions on Signal Processing, 2019, 67(12): 3181–3196. doi: 10.1109/TSP.2019.2912878 [10] LIU Yifei, ZHAO Yuan, ZHU Jun, et al. Iterative high-accuracy parameter estimation of uncooperative OFDM-LFM radar signals based on FRFT and fractional autocorrelation interpolation[J]. Sensors, 2018, 18(10): 3550. doi: 10.3390/s18103550 [11] 赵兴浩, 邓兵, 陶然. 分数阶傅里叶变换数值计算中的量纲归一化[J]. 北京理工大学学报, 2005, 25(4): 360–364. doi: 10.3969/j.issn.1001-0645.2005.04.019ZHAO Xinghao, DENG Bing, and TAO Ran. Dimensional normalization in the digital computation of the fractional fourier transform[J]. Transactions of Beijing Institute of Technology, 2005, 25(4): 360–364. doi: 10.3969/j.issn.1001-0645.2005.04.019 [12] 仇兆炀, 陈蓉, 汪一鸣. 基于FRFT的线性调频信号欠采样快速检测方法[J]. 电子学报, 2012, 40(11): 2165–2170.QIU Zhaoyang, CHEN Rong, and WANG Yiming. Fast detection of LFM signal based on FRFT and sub-nyquist sampling[J]. Acta Electronica Sinica, 2012, 40(11): 2165–2170. [13] ALDIMASHKI O and SERBES A. Performance of chirp parameter estimation in the fractional fourier domains and an algorithm for fast chirp-rate estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(5): 3685–3700. doi: 10.1109/TAES.2020.2981268 [14] 黄响, 唐世阳, 张林让, 等. 一种基于高效FRFT的LFM信号检测与参数估计快速算法[J]. 电子与信息学报, 2017, 39(12): 2905–2911.HUANG Xiang, TANG Shiyang, ZHANG Linrang, et al. A fast algorithm of LFM signal detection and parameter estimation based on efficient FRFT[J]. Journal of Electronics &Information Technology, 2017, 39(12): 2905–2911. [15] 宋耀辉, 黄仰超, 张衡阳, 等. 基于FRFT的多分量LFM信号检测与参数估计方法[J]. 北京航空航天大学学报, 2020, 46(6): 1221–1228. doi: 10.13700/j.bh.1001-5965.2019.0430SONG Yaohui, HUANG Yangchao, ZHANG Hengyang, et al. Multicomponent LFM signal detection and parameter estimation method based on FRFT[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(6): 1221–1228. doi: 10.13700/j.bh.1001-5965.2019.0430 [16] YIN Zhiping, ZHANG Dongchen, CHEN Weidong, et al. LFM signal detection using the origin moment of fractional spectrum[C]. 2008 9th International Conference on Signal Processing, Beijing, China, 2008: 191–194. -





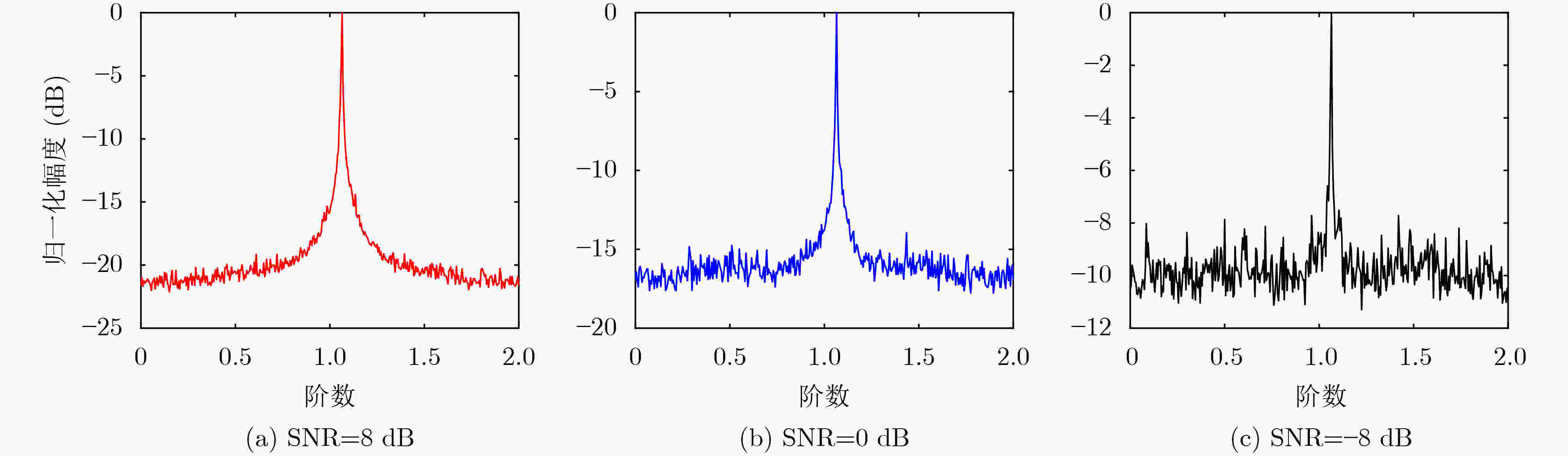
 下载:
下载:
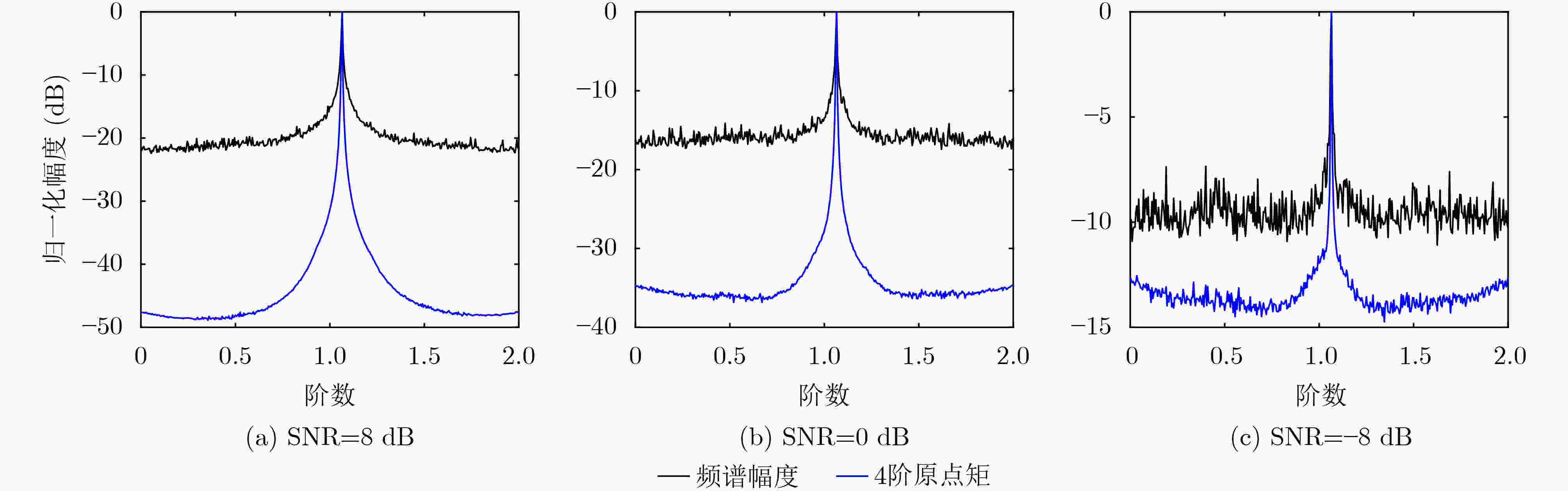

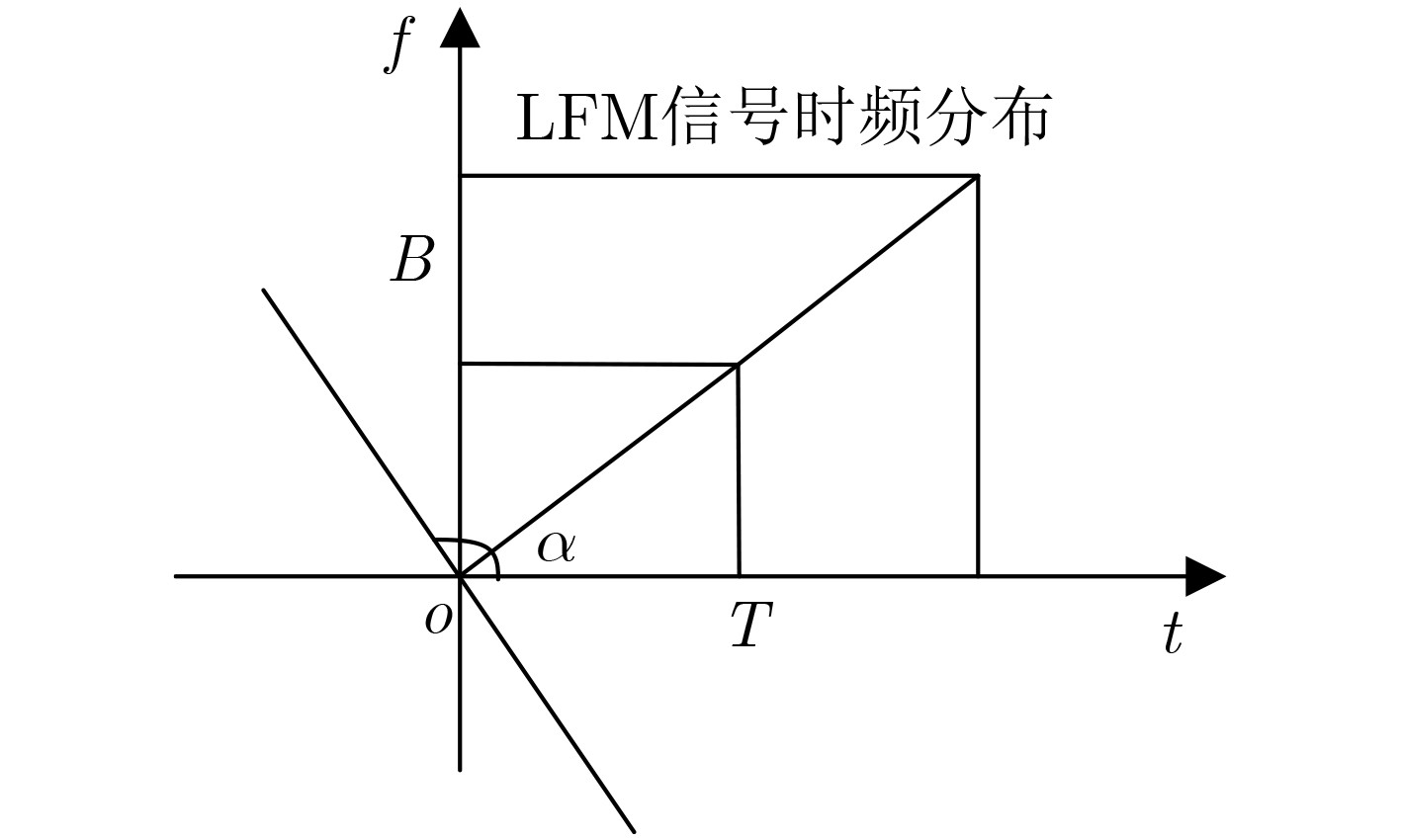

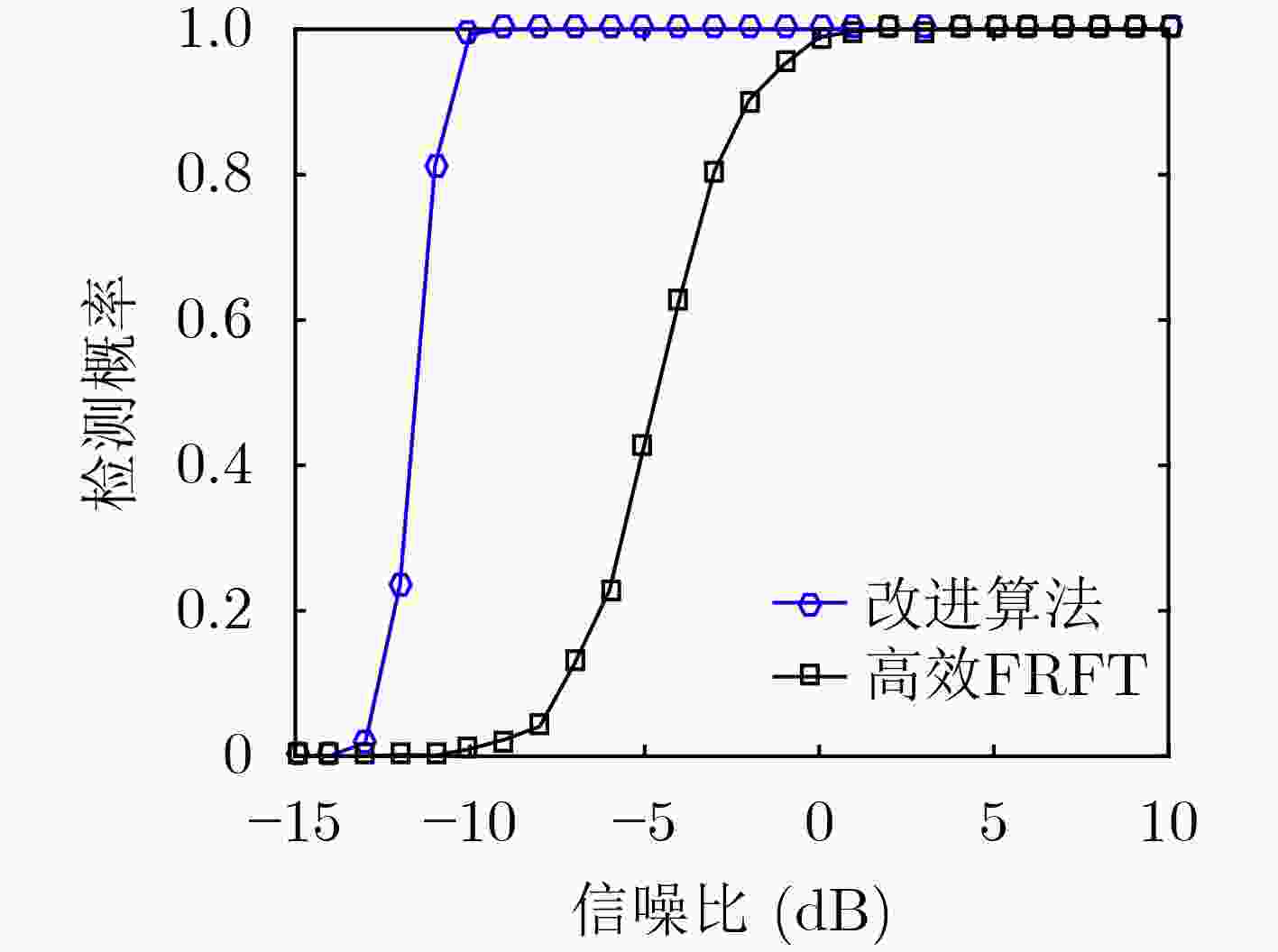


 下载:
下载:
