信号相关杂波背景中极化雷达发射波形优化

孙挺; 程旭

doi:10.11999/JEIT200138

信号相关杂波背景中极化雷达发射波形优化

doi: 10.11999/JEIT200138

孙挺¹,
程旭^2, ,

1.
周口师范学院网络工程学院周口 466000
2.
中山大学电子与通信工程学院深圳 518107

基金项目: 国家自然科学基金(61801527)，深圳市科技计划项目(KQTD20190929172704911)，电子信息系统复杂电磁环境效应国家重点实验室开放基金（CEMEE2021K0201B）

详细信息

作者简介:
孙挺：男，1972年生，教授，主要研究方向为信号与信息处理技术

程旭：男，1987年生，博士后，主要研究方向为统计信号处理、雷达信号处理等

通讯作者:
程旭　chengx95@mail.sysu.edu.cn

¹⁾ Q的值由雷达视线方向上目标径向长度和雷达的距离分辨率决定。
²⁾根据T-72坦克的长度信息和雷达的距离分辨率选定。
³⁾可取满足步进条件的\begin{document}$ \theta\in[0^\circ,~360^\circ]$\end{document}范围的任一值。
中图分类号: TN958
计量
- 文章访问数: 1192
- HTML全文浏览量: 375
- PDF下载量: 83
- 被引次数: 0
出版历程
- 收稿日期: 2020-02-28
- 修回日期: 2020-10-18
- 网络出版日期: 2020-11-16
- 刊出日期: 2021-05-18

Transmit Waveform Optimization of Polarimetric Radar in Signal-dependent Clutter

Ting SUN¹,
Xu CHENG^{2
, ,}

1.
College of Network Engineering, Zhoukou Normal University, Zhoukou 466000, China
2.
School of Electronic and Communication Engineering, Sun Yat-Sen University, Shenzhen 518107, China

Funds: The National Natural Science Foundation of China (61801527), Shenzhen Science and Technology Program (KQTD20190929172704911), China State Key Laboratory of Complex Electromagnetic Environment Effects on Electronic and Information System（CEMEE2021K0201B）

摘要

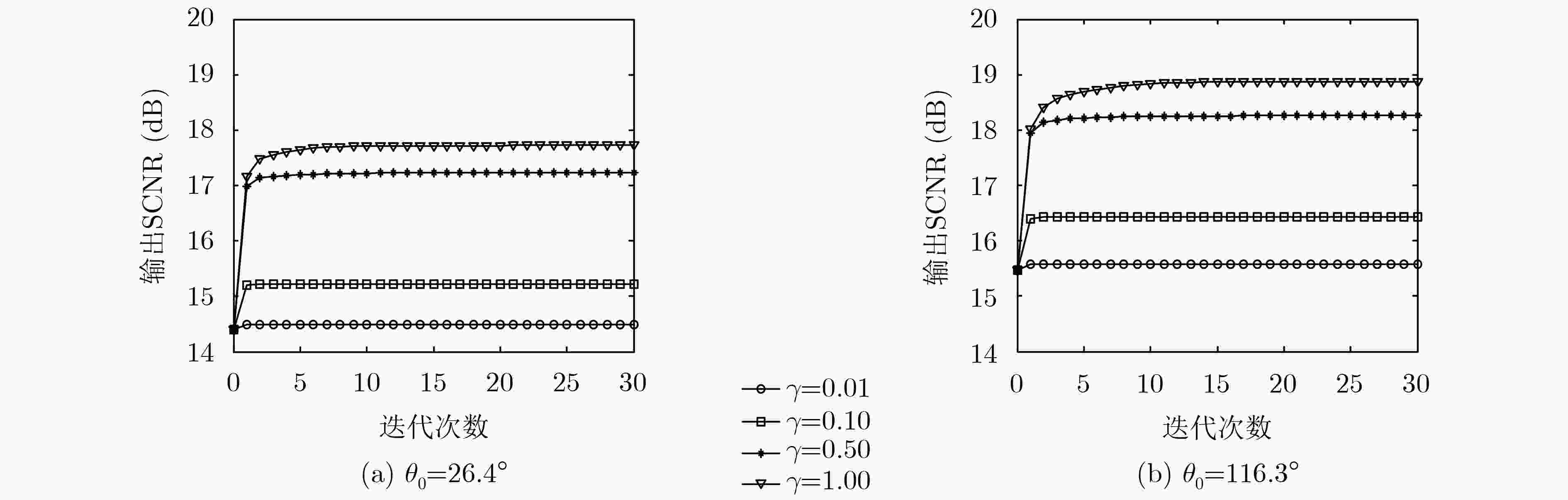
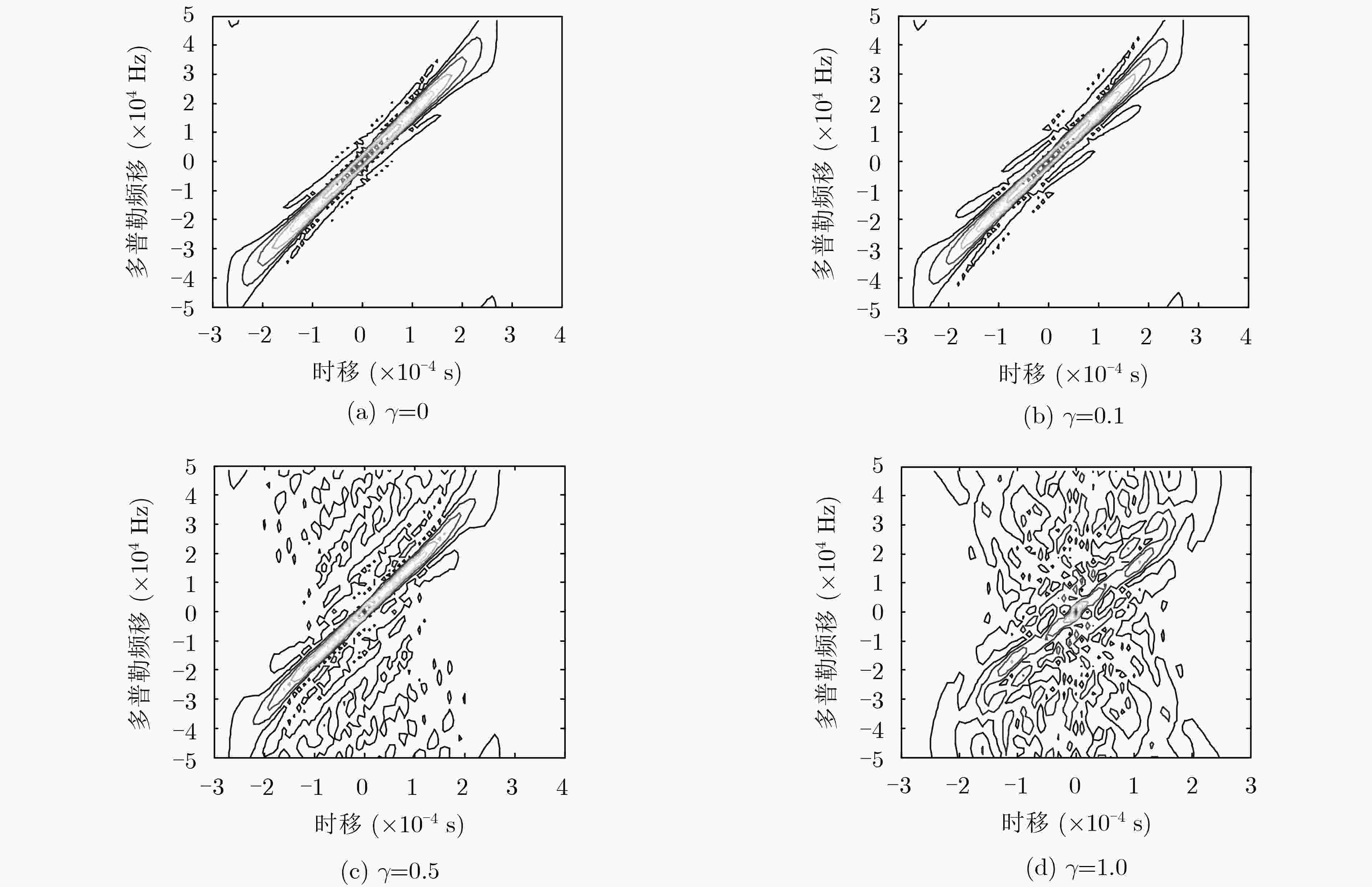
摘要: 波形优化可有效抑制干扰，显著改善雷达探测性能。针对全极化雷达，考虑发射波形满足能量和相似性双重约束，以最大化信杂噪比为准则，对发射波形和接收滤波器进行联合优化。该文设计了一种波形和滤波器的迭代优化算法，该方法序贯提高输出信杂噪比。算法的每一次迭代需要分别解决一个凸问题和隐凸问题，整个算法的计算量与迭代次数和接收滤波器长度分别呈线性和多项式关系。最后，通过仿真实验分析了算法的收敛性、优化波形的模糊度函数方面的性质，与其他算法进行了对比，结果表明：与现有方法相比，该文方法可实现信杂噪比的有效提升。
- 极化雷达 /
- 波形优化 /
- 波形设计 /
- 相似性约束
Abstract: Waveform optimization can effectively suppress the interference, and improve significantly radar performance. With considering polarimetric radars as the object of study and to maximize the output Signal-to-Clutter plus Noise Ratio (SCNR) as the merit of figure, an optimization problem of joint transmit waveform and receive filter design under both the energy and similarity constraints is constructed. Then, an optimization procedure for transmit signal and receive filter which improves sequentially the SCNR is exploited. Each iteration of the algorithm requires the solution of both a convex and a hidden convex optimization problem, and the resulting computational complexity is linear with the number of iterations and polynomial with the receive filter length. Finally, the convergence of the algorithm and the property of the optimized waveform in the ambiguous domain are analyzed through numerical experiments. Results show that, compared to the existing methods, the proposed approach improves significantly the SCNR.
- Polarimetric radar /
- Waveform optimization /
- Waveform design /
- Similarity constraint
¹⁾ Q的值由雷达视线方向上目标径向长度和雷达的距离分辨率决定。

²⁾根据T-72坦克的长度信息和雷达的距离分辨率选定。

³⁾可取满足步进条件的$ \theta\in[0^\circ,~360^\circ]$范围的任一值。

HTML全文

图 1 信杂噪比随迭代次数的变化曲线

下载: 全尺寸图片幻灯片

图 2 经优化后的全极化雷达水平极化通道发射波形模糊度函数幅度图

下载: 全尺寸图片幻灯片

图 3 本文方法和Pillai方法、Chen方法的性能对比结果

下载: 全尺寸图片幻灯片

表 1 算法1：Dinkelbach算法求解$ {\cal{P}}_{\rm{FP}} $

　已知：$ {\cal{X}}\subseteq \mathbb{C}^N $, $ f({{x}}) $和$ g({{x}}) $

　求：优化问题$ {\cal{P}}_{\rm{FP}} $的解$ {{x}}^\star $

　　　(1) 令$ m=0,~\lambda_m=0 $；

　　　(2) 重复

　　　(3)　　　计算$ {{x}}_m^\star= \arg \displaystyle{\max_{{{x}}\in {\cal{X}}}}\left\{f({{x}})-\lambda_m g({{x}})\right\}$；

　　　(4)　　　$ F_{\lambda}=f({{x}}_m^\star)-\lambda_m g({{x}}_m^\star) $；

　　　(5)　　　$ m=m+1 $；

　　　(6)　　　$\lambda_m=\dfrac{f({{x} }_m^\star)}{g({{x} }_m^\star)}$；

　　　(7) 直到 $ F_\lambda=0 $；

　　　(8) 输出 $ {{x}}^\star={{x}}^\star_m$。

下载: 导出CSV

表 2 算法2：发射波形-接收滤波器联合优化算法

　已知：$ \sigma_v^2 $, $\Big\{(r_{ij}(n,n'),\sigma_n,\epsilon_n,\chi_n),$$ \{i,j\}\in\{1,2,3\},\{n,n'\}= $$ -N+1,···,M-1\Big\} $, $ {{T}}(\theta) $, $ {{s}}_0 $, $ \gamma $和$ \zeta $

　求：优化问题$ \cal{P} $的解$ \left({{s}}^\star,{{w}}^\star\right) $

　　　(1) 令$ m:=0,{{s}}^{(m)}={{s}}_0 $，代入式(15)得到$ {{w}}^{(0)} $，对应$ {\rm{SINR}}^{(0)}=\left(g\left({{s}}_0, {{w}}^{(0)}\right)\right)^2 $；

　　　(2) 重复

　　　(3)　　　　$ m:=m+1 $；

　　　(4)　　　　采用算法1解$ {\cal{P}}_{{{s}}^{(m)}} $得到第$ m$步的最优发射波形
　　　　　　　　 $ {{s}}^{(m)} $；

　　　(5)　　　　将$ {{s}}^{(m)} $代入式(15)得到第$ m$步的最优接收滤波
　　　　　　　　器$ {{w}}^{(m)} $；

　　　(6)　　　　计算$ {\rm{SINR}}^{(m)}=\left(g\left({{s}}^{(m)}, {{w}}^{(m)}\right)\right)^2 $；

　　　(7)　　　直到$ |{\rm{SCNR}}^{(m)}-{\rm{SCNR}}^{(m-1)}|<\zeta $；

　　　(8)　　　输出$ {{s}}^\star={{s}}^{(m)} $, $ {{w}}^\star={{w}}^{(m)} $。

下载: 导出CSV

参考文献(18)

[1]	LEE J S and ERIC P. Polarimetric Radar Imaging: Basics to Applications[M]. 2nd ed. Boca Raton: CRC Press, 2020.
[2]	TREUHAFT R N and SIQUEIRA P R. Vertical structure of vegetated land surfaces from interferometric and polarimetric radar[J]. Radio Science, 2000, 35(1): 141–177. doi: 10.1029/1999RS900108
[3]	王雪松. 雷达极化技术研究现状与展望[J]. 雷达学报, 2016, 5(2): 119–131. doi: 10.12000/JR16039 WANG Xuesong. Status and prospects of radar polarimetry techniques[J]. Journal of Radars, 2016, 5(2): 119–131. doi: 10.12000/JR16039
[4]	LEI Lei, ZHANG Guifu, DOVIAK R J, et al. Comparison of theoretical biases in estimating polarimetric properties of precipitation with weather radar using parabolic reflector, or planar and cylindrical arrays[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(8): 4313–4327. doi: 10.1109/TGRS.2015.2395714
[5]	CHENG Ziyang, HE Zishu, LIAO Bin, et al. MIMO radar waveform design with PAPR and similarity constraints[J]. IEEE Transactions on Signal Processing, 2018, 66(4): 968–981. doi: 10.1109/TSP.2017.2780052
[6]	庞晓娇, 赵永波, 徐保庆, 等. 基于原子范数的MIMO雷达发射波形设计方法[J]. 电子与信息学报, 2019, 41(9): 2143–2150. doi: 10.11999/JEIT181107 PANG Xiaojiao, ZHAO Yongbo, XU Baoqing, et al. An atomic norm-based transmit waveform design method in MIMO radar[J]. Journal of Electronics &Information Technology, 2019, 41(9): 2143–2150. doi: 10.11999/JEIT181107
[7]	李慧, 赵永波, 程增飞. 基于线性调频时宽的MIMO雷达正交波形设计[J]. 电子与信息学报, 2018, 40(5): 1151–1158. doi: 10.11999/JEIT170426 LI Hui, ZHAO Yongbo, and CHENG Zengfei. MIMO Radar orthogonal waveform set design based on chirp durations[J]. Journal of Electronics &Information Technology, 2018, 40(5): 1151–1158. doi: 10.11999/JEIT170426
[8]	NOVAK L M, SECHTIN M B, and CARDULLO M J. Studies of target detection algorithms that use polarimetric radar data[J]. IEEE Transactions on Aerospace and Electronic Systems, 1989, 25(2): 150–165. doi: 10.1109/7.18677
[9]	GARREN D A, ODOM A C, OSBORN M K, et al. Full-polarization matched-illumination for target detection and identification[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(3): 824–837. doi: 10.1109/TAES.2002.1039402.
[10]	CHEN Chunyang and VAIDYANATHAN P P. MIMO radar waveform optimization with prior information of the extended target and clutter[J]. IEEE Transactions on Signal Processing, 2009, 57(9): 3533–3544. doi: 10.1109/TSP.2009.2021632
[11]	YUAN Mengxin, CHENG Xu, ZHANG Jing, et al. Adaptive waveform design of polarimetric radar for extended targets in signal-dependent clutter[C]. Web, Artificial Intelligence and Network Applications-Proceedings of the Workshops of the 33rd International Conference on Advanced Information Networking and Applications, Matsue, Japan, 2019: 3–13.
[12]	包本刚, 朱湘萍, 谭永宏. 极化雷达发射波形和接收滤波器联合优化新方法[J]. 重庆大学学报, 2019, 42(1): 124–134. BAO Bengang, ZHU Xiangping, and TAN Yonghong. A novel method to jointly optimize transmit waveform and receive filter of polarimetric radar[J]. Journal of Chongqing University, 2019, 42(1): 124–134.
[13]	程旭. 全极化雷达目标检测与参数估计方法研究[D]. [博士论文], 国防科学技术大学, 2016. CHENG Xu. Study on target detection and parameter estimation approaches of fully polarimetric radar[D]. [Ph. D. dissertation], National University of Defense Technology, 2016.
[14]	CHENG Xu, AUBRY A, CIUONZO D, et al. Robust waveform and filter bank design of polarimetric radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(1): 370–384. doi: 10.1109/TAES.2017.2650619
[15]	TKACENKO A and VAIDYANATHAN P P. Iterative greedy algorithm for solving the FIR paraunitary approximation problem[J]. IEEE Transactions on Signal Processing, 2006, 54(1): 146–160. doi: 10.1109/TSP.2005.861054
[16]	LI Jian, STOICA P, and WANG Zhisong. On robust Capon beamforming and diagonal loading[J]. IEEE Transactions on Signal Processing, 2003, 51(7): 1702–1715. doi: 10.1109/TSP.2003.812831
[17]	CROUZEIX J P and FERLAND J A. Algorithms for generalized fractional programming[J]. Mathematical Programming, 1991, 52(1/3): 191–207.
[18]	BEN-TAL A and NEMIROVSKI A. Lectures on Modern Convex Optimization: Analysis, Algorithms, and Engineering Applications [M]. Philadelphia: Society for Industrial and Applied Mathematics, 2001.