基于电离层色散的短波信道多径特性分析

吴永宏; 王程林; 任渊博; 周福厚

doi:10.11999/JEIT190384

基于电离层色散的短波信道多径特性分析

doi: 10.11999/JEIT190384

吴永宏^{1, 2, ,},
王程林^{1, 2},
任渊博^{1, 2},
周福厚³

1.
中国电波传播研究所青岛 266107
2.
青岛海洋科学与技术试点国家实验室青岛 266235
3.
山东航天电子技术研究所烟台 264003

基金项目: 山东省支持青岛海洋科学与技术试点国家实验室重大科技专项(2018SDKJ0210)

详细信息

作者简介:
吴永宏：男，1974年生，高级工程师，主要研究方向为短波通信、网络规划和信号处理等

王程林：男，1985年生，工程师，主要研究方向为短波通信及嵌入式软件开发

任渊博：女，1980年生，工程师，主要研究方向为短波通信及嵌入式软件开发

周福厚：男，1972年生，工程师，主要研究方向为无线通信及信息系统总体设计

通讯作者:
吴永宏　wyh7426@sina.com

中图分类号: TN92
计量
- 文章访问数: 2487
- HTML全文浏览量: 1201
- PDF下载量: 111
- 被引次数: 0
出版历程
- 收稿日期: 2019-05-29
- 修回日期: 2020-03-02
- 网络出版日期: 2020-03-31
- 刊出日期: 2020-08-18

High Frequency Channel Multipath Analysis Based on Ionosphere Dispersion

Yonghong WU^{1, 2
, ,},
Chenglin WANG^{1, 2},
Yuanbo REN^{1, 2},
Fuhou ZHOU³

1.
China Research Institute of Radio Wave Propagation, Qingdao 266071, China
2.
Pilot National Laboratory for Marine Science and Technology, Qingdao 266235, China
3.
Shandong Institute of Space Electronic Technology, Yantai 264003, China

Funds: The Marine S&T Fund of Shandong Province for Pilot National Laboratory for Marine Science and Technology (Qingdao) (2018SDKJ0210)

摘要

摘要:
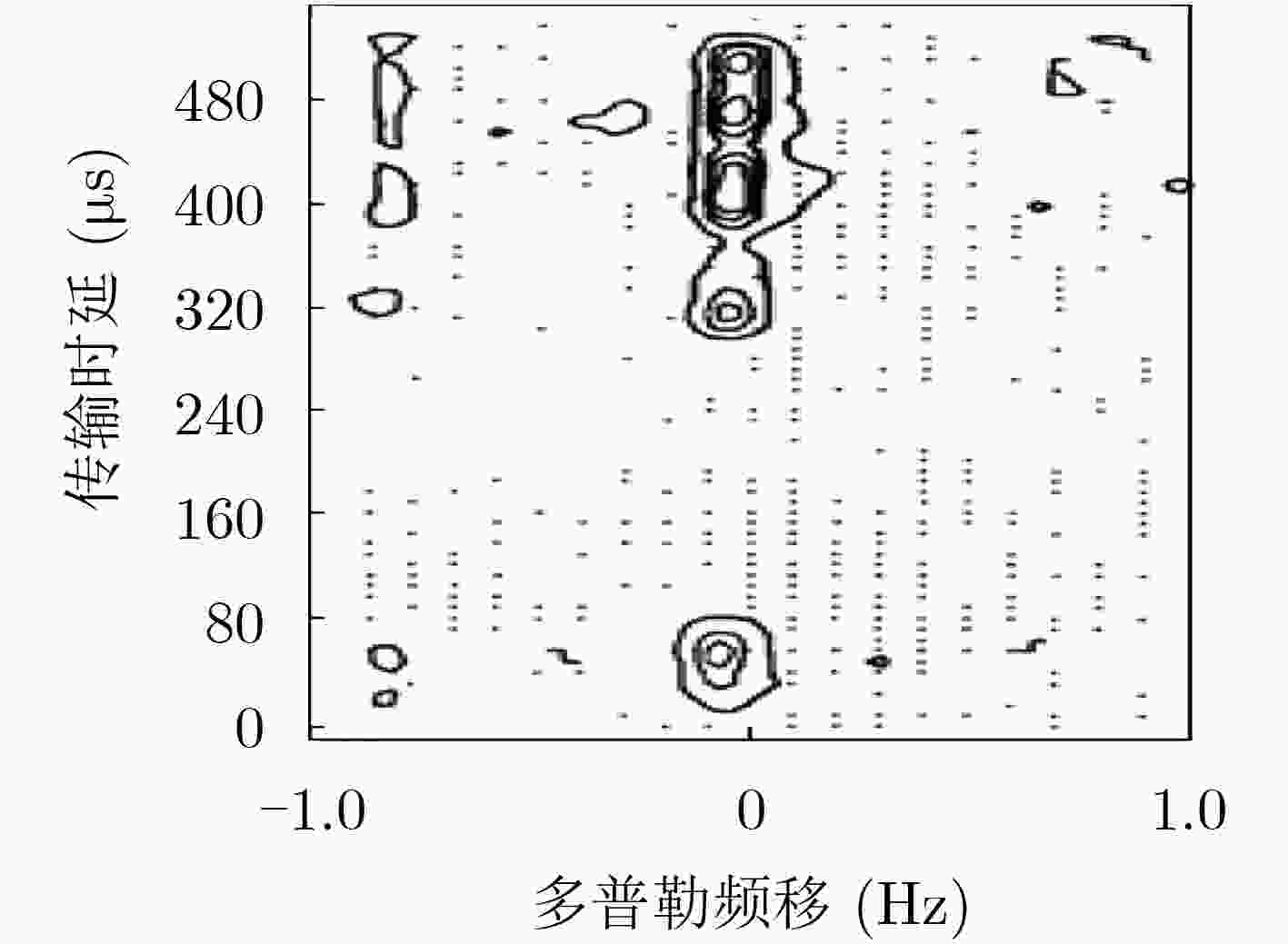
短波链路不同传播模式的多径时延通常为0.5～2.0 ms，该文研究同一传播模式的多径时延，在考虑地磁场影响的情况下，将电离层短波传播的折射指数和射线追踪结合起来，给出了数值迭代算法，实现了用数值方法来描述电离层色散引起的多径时延，并进行了数值仿真，得出短波宽带通信的模拟带宽应为48 kHz。
- 射线追踪 /
- 电离层色散 /
- 多径时延 /
- 折射指数 /
- 寻常波 /
- 非寻常波
Abstract:
The multipath delay for different propagation mode is 0.5～2.0 ms, and the multipath delay for the same propagation mode is analyzed. Taking into account the earth magnetic field effects, the refractive index of High frequency propagation in ionosphere is combined with ray tracing, and then a new numerical iteration algorithm is given. The multipath delay caused by ionosphere dispersion is analyzed by numerical method, and the simulation is realized. Thus the analogue bandwidth of wideband communication for high frequency should be 48 kHz.
- Ray tracing /
- Ionosphere dispersion /
- Multipath delay /
- Refractive index /
- Ordinary wave /
- Extraordinary wave

HTML全文

图 1 北美大陆天波链路(8 km)实测数据得到的散射函数

下载: 全尺寸图片幻灯片

表 1 青岛-许昌链路多径时延实测结果

序号	1	2	3	4	5	6	7	8	9	10	11	12	13	14
多径时延(µs)	55	11	30	8	22	8	19	31	31	53	22	30	10	40

下载: 导出CSV

表 2 北美大陆天波链路(80 km)路径时延和多径时延仿真结果

频率(MHz)	3.5	3.8	4.1	4.4	4.7	5.0
寻常波时延(ms)	1.228	1.312	1.875	1.916	2.000	2.144
非寻常波时延(ms)	1.544	1.540	1.624	1.868	2.180	2.308
多径时延(µs)	316	228	251	48	180	164

下载: 导出CSV

表 3 青岛-许昌链路路径时延和多径时延仿真结果

频率(MHz)	6.5	7.0	7.5	8.0	8.5	9.0
寻常波时延(ms)	2.760	2.912	2.928	2.996	3.168	3.480
非寻常波时延(ms)	2.516	3.052	3.000	2.928	2.960	3.164
多径时延(µs)	244	140	72	68	208	316

下载: 导出CSV

表 4 青岛-北京链路5点时段路径时延和多径时延

频率(MHz)	4.0	4.5	5.0	5.5	6.0
寻常波时延(ms)	2.292	2.280	2.372	2.560	2.764
非寻常波时延(ms)	2.264	2.304	2.352	2.408	2.488
多径时延(µs)	28	24	20	152	276

下载: 导出CSV

表 5 青岛-北京链路13点时段路径时延和多径时延

频率(MHz)	6.0	6.5	7.0	7.5	8.0	8.5	9.0
寻常波时延(ms)	2.572	2.464	2.408	2.484	2.520	2.628	2.944
非寻常波时延(ms)	2.776	2.512	2.452	2.440	2.336	2.484	2.644
多径时延(µs)	204	48	44	40	184	144	300

下载: 导出CSV

表 6 青岛-北京链路21点时段路径时延和多径时延

频率(MHz)	4.5	5.0	5.5	6.0	6.5	7.0	7.5	8.0
寻常波时延(ms)	2.308	2.304	2.356	2.408	2.448	2.764	2.688	2.900
非寻常波时延(ms)	2.276	2.308	2.340	2.320	2.396	2.472	2.552	2.720
多径时延(µs)	32	4	16	88	52	292	136	18

下载: 导出CSV

表 7 青岛-上海链路5点时段路径时延和多径时延

频率(MHz)	4.0	4.5	5.0	5.5	6.0
寻常波时延(ms)	2.440	2.496	2.704	2.624	2.940
非寻常波时延(ms)	2.408	2.412	2.412	2.460	2.504
多径时延(µs)	32	84	292	164	436

下载: 导出CSV

表 8 青岛-上海链路13点时段路径时延和多径时延

频率(MHz)	6.0	6.5	7.0	7.5	8.0	8.5	9.0	9.5	10.0	10.5
寻常波时延(ms)	2.388	2.600	2.536	2.516	2.548	2.580	2.676	2.812	2.716	2.792
非寻常波时延(ms)	2.463	2.532	2.420	2.464	2.452	2.540	2.528	2.504	2.608	2.768
多径时延(µs)	85	68	116	52	96	40	148	308	108	24

下载: 导出CSV

表 9 青岛-上海链路21点时段路径时延和多径时延

频率(MHz)	5.0	5.5	6.0	6.5	7.0	7.5	8.0
寻常波时延(ms)	2.536	2.568	2.616	2.684	2.572	2.912	3.160
非寻常波时延(ms)	2.472	2.492	2.528	2.572	2.608	2.572	2.788
多径时延(µs)	64	76	88	112	36	340	372

下载: 导出CSV

表 10 青岛-重庆链路5点时段路径时延和多径时延

频率(MHz)	6.0	6.5	7.0	7.5	8.0	8.5	9.0	9.5	10.0
寻常波时延(ms)	5.304	5.296	5.292	5.308	5.324	5.320	5.292	5.372	5.472
非寻常波时延(ms)	5.296	5.224	5.276	5.288	5.292	5.304	5.240	5.364	5.320
多径时延(µs)	8	72	16	20	32	16	52	8	152

下载: 导出CSV

表 11 青岛-重庆链路13点时段路径时延和多径时延

频率(MHz)	11.5	12.0	12.5	13.0	13.5	14.0	14.5
寻常波时延(ms)	5.328	5.228	5.316	5.404	5.372	5.360	5.272
非寻常波时延(ms)	5.496	5.196	5.144	5.256	5.388	5.364	5.340
多径时延(µs)	168	32	172	148	16	4	68
频率(MHz)	15.0	15.5	16.0	16.5	17.0	17.5	18.0
寻常波时延(ms)	5.332	5.328	5.332	5.332	5.368	5.380	5.420
非寻常波时延(ms)	5.352	5.280	5.324	5.348	5.360	5.356	5.348
多径时延(µs)	20	48	8	16	8	24	72

下载: 导出CSV

表 12 青岛-重庆链路21点时段路径时延和多径时延

频率(MHz)	7.0	7.5	8.0	8.5	9.0	9.5	10.0	10.5
寻常波时延(ms)	5.226	5.235	5.241	5.304	5.259	5.259	5.280	5.292
非寻常波时延(ms)	5.243	5.238	5.253	5.253	5.244	5.274	5.284	5.295
多径时延(µs)	17	3	12	51	15	15	4	3
频率(MHz)	11.0	11.5	12.0	12.5	13.0	13.5	14.0	14.5
寻常波时延(ms)	5.248	5.308	5.260	5.284	5.340	5.356	5.428	5.388
非寻常波时延(ms)	5.256	5.292	5.300	5.308	5.304	5.312	5.352	5.340
多径时延(µs)	8	16	40	24	36	44	76	48

下载: 导出CSV

表 13 青岛-北京链路多径时延的期望和标准差

时段(点)	5	13	21
期望(µs)	100.0	137.7	79.8
标准差(µs)	101.0	99.4	90.1

下载: 导出CSV

表 14 青岛-上海链路多径时延的期望和标准差

时段(点)	5	13	21
期望(µs)	201.6	104.5	155.4
标准差(µs)	146.4	76.6	128.9

下载: 导出CSV

表 15 青岛-重庆链路多径时延的期望和标准差

时段(点)	5	13	21
期望(µs)	41.8	57.4	25.8
标准差(µs)	43.9	58.7	20.5

下载: 导出CSV

参考文献(21)

WANG Jinlong, LI Shaoqian, and WEI Jibo. Wideband, intelligent and integrated HF communications[J]. China Communications, 2018, 15(9): iii–v. doi: 10.1109/CC.2018.8456446.

LOBOVA E O and KANDAUROV N A. Experimental results of dispersion distortion compensation of wideband signals with a device based on a digital filter bank[C]. 2019 Systems of Signals Generating and Processing in the Field of on Board Communications, Moscow, Russia, 2019. doi: 10.1109/SOSG.2019.8706758.

LOBOV E M and SHUBIN D N. A narrow-band interference compensation device based on a digital filter bank for broadband low-energy HF radio lines[C]. 2019 Systems of signals generating and processing in the field of on board communication, Moscow, Russia, 2019. doi: 10.1109/SOSG.2019.8706791.

VOGLER L E and HOFFMEYER J A. A new approach to HF channel modeling and simulation, Part I: Deterministic model[R]. NTIA Report 88–240, 1988.

VOGLER L E and HOFFMEYER J A. A new approach to HF channel modeling and simulation, Part Ⅱ: Stochastic model[R]. NTIA Report 90–255, 1990.

VOGLER L E and HOFFMEYER J A. A new approach to HF channel modeling and simulation, Part Ⅲ: Transfer function[R]. NTIA Report 93–284, 1992.

VOGLER L E and HOFFMEYER J A. A model for wideband HF propagation channels[J]. Radio Science, 1993, 28(6): 1131–1142. doi: 10.1029/93RS01607

MIL-STD-188-110D Interoperability and performance standards for data modems[S]. 2017: 142–145.

NELSON R, JORGENSON M, and JOHNON R W. Extension of wideband HF capabilities[EB/OL]. https://www.hfindustry.com/account/my-account. 2014.5.

DAVIS K. Ionospheric Radio[M]. London: P. Peregrinus on behalf of the Institution of Electrical Engineers, 1990: 18–20.

索玉成. 电离层短波射线追踪[J]. 空间科学学报, 1993, 13(4): 306–312.

SUO Yucheng. Short wave ray tracing in the ionosphere[J]. Chinese Journal of Space Science, 1993, 13(4): 306–312.

柳文, 焦培南, 王世凯, 等. 电离层短波三维射线追踪及其应用研究[J]. 电波科学学报, 2008, 23(1): 41–48, 67. doi: 10.3969/j.issn.1005-0388.2008.01.007

LIU Wen, JIAO Peinan, WANG Shikai, et al. Short wave ray tracing in the ionosphere and its application[J]. Chinese Journal of Radio Science, 2008, 23(1): 41–48, 67. doi: 10.3969/j.issn.1005-0388.2008.01.007

THAYAPARAN T, DUPONT D, IBRAHIM Y, et al. High-frequency ionospheric monitoring system for over-the-horizon radar in Canada[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(9): 6372–6384. doi: 10.1109/TGRS.2019.2905757

THAYAPARAN T, IBRAHIM Y, POLAK J, et al. High-frequency over-the-horizon radar in Canada[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(11): 1700–1704. doi: 10.1109/LGRS.2018.2856185

KLIMENKO M V, CHIRIK N V, KOTOVA D S, et al. Development of improved ionospheric empirical model and software for HF ray tracing[C]. 2018 2nd URSI Atlantic Radio Science Meeting, Meloneras, Spain, 2018. doi: 10.23919/URSI-AT-RASC.2018.8471348.

JONES R M and STEPHENSON J J. A versatile three-dimensional ray tracing computer program for radio waves in the ionosphere[R]. OT Report 75–76, 1975.

攸阳, 钱志刚, 李吉宁, 等. 短波时差定位中电离层参数对定位影响仿真[J]. 电波科学学报, 2017, 32(4): 462–466. doi: 10.13443/J.CJORS.2017033002

YOU Yang, QIAN Zhigang, LI Jining, et al. Simulation on the effect of ionospheric parameters on TDOA location in short wave[J]. Chinese Journal of Radio Science, 2017, 32(4): 462–466. doi: 10.13443/J.CJORS.2017033002

HUANG Xiaoguo. Extended beam approximation for high-frequency wave propagation[J]. IEEE Access, 2018, 6: 37214–37224. doi: 10.1109/ACCESS.2018.2849595

SAITO S, YAMAMOTO M, and MARUYAMA T. Arrival angle and travel time measurements of HF transequatorial propagation for plasma bubble monitoring[J]. Radio Science, 2018, 53(11): 1304–1315. doi: 10.1029/2017RS006518

TAYGUR M M, EIBERT T F, and SUKHAREVSKY I O. A bidirectional ray-tracing method for antenna coupling evaluation based on the reciprocity theorem[J]. IEEE Transactions on Antennas and Propagation, 2018, 66(12): 6654–6664. doi: 10.1109/TAP.2018.2876680

YAN Zhaowen, ZHANG Lanlan, RAHMAN T, et al. Prediction of the HF ionospheric channel stability based on the modified ITS model[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(6): 3321–3333. doi: 10.1109/TAP.2013.2249571

施引文献

资源附件(0)

访问统计