Sensor Selection Method for TDOA Passive Localization
-
摘要:
该文主要研究一种面向到达时间差(TDOA)被动定位的定位节点选择方法。首先,通过经典的闭式解析算法将TDOA非线性方程转化为伪线性方程,并使用位置误差的协方差矩阵来度量定位精度。其次,在可用节点数量给定的条件下,在数学上将定位节点选择问题转化为最小化位置误差协方差矩阵的迹这一非凸优化问题。然后,将非凸优化问题凸松弛并化为半正定规划问题,从而快速有效地求解出最优的定位节点组合。仿真结果表明,所提节点优选方法的性能非常接近穷尽搜索方法,而且克服了穷尽搜索方法运算复杂度高、时效性差的不足,从而验证了所提方法的有效性。
Abstract:This paper focuses on the sensor selection optimization problem in Time Difference Of Arrival (TDOA) passive localization scenario. Firstly, the localization accuracy metric is given by the error covariance matrix of classical closed-form solution, which is introduced to convert the TDOA nonlinear equations into pseudo linear equations. Secondly, the problem of sensor selection can be mathematically transformed into the non-convex optimization problem, to minimize the trace of localization error covariance matrix under the condition that the number of active sensors is given. Then, the non-convex optimization problem is relaxed and transformed into a positive semi-definite programming problem so that the optimal subset of positioning nodes can be solved quickly and effectively. Simulation results validate that the performance of proposed sensor selection method is very close to the exhausted-search method, and overcomes the shortcomings of the high computation complexity and poor timeliness of the exhausted-search method.
-
胡勤振, 苏洪涛, 刘子威, 等. 配准误差下的多基地雷达目标检测算法[J]. 电子与信息学报, 2017, 39(1): 88–94. doi: 10.11999/JEIT160207HU Qinzhen, SU Hongtao, LIU Ziwei, et al. Target detection algorithm for multistatic radar with registration errors[J]. Journal of Electronics &Information Technology, 2017, 39(1): 88–94. doi: 10.11999/JEIT160207 YASSIN A, NASSER Y, AWAD M, et al. Recent advances in indoor localization: A survey on theoretical approaches and applications[J]. IEEE Communications Surveys & Tutorials, 2017, 19(2): 1327–1346. doi: 10.1109/COMST.2016.2632427 CHEN Hongyang, WANG Gang, WANG Zizhuo, et al. Non-line-of-sight node localization based on semi-definite programming in wireless sensor networks[J]. IEEE Transactions on Wireless Communications, 2012, 11(1): 108–116. doi: 10.1109/TWC.2011.110811.101739 CHEN Hongyang, SHI Qingjiang, TAN Rui, et al. Mobile element assisted cooperative localization for wireless sensor networks with obstacles[J]. IEEE Transactions on Wireless Communications, 2010, 9(3): 956–963. doi: 10.1109/TWC.2010.03.090706 SHI Qingjiang, HE Chen, CHEN Hongyang, et al. Distributed wireless sensor network localization via sequential greedy optimization algorithm[J]. IEEE Transactions on Signal Processing, 2010, 58(6): 3328–3340. doi: 10.1109/TSP.2010.2045416 HENTATI A, DRIOUCH E, FRIGON J, et al. Fair and low complexity node selection in energy harvesting wireless sensor networks[J]. IEEE Systems Journal, 2018, 99(1): 1–11. doi: 10.1109/JSYST.2017.2771294 JOSHI S and BOYD S. Sensor selection via convex optimization[J]. IEEE Transactions on Signal Processing, 2009, 57(2): 451–462. doi: 10.1109/TSP.2008.2007095 LIU S, CHEPURI S P, FARDAD M, et al. Sensor selection for estimation with correlated measurement noise[J]. IEEE Transactions on Signal Processing, 2016, 64(13): 3509–3522. doi: 10.1109/TSP.2016.2550005 CHEPURI S P and LEUS G. Sparsity-promoting sensor selection for non-linear measurement models[J]. IEEE Transactions on Signal Processing, 2014, 63(3): 684–698. doi: 10.1109/TSP.2014.2379662 RAO S, CHEPURI S P, and LEUS G. Greedy sensor selection for non-linear models[C]. IEEE 6th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing(CAMSAP), Cancun, Mexico, 2015, (2): 241–244. HO K C, LU Xiaoming, and KOVAVISARUCH L. Source localization using TDOA and FDOA measurements in the presence of receiver location errors: Analysis and solution[J]. IEEE Transactions on Signal Processing, 2007, 55(2): 684–696. doi: 10.1109/TSP.2006.885744 QU Xiaomei and XIE Lihua. An efficient convex constrained weighted least squares source localization algorithm based on TDOA measurements[J]. Signal Processing, 2016, 119(2): 142–152. HO K C and XU Wenwei. An accurate algebraic solution for moving source location using TDOA and FDOA measurements[J]. IEEE Transactions on Signal Processing, 2004, 52(9): 2453–2463. doi: 10.1109/TSP.2004.831921 曲付勇, 孟祥伟. 基于约束总体最小二乘方法的到达时差到达频差无源定位算法[J]. 电子与信息学报, 2014, 36(5): 1075–1081. doi: 10.3724/SP.J.1146.2013.01019QU Fuyong and MENG Xiangwei. Source localization using TDOA and FDOA measurements based on constrained total least squares algorithm[J]. Journal of Electronics &Information Technology, 2014, 36(5): 1075–1081. doi: 10.3724/SP.J.1146.2013.01019 RUI Liyang, CHEN Shanjie, and HO K C. Anchor nodes refinement in joint localization and synchronization of a sensor node[C]. IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP), Brisbane, Australia, 2015: 2834–2838. HO K C and SUN Ming. Passive source localization using time differences of arrival and gain ratios of arrival[J]. IEEE Transactions on Signal Processing, 2008, 56(2): 464–477. doi: 10.1109/TSP.2007.906728 HO K C. Bias reduction for an explicit solution of source localization using TDOA[J]. IEEE Transactions on Signal Processing, 2012, 60(5): 2101–2114. doi: 10.1109/TSP.2012.2187283 YANG Xiaojun and NIU Ruixin. Adaptive sensor selection for nonlinear tracking via sparsity-promoting approaches[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018. doi: 10.1109/TAES.2018.2805258 GRANT M, BOYD S, and YE Y. CVX Version 2.1. Matlab Software for Disciplined Convex Programming[OL]. www.stanford.edu/boyd/cvx/, 2017. -





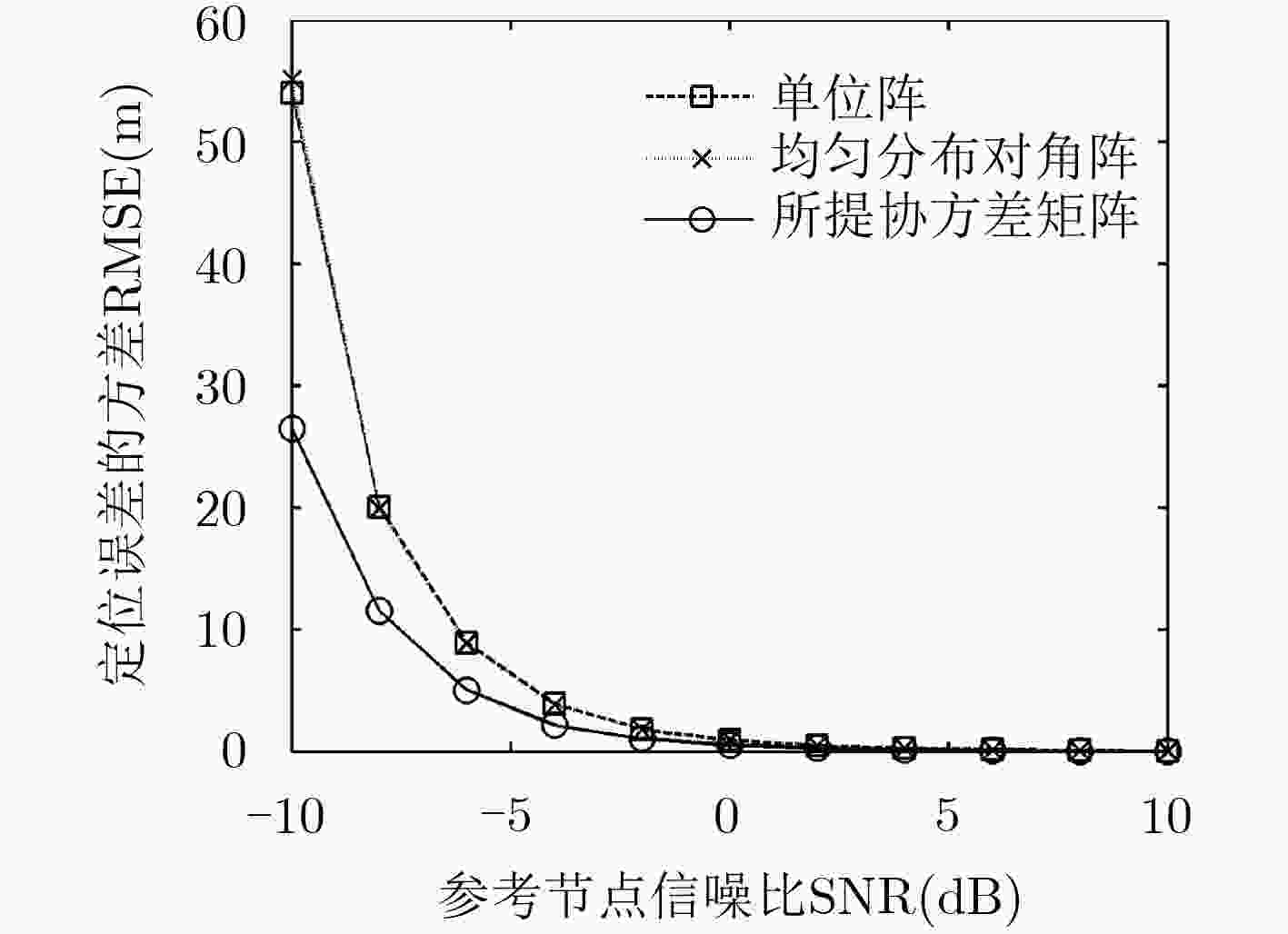
 下载:
下载:
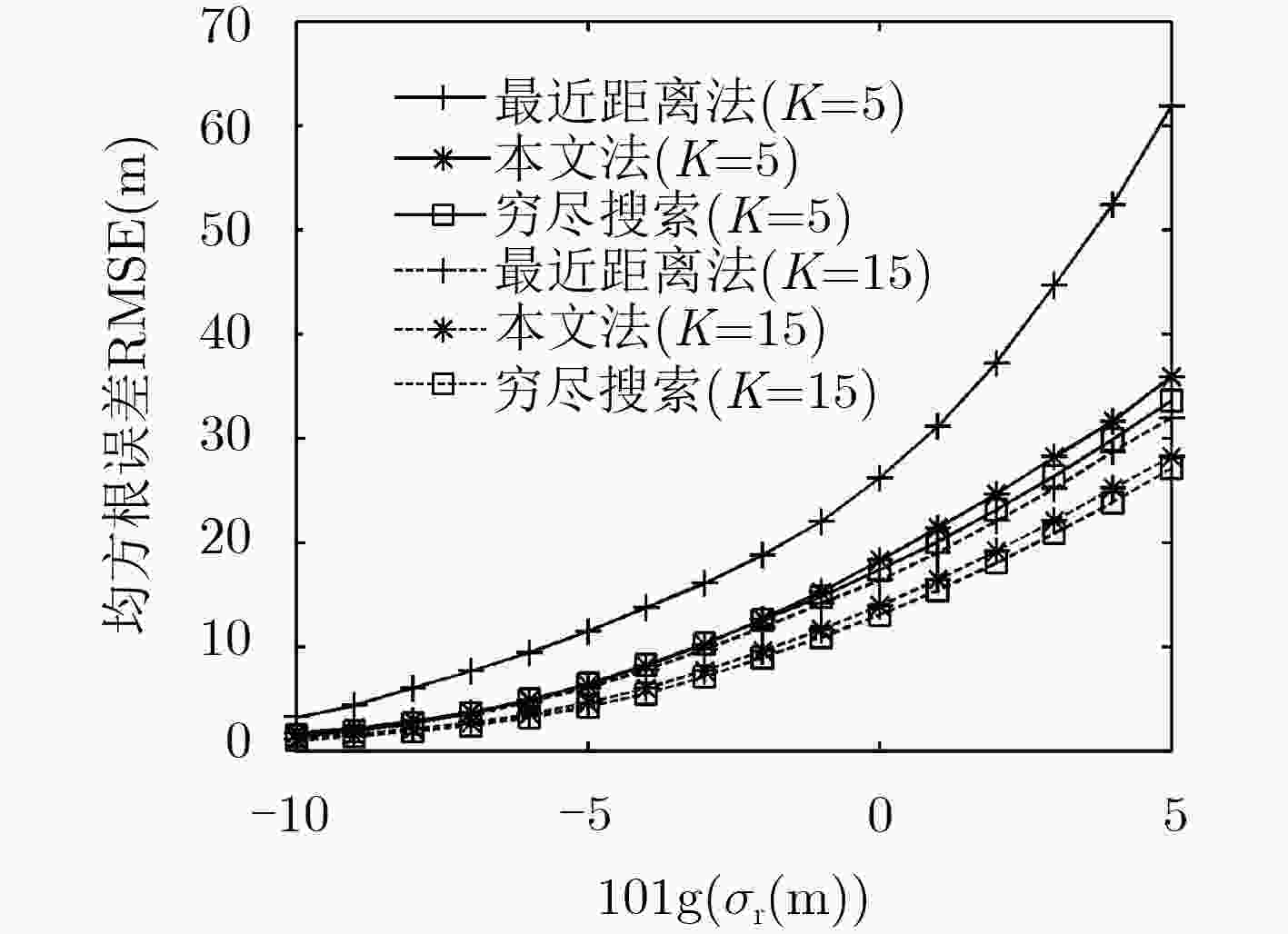
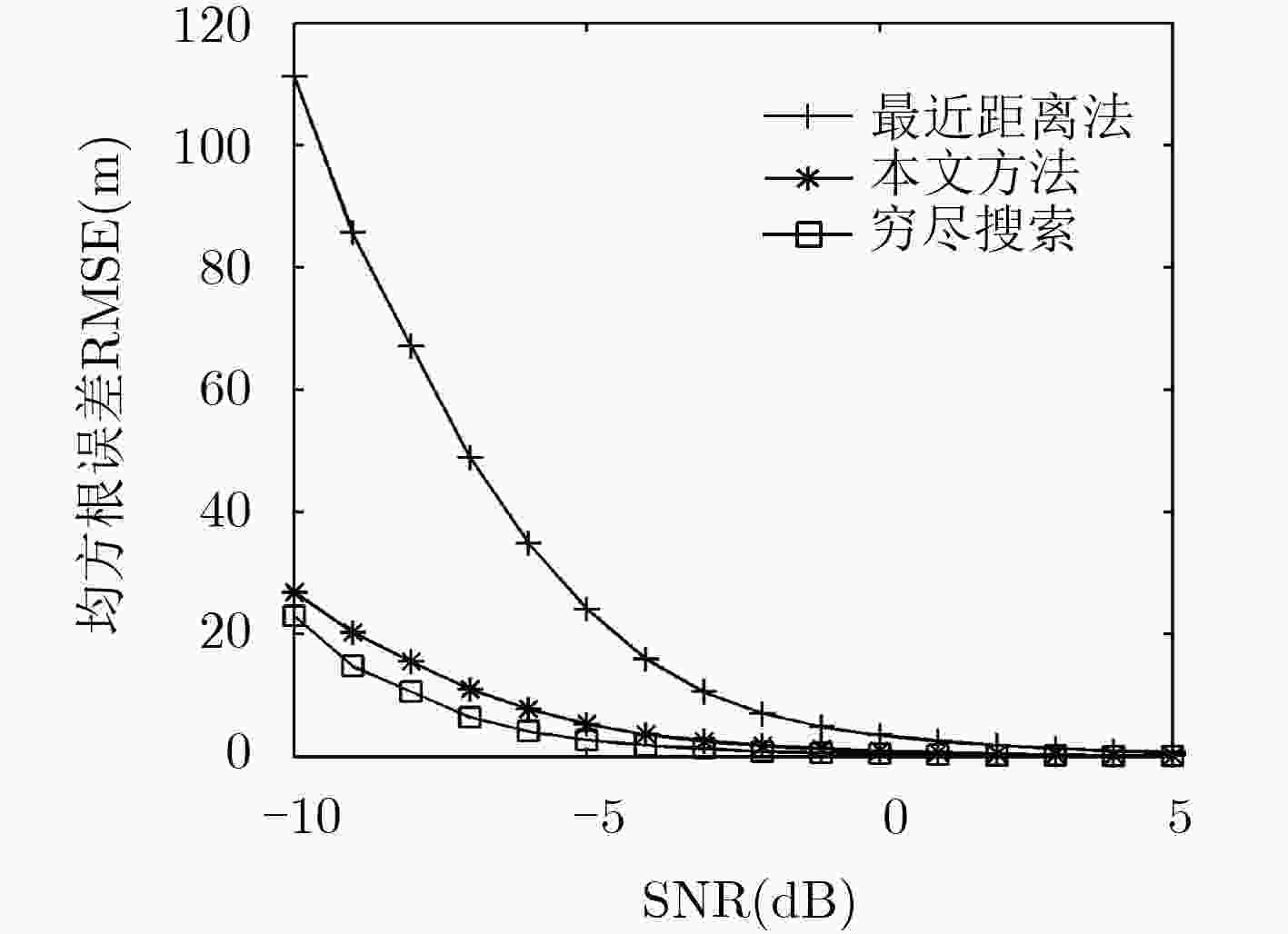
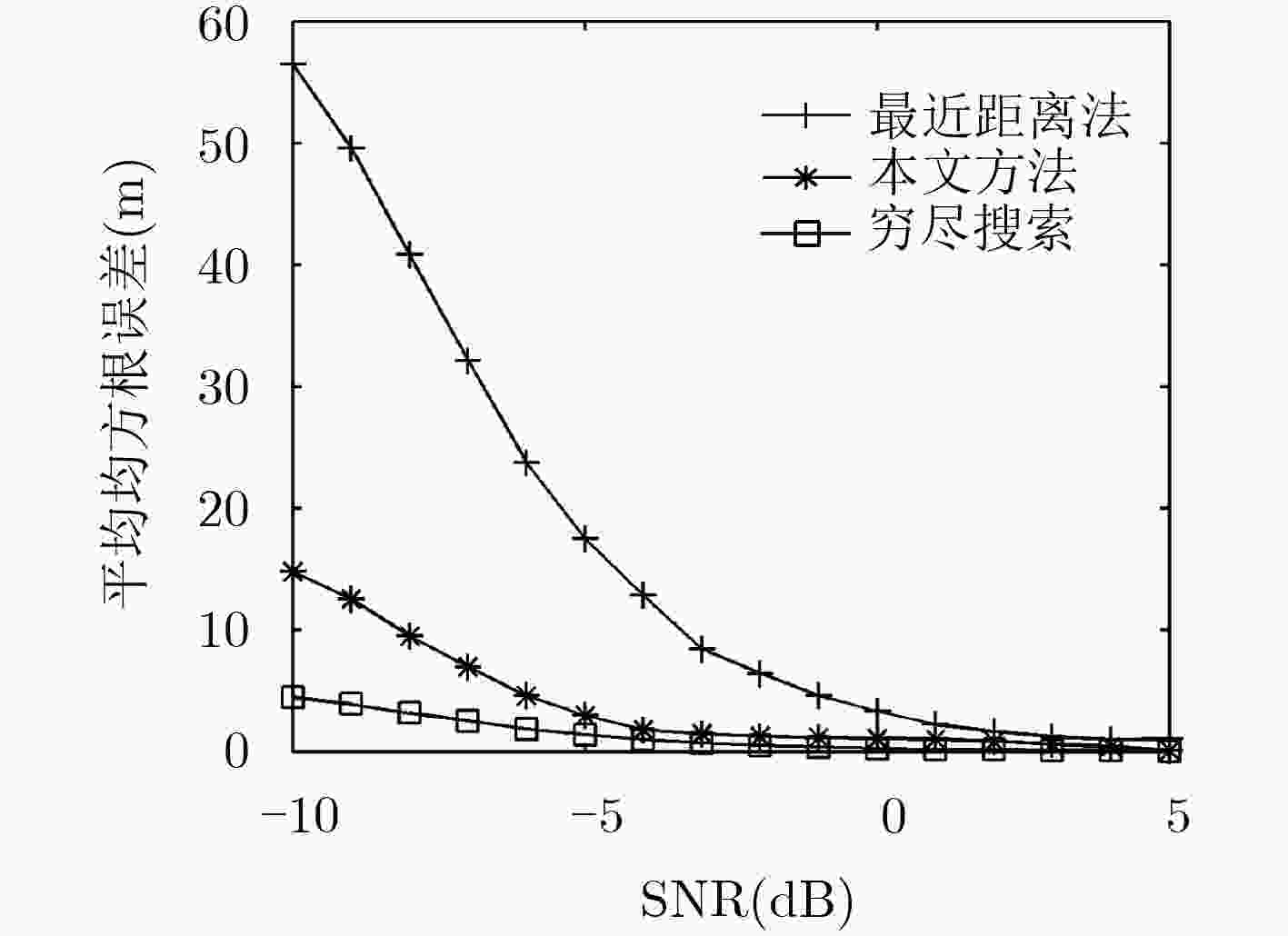


 下载:
下载:
