参数灵活的二维格雷-零相关区阵列集构造方法

王美悦; 刘涛; 陈晓玉; 李玉博

doi:10.11999/JEIT251360

参数灵活的二维格雷-零相关区阵列集构造方法

doi: 10.11999/JEIT251360 cstr: 32379.14.JEIT251360

1.
燕山大学信息科学与工程学院秦皇岛 066004
2.
河北省信息传输与信号处理重点实验室秦皇岛 066004
3.
燕山大学深圳研究院深圳 518063

基金项目: 国家自然科学基金(62501520, 62471427)，河北省中央引导地方科技发展资金项目(246Z0403G)，河北省自然科学基金(F2025203055)

详细信息

作者简介:
王美悦：女，博士生，研究方向为序列设计与编码理论

刘涛：女，讲师，研究方向为序列设计与编码理论

陈晓玉：女，副教授，研究方向为为信号设计与无线通信技术

李玉博：男，教授，研究方向为为序列设计与编码、码域非正交多址技术、通信与雷达信号设计

通讯作者:
李玉博　liyubo6316@ysu.edu.cn

中图分类号: TN911.2
计量
- 文章访问数: 12
- HTML全文浏览量: 7
- PDF下载量: 1
- 被引次数: 0
出版历程
- 修回日期: 2026-02-05
- 录用日期: 2026-02-05
- 网络出版日期: 2026-02-15

Construction Methods of Two-Dimensional Golay-Zero Correlation Zone Array Sets with Flexible Parameters

1.
School of Information Science and Engineering, Yanshan University, Qinhuangdao 066004, China
2.
Hebei Province Key Laboratory of Information Transmission and Signal Processing, Qinhuangdao 066004, China
3.
Shenzhen Research Institute of Yanshan University, Shenzhen 518063, China

Funds: The National Natural Science Foundation of China (62501520, 62471427), The Central Guiding Local Science and Technology Development Fund Project of Hebei Province (246Z0403G), The Natural Science Foundation of Hebei Province (F2025203055)

摘要

摘要: 二维(2-D)格雷-零相关区(Golay-ZCZ)阵列集在多输入多输出(MIMO)全向传输系统中具有潜在的应用前景，例如用于预编码矩阵、相控阵天线和声源阵列。然而，针对其构造研究的现有文献仍较为有限。该文分别基于2-D多变量函数和级联法提出了三种2-D Golay-ZCZ阵列集的构造方法，构造的阵列集具有灵活阵列尺寸和大的零相关区。构造得到的阵列集不仅可以得到现有文献中没有的新参数，还可包含已有的结果为特例。
- 二维格雷-零相关区阵列集 /
- 二维多变量函数 /
- 零相关区 /
- 全向传输
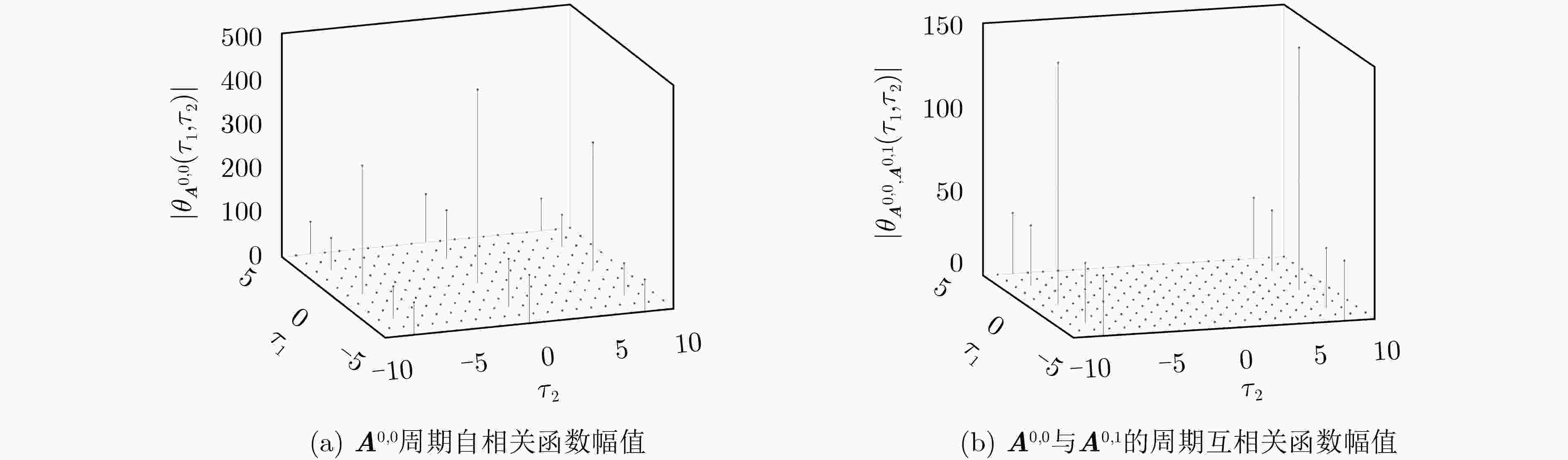
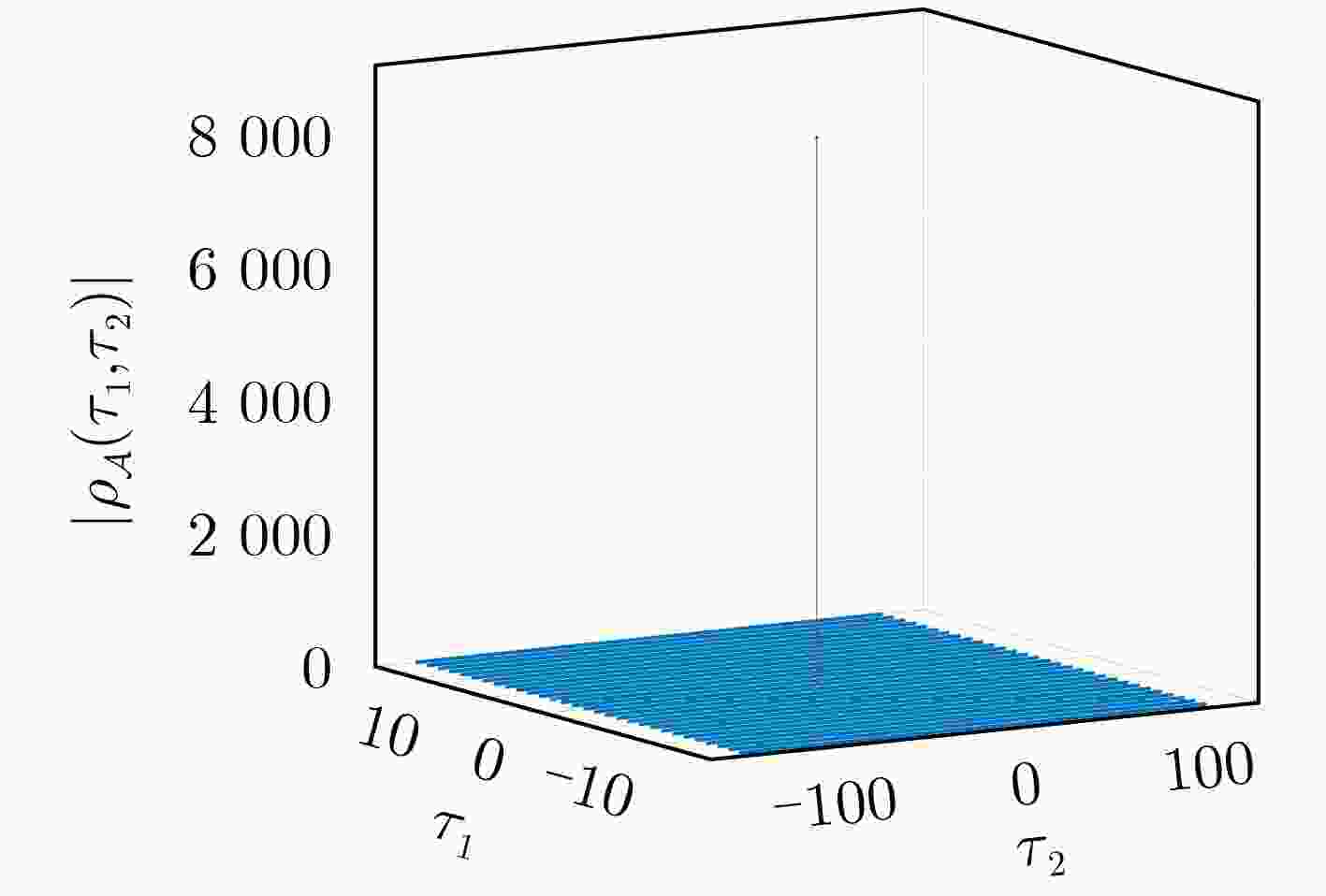
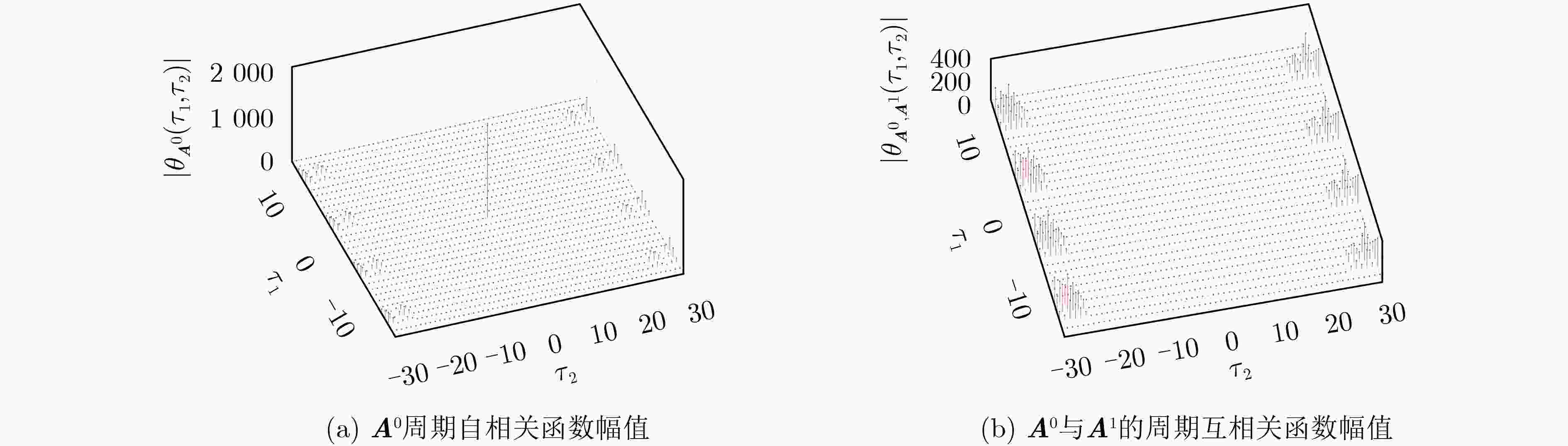
Abstract: Objective Sequences with good correlation properties have important applications in wireless communications, cryptography and radar. However, a sequence set cannot simultaneously achieve ideal autocorrelation and ideal cross-correlation. This limitation has driven the study of two signal classes with ideal correlation properties: Zero Correlation Zone (ZCZ) sequences and Golay Complementary Sets (GCS). The Golay-ZCZ sequence set combines their advantages: its constituent sequences exhibit ideal periodic autocorrelation and cross-correlation within the ZCZ, while their aperiodic autocorrelations sum to zero at all non-zero shifts. That is, a Golay-ZCZ set is a ZCZ set and also a GCS. Therefore, it can be used in the original applications of GCSs and those of ZCZ sets. An array set is a two-dimensional extension of a sequence set. Although Golay-ZCZ sequence sets have been extensively constructed and studied, research on Two-Dimensional (2-D) Golay-ZCZ array sets remains relatively limited. This study proposes three constructions of 2-D Golay-ZCZ array sets using 2-D multivariate functions and concatenation operator, which can be applied as precoding matrices for massive Multiple Input Multiple Output (MIMO) omnidirectional transmission. Methods This paper proposes three construction methods for constructing 2-D Golay-ZCZ array sets, including both direct and indirect construction approaches. The parameters of these methods have not been reported in the existing literature. In the first construction, the 2-D Golay-ZCZ array set is generated based on 2-D multivariate functions, with its parameters taking the form of prime powers. This function-based direct construction enables more efficient synthesis of the target arrays. The second and third construction methods generate 2-D Golay-ZCZ array sets by horizontally cascading and vertically cascading two-dimensional complete complementary codes, respectively. The parameters of these indirect construction methods are not restricted to prime powers, thereby broadening the applicability and parametric flexibility of the approaches. Results and Discussions The first construction generates a 2-D Golay-ZCZ array set with array size $ p_{1}^{{m}_{1}}\times p_{2}^{{m}_{2}} $ and ZCZ size $ ({p}_{1}-1)p_{1}^{{\pi }_{1}(2)-1}\times ({p}_{2}-1)p_{2}^{{\sigma }_{1}(2)-1} $ through a direct function-based method, where $ {p}_{1} $ and $ {p}_{2} $ are primes. For ease of understanding, the magnitudes of the 2-D periodic cross-correlation function of the constructed array set in example 1 (Fig. 1). The second construction presents a ZCZ array set with array size $ {L}_{1}\times {N}^{2}{L}_{2} $ and ZCZ size $ ({L}_{1}-1)\times (N-1){L}_{2} $ based the horizontal concatenation of $ (N,N,{L}_{1},{L}_{2}) $ 2-D CCC. The third construction presents a ZCZ array set with array size $ {N}^{2}{L}_{1}\times {L}_{2} $ and ZCZ size $ (N-1){L}_{1}\times ({L}_{2}-1) $based the vertical concatenation of $ (N,N,{L}_{1},{L}_{2}) $ 2-D CCC. An illustrative example for construction 2 is provided. The corresponding correlation magnitudes are detailed accordingly (Figs. 2 and 3). As shown in (Table 1), the construction methods proposed in this paper produce parameters that have not been reported in the existing literature. The constructed array sets exhibit significant flexibility in terms of array dimensions and ZCZ sizes, which is of substantial practical importance for the design of precoding matrices in MIMO omnidirectional transmission systems. In practical implementations, the dimensionality of a precoding matrix is typically determined by the number of transmit antennas, while the size of the ZCZ must align with the maximum multipath delay spread of the channel. Owing to the parameter flexibility, the proposed 2-D Golay-ZCZ array sets facilitate adaptive selection based on diverse antenna configurations and channel conditions. Conclusions This paper proposes three constructions of 2-D Golay-ZCZ array sets, which can provide flexible array size and large ZCZ width. Based on the 2-D multivariable function, the first proposed construction can include the previous result as a special case without utilizing any kernels. The second and third constructions exhibit more parametric flexibility based on concatenation operator. The proposed 2-D Golay-ZCZ arrays have potential applications in MIMO omnidirectional transmission. The parameter-flexible 2-D Golay-ZCZ array set can adaptively select according to different antenna configurations and channel conditions, thereby effectively suppressing multi-antenna interference within the zero-correlation zone while maintaining the uniformity of the transmitted energy.
- 2-D Golay-ZCZ Array Set /
- 2-D Multivariable Function /
- Zero Correlation Zone (ZCZ) /
- Omnidirectional Transmission

HTML全文

图 1 例1中阵列集的二维周期相关函数幅值

下载: 全尺寸图片幻灯片

图 2 例2中阵列集${\mathcal{A}}$的二维非周期自相关函数幅值

下载: 全尺寸图片幻灯片

图 3 例2中阵列集的二维周期相关函数幅值

下载: 全尺寸图片幻灯片

表 1 二维Golay-ZCZ阵列集参数比较

方法	集合大小	阵列尺寸	零相关区宽度	基于	相位$ q $
文献[26]定理1	2	$ (m,4n) $	$ (m-1,n) $	GCAP	同GCAP的相位
文献[27]定理1	$ {2}^{k} $	$ ({2}^{n},{2}^{m}) $	$ ({2}^{n}-1,{2}^{{{\pi }_{1}}(2)-1}) $	2-D GBF	$ q\geq 2 $且为偶数
文献[27]定理2	$ {4}^{k} $	$ ({2}^{n},{2}^{m}) $	$ ({2}^{{{\sigma }_{1}}(2)-1},{2}^{{{\pi }_{1}}(2)-1}) $	2-D GBF	$ q\geq 2 $且为偶数
本文定理1	$ p_{1}^{{k}_{1}}p_{2}^{{k}_{2}} $	$ (p_{1}^{{m}_{1}},p_{2}^{{m}_{2}}) $	$ \left(({p}_{1}-1)p_{1}^{{\pi }_{1}(2)-1},({p}_{2}-1)p_{2}^{{\sigma }_{1}(2)-1}\right) $	2-D MVF	$ \text{lcm}({p}_{1},{p}_{2})\left\| q\right. $， $ {p}_{1},{p}_{2} $为素数
本文定理2	$ N $	$ ({L}_{1},{N}^{2}{L}_{2}) $	$ \left(\begin{array}{c}({L}_{1}-1),(N-1){L}_{2}\end{array}\right) $	2-D CCC和DFT矩阵	$ \text{lcm}(Q,N)\left\| q\right. $，$ Q $为2-D CCC相位， $ N $为DFT矩阵阶数
本文定理3	$ N $	$ ({N}^{2}{L}_{1},{L}_{2}) $	$ \left((N-1){L}_{1},({L}_{2}-1)\right) $	2-D CCC和DFT矩阵.

下载: 导出CSV

参考文献(28)

[1]	沈炳声, 周正春, 杨洋, 等. 一种无扰的多载波互补码分多址通信雷达一体化方案[J]. 电子与信息学报, 2025, 47(1): 201–210. doi: 10.11999/JEIT240297. SHEN Bingsheng, ZHOU Zhengchun, YANG Yang, et al. A non-interference multi-carrier complementary coded division multiple access dual-functional radar-communication scheme[J]. Journal of Electronics & Information Technology, 2025, 47(1): 201–210. doi: 10.11999/JEIT240297.
[2]	GOLAY M. Complementary series[J]. IEEE Transactions on Information Theory, 1961, 7(2): 82–87. doi: 10.1109/TIT.1961.1057620.
[3]	TSENG C C and LIU C. Complementary sets of sequences[J]. IEEE Transactions on Information Theory, 1972, 18(5): 644–652. doi: 10.1109/TIT.1972.1054860.
[4]	沈炳声, 周正春, 杨洋, 等. 基于基序列构造二元互补序列集[J]. 电子与信息学报, 2024, 46(9): 3757–3762. doi: 10.11999/JEIT240309. SHEN Bingsheng, ZHOU Zhengchun, YANG Yang, et al. Constructions of binary complementary sequence set based on base sequences[J]. Journal of Electronics & Information Technology, 2024, 46(9): 3757–3762. doi: 10.11999/JEIT240309.
[5]	LIU Zilong, PARAMPALLI U, GUAN Yongliang, et al. Constructions of optimal and near-optimal quasi-complementary sequence sets from singer difference sets[J]. IEEE Wireless Communications Letters, 2013, 2(5): 487–490. doi: 10.1109/wcl.2013.061213.130286.
[6]	刘涛, 王玉含, 李玉博. 低相关区互补序列集的构造方法研究[J]. 电子与信息学报, 2024, 46(8): 3410–3418. doi: 10.11999/JEIT231332. LIU Tao, WANG Yuhan, and LI Yubo. Research on construction methods of low correlation zone complementary sequence sets[J]. Journal of Electronics & Information Technology, 2024, 46(8): 3410–3418. doi: 10.11999/JEIT231332.
[7]	PAI Chengyu and CHEN Chaoyu. Two-dimensional Golay complementary array pairs/sets with bounded row and column sequence PAPRs[J]. IEEE Transactions on Communications, 2022, 70(6): 3695–3707. doi: 10.1109/TCOMM.2022.3166903.
[8]	SHEN Bingsheng, YANG Yang, and REN Ruibin. Three constructions of Golay complementary array sets[J]. Advances in Mathematics of Communications, 2024, 18(3): 696–710. doi: 10.3934/amc.2022019.
[9]	LIU Tao, MEN Xinyu, LI Yubo, et al. Constructions of 2-D Golay complementary array sets for MIMO omnidirectional transmission[J]. IEEE Communications Letters, 2022, 26(7): 1459–1463. doi: 10.1109/LCOMM.2022.3160267.
[10]	ZHAO Youqi, PAI Chengyu, HUANG Zhenming, et al. Two-dimensional Golay complementary array sets with arbitrary lengths for omnidirectional MIMO transmission[J]. IEEE Transactions on Communications, 2024, 72(2): 1135–1145. doi: 10.1109/TCOMM.2023.3326498.
[11]	XIAO Hongyang and CAO Xiwang. Two constructions of two-dimensional Golay complementary array sets with flexible sizes in two dimensions[J]. Computational and Applied Mathematics, 2024, 43(4): 174. doi: 10.1007/s40314-024-02694-7.
[12]	FAN Pingzhi, YUAN Weina, and TU Yifeng. Z-complementary binary sequences[J]. IEEE Signal Processing Letters, 2007, 14(8): 509–512. doi: 10.1109/LSP.2007.891834.
[13]	TANG Xiaohu, FAN Pingzhi, and LINDNER J. Multiple binary ZCZ sequence sets with good cross-correlation property based on complementary sequence sets[J]. IEEE Transactions on Information Theory, 2010, 56(8): 4038–4045. doi: 10.1109/TIT.2010.2050796.
[14]	ZHOU Zhengchun, ZHANG Dan, HELLESETH T, et al. A construction of multiple optimal ZCZ sequence sets with good cross correlation[J]. IEEE Transactions on Information Theory, 2018, 64(2): 1340–1346. doi: 10.1109/TIT.2017.2756845.
[15]	CHEN Xiaoyu, GAO Xichao, and PENG Xiuying. Construction of multiple optimal polyphase zero correlation zone sequence sets with inter-set zero cross-correlation zone[J]. IEEE Communications Letters, 2021, 25(9): 2795–2799. doi: 10.1109/LCOMM.2021.3085312.
[16]	LIU Zilong, GUAN Yongliang, and PARAMPALLI U. A new construction of zero correlation zone sequences from generalized reed-muller codes[C]. Proceedings of 2014 IEEE Information Theory Workshop, Hobart, Australia, 2014: 591–595. doi: 10.1109/ITW.2014.6970900.
[17]	HU Su, LIU Zilong, GUAN Yongliang, et al. Training sequence design for efficient channel estimation in MIMO-FBMC systems[J]. IEEE Access, 2017, 5: 4747–4758. doi: 10.1109/ACCESS.2017.2688399.
[18]	ZHANG Rongqing, CHENG Xiang, MA Meng, et al. Interference-avoidance pilot design using ZCZ sequences for multi-cell MIMO-OFDM systems[C]. Proceedings of 2012 IEEE Global Communications Conference, Anaheim, USA, 2012: 5056–5061. doi: 10.1109/GLOCOM.2012.6503922.
[19]	LONG Biqi, ZHANG Ping, and HU Jiandong. A generalized QS-CDMA system and the design of new spreading codes[J]. IEEE Transactions on Vehicular Technology, 1998, 47(4): 1268–1275. doi: 10.1109/25.728516.
[20]	TANG Xiaohu, FAN Pingzhi, LI Dingbo, et al. Binary array set with zero correlation zone[J]. Electronics Letters, 2001, 37(13): 841–842. doi: 10.1049/el:20010576. (查阅网上资料,请核对作者的全拼信息).
[21]	ZHANG Hui, FAN Cuiling, and MESNAGER S. Constructions of two-dimensional Z-complementary array pairs with large ZCZ ratio[J]. Designs, Codes and Cryptography, 2022, 90(5): 1221–1239. doi: 10.1007/s10623-022-01035-1.
[22]	GONG Guang, HUO Fei, and YANG Yang. Large zero autocorrelation zones of Golay sequences and their applications[J]. IEEE Transactions on Communications, 2013, 61(9): 3967–3979. doi: 10.1109/TCOMM.2013.072813.120928.
[23]	CHEN Chaoyu and WU Shingwei. Golay complementary sequence sets with large zero correlation zones[J]. IEEE Transactions on Communications, 2018, 66(11): 5197–5204. doi: 10.1109/TCOMM.2018.2857485.
[24]	PAI Chengyu, LIN Y, and CHEN Chaoyu. Optimal and almost-optimal Golay-ZCZ sequence sets with bounded PAPRs[J]. IEEE Transactions on Communications, 2023, 71(2): 728–740. doi: 10.1109/TCOMM.2022.3228932.
[25]	GU Zhi, ZHOU Zhengchun, ADHIKARY A R, et al. Asymptotically optimal Golay-ZCZ sequence sets with flexible length[J]. Chinese Journal of Electronics, 2023, 32(4): 806–820. doi: 10.23919/cje.2022.00.266.
[26]	GU Zhi, ZHOU Zhengchun, ADHIKARY A R, et al. Two-dimensional Golay complementary array pairs with flexible size and large zero correlation zone[J]. Cryptography and Communications, 2023, 15(3): 709–717. doi: 10.1007/s12095-023-00633-7.
[27]	PRAKASH A, KAO T C, MAJHI S, et al. Constructions of two-dimensional Golay-ZCZ array sets based on generalized boolean functions[J]. IEEE Signal Processing Letters, 2025, 32: 321–325. doi: 10.1109/LSP.2024.3516562.
[28]	PAI Chengyu, LIU Zilong, ZHAO Youqi, et al. Designing two-dimensional complete complementary codes for omnidirectional transmission in massive MIMO systems[C]. Proceedings of 2022 IEEE International Symposium on Information Theory, Espoo, Finland, 2022: 2285–2290. doi: 10.1109/ISIT50566.2022.9834723.