A Complexity-Reduced Active Interference Cancellation Algorithm in f-OFDM
-
摘要: 滤波正交频分复用(f-OFDM)使用子带滤波器对不同子带进行了有效隔离,实现了子带参数的灵活配置和异步传输,但代价是引入了一定量的固有干扰,尤其是由于子带的带外辐射(OOBE)而导致的子带间干扰(ITBI),造成了系统性能下降。因此抑制子带的OOBE对于降低ITBI,提升f-OFDM系统性能具有重要作用。该文根据f-OFDM的系统结构特点,构建了f-OFDM中的降复杂度主动干扰抵消(CRAIC)优化模型,并设计了对应的数域转换和类型转换方法,将CRAIC的优化模型转化为二阶锥规划问题进行了求解。该文还通过计算机仿真对所提CRAIC算法进行了验证,仿真结果显示,该文提出的CRAIC算法可以有效降低f-OFDM子带的OOBE,从而降低对相邻子带的ITBI,提高其性能。此外,该文还对消除子载波(CCs)个数、参与生成CCs的数据子载波个数,以及带外目标抑制频点个数等主要参数对CRAIC算法性能的影响进行了仿真分析,从功率谱密度、误码率等角度揭示了f-OFDM中CRAIC算法参数设置的内在特性。Abstract:
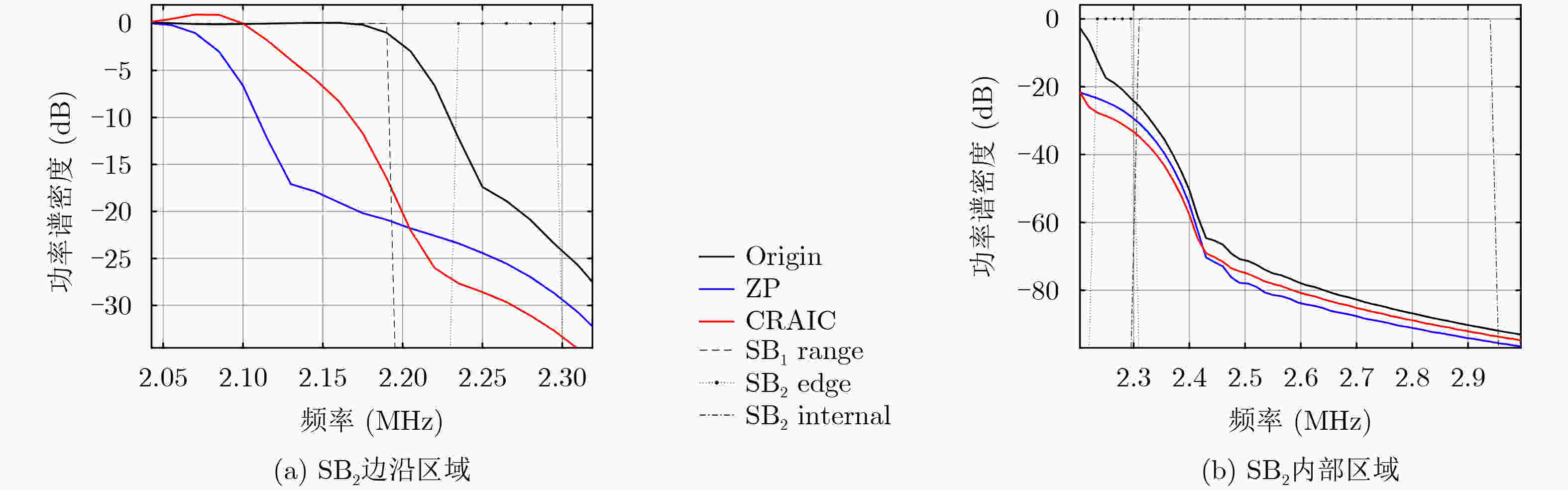
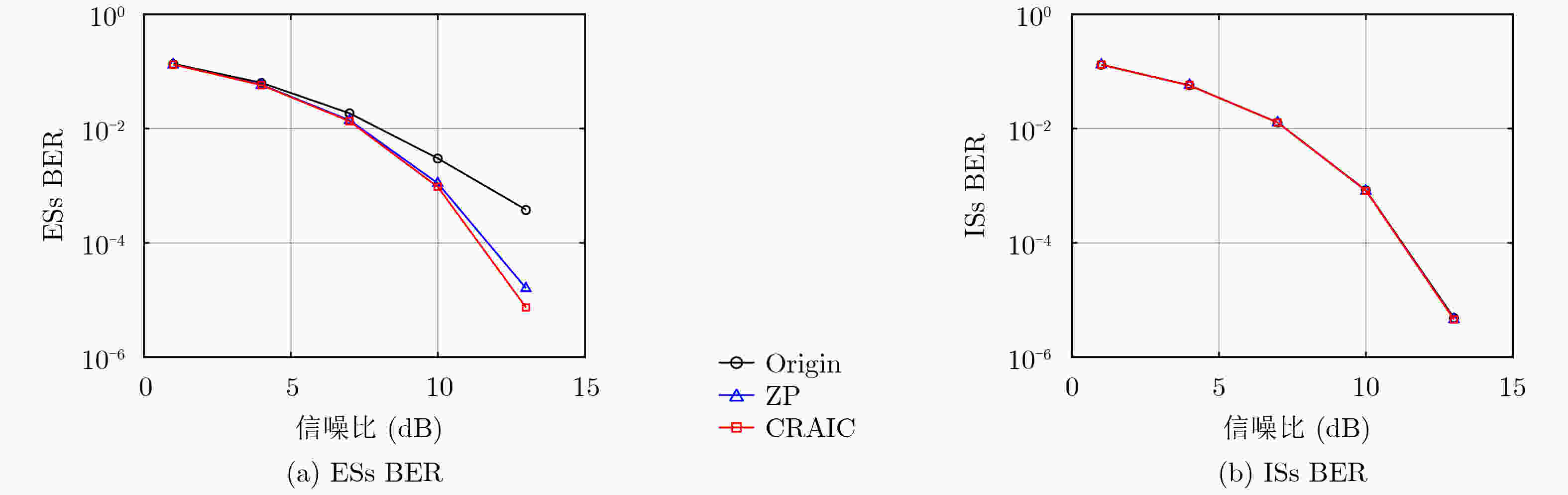
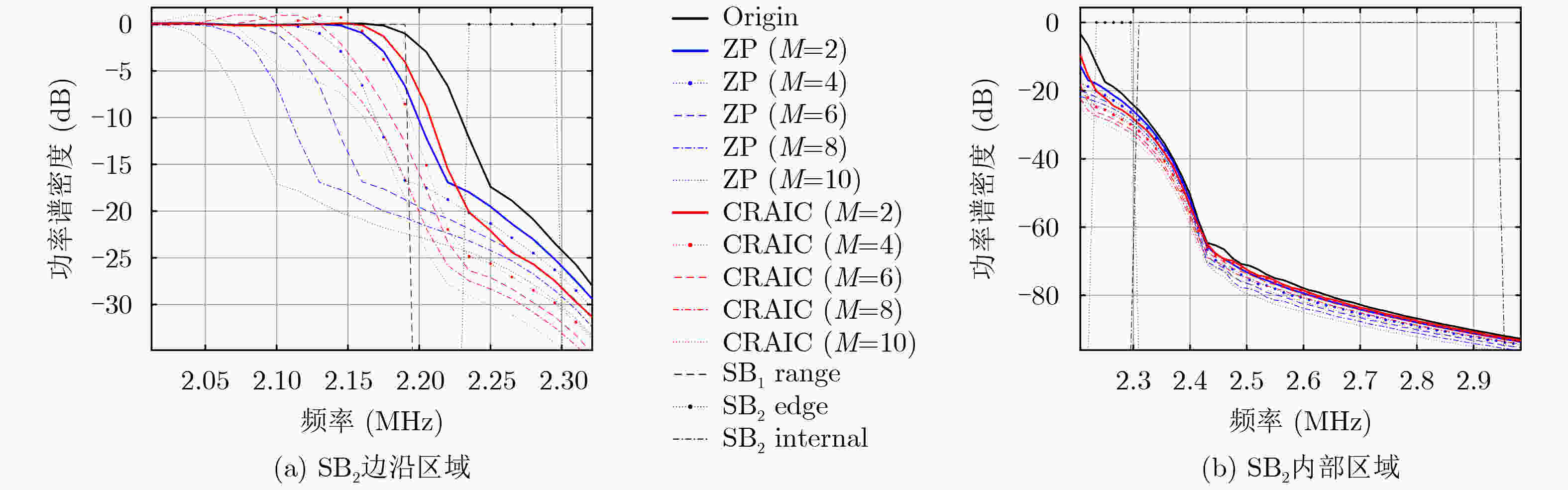
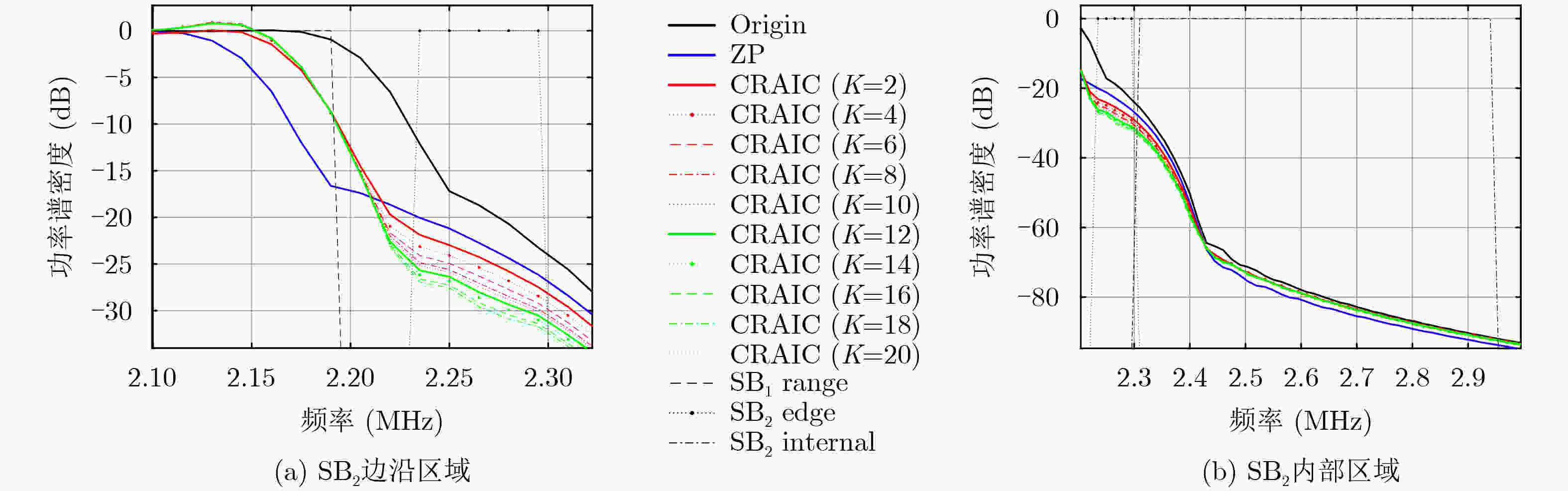
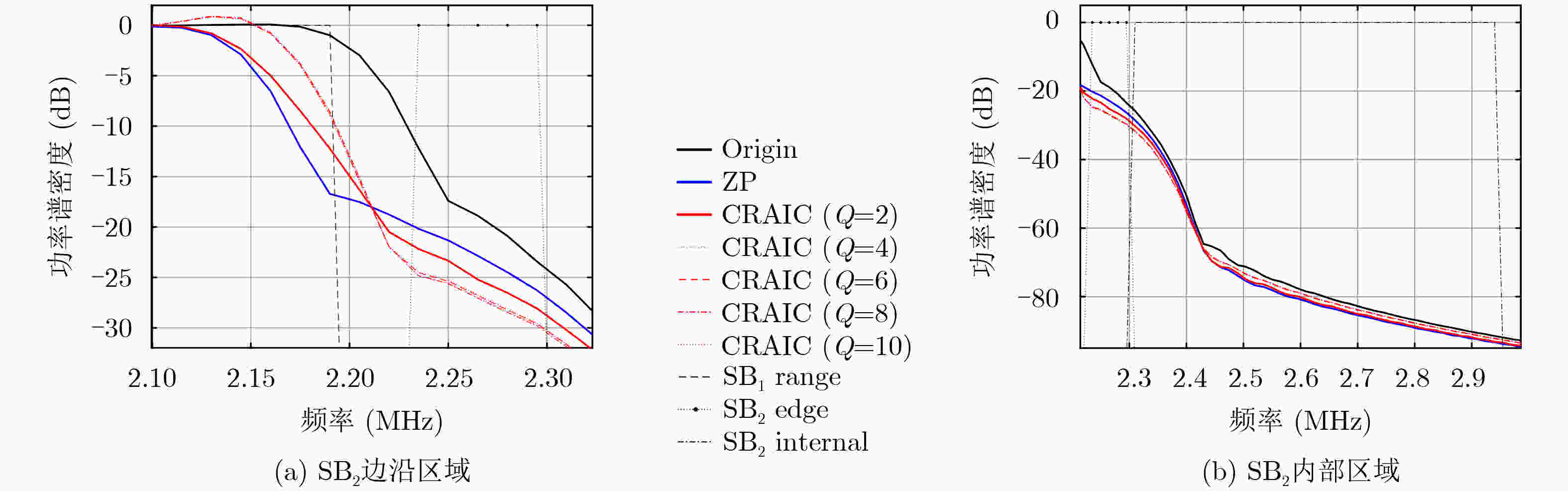
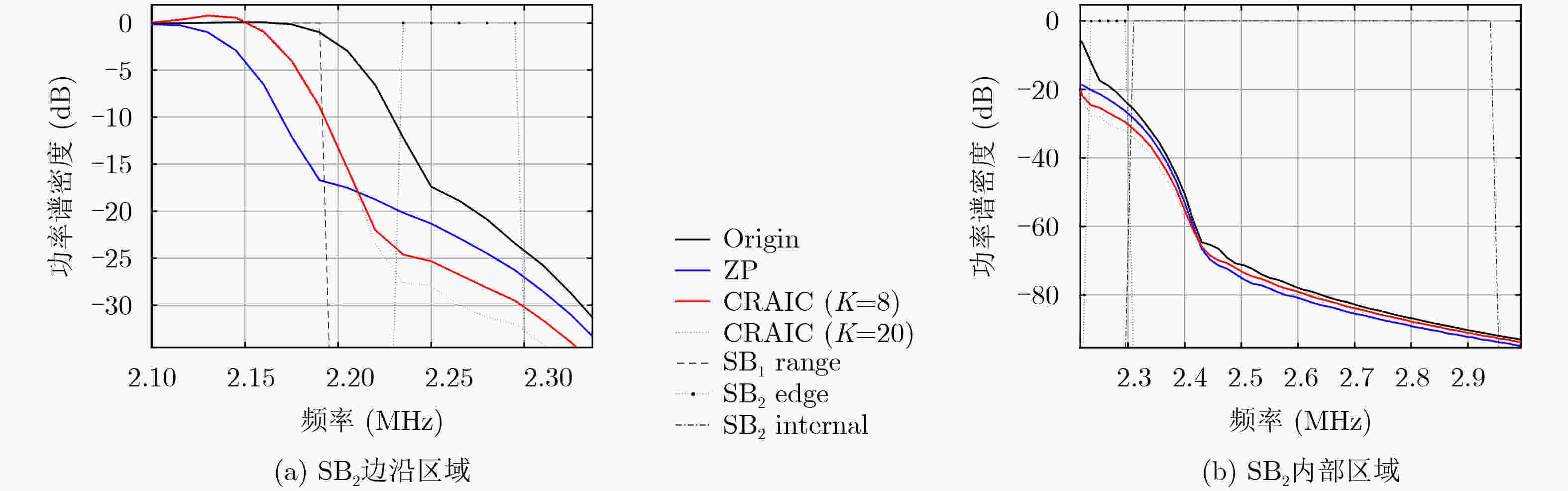
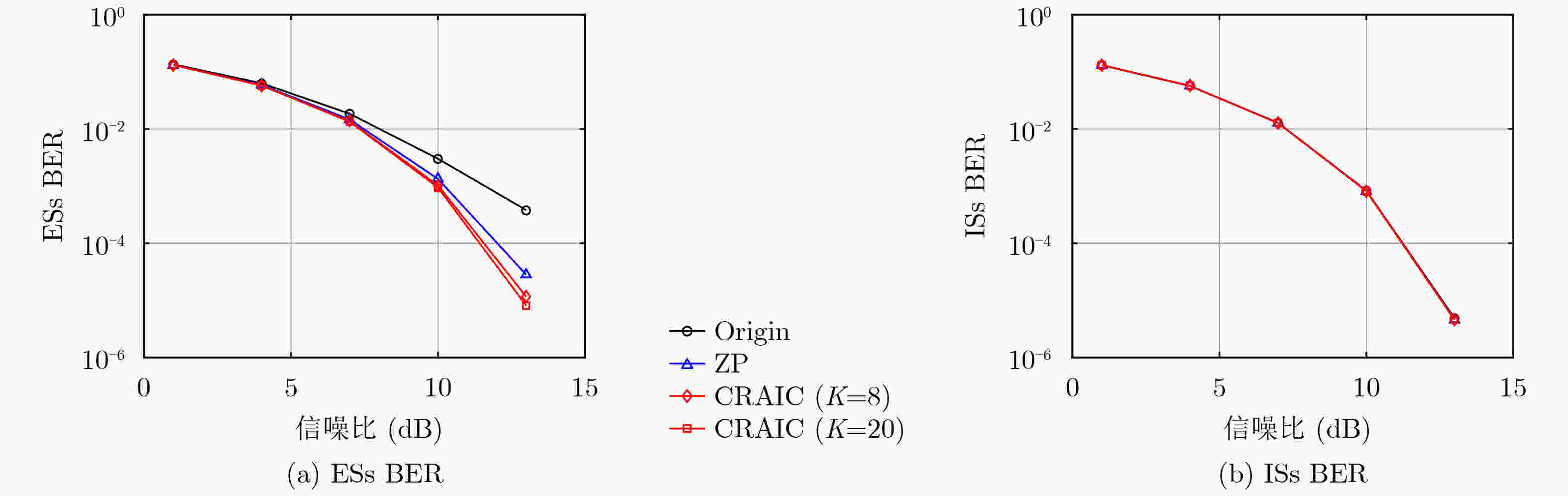
Objective Due to spectrum scarcity and diverse communication needs, there is an urgent need for a waveform technology with high spectral efficiency, flexible subband configuration, and support for asynchronous communication in the Sixth Generation mobile communication (6G). Among the candidate waveforms, filtered Orthogonal Frequency Division Multiplexing (f-OFDM) has emerged as a promising solution that satisfies all these requirements. By applying subband filtering, capabilities such as flexible subband configuration as well as asynchronous transmission are achieved by f-OFDM. Nevertheless, this filtering mechanism inevitably introduces a certain level of intrinsic interference into the system. Notably, a dominant component of such interference is the Inter-subband Interference (ITBI), which primarily caused by the Out-Of-Band Emission (OOBE) leaking from adjacent subbands. Therefore, subband OOBE suppression plays a crucial role in reducing ITBI and enhancing the performance of f-OFDM systems. Based on the system structure of f-OFDM, the study proposes a Complexity-Reduced Active Interference Cancellation (CRAIC) algorithm in f-OFDM, so as to suppress the OOBE of f-OFDM subbands, and then enhance the system performance. Methods First, base on the spectral structure of f-OFDM, the paper exploits a subset of data subcarriers within the target subband to generate Cancellation Carriers (CCs). Then, the CRAIC optimization model for f-OFDM systems is constructed under the constraint of CCs power, and the cost function is defined addressing the superposed spectrum of both data subcarriers and CCs at Desired Frequency Points (DFPs). Second, by introducing the real-complex domain transformation and the reformulation of optimization model, the above complex-domain CRAIC programming problem is transformed into a real-domain Second-Order Cone Programming (SOCP) problem, enabling an efficient solution. Furthermore, through computer simulations, the impact of key parameters on CRAIC performance has been evaluated, including the number of cancellation carriers ($ M $), the number of data subcarriers involved in CCs generation ($ K $), and the number of DFPs ($ Q $). Then practical recommendations are provided for the rational configuration of CRAIC parameters in f-OFDM systems. Results and Discussions The simulation results demonstrate that in the edge region of the adjacent subband, the proposed CRAIC algorithm exhibits the steepest PSD roll-off rate compared to the conventional ZP and Origin schemes. This indicates that CRAIC possesses the strongest ITBI suppression capability in such region, consequently achieving the lowest Edge Subcarriers (ESs) Bit Error Rate (BER) of the adjacent subband. Specifically, CRAIC achieves a maximum PSD reduction of 4 dB and 12 dB relative to ZP and Origin ( Fig. 2a ). This is attributed to the fact that the right Q/2 DFPs largely fall within the edge region of SB2, leading to effective suppression of the spectrum in this area. Consequently, in terms of the BER at the edge of SB2, RCAIC achieves a significantly lower BER compared to Origin. A visible performance improvement is also observed relative to ZP (Fig. 3a ). Furthermore, the impact of key parameters, i.e. $ M $, $ K $ and $ Q $ is evaluated through computer simulations. The results indicate that while increasing $ M $ continuously improves the OOBE suppression capability (Fig. 4a ), it concurrently leads to a gradual degradation in spectral efficiency. In contrast to $ M $, increasing $ K $ and $ Q $ exhibits a marginal effect on enhancing the performance of CRAIC, continual increments beyond a certain point do not yield sustained performance improvements (Fig. 5a andFig. 6a ). Based on these analyses, we consider $ M=4 $, $ K=8 $, $ Q=4 $ to be a typical parameter configuration in the scenario of the paper. Under this typical setting, CRAIC (with $ K=8 $) achieves significant performance gains in ESs BER compared to Origin and ZP (Fig. 8a ), while maintaining nearly the same Internal Subcarriers (ISs) BER performance as the two benchmark schemes (Fig.8b ). Even when compared to the full-scale CRAIC ($ K=20 $), CRAIC ($ K=8 $) achieves a remarkable 60% reduction in the size of the data subcarrier mapping matrix, while incurring merely limited degradation in BER performance (Fig. 8a ). This result convincingly demonstrates that the proposed algorithm effectively preserves the performance of the full-scale AIC while substantially lowering its computational complexity.Conclusions An algorithm named CRAIC for filtered OFDM systems is investigated in the paper. The proposed CRAIC optimization model is constructed under the constraint of CCs power, in which the cost function is defined addressing the superposed spectrum of a subset of data subcarriers as well as CCs at DFPs. Through designed real-imaginary domain conversion and model reformulation, the complex-domain optimization problem is then converted into a real-domain SOCP problem. Simulation results demonstrate that the CRAIC algorithm significantly reduces the PSD of the target subband, particularly in the transition region of the adjacent subband, leading to notable improvements in edge BER. Furthermore, the influence of key parameters is evaluated. The results indicate that increasing $ M $ enlarges the performance gain of CRAIC over ZP, though at the expense of reduced spectral efficiency. While a larger $ K $ improves the OOBE suppression capability, with diminishing marginal returns and increased computational complexity. Moreover, simply increasing $ Q $ does not yield continuous PSD reduction. In summary, the application of CRAIC in f-OFDM systems enhances isolation between subbands and reduces ITBI, then improves the system performance. -
Key words:
- f-OFDM /
- subband filtering /
- Active Interference Cancellation /
- OOBE suppression
-
表 1 主要仿真参数
参数 SB1 SB2 SCS/kHz 30 15 滤波器长度/样点 512 1024 IFFT尺寸/样点 1024 2048 CP长度/样点 16 32 子载波序号 50~73 149~196 每帧符号数 28 14 -
[1] ATAEEBOJD E, RASTI M, and LATVA-AHO M. Network selection and resource allocation for coexistence of eMBB and URLLC services in a 6G multi-band HetNet[J]. IEEE Transactions on Green Communications and Networking, 2025, 9(3): 1179–1194. doi: 10.1109/TGCN.2024.3481281. [2] 徐金雷, 赵俊湦, 卢华兵, 等. 面向6G的多维扩展通感一体化研究综述[J]. 电子与信息学报, 2024, 46(5): 1672–1683. doi: 10.11999/JEIT231045.XU Jinlei, ZHAO Junsheng, LU Huabing, et al. An overview on multi-dimensional expanded integrated sensing and communication for 6G[J]. Journal of Electronics & Information Technology, 2024, 46(5): 1672–1683. doi: 10.11999/JEIT231045. [3] CHEN Zirui, ZHANG Zhaoyang, and YANG Zhaohui. Big AI models for 6G wireless networks: Opportunities, challenges, and research directions[J]. IEEE Wireless Communications, 2024, 31(5): 164–172. doi: 10.1109/MWC.015.2300404. [4] RAWAT B S, SRIVASTAVA A, SHRIVASTAVA V, et al. A comprehensive analysis of applications in internet of things networks in 5G and 6G[C]. 2024 2nd International Conference on Computer, Communication and Control (IC4), Indore, India, 2024: 1–6. doi: 10.1109/IC457434.2024.10486565. [5] 束锋, 张钧豪, 张旗, 等. 混合智能反射面辅助感通算一体化车联网的联合功率时间分配方法[J]. 电子与信息学报, 2025, 47(4): 1026–1042. doi: 10.11999/JEIT240719.SHU Feng, ZHANG Junhao, ZHANG Qi, et al. Hybrid reconfigurable intelligent surface assisted sensing communication and computation for joint power and time allocation in vehicle ad-hoc network[J]. Journal of Electronics & Information Technology, 2025, 47(4): 1026–1042. doi: 10.11999/JEIT240719. [6] GUO Fengxian, YU F R, ZHANG Heli, et al. Enabling massive IoT toward 6G: A comprehensive survey[J]. IEEE Internet of Things Journal, 2021, 8(15): 11891–11915. doi: 10.1109/JIOT.2021.3063686. [7] YUAN Yifei, WANG Sen, WU Yongpeng, et al. NOMA for next-generation massive IoT: Performance potential and technology directions[J]. IEEE Communications Magazine, 2021, 59(7): 115–121. doi: 10.1109/MCOM.001.2000997. [8] 曾嵘, 邵智敏. 零前缀OFDM中智能反射表面环境下干扰抑制算法研究[J]. 电子与信息学报, 2022, 44(7): 2358–2365. doi: 10.11999/JEIT211389.ZENG Rong and SHAO Zhimin. Research on interference suppression algorithm in reconfigurable intelligent surface environment in ZP-OFDM[J]. Journal of Electronics & Information Technology, 2022, 44(7): 2358–2365. doi: 10.11999/JEIT211389. [9] EL HOUDA BOUDA N, ELAHMAR S A, and DAYOUB I. 5G MCM based NOMA in vehicular environments: A comparative analysis of F-OFDM and W-OFDM[C]. 2024 3rd International Conference on Advanced Electrical Engineering (ICAEE), Sidi-Bel-Abbes, Algeria, 2024: 1–5. doi: 10.1109/ICAEE61760.2024.10783226. [10] ABDOLI J, JIA Ming, and MA Jianglei. Filtered OFDM: A new waveform for future wireless systems[C]. 2015 IEEE 16th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Stockholm, Sweden, 2015: 66–70. doi: 10.1109/SPAWC.2015.7227001. [11] 华惊宇, 杨乐, 闻建刚, 等. 通用滤波多载波系统原型滤波器的连续凸近似优化设计方法[J]. 电子与信息学报, 2025, 47(10): 3793–3803. doi: 10.11999/JEIT250278.HUA Jingyu, YANG Le, WEN Jian’gang, et al. A successive convex approximation optimization based prototype filter design method for universal filtered multi-carrier systems[J]. Journal of Electronics & Information Technology, 2025, 47(10): 3793–3803. doi: 10.11999/JEIT250278. [12] ZHANG Xi, JIA Ming, CHEN Lei, et al. Filtered-OFDM - enabler for flexible waveform in the 5th generation cellular networks[C]. Proceedings of 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, USA, 2015: 1–6. doi: 10.1109/GLOCOM.2015.7417854. [13] CHEN Hao, HUA Jingyu, LI Feng, et al. Interference analysis in the asynchronous f-OFDM systems[J]. IEEE Transactions on Communications, 2019, 67(5): 3580–3596. doi: 10.1109/TCOMM.2019.2898867. [14] CHENG Xudong, HE Yejun, GE Baohong, et al. A filtered OFDM using FIR filter based on window function method[C]. Proceedings of 2016 IEEE 83rd Vehicular Technology Conference (VTC Spring), Nanjing, China, 2016: 1–5. doi: 10.1109/VTCSpring.2016.7504065. [15] LIU Mingxin, XUE Wei, XU Yidong, et al. Design of filters based on generic function model for reducing out-of-band emissions of the F-OFDM systems[J]. AEU - International Journal of Electronics and Communications, 2021, 139: 153908. doi: 10.1016/j.aeue.2021.153908. [16] CHEN Hao, HUA Jingyu, WEN Jiangang, et al. Uplink interference analysis of F-OFDM systems under non-ideal synchronization[J]. IEEE Transactions on Vehicular Technology, 2020, 69(12): 15500–15517. doi: 10.1109/TVT.2020.3041938. [17] VAN DE BEEK J and BERGGREN F. Out-of-band power suppression in OFDM[J]. IEEE Communications Letters, 2008, 12(9): 609–611. doi: 10.1109/LCOMM.2008.080587. [18] BRANDES S, COSOVIC I, and SCHNELL M. Reduction of out-of-band radiation in OFDM systems by insertion of cancellation carriers[J]. IEEE Communications Letters, 2006, 10(6): 420–422. doi: 10.1109/LCOMM.2006.1638602. [19] ALIZADEH F and GOLDFARB D. Second-order cone programming[J]. Mathematical Programming, 2003, 95(1): 3–51. doi: 10.1007/s10107-002-0339-5. [20] LOBO M S, VANDENBERGHE L, BOYD S, et al. Applications of second-order cone programming[J]. Linear Algebra and its Applications, 1998, 284(1/3): 193–228. doi: 10.1016/S0024-3795(98)10032-0. [21] ZHANG Ruijin, WANG Zhaowei, LIU Xinwei, et al. IPRSOCP: A primal-dual interior-point relaxation algorithm for second-order cone programming[J]. Journal of the Operations Research Society of China, 2024: 1–31. doi: 10.1007/s40305-024-00538-z. (查阅网上资料,未找到对应的卷期页码信息,请确认). [22] FENG Zengzhe. A new $ O(\sqrt{n} L) $ iteration large-update primal-dual interior-point method for second-order cone programming[J]. Numerical Functional Analysis and Optimization, 2012, 33(4): 397–414. doi: 10.1080/01630563.2011.652269. [23] ZAIDI A A, BALDEMAIR R, MOLES-CASES V, et al. OFDM numerology design for 5G new radio to support IoT, eMBB, and MBSFN[J]. IEEE Communications Standards Magazine, 2018, 2(2): 78–83. doi: 10.1109/MCOMSTD.2018.1700021. -





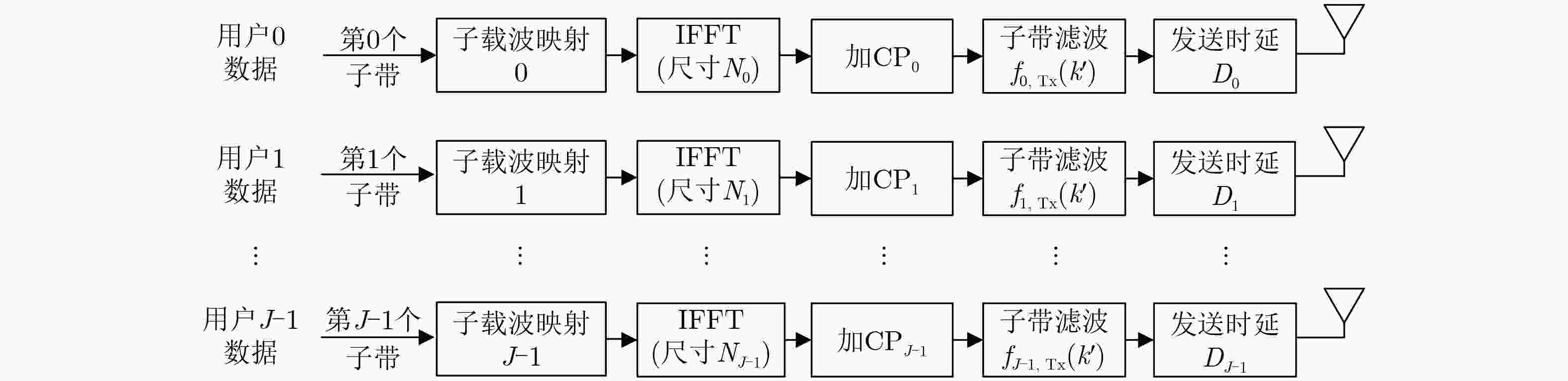
 下载:
下载:


 下载:
下载:
