二阶多智能体系统的弹性平均一致性算法及其应用

方崇荣; 还约辉; 郑文喆; 包贤晨; 李政

doi:10.11999/JEIT251155

二阶多智能体系统的弹性平均一致性算法及其应用

doi: 10.11999/JEIT251155 cstr: 32379.14.JEIT251155

1.
上海交通大学自动化与感知学院上海，200400
2.
浙江国利网安科技有限公司宁波 315000

基金项目: 浙江省“尖兵领雁+X”研发攻关计划(2024SJCZX0003, 2024SJCZX0004)

详细信息

作者简介:
方崇荣：男，副教授，研究方向为信息物理系统安全

还约辉：男，总经理，研究方向为工业控制系统安全

郑文喆：男，硕士，研究方向为多智能体系统安全

包贤晨：男，技术经理，研究方向为工业信息安全

李政：男，博士在读，研究方向为信息物理系统攻击检测

通讯作者:
还约辉　huanyuehui@guolisec.com

中图分类号: TP278
计量
- 文章访问数: 78
- HTML全文浏览量: 34
- PDF下载量: 3
- 被引次数: 0
出版历程
- 收稿日期: 2025-11-01
- 修回日期: 2025-12-31
- 录用日期: 2025-12-31
- 网络出版日期: 2026-01-15

Resilient Average Consensus for Second-Order Multi-Agent Systems: Algorithms and Application

1.
School of Automation and Intelligent Sensing, Shanghai Jiao Tong University , Shanghai, 200400, China
2.
Zhejiang Guoli Security Technology Co. Ltd., Ningbo, 315000, China

Funds: Pioneer Leading Goose+X R&D Program of Zhejiang (2024SJCZX0003, 2024SJCZX0004)

摘要

摘要: 多智能体系统是实现协同协作的重要途径，而弹性一致性则是其安全支撑技术之一。该文针对二阶多智能体系统，研究在存在异常行为节点(包括恶意攻击和意外故障)情况下保证系统协同性能的弹性平均一致性问题。该问题面临双重挑战：如何实现分布式异常检测，以及如何通过一维加速度输入精确补偿二维状态误差。为解决该问题，该文首先推导了二阶平均一致性实现的充分条件。基于此，通过引入两跳通信信息设计了分布式检测机制，并提出能够精确补偿有限控制输入误差的方案。针对输入、速度、位置维度可能遭受的持续攻击，进一步提出具有容错机制的扩展算法。理论证明表明，所提算法能使节点在存在异常节点情况下渐近实现二阶平均一致性。最后，通过大量数值仿真和实验验证了所提方法的有效性。
- 二阶多智能体系统 /
- 弹性一致性 /
- 攻击检测 /
- 误差补偿.
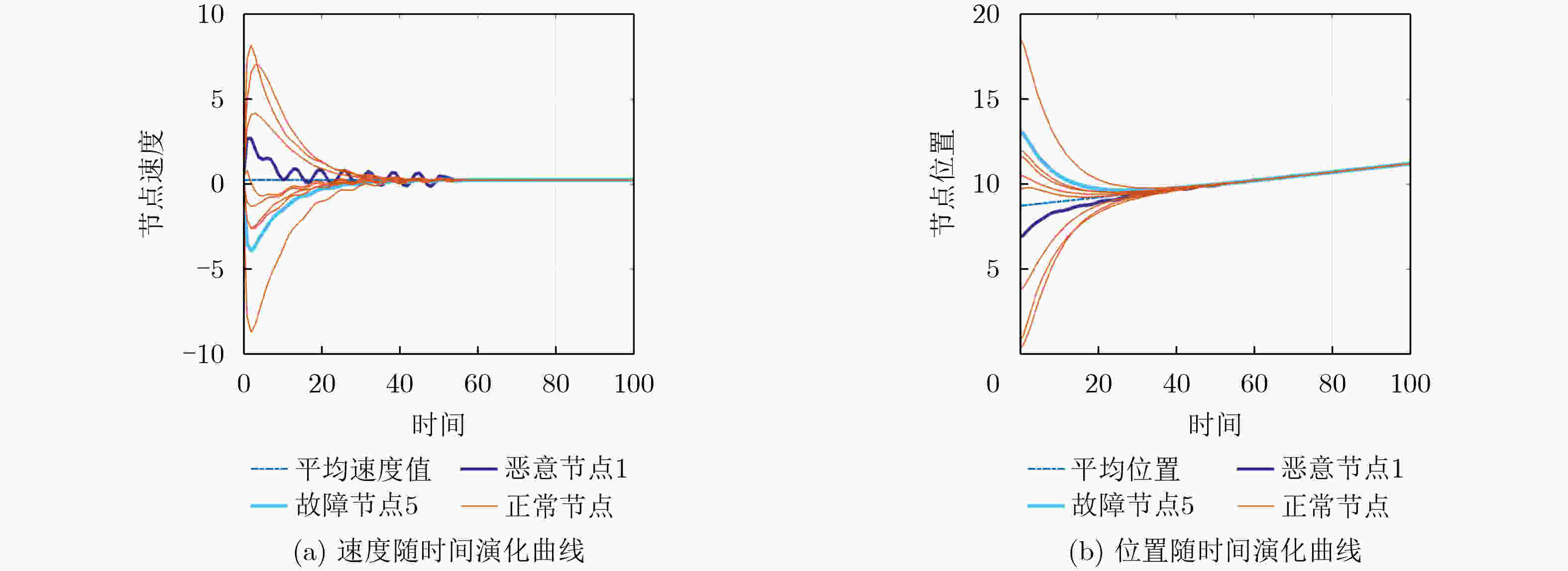
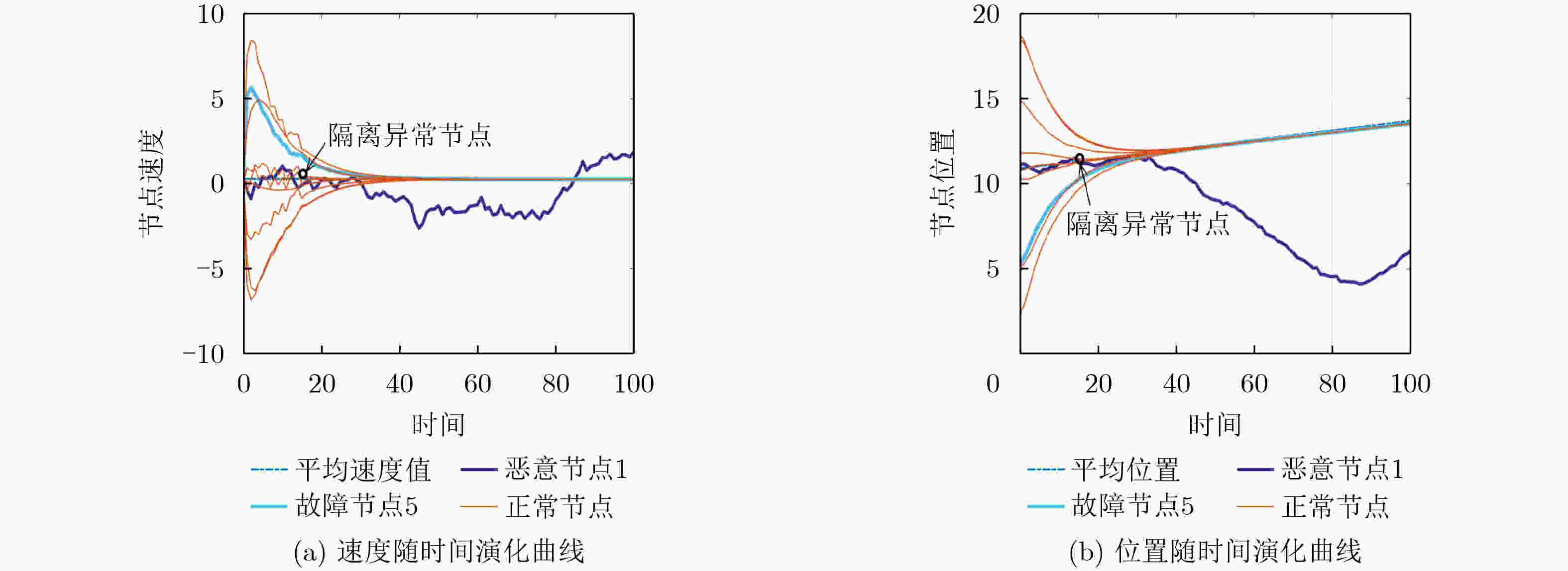
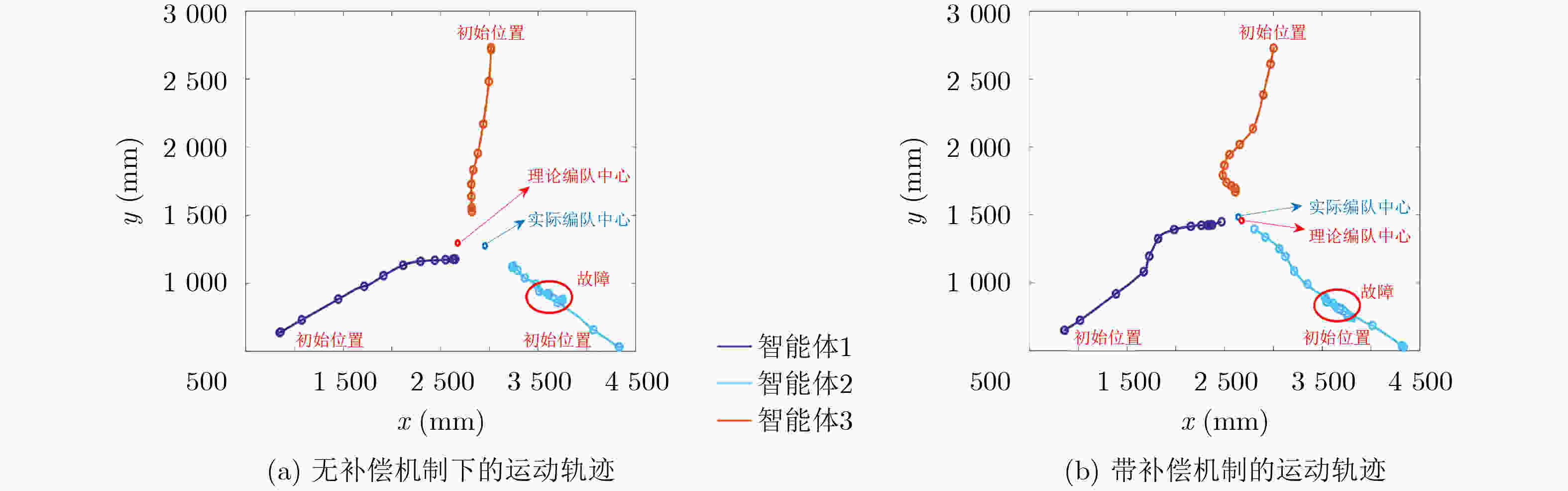
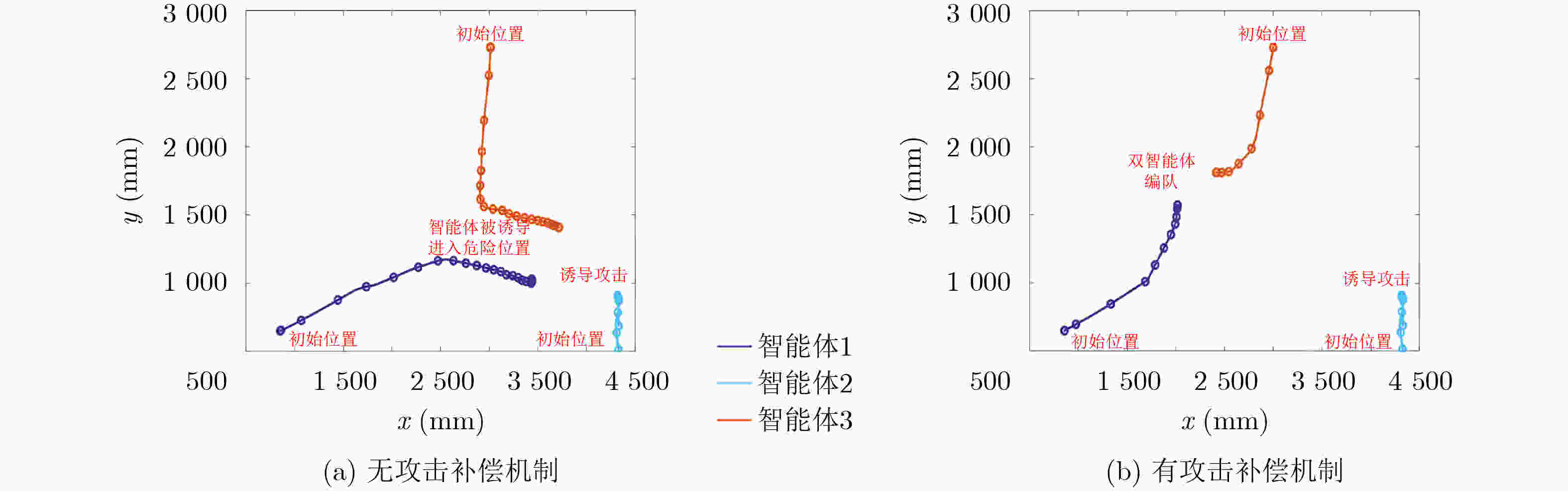
Abstract: Objective Multi-Agent Systems (MASs) are central to collaborative tasks in dynamic environments, and consensus algorithms are essential for applications such as formation control. However, MASs are vulnerable to misbehaviors (e.g., malicious attacks or accidental faults) that disrupt consensus and degrade system performance. Existing resilient consensus methods for first-order systems are insufficient for second-order MASs, where both position and velocity states must be considered. This study develops a resilient average consensus framework for second-order MASs that maintains accurate collaboration under misbehaviors. The main challenges are distributed error detection and compensation for two-dimensional state errors (position and velocity) using one-dimensional acceleration inputs. Methods The study derives sufficient conditions for second-order average consensus under misbehaviors using graph theory and Lyapunov stability analysis. The system is modeled as an undirected graph $ \mathcal{G}=(\mathcal{V},\mathcal{E}) $, and agents follow double-integrator dynamics. Two algorithms are proposed. Finite Input-Errors Detection–Compensation (FIDC): For finite control input errors, Detection Strategies 1 and 2 use two-hop communication to detect discrepancies in neighbors’ states or control inputs. Compensation Scheme 1 generates input sequences that satisfy the consensus conditions in Corollary 1. Infinite Attack Detection–Compensation (IADC): For infinite errors in control inputs, velocities, and positions, the detection strategies are extended to identify falsified data. Compensation Schemes 2 and 3 reduce the effect of these errors, and an exponentially decaying error bound isolates persistent attackers. The algorithms are fully distributed and require no global information. Results and Discussions Simulations on a 10-agent network demonstrate the effectiveness of the algorithms. Under FIDC, agents reach exact average consensus despite finite input errors caused by malicious or faulty agents (Fig. 3). IADC ensures consensus among normal agents after isolating malicious agents that exceed the error bound (Fig. 4). Experiments on a multi-robot platform confirm resilience to real-world faults (e.g., actuator failures) and attacks (e.g., false data injection). In fault scenarios, FIDC reduces the deviation of the formation center from 180 mm to 34 mm (Fig. 6). Under attacks, IADC isolates malicious robots, allowing normal agents to converge correctly (Fig. 7). Analyses of relaxed Assumption 1 (non-adjacent misbehaving agents) show that Detection Strategy 3 and majority voting address certain connected malicious topologies (Fig. 2), although complex cases need further study. Conclusions This work presents a resilient average consensus framework for second-order MASs. Theoretically, the study provides sufficient conditions for consensus under misbehaviors. The FIDC and IADC algorithms enable distributed detection, compensation, and isolation of errors. Simulations and physical experiments verify that the methods achieve accurate average consensus under both finite and infinite errors. Future research will explore extensions to directed networks, time-varying topologies, and higher-dimensional systems.
- Second-order multi-agent system /
- Resilient consensus /
- Attack detection /
- Compensation

HTML全文

图 1 弹性平均一致性方法的整体设计框架

下载: 全尺寸图片幻灯片

图 2 典型拓扑结构

下载: 全尺寸图片幻灯片

图 3 FIDC算法下的弹性一致性性能表现

下载: 全尺寸图片幻灯片

图 4 IADC算法下的弹性一致性性能表现

下载: 全尺寸图片幻灯片

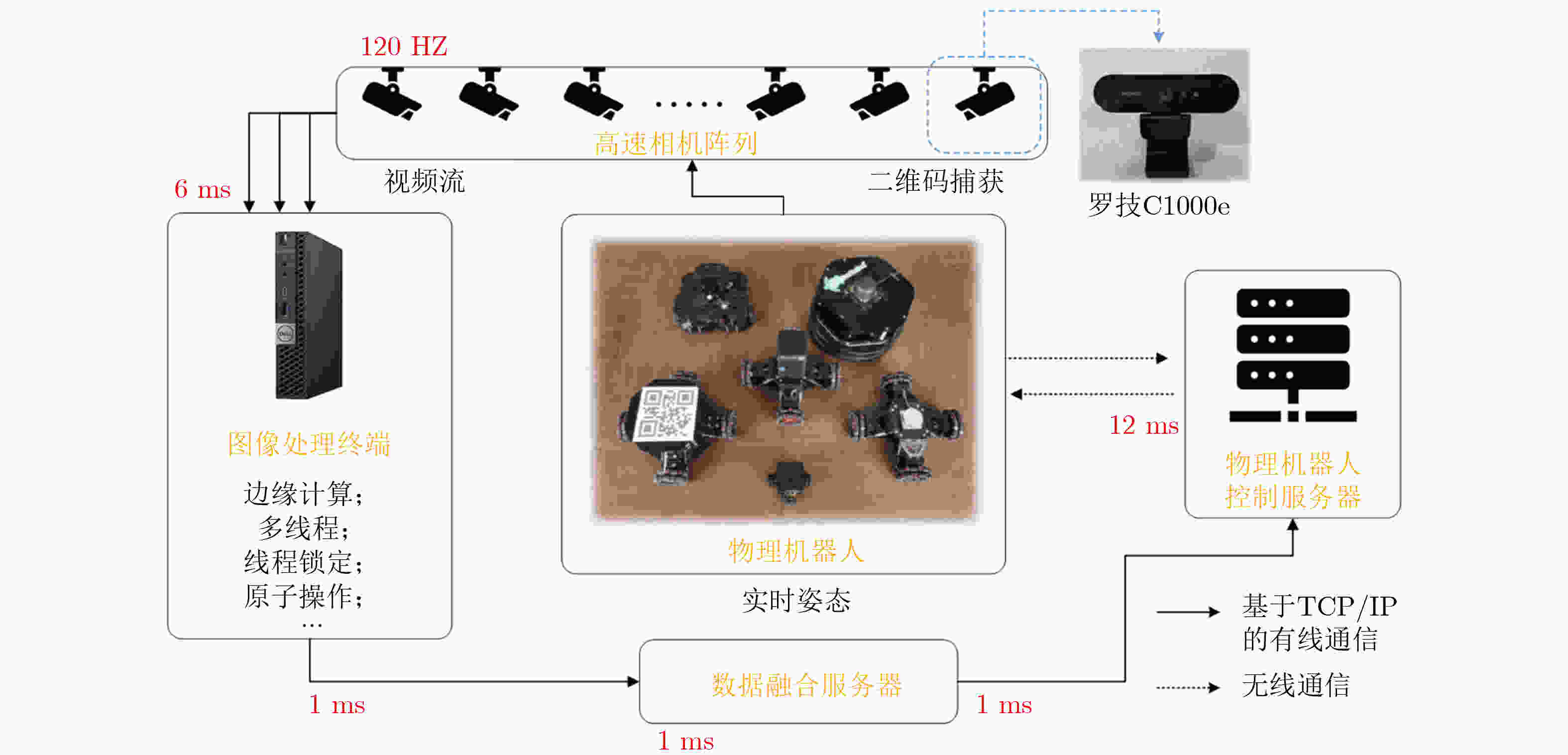
图 5 多机器人平台架构^[23]

下载: 全尺寸图片幻灯片

图 6 故障存在时多机器人系统节点运动轨迹

下载: 全尺寸图片幻灯片

图 7 攻击存在时多机器人系统节点运动轨迹

下载: 全尺寸图片幻灯片

1 FIDC

1：初始化：设置补偿周期$ {T}_{c} $，并交换各节点的邻居数量$ \|{\mathcal{N}}_{j}\| $信息
2：$ \rm{f}\rm{o}\rm{r} $$ k=0\colon {\mathrm{Max}}\_ {\mathrm{time}} $ $ \rm{d}\rm{o} $
3：　　$ \rm{f}\rm{o}\rm{r} $ $ i\in {\mathcal{N}}_{j} $ $ \rm{d}\rm{o} $
4：　　　节点$ j $基于公式计算节点$ i $引起的误差
5：　　　$ \rm{i}\rm{f} $ $ \varepsilon _{i}^{j}(k)\neq 0 $
6：　　　　通过公式计算补偿序列$ {\varepsilon }_{j}(k+l\|k),l=1,2,\cdots ,{T}_{c} $
7：　　$ \rm{e}\rm{n}\rm{d} $ $ \rm{i}\rm{f} $
8：　$ \rm{e}\rm{n}\rm{d} $$ \boldsymbol{f}\boldsymbol{o}\boldsymbol{r} $
9：　通过公式和式(6)分别计算$ {\varepsilon }_{j}(k+1) $和控制输入并施加
10：更新$ {v}_{j}(k+2) $和$ {\tilde{r}}_{j}(k+2) $状态值
11：$ \rm{e}\rm{n}\rm{d} $ $ \rm{f}\rm{o}\rm{r} $

下载: 导出CSV

2 IADC

1：初始化：设置补偿周期$ {T}_{c} $，并交换各节点的邻居数量$ \|{\mathcal{N}}_{j}\| $信息
2：$ \rm{f}\rm{o}\rm{r} $$ k=0\colon {\mathrm{Max}}\_ {\mathrm{time}} $ $ \rm{d}\rm{o} $
3：　$ \rm{f}\rm{o}\rm{r} $ $ i\in {\mathcal{N}}_{j} $ $ \rm{d}\rm{o} $
4：　　通过公式计算$ i $在控制输入、速度和位置上的误差。
5：　　$ \rm{i}\rm{f} $ $ {\omega }_{i}(k)\neq 0 $或$ {\delta }_{i}(k)\neq 0 $或$ \varepsilon _{i}^{j}(k)\neq 0 $
6：　　　根据公式和获取补偿序列。
7：　　$ \rm{e}\rm{n}\rm{d} $ $ \rm{i}\rm{f} $
8：　　$ \rm{i}\rm{f} $ $ \varepsilon _{i}^{j}(k)\geq {\alpha }_{j}\rho _{j}^{k} $或$ {\omega }_{i}(k)\geq {\alpha }_{j}\rho _{j}^{k} $或$ {\delta }_{i}(k)\geq {\alpha }_{j}\rho _{j}^{k} $
9：　　　节点$ j $隔离节点$ i $，通过公式计算补偿序列。
10：　 $ \rm{e}\rm{n}\rm{d} $ $ \rm{i}\rm{f} $
11： $ \rm{e}\rm{n}\rm{d} $$ \rm{f}\rm{o}\rm{r} $
12：通过公式计算$ {\varepsilon }_{j}(k+1) $，基于公式计算控制输入并施加
13：更新$ {v}_{j}(k+2) $和$ {\tilde{r}}_{j}(k+2) $状态值
14：$ \rm{e}\rm{n}\rm{d} $ $ \rm{f}\rm{o}\rm{r} $

下载: 导出CSV

参考文献(24)

[1]	OLFATI-SABER R, FAX J A, and MURRAY R M. Consensus and cooperation in networked multi-agent systems[J]. Proceedings of the IEEE, 2007, 95(1): 215–233. doi: 10.1109/JPROC.2006.887293.
[2]	WANG Xin, HE Jianping, CHENG Peng, et al. Differentially private maximum consensus: Design, analysis and impossibility result[J]. IEEE Transactions on Network Science and Engineering, 2019, 6(4): 928–939. doi: 10.1109/TNSE.2018.2879795.
[3]	LIU Mengxiang, ZHAO Chengcheng, DENG Ruilong, et al. False data injection attacks and the distributed countermeasure in DC microgrids[J]. IEEE Transactions on Control of Network Systems, 2022, 9(4): 1962–1974. doi: 10.1109/TCNS.2022.3181483.
[4]	WU Yanfang, GUO Peng, WANG Ying, et al. Attack-defense game modeling framework from a vulnerability perspective to protect critical infrastructure systems[J]. Reliability Engineering & System Safety, 2025, 256: 110740. doi: 10.1016/j.ress.2024.110740.
[5]	KIECKHAFER R M and AZADMANESH M H. Low cost approximate agreement in partially connected networks[J]. Journal of Computing and Information, 1993, 3(2). (查阅网上资料, 未找到页码信息, 请补充).
[6]	KIECKHAFER R M and AZADMANESH M H. Reaching approximate agreement with mixed-mode faults[J]. IEEE Transactions on Parallel and Distributed Systems, 1994, 5(1): 53–63. doi: 10.1109/71.262588.
[7]	LEBLANC H J, ZHANG Haotian, KOUTSOUKOS X, et al. Resilient asymptotic consensus in robust networks[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(4): 766–781. doi: 10.1109/JSAC.2013.130413.
[8]	DIBAJI S M and ISHII H. Consensus of second-order multi-agent systems in the presence of locally bounded faults[J]. Systems & Control Letters, 2015, 79: 23–29. doi: 10.1016/j.sysconle.2015.02.005.
[9]	SUNDARAM S and HADJICOSTIS C N. Distributed function calculation via linear iterative strategies in the presence of malicious agents[J]. IEEE Transactions on Automatic Control, 2011, 56(7): 1495–1508. doi: 10.1109/TAC.2010.2088690.
[10]	WU Hanyu, LIU Qingshan, and PARK J H. Observer-based secure consensus for multiagent systems under multimode DoS attacks with application to power system[J]. IEEE Transactions on Cybernetics, 2025, 55(3): 1032–1044. doi: 10.1109/TCYB.2025.3528200.
[11]	PASQUALETTI F, BICCHI A, and BULLO F. Consensus computation in unreliable networks: A system theoretic approach[J]. IEEE Transactions on Automatic Control, 2012, 57(1): 90–104. doi: 10.1109/TAC.2011.2158130.
[12]	SHAMES I, TEIXEIRA A M H, SANDBERG H, et al. Distributed fault detection for interconnected second-order systems[J]. Automatica, 2011, 47(12): 2757–2764. doi: 10.1016/j.automatica.2011.09.011.
[13]	GUO Meng, DIMAROGONAS D V, and JOHANSSON K H. Distributed real-time fault detection and isolation for cooperative multi-agent systems[C]. 2012 American Control Conference, Montreal, Canada, 2012: 5270–5275. doi: 10.1109/ACC.2012.6315178.
[14]	FANG Chongrong, ZHENG Wenzhe, HE Zhiyu, et al. Towards resilient average consensus in multi-agent systems: A detection and compensation approach[J]. Frontiers of Information Technology & Electronic Engineering, 2024, 25(2): 182–196. doi: 10.1631/FITEE.2300467.
[15]	YUAN Liwei and ISHII H. Resilient average consensus with adversaries via distributed detection and recovery[J]. IEEE Transactions on Automatic Control, 2025, 70(1): 415–430. doi: 10.1109/TAC.2024.3426387.
[16]	LIU Zeqiang, LIU Zhiwei, HE Dingxin, et al. Dynamic resilient consensus of second-order multiagent networks with a time-varying malicious agent set[J]. IEEE Transactions on Automatic Control, 2025, 70(5): 3308–3315. doi: 10.1109/TAC.2024.3507672.
[17]	XIAO Lin, BOYD S, and KIM S J. Distributed average consensus with least-mean-square deviation[J]. Journal of Parallel and Distributed Computing, 2007, 67(1): 33–46. doi: 10.1016/j.jpdc.2006.08.010.
[18]	ZHENG Wenzhe, FANG Chongrong, HE Jianping, et al. Resilient average consensus of second-order multi-agent systems[C]. 2022 American Control Conference, Atlanta, USA, 2022: 1466–1471. doi: 10.23919/ACC53348.2022.9867735.
[19]	CAO Yongcan and REN Wei. Sampled-data discrete-time coordination algorithms for double-integrator dynamics under dynamic directed interaction[J]. International Journal of Control, 2010, 83(3): 506–515. doi: 10.1080/00207170903214338.
[20]	HE Jianping, CHENG Peng, SHI Ling, et al. SATS: Secure average-consensus-based time synchronization in wireless sensor networks[J]. IEEE Transactions on Signal Processing, 2013, 61(24): 6387–6400. doi: 10.1109/TSP.2013.2286102.
[21]	ZHAO Chengcheng, HE Jianping, and CHEN Jiming. Resilient consensus with mobile detectors against malicious attacks[J]. IEEE Transactions on Signal and Information Processing over Networks, 2018, 4(1): 60–69. doi: 10.1109/TSIPN.2017.2742859.
[22]	E-ISAC. Analysis of the Cyber Attack on the Ukrainian Power Grid[M]. Washington, USA: E-ISAC, 2016: 3.
[23]	DING Xuda, WANG Han, LI Hongbo, et al. Robopheus: A virtual-physical interactive mobile robotic testbed[J]. arXiv: 2103.04391, 2021. doi: 10.48550/arXiv.2103.04391.
[24]	LI Yushan, HE Jianping, CHEN Cailian, et al. Intelligent physical attack against mobile robots with obstacle-avoidance[J]. IEEE Transactions on Robotics, 2023, 39(1): 253–272. doi: 10.1109/TRO.2022.3201394.