Group-based Sparse Vector Codes for Short-Packet Communications
-
摘要: 稀疏矢量码(SVC)技术因其实施简单、传输可靠等优点在短包高可靠低时延通信方面获得了广泛关注。构造短稀疏矢量并使用小尺寸随机扩频码本是确保其系统性能的关键。为此,该文提出一种基于分组的SVC(Group-based SVC, GSVC)方案。该方案摒弃了经典的索引调制全局稀疏变换方式,通过对索引比特分组划分,以分组稀疏变换的形式在同一预定稀疏矢量上逐次选取出各分组的非零位置,从而实现位置资源对所有分组的共享,达到压缩稀疏矢量的目的。因此,所提GSVC方案具有高的位置资源利用率,能够构造出比常规全局选取方式要短的稀疏矢量来传输既定信息比特。与现有多种SVC改进方案的仿真对比结果表明,所提方案在低阶调制模式下具有更优的误块率性能。Abstract:
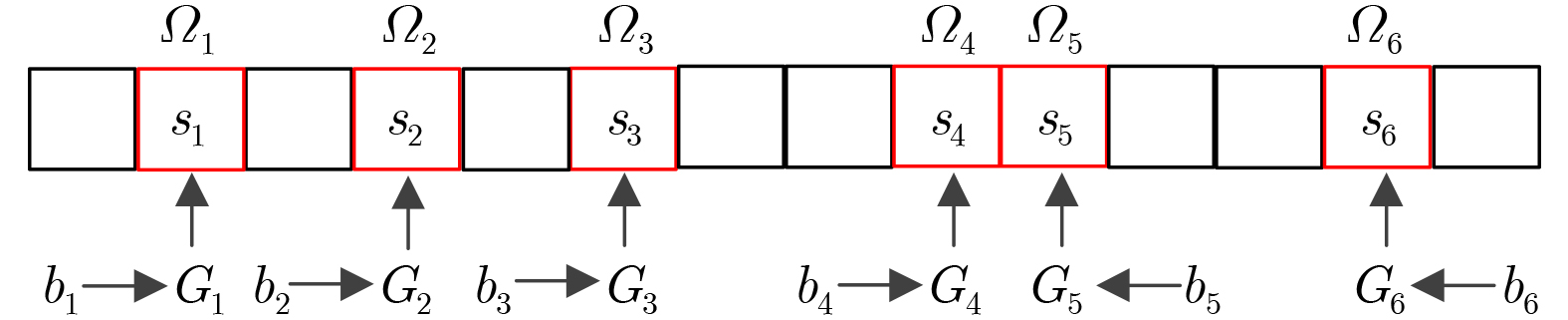
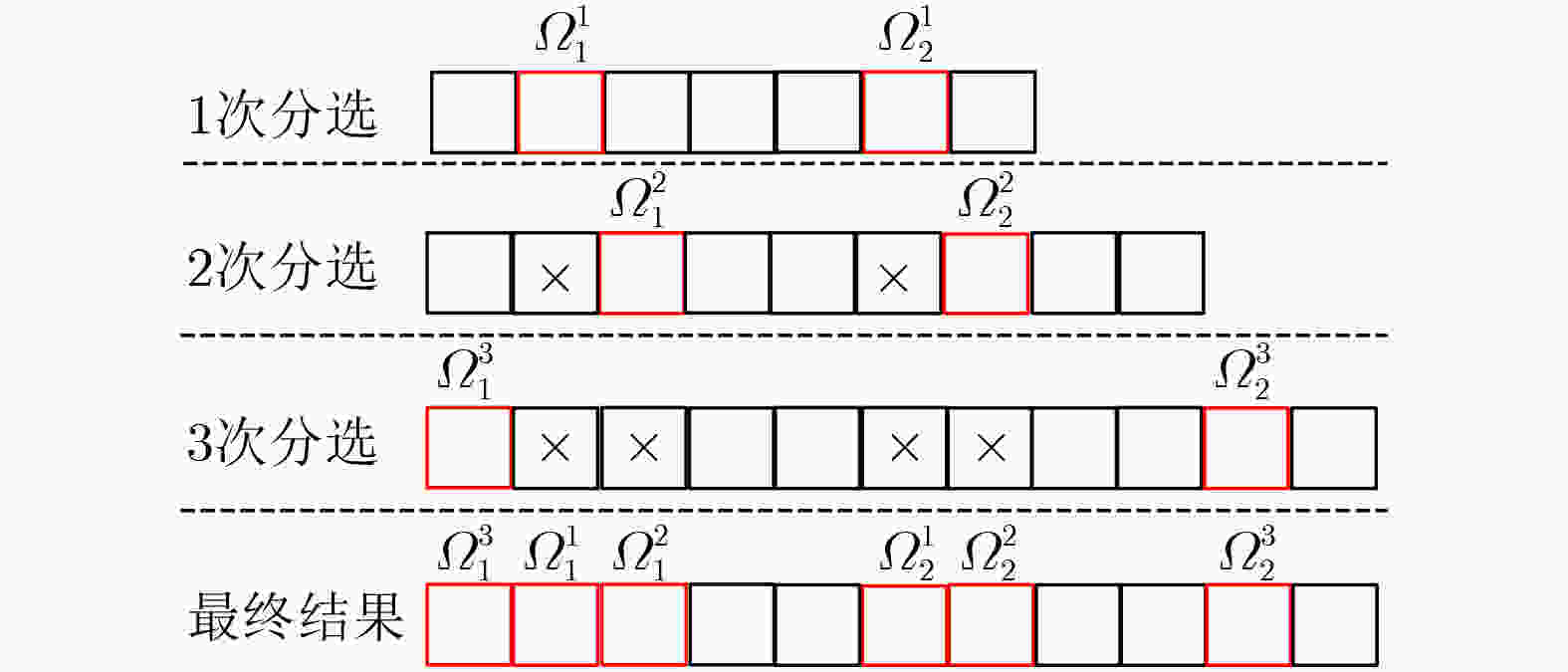
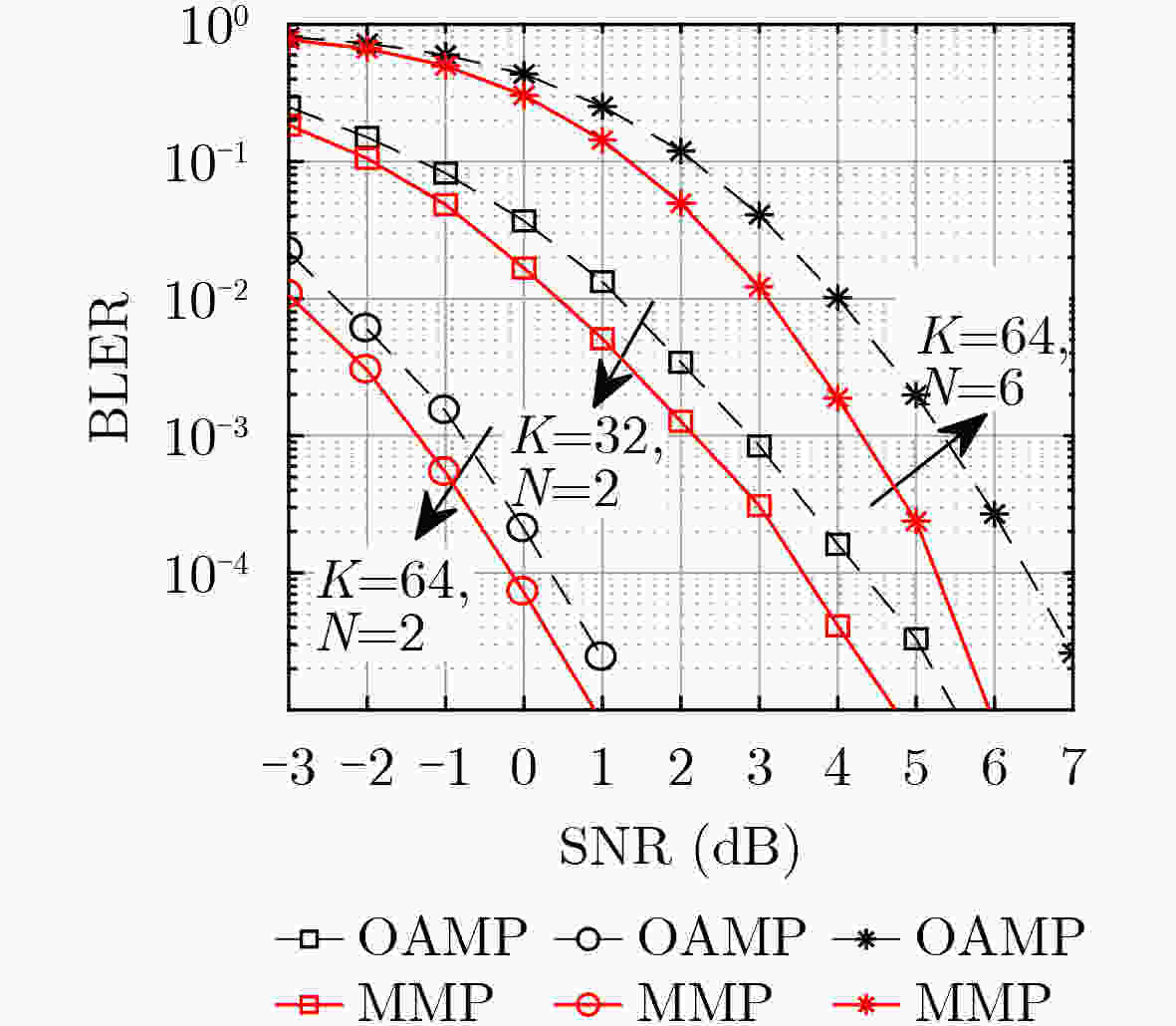
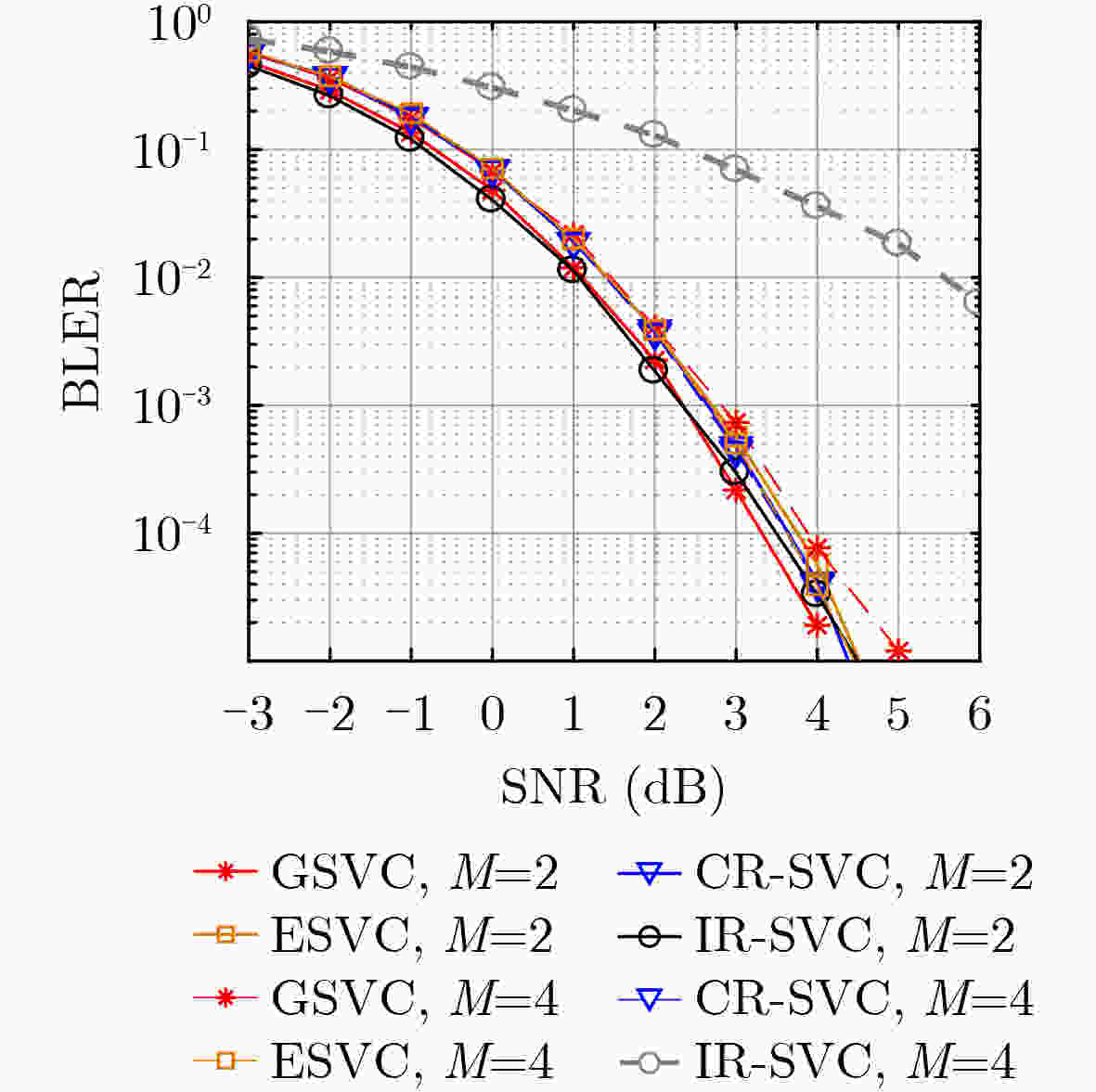
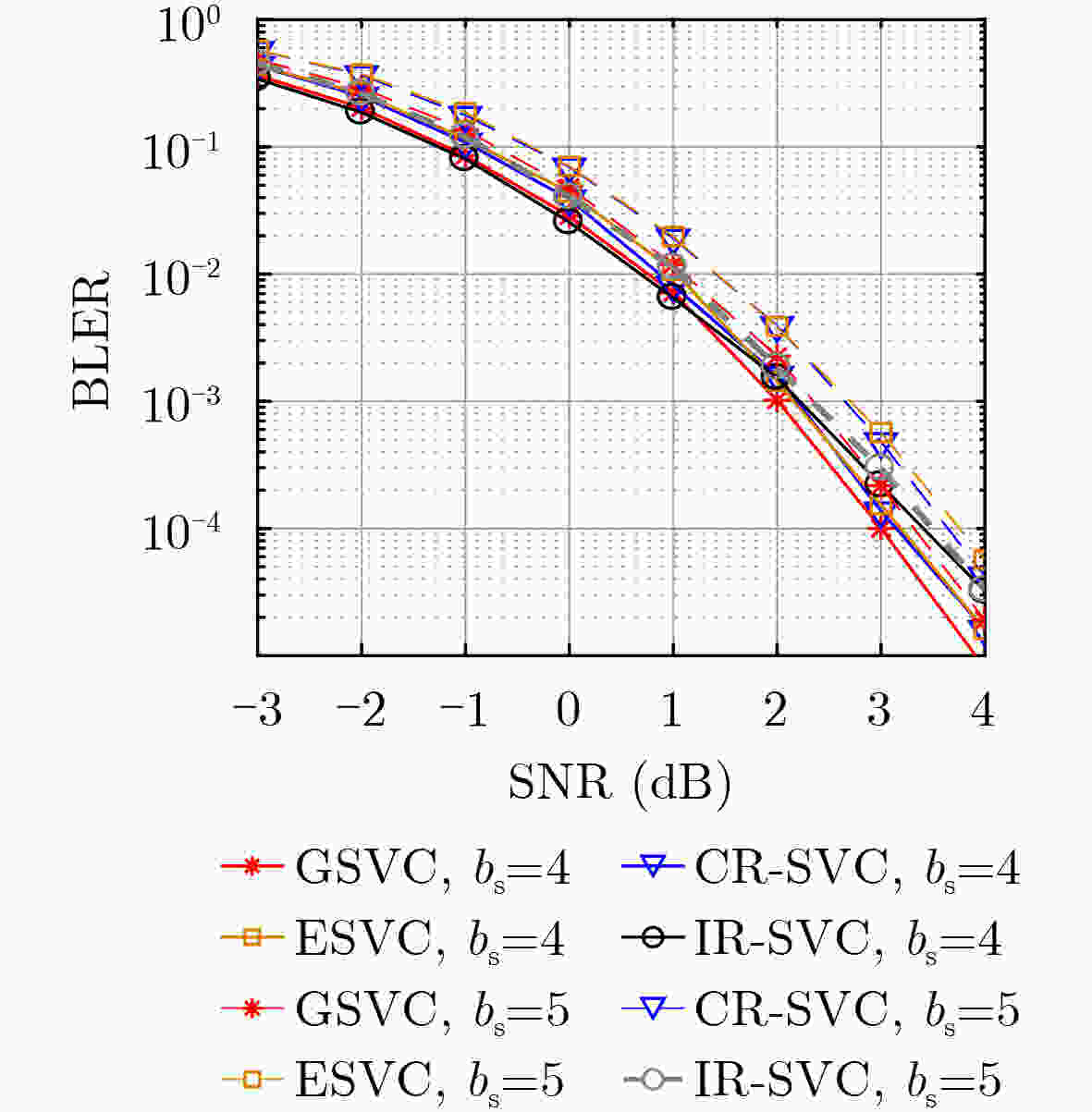
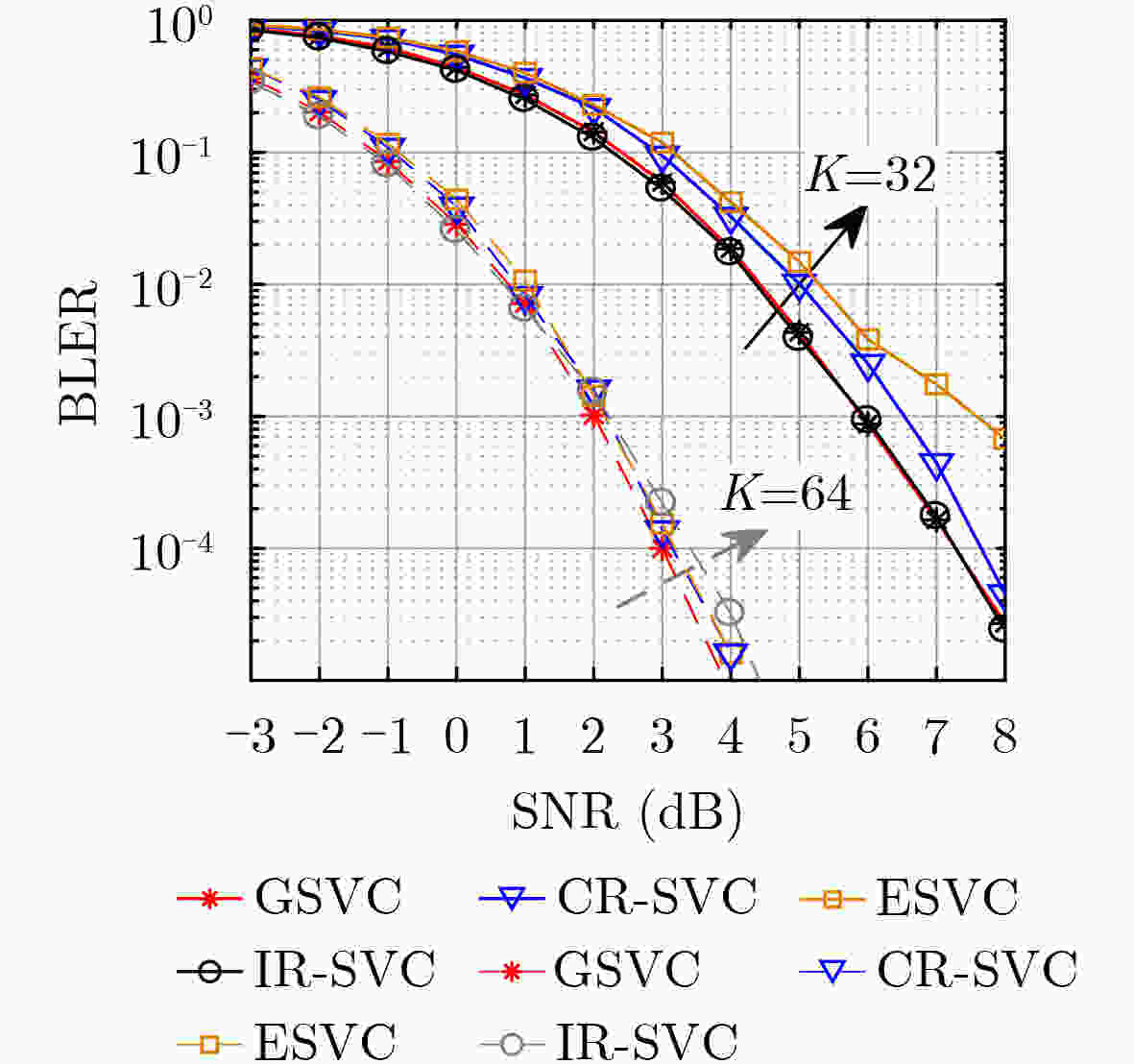
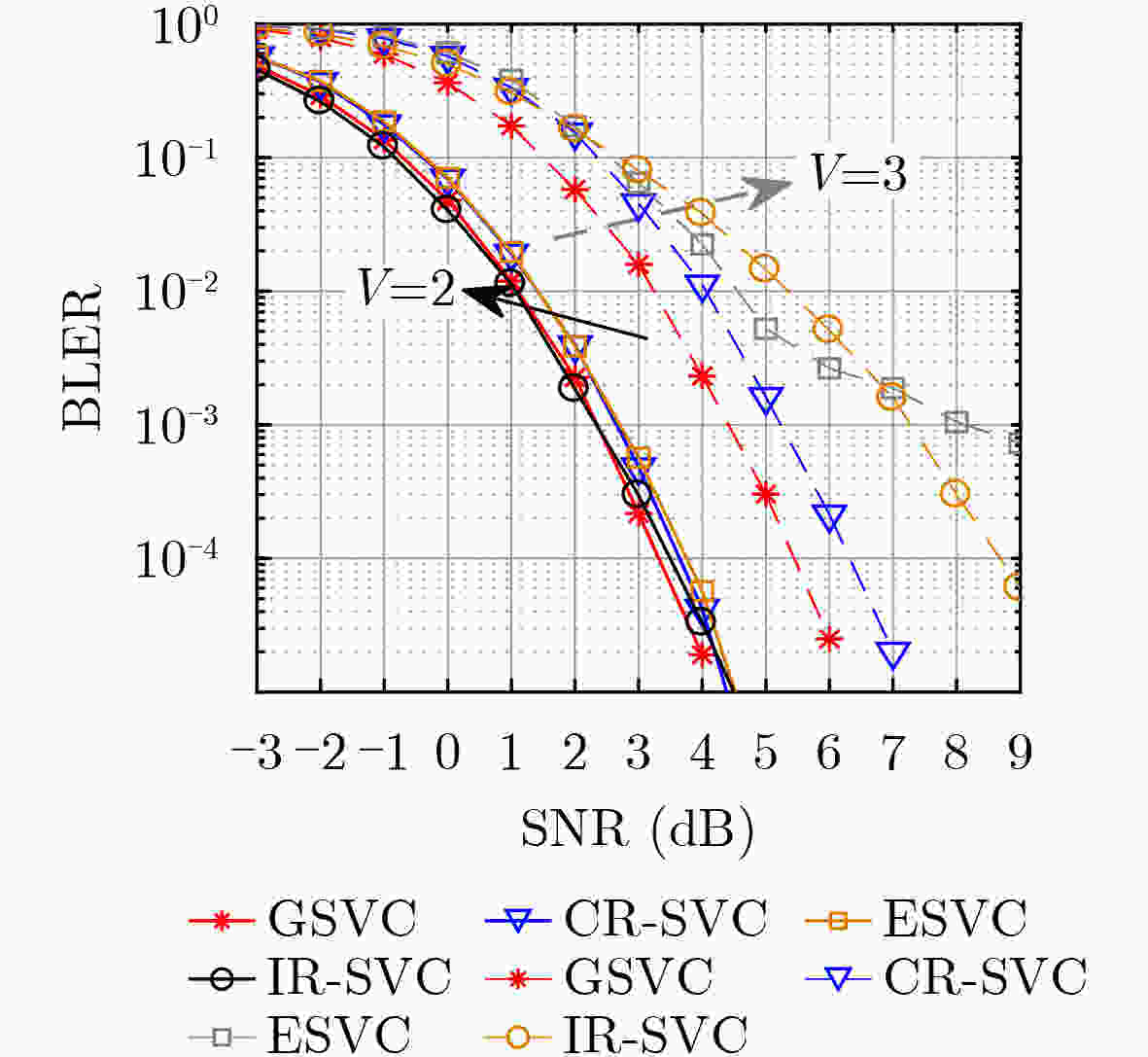
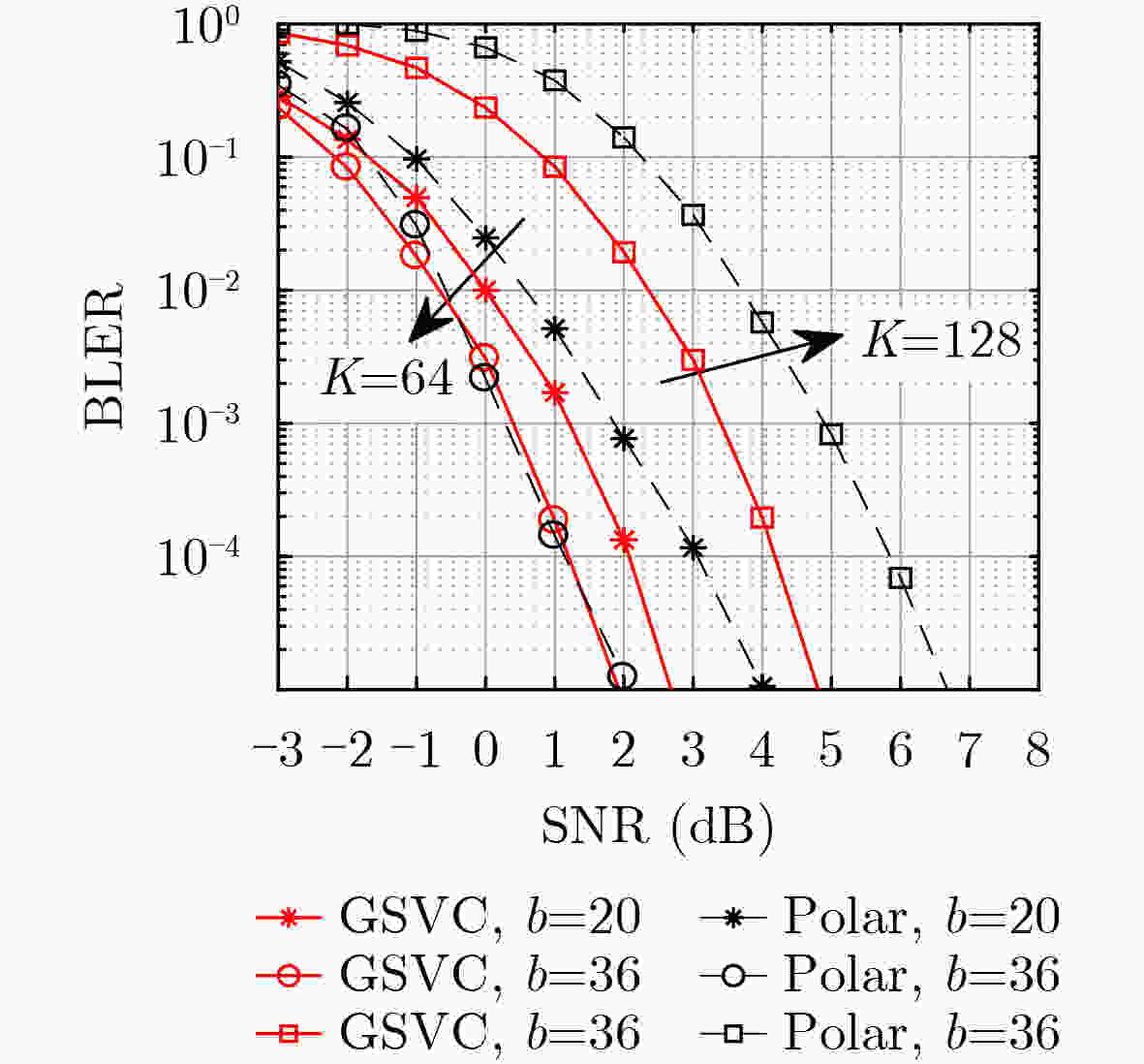
Objective Sparse Vector Codes (SVC) aim to construct sparse underdetermined linear systems and have attracted wide interest for short-packet Ultra-Reliable and Low-Latency Communications (URLLC) because of their simple implementation and reliable transmission. To guarantee system performance, short sparse vectors that can be transmitted using small-size random spreading codebooks are required. However, most existing sparse transformation schemes based on index modulation adopt a global selection strategy, where nonzero positions, to which transmission bits are mapped, are selected directly from the entire set of available positional resources in the sparse vector. Under high coding efficiency requirements, this strategy often leads to excessively long sparse vectors and a sharp degradation in transmission performance. To address this issue, a Group-based Sparse Vector Code (GSVC) scheme is proposed. Unlike the conventional global sparse mapping approach, GSVC divides index bits into groups and sequentially determines the nonzero positions for each group within a predefined sparse vector. This design enables positional resource sharing among all groups and generates compressed sparse vectors with higher positional resource utilization, thereby achieving Better Block Error Rate (BLER) performance than conventional SVC schemes. Methods The proposed GSVC scheme partitions the total number of nonzero positions N into V groups. Within a single predefined sparse vector, each group sequentially selects its N/V nonzero positions through index modulation. To prevent position selection conflicts among groups, a resource supplementation and elimination mechanism is applied. This mechanism ensures that the selected positions are mutually exclusive and that each group maintains the same number of available positional resources throughout the selection process. Given the sparsity of the constructed vector, a low-complexity sparse recovery algorithm is employed at the receiver. Accordingly, a GSVC decoder based on the Multipath Matching Pursuit (MMP) algorithm is designed. To enable accurate identification of the group affiliation associated with each nonzero position, GSVC adopts a multi-constellation mapping strategy for the nonzero elements. The receiver performs constellation matching by exploiting the unique characteristics of each constellation, thereby determining group affiliation and ensuring a high probability of successful decoding. Results and Discussions By enabling different groups to share positional resources through group-based nonzero position selection, GSVC effectively compresses the sparse vector and improves transmission reliability. Simulation results show that the GSVC decoder based on MMP significantly outperforms the decoder based on the Orthogonal Approximate Message Passing (OAMP) algorithm ( Fig. 3 ). At lower modulation orders, GSVC achieves better BLER performance than existing schemes, including enhanced SVC, multi-rotation constellation-based SVC, and index-redefined SVC (Fig. 4 andFig. 5 ). When the number of Orthogonal Frequency Division Multiplexing (OFDM) subcarriers is large, GSVC provides the best BLER performance among all compared schemes (Fig. 6 ). In addition, for a fixed number of nonzero entries per group, the BLER performance advantage of GSVC increases as the number of groups increases. A performance gain exceeding 1 dB over the second-best SVC scheme is observed at a BLER of 10–5 (Fig. 7 ). Compared with polar codes (Fig. 8 ), GSVC achieves better BLER performance without Cyclic Redundancy Check (CRC) assistance and even outperforms CRC-aided polar codes.Conclusions This paper proposes a GSVC scheme to address the excessive sparse vector length encountered in conventional index modulation-based SVC systems. The central feature of GSVC is a grouped nonzero position selection mechanism that enables multiple groups to share positional resources within a predefined sparse vector, thereby reducing the overall vector length. A dedicated multi-constellation mapping design, together with well-defined resource allocation rules, ensures conflict-free and efficient utilization of positional resources. Simulation results demonstrate that (1) the GSVC decoder implemented using MMP significantly outperforms decoders based on the OAMP algorithm; (2) GSVC achieves superior BLER performance compared with enhanced SVC, multi-rotation constellation-based SVC, and index-redefined SVC schemes, particularly at lower modulation orders and with a large number of OFDM subcarriers; and (3) GSVC surpasses the BLER performance of CRC-aided polar codes without requiring CRC. Future work will focus on optimizing the grouping strategy and examining the transmission performance of SVC under imperfect channel estimation to improve robustness in practical communication systems. -
1 GSVC的译码过程
(1) 初始化$ {\boldsymbol{r}}_{{\mathrm{end}}}=+\mathrm{\infty } $, $ {\boldsymbol{r}}_{0}=\boldsymbol{y} $, $ \varepsilon $, D, $ {l}_{\max } $, $ l=1 $; (2) 利用MMP获得合成矢量的位置估计$ \hat{\varOmega } $和元素估计$ \hat{s} $: (3) while ($ \varepsilon \lt {\boldsymbol{r}}_{{\mathrm{end}}} $&&$ l\leq {l}_{\max } $) (4) 令t = l – 1; (5) for n = 1 : N (6) $ {d}_{n}=\mathrm{mod}\left(t\right)+1 $; $ t=\left\lfloor t/D\right\rfloor $; // 式(19) (7) end for (8) for n = 1 : N (9) 根据式(20)、式(21)、式(22)计算$ \tilde{\pi }_{{d}_{n}}^{l} $, $ \hat{s}_{n}^{l} $, $ \boldsymbol{r}_{n}^{l} $; (10) end for (11) if ($ {\boldsymbol{r}}_{{\mathrm{end}}} \gt \left|\left|\boldsymbol{r}_{N}^{l}\right|\right| $) (12) $ {\boldsymbol{r}}_{{\mathrm{end}}}=\left|\left|\boldsymbol{r}_{N}^{l}\right|\right| $; $ \hat{\varOmega }=\left\{\tilde{\pi }_{{d}_{n}}^{l}\right\}_{n=1}^{N} $; $ \hat{s}=\left\{\hat{s}_{n}^{l}\right\}_{n=1}^{N} $; (13) end if (14) $ l=l+1 $; (15) end while (16) 利用$ \hat{s} $完成解层映射并输出比特流: (17) 依据步骤1对$ \hat{s} $中N个元素实施分组; (18) for t = 1 : T (19) 根据式(23)获取Val; (20) end for (21) 获取最小Val对应下的分组,依据步骤3输出比特流。 -
[1] SONG Lulu, ZHANG Di, JIA Shaobo, et al. STAR-RIS-aided NOMA for secured xURLLC[J]. IEEE Transactions on Vehicular Technology, 2025, 74(8): 13249–13254. doi: 10.1109/TVT.2025.3556542. [2] POURKABIRIAN A, KORDAFSHARI M S, JINDAL A, et al. A vision of 6G URLLC: Physical-layer technologies and enablers[J]. IEEE Communications Standards Magazine, 2024, 8(2): 20–27. doi: 10.1109/MCOMSTD.0003.2300018. [3] 蔡穗华, 王义文, 白宝明, 等. 面向高可靠低时延通信的信道编码技术研究综述[J]. 电子学报, 2025, 53(2): 629–644. doi: 10.12263/DZXB.20240137.CAI Suihua, WANG Yiwen, BAI Baoming, et al. Channel coding techniques for ultra-reliable and low-latency communication[J]. Acta Electronica Sinica, 2025, 53(2): 629–644. doi: 10.12263/DZXB.20240137. [4] 戴景鑫, 尹航, 王玉环, 等. 面向短包通信的PAC码低复杂度序贯译码算法[J]. 电子与信息学报, 2025, 47(12): 1–12. doi: 10.11999/JEIT250533.DAI Jingxin, YIN Hang, WANG Yuhuan, et al. Low complexity sequential decoding algorithm of PAC code for short packet communication[J]. Journal of Electronics & Information Technology, 2025, 47(12): 1–12. doi: 10.11999/JEIT250533. [5] BILBAO I, FANARI L, IRADIER E, et al. Sparse vector coding for short-packet transmission on industrial communications: Reference architecture and design challenges[J]. IEEE Open Journal of the Industrial Electronics Society, 2023, 4: 1–13. doi: 10.1109/OJIES.2022.3230142. [6] SHIM B. Sparse vector coding for ultra-reliable and low-latency communications[M]. DUONG T Q, KHOSRAVIRAD S R, SHE Changyang, et al. Ultra-Reliable and Low-Latency Communications (URLLC) Theory and Practice: Advances in 5G and Beyond. Wiley, 2023: 169–213. doi: 10.1002/9781119818366.ch6. [7] ZHANG Xuewan and ZHANG Dalong. Sparse superimposed coding based on index redefinition[J]. IEEE Communications Letters, 2023, 27(5): 1467–1471. doi: 10.1109/LCOMM.2023.3257314. [8] SABAPATHY S, MARUTHU S, and JAYAKODY D N K. Multi-user sparse vector coding for eXtreme ultra-reliable low-latency communication in beyond 5G[J]. IEEE Access, 2025, 13: 56780–56792. doi: 10.1109/ACCESS.2025.3551398. [9] LIU Huiqi, MOW H M, and LIANG Shansuo. Generalization and construction of single-section sparse regression codes[C]. ICC 2024 - IEEE International Conference on Communications, Denver, USA, 2024: 611–616. doi: 10.1109/ICC51166.2024.10622751. [10] ZHANG Yanfeng, ZHU Xu, XU Zhixiang, et al. Sparse superimposed codes for vehicular communications with low-resolution ADCs[C]. 2024 IEEE/CIC International Conference on Communications in China (ICCC Workshops), Hangzhou, China, 2024: 277–281. doi: 10.1109/ICCCWorkshops62562.2024.10693757. [11] HSIEH K and VENKATARAMANAN R. Modulated sparse superposition codes for the complex AWGN channel[J]. IEEE Transactions on Information Theory, 2021, 67(7): 4385–4404. doi: 10.1109/TIT.2021.3081368. [12] KIM W, BANDARI S K, and SHIM B. Enhanced sparse vector coding for ultra-reliable and low latency communications[J]. IEEE Transactions on Vehicular Technology, 2020, 69(5): 5698–5702. doi: 10.1109/TVT.2020.2982943. [13] SABAPATHY S, MARUTHU S, and JAYAKODY D N K. Rate-splitting sparse vector code for next-generation URLLC systems[J]. IEEE Wireless Communications Letters, 2024, 13(7): 1993–1997. doi: 10.1109/LWC.2024.3400452. [14] ZHANG Xuewan, ZHANG Di, SHIM B, et al. Sparse superimposed coding for short-packet URLLC[J]. IEEE Internet of Things Journal, 2022, 9(7): 5275–5289. doi: 10.1109/JIOT.2021.3108161. [15] ZHANG Xuewan, CHEN Hongyang, ZHANG Di, et al. Uniquely decomposable constellation group-based sparse vector coding for short packet communications[J]. China Communications, 2023, 20(5): 119–134. doi: 10.23919/JCC.fa.2022-0253.202305. [16] ARSLAN E, DOGUKAN A T, and BASAR E. Sparse-encoded codebook index modulation[J]. IEEE Transactions on Vehicular Technology, 2020, 69(8): 9126–9130. doi: 10.1109/TVT.2020.2996023. [17] HAN D, LEE B, JANG M, et al. Block orthogonal sparse superposition codes for L3 communications: Low error rate, low latency, and low transmission power[J]. IEEE Journal on Selected Areas in Communications, 2025, 43(4): 1183–1199. doi: 10.1109/JSAC.2025.3531569. [18] YANG Linjie and FAN Pingzhi. Multiple-mode sparse superposed code with low block error rate for short packet URLLC[J]. IEEE Communications Letters, 2024, 28(2): 248–252. doi: 10.1109/LCOMM.2023.3348570. [19] ZHANG Xuewan, LIU Pengxue, and XU Xiumei. One-hot vector-based sparse vector transmission for short packet URLLC[J]. IEEE Transactions on Vehicular Technology, accepted, September 2025. doi: 10.1109/TVT.2025.3608466. [20] ZHANG Xuewan, CHEN Yadi, and GUO Jingjing. A pairwise grouping-based sparse mapping for sparse vector transmission[J]. IEEE Communications Letters, 2024, 28(12): 2844–2848. doi: 10.1109/LCOMM.2024.3481003. [21] HUI Ming, ZHANG Xuewan, and GUO Jingjing. Generalized multi-user sparse superposition transmission for massive machine-type communications[J]. Journal of Communications and Networks, 2024, 26(4): 433–444. doi: 10.23919/JCN.2024.000029. [22] LI Jun, DANG Shuping, HUANG Yu, et al. Composite multiple-mode orthogonal frequency division multiplexing with index modulation[J]. IEEE Transactions on Wireless Communications, 2023, 22(6): 3748–3761. doi: 10.1109/TWC.2022.3220752. [23] RUSH C, HSIEH K, and VENKATARAMANAN R. Capacity-achieving spatially coupled sparse superposition codes with AMP decoding[J]. IEEE Transactions on Information Theory, 2021, 67(7): 4446–4484. doi: 10.1109/TIT.2021.3083733. [24] LIU Lei, LIANG Shansuo, and PING Li. On capacity optimality of OAMP: Beyond IID sensing matrices and Gaussian signaling[J]. IEEE Transactions on Communications, 2024, 72(5): 2519–2535. doi: 10.1109/TCOMM.2024.3354201. -





 下载:
下载:


 下载:
下载:
