融合特征提取与恢复机制的SCUNet瑞利衰落信道译码算法

王磊军; 王宽; 谢晋发; 彭栖栋; 黎嘉文; 陈荣军

doi:10.11999/JEIT251138

融合特征提取与恢复机制的SCUNet瑞利衰落信道译码算法

doi: 10.11999/JEIT251138 cstr: 32379.14.JEIT251138

广东技术师范大学计算机科学学院广州 510665

基金项目: 广东省重点学科建设项目(2022ZDJS015, 2025ZDJS023)，广东技术师范大学博士点建设单位科研能力提升项目(22GPNUZDJS17)，广东技术师范大学研究生教育示范基地项目(2023YJSY04002)，广州市科技计划项目(2024B03J1361, 2023B03J1327)

详细信息

作者简介:
王磊军：男，讲师，研究方向为智能编码调制理论及技术、无线通信、信息论等

王宽：男，硕士生，研究方向为智能编译码技术

谢晋发：男，硕士生，研究方向为智能编码调制技术

彭栖栋：男，硕士生，研究方向为智能编码调制技术

黎嘉文：男，副教授，研究方向为生物医学信号处理、机器学习等

陈荣军：男，教授，研究方向为智联网、图像智能感知与处理等

通讯作者:
陈荣军　chenrongjun@gpnu.edu.cn

中图分类号: TN919.32
计量
- 文章访问数: 18
- HTML全文浏览量: 8
- PDF下载量: 0
- 被引次数: 0
出版历程
- 修回日期: 2026-01-22
- 录用日期: 2026-01-22
- 网络出版日期: 2026-02-11

SCUNet-Based Decoding Algorithm for Rayleigh Fading Channels Integrating Feature Extraction and Recovery Mechanisms

School of Computer Science, Guangdong Polytechnic Normal University, Guangzhou 510665, China

Funds: The Key Discipline Improvement Project of Guangdong Province (2022ZDJS015, 2025ZDJS023), The Scientific Research Capacity Improvement Project of the Doctoral Program Construction Unit of Guangdong Polytechnic Normal University (22GPNUZDJS17), The Graduate Education Demonstration Base Project of Guangdong Polytechnic Normal University (2023YJSY04002), The Guangzhou Science and Technology Plan Project (2024B03J1361, 2023B03J1327)

摘要

摘要: 人工智能的快速发展为无线通信系统性能的优化和提升提供了新思路。针对瑞利衰落信道下常规深度神经网络(DNN)译码算法性能受限的问题，提出了一种融合特征提取与恢复机制的SCUNet译码算法，记为SCUNetDec。该网络设计中融入了数据预处理、特征提取与恢复以及噪声水平图三方面机制：首先通过升维操作将一维信号映射为二维特征图，以挖掘更丰富的结构信息；继而利用特征提取与恢复模块削弱维度转换中产生的不相关干扰，从而提升译码效果；同时引入噪声水平图，使网络能够更敏锐地感知和建模信噪比的变化，进一步增强在复杂信道环境下的适应能力。仿真结果表明，SCUNetDec在瑞利衰落信道下的误码性能优于常规神经网络译码方法，接近传统最优译码算法，且同时具备更快的译码速度。
- 智能译码 /
- SCUNet /
- 特征提取 /
- 短码 /
- 瑞利衰落信道
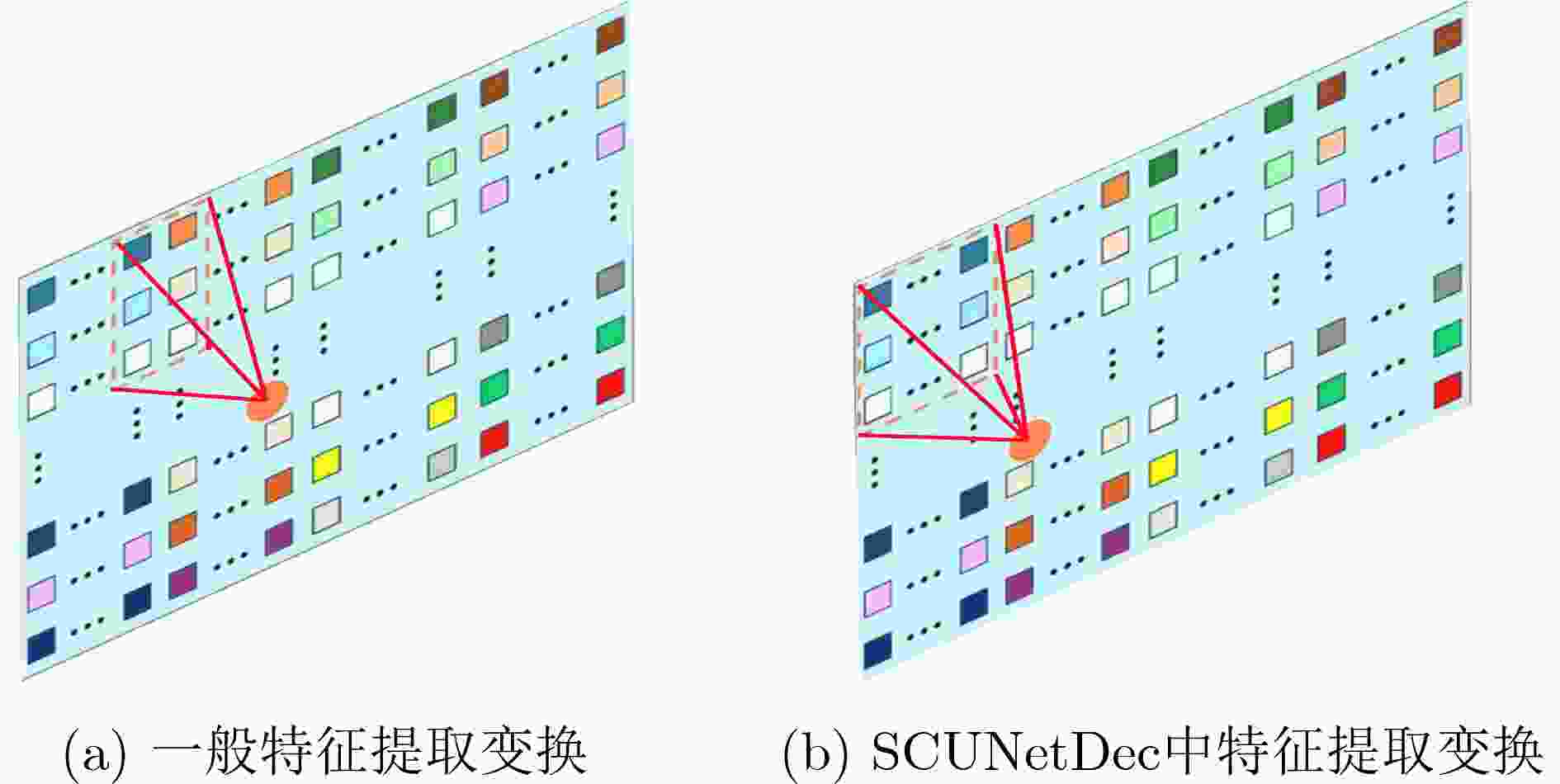
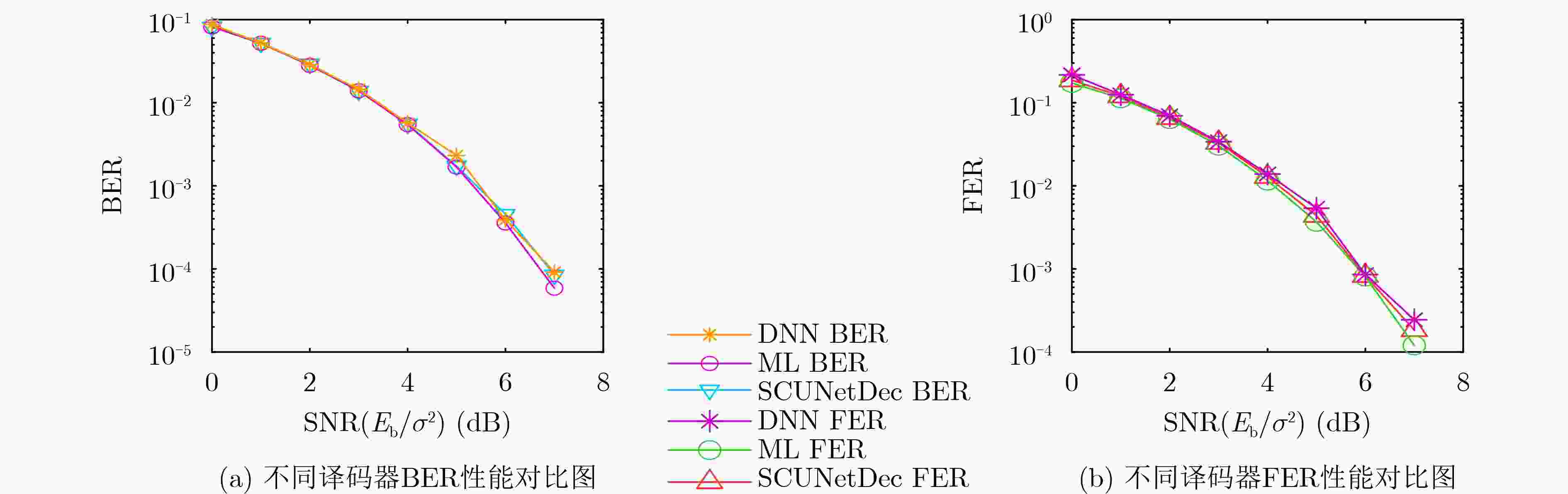
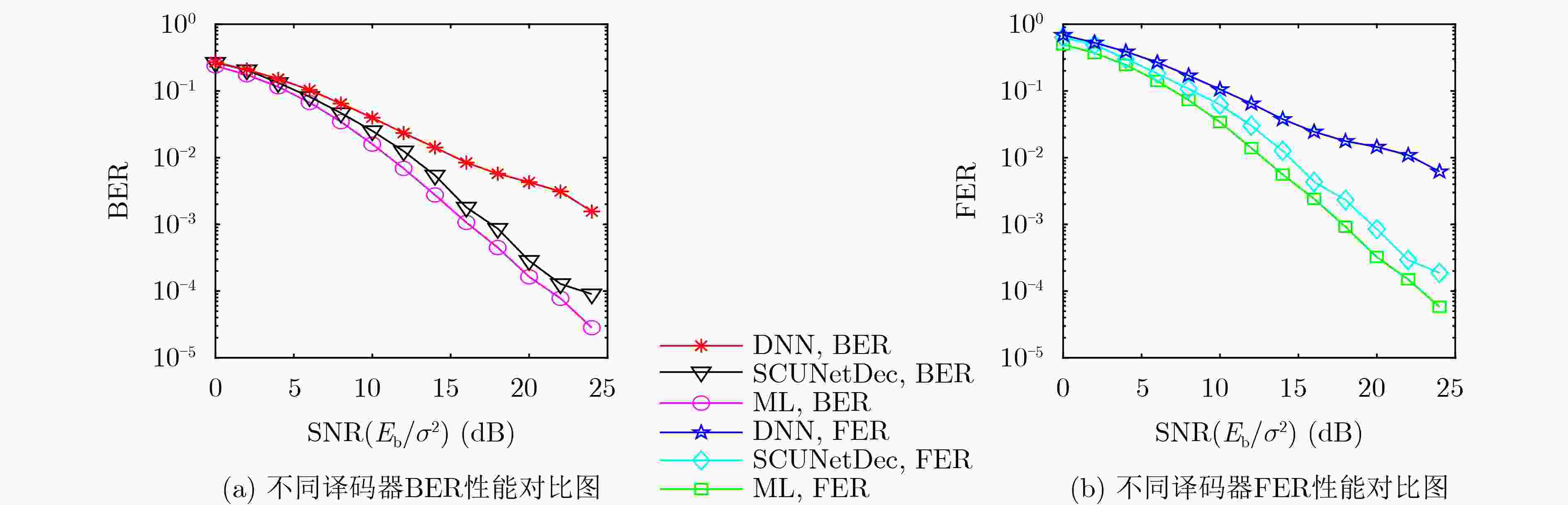
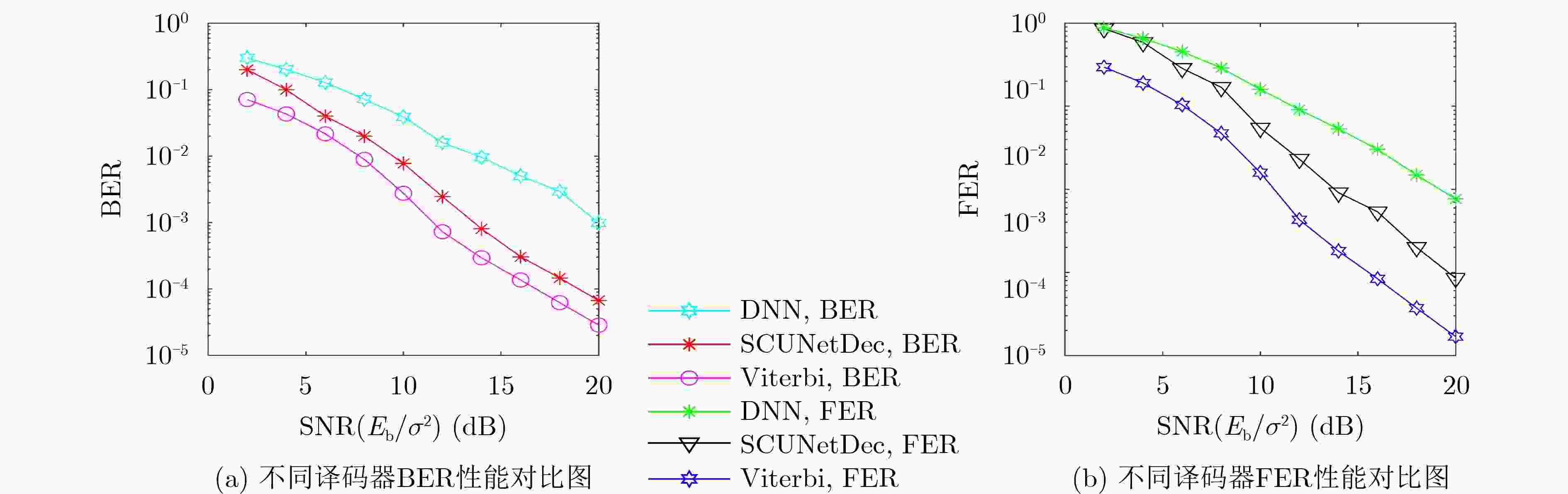
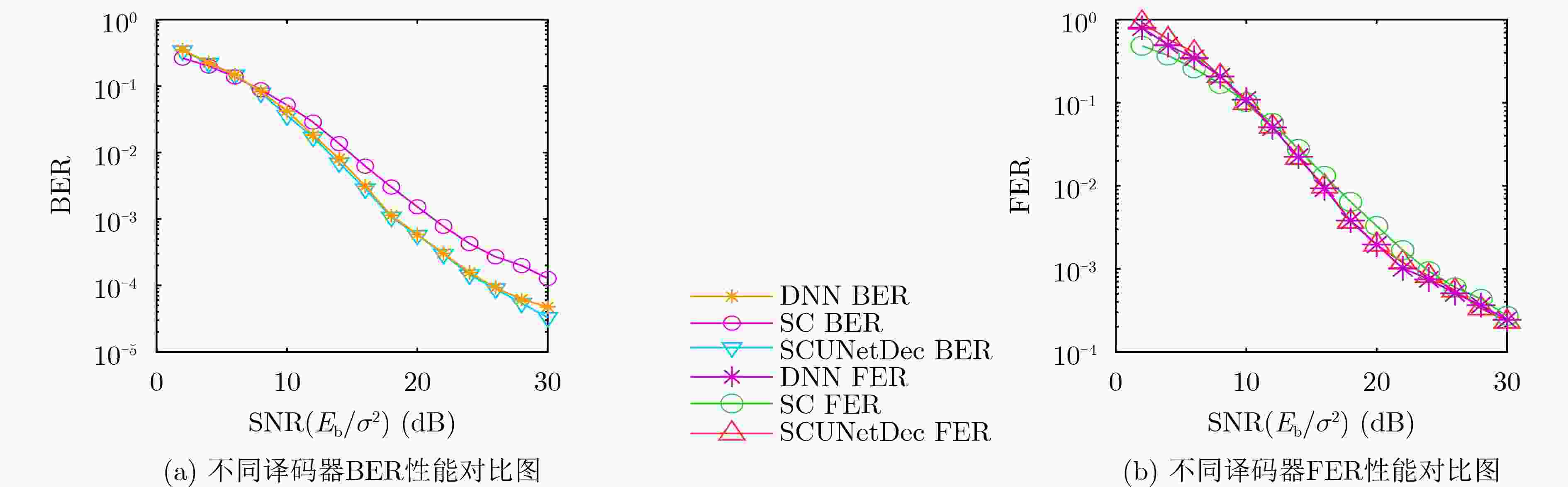
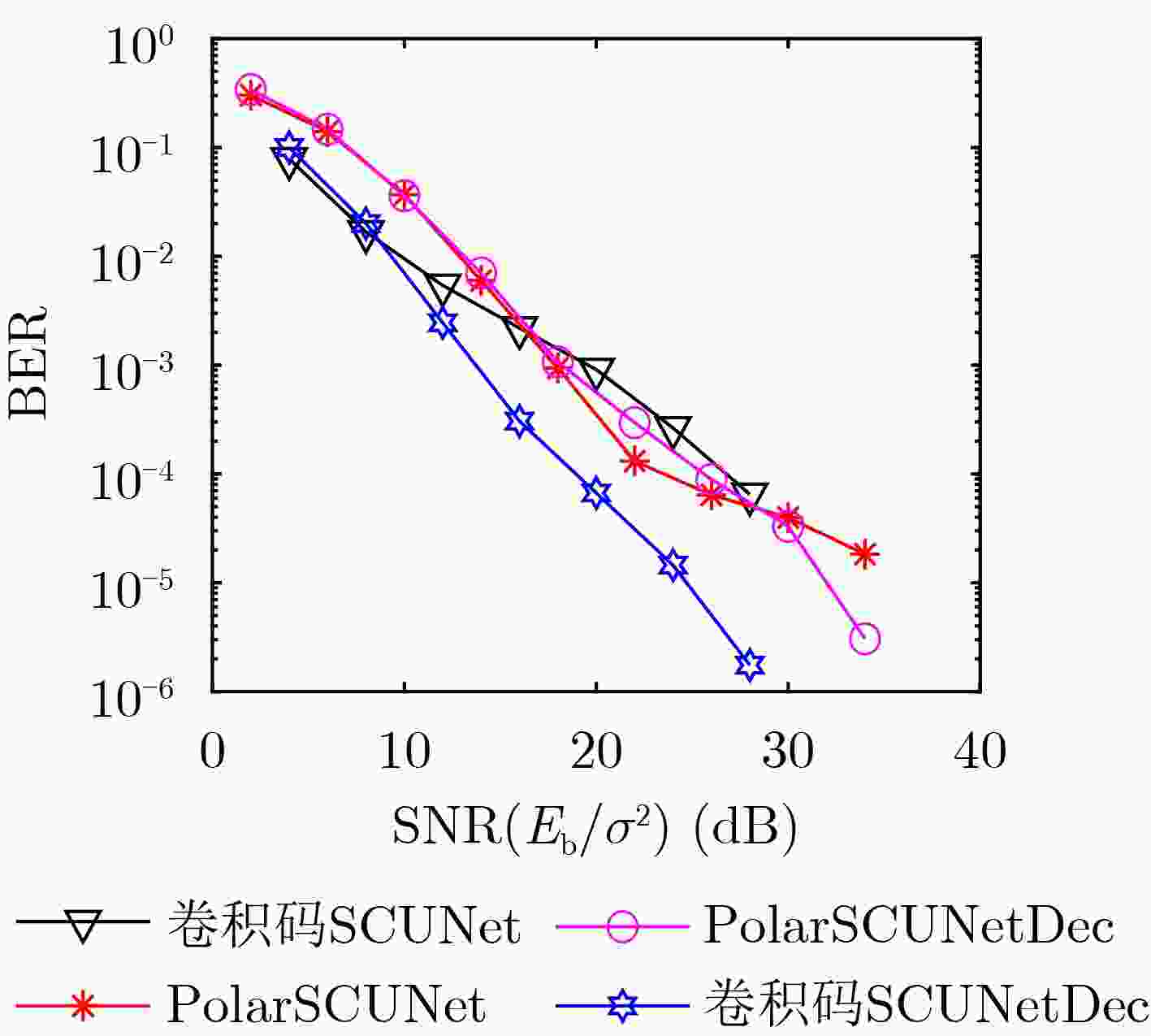
Abstract: Objective This study addresses the limitations of conventional deep neural network (DNN) decoding algorithms in Rayleigh fading channels, such as constrained performance, insufficient generalization capability, and weak resistance to fading. To tackle these issues, a feature extraction and recovery decoding algorithm based on the SCUNet architecture, termed SCUNetDec, is proposed. In the 6G communication era, wireless channels are characterized by high dynamics and complexity, making it difficult for traditional decoding methods to meet the strict requirements for high reliability, low latency, and strong robustness. Therefore, exploring intelligent decoding mechanisms with adaptive feature learning capabilities holds significant theoretical and practical importance. By integrating a multi-dimensional feature extraction and recovery mechanism and incorporating a noise-level map to enhance the network’s perception of channel states, SCUNetDec effectively learns channel characteristics, mitigates fading effects, and significantly improves decoding performance. This research not only provides a new approach to the design of intelligent decoding in complex channel environments but also lays a key technical foundation for building efficient and intelligent 6G communication systems. Methods In the construction of the research methodology, the proposed SCUNetDec network deeply integrates three core mechanisms—data preprocessing, feature extraction and recovery, and noise-level mapping—to achieve efficient and robust signal representation learning and decoding performance enhancement in Rayleigh fading channel environments. First, in the data preprocessing stage, dimensionality expansion operations are employed to map the original one-dimensional received signal into a two-dimensional feature map, enhancing the discernibility of the signal structure and providing a spatial correlation foundation for subsequent deep feature extraction. Second, a feature extraction and recovery module is constructed: the extraction module combines multi-layer convolutional layers with attention mechanisms to effectively capture essential channel features in the signal, while the recovery module utilizes deconvolutional layers and residual connections to suppress irrelevant interference introduced during the dimensionality transformation process, thereby improving signal reconstruction quality and decoding accuracy. Furthermore, a noise-level map mechanism is incorporated into the network. By embedding SNR-aware information that aligns with the feature maps, the model can dynamically adapt to changes in channel conditions and adjust its decoding strategy and feature extraction intensity accordingly. The synergistic interaction of these three mechanisms significantly enhances the noise robustness, generalization capability, and decoding stability of SCUNetDec in Rayleigh fading channels, providing a systematic solution for intelligent decoding in complex 6G wireless environments. Results and Discussions The SCUNetDec decoding algorithm, built upon the SCUNet architecture, significantly enhances signal learning and decoding capabilities in Rayleigh fading channels by integrating a feature extraction-recovery module and a noise-level map. Its performance was evaluated through simulations under various coding schemes. For (7,4) Hamming code, SCUNetDec outperformed conventional DNN decoding and closely approached Maximum Likelihood (ML) performance. Specifically, at a BER of $ {10}^{-4} $, the performance gap to ML decoding was about 1.5 dB, and at a FER of $ {10}^{-3} $, the gap was approximately 2.0 dB (Fig. 4). This shows that SCUNetDec can capture complex relationships within signals, thereby effectively learning the latent associations between information and parity-check nodes. For (2,1,3) Convolutional code, SCUNetDec's performance at BER=$ {10}^{-3} $ was close to the Viterbi algorithm, with a marginal gap of only about 2.0 dB. In contrast, DNN decoding performance degraded significantly at high SNRs, demonstrating SCUNetDec's superior decoding capability and robustness (Fig. 5). For Polar codes with a rate of 0.5, SCUNetDec exhibited strong learning and generalization capabilities. It achieved a gain of approximately 4.0 dB over Successive Cancellation (SC) decoding at BER=$ {10}^{-4} $ and maintained an advantage of about 1.0 dB at FER=$ {10}^{-3} $, whereas SC decoding only showed a slight advantage in the low SNR region (Fig. 6). The comparison results of decoding time indicate that the SCUNetDec decoder can reduce decoding time compared to traditional decoding algorithms (Table 2). The ablation experiments demonstrate that combining the designed feature extraction and recovery modules with SCUNet leads to better decoding performance (Fig. 7). In summary, comprehensive analysis confirms that SCUNetDec delivers outstanding and robust decoding performance across multiple coding schemes and varying signal-to-noise ratio conditions. Conclusions To address the limited decoding performance of DNNs in Rayleigh fading channels, this paper proposes a decoding method named SCUNetDec based on the SCUNet network. The method enhances SCUNet by designing signal feature extraction and signal recovery modules. Simulations and ablation studies on Hamming codes, convolutional codes, and Polar codes demonstrate that the proposed modules exhibit strong generalization capability and effectiveness, making them suitable for various coding schemes. Compared with traditional DNN models, SCUNetDec shows superior decoding performance in Rayleigh fading channels, approaching that of conventional optimal decoding algorithms while significantly reducing decoding time. These results indicate that the SCUNetDec decoding algorithm possesses certain performance advantages and practical application potential in complex channel environments. Future work will focus on algorithm fusion and engineering implementation. On one hand, we aim to deepen the co-design of neural networks and traditional algorithms to achieve an optimal trade-off between performance and complexity via dynamic parameter optimization, while further exploring intelligent decoding schemes for long codes. On the other hand, research will be conducted on joint modulation-decoding modeling and end-to-end architectures to enhance the model's adaptability and practical value under high-order modulation and complex channel environments.
- Intelligent decoding /
- SCUNet /
- Feature extraction /
- Short codes /
- Rayleigh fading channel

HTML全文

图 1 SCUNetDec网络模型

下载: 全尺寸图片幻灯片

图 2 (a) 一般特征提取变换

下载: 全尺寸图片幻灯片

图 3 AWGN信道不同译码器下汉明码译码性能

下载: 全尺寸图片幻灯片

图 4 不同译码器对汉明码译码性能对比

下载: 全尺寸图片幻灯片

图 5 卷积码不同译码器性能对比

下载: 全尺寸图片幻灯片

图 6 Polar码不同译码器性能对比

下载: 全尺寸图片幻灯片

图 7 模块有效性对比

下载: 全尺寸图片幻灯片

表 1 SCUNetDec信号特征提取与恢复译码算法

输入：译码器接收L，信号大小为$ 1\times n $，即$ \boldsymbol{L}=\left({L}_{0},{L}_{1},\cdots ,{L}_{n-1}\right) $, n代表信号点的个数，然后将数量足够多的信号L转换为$ g\times g $大小的　二维信号，其中将每一行信号L的数量记为l,则$ g=n\times l $。
输出：恢复的消息序列$ \hat{\boldsymbol{u}} $。
(1) 初始化f = Conv2d，卷积核大小为(3,2)，步幅为(1,2)，填充为(1,0)；
(2) 初始化$ {f}^{-1}=\mathrm{ConvTranspose}2\mathrm{d} $，根据不同消息序列长度选择合适的卷积核大小和步幅；
(3) 初始化fSCUNet = SCUNet;
(4) if$ n\geq 2 $且$ n\neq {2}^{q} $时,$ q\geq 1 $then
特征提取设计
(5) 　$ \left({L}_{0},{L}_{1},\cdots ,{L}_{n-1}\right)\rightarrow \left({L}_{0},{L}_{1},\cdots ,{L}_{n-1},0,\cdots ,0\right) $，给信号L尾部补0，将其长度补齐为$ {2}^{q} $，即需补$ {2}^{q}-n $个0，记为$ \overline{\boldsymbol{L}} $;
(6) 　$ {\boldsymbol{L}}_{\mathrm{feature}}=f\cdots f\left(\overline{\boldsymbol{L}}\right) $，f层数为k;
(7) 　$ {\boldsymbol{L}}_{\mathrm{SCUNetfeature}}=fSCUNet\left({\boldsymbol{L}}_{\mathrm{feature}}\right) $;
信号恢复设计
(8) 　$ \hat{\boldsymbol{u}}=f{f}^{-1}\cdots {f}^{-1}\left({\boldsymbol{L}}_{\mathrm{SCUNetfeature}}\right) $;
else$ n\geq 2 $且$ n={2}^{\mathrm{q}} $时，$ q\geq 1 $
特征提取设计
(9) 　$ {\boldsymbol{L}}_{\mathrm{feature}}=f\cdots f\left(\boldsymbol{L}\right) $, f层数为k;
(10) $ {\boldsymbol{L}}_{\mathrm{SCUNetfeature}}=fSCUNet\left({\boldsymbol{L}}_{\mathrm{feature}}\right) $;
信号恢复设计
(11) $ \hat{\boldsymbol{u}}=f{f}^{-1}\cdots {f}^{-1}\left({\boldsymbol{L}}_{\mathrm{SCUNetfeature}}\right) $;

下载: 导出CSV

表 2 不同译码器译码时间对比

译码器	编码方式	码长	译码时间(s)
SCUNetDec	汉明码	L = 7	0.65
ML	汉明码	L = 7	149.09
DNN	汉明码	L = 7	0.63
SCUNetDec	卷积码	L = 16	0.60
Viterbi	卷积码	L = 16	5.43
DNN	卷积码	L = 16	1.54
SCUNetDec	Polar	L = 16	0.70
SC	Polar	L = 16	60.00
DNN	Polar	L = 16	0.68

下载: 导出CSV

参考文献(39)

[1]	LIU Fan, CUI Yuanhao, MASOUROS C, et al. Integrated sensing and communications: Toward dual-functional wireless networks for 6G and beyond[J]. IEEE Journal on Selected Areas in Communications, 2022, 40(6): 1728–1767. doi: 10.1109/JSAC.2022.3156632.
[2]	O’SHEA T and HOYDIS J. An introduction to deep learning for the physical layer[J]. IEEE Transactions on Cognitive Communications and Networking, 2017, 3(4): 563–575. doi: 10.1109/TCCN.2017.2758370.
[3]	CHEN Rongjun, YAO Chengsi, ZENG Xianxian, et al. Large-scale cross-modal hashing via Kolmogorov-Arnold representation theorem and optimal transport[J]. Knowledge-Based Systems, 2025, 330: 114698. doi: 10.1016/j.knosys.2025.114698.
[4]	YUE Chentao, SHIRVANIMOGHADDAM M, LI Yonghui, et al. Segmentation-discarding ordered-statistic decoding for linear block codes[C]. Proceedings of 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, USA, 2019: 1–6. doi: 10.1109/GLOBECOM38437.2019.9014173.
[5]	YUE Chentao, SHIRVANIMOGHADDAM M, PARK G, et al. Linear-equation ordered-statistics decoding[J]. IEEE Transactions on Communications, 2022, 70(11): 7105–7123. doi: 10.1109/TCOMM.2022.3207206.
[6]	LIANG Jifan, WANG Yiwen, CAI Suihua, et al. A low-complexity ordered statistic decoding of short block codes[J]. IEEE Communications Letters, 2023, 27(2): 400–403. doi: 10.1109/LCOMM.2022.3222819.
[7]	WANG Yiwen, LIANG Jifan, and MA Xiao. Local constraint-based ordered statistics decoding for short block codes[C]. Proceedings of 2022 IEEE Information Theory Workshop (ITW), Mumbai, India, 2022: 107–112. doi: 10.1109/ITW54588.2022.9965916.
[8]	WANG Qianfan, CHEN Yanzhi, LIANG Jifan, et al. A new joint source-channel coding for short-packet communications[J]. IEEE Transactions on Communications, 2024, 72(1): 28–37. doi: 10.1109/TCOMM.2023.3320699.
[9]	WANG Qianfan, CHEN Yanzhi, LIANG Jifan, et al. A new joint source-channel coding in the short blocklength regime[C]. Proceedings of IEEE Global Communications Conference Workshops (GLOBECOM Workshops), Kuala Lumpur, Malaysia, 2023: 1566–1571. doi: 10.1109/GCWkshps58843.2023.10464813.
[10]	CHEN Yanzhi, LIANG Jifan, WANG Qianfan, et al. A new joint source-channel coding scheme with overlay spread spectrum transmission[C]. Proceedings of IEEE International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 2023: 239–244. doi: 10.1109/WCSP58612.2023.10404761.
[11]	ZHENG Xiangping, WANG Qianfan, WEI Baodian, et al. Quasi-OSD of binary image of RS codes with applications to JSCC[C]. Proceedings of 2024 IEEE International Symposium on Information Theory (ISIT), Athens, Greece, 2024: 3576–3581. doi: 10.1109/ISIT57864.2024.10619269.
[12]	WANG Qianfan, WANG Yiwen, WANG Yixin, et al. Random staircase generator matrix codes: Coding theorem, performance analysis, and code design[J]. IEEE Transactions on Information Theory, 2025, 71(5): 3497–3509. doi: 10.1109/TIT.2025.3541734.
[13]	WANG Qianfan, WANG Yiwen, WANG Yixin, et al. Random staircase generator matrix codes[C]. Proceedings of 2024 IEEE International Symposium on Information Theory (ISIT), Athens, Greece, 2024: 2622–2627. doi: 10.1109/ISIT57864.2024.10619485.
[14]	WANG Yiwen, LIANG Jifan, WANG Qianfan, et al. Representative ordered statistics decoding of staircase matrix codes[J]. IEEE Transactions on Communications, 2025, 73(4): 2148–2158. doi: 10.1109/TCOMM.2024.3478114.
[15]	WANG Yiwen, WANG Qianfan, LIANG Jifan, et al. Representative ordered statistics decoding of polar codes[C]. Proceedings of IEEE 99th Vehicular Technology Conference (VTC2024-Spring), Singapore, Singapore, 2024: 1–5. doi: 10.1109/VTC2024-Spring62846.2024.10683273.
[16]	WANG Yiwen, WANG Qianfan, LIANG Jifan, et al. Representative OSD with local constraints of CA-polar codes[J]. Chinese Journal of Electronics, 2025, 34(4): 1111–1119. doi: 10.23919/cje.2024.00.220.
[17]	钟卓宏, 王千帆, 王义文, 等. 双向叠加BCH码及其高性能译码[J]. 电子学报, 2025, 53(9): 3192–3201. doi: 10.12263/dzxb.20250582. ZHONG Zhuohong, WANG Qianfan, WANG Yiwen, et al. TPST-BCH coding scheme with high-performance decoding[J]. Acta Electronica Sinica, 2025, 53(9): 3192–3201. doi: 10.12263/dzxb.20250582.
[18]	WANG Yiwen, WANG Qianfan, ZHENG Xiangping, et al. Reduced-complexity guessing codeword decoding of BCH codes with most reliable cyclic basis[C]. Proceedings of the IEEE Global Communications Conference (GLOBECOM), 2025. (查阅网上资料, 未找到本条文献信息, 请确认).
[19]	WANG Qianfan, WANG Yiwen, ZHENG Xiangping, et al. Ordered reliability bits guessing codeword decoding of short codes[J]. IEEE Wireless Communications Letters, 2025, 14(9): 2823–2827. doi: 10.1109/LWC.2025.3580156.
[20]	ZHENG Xiangping, WANG Qianfan, and MA Xiao. SCL-GCD of short polar codes[C]. Proceedings of GLOBECOM 2024-2024 IEEE Global Communications Conference, Cape Town, South Africa, 2024: 686–691. doi: 10.1109/GLOBECOM52923.2024.10901715.
[21]	王义文, 王千帆, 梁济凡, 等. 多矩阵的代表性顺序统计量译码算法[J]. 电子与信息学报, 2026. doi: 10.11999/JEIT250854. (查阅网上资料,未找到本条文献卷期页码信息,请确认). WANG Yiwen, WANG Qianfan, LIANG Jifan, et al. Multi-matrix representative ordered statistics decoding[J]. Journal of Electronics & Information Technology, 2026. doi: 10.11999/JEIT250854.
[22]	王千帆, 郭延庚, 宋林琦, 等. 基于跳过机制的低复杂度顺序统计译码算法[J]. 电子与信息学报, 2025, 47(11): 4275–4284. doi: 10.11999/JEIT250447. WANG Qianfan, GUO Yangeng, SONG Linqi, et al. Low-complexity ordered statistic decoding algorithm based on skipping mechanisms[J]. Journal of Electronics & Information Technology, 2025, 47(11): 4275–4284. doi: 10.11999/JEIT250447.
[23]	王义文, 王千帆, 马强. 干扰环境下无速率随机码编译码方案及其性能分析[J]. 电子与信息学报, 2024, 46(10): 4017–4023. doi: 10.11999/JEIT230879. WANG Yiwen, WANG Qianfan, and MA Xiao. Rateless random coding scheme and performance analysis in strong interference environments[J]. Journal of Electronics & Information Technology, 2024, 46(10): 4017–4023. doi: 10.11999/JEIT230879.
[24]	梁济凡, 王千帆, 宋林琦, 等. 参数列表化置信传播-顺序统计译码算法[J]. 电子与信息学报, 2025, 47(11): 4254–4263. doi: 10.11999/JEIT250552. LIANG Jifan, WANG Qianfan, SONG Linqi, et al. Belief propagation-ordered statistics decoding algorithm with parameterized list structures[J]. Journal of Electronics & Information Technology, 2025, 47(11): 4254–4263. doi: 10.11999/JEIT250552.
[25]	LIANG Jifan, WANG Qianfan, LI Lvzhou, et al. The BP-LCOSD algorithm for toric codes[C]. Proceedings of IEEE International Symposium on Information Theory Workshops (ISIT-W), Athens, Greece, 2024: 1–6. doi: 10.1109/ISIT-W61686.2024.10591758.
[26]	LIANG Jifan, WANG Qianfan, LI Lvzhou, et al. A low-complexity BP-OSD algorithm for quantum LDPC codes[J]. The European Physical Journal Special Topics, 2025, 234(20): 6211–6222. doi: 10.1140/epjs/s11734-025-01712-x.
[27]	LIANG Jifan, WANG Qianfan, LI Lvzhou, et al. A high-performance list decoding algorithm for surface codes with erroneous syndrome[J]. arXiv preprint arXiv: 2409.06979, 2024. doi: 10.48550/arXiv.2409.06979. (查阅网上资料,不确定文献类型及格式是否正确,请确认).
[28]	WANG Qianfan, Liang Jifan, LI Lvzhou, et al. BP-LCGCD: A Gaussian-elimination-free and high-performance decoder for surface codes[J]. IEEE Communications Letters, 2026, 30: 782–786. doi: 10.1109/LCOMM.2025.3646724.
[29]	赵生妹, 徐鹏, 张南, 等. 基于CNN扰动的极化码译码算法[J]. 电子与信息学报, 2021, 43(7): 1900–1906. doi: 10.11999/JEIT200136. ZHAO Shengmei, XU Peng, ZHANG Nan, et al. A decoding algorithm of polar codes based on perturbation with CNN[J]. Journal of Electronics & Information Technology, 2021, 43(7): 1900–1906. doi: 10.11999/JEIT200136.
[30]	FENG Haogang, XIAO Haiyu, ZHONG Shida, et al. Deep-learning-aided fast successive cancellation decoding of polar codes[J]. Journal of Communications and Networks, 2024, 26(6): 593–602. doi: 10.23919/JCN.2024.000070.
[31]	周华, 周鸣, 张立康. 低密度奇偶校验码正则化神经网络归一化最小和译码算法[J]. 电子与信息学报, 2025, 47(5): 1486–1493. doi: 10.11999/JEIT240860. ZHOU Hua, ZHOU Ming, and ZHANG Likang. Regularized neural network-based normalized min-sum decoding for LDPC codes[J]. Journal of Electronics & Information Technology, 2025, 47(5): 1486–1493. doi: 10.11999/JEIT240860.
[32]	GRUBER T, CAMMERER S, HOYDIS J, et al. On deep learning-based channel decoding[C]. Proceedings of IEEE 2017 51st Annual Conference on Information Sciences and Systems (CISS), Baltimore, USA, 2017: 1–6. doi: 10.1109/CISS.2017.7926071.
[33]	WANG Yaohan, ZHANG Zhichao, ZHANG Shunqing, et al. A unified deep learning based polar-LDPC decoder for 5G communication systems[C]. Proceedings of IEEE 2018 10th International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 2018: 1–6. doi: 10.1109/WCSP.2018.8555891.
[34]	ZHENG Shilian, CHEN Shichuan, and YANG Xiaoniu. DeepReceiver: A deep learning-based intelligent receiver for wireless communications in the physical layer[J]. IEEE Transactions on Cognitive Communications and Networking, 2021, 7(1): 5–20. doi: 10.1109/TCCN.2020.3018736.
[35]	YE Hao and LI G Y. Initial results on deep learning for joint channel equalization and decoding[C]. Proceedings of IEEE 2017 IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, Canada, 2017: 1–5. doi: 10.1109/VTCFall.2017.8288419.
[36]	TEICH W G, LIU Ruiqi, and BELAGIANNIS V. Deep learning versus high-order recurrent neural network based decoding for convolutional codes[C]. Proceedings of IEEE GLOBECOM 2020-2020 IEEE Global Communications Conference, 2020: 1–7. doi: 10.1109/GLOBECOM42002.2020.9348117.
[37]	ZHANG Kai, LI Yawei, LIANG Jingyun, et al. Practical blind image denoising via Swin-Conv-UNet and data synthesis[J]. Machine Intelligence Research, 2023, 20(6): 822–836. doi: 10.1007/s11633-023-1466-0.
[38]	CHEN Kecheng, PU Xiaorong, REN Yazhou, et al. TEMDnet: A novel deep denoising network for transient electromagnetic signal with signal-to-image transformation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5900318. doi: 10.1109/TGRS.2020.3034752.
[39]	ZHANG Kai, ZUO Wangmeng, and ZHANG Lei. FFDNet: Toward a fast and flexible solution for CNN-based image denoising[J]. IEEE Transactions on Image Processing, 2018, 27(9): 4608–4622. doi: 10.1109/TIP.2018.2839891.