Delay Deterministic Routing Algorithm Based on Inter-Controller Cooperation for Multi-Layer LEO Satellite Networks
-
摘要: 针对多层低轨星座在软件定义网络架构下节点数量庞大、网络拓扑动态性强以及控制器对全网状态的感知滞后导致难以确定端到端数据传输时延的问题,提出了一种基于控制器间协作的多层低轨星座确定性时延路由算法。首先,构建多层低轨星座的区域划分与控制器部署策略,以及星间链路的建立准则,消除节点数量和状态感知滞后的影响;其次,设计时变增量图模型刻画卫星网络拓扑与链路资源属性,在链路的带宽、卫星队列大小与链路间持续时间的约束下,提出基于控制器间协作的确定性时延路由算法,并通过控制器间状态实时感知和交互,及多目的拉格朗日的松弛聚合算法优化传输路径;最后,构建基于NS-3和Ryu的仿真平台验证可行性。结果表明,相较链路效用的自适应路由算法,所提算法在平均端到端时延、时延抖动与丢包率上分别降低16.0%、37.9%、37.2%,平均吞吐量提升约 2%,且具有较低计算复杂度与信令开销。Abstract:
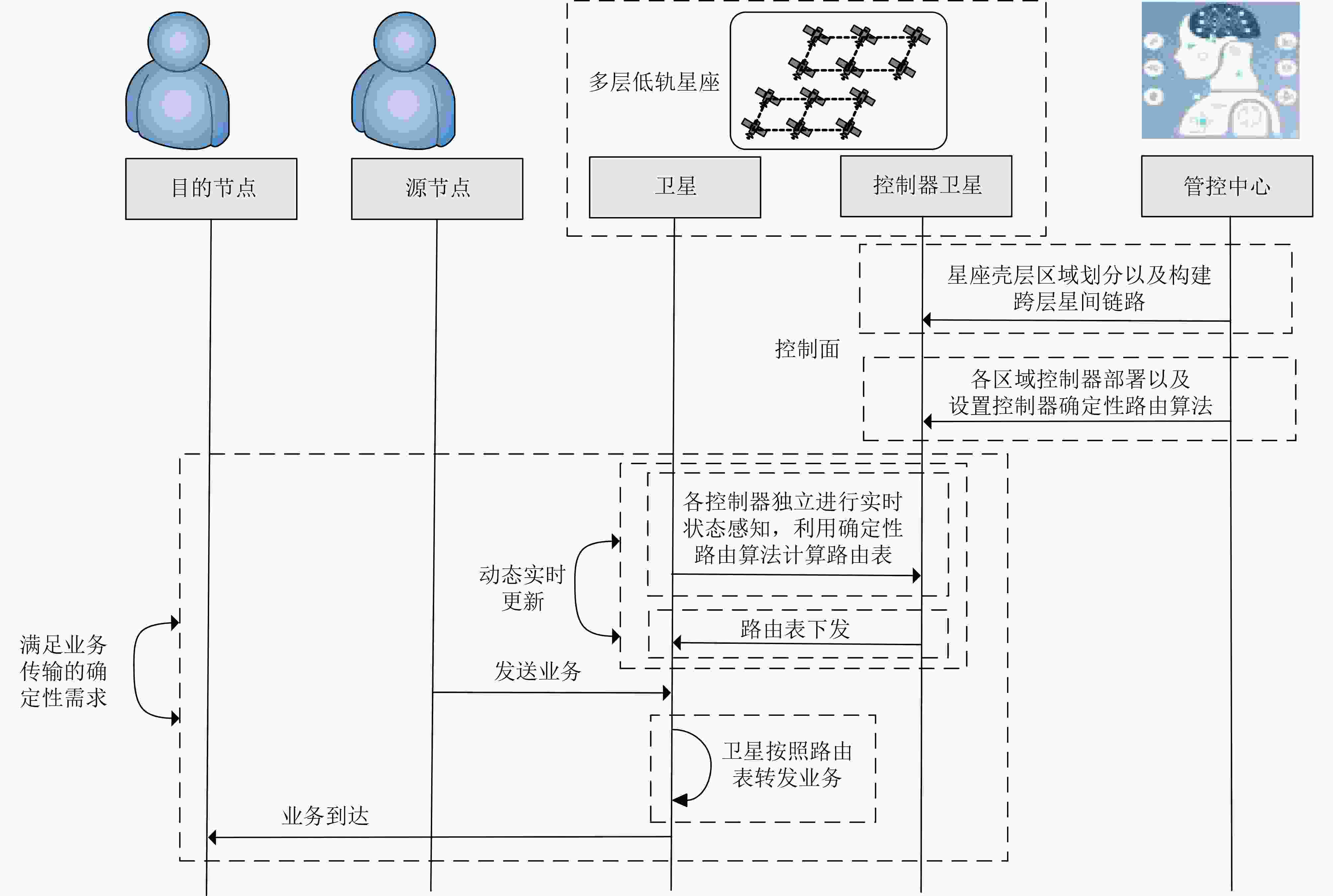
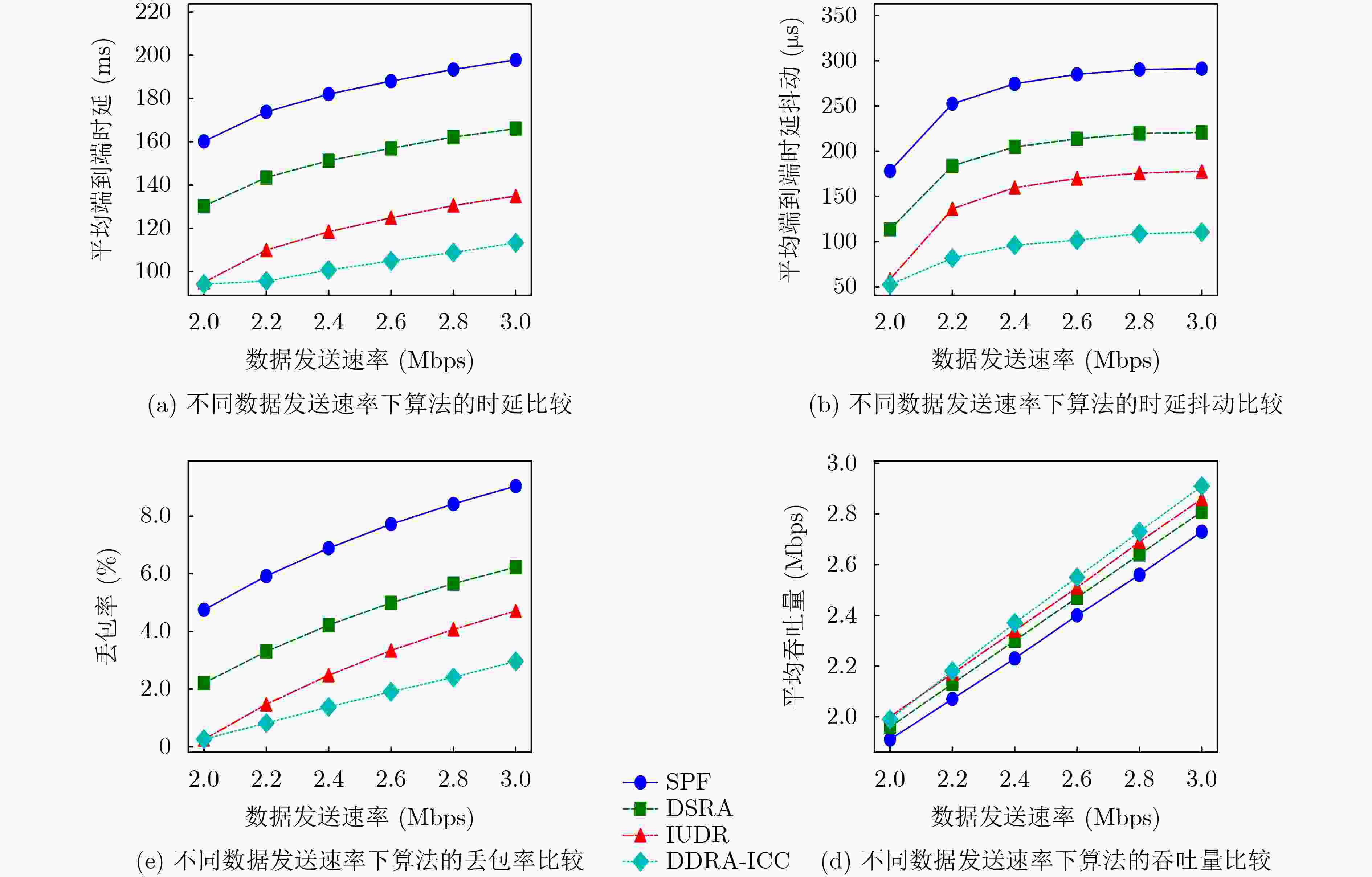
Objective The massive scale and large number of satellites in multi-layer Low Earth Orbit (LEO) constellations result in highly dynamic network topologies. Coupled with the time-varying traffic load, this leads to temporal fluctuations in satellite network resources (e.g., available link queue sizes, available link bandwidth), making it challenging to establish stable end-to-end transmission paths and guarantee Quality of Service (QoS). To address these issues, this study introduces Software-Defined Networking (SDN) into multi-layer LEO constellations. By leveraging SDN controllers to collect network state information, unified management of network resources is achieved. The constellation is partitioned into regions, with a controller deployed in each region to manage the entire constellation. Furthermore, a deterministic delay routing algorithm is designed within the SDN controller to compute inter-region transmission paths for traffic, thereby meeting its deterministic delay requirements. Methods This paper proposes a deterministic delay routing algorithm for multi-layer LEO constellations based on controller collaboration. Firstly, a regional division strategy and controller deployment scheme are proposed, dividing the satellite network into multiple regions, each managed by an assigned controller. Subsequently, criteria are established for Inter-Satellite Links (ISLs) between satellites within the same layer and across different layers to characterize link communication states. Finally, a Time-Varying Graph (TVG) model is employed to represent the network topology and link resource attributes, including bandwidth, queue size, and link duration. This is combined with a multi-destination LaGrange relaxation method to optimize path selection, ensuring the chosen paths satisfy both delay and delay jitter constraints. Through collaboration between adjacent regional controllers, which exchange state information, the proposed algorithm enables the computation of feasible inter-region paths. Results and Discussions To validate the effectiveness of the proposed method, a simulation system for multi-layer LEO constellations was designed, and the algorithm’s performance was tested under different data transmission rates. Compared to IUDR, the proposed method significantly enhances network performance by reducing end-to-end delay, delay jitter, and packet loss rate, while improving throughput. Specifically, at a data transmission rate of 3 Mbps, the average end-to-end delay was reduced by 16.0% ( Fig. 3(a) ), delay jitter by 37.9% (Fig. 3(b) ), packet loss rate by 37.2% (Fig. 3(c) ), and throughput increased by approximately 2%(Fig. 3(d) ). Regarding signaling overhead, the proposed algorithm achieves a higher Reduction-Improvement Gain Ratio, improved by approximately 111.8% compared to IUDR, indicating the superior comprehensive performance of the DDRA-ICC. Additionally, the proposed method exhibits lower time complexity for route computation compared to IUDR.Conclusions To solve the problem of deterministic delay for traffic transmission in multi-layer LEO constellations, this study proposed a controller collaboration-based deterministic delay routing algorithm. Performance evaluation under different load scenarios demonstrates that: (1) Compared to IUDR, the proposed algorithm reduces average end-to-end delay, delay jitter, and packet loss rate by 16.0%, 37.9%, and 37.2% respectively, while increasing average throughput by approximately 2%. (2) While the additional overhead increase of the DDRA-ICC is comparable to IUDR, it further reduces the packet loss rate to 2.96%—a reduction of 52.49%—and achieves a Reduction-Improvement Gain Ratio of 1.97. This indicates lower packet loss, a higher Reduction-Improvement Gain Ratio, and demonstrates a better balance between overhead and reliability, granting it greater advantage in ensuring deterministic traffic transmission. Future work could incorporate more practical factors, such as the impact of satellite node failures on network performance, to further enhance network capabilities. -
1 DDRA-ICC
输入: 业务发送的持续时间$ {T}_{c} $,数据传输的源用户终端节点$ {S}_{G} $,数据传输目的用户终端节点$ {D}_{G} $,区域拓扑图$ {G}_{R} $,$ {S}_{G} $与$ {D}_{G} $之间的时
延约束$ D $和时延抖动约束$ J $输出: 当前区域内从$ {S}_{G} $到$ {D}_{G} $满足确定性时延需求的路径$ \text{path} $ 1: 确定$ {S}_{G} $和$ {D}_{G} $所在的区域,源用户终端节点$ {S}_{G} $所在的区域称为源区域$ {S}_{R} $,目的用户终端节点$ {D}_{G} $所在的区域称为目的区域$ {D}_{R} $ 2: 基于最小跳数在$ {G}_{R} $中,计算源区域到目的区域的所需经历的区域集合$ {p}_{r} $ 3: 针对区域集合$ {p}_{r} $中每个区域的控制器更新时变增量图$ {G}_{{{r}_{i}}} $ 4: 给定$ D $和$ J $,按照公式(10)计算区域集合$ {p}_{r} $中每个区域对应的时延约束$ {D}_{{{r}_{i}}} $和时延抖动约束$ {J}_{{{r}_{i}}} $,令$ i=0 $ 5: 判断当前区域$ {r}_{i} $是否为源区域$ {S}_{R} $,若是,则设置当前区域$ {r}_{i} $的源节点$ {S}_{s} $为$ {S}_{G} $,若不是,则令$ {S}_{s} $为$ {r}_{i} $第一个接收到业务的卫星节点 6: 判断当前区域$ {r}_{i} $是否为目的区域$ {\mathrm{D}}_{\mathrm{R}} $$ {D}_{R} $,若是,则把$ {D}_{G} $加入到$ {r}_{i} $的目的节点集合$ {\text{Dest}}_{{{r}_{i}}} $中,并转至步骤10,若不是,则转至步骤7 7: 由$ {r}_{i} $内的控制器$ {C}_{{{r}_{i}}} $向$ {r}_{i+1} $内的控制器$ {C}_{{{r}_{i+1}}} $发送请求,$ {C}_{{{r}_{i+1}}} $收到请求后把$ {r}_{i} $与$ {r}_{i+1} $之间的边界卫星的状态信息发送给$ {C}_{{{r}_{i}}} $ 8: $ {C}_{{{r}_{i}}} $收到状态信息后,筛选出$ {r}_{i} $与$ {r}_{i+1} $之间边界星间链路中的所有可行星间链路,得到边界可行链路集合$ E_{{r}_{i},{r}_{i+1}}^{e} $对应的带宽集合
$ B_{{r}_{i},{r}_{i+1}}^{e} $、时延集合$ D_{{r}_{i},{r}_{i+1}}^{e} $、时延抖动集合$ J_{{r}_{i},{r}_{i+1}}^{e} $9: 把$ E_{{r}_{i},{r}_{i+1}}^{e} $中属于$ {r}_{i+1} $内的边界卫星节点加入到$ Des{t}_{{{r}_{i}}} $中,并把$ {S}_{s} $和$ Des{t}_{{{r}_{i}}} $加入到$ {G}_{{{r}_{i}}} $ 10: 给定$G_{r_i} $、$B^e_{r_i,r_{i+1}} $、$D^e_{r_i,r_{i+1}} $、$J^e_{r_i, r_{i+1}} $、$ {D}_{{{r}_{i}}} $和$ {J}_{{{r}_{i}}} $,调用MD-LARAC算法,计算出满足条件的路径$ {\text{path}}_{{{r}_{i}}} $,并将其加入到
$ \text{path} $. 若 $ i \lt \left| {p}_{r}\right| $,$ i=i+1 $并返回到步骤5;否则进入步骤1111: 返回$ \text{path} $ 2 DC-LARAC算法
输入:时变增量图$ {G}_{{{r}_{i}}} $,目的节点$ \text{Dest} $,时延约束$ {D}_{{{r}_{i}}} $,时延抖动约束$ {J}_{{{r}_{i}}} $ 输出:从$ \text{Src} $到$ \text{Dest} $满足时延和时延抖动约束的路径$ P $ 初始化:归一化权重:$ {\alpha }_{d} $和$ {\alpha }_{j} $ ($ {\alpha }_{d}+{\alpha }_{j}=1 $),最大迭代次数$ K $,$ {\mu }_{\mathrm{d}}={\mu }_{\mathrm{j}}=0 $$ {\mu }_{d}={\mu }_{j}=0 $,$ \mathrm{k}=0 $$ k=0 $,步长$ \eta \gt 0 $ 1:从$ {G}_{{{r}_{i}}} $中分别取出$ {S}_{s} $,并赋值给$ \text{Src} $,给定时变增量图$ {G}_{{{r}_{i}}} $,以$ {G}_{{{r}_{i}}} $中链路时延为权重,利用Dijkstra算法计算从源节点到目的节点的最短时延路径$ {P}_{\min D} $ 2:if 路径$ {P}_{\text{minD}} $的时延满足$ {D}_{{{r}_{i}}} $且时延抖动满足$ {J}_{{{r}_{i}}} $then 3: return $ {P}_{\text{minD}} $ 4:end if 5:给定时变增量图$ {G}_{{{r}_{i}}} $,以$ {G}_{{{r}_{i}}} $中链路时延抖动为权重,利用Dijkstra算法计算从源节点到目的节点的最短时延路径$ {P}_{\text{minJ}} $ 6:if 路径$ {P}_{\text{minJ}} $的时延满足$ {D}_{{{r}_{i}}} $且时延抖动满足$ {J}_{{{r}_{i}}} $then 7: return $ {P}_{\text{minJ}} $ 8:end if 9:if 路径$ {P}_{\text{minD}} $的时延无法满足$ {D}_{{{r}_{i}}} $或者路径$ {P}_{\text{minJ}} $的时延抖动无法满足$ {J}_{{{r}_{i}}} $then 10: return “无解” 11:end if 12:对$ {G}_{{{r}_{i}}} $中的时延集合$ D_{{r}_{i},{r}_{i+1}}^{e} $和时延抖动集合$ J_{{r}_{i},{r}_{i+1}}^{e} $,分别用$ {D}_{{{r}_{i}}} $和$ {J}_{{{r}_{i}}} $进行归一化,并赋值给$ \overline{d}_{{r}_{i}}^{e} $和$ \overline{j}_{{r}_{i}}^{e} $ ,令
$ a_{{r}_{i}}^{e}={\alpha }_{d}\cdot \overline{d}_{{r}_{i}}^{e}+{\alpha }_{j}\cdot \overline{j}_{{r}_{i}}^{e} $13:给定$ {G}_{{{r}_{i}}} $,以$ a_{{r}_{i}}^{e} $为权重,利用Dijkstra算法计算从源节点到目的节点的最短时延路径$ {P}_{0} $ 14:if 路径$ {P}_{0} $的时延满足$ {D}_{{{r}_{i}}} $且时延抖动满足$ {J}_{{{r}_{i}}} $then 15: return $ {P}_{0} $ 17:end if 19:while $ k \lt K $ do 20: $ k=k+1 $ 21: 令$ a_{{r}_{i}}^{e}=({\alpha }_{d}+{\mu }_{d})\cdot \overline{d}_{{r}_{i}}^{e}+({\alpha }_{j}+{\mu }_{j})\cdot \overline{j}_{{r}_{i}}^{e} $ 22: 给定$ {G}_{{{r}_{i}}} $,以$ a_{{r}_{i}}^{e} $为权重,利用Dijkstra算法计算从源节点到目的节点的最短时延路径$ {P}_{\mu } $ 23: if 路径$ {P}_{\mu } $的时延满足$ {D}_{{{r}_{i}}} $且时延抖动满足$ {J}_{{{r}_{i}}} $then 24: return $ {P}_{\mu } $ 25: 计算$ {P}_{\mu } $的时延和时延抖动得到$ P_{\mu }^{\text{Deday}} $和$ P_{\mu }^{\text{Jitter}} $,令$ {g}_{d}=P_{\mu }^{\text{Deday}}/D-1 $$ {\mathrm{g}}_{\mathrm{j}}=\mathrm{jitter}({\mathrm{p}}_{\mu })/\mathrm{J}-1 $,$ {g}_{j}=P_{\mu }^{\text{Jitter}}/J-1 $ 26: 设步长:$ {\alpha }_{\mathrm{s}}=\eta /\sqrt{\mathrm{k}} $$ {\alpha }_{s}=\eta /\sqrt{k} $ 27: 更新乘子:$ {\mu }_{\mathrm{d}}=\max (0,{\mu }_{\mathrm{d}}+{\alpha }_{\mathrm{s}}\mathrm{*}{\mathrm{g}}_{\mathrm{d}}) $$ {\mu }_{d}=\max (0,{\mu }_{d}+{\alpha }_{s}\cdot {g}_{d}) $,$ {\mu }_{j}=\max (0,{\mu }_{j}+{\alpha }_{s}\cdot {g}_{j}) $$ {\mu }_{\mathrm{j}}=\max (0,{\mu }_{\mathrm{j}}+{\alpha }_{\mathrm{s}}\mathrm{*}{\mathrm{g}}_{\mathrm{j}}) $ 28:end while 29:return “无解” 表 1 仿真参数设置
仿真参数 数值 仿真参数 数值 地面用户数 100 壳层1/2卫星数量 108/60 跨层链路数量 12 壳层1/2轨道高度 1150 /1175 Km链路缓存大小 100 Packets 壳层1/2倾角 50°/86.5° GSL/ISL带宽 10 Mbps 数据包大小 1024 B控制器数量 10 信息搜集周期$ \Delta T $ 5 s 表 2 算法开销对比
算法 额外开销包数(个) 丢包率(%) 额外开销提升率(%) 丢包率降低(%) 降低-提升增益比 DSRA 9836 6.23 0.00 0.00 0.00 IUDR 12412 4.71 26.19 24.39 0.93 DDRA-ICC 12454 2.96 26.61 52.49 1.97 -
[1] 倪少杰, 岳洋, 左勇, 等. 卫星网络路由技术现状及展望[J]. 电子与信息学报, 2023, 45(2): 383–395. doi: 10.11999/JEIT211393.NI Shaojie, YUE Yang, ZUO Yong, et al. The status quo and prospect of satellite network routing technology[J]. Journal of Electronics & Information Technology, 2023, 45(2): 383–395. doi: 10.11999/JEIT211393. [2] DENG Xia, CHANG Le, ZENG Shouyuan, et al. Distance-based back-pressure routing for load-balancing LEO satellite networks[J]. IEEE Transactions on Vehicular Technology, 2023, 72(1): 1240–1253. doi: 10.1109/TVT.2022.3206616. [3] ZHANG Shengyu and YEUNG K L. Scalable routing in low-earth orbit satellite constellations: Architecture and algorithms[J]. Computer Communications, 2022, 188: 26–38. doi: 10.1016/j.comcom.2022.02.015. [4] ELBEHIRY E A, FARES A, ELHALAWANY B M, et al. Inter-mesh routing algorithms in LEO satellite constellations networks[J]. Computing, 2025, 107(2): 57. doi: 10.1007/s00607-024-01409-4. [5] HUANG Yunxue, FENG Bohao, TIAN A, et al. An efficient differentiated routing scheme for MEO/LEO-based multi-layer satellite networks[J]. IEEE Transactions on Network Science and Engineering, 2024, 11(1): 1026–1041. doi: 10.1109/TNSE.2023.3313119. [6] MAO Bomin, ZHOU Xueming, LIU Jiajia, et al. On an intelligent hierarchical routing strategy for ultra-dense free space optical low earth orbit satellite networks[J]. IEEE Journal on Selected Areas in Communications, 2024, 42(5): 1219–1230. doi: 10.1109/JSAC.2024.3365880. [7] Wang Ruibo, KISHK M A, and ALOUINI M S. Reliability analysis of multi-hop routing in multi-tier LEO satellite networks[J]. IEEE Transactions on Wireless Communications, 2024, 23(3): 1959–1973. doi: 10.1109/TWC.2023.3293467. [8] 石怀峰, 周龙, 潘成胜, 等. 基于链路状态感知增强的战术通信网络智能路由算法[J]. 电子与信息学报, 2025, 47(7): 2127–2139. doi: 10.11999/JEIT241132.SHI Huaifeng, ZHOU Long, PAN Chengsheng, et al. Link state awareness enhanced intelligent routing algorithm for tactical communication networks[J]. Journal of Electronics & Information Technology, 2025, 47(7): 2127–2139. doi: 10.11999/JEIT241132. [9] 李学华, 廖海龙, 张贤, 等. 面向低轨卫星通信网络的联邦深度强化学习智能路由方法[J]. 电子与信息学报, 2025, 47(8): 2652–2664. doi: 10.11999/JEIT250072.LI Xuehua, LIAO Hailong, ZHANG Xian, et al. Federated deep reinforcement learning-based intelligent routing design for LEO satellite networks[J]. Journal of Electronics & Information Technology, 2025, 47(8): 2652–2664. doi: 10.11999/JEIT250072. [10] KUMAR P, BHUSHAN S, HALDER D, et al. fybrrLink: Efficient QoS-aware routing in SDN enabled future satellite networks[J]. IEEE Transactions on Network and Service Management, 2022, 19(3): 2107–2118. doi: 10.1109/TNSM.2021.3129876. [11] QI Hui, GUO Yingjun, HOU DingHui, et al. SDN-based dynamic multi-path routing strategy for satellite networks[J]. Future Generation Computer Systems, 2022, 133: 254–265. doi: 10.1016/j.future.2022.03.012. [12] GUO Jianming, YANG Lei, RINCÓN D, et al. Static placement and dynamic assignment of SDN controllers in LEO satellite networks[J]. IEEE Transactions on Network and Service Management, 2022, 19(4): 4975–4988. doi: 10.1109/TNSM.2022.3184989. [13] ROTH M M H, BRANDT H, and BISCHL H. Distributed SDN-based load-balanced routing for low earth orbit satellite constellation networks[C]. 2022 11th Advanced Satellite Multimedia Systems Conference and the 17th Signal Processing for Space Communications Workshop, Graz, Austria, 2022: 1–8. doi: 10.1109/ASMS/SPSC55670.2022.9914690. [14] HU Yun, GUO Binquan, YANG Chungang, et al. Time-deterministic networking for satellite-based internet-of-things services: Architecture, key technologies, and future directions[J]. IEEE Network, 2024, 38(4): 111–118. doi: 10.1109/MNET.2024.3380073. [15] 李红艳, 张焘, 张靖乾, 等. 基于时变图的天地一体化网络时间确定性路由算法与协议[J]. 通信学报, 2020, 41(10): 116–129. doi: 10.11959/j.issn.1000-436x.2020188.LI Hongyan, ZHANG Tao, ZHANG Jingqian, et al. Time deterministic routing algorithm and protocol based on time-varying graph over the space-ground integrated network[J]. Journal on Communications, 2020, 41(10): 116–129. doi: 10.11959/j.issn.1000-436x.2020188. [16] ZHENG Gao, WANG Ning, and TAFAZOLLI R R. SDN in space: A virtual data-plane addressing scheme for supporting LEO satellite and terrestrial networks integration[J]. IEEE/ACM Transactions on Networking, 2024, 32(2): 1781–1796. doi: 10.1109/TNET.2023.3330672. [17] LIANG Jintao, CHAUDHRY A U, CHINNECK J W, et al. Latency versus transmission power trade-off in free-space optical (FSO) satellite networks with multiple inter-continental connections[J]. IEEE Open Journal of the Communications Society, 2023, 4: 3014–3029. doi: 10.1109/OJCOMS.2023.3325203. [18] TAN Haichao and ZHU Lidong. A novel routing algorithm based on virtual topology snapshot in LEO satellite networks[C]. 2014 IEEE 17th International Conference on Computational Science and Engineering, Chengdu, China. 2014: 357–361. doi: 10.1109/CSE.2014.93. [19] XU Xin, ZHANG Senbai, and LIU Aijun. Topology dynamic of mega-constellation networks[J]. IEEE Internet of Things Journal, 2025, 12(13): 22975–22988. doi: 10.1109/JIOT.2025.3550920. [20] JUTTNER A, SZVIATOVSKI B, MÉCS I, et al. Lagrange relaxation based method for the QoS routing problem[C]. Proceedings IEEE INFOCOM 2001. Conference on Computer Communications. Twentieth Annual Joint Conference of the IEEE Computer and Communications Society, Anchorage, USA, 2001: 859–868. doi: 10.1109/INFCOM.2001.916277. [21] QI Xiaoxin, ZHANG Bing, and QIU Zhiliang. A distributed survivable routing algorithm for mega-constellations with inclined orbits[J]. IEEE Access, 2020, 8: 219199–219213. doi: 10.1109/ACCESS.2020.3041346. [22] HAN Zhenzhen, XU Chuan, ZHAO Guofeng, et al. Time-varying topology model for dynamic routing in LEO satellite constellation networks[J]. IEEE Transactions on Vehicular Technology, 2023, 72(3): 3440–3454. doi: 10.1109/TVT.2022.3217952. [23] CHEN Quan, YANG Lei, ZHAO Yong, et al. Shortest path in LEO satellite constellation networks: An explicit analytic approach[J]. IEEE Journal on Selected Areas in Communications, 2024, 42(5): 1175–1187. doi: 10.1109/JSAC.2024.3365873. [24] KASSING S, BHATTACHERJEE D, ÁGUAS A B, et al. Exploring the "Internet from space" with Hypatia[C]. Proceedings of the ACM Internet Measurement Conference, 2020: 214–229. doi: 10.1145/3419394.3423635. (查阅网上资料,未找到出版地信息,请补充). -





 下载:
下载:


 下载:
下载:
