Convolutional Mixed Multi-Attention Encoder-Decoder Network for Radar Signal Sorting
-
摘要: 雷达信号分选是电磁环境感知领域中的关键技术之一。随着雷达辐射源调制样式、工作模式和协同方式日益复杂,对雷达辐射源的侦收过程中,虚假脉冲、脉冲丢失和参数测量误差等问题日益突出,常规信号分选方法性能严重下降。针对上述问题,该文提出一种卷积混合多注意力的编解码网络,其中编码器与解码器均基于双分支扩张瓶颈模块构建,通过并行膨胀卷积路径捕获多尺度时序模式,逐步扩大感受野以融合上下文信息;在编解码器间嵌入局部注意力模块,用于建模脉冲序列的时序依赖关系并增强全局表征能力;同时在跳跃连接中引入特征选择模块,自适应地筛选多阶段特征图中的关键信息,最终通过分类器实现逐脉冲的雷达信号分类,进而实现分选。仿真实验表明,与主流基线方法相比,在脉冲丢失和虚假脉冲概率高且存在脉冲到达时间估计误差等复杂条件下,所提出方法具有更好的信号分选性能。Abstract:
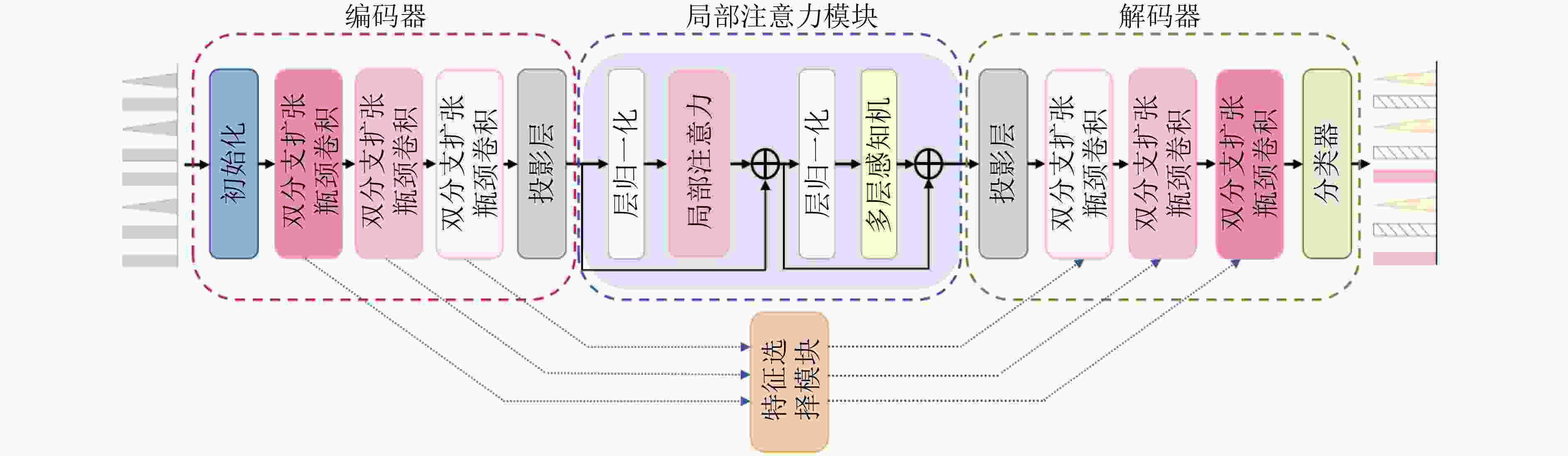
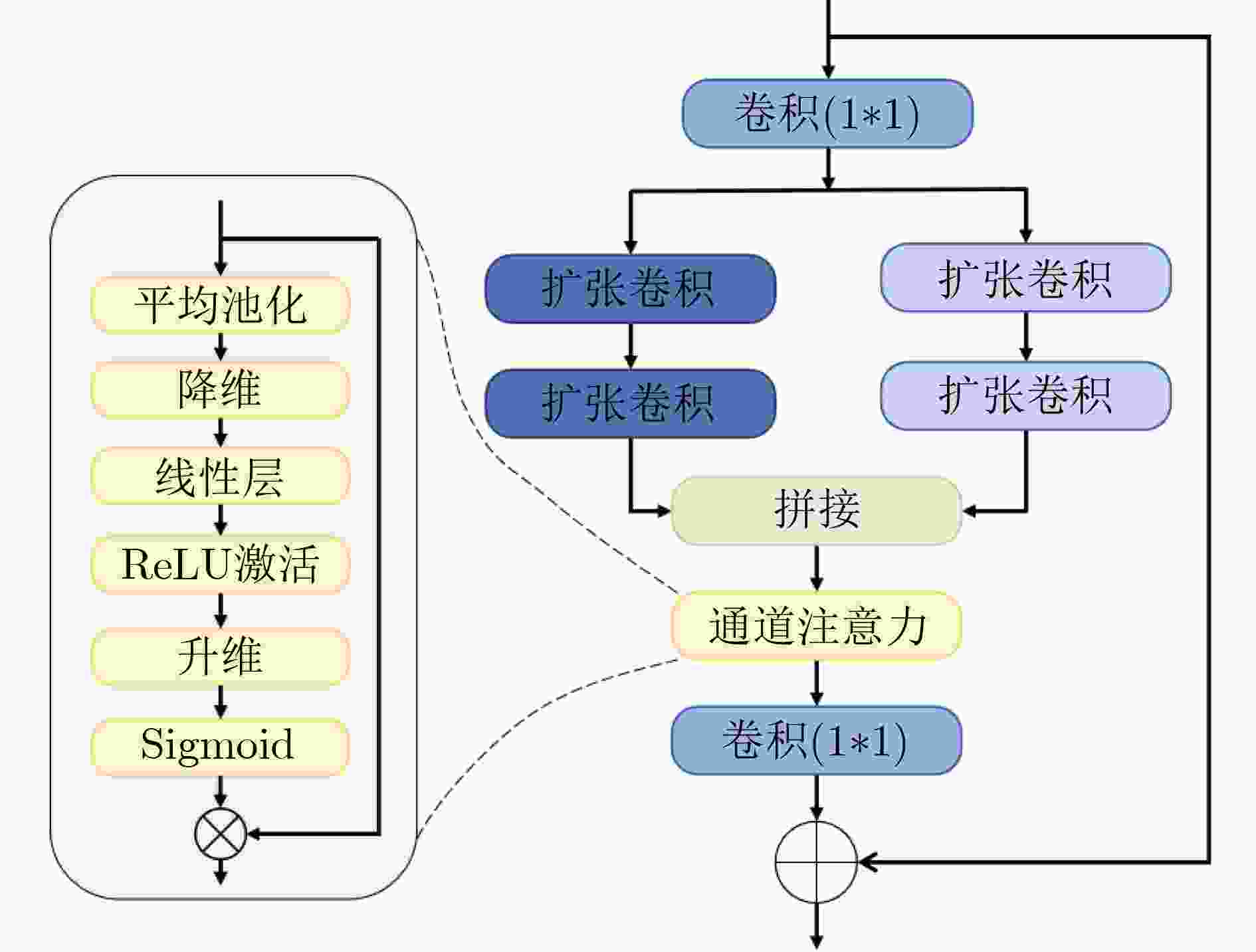
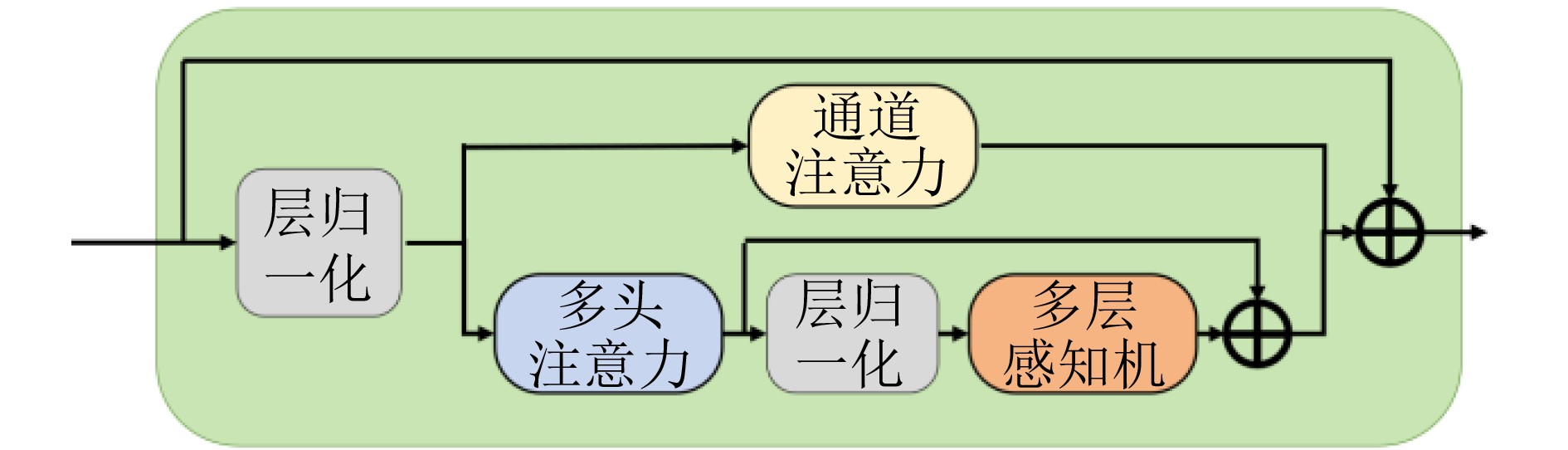
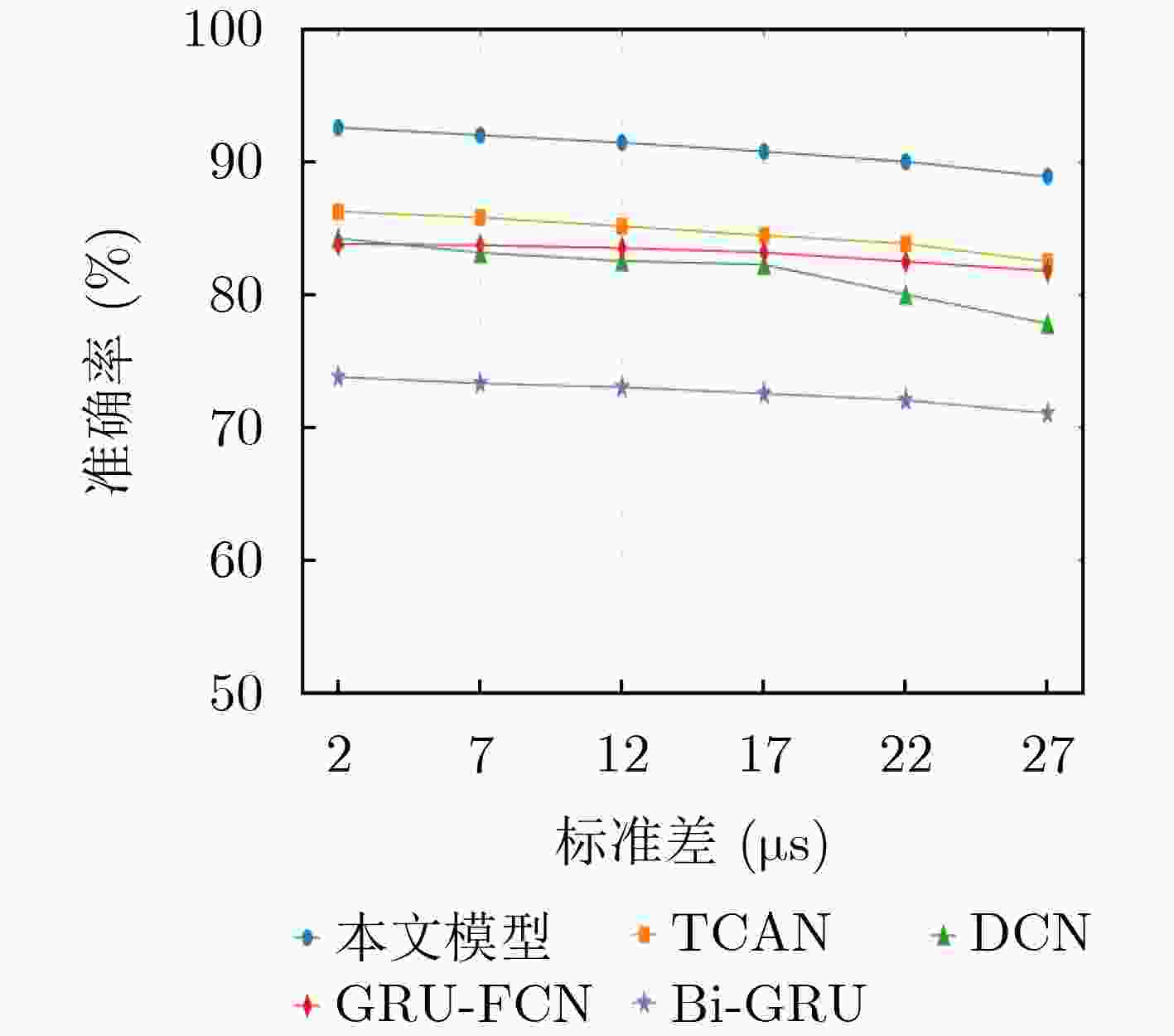
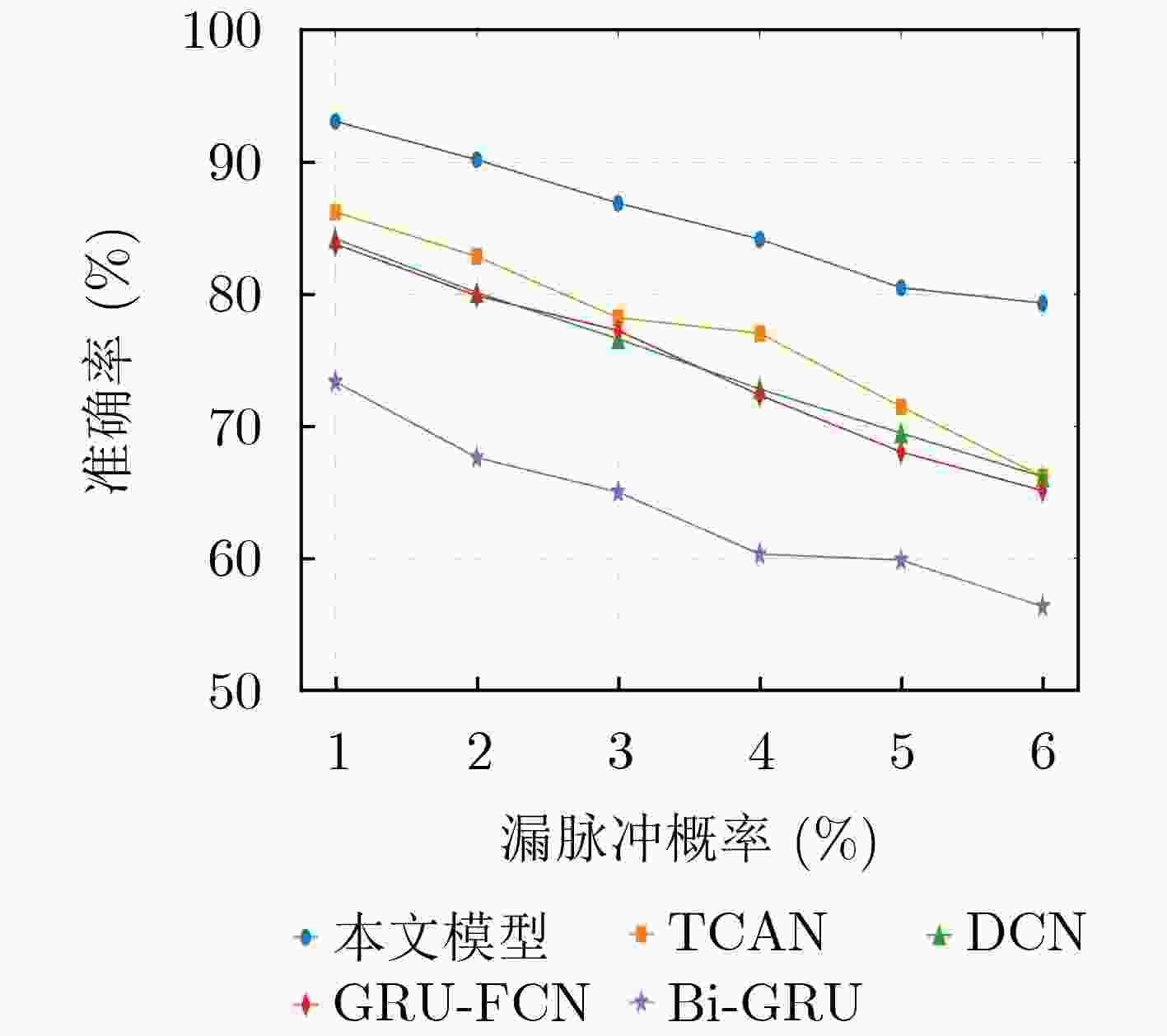
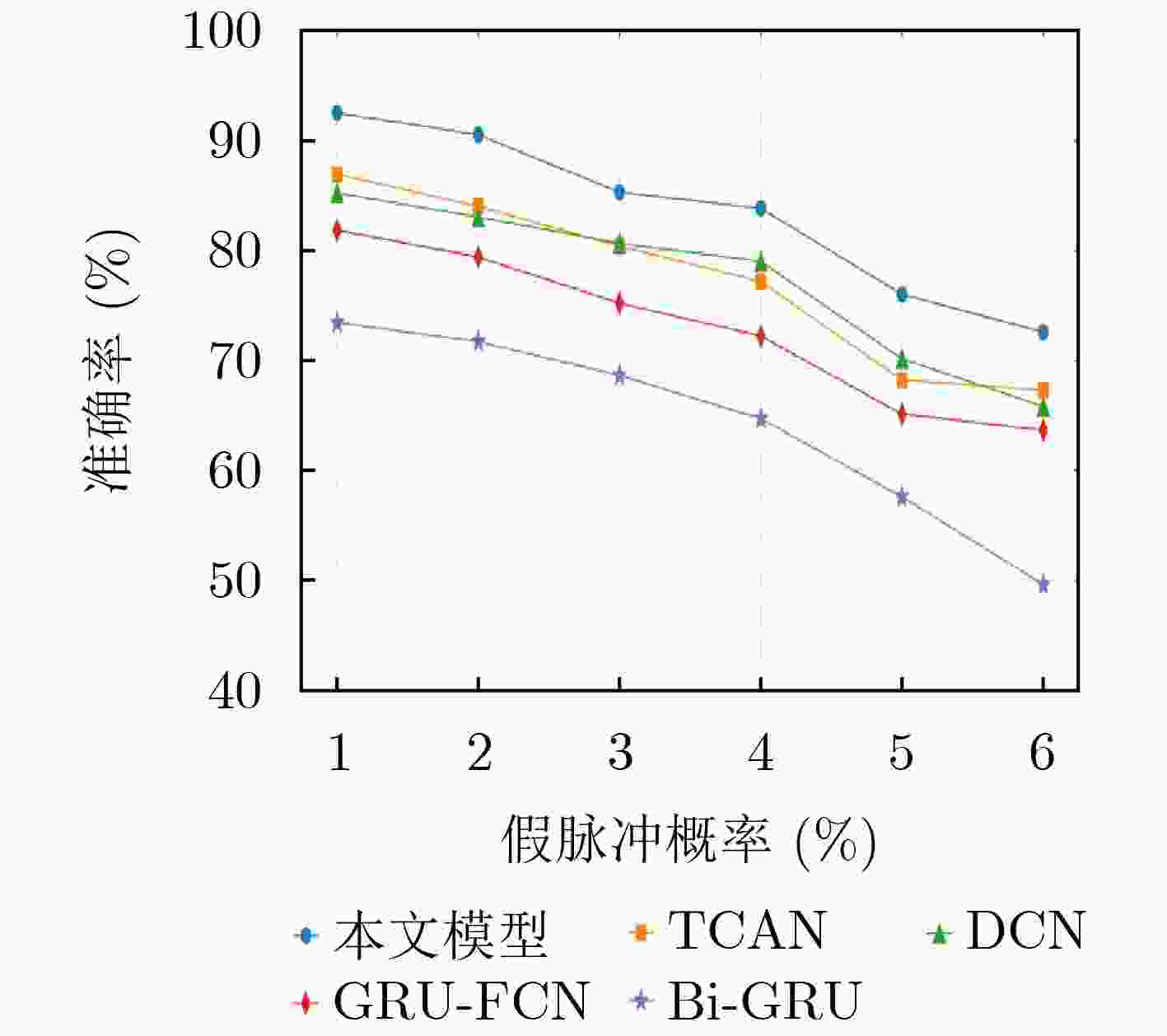
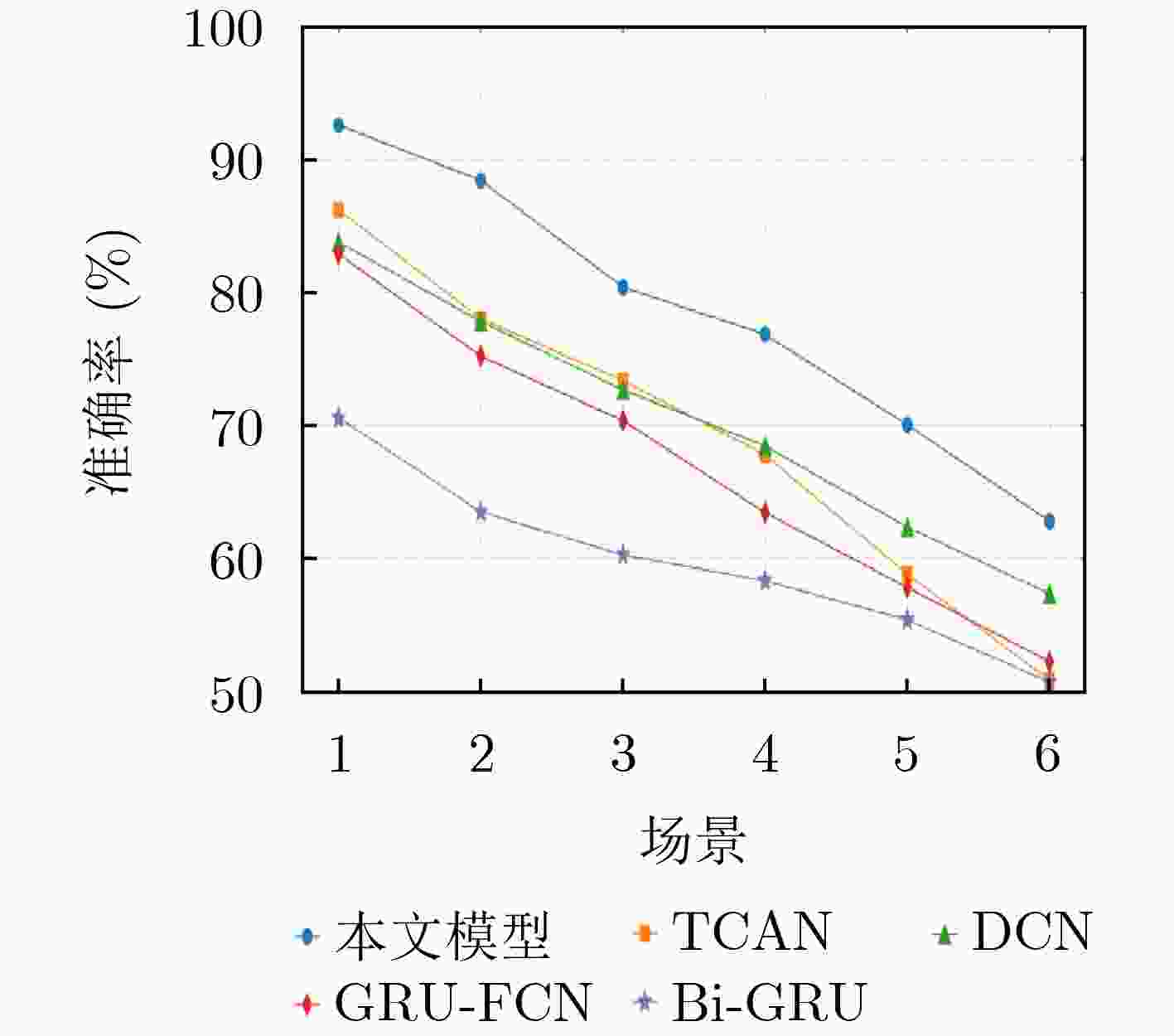
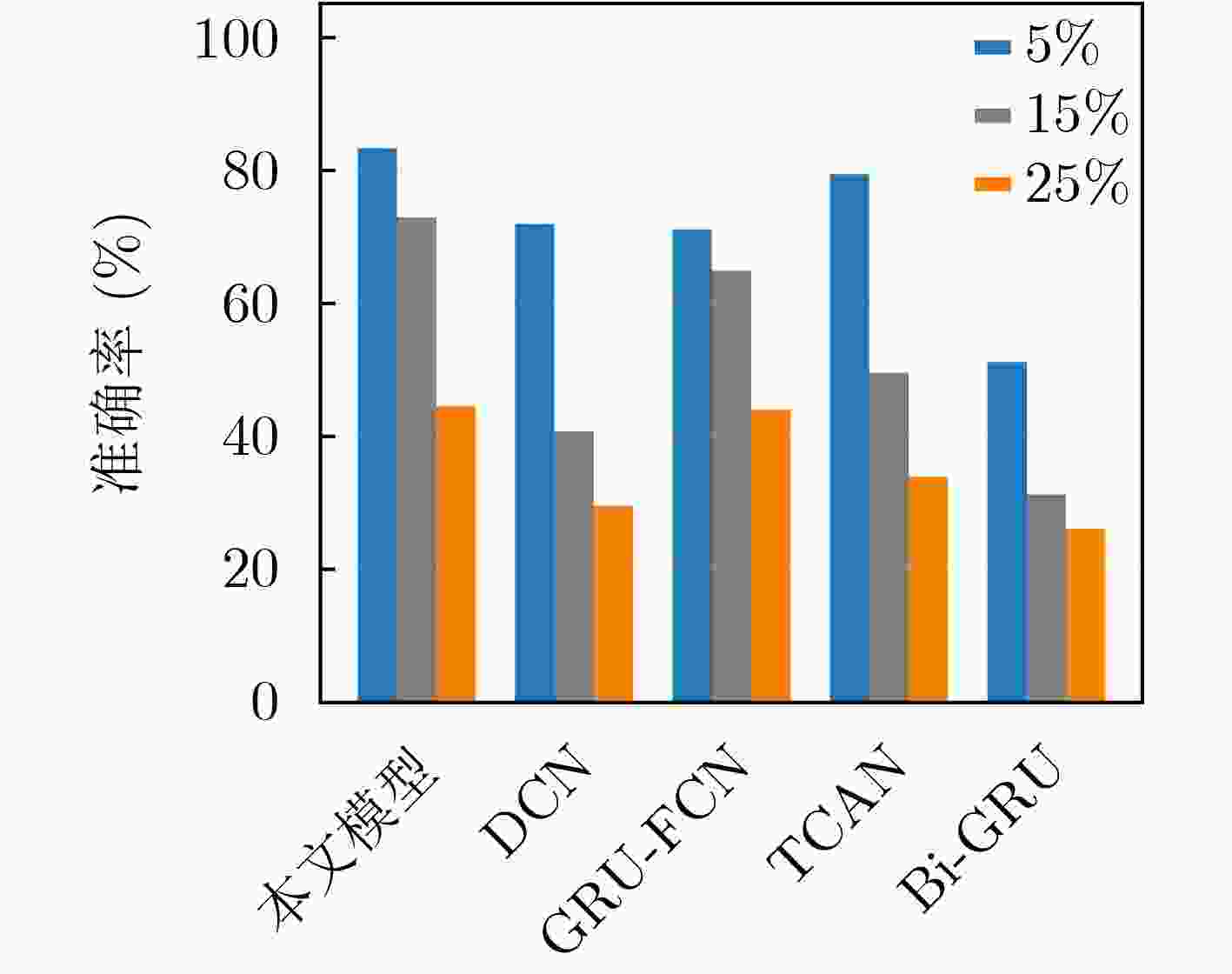
Objective Radar signal sorting is a fundamental technology for electromagnetic environment awareness and electronic warfare systems. The objective of this study is to develop an effective radar signal sorting method that accurately separates intercepted pulse sequences and assigns them to different radiation sources in complex electromagnetic environments. With the increasing complexity of modern radar systems, intercepted pulse sequences are severely affected by pulse overlap, pulse loss, false pulses, and pulse arrival time measurement errors, which substantially reduce the performance of conventional sorting approaches. Therefore, a robust signal sorting framework that maintains high accuracy under non-ideal conditions is required. Methods Radar signal sorting in complex electromagnetic environments is formulated as a pulse-level time-series semantic segmentation problem, where each pulse is treated as the minimum processing unit and classified in an end-to-end manner. Under this formulation, sorting is achieved through unified sequence modeling and label prediction without explicit pulse subsequence extraction or iterative stripping procedures, which reduces error accumulation. To address this task, a convolutional mixed multi-attention encoder-decoder network is proposed ( Fig. 1 ). The network consists of an encoder-decoder backbone, a local attention module, and a feature selection module. The encoder-decoder backbone adopts a symmetric structure with progressive downsampling and upsampling to aggregate contextual information while restoring pulse-level temporal resolution. Its core component is a dual-branch dilated bottleneck module (Fig. 2 ), in which a 1$* $1 temporal convolution is applied for channel projection. Two parallel dilated convolution branches with different dilation rates are then employed to construct multi-scale receptive fields, which enable simultaneous modeling of short-term local variations and long-term modulation patterns across multiple pulses and ensure robust temporal representation under pulse time shifts and missing pulses. To enhance long-range dependency modeling beyond convolutional operations, a local Transformer module is inserted between the encoder and the decoder. By applying local self-attention to temporally downsampled feature maps, temporal dependencies among pulses are captured with reduced computational complexity, whereas the influence of false and missing pulses is suppressed during feature aggregation. In addition, a feature selection module is integrated into skip connections to reduce feature redundancy and interference (Fig. 3 ). Through hybrid attention across temporal and channel dimensions, multi-level features are adaptively filtered and fused to emphasize discriminative information for radiation source identification. During training, focal loss is applied to alleviate class imbalance and improve the discrimination of difficult and boundary pulses.Results and Discussions Experimental results demonstrate that the proposed network achieves pulse-level fine-grained classification for radar signal sorting and outperforms mainstream baseline methods across various complex scenarios. Compared with existing approaches, an average sorting accuracy improvement of more than 6% is obtained under moderate interference conditions. In MultiFunctional Radar (MFR) overlapping scenarios, recall rates of 88.30%, 85.48%, 86.89%, and 86.48% are achieved for four different MFRs, respectively, with an overall average accuracy of 86.82%. For different pulse repetition interval modulation types, recall rates exceed 90% for fixed patterns and remain above 85% for jittered, staggered, and group-varying modes. In staggered and group-varying cases, performance improvements exceeding 3.5% relative to baseline methods are observed. Generalization experiments indicate that high accuracy is maintained under parameter distribution shifts of 5% and 15%, which demonstrates strong robustness to distribution perturbations ( Fig. 8 ). Ablation studies confirm the effectiveness of each proposed module in improving overall performance (Table 7 ).Conclusions A convolutional mixed multi-attention encoder-decoder network is proposed for radar signal sorting in complex electromagnetic environments. By modeling radar signal sorting as a pulse-level time-series semantic segmentation task and integrating multi-scale dilated convolutions, local attention modeling, and adaptive feature selection, high sorting accuracy, robustness, and generalization capability are achieved under severe interference conditions. The experimental results indicate that the proposed approach provides an effective and practical solution for radar signal sorting in complex electromagnetic environments. -
表 1 雷达参数设置
雷达 RF(GHz) PW(μs) PRI(μs) PRI调制方式 1 8.1~8.5 20~40 540 固定 2 8.15~8.3 30~45 370, J=0.25 抖动 3 8.1~8.45 15~40 110/280/ 800 参差 4 8.25~8.6 25~45 400·20, 600·15, 900·10 组变 表 2 MFR参数设置
雷达 RF(GHz) PW(μs) PRI(μs) PRI调制方式 1 8.15~8.4 15~45 240 固定 8.2~8.45 20~50 310,J=0.1 抖动 8.25~8.5 25~40 370/410/260 参差 2 8.1~8.5 20~40 480,J=0.1 抖动 8.2~8.45 30~50 190/240/380 参差 8.15~8.4 25~45 290·20,330·14,210·10 组变 3 8.2~8.4 10~25 430,340 参差 8.45~8.8 15~40 230·10,330·8,180·24,280·12 组变 8.3~8.55 20~40 320 固定 4 8.1~8.45 25~45 410·15,350·20 组变 8.2~8.5 30~50 390 固定 8.15~8.6 20~40 150,J=0.2 抖动 注:A·B表示脉冲序列参数,A代表PRI值,B代表该PRI的脉冲组长度 表 3 仿真实验结果(%)
类别 本文模型 TCAN DCN GRU-FCN Bi-GRU 总体准确率 92.58 86.24 84.22 83.81 73.38 雷达1 90.72 88.03 83.80 77.69 50.73 雷达2 91.65 80.92 85.66 85.81 76.40 雷达3 96.98 96.91 97.32 96.42 99.81 雷达4 89.72 77.08 63.28 69.21 55.32 表 4 MFR仿真实验结果(%)
类别 本文模型 TCAN DCN GRU-FCN Bi-GRU 总体准确率 86.82 83.52 82.32 76.72 68.44 雷达1 88.30 83.78 84.16 82.99 75.01 雷达2 85.48 80.64 78.27 72.71 67.48 雷达3 86.89 82.54 82.59 72.86 60.74 雷达4 86.48 87.04 84.03 77.95 70.36 表 5 各调制模式对比(%)
类别 本文模型 TCAN DCN GRU-FCN Bi-GRU 固定 90.47 87.77 86.33 79.56 78.67 抖动 85.11 85.22 82.40 77.22 72.37 参差 88.68 81.62 84.51 79.48 66.79 组变 85.46 81.90 78.37 72.79 57.78 表 6 模型计算开销对比
算法模型 本文模型 TCAN DCN GRU-FCN 参数量 401.68 k 329.50 k 158.17 k 38.15 k FLOPs 103.88 M 165.40 M 80.50 M 20.02 M 存储空间 1.53 MB 1.26 MB 0.60 MB 0.15 MB 表 7 消融实验结果(%)
模型 场景1 场景2 场景3 Baseline 81.4 76.2 72.0 Baseline+A 86.1 82.6 75.9 Baseline+A+B 88.2 84.3 76.2 Baseline+A+B+C 92.6 87.4 80.4 -
[1] WANG Shiqiang, HU Guoping, ZHANG Qiliang, et al. The background and significance of radar signal sorting research in modern warfare[J]. Procedia Computer Science, 2019, 154: 519–523. doi: 10.1016/j.procs.2019.06.080. [2] HAIGH K and ANDRUSENKO J. Cognitive Electronic Warfare: An Artificial Intelligence Approach[M]. Norwood: Artech House, 2021: 239. [3] LANG Ping, FU Xiongjun, DONG Jian, et al. A novel radar signals sorting method via residual graph convolutional network[J]. IEEE Signal Processing Letters, 2023, 30: 753–757. doi: 10.1109/LSP.2023.3287404. [4] WAN Liangtian, LIU Rong, SUN Lu, et al. UAV Swarm based radar signal sorting via multi-source data fusion: A deep transfer learning framework[J]. Information Fusion, 2022, 78: 90–101. doi: 10.1016/j.inffus.2021.09.007. [5] ZHOU Zixiang, FU Xiongjun, DONG Jian, et al. Radar signal sorting with multiple self-attention coupling mechanism based transformer network[J]. IEEE Signal Processing Letters, 2024, 31: 1765–1769. doi: 10.1109/LSP.2024.3421948. [6] CAO Sheng, WANG Shucheng, and ZHANG Yan. Density-based fuzzy C-means multi-center re-clustering radar signal sorting algorithm[C].17th IEEE International Conference on Machine Learning and Applications, Orlando, USA, 2018: 891–896. doi: 10.1109/ICMLA.2018.00144. [7] SU Yuhang, CHEN Zhao, GONG Linfu, et al. An improved adaptive radar signal sorting algorithm based on DBSCAN by a novel CVI[J]. IEEE Access, 2024, 12: 43139–43154. doi: 10.1109/ACCESS.2024.3361221. [8] AHMED M G S and TANG B. New FCM's validity index for sorting radar signal[C]. IEEE 17th International Conference on Computational Science and Engineering, Chengdu, China, 2014: 127–131. doi: 10.1109/CSE.2014.55. [9] ZHU Mengtao, LI Yunjie, and WANG Shafei. Model-based time series clustering and interpulse modulation parameter estimation of multifunction radar pulse sequences[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(6): 3673–3690. doi: 10.1109/TAES.2021.3082660. [10] WEI Xiuxi, PENG Maosong, HUANG Huajuan, et al. An overview on density peaks clustering[J]. Neurocomputing, 2023, 554: 126633. doi: 10.1016/j.neucom.2023.126633. [11] LIU Zhangmeng and YU P S. Classification, denoising, and deinterleaving of pulse streams with recurrent neural networks[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(4): 1624–1639. doi: 10.1109/TAES.2018.2874139. [12] NOTARO P, PASCHALI M, HOPKE C, et al. Radar emitter classification with attribute-specific recurrent neural networks[J/OL]. arXiv preprint arXiv: 1911.07683, 2019. doi: 10.48550/arXiv.1911.07683. [13] ZHANG Jiaxiang, WANG Bo, HAN Xinrui, et al. A multi-radar emitter sorting and recognition method based on hierarchical clustering and TFCN[J]. Digital Signal Processing, 2025, 160: 105005. doi: 10.1016/j.dsp.2025.105005. [14] WANG Haojian, TAO Zhenji, HE Jin, et al. Deinterleaving of intercepted radar pulse streams via temporal convolutional attention network[J]. IEEE Transactions on Aerospace and Electronic Systems, 2025, 61(4): 9327–9343. doi: 10.1109/TAES.2025.3555244. [15] AL-MALAHI A, FARHAN A, FENG Hancong, et al. An intelligent radar signal classification and deinterleaving method with unified residual recurrent neural network[J]. IET Radar, Sonar & Navigation, 2023, 17(8): 1259–1276. doi: 10.1049/rsn2.12417. [16] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. The IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 770–778. doi: 10.1109/CVPR.2016.90. [17] WANG Qilong, WU Banggu, ZHU Pengfei, et al. ECA-Net: Efficient channel attention for deep convolutional neural networks[C]. The IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, USA, 2020: 11531–11539. doi: 10.1109/CVPR42600.2020.01155. [18] HU Jie, SHEN Li, and SUN Gang. Squeeze-and-excitation networks[C]. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA, 2018: 7132–7141. doi: 10.1109/CVPR.2018.00745. [19] LIN T Y, GOYAL P, GIRSHICK R, et al. Focal loss for dense object detection[C]. IEEE International Conference on Computer Vision, Venice, Italy, 2017: 2999–3007. doi: 10.1109/ICCV.2017.324. [20] ELSAYED N, MAIDA A S, and BAYOUMI M. Deep gated recurrent and convolutional network hybrid model for univariate time series classification[J/OL]. arXiv preprint arXiv: 1812.07683, 2018. doi: 10.48550/arXiv.1812.07683. [21] CHEN Hongyu, FENG Kangan, KONG Yukai, et al. Multi-function radar work mode recognition based on encoder-decoder model[C]. IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 2022: 1189–1192. doi: 10.1109/IGARSS46834.2022.9884556. -





 下载:
下载:


 下载:
下载:
