改进的全轮HALFLOOP-48相关调柄攻击

孙晓萌; 张文英; 苑兆忠

doi:10.11999/JEIT251014

改进的全轮HALFLOOP-48相关调柄攻击

doi: 10.11999/JEIT251014 cstr: 32379.14.JEIT251014

山东师范大学信息科学与工程学院济南 250014

基金项目: 国家自然科学基金(62272282)

详细信息

作者简介:
孙晓萌：女，博士生，研究方向为分组密码算法的安全性分析

张文英：女，教授，博士生导师，研究方向为哈希函数，分组密码算法设计与分析，口令安全

苑兆忠：男，副教授，研究方向为信息安全

通讯作者:
张文英　zhangwenying@sdnu.edu.cn

中图分类号: TN918; TP309
计量
- 文章访问数: 13
- HTML全文浏览量: 6
- PDF下载量: 1
- 被引次数: 0
出版历程
- 修回日期: 2026-01-12
- 录用日期: 2026-01-12
- 网络出版日期: 2026-01-27

Improved Related-Tweak Attack on Full-Round HALFLOOP-48

School of Information Science and Engineering, Shandong Normal University, Jinan 250358, China

Funds: The National Natural Science Foundation of China (62272282)

摘要

摘要: HALFLOOP是一类基于调柄机制、结构类似AES的轻量级分组密码，用于保护第四代高频无线电系统中的自动链路消息。由于其行移位与列混合操作具有使差分快速扩散的特点，寻找具有实际可行性的长轮数、高概率的差分区分器，并实现对完整轮HALFLOOP-48的有效攻击仍是亟待解决的关键问题。为此，该文提出了一个新的截断差分三明治区分器框架，并基于布尔可满足性(Boolean Satisfiability Problem，SAT)方法实现自动化搜索最优差分区分器。该框架将密码分为三个子密码层， $ {\mathrm{E}}_{0} $和$ {\mathrm{E}}_{1} $使用字节级模型，$ {\mathrm{E}}_{\mathrm{m}} $使用比特级模型。为突破大型S盒差分特征建模的瓶颈，该文提出了基于仿射子空间的降维方法，将高维向量的差分特征分解为两个低维子向量，显著降低了SAT的约束规模。其次，为提高区分器概率，该文将$ {\mathrm{E}}_{0} $与$ {\mathrm{E}}_{1} $的依赖关系系统地分为三层，逐一计算每层概率并相乘，得到了概率高达$ {2}^{-43.2} $的8轮HALFLOOP-48截断差分三明治区分器，且给出了满足该差分路径的明文对实例。最终，利用该实际差分路径，对完整轮数的HALFLOOP-48算法发起密钥恢复攻击。与已有结果相比，该文结果在时间复杂度上减少了$ {2}^{25.4} $，在内存复杂度上减少了$ {2}^{10} $。结果说明HALFLOOP算法无法抵抗相关调柄下的三明治攻击。
- 轻量级分组密码 /
- 相关调柄攻击 /
- 截断三明治区分器 /
- 布尔可满足性问题 /
- 密钥恢复攻击
Abstract: Objective HALFLOOP, a family of tweakable AES-like lightweight block cipher used to encrypt automatic link establishment messages in the fourth-generation high frequency radio systems. Since the RotateRows and MixColumns operations of HALFLOOP diffuse differences rapidly, it is difficult to build long differentials with higher probability in general, further to attack full cipher. This study aims to attack full HALFLOOP-48 and evaluates the cipher’s resistance to sandwich attacks in setting of related tweak, a critical cryptanalysis method for lightweight ciphers. Methods To attack full HALFLOOP-48, the paper proposes a new truncated sandwich distinguisher framework, which decomposes the cipher into three sub-ciphers:$ {\mathrm{E}}_{0} $, $ {\mathrm{E}}_{1} $ and $ {\mathrm{E}}_{\mathrm{m}} $ to connect with $ {\mathrm{E}}_{0} $, $ {\mathrm{E}}_{1} $. A model is built by using an automatic search method -- Boolean Satisfiability Problem (SAT) for three parts respectively: byte-wise models for $ {\mathrm{E}}_{0} $, $ {\mathrm{E}}_{1} $ together with a bit-wise model for $ {\mathrm{E}}_{\mathrm{m}} $. In $ {\mathrm{E}}_{\mathrm{m}} $, we propose a novel method to effectively model large S-boxes using SAT -- the Affine Subspace Dimensional Reduction method (ADR). The ADR method can turn the problem of modeling a high-dimensional set into two sub-problems for a low-dimensional set. The ADR method makes sure the differentials searched by SAT exist and the accurate probability with reducing the size of Conjunctive Normal Form(CNF) clauses. It also makes the SAT method to search for the longer differentials with large S-boxes effectively. To improve the accuracy of the probability in $ {\mathrm{E}}_{\mathrm{m}} $, we comprehensively evaluate the dependencies between$ {\mathrm{E}}_{0} $ and $ {\mathrm{E}}_{1} $ by considering three layers with multiplying their probability of each layer. The two key-recovery attacks -- a sandwich attack and a rectangle-like sandwich attack can be launched on the sandwich distinguisher in related-tweak scenario. Results and Discussions The SAT-based model reveals a critical vulnerability of the HALFLOOP-48 cipher. We find the first 8 round practical sandwich distinguisher with probability $ {2}^{-43.415} $. Then, an optimal truncated sandwich distinguisher for 8-round HALFLOOP-48 with probability$ {2}^{-43.2} $ is established via the clustering effect of the founded differentials. Compared with the previous results, our distinguisher is practical with extending two more rounds. Employing the 8-round distinguisher, we mount two key-recovery attacks -- a sandwich attack and a rectangle-like sandwich attack on full-round HALFLOOP-48 in related-tweak scenario. The proposed sandwich attack has a data complexity of $ {2}^{32.8} $, time complexity $ {2}^{92.2} $ and memory complexity $ {2}^{42.8} $. For our rectangle-like sandwich attack, the data complexity is $ {2}^{16.2} $, with time complexity $ {2}^{99.2} $ and memory complexity $ {2}^{26.2} $. Compared with the previous results, the key recovery attacks decrease time complexity by $ {2}^{25.4} $and decrease memory complexity by $ {2}^{10} $. Conclusions To overcome the rapidly difference diffusion of HALFLOOP, we derive a new perspective on sandwich attacks with truncated differentials by combining byte-wise and bit-wise models. The models for $ {\mathrm{E}}_{0} $ and $ {\mathrm{E}}_{1} $ are based on bytes-wise and extend these two parts in forward and backward directions into the middle part $ {\mathrm{E}}_{\mathrm{m}} $, which is based on bit-wise. To efficiently model the 8-bit S-box in the layer $ {\mathrm{E}}_{\mathrm{m}} $, we propose a new approach based on affine subspace dimension reduction. This model ensures that the two truncated differential trails are compatible and covers as many rounds as possible with high probability. It allows us to introduce a new 8-round truncated boomerang distinguisher that performs better than earlier distinguishers of HALFLOOP-48. Based on the 8-round truncated boomerang distinguisher, we launch the key-recovery attack successfully with probability 63%. The results show that (1) The proposed ADR method provides a new perspective to efficiently apply large S-box to lightweight ciphers. (2) The constructure of the truncated boomerang distinguisher could be applied to other AES-like lightweight block cipher. (3) HALFLOOP-48 has not enough security margin to be applied on the U.S. military standard.
- Lightweight block cipher /
- Related-tweak attack /
- Truncated sandwich distinguisher /
- Boolean Satisfiability Problem (SAT) /
- Key recovery attack

HTML全文

图 1 HALFLOOP-48的轮函数

下载: 全尺寸图片幻灯片

图 2 截断三明治区分器

下载: 全尺寸图片幻灯片

图 3 活跃字节$ {S}_{2,2} $在RR下产生的两条差分特征

下载: 全尺寸图片幻灯片

图 4 $ {\mathrm{E}}_{\mathrm{m}} $的3轮最优截断差分

下载: 全尺寸图片幻灯片

图 5 对完整轮数HALFLOOP-48算法的密钥恢复攻击

下载: 全尺寸图片幻灯片

表 1 HALFLOOP-48算法分析结果

攻击场景	攻击轮数	时间复杂度	数据复杂度	存储复杂度	文献
DS中间相遇攻击	$ 10 $	$ {2}^{122} $	$ 13 $	$ {2}^{57} $B	[3]
相关调柄攻击	$ 8 $	$ {2}^{92.71} $	$ {2}^{33.27} $	$ {2}^{36.385} $B	[4]
相关调柄三明治攻击	$ 10 $	$ {2}^{96.2} $	$ {2}^{32.8} $	$ {2}^{42.8} $B	第5节
相关调柄矩形攻击	$ 10 $	$ {2}^{99.2} $	$ {2}^{16.2} $	$ {2}^{26.2} $B	第5节

下载: 导出CSV

表 2 轮密钥差分特征

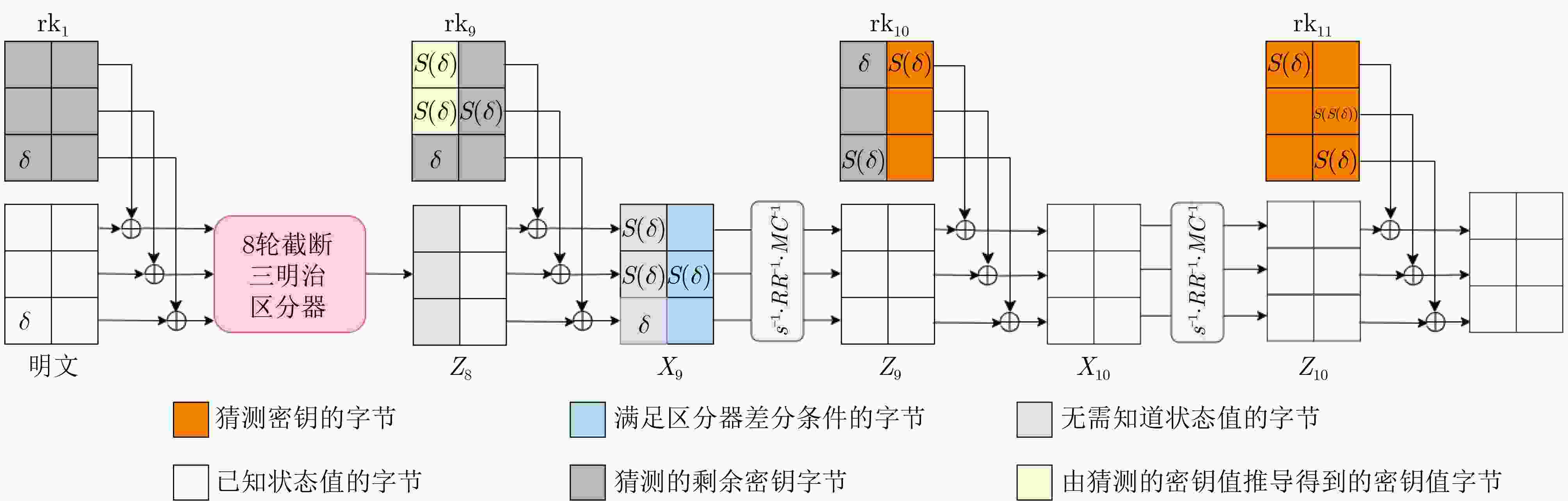
轮密钥	差分特征
$ \Delta {\text{rk}}_{1} $	$ {0}^{16}\parallel \delta \parallel {0}^{24} $
$ \Delta {\text{rk}}_{2} $	0
$ \Delta {\text{rk}}_{3} $	0
$ \Delta {\text{rk}}_{4} $	$ \delta \parallel {0}^{24}\parallel \delta \parallel {0}^{8} $
$ \Delta {\text{rk}}_{5} $	$ {0}^{16}\parallel \delta \parallel {0}^{24} $
$ \Delta {\text{rk}}_{6} $	$ \delta \parallel {0}^{16}\parallel S\left(\delta \right)\parallel \delta \parallel {0}^{8} $
$ \Delta {\text{rk}}_{7} $	$ {0}^{8}\parallel S\left(\delta \right){\parallel 0}^{24}\parallel S\left(\delta \right) $
$ \Delta {\text{rk}}_{8} $	$ \delta \parallel {0}^{16}\parallel S\left(\delta \right)\parallel {0}^{16} $
$ \Delta {\text{rk}}_{9} $	$ S\left(S\left(\delta \right)\right)\parallel S\left(\delta \right)\parallel \delta \parallel {0}^{8}\parallel \delta \parallel {0}^{8} $
$ \Delta {\text{rk}}_{10} $	$ \delta \parallel {0}^{8}\parallel S\left(\delta \right)\parallel S\left(\delta \right){\parallel 0}^{16} $
$ \Delta {\text{rk}}_{11} $	$ S(\delta )\parallel {0}^{24}\parallel S\left(\left(\delta \right)\right)\parallel S\left(\delta \right) $

下载: 导出CSV

表 3 HALFLOOP的8轮区分器

轮数	$ \Delta \text{rk} $	$ \Delta x $	$ \Delta y $	$ \Delta w $	$ r $	轮数	$ \nabla \text{rk} $	$ \nabla x $	$ \nabla y $	$ \nabla w $	r
上差分特征						下差分特征
$ {R}_{1} $	00 00 00 00 b0 00	00 00 00 00 b0 00	00 00 00 00 00 00	00 00 00 00 b0 00	$ 1 $	$ {R}_{5} $	00 00 00 00 b0 00	98 91 00 ca 6c 60	25 5b 00 17 33 ab	fc ee 00 3d 00 00	$ {2}^{-11.415}\dagger $
$ {R}_{2} $	00 00 00 00 00 00	00 00 00 00 00 00	00 00 00 00 00 00	00 00 00 00 00 00	$ 1 $	$ {R}_{6} $	b0 01 00 b0 00 00	4c 76 00 8d 00 00	4a 5b 00 3e 00 00	d9 57 db 27 00 00	$ {2}^{-18}\dagger $
$ {R}_{3} $	00 00 00 00 00 00	00 00 00 00 00 00	00 00 00 00 00 00	00 00 00 00 00 00	$ 1 $	$ {R}_{7} $	00 00 db 00 00 db	d9 57 00 27 00 db	56 38 00 af 00 da	b0 a0 00 00 00 00	$ {2}^{-5.415}\dagger $
$ {R}_{4} $	b0 00 00 b0 00 00	b0 00 00 b0 00 00	84 00 00 84 00 00	89 00 6c 00 b0 00	$ {\left({2}^{-2}\right)}^{2} $	$ {R}_{8} $	b0 a0 00 00 00 00	00 00 00 00 00 00	00 00 00 00 00 00	00 00 00 00 00 00	$ 1 $
$ {R}_{5} $	00 00 00 00 b0 00	89 00 6c 00 00 00	c4 00 33 00 00 00	b0 01 38 b0 a4 06	$ {2}^{-11.415}\dagger $	$ {R}_{9} $	c9 00 a0 b0 b0 00	c9 00 a0 b0 b0 00
$ {R}_{6} $	b0 01 00 b0 00 00	00 00 38 00 a4 06	00 00 64 00 2a 0c	a0 00 aa 00 30 00	$ {2}^{-18}\dagger $
$ {R}_{7} $	00 00 31 00 00 31	a0 00 9b 00 30 31	83 00 77 00 67 a4	4e 53 98 a4 1f f3	$ {2}^{-5.415}\dagger $

下载: 导出CSV

参考文献(19)

[1]	Department of Defense. MILSTD-188-141D Interoperability and performance standardsfor medium and high frequencyradio systems[S]. Washington: Department of Defense, 2017. (查阅网上资料, 未找到本条文献出版地, 请确认).
[2]	DANSARIE M, DERBEZ P, LEANDER G, et al. Breaking HALFLOOP-24[J]. IACR Transactions on Symmetric Cryptology, 2022, 2022(3): 217–238. doi: 10.46586/tosc.v2022.I3.217-238.
[3]	LEANDER G, RASOOLZADEH S, and STENNES L. Cryptanalysis of HALFLOOP block ciphers: Destroying HALFLOOP-24[J]. IACR Transactions on Symmetric Cryptology, 2023, 2023(4): 58–82. doi: 10.46586/tosc.v2023.I4.58-82.
[4]	LIN Yunxue and SUN Ling. Related-tweak and related-key differential attacks on HALFLOOP-48[C]. Proceedings of the 22nd International Conference on Applied Cryptography and Network Security, Abu Dhabi, United Arab Emirates, 2024: 355–377. doi: 10.1007/978-3-031-54776-8_14.
[5]	WAGNER D A. The boomerang attack[C]. Proceedings of the 6th International Workshop on Fast Software Encryption, Rome, Italy, 1999: 156–170. doi: 10.1007/3-540-48519-8_12.
[6]	MURPHY S. The return of the cryptographic boomerang[J]. IEEE Transactions on Information Theory, 2011, 57(4): 2517–2521. doi: 10.1109/TIT.2011.2111091.
[7]	DUNKELMAN O, KELLER N, and SHAMIR A. A practical-time related-key attack on the KASUMI cryptosystem used in GSM and 3G telephony[C]. Proceedings of the 30th Annual Cryptology Conference on Advances in Cryptology, Santa Barbara, USA, 2010: 393–410. doi: 10.1007/978-3-642-14623-7_21.
[8]	BIRYUKOV A and KHOVRATOVICH D. Related-key cryptanalysis of the full AES-192 and AES-256[C]. Proceedings of the 15th International Conference on the Theory and Application of Cryptology and Information Security, Tokyo, Japan, 2009: 1–18. doi: 10.1007/978-3-642-10366-7_1.
[9]	谭林, 曾新皓, 刘加美. AES-192的相关密钥飞去来器攻击和矩形攻击[J]. 密码学报(中英文), 2024, 11(5): 1018–1028. doi: 10.13868/j.cnki.jcr.000723. TAN Lin, ZENG Xinhao, and LIU Jiamei. Related-key boomerang and rectangle attacks on AES-192[J]. Journal of Cryptologic Research, 2024, 11(5): 1018–1028. doi: 10.13868/j.cnki.jcr.000723.
[10]	BOURA C and COGGIA D. Efficient MILP modelings for Sboxes and linear layers of SPN ciphers[J]. IACR Transactions on Symmetric Cryptology, 2020, 2020(3): 327–361. doi: 10.13154/tosc.v2020.i3.327-361.
[11]	ANKELE R and KÖLBL S. Mind the gap - a closer look at the security of block ciphers against differential cryptanalysis[C]. Proceedings of the 25th International Conference on Selected Areas in Cryptography, Calgary, Canada, 2018: 163–190. doi: 10.1007/978-3-030-10970-7_8.
[12]	MA Sudong, JIN Chenhui, SHI Zhen, et al. Correlation attacks on snow-v-like stream ciphers based on a heuristic MILP model[J]. IEEE Transactions on Information Theory, 2024, 70(6): 4478–4491. doi: 10.1109/TIT.2023.3326348.
[13]	DAEMEN J and RIJMEN V. The Design of Rijndael: AES - The Advanced Encryption Standard[M]. Berlin, Heidelberg: Springer, 2002. doi: 10.1007/978-3-662-04722-4. .
[14]	CID C, HUANG T, PEYRIN T, et al. Boomerang connectivity table: A new cryptanalysis tool[C]. Proceedings of the 37th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Tel Aviv, Israel, 2018: 683–714. doi: 10.1007/978-3-319-78375-8_22.
[15]	蒋梓龙, 金晨辉. 对TweAES的相关调柄多重不可能差分攻击[J]. 电子与信息学报, 2023, 45(1): 344–352. doi: 10.11999/JEIT211147. JIANG Zilong and JIN Chenhui. Related-tweak multiple impossible differential attack for TweAES[J]. Journal of Electronics & Information Technology, 2023, 45(1): 344–352. doi: 10.11999/JEIT211147.
[16]	张丽, 吴文玲, 张蕾, 等. 基于交换等价的缩减轮AES-128的密钥恢复攻击[J]. 计算机研究与发展, 2021, 58(10): 2213–2221. doi: 10.7544/issn1000-1239.2021.20210549. ZHANG Li, WU Wenling, ZHANG Lei, et al. Key-recovery attack on reduced-round AES-128 using the exchange-equivalence[J]. Journal of Computer Research and Development, 2021, 58(10): 2213–2221. doi: 10.7544/issn1000-1239.2021.20210549.
[17]	SONG Ling, ZHANG Nana, YANG Qianqian, et al. Optimizing rectangle attacks: A unified and generic framework for key recovery[C]. Proceedings of the 28th International Conference on the Theory and Application of Cryptology and Information Security, Taipei, China, 2022: 410–440. doi: 10.1007/978-3-031-22963-3_14.
[18]	BLONDEAU C, GÉRARD B, and TILLICH J P. Accurate estimates of the data complexity and success probability for various cryptanalyses[J]. Design Codes Cryptography, 2011, 59(1/3): 3–34. doi: 10.1007/S10623-010-9452-2.
[19]	严智广, 韦永壮, 叶涛. 全轮超轻量级分组密码PFP的相关密钥差分分析[J]. 电子与信息学报, 2025, 47(3): 729–738. doi: 10.11999/JEIT240782. YAN Zhiguang, WEI Yongzhuang, and YE Tao. Related-key differential cryptanalysis of full-round PFP ultra-lightweight block cipher[J]. Journal of Electronics & Information Technology, 2025, 47(3): 729–738. doi: 10.11999/JEIT240782.