DetDiffRS: 面向细节优化的遥感图像超分辨率扩散模型

宋淼; 陈志强; 王培松; 邢相薇; 黄立威; 程健

doi:10.11999/JEIT250995

DetDiffRS: 面向细节优化的遥感图像超分辨率扩散模型

doi: 10.11999/JEIT250995 cstr: 32379.14.JEIT250995

宋淼^{1, 2},
陈志强³,
王培松^{1, 2, ,},
邢相薇⁴,
黄立威⁴,
程健^{1, 2}

1.
中国科学院自动化研究所，北京，100190
2.
中国科学院大学，北京，100049
3.
东南大学，南京，210096
4.
北京市遥感信息研究所，北京，100192

基金项目: 国家自然科学基金(62572471, 62341130)

详细信息

作者简介:
宋淼：女，硕士生，研究方向为模型轻量化、扩散模型

陈志强：男，硕士生，研究方向为神经网络推理加速和领域特定架构

王培松：男，副研究员，研究方向为轻量化人工智能

邢相薇：男，副研究员，研究方向为遥感图像智能解译

黄立威：男，高级工程师，研究方向为卫星信息处理

程健：男，研究员，研究方向为轻量化人工智能

通讯作者:
王培松　peisong.wang@nlpr.ia.ac.cn

中图分类号: TN919.81
计量
- 文章访问数: 14
- HTML全文浏览量: 10
- PDF下载量: 2
- 被引次数: 0
出版历程
- 收稿日期: 2025-09-25
- 修回日期: 2025-11-22
- 录用日期: 2025-12-24
- 网络出版日期: 2025-12-31

DetDiffRS: A Detail-Enhanced Diffusion Model for Remote Sensing Image Super-Resolution

SONG Miao^{1, 2},
CHEN Zhiqiang³,
WANG Peisong^{1, 2
, ,},
XING Xiangwei⁴,
HUANG Liwei⁴,
CHENG Jian^{1, 2}

1.
Institute of Automation, Chinese Academy of Sciences, Beijing 100190, China
2.
University of Chinese Academy of Sciences, Beijing 100049, China
3.
Southeast University, Nanjing 210096, China
4.
Beijing Institute of Remote Sensing Information, Beijing 100192, China

Funds: The National Natural Science Foundation of China (62572471, 62341130)

摘要

摘要: 遥感图像超分辨率技术对精确解析地物、支持城市规划与环境监测等下游应用具有至关重要的价值。近期基于扩散模型的方法在自然图像超分辨率任务中展现了卓越的性能，其强大的生成能力使其能够恢复精细的纹理。然而，当直接应用于遥感领域时，模型会面临由遥感影像特有的数据高低频信息分布不均衡所带来的挑战。影像中大面积、纹理单一的低频区域在训练中占据主导地位，导致模型对承载着关键信息的稀疏高频细节学习不足，最终的重建结果往往呈现全局平滑、细节模糊的特征。因此，为解决这一问题，该文提出一种能够显著增强高频细节重建能力的遥感图像超分辨率扩散模型DetDiffRS。首先在数据输入端提出多尺度图块采样策略以应对低频区域在训练过程中占主导问题，该策略通过对多尺度图块进行加权采样，提升了富含高频信息图块的采样频率，从而引导模型更充分地学习这些关键细节。其次在优化端设计了一种复合感知损失函数，该损失函数在深度特征空间中约束高维感知损失，并且在傅里叶频域中对高频分量进行高频感知损失。这一设计从空间域和频率域两个维度增强了模型对高频细节的精确恢复能力。大量的实验结果表明，在AID、DOTA和DIOR等多个公开数据集上，DetDiffRS在客观量化指标(FID, PSNR, SSIM)与视觉真实感方面均超越了现有的先进方法，尤其在细节恢复的清晰度上优势显著。
- 遥感图像超分辨率 /
- 扩散概率模型 /
- 高频细节恢复
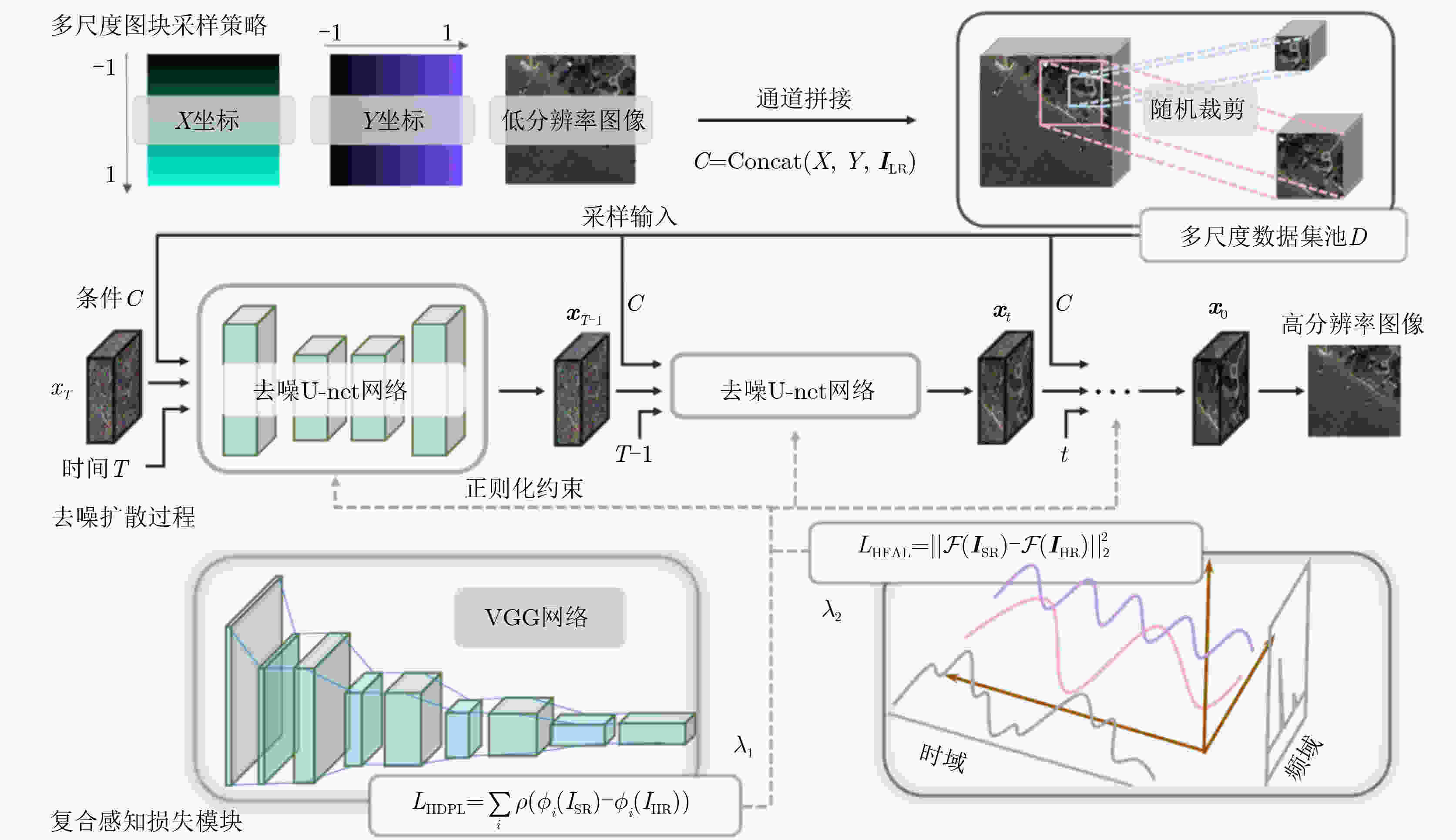
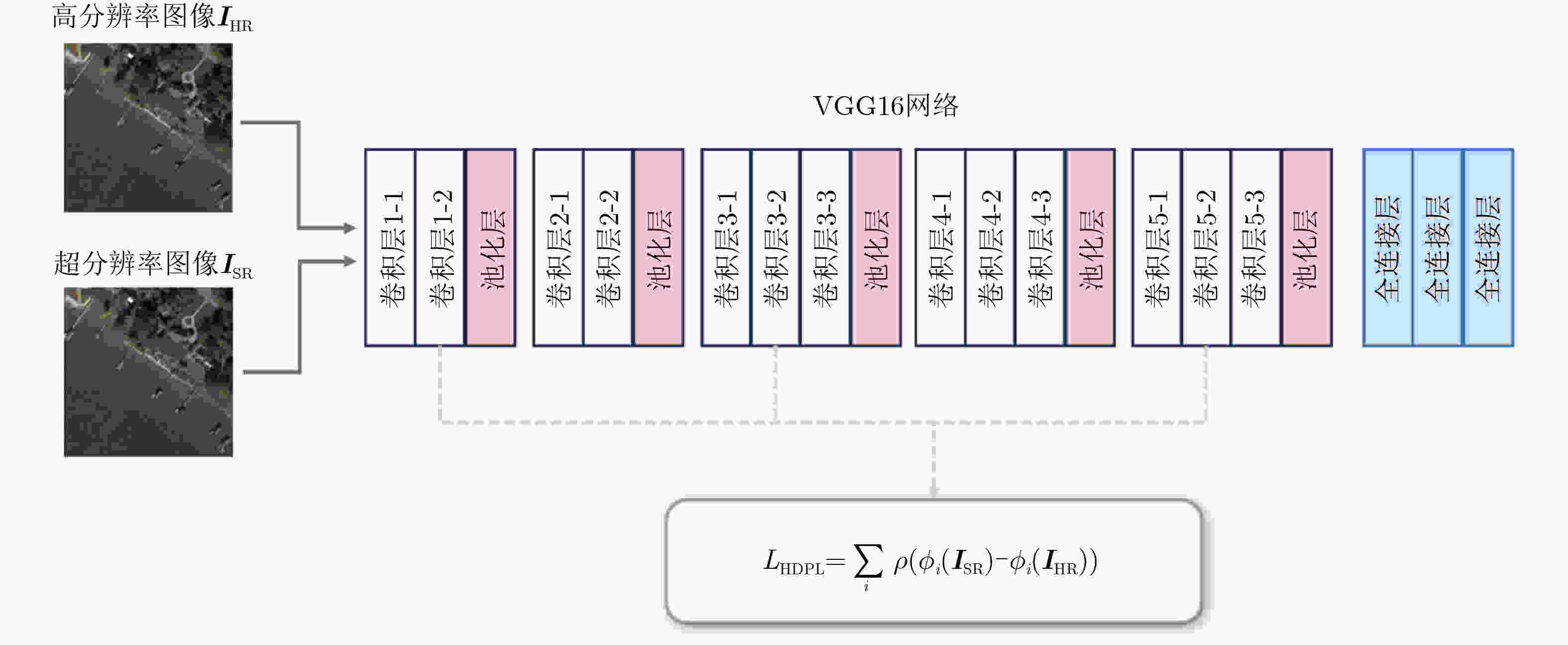
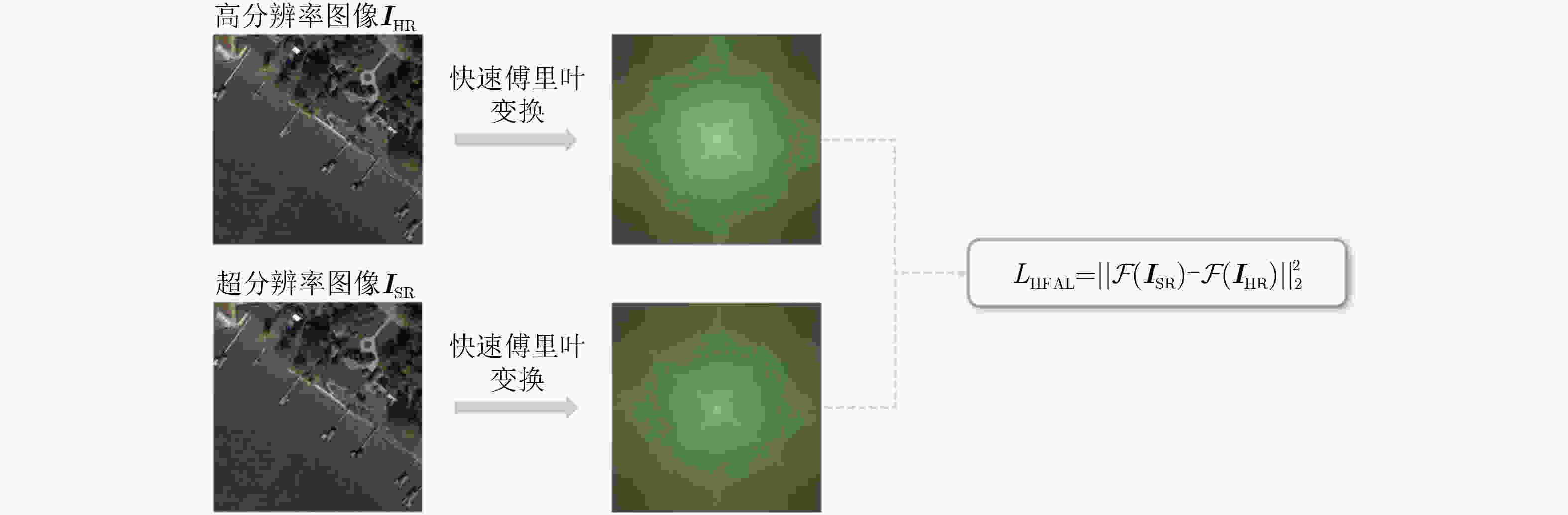
Abstract: Objective This study aims to enhance the reconstruction of fine structural details in high-resolution (HR) remote sensing image super-resolution by leveraging diffusion models. Although diffusion-based approaches have achieved remarkable success in natural image restoration, their direct application to remote sensing imagery remains suboptimal due to the pronounced imbalance between extensive low-frequency homogeneous regions (e.g., water bodies, farmland) and localized high-frequency regions with complex structures (e.g., buildings, ports, aircraft). This imbalance often leads to insufficient learning of crucial high-frequency details, resulting in reconstructions that appear globally smooth but lack sharpness and realism. To overcome this limitation, we propose DetDiffRS—a detail-enhanced diffusion-based framework—designed to explicitly improve the model’s sensitivity to high-frequency information during both data sampling and optimization, thereby achieving superior perceptual quality and structural fidelity. Methods The proposed DetDiffRS framework introduces innovations at both the data input and loss function levels to mitigate the high–low frequency imbalance in remote sensing imagery. First, a Multi-Scale Patch Sampling (MSPS) strategy is developed to increase the likelihood of selecting patches containing high-frequency structures during training. This is achieved by constructing a multi-scale patch pool and applying weighted sampling to prioritize complex regions. Second, a composite perceptual loss is designed to provide richer supervision beyond conventional denoising objectives. This loss integrates: (1) a High-Dimensional Perceptual Loss (HDPL) to enforce structural consistency in deep feature space, and (2) a High-Frequency-Aware Loss (HFAL) to directly constrain high-frequency components in the frequency domain. The combination of MSPS and the composite perceptual loss enables the diffusion model to more effectively capture and reconstruct fine details, thereby improving both objective quality metrics and visual realism. Results and Discussions Extensive experiments were conducted on three publicly available remote sensing datasets—AID, DOTA, and DIOR—against a diverse set of state-of-the-art super-resolution methods, including CNN-based (EDSR, RCAN), Transformer-based (HAT-L, TTST), GAN-based (MSRGAN, ESRGAN, SPSR), and diffusion-based (SR3, IRSDE) approaches. Quantitative evaluation using Fréchet Inception Distance (FID) on the AID dataset demonstrated that DetDiffRS achieved the best performance in 21 out of 30 scene categories, yielding an average FID of 48.37, surpassing the second-best method by 1.14. The improvements were particularly pronounced in texture-rich and structurally complex categories such as Dense Residential, Meadow, and River, where FID reductions exceeded 3.0 compared to competing diffusion models (Table 1). While PSNR-oriented methods like RCAN obtained the highest PSNR/SSIM values in some cases, they produced overly smooth reconstructions lacking fine details. In contrast, DetDiffRS, benefiting from its High-Dimensional Perceptual Loss (HDPL) and High-Frequency-Aware Loss (HFAL), achieved a balanced enhancement in both objective metrics and perceptual quality—for instance, improving PSNR by 1.06 dB over SR3 on AID and SSIM by 0.0846 on DOTA (Table 2). Visual comparisons further confirmed that DetDiffRS consistently generated sharper edges, clearer structures, and more realistic textures, effectively mitigating the over-smoothing of PSNR-focused methods and the artifacts often observed in GAN-based approaches (Fig. 5, Fig. 6). Conclusions This study presents DetDiffRS, a detail-enhanced diffusion-based super-resolution framework tailored for the unique frequency distribution characteristics of remote sensing imagery. By integrating the Multi-Scale Patch Sampling (MSPS) strategy with a composite perceptual loss combining HDPL and HFAL, the proposed method effectively addresses the underrepresentation of high-frequency regions during training, leading to substantial improvements in detail preservation and perceptual fidelity. Experimental results across multiple datasets and diverse scene types demonstrate that DetDiffRS not only outperforms existing CNN-, Transformer-, GAN-, and diffusion-based methods in FID, but also achieves a competitive balance between PSNR/SSIM and visual realism. These findings suggest that DetDiffRS offers a robust and generalizable solution for high-quality remote sensing image super-resolution, with strong potential for application in urban planning, environmental monitoring, and other geospatial analysis tasks requiring both structural accuracy and fine detail reconstruction.
- Remote sensing super-resolution(RSSR) /
- Diffusion model(DM) /
- High-frequency detail restoration

HTML全文

图 1 来自 DOTA[50]数据集的街道汽车图像(左)与来自 ImageNet[20]数据集的街道汽车图像(右)对比

下载: 全尺寸图片幻灯片

图 2 DetDiffRS整体架构

下载: 全尺寸图片幻灯片

图 3 HDPL计算流程

高维感知损失

下载: 全尺寸图片幻灯片

图 4 HFAL计算流程

下载: 全尺寸图片幻灯片

图 5 AID数据集×4超分辨率结果可视化

下载: 全尺寸图片幻灯片

图 6 DOTA数据集×4超分辨率结果可视化

下载: 全尺寸图片幻灯片

表 6 不同 $ {\lambda }_{1} $ 与$ {\lambda }_{2} $设置对性能的影响

$ {\lambda }_{1} $	$ {\lambda }_{2} $	PSNR↑	SSIM↑
$ 1\times {10}^{-2} $	0	27.3054	0.6912
$ 6\times {10}^{-3} $	$ 4\times {10}^{-3} $	27.3366	0.7002
$ 4\times {10}^{-3} $	$ 6\times {10}^{-3} $	27.4372	0.7093
$ 2\times {10}^{-3} $	$ 8\times {10}^{-3} $	27.3298	0.6958
0	$ 1\times {10}^{-2} $	27.3155	0.6954

下载: 导出CSV

表 1 AID遥感图像分类数据集FID指标

类别	Bicubic	EDSR^[33]	RCAN^[34]	HAT-L^[41]	TTST^[59]	MSRGAN^[44]	ESRGAN^[12]	SPSR^[45]	SR3^[16]	IRSDE^[48]	EDiffSR^[51]	Ours
Airport	126.84	86.77	88.27	87.46	86.47	54.23	55.23	57.55	56.93	54.47	53.33	50.83
Bare Land	112.58	91.31	93.86	90.81	90.12	66.66	61.83	70.93	77.75	80.25	66.38	67.13
Baseball Field	130.83	88.67	92.01	90.85	90.91	50.48	46.39	56.85	71.56	57.95	52.58	51.53
Beach	122.18	105.67	104.97	101.97	102.06	50.07	48.45	52.34	51.38	42.39	43.49	40.55
Bridge	138.11	80.77	81.96	81.63	80.84	48.34	50.85	49.93	74.43	45.64	50.45	46.02
Center	139.63	71.68	73.32	70.99	72.19	49.88	55.44	48.15	53.27	44.93	42.73	44.09
Church	122.35	86.47	88.44	88.57	87.67	52.38	51.59	54.86	62.99	49.66	50.12	50.85
Commercial	111.69	110.98	110.77	103.94	105.05	54.75	56.53	60.38	70.82	51.92	55.44	54.69
Dense Residential	126.94	112.81	126.07	125.57	122.28	51.21	58.55	55.76	64.04	39.87	40.59	37.57
Desert	114.92	77.88	77.49	76.88	75.41	55.61	54.88	63.27	59.86	60.11	53.79	53.02
Farmland	144.04	91.86	94.38	95.59	95.03	67.17	55.39	57.49	78.23	61.11	50.94	51.68
Forest	103.82	88.32	94.51	95.85	95.64	59.53	64.44	62.13	72.79	48.49	46.28	43.26
Industrial	106.64	78.49	81.02	75.68	72.80	38.94	37.65	45.88	45.09	36.92	42.26	37.69
Meadow	134.26	108.74	105.79	102.09	101.07	96.61	69.71	65.49	86.11	69.64	65.95	68.78
Medium Residential	116.72	99.53	104.77	101.10	102.32	46.65	50.76	48.85	74.12	42.18	40.58	39.43
Mountain	103.45	106.11	106.29	103.11	101.10	58.24	54.94	70.40	71.89	58.55	51.93	52.48
Park	137.36	110.36	112.83	110.82	103.57	60.05	61.47	73.19	81.58	63.76	63.28	60.35
Parking	134.26	60.09	67.81	63.55	65.14	42.25	42.43	44.32	55.42	36.74	35.69	35.77
Playground	113.08	58.52	62.03	59.91	58.72	41.34	39.49	40.78	54.89	38.47	36.26	33.88
Pond	162.09	123.54	124.05	127.08	126.09	61.91	54.44	63.54	103.73	55.69	56.77	55.42
Port	134.49	77.28	79.89	80.11	82.35	46.27	46.94	51.13	58.19	47.90	47.62	47.54
Railway Station	113.93	92.81	94.43	88.41	87.88	49.58	53.01	57.65	56.99	49.01	51.57	50.06
Resort	131.65	100.04	104.77	105.61	105.13	59.20	61.23	68.16	68.03	59.86	57.76	57.43
River	150.87	105.66	108.52	108.43	107.60	54.18	59.81	64.47	83.71	59.55	57.15	58.21
School	109.36	85.29	89.02	81.65	82.24	50.59	49.66	53.26	59.63	48.28	46.63	46.39
Sparse Residential	148.27	134.92	141.27	133.06	132.01	72.99	75.88	76.72	84.86	69.16	71.89	69.32
Square	109.76	71.02	75.39	72.66	72.68	43.70	45.55	45.85	53.65	44.67	42.95	42.38
Stadium	121.39	55.55	59.47	59.77	56.22	37.02	35.74	37.65	38.71	33.05	33.94	32.49
Storage Tanks	162.28	90.12	92.94	88.55	90.39	46.16	50.93	50.82	52.71	45.45	43.74	41.16
Viaduct	109.63	67.43	68.73	66.48	65.54	35.84	33.86	38.17	45.65	33.84	33.26	31.02
Average	126.48	90.62	93.50	91.27	90.55	53.39	52.77	56.20	65.63	50.98	49.51	48.37

下载: 导出CSV

表 2 AID、DOTA 和 DIOR数据集上 PSNR/SSIM 对比结果

模型	AID			DOTA			DIOR			参数量(M)
指标	PSNR↑	SSIM↑	FID↓	PSNR↑	SSIM↑	FID↓	PSNR↑	SSIM↑	FID↓	参数量(M)
EDSR^[33]	30.5987	0.8034	90.6217	33.6742	0.8571	56.3559	30.6519	0.8085	41.1396	43.096
RCAN^[34]	30.8543	0.8126	93.5024	33.8764	0.8622	51.6321	30.8684	0.8157	44.1177	15.673
HAT-L^[41]	30.8732	0.8133	91.2743	33.9388	0.8745	43.2568	30.8892	0.8283	40.9004	40.396
TTST^[59]	30.9274	0.8169	90.5602	34.1066	0.8742	40.8301	30.9246	0.8296	39.2227	37.573
MSRGAN^[40]	28.8027	0.7481	53.3889	29.4572	0.7859	27.8021	28.8469	0.7596	23.2691	1.510
ESRGAN^[12]	28.3994	0.7248	52.7719	28.9591	0.7793	24.9884	28.1226	0.7015	23.2864	16.706
SPSR^[45]	27.6995	0.7098	56.2035	28.0487	0.7792	25.9249	27.4461	0.7169	24.2751	24.872
SR3^[16]	26.2583	0.6695	65.6274	27.5896	0.6781	34.8752	26.2508	0.6691	31.9048	92.654
IRSDE^[48]	27.2186	0.6647	50.9811	27.9721	0.7093	24.3797	27.0014	0.6482	22.8679	137.255
EDiffSR^[51]	27.3817	0.6752	50.5063	28.2049	0.7294	22.3208	27.5169	0.6792	22.7289	26.790
DDIM^[15]	27.1338	0.6519	51.4447	28.0186	0.6914	26.0746	27.1224	0.6523	26.6102	26.166
Ours	27.4372	0.7093	48.3711	28.4218	0.7425	21.1314	27.6715	0.6987	22.1396	26.532

下载: 导出CSV

表 3 多尺度图块采样策略消融实验结果

方法	多尺度	加权采样策略	位置编码	N	PSNR↑	SSIM↑
Baseline	×	×	×	-	27.1596	0.6660
MS-uniform-noPos	√	×	×	4	27.2645	0.6899
MS-weighted-noPos	√	√	×	4	27.2990	0.6954
MS-weighted-noPos(Ours)	√	√	√	4	27.4372	0.7093

下载: 导出CSV

表 4 不同尺度数量 N的性能对比

N	PSNR↑	SSIM↑
2	27.1997	0.6705
3	27.2659	0.6914
4	27.4372	0.7093
5	27.3027	0.6988

下载: 导出CSV

表 5 复合感知损失消融实验结果

方法	$ {L}_{\text{denoise}} $	HDPL	HFAL	PSNR↑	SSIM↑
Baseline	√	×	×	27.2823	0.6899
+HDPL	√	√	×	27.3054	0.6912
+HFAL	√	×	√	27.3155	0.6954
+HDPL +HFAL	√	√	√	27.4372	0.7093

下载: 导出CSV

参考文献(63)

[1]	张永生, 巩丹超, 刘军, 等. 高分辨率遥感卫星应用: 成像模型、处理算法及应用技术[M]. 北京: 科学出版社, 2004. ZHANG Yongsheng, GONG Danchao, LIU Jun, et al. Applications of High-Resolution Remote Sensing Satellites[M]. Beijing: Science Press, 2004. (查阅网上资料, 未找到本条文献英文翻译, 请确认).
[2]	LI Songnian, DRAGICEVIC S, CASTRO F A, et al. Geospatial big data handling theory and methods: A review and research challenges[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2016, 115: 119–133. doi: 10.1016/j.isprsjprs.2015.10.012.
[3]	童旭东. 中国高分辨率对地观测系统重大专项建设进展[J]. 遥感学报, 2016, 20(5): 775–780. doi: 10.11834/jrs.20166302. TONG Xudong. Development of China high-resolution earth observation system[J]. Journal of Remote Sensing, 2016, 20(5): 775–780. doi: 10.11834/jrs.20166302.
[4]	ZHU Xiaoxiang, TUIA D, MOU Lichao, et al. Deep learning in remote sensing: A comprehensive review and list of resources[J]. IEEE Geoscience and Remote Sensing Magazine, 2017, 5(4): 8–36. doi: 10.1109/MGRS.2017.2762307.
[5]	FARSIU S, ROBINSON M D, ELAD M, et al. Fast and robust multiframe super resolution[J]. IEEE Transactions on Image Processing, 2004, 13(10): 1327–1344. doi: 10.1109/TIP.2004.834669.
[6]	WANG Qi, LI Qiang, and LI Xuelong. Spatial-spectral residual network for hyperspectral image super-resolution[J]. arXiv preprint arXiv: 2001.04609, 2020. doi: 10.48550/arXiv.2001.04609. (查阅网上资料,请作者核对文献类型及格式是否正确).
[7]	成科扬, 荣兰, 蒋森林, 等. 基于深度学习的遥感图像超分辨率重建方法综述[J]. 郑州大学学报: 工学版, 2022, 43(5): 8–16. doi: 10.13705/j.issn.1671-6833.2022.05.013. CHENG Keyang, RONG Lan, JIANG Senlin, et al. Overview of methods for remote sensing image super-resolution reconstruction based on deep learning[J]. Journal of Zhengzhou University: Engineering Science, 2022, 43(5): 8–16. doi: 10.13705/j.issn.1671-6833.2022.05.013.
[8]	DONG Chao, LOY C C, HE Kaiming, et al. Image super-resolution using deep convolutional networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(2): 295–307. doi: 10.1109/TPAMI.2015.2439281.
[9]	JOHNSON J, ALAHI A, and FEI-FEI L. Perceptual losses for real-time style transfer and super-resolution[C]. 14th European Conference on Computer Vision, Amsterdam, The Netherlands, 2016: 694–711. doi: 10.1007/978-3-319-46475-6_43.
[10]	GOODFELLOW I J, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[C]. Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, Canada, 2014: 2672–2680.
[11]	TIAN Chunwei, ZHANG Xuanyu, ZHU Qi, et al. Generative adversarial networks for image super-resolution: A survey[J]. arXiv preprint arXiv: 2204.13620, 2022. doi: 10.48550/arXiv.2204.13620.
[12]	WANG Xintao, YU Ke, WU Shixiang, et al. ESRGAN: Enhanced super-resolution generative adversarial networks[C]. Proceedings of the European Conference on Computer Vision Workshops, Munich, Germany, 2019: 63–79. doi: 10.1007/978-3-030-11021-5_5.
[13]	彭晏飞, 高艺, 杜婷婷, 等. 生成对抗网络的单图像超分辨率重建方法[J]. 计算机科学与探索, 2020, 14(9): 1612–1620. doi: 10.3778/j.issn.1673-9418.1910067. PENG Yanfei, GAO Yi, DU Tingting, et al. Single image super-resolution reconstruction method for generative adversarial network[J]. Journal of Frontiers of Computer Science and Technology, 2020, 14(9): 1612–1620. doi: 10.3778/j.issn.1673-9418.1910067.
[14]	HO J, JAIN A, and ABBEEL P. Denoising diffusion probabilistic models[C]. Proceedings of the 34th International Conference on Neural Information Processing Systems, Vancouver, Canada, 2020: 574.
[15]	SONG Jiaming, MENG Chenlin, and ERMON S. Denoising diffusion implicit models[C]. 9th International Conference on Learning Representations, 2021. (查阅网上资料, 未找到本条文献出版地信息, 请确认并补充).
[16]	SAHARIA C, HO J, CHAN W, et al. Image super-resolution via iterative refinement[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2023, 45(4): 4713–4726. doi: 10.1109/TPAMI.2022.3204461.
[17]	ROMBACH R, BLATTMANN A, LORENZ D, et al. High-resolution image synthesis with latent diffusion models[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, USA, 2022: 10674–10685. doi: 10.1109/CVPR52688.2022.01042.
[18]	韩阳, 朱军鹏, 郭春雨, 等. 基于扩散模型的流场超分辨率重建方法[J]. 力学学报, 2023, 55(10): 2309–2320. doi: 10.6052/0459-1879-23-167. HAN Yang, ZHU Junpeng, GUO Chunyu, et al. A flow field super-resolution reconstruction method based on diffusion model[J]. Chinese Journal of Theoretical and Applied Mechanics, 2023, 55(10): 2309–2320. doi: 10.6052/0459-1879-23-167.
[19]	XIA Guisong, BAI Xiang, DING Jian, et al. DOTA: A large-scale dataset for object detection in aerial images[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA, 2018: 3974–3983. doi: 10.1109/CVPR.2018.00418.
[20]	DENG Jia, DONG Wei, SOCHER R, et al. ImageNet: A large-scale hierarchical image database[C]. 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, USA, 2009: 248–255. doi: 10.1109/CVPR.2009.5206848.
[21]	JUSTICE C O, VERMOTE E, TOWNSHEND J R G, et al. The Moderate Resolution Imaging Spectroradiometer (MODIS): Land remote sensing for global change research[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(4): 1228–1249. doi: 10.1109/36.701075.
[22]	甘甫平, 王润生, 王永江, 等. 基于遥感技术的土地利用与土地覆盖的分类方法[J]. 国土资源遥感, 1999, 11(4): 40–45. doi: 10.3969/j.issn.1001-070X.1999.04.008. GAN Fuping, WANG Runsheng, WANG Yongjiang, et al. The classification method based on remote sensing techniques for land use and cover[J]. Remote Sensing for Land & Resources, 1999, 11(4): 40–45. doi: 10.3969/j.issn.1001-070X.1999.04.008.
[23]	张秀再, 沈涛, 许岱. 基于改进YOLOv8算法的遥感图像目标检测[J]. 激光与光电子学进展, 2024, 61(10): 1028001. doi: 10.3788/LOP231803. ZHANG Xiuzai, SHEN Tao, and XU Dai. Remote-sensing image object detection based on improved YOLOv8 algorithm[J]. Laser & Optoelectronics Progress, 2024, 61(10): 1028001. doi: 10.3788/LOP231803.
[24]	SHAO Zhenfeng, WANG Lei, WANG Zhongyuan, et al. Remote sensing image super-resolution using sparse representation and coupled sparse autoencoder[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(8): 2663–2674. doi: 10.1109/JSTARS.2019.2925456.
[25]	ZHOU Weixun, GUAN Haiyan, LI Ziyu, et al. Remote sensing image retrieval in the past decade: Achievements, challenges, and future directions[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2023, 16: 1447–1473. doi: 10.1109/JSTARS.2023.3236662.
[26]	王海波, 马明国. 基于遥感的湖泊水域动态变化监测研究进展[J]. 遥感技术与应用, 2009, 24(5): 674–684. doi: 10.11873/j.issn.1004-0323.2009.5.674. WANG Haibo and MA Mingguo. A review of monitoring change in lake water areas based on remote sensing[J]. Remote Sensing Technology and Application, 2009, 24(5): 674–684. doi: 10.11873/j.issn.1004-0323.2009.5.674.
[27]	BILJECKI F, STOTER J, LEDOUX H, et al. Applications of 3D city models: State of the art review[J]. ISPRS International Journal of Geo-Information, 2015, 4(4): 2842–2889. doi: 10.3390/ijgi4042842.
[28]	PARK S C, PARK M K, and KANG M G. Super-resolution image reconstruction: A technical overview[J]. IEEE Signal Processing Magazine, 2003, 20(3): 21–36. doi: 10.1109/MSP.2003.1203207.
[29]	KEYS R. Cubic convolution interpolation for digital image processing[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1981, 29(6): 1153–1160. doi: 10.1109/TASSP.1981.1163711.
[30]	KIM J, LEE J K, and LEE K M. Accurate image super-resolution using very deep convolutional networks[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 1646–1654. doi: 10.1109/CVPR.2016.182.
[31]	KIM J, LEE J K, and LEE K M. Deeply-recursive convolutional network for image super-resolution[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 1637–1645. doi: 10.1109/CVPR.2016.181.
[32]	DONG Chao, LOY C C, and TANG Xiao’ou. Accelerating the super-resolution convolutional neural network[C]. 14th European Conference on Computer Vision, Amsterdam, The Netherlands, 2016: 391–407. doi: 10.1007/978-3-319-46475-6_25.
[33]	LIM B, SON S, KIM H, et al. Enhanced deep residual networks for single image super-resolution[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, USA, 2017: 1132–1140. doi: 10.1109/CVPRW.2017.151.
[34]	ZHANG Yulun, LI Kunpeng, LI Kai, et al. Image super-resolution using very deep residual channel attention networks[C]. Proceedings of the 15th European Conference on Computer Vision, Munich, Germany, 2018: 294–310. doi: 10.1007/978-3-030-01234-2_18.
[35]	MEI Yiqun, FAN Yuchen, and ZHOU Yuqian. Image super-resolution with non-local sparse attention[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, USA, 2021: 3516–3525. doi: 10.1109/CVPR46437.2021.00352.
[36]	NIU Ben, WEN Weilei, REN Wenqi, et al. Single image super-resolution via a holistic attention network[C]. 16th European Conference on Computer Vision, Glasgow, UK, 2020: 191–207. doi: 10.1007/978-3-030-58610-2_12.
[37]	HAUT J M, FERNANDEZ-BELTRAN R, PAOLETTI M E, et al. Remote sensing image superresolution using deep residual channel attention[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 9277–9289. doi: 10.1109/TGRS.2019.2924818.
[38]	KONG Dezhi, GU Lingjia, LI Xiaofeng, et al. Multiscale residual dense network for the super-resolution of remote sensing images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 5612612. doi: 10.1109/TGRS.2024.3370826.
[39]	WANG Hongyuan, CHENG Shuli, LI Yongming, et al. Lightweight remote-sensing image super-resolution via attention-based multilevel feature fusion network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 2005715. doi: 10.1109/TGRS.2023.3336524.
[40]	XIAO Huanling, CHEN Xintong, LUO Liuhui, et al. A dual-path feature reuse multi-scale network for remote sensing image super-resolution[J]. The Journal of Supercomputing, 2025, 81(1): 17. doi: 10.1007/s11227-024-06569-w.
[41]	CHEN Xiangyu, WANG Xintao, ZHOU Jiantao, et al. Activating more pixels in image super-resolution transformer[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, Canada, 2023: 22367–22377. doi: 10.1109/CVPR52729.2023.02142.
[42]	LIU Jingyi and YANG Xiaomin. Multi-stage remote sensing super-resolution network with deep fusion and structure enhancement based on CNN and transformer[J]. Signal, Image and Video Processing, 2025, 19(5): 407. doi: 10.1007/s11760-025-03988-x.
[43]	LUGMAYR A, DANELLJAN M, VAN GOOL L, et al. SRFlow: Learning the super-resolution space with normalizing flow[C]. 16th European Conference on Computer Vision, Glasgow, UK, 2020: 715–732. doi: 10.1007/978-3-030-58558-7_42.
[44]	LEDIG C, THEIS L, HUSZÁR F, et al. Photo-realistic single image super-resolution using a generative adversarial network[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, USA, 2017: 105–114. doi: 10.1109/CVPR.2017.19.
[45]	MA Cheng, RAO Yongming, LU Jiwen, et al. Structure-preserving image super-resolution[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(11): 7898–7911. doi: 10.1109/TPAMI.2021.3114428.
[46]	SONG Yang and ERMON S. Generative modeling by estimating gradients of the data distribution[C]. Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, Canada, 2019: 1067.
[47]	LI Haoying, YANG Yifan, CHANG Meng, et al. SRDiff: Single image super-resolution with diffusion probabilistic models[J]. Neurocomputing, 2022, 479: 47–59. doi: 10.1016/j.neucom.2022.01.029.
[48]	LUO Ziwei, GUSTAFSSON F K, ZHAO Zheng, et al. Image restoration with mean-reverting stochastic differential equations[C]. Proceedings of the 40th International Conference on Machine Learning, Honolulu, USA, 2023: 23045–23066.
[49]	LIU Jinzhe, YUAN Zhiqiang, PAN Zhaoying, et al. Diffusion model with detail complement for super-resolution of remote sensing[J]. Remote Sensing, 2022, 14(19): 4834. doi: 10.3390/rs14194834.
[50]	HAN Lintao, ZHAO Yuchen, LV Hengyi, et al. Enhancing remote sensing image super-resolution with efficient hybrid conditional diffusion model[J]. Remote Sensing, 2023, 15(13): 3452. doi: 10.3390/rs15133452.
[51]	XIAO Yi, YUAN Qiangqiang, JIANG Kui, et al. EDiffSR: An efficient diffusion probabilistic model for remote sensing image super-resolution[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 5601514. doi: 10.1109/TGRS.2023.3341437.
[52]	张文雪, 罗一涵, 刘雅卿, 等. 基于主动位移成像的图像超分辨率重建[J]. 光电工程, 2024, 51(1): 230290. doi: 10.12086/oee.2024.230290. ZHANG Wenxue, LUO Yihan, LIU Yaqing, et al. Image super-resolution reconstruction based on active displacement imaging[J]. Opto-Electronic Engineering, 2024, 51(1): 230290. doi: 10.12086/oee.2024.230290.
[53]	房垚鑫, 郭宝峰, 马超. 基于改进点扩散函数的遥感图像超分辨率重建[J]. 激光技术, 2019, 43(5): 713–718. doi: 10.7510/jgjs.issn.1001-3806.2019.05.024. FANG Yaoxin, GUO Baofeng, and MA Chao. Super-resolution reconstruction of remote sensing images based on the improved point spread function[J]. Laser Technology, 2019, 43(5): 713–718. doi: 10.7510/jgjs.issn.1001-3806.2019.05.024.
[54]	SIMONYAN K and ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[C]. 3rd International Conference on Learning Representations, San Diego, USA, 2015.
[55]	XIA Guisong, HU Jingwen, HU Fan, et al. AID: A benchmark data set for performance evaluation of aerial scene classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(7): 3965–3981. doi: 10.1109/TGRS.2017.2685945.
[56]	LI Ke, WAN Gang, CHENG Gong, et al. Object detection in optical remote sensing images: A survey and a new benchmark[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2020, 159: 296–307. doi: 10.1016/j.isprsjprs.2019.11.023.
[57]	HEUSEL M, RAMSAUER H, UNTERTHINER T, et al. GANs trained by a two time-scale update rule converge to a local Nash equilibrium[C]. Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, USA, 2017: 6629–6640.
[58]	WANG Zhou, BOVIK A C, SHEIKH H R, et al. Image quality assessment: From error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600–612. doi: 10.1109/TIP.2003.819861.
[59]	XIAO Yi, YUAN Qiangqiang, JIANG Kui, et al. TTST: A top-k token selective transformer for remote sensing image super-resolution[J]. IEEE Transactions on Image Processing, 2024, 33: 738–752. doi: 10.1109/TIP.2023.3349004.
[60]	LIU Quanyong, PENG Jiangtao, ZHANG Genwei, et al. Deep contrastive learning network for small-sample hyperspectral image classification[J]. Journal of Remote Sensing, 2023, 3: 0025. doi: 10.34133/remotesensing.0025.
[61]	SHI Qian, ZHU Jiajun, LIU Zhengyu, et al. The last puzzle of global building footprints—Mapping 280 million buildings in East Asia based on VHR images[J]. Journal of Remote Sensing, 2024, 4: 0138. doi: 10.34133/remotesensing.0138.
[62]	LIU Shuaijun, LIU Jia, TAN Xiaoyue, et al. A hybrid spatiotemporal fusion method for high spatial resolution imagery: Fusion of Gaofen-1 and Sentinel-2 over agricultural landscapes[J]. Journal of Remote Sensing, 2024, 4: 0159. doi: 10.34133/remotesensing.0159.
[63]	MEI Shaohui, LIAN Jiawei, WANG Xiaofei, et al. A comprehensive study on the robustness of deep learning-based image classification and object detection in remote sensing: Surveying and benchmarking[J]. Journal of Remote Sensing, 2024, 4: 0219. doi: 10.34133/remotesensing.0219.