地磁背景下磁异常空间延拓的优化多层等效源方法

管宇; 张慧强

doi:10.11999/JEIT250958

地磁背景下磁异常空间延拓的优化多层等效源方法

doi: 10.11999/JEIT250958 cstr: 32379.14.JEIT250958

管宇^,,
张慧强

哈尔滨理工大学自动化学院，哈尔滨，150006

详细信息

作者简介:
管宇：女，讲师，研究方向为容错控制与故障诊断

张慧强：男，硕士生，研究方向为地磁导航

通讯作者:
管宇　gy_hlg@163.com

中图分类号: O411.5; TN911.7
计量
- 文章访问数: 22
- HTML全文浏览量: 7
- PDF下载量: 1
- 被引次数: 0
出版历程
- 修回日期: 2026-01-22
- 录用日期: 2026-01-22
- 网络出版日期: 2026-02-11

An Optimized Multi-Layer Equivalent Source Method for Spatial Continuation of Magnetic Anomalies in the Geomagnetic Background

GUAN Yu^,,
ZHANG Huiqiang

Institute of Automation, Harbin University of Science and Technology, Harbin 150006, China

摘要

摘要: 磁异常延拓是地磁空间信息获取与处理的重要技术手段。针对现有的频率域方法在向下延拓中具有不适定性，以及传统等效源方法难以兼顾多尺度场源拟合精度的问题，该文提出了一种磁异常空间延拓的优化多层等效源方法。该方法采用基于功率谱分析的深度估计与变分模态分解技术构建多层等效源参数设定框架，并引入真菌生长算法对等效源反演过程进行协同优化。理论模型与EMAG2仿真实验表明，该方法显著降低了模型构建的主观性，在5%高斯噪声干扰下仍能保持较高的信号保真度与抗噪鲁棒性。基于澳大利亚实测磁异常网格数据的应用验证，该方法在复杂构造区与平缓基底区均具有优异的普适性与延拓精度。
- 磁异常延拓 /
- 等效源 /
- 功率谱分析 /
- 地磁背景
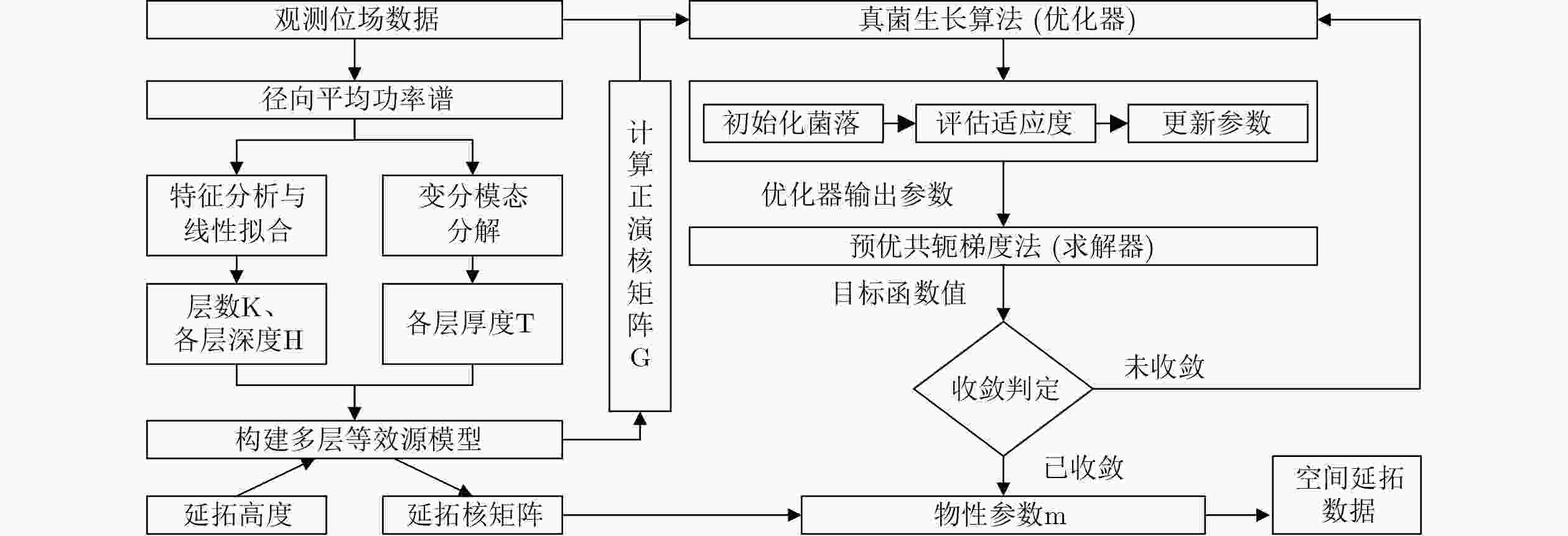
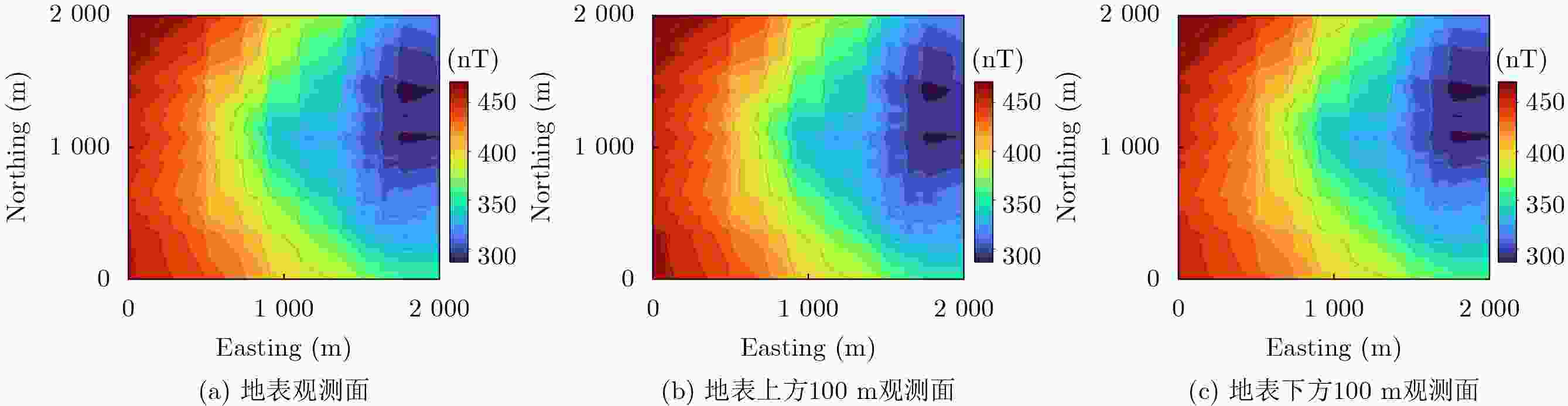
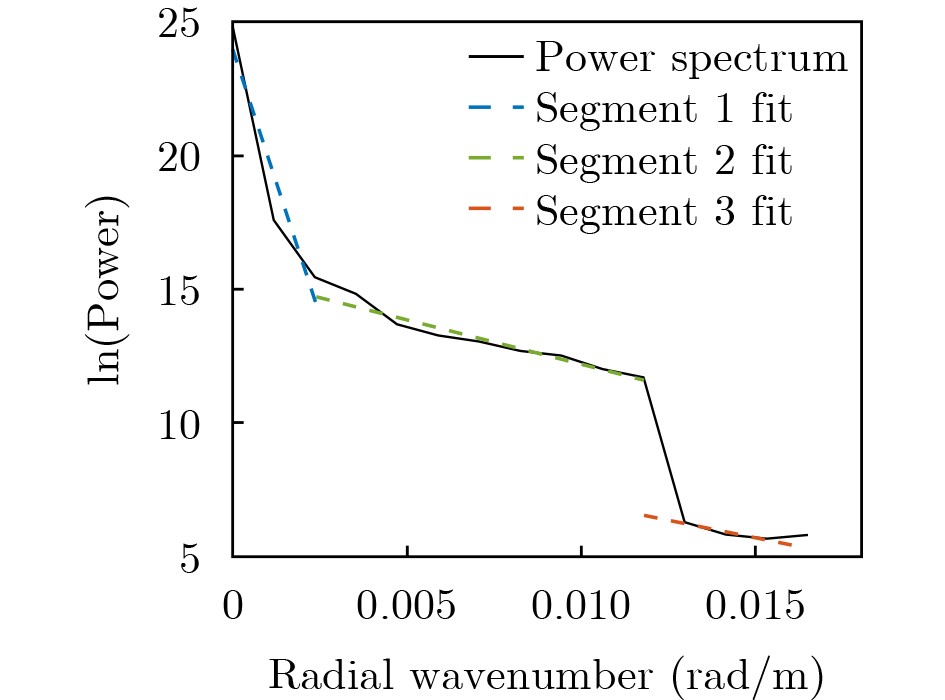
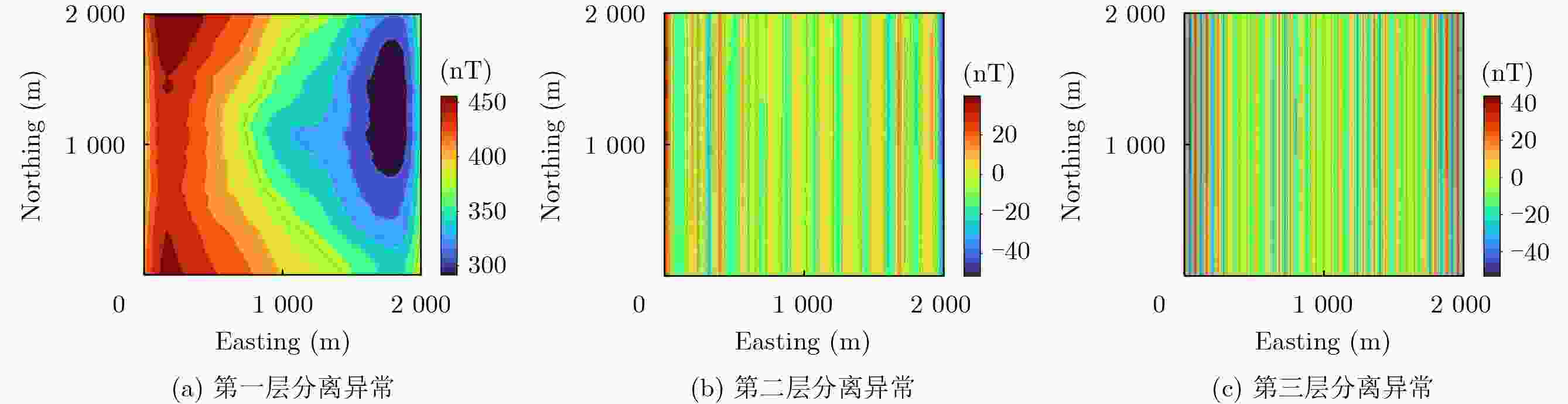
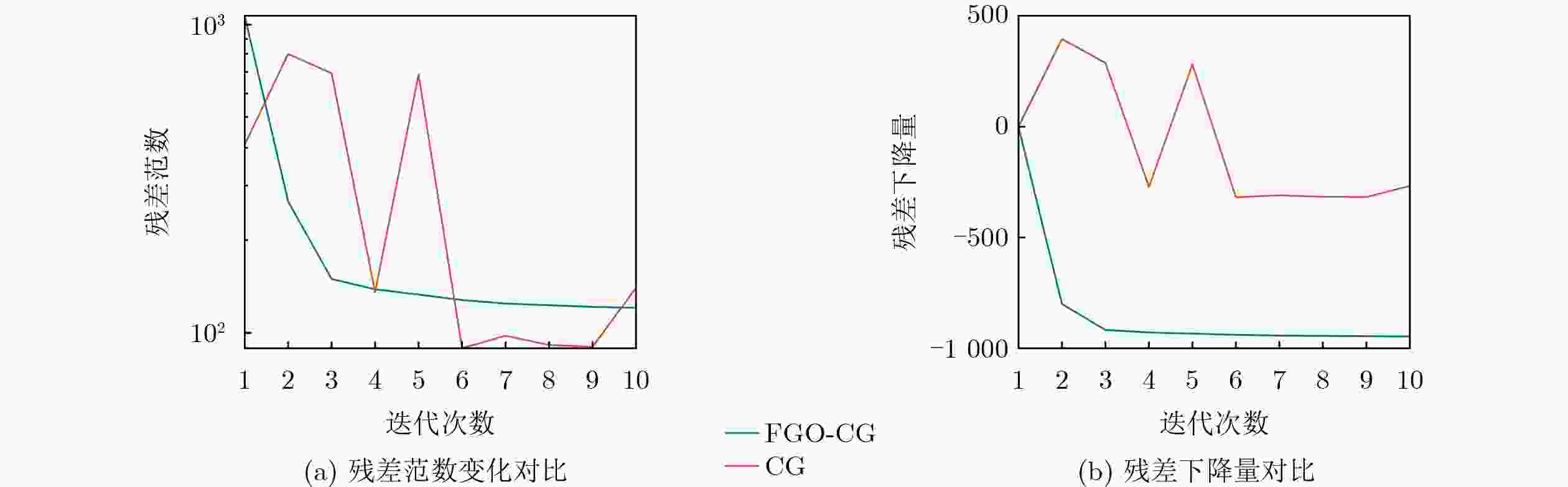
Abstract: Objective Spatial continuation of magnetic anomalies is a pivotal technique in potential field data processing, serving as a prerequisite for geological interpretation and geomagnetic navigation. However, existing methods face inherent limitations: frequency-domain methods suffer from severe ill-posedness and high-frequency noise amplification during downward continuation, while traditional single-layer equivalent source methods often struggle to simultaneously fit multi-scale anomalies caused by sources at varying depths. Although the Multi-layer Equivalent Source (MES) model offers a solution for depth resolution, its application is hindered by the subjectivity in structural parameter setting and the instability of large-scale inversion, leading to the loss of high-frequency structural details. To overcome these bottlenecks, this study proposes an optimized MES method designed for high-precision continuation in complex geological environments. The method establishes an objective parameterization framework by combining Radially Averaged Power Spectrum (RAPS) analysis with Variational Mode Decomposition (VMD) to accurately separate sources. Furthermore, it introduces a collaborative inversion scheme based on the Fungal Growth Optimizer (FGO) and Preconditioned Conjugate Gradient (PCG) to adaptively optimize regularization parameters, thereby effectively suppressing ill-posedness and enhancing the robustness and fidelity of signal reconstruction under noisy conditions. Methods To achieve high-precision spatial continuation of magnetic anomalies, this study establishes a systematic four-step technical framework. (1) Model Construction: A multi-layer equivalent source (MES) model is constructed using a layered strategy, where uniformly magnetized rectangular prisms are selected as the fundamental source units to accurately represent subsurface field sources. (2) Parameter Configuration: To objectively determine model parameters, a hybrid approach integrating Radially Averaged Power Spectrum (RAPS) analysis and Variational Mode Decomposition (VMD) is proposed. RAPS is utilized to estimate the average depths of source layers by analyzing the slope variations in the logarithmic power spectrum. Subsequently, VMD decomposes the original magnetic signal into intrinsic mode functions corresponding to different depths, allowing for the precise calculation of layer thickness based on the ratio of Mean Total Horizontal Gradient (MTHD). (3) Collaborative Inversion: A robust inversion strategy is implemented by introducing the Fungal Growth Optimizer (FGO) into the Preconditioned Conjugate Gradient (PCG) method. Tikhonov regularization is employed to construct the objective function to mitigate the ill-posedness of the linear system. FGO adaptively searches for optimal hyperparameters—including the regularization parameter, step size scaling factor, and preconditioner weights—thereby balancing solution stability with convergence efficiency. (4) Comprehensive Validation: The method's effectiveness is rigorously verified through three stages: first, a theoretical model comprising five prisms is established to validate the reliability of the proposed method by benchmarking its continuation performance against single-layer, double-layer equivalent source models, and frequency-domain methods; second, the global EMAG2 magnetic anomaly model is used to test robustness under 5% Gaussian noise, ensuring stability in downward continuation; finally, real measured data from the Australian magnetic anomaly grid are applied. Two distinct sub-regions—a complex tectonic zone (Area A) and a gentle sedimentary basin (Area B)—are selected for downward continuation experiments (2000 m to 0 m), using quantitative indicators (RMSE, GOF) to demonstrate the method's universality across different geological textures. Results and Discussions The performance of the proposed method is validated through three progressive stages: (1) Theoretical Model Verification: The radial average logarithmic power spectrum (Fig. 3) and VMD analysis (Fig. 4) successfully identified three equivalent source layers, confirming the objectivity of the parameter configuration framework. The FGO-optimized inversion strategy accelerated convergence by approximately 5-6 times and reduced the residual norm by 13% compared to the traditional Conjugate Gradient (CG) method (Fig. 7). In the 100 m upward continuation (Fig. 8, Table 4) and downward continuation (Fig. 9, Table 5) experiments, the proposed method achieved the lowest RMSE and highest GOF, effectively overcoming the ill-posedness of frequency-domain methods and the large fitting errors of single/double-layer models.(2) Robustness Analysis: Using the EMAG2 data (Fig. 10), the method demonstrated exceptional anti-noise capabilities. Even with 5% Gaussian noise added to the 1000 m observation data, the downward continuation results remained stable without significant artifacts. Quantitative evaluation (Table 6) shows an RMSE of 7.36 nT and a GOF of 82.65%, verifying the method's robustness in low signal-to-noise ratio environments. (3) Generalization Verification: In the application to real Australian magnetic anomaly grid data, two distinct geological regions were analyzed (Fig. 11, Fig. 12). For Area B (Sedimentary Basin), characterized by smooth gradients, the method achieved high-fidelity reconstruction with a GOF of 84.28% and an RMSE of 29.06 nT. For Area A (Complex Tectonic Zone), despite the exponential decay of high-frequency signals, the method effectively recovered main structural features (GOF = 76.14%), although localized residuals occurred in high-gradient zones due to the physical limits of field transformation (Table 8). These results confirm the method's universality across diverse geological textures. Conclusions This study proposes a robust spatial continuation method for magnetic anomalies based on an optimized multi-layer equivalent source (MES) framework. By integrating Radially Averaged Power Spectrum (RAPS) analysis with Variational Mode Decomposition (VMD), the method establishes an objective parameterization scheme, effectively reducing the subjectivity in model construction. Furthermore, the introduction of the Fungal Growth Optimizer (FGO) into the inversion algorithm significantly enhances convergence speed and stability, successfully mitigating the ill-posedness inherent in downward continuation. Experimental results indicate that:(1)The method exhibits exceptional robustness, maintaining high signal fidelity even under 5% Gaussian noise interference, as verified by the EMAG2 model tests; (2) The method demonstrates excellent geological universality. In applications to real Australian aeromagnetic grid data, it achieves high-precision reconstruction in deep sedimentary basins (Area B) and effectively recovers main structural features in complex tectonic zones (Area A), outperforming traditional single-layer and frequency-domain methods. However, the method currently faces challenges regarding high memory consumption due to the storage of large-scale dense kernel matrices. Future research will focus on implementing matrix compression techniques or exploring matrix-free inversion strategies to further enhance computational efficiency for large-scale geomagnetic data processing.
- Magnetic Anomaly Continuation /
- Equivalent Source /
- Power Spectrum Analysis /
- Geomagnetic Background

HTML全文

图 1 磁异常空间延拓的优化多层等效源方法流程图

下载: 全尺寸图片幻灯片

图 2 模型理论磁异常示意图

下载: 全尺寸图片幻灯片

图 3 径向平均功率谱曲线

下载: 全尺寸图片幻灯片

图 4 地表磁异常分离异常

下载: 全尺寸图片幻灯片

图 5 等效源分布范围实验结果

下载: 全尺寸图片幻灯片

图 6 关键参数敏感性曲线

下载: 全尺寸图片幻灯片

图 7 反演算法对比

下载: 全尺寸图片幻灯片

图 8 不同方法向上延拓100 m结果及对比残差

下载: 全尺寸图片幻灯片

图 9 不同方法向下延拓100 m结果及对比残差

下载: 全尺寸图片幻灯片

图 10 基于EMAG2区域数据的鲁棒性验证结果

下载: 全尺寸图片幻灯片

图 11 基于复杂构造区(A区)实测数据的向下延拓结果与残差分布

下载: 全尺寸图片幻灯片

图 12 基于平缓背景区(B区)实测数据的向下延拓结果与残差分布

下载: 全尺寸图片幻灯片

表 1 理论模型参数表

模型编号	中心深度(m)	水平坐标(m)	长a(m)	宽b(m)	高c(m)	磁化率(无量纲)
1	250	(1000, 1000)	200	200	300	0.2
2	450	(1600, 1600)	300	300	300	0.2
3	425	(1200, 800)	150	150	250	0.2
4	500	(500, 1500)	250	250	200	0.2
5	950	(1000, 1000)	1000	1000	100	0.2

下载: 导出CSV

表 2 功率谱分段、谱斜率深度估计与VMD分解的参数设置

模块	参数	设定	说明
功率谱分段	分段区间(rad/m)	0–0.0024, 0.0024–0.0118, 0.0118–0.0168.	依据功率谱曲线斜率突变位置识别线性段区间
谱斜率深度	拟合方法	线性最小二乘法	拟合线性段
谱斜率深度	深度公式	公式(9)	符合二维指数衰减模型
VMD 分解	模态数	5	控制分解模态数量
	带宽因子	1000	控制带宽和分解稳定性
	拉格朗日步长	0	采用无约束稳态更新形式
	收敛阈值	10⁻⁶	控制迭代终止条件

下载: 导出CSV

表 3 变分模态分解参数扰动敏感性分析

参数类型	设定值	频带表现	结果
模态数	5	中间层混叠	边界波动明显
	8	三层分量分离清晰	分解稳定可重复
	10	过度分解	分解稳定性降低
带宽因子	1000	频带重叠	收敛不稳定
	2000	结构层次明显	收敛快速稳定
	5000	过度压缩	高频成分被过度抑制

下载: 导出CSV

表 4 不同方法向上100m延拓结果的量化精度评估

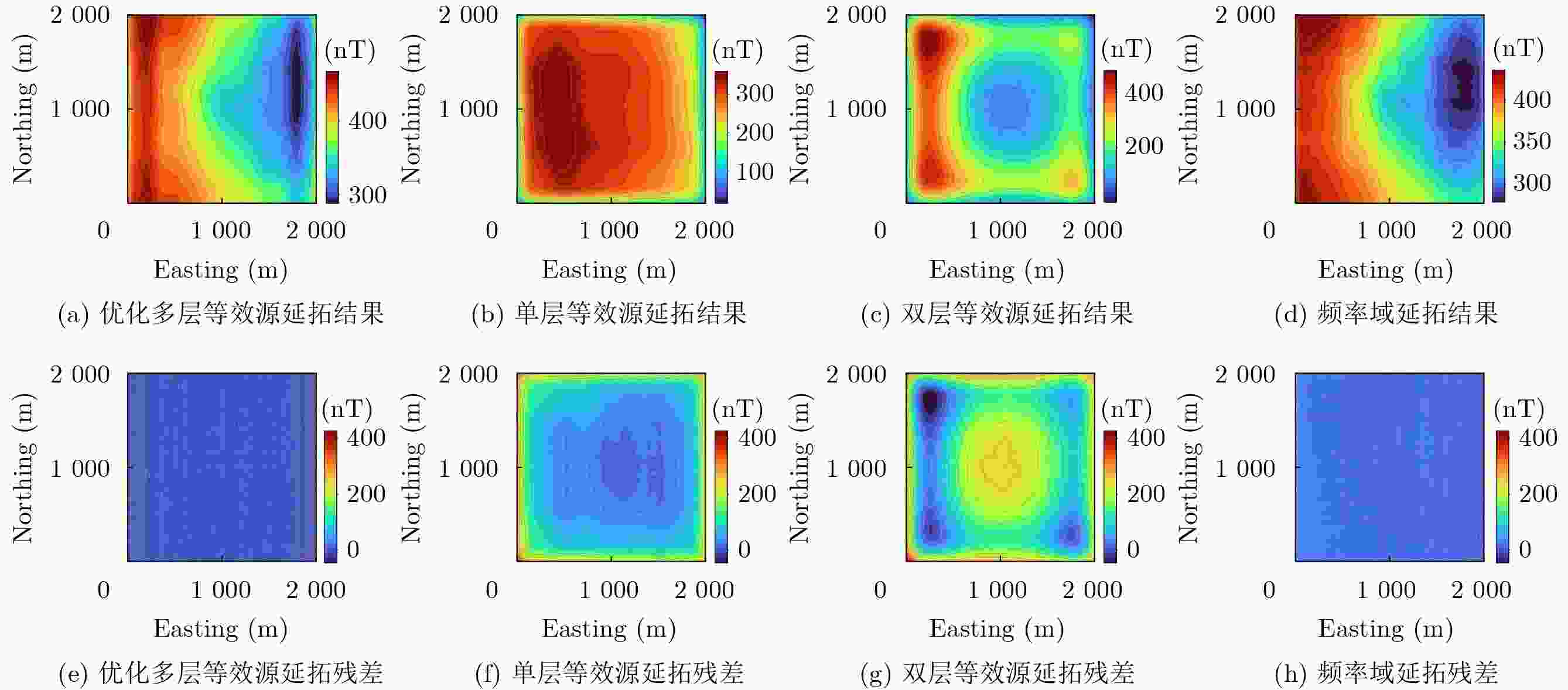
方法	RMSE(nT)	MaxAbsError(nT)	GradRMS(nT/m)	GOF(%)
优化多层等效源	2.17	10.90	2.23	99.43
单层等效源	118.29	407.06	25.45	69.25
双层等效源	173.73	427.58	30.40	54.85
频率域	21.58	54.98	4.71	94.39

下载: 导出CSV

表 5 不同方法向下100m延拓结果的量化精度评估

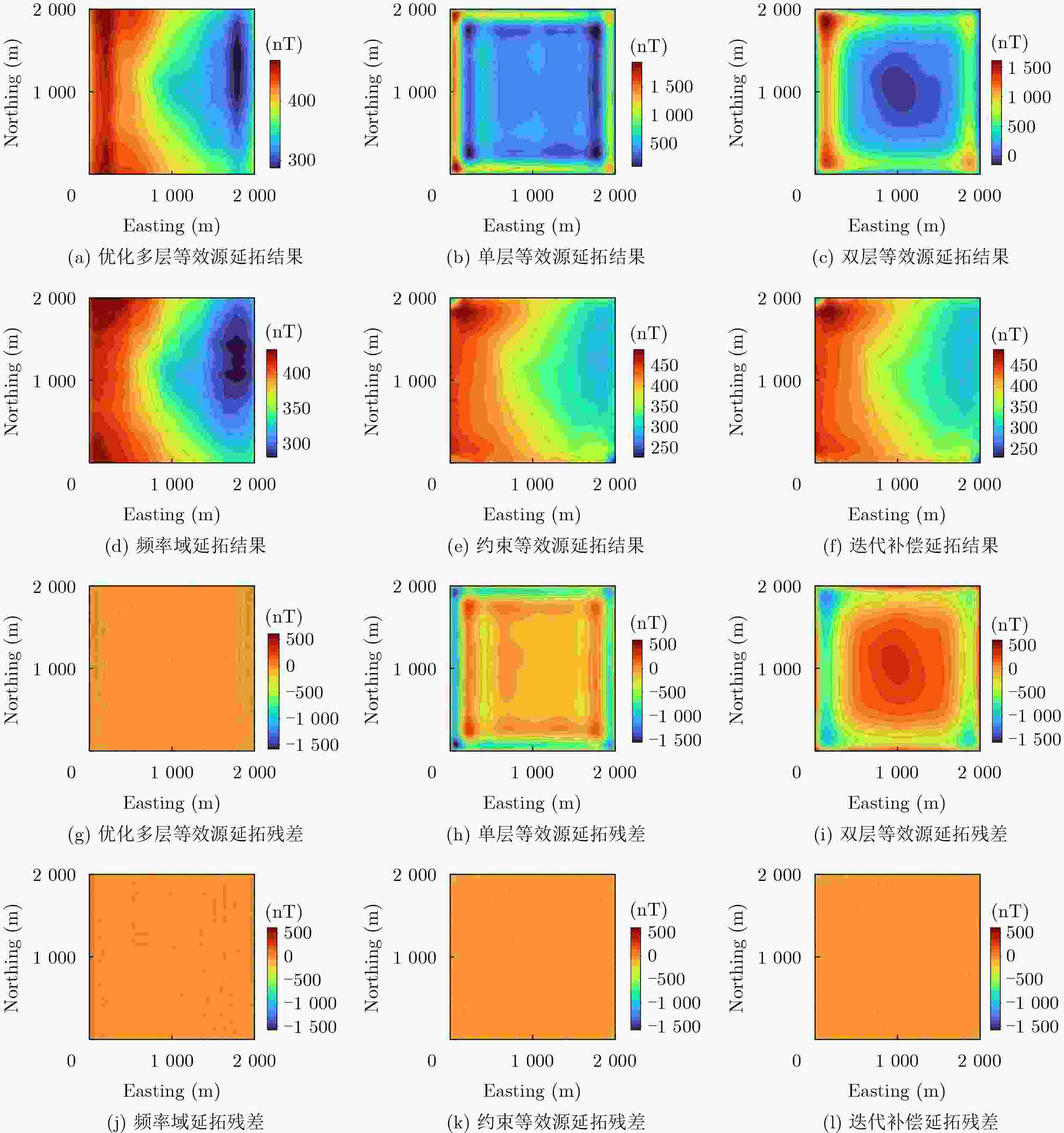
方法	RMSE(nT)	MaxAbsError(nT)	GradRMS(nT/m)	GOF(%)
优化多层等效源	4.88	16.56	2.31	98.94
单层等效源	251.06	1574.95	226.55	7.76
双层等效源	280.05	1228.15	181.48	12.15
频率域	93.69	160.52	1.95	67.76
约束等效源	12.83	202.38	7.22	96.67
迭代补偿	12.38	218.11	7.15	96.79

下载: 导出CSV

表 6 不同噪声水平下向下延拓结果的量化精度评估

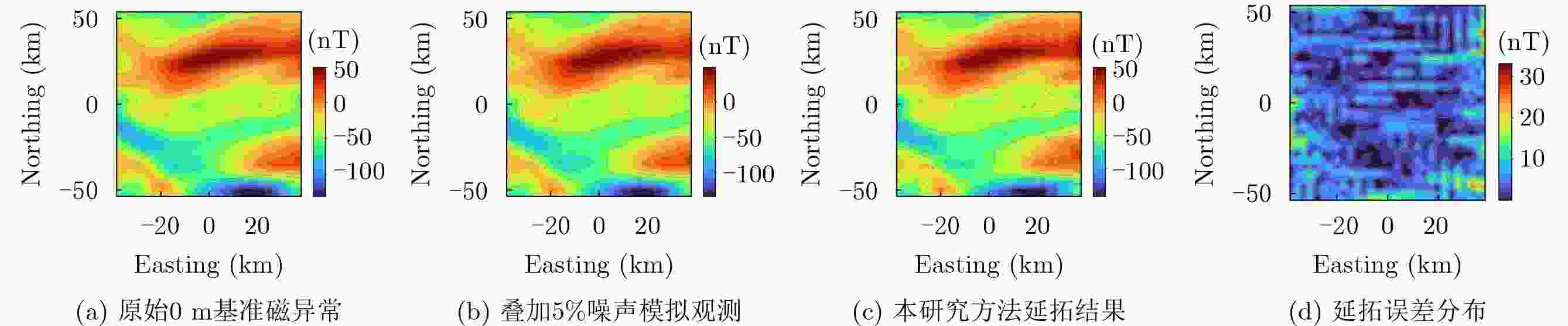
噪声水平	RMSE(nT)	MaxAbsError(nT)	GradRMS(nT/km)	GOF(%)
无噪声	2.53	10.93	0.78	94.04
含1%噪声	5.83	25.46	1.40	86.25
含5%噪声	7.36	34.71	1.90	82.65

下载: 导出CSV

表 7 不同地质区域参数

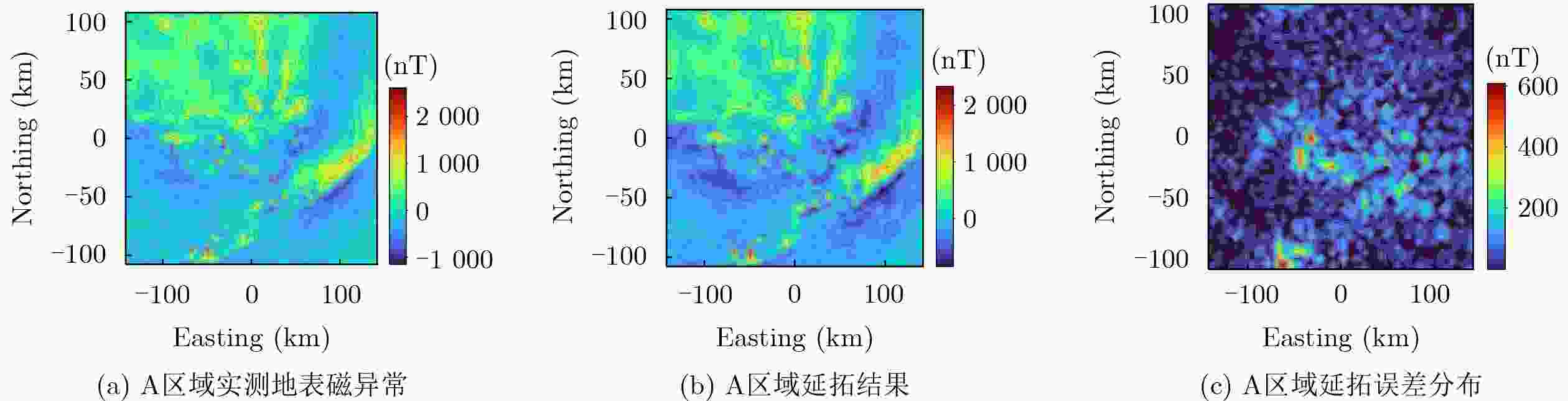
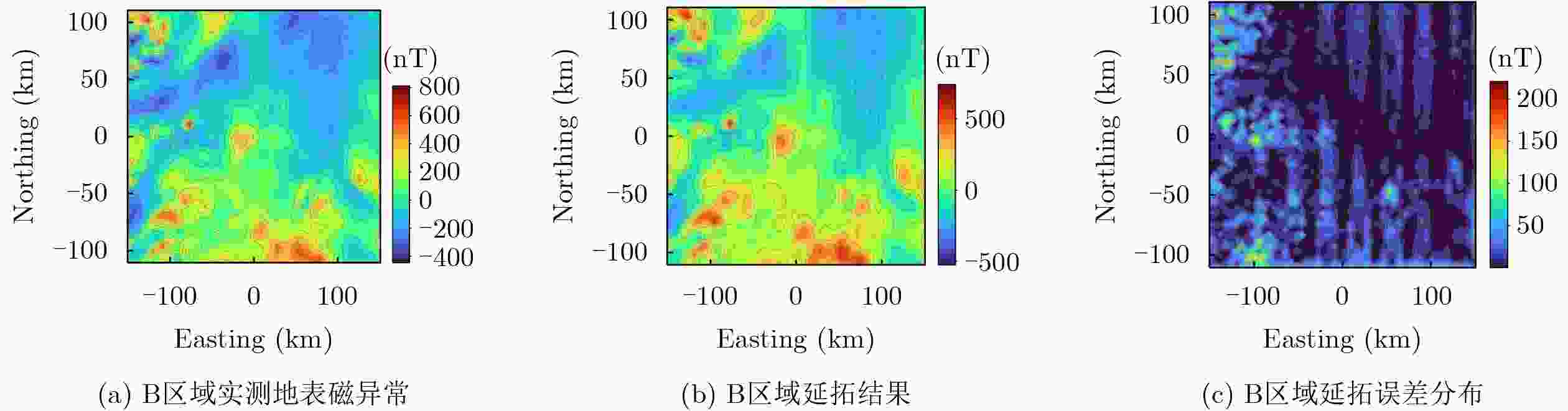
参数类别	实验区 A(浅部复杂构造区)	实验区 B(深部平缓基底区)
纬度范围	–30.9950°S～–29.0050°S	–25.9950°S ～–24.0050°S
经度范围	139.0050°E～141.9950°E	134.0050°E～136.9950°E
异常幅度范围	–2585 nT～5112 nT	–538 nT～2419 nT
地质特征	构造破碎、磁性梯度大、纹理复杂	构造平缓、磁性梯度弱、纹理简单

下载: 导出CSV

表 8 不同地质区域向下延拓结果的量化精度评估

区域	RMSE(nT)	MaxAbsError(nT)	GradRMS(nT/km)	GOF(%)
A	90.60	637.28	127.76	76.14
B	29.06	231.93	5.26	84.28

下载: 导出CSV

参考文献(21)

[1]	DAMPNEY C N G. The equivalent source technique[J]. Geophysics, 1969, 34(1): 39–53. doi: 10.1190/1.1439996.
[2]	BHATTACHARYYA B K and CHAN K C. Reduction of magnetic and gravity data on an arbitrary surface acquired in a region of high topographic relief[J]. Geophysics, 1977, 42(7): 1411–1430. doi: 10.1190/1.1440802.
[3]	王万银, 潘作枢, 李家康. 三维高精度重磁位场曲面延拓方法[J]. 物探与化探, 1991, 15(6): 415–422. WANG Wanyin, PAN Zuoshu, and LI Jiakang. Continuation methods for curved surface of the three-dimensional high-precision gravity and magnetic potential field[J]. Geophysical and Geochemical Exploration, 1991, 15(6): 415–422.
[4]	安玉林, 柴玉璞, 张明华, 等. 曲化平用最佳等效源模型及其单位位场表达式推导的新方法[J]. 地球物理学报, 2013, 56(7): 2473–2483. doi: 10.6038/cjg20130733. AN Yulin, CHAI Yupu, ZHANG Minghua, et al. An optimal model of the equivalent source for reduction-to-plane of potential field on uneven surface and the new method to deduce unit potential field expression of the optimal model[J]. Chinese Journal of Geophysics, 2013, 56(7): 2473–2483. doi: 10.6038/cjg20130733.
[5]	李端, 陈超, 杜劲松, 等. 多层等效源曲面磁异常转换方法[J]. 地球物理学报, 2018, 61(7): 3055–3073. doi: 10.6038/cjg2018L0362. LI Duan, CHEN Chao, DU Jinsong, et al. Transformation of magnetic anomaly data on an arbitrary surface by multi-layer equivalent sources[J]. Chinese Journal of Geophysics, 2018, 61(7): 3055–3073. doi: 10.6038/cjg2018L0362.
[6]	高宝龙, 胡正旺, 李端, 等. 多层等效源方法在地面与航空磁异常数据融合中的应用[J]. 地球科学, 2021, 46(5): 1881–1895. doi: 10.3799/dqkx.2020.134. GAO Baolong, HU Zhengwang, LI Duan, et al. Fusion of ground and airborne magnetic data using multi-layer equivalent source method[J]. Earth Science, 2021, 46(5): 1881–1895. doi: 10.3799/dqkx.2020.134.
[7]	LIU Tianyou, ZENG Xiaoniu, LI Xihai, et al. A nonnegative constrained method for high-precision downward continuation of gravity field data[J]. Journal of Applied Geophysics, 2025, 233: 105625. doi: 10.1016/j.jappgeo.2025.105625.
[8]	FENG Jinkai, LI Shanshan, FAN Haopeng, et al. An ACGLSR method for multi-layer equivalent source model inversion[J]. Journal of Applied Geophysics, 2025, 241: 105827. doi: 10.1016/j.jappgeo.2025.105827.
[9]	HUANG Shuanglong, QIU Jing, LI Mingyu, et al. 3D inversion of magnetic gradient data based on equivalent source weighting method[J]. AIP Advances, 2024, 14(1): 015057. doi: 10.1063/9.0000768.
[10]	ZUO Boxin, HU Xiangyun, WANG Lizhe, et al. Three-dimensional unstructured magnetization vector inversion and modeling of planetary equivalent toroidal currents for Earth’s magnetic field analysis[J]. Journal of Geophysical Research: Solid Earth, 2025, 130(1): e2024JB029224. doi: 10.1029/2024JB029224.
[11]	王泽庆, 孟小红, 王俊, 等. 一种改进的等效源模型设置方案[J]. 地球物理学进展, 2022, 37(3): 1189–1196. doi: 10.6038/pg2022FF0337. WANG Zeqing, MENG Xiaohong, WANG Jun, et al. Improved equivalent source model setting scheme[J]. Progress in Geophysics, 2022, 37(3): 1189–1196. doi: 10.6038/pg2022FF0337.
[12]	GHANBARIFAR S, HOSSEINI S H, GHIASI S M, et al. Joint Euler deconvolution for depth estimation of potential field magnetic and gravity data[J]. International Journal of Mining and Geo-Engineering, 2024, 58(2): 121–134. doi: 10.22059/ijmge.2023.363558.595090.
[13]	杨青青, 蒲雪莱, 彭艺, 等. HRIS辅助的分层稀疏重构混合远近场源定位算法[J]. 电子与信息学报, 2025, 47(11): 4220–4230. doi: 10.11999/JEIT250429. YANG Qingqing, PU Xuelai, PENG Yi, et al. HRIS-aided layered sparse reconstruction hybrid near-and far-field source localization algorithm[J]. Journal of Electronics & Information Technology, 2025, 47(11): 4220–4230. doi: 10.11999/JEIT250429.
[14]	张琪烁, 张文鑫, 高梦宇, 等. 基于双模微波雷达联合雨量计的降雨强度动态反演算法[J]. 电子与信息学报, 2025, 47(11): 4363–4372. doi: 10.11999/JEIT250535. ZHANG Qishuo, ZHANG Wenxin, GAO Mengyu, et al. Dynamic inversion algorithm for rainfall intensity based on dual-mode microwave radar combined rain gauge[J]. Journal of Electronics & Information Technology, 2025, 47(11): 4363–4372. doi: 10.11999/JEIT250535.
[15]	BLAKELY R J. Potential Theory in Gravity and Magnetic Applications[M]. Cambridge: Cambridge University Press, 1996: 45–50.
[16]	TIAN Hongjun, GU Zhiwen, ZHANG Guangda, et al. Exploration of anomaly separation technology of wide-field electromagnetic method[J]. Applied Geophysics, 2024, 21(2): 343–357. doi: 10.1007/s11770-021-0965-4.
[17]	刘高辉, 席宏恩. 改进变分模态分解与多特征的通信辐射源个体识别方法[J]. 电子与信息学报, 2024, 46(10): 4044–4052. doi: 10.11999/JEIT231348. LIU Gaohui and XI Hongen. Individual identification method for communication emitters based on improved variational modal decomposition and multiple features[J]. Journal of Electronics & Information Technology, 2024, 46(10): 4044–4052. doi: 10.11999/JEIT231348.
[18]	ATTOUCH H and LÁSZLÓ S C. Convex optimization via inertial algorithms with vanishing Tikhonov regularization: Fast convergence to the minimum norm solution[J]. Mathematical Methods of Operations Research, 2024, 99(3): 307–347. doi: 10.1007/s00186-024-00867-y.
[19]	ABDEL-BASSET M, MOHAMED R, and ABOUHAWWASH M. Fungal growth optimizer: A novel nature-inspired metaheuristic algorithm for stochastic optimization[J]. Computer Methods in Applied Mechanics and Engineering, 2025, 437: 117825. doi: 10.1016/j.cma.2025.117825.
[20]	周智文, 河水原, 孟小红, 等. 约束等效源稳定向下延拓方法研究[J]. 地球物理学报, 2022, 65(2): 754–762. doi: 10.6038/cjg2022P0121. ZHOU Zhiwen, HE Shuiyuan, MENG Xiaohong, et al. Stable downward continuation of potential field data using an equivalent source method and a constrained strategy[J]. Chinese Journal of Geophysics, 2022, 65(2): 754–762. doi: 10.6038/cjg2022P0121.
[21]	李晓杰, 王真理. 正则化等效层重力向下延拓方法[J]. 地球物理学报, 2018, 61(7): 3028–3036. doi: 10.6038/cjg2018L0249. LI XiaoJie and WANG Zhenli. A study on gravity field downward continuation using the regularized equivalent-layer method[J]. Chinese Journal of Geophysics, 2018, 61(7): 3028–3036. doi: 10.6038/cjg2018L0249.