鲁棒自适应稀疏阵列波束形成

范旭慧; 王宇翼; 王安义; 徐艳红; 崔灿

doi:10.11999/JEIT250952

鲁棒自适应稀疏阵列波束形成

doi: 10.11999/JEIT250952 cstr: 32379.14.JEIT250952

西安科技大学通信与信息工程学院西安 710054

基金项目: 国家自然科学基金(62471384, 62301414, 62301415)

详细信息

作者简介:
范旭慧：女，副教授，研究方向为阵列信号处理、优化算法

王宇翼：女，硕士生，研究方向为阵列信号处理

王安义：男，教授，研究方向为宽带数字移动通信与智能信息处理技术及煤矿智能化

徐艳红：女，教授，研究方向为新体制阵列波束综合与控制、宽带毫米波天线设计与矿业应用

崔灿：女，副教授，研究方向为阵列天线综合与优化、新体制阵列天线设计

通讯作者:
王安义　wanganyi@xust.edu.cn

中图分类号: TN911.7
计量
- 文章访问数: 69
- HTML全文浏览量: 30
- PDF下载量: 11
- 被引次数: 0
出版历程
- 收稿日期: 2025-09-22
- 修回日期: 2025-12-04
- 录用日期: 2025-12-04
- 网络出版日期: 2025-12-09

Robust Adaptive Beamforming for Sparse Arrays

School of Communication and Information Engineering, Xi’an University of Science and Technology, Xi’an 710054, China

Funds: The National Natural Science Foundation of China(62471384, 62301414, 62301415)

摘要

摘要: 波束形成技术在阵列信号处理，尤其是在波达方向估计方面发挥着关键作用。尽管传统的鲁棒波束形成方法能够处理导向矢量失配的问题，但它们未能充分利用阵列稀疏化带来的硬件优势，并且在存在干扰源时，难以有效抑制副瓣。因此，该文提出一种能够协同优化鲁棒性、波束性能、副瓣电平与阵列稀疏性的统一框架。通过将l₀范数作为稀疏约束、引入导向矢量误差以增强鲁棒性，并联合副瓣抑制约束，构建了一个全面的凸优化问题。特别地，该文在建模时进一步考虑了实际天线间的互耦效应，通过引入包含互耦参数的精确导向矢量模型，显著提升了算法在实际天线阵列中的适用性。仿真结果表明，在信噪比为5 dB、存在单个干扰源的条件下，所提算法能实现低于–40 dB的干扰抑制深度，并将峰值旁瓣电平稳定在–24.5 dB以下，同时减少10%的激活阵元。在与现有方法的定量对比中，该算法在信噪比为5 dB场景下的输出信干噪比相较于最小方差无失真响应方法提升11.37 dB。实验结果证明该框架能够在导向矢量失配及低信噪比等非理想条件下，以较少的阵元实现较高的输出信干噪比和较强的干扰抑制能力，对导向矢量误差与阵元间的相互耦合均表现出良好的鲁棒性。
- 自适应波束形成 /
- 稀疏阵列 /
- 鲁棒性约束 /
- 凸优化方法
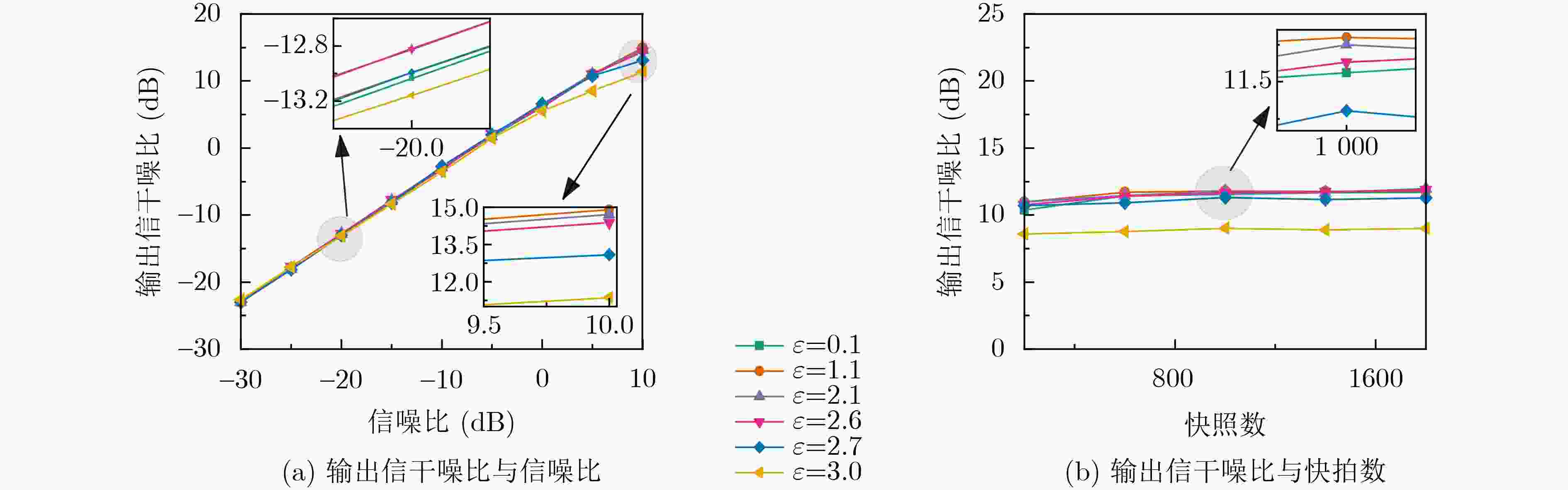
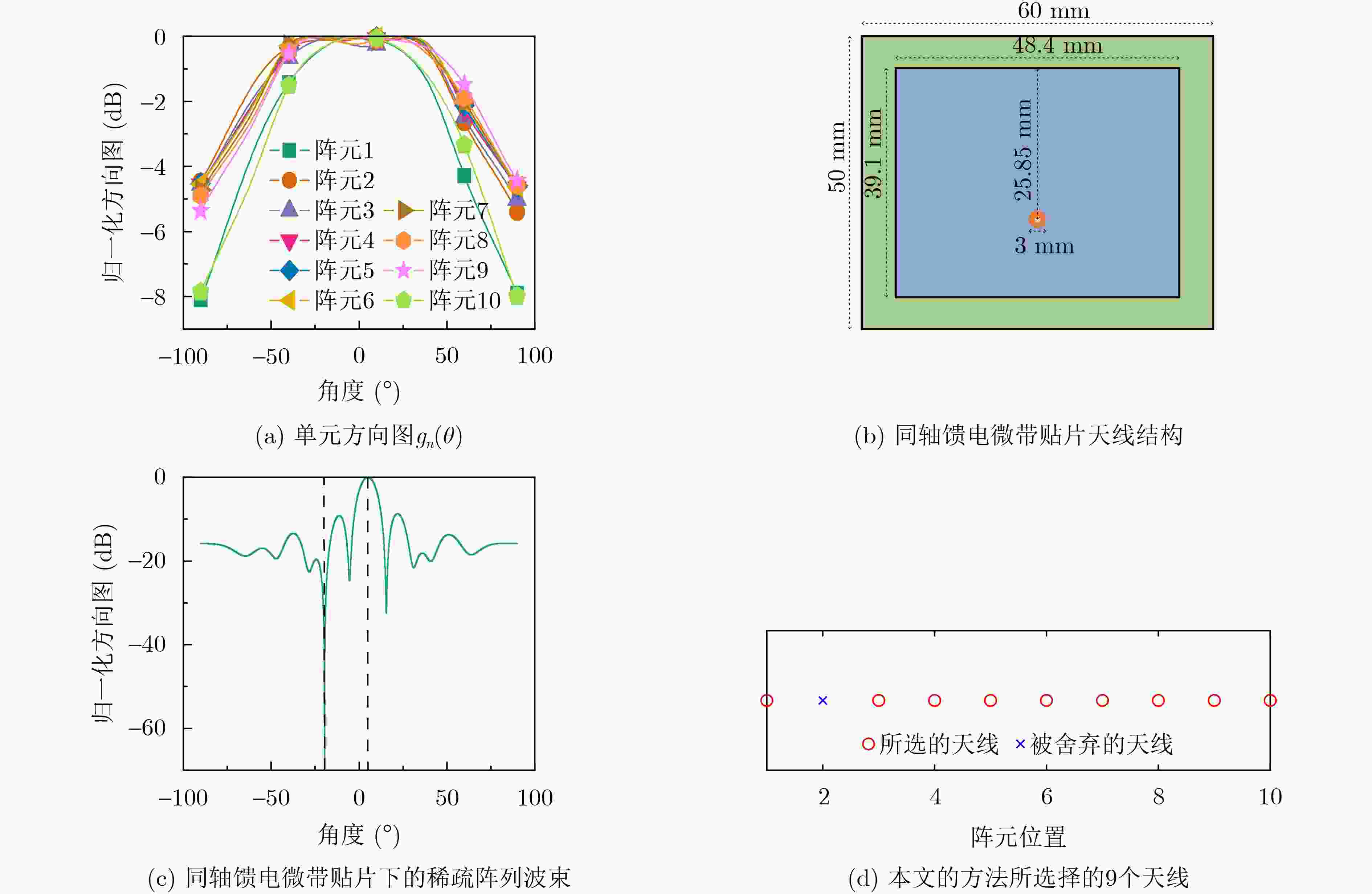
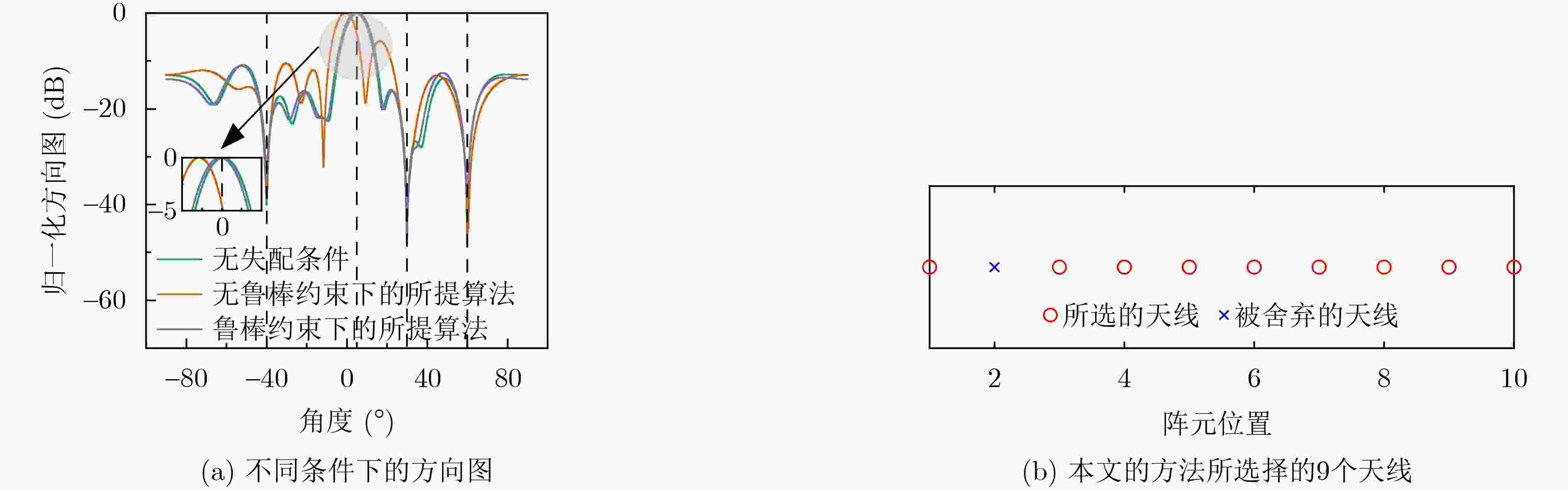
Abstract: Objective The rapid development of modern communication technologies, such as 5G networks and Internet of Things (IoT) applications, increases the complexity of signal processing in wireless communication and radar systems. Adaptive beamforming is widely used because it extracts the signal of interest in the presence of interference and noise. Traditional robust adaptive beamforming methods address steering vector mismatch, which may result from environmental nonstationarity, Direction-Of-Arrival (DOA) estimation errors, imperfect array calibration, antenna deformation, and local scattering. However, they do not leverage the advantages of the Sparse Array (SA), which reduces hardware complexity and system cost. They also often fail to suppress SideLobe Levels (SLLs) under interference conditions, limiting their effectiveness in complex electromagnetic environments. To address these issues, a robust adaptive beamforming algorithm is proposed that incorporates SA and low-SLL constraints. Methods Unlike conventional sparse approaches that place thel₀ norm penalty in the objective function, the proposed method introduces the l₀ norm into the constraint. This formulation ensures that the optimized array configuration meets the pre-specified number of active sensors and avoids the uncertainty associated with sparse-weight tuning in multi-objective optimization models. In addition to the sparsity constraint, an SLL suppression constraint is incorporated to impose an upper bound on array response in interference and clutter directions. By integrating these constraints into a unified optimization framework, the method achieves a robust Minimum Variance Distortionless Response (MVDR) beamforming scheme that exhibits sparsity, adaptivity, and robustness. To address the nonconvexity of the formulated optimization problem, a convex relaxation strategy is used to convert the nonconvex constraint into a convex one. Based on this formulation, robust adaptive beamforming methods are developed to generate a sparse weight solution from a Uniform Linear Array (ULA). Although the method is derived from a ULA, the sparse weight solution provides practical advantages. By assigning zero weights to selected sensors, the number of active elements is reduced, lowering hardware cost and computational burden while preserving desirable beamforming performance. The main contribution of this work lies in establishing a unified framework that enables collaborative optimization of robustness, beam performance, SLL, and array sparsity. Results and Discussions A series of simulation experiments were conducted to evaluate the performance of the proposed sparse robust beamforming algorithm under multiple scenarios, including multi-interference environments, steering vector mismatch, Angle-Of-Arrival (AOA) mismatch, low Signal-to-Noise Ratio (SNR) conditions, and complex electromagnetic environments based on practical antenna arrays. The results show that the algorithm maintains stable mainlobe gain in the desired signal direction while forming deep nulls in interference directions. First, in the presence of steering vector mismatch, conventional MVDR beamformers often exhibit reduced mainlobe gain or beam pointing deviation, which compromises desired-signal reception. By contrast, the proposed method maintains a stable, distortionless mainlobe direction under mismatch conditions, ensuring high gain in the desired signal direction (Fig. 2(a), Fig. 3(a)). Second, with the introduction of an SLL constraint, clutter is suppressed effectively and peak SLLs are reduced markedly (Fig. 2(b)). Third, under low-SNR conditions, the method shows strong noise resistance. Even in heavily noise-contaminated scenarios, it maintains effective interference suppression and achieves high output Signal-to-Interference-plus-Noise Ratio (SINR), demonstrating adaptability to weak-target detection and cluttered environments. Moreover, the optimized SA configuration achieves beamforming performance close to that of a ULA while activating only part of the sensors (Fig. 2). Finally, experimental validation using real antenna arrays further confirms the method’s effectiveness (Fig. 3). Stable performance is maintained, and high gain is achieved in the desired direction even under AOA estimation mismatch (Fig. 4). Overall, the results indicate that the proposed method enhances robustness and hardware efficiency and provides reliable performance in complex electromagnetic environments. Conclusions A robust adaptive beamforming algorithm for sparse arrays is proposed. The central innovation is the construction of a joint optimization model that integrates array sparsity, robustness to steering vector mismatch, and low SLL constraints within a unified framework. Compared with approaches such as MVDR, which emphasizes interference suppression, Covariance Matrix Reconstruction (CMR), which enhances robustness, and Non-Adjacent Constrained Sparsity (NACS), which achieves array sparsity, the proposed method attains a balanced improvement across these dimensions. Simulation results show that in scenarios featuring steering vector errors, AOA estimation mismatches, and low-SNR conditions, the method maintains satisfactory beamforming performance with reduced hardware cost, demonstrating strong practical engineering utility and application potential.
- Adaptive beamforming /
- Sparse Array (SA) /
- Robust constraints /
- Convex optimization

HTML全文

图 1 不同$ \varepsilon $值下的输出信干噪比变化

下载: 全尺寸图片幻灯片

图 2 不同算法的性能对比

下载: 全尺寸图片幻灯片

图 3 辐射以及波束成形的结果

下载: 全尺寸图片幻灯片

图 4 不同失配条件下优化的稀疏阵列结果

下载: 全尺寸图片幻灯片

表 1 各种算法的计算复杂度对比

算法	计算复杂度	主要计算来源
所提算法	$ O\left(\sqrt{N+J}\left({N}^{3}+N{K}^{2}+NJ\right)\right) $	多约束SOCP内点法求解
MVDR^[9]	$ O\left({N}^{3}\right) $	协方差矩阵求逆
CMR^[12]	$ O\left({N}^{3.5}\right) $	协方差矩阵重构与优化
NA-CS^[30]	$ O\left({N}^{2}D+{D}^{3}\right) $	稀疏重构与字典矩阵构建
注：$ N $是天线个数，$ K $是接收信号的采样点数，$ J $是副瓣区域采样点数，$ D $是离散化空域点数，通常远大于$ N $，导致其实际计算负担较重。

下载: 导出CSV

表 2 各种算法的性能对比

性能	MVDR^[9]	CMR^[12]	NA-CS^[30]	所提算法-考虑稀疏约束	所提算法-不考虑稀疏约束
输出信干噪比 (dB)(信噪比=5 dB)	0.17	11.24	8.68	11.54	12.63
干扰方向是否对齐	否	否	否	是	是
目标方向是否对齐	否	是	否	是	是
峰值旁瓣(dB)	–13.2	–16.8	–10.03	–24.5	–11.97
天线个数	10	10	6	9	10
是否具有鲁棒性	否	是	否	是	是
CPU时间(s)	0.19	0.59	10.35	1.13	1.09

下载: 导出CSV

参考文献(36)

[1]	LUO Jie, ZHANG Shurui, HAN Yubing, et al. Low complexity robust subband adaptive beamforming with frequency-angle coupling[J]. Digital Signal Processing, 2025, 164: 105288. doi: 10.1016/j.dsp.2025.105288.
[2]	BUI V P, VAN CHIEN T, LAGUNAS E, et al. Demand-based adaptive multi-beam placement and resource allocation in non-GSO satellite systems[J]. IEEE Transactions on Vehicular Technology, 2025. doi: 10.1109/TVT.2025.3610334.
[3]	SOMASUNDARAM S D. Linearly constrained robust Capon beamforming[J]. IEEE Transactions on Signal Processing, 2012, 60(11): 5845–5856. doi: 10.1109/TSP.2012.2212889.
[4]	巩朋成, 陈伟, 柯航, 等. 导向矢量失配条件下多约束鲁棒波束形成算法[J]. 信号处理, 2024, 40(10): 1855–1865. doi: 10.12466/xhcl.2024.10.010. GONG Pengcheng, CHEN Wei, KE Hang, et al. Multiple constraints robust beamforming algorithm under steering vector mismatch conditions[J]. Journal of Signal Processing, 2024, 40(10): 1855–1865. doi: 10.12466/xhcl.2024.10.010.
[5]	王兆彬, 巩朋成, 邓薇, 等. 联合协方差矩阵重构和ADMM的鲁棒波束形成[J]. 哈尔滨工业大学学报, 2023, 55(4): 64–71. doi: 10.11918/202107104. WANG Zhaobin, GONG Pengcheng, DENG Wei, et al. Robust beamforming by joint covariance matrix reconstruction and ADMM[J]. Journal of Harbin Institute of Technology, 2023, 55(4): 64–71. doi: 10.11918/202107104.
[6]	巩朋成, 刘永康, 吴云韬, 等. 基于多近似一致性ADMM的阵列方向图合成[J/OL]. https://link.cnki.net/urlid/32.1353.TN.20230113.1313.001, 2023. GONG Pengcheng, LIU Yongkang, WU Yuntao, et al. Array pattern synthesis based on multi-approximate Consistent-ADMM[J/OL]. https://link.cnki.net/urlid/32.1353.TN.20230113.1313.001, 2023.
[7]	LIU Yujin, WANG Zedan, and SUN Xuekai. Connections between least-squares migration, capon beamforming, and phase correction for seismic resolution enhancement[J]. IEEE Geoscience and Remote Sensing Letters, 2025, 22: 3002505. doi: 10.1109/LGRS.2025.3575170.
[8]	COX H, ZESKIND R, and OWEN M. Robust adaptive beamforming[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1987, 35(10): 1365–1376. doi: 10.1109/TASSP.1987.1165054.
[9]	CAPON J. High-resolution frequency-wavenumber spectrum analysis[J]. Proceedings of the IEEE, 1969, 57(8): 1408–1418. doi: 10.1109/PROC.1969.7278.
[10]	HUANG Yongwei, ZHOU Mingkang, and VOROBYOV S A. New designs on MVDR robust adaptive beamforming based on optimal steering vector estimation[J]. IEEE Transactions on Signal Processing, 2019, 67(14): 3624–3638. doi: 10.1109/TSP.2019.2918997.
[11]	ALI M, HAMEED K, and NATHWANI K. Enhancing traditional underwater DoA estimation techniques using convolutional autoencoder-based covariance matrix reconstruction[J]. IEEE Sensors Letters, 2025, 9(1): 7000304. doi: 10.1109/LSENS.2024.3516859.
[12]	LUO Tao, CHEN Peng, CAO Zhenxin, et al. URGLQ: An efficient covariance matrix reconstruction method for robust adaptive beamforming[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(5): 5634–5645. doi: 10.1109/TAES.2023.3263386.
[13]	YANG Yue, XU Xu, YANG Huichao, et al. Robust adaptive beamforming via covariance matrix reconstruction with diagonal loading on interference sources covariance matrix[J]. Digital Signal Processing, 2023, 136: 103977. doi: 10.1016/j.dsp.2023.103977.
[14]	SU Leqiang, LIU Hongwei, XU Xu, et al. Robust adaptive beamforming algorithm for multipath coherent reception based on iterative adaptive approach and covariance matrix reconstruction[J]. Digital Signal Processing, 2026, 168: 105532. doi: 10.1016/j.dsp.2025.105532.
[15]	MOHAMMADZADEH S, NASCIMENTO V H, DE LAMARE R C, et al. Maximum entropy-based interference-plus-noise covariance matrix reconstruction for robust adaptive beamforming[J]. IEEE Signal Processing Letters, 2020, 27: 845–849. doi: 10.1109/LSP.2020.2994527.
[16]	THOMAS J K, SCHARF L L, and TUFTS D W. The probability of a subspace swap in the SVD[J]. IEEE Transactions on Signal Processing, 1995, 43(3): 730–736. doi: 10.1109/78.370627.
[17]	MOLU M M, XIAO P, KHALILY M, et al. Low-complexity and robust hybrid beamforming design for multi-antenna communication systems[J]. IEEE Transactions on Wireless Communications, 2018, 17(3): 1445–1459. doi: 10.1109/TWC.2017.2778258.
[18]	SUN Linlin, QIN Yaolu, ZHUANG Zhihong, et al. A robust secure hybrid analog and digital receive beamforming scheme for efficient interference reduction[J]. IEEE Access, 2019, 7: 22227–22234. doi: 10.1109/ACCESS.2019.2899154.
[19]	CHAHROUR H, RAJAN S, DANSEREAU R, et al. Hybrid beamforming for interference mitigation in MIMO radar[C]. 2018 IEEE Radar Conference, Oklahoma City, USA, 2018: 1005–1009. doi: 10.1109/RADAR.2018.8378698.
[20]	AL KASSIR H, ZAHARIS Z D, LAZARIDIS P I, et al. A review of the state of the art and future challenges of deep learning-based beamforming[J]. IEEE Access, 2022, 10: 80869–80882. doi: 10.1109/ACCESS.2022.3195299.
[21]	LIU Fulai, QIN Hao, SUN Ziyuan, et al. WS-CACNN algorithm for robust adaptive beamforming[J]. Physical Communication, 2025, 71: 102666. doi: 10.1016/j.phycom.2025.102666.
[22]	SINGMAN M P and NARAYANAN R M. Applying machine learning to adaptive array signal processing weight generation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2024, 60(4): 4952–4962. doi: 10.1109/TAES.2024.3382620.
[23]	YE Sicong, XIAO Ming, KWAN M W, et al. Extremely large aperture array (ELAA) communications: Foundations, research advances and challenges[J]. IEEE Open Journal of the Communications Society, 2024, 5: 7075–7120. doi: 10.1109/OJCOMS.2024.3486172.
[24]	SHI Wanlu, VOROBYOV S A, and LI Yingsong. ULA fitting for sparse array design[J]. IEEE Transactions on Signal Processing, 2021, 69: 6431–6447. doi: 10.1109/TSP.2021.3125609.
[25]	WANG Xiangrong, GRECO M S, and GINI F. Adaptive sparse array beamformer design by regularized complementary antenna switching[J]. IEEE Transactions on Signal Processing, 2021, 69: 2302–2315. doi: 10.1109/TSP.2021.3064183.
[26]	NOSRATI H and ABOUTANIOS E. Online antenna selection for adaptive beamforming in MIMO radar[C]. 2020 IEEE Radar Conference, Florence, Italy, 2020: 1–6. doi: 10.1109/RadarConf2043947.2020.9266672.
[27]	LI Hongtao, RAN Longyao, HE Cheng, et al. Adaptive beamforming with sidelobe level control for multiband sparse linear array[J]. Remote Sensing, 2023, 15(20): 4929. doi: 10.3390/rs15204929.
[28]	ZHANG Xuan and WANG Xiangrong. Sparse adaptive beamformer design with a good quiescent beampattern[C]. 2019 IEEE International Conference on Signal, Information and Data Processing, Chongqing, China, 2019: 1–5. doi: 10.1109/ICSIDP47821.2019.9173179.
[29]	HUANG Jiayi, ZHANG Xuan, WANG Xiangrong, et al. Transmit sparse array beamformer design for dual-function radar communication systems[C]. 2023 IEEE International Radar Conference, Sydney, Australia, 2023: 1–6. doi: 10.1109/RADAR54928.2023.10371099.
[30]	陈力恒, 马晓川, 李璇, 等. 结合压缩感知模型的稀疏阵列波束形成方法[J]. 信号处理, 2020, 36(4): 475–485. doi: 10.16798/j.issn.1003-0530.2020.04.001. CHEN Liheng, MA Xiaochuan, LI Xuan, et al. Sparse array beamforming method combined with compressed sensing model[J]. Journal of Signal Processing, 2020, 36(4): 475–485. doi: 10.16798/j.issn.1003-0530.2020.04.001.
[31]	赵友瑜, 罗桂宁, 王姣, 等. 基于改进平滑L0范数的压缩感知重构算法[J]. 电脑知识与技术, 2024, 20(12): 35–38, 41. doi: 10.14004/j.cnki.ckt.2024.0596. ZHAO Youyu, LUO Guining, WANG Jiao, et al. Compressed sensing reconstruction algorithm based on improved smooth L0norm[J]. Computer Knowledge and Technology, 2024, 20(12): 35–38, 41. doi: 10.14004/j.cnki.ckt.2024.0596.
[32]	OLIVERI G, BEKELE E T, ROBOL F, et al. Sparsening conformal arrays through a versatile BCS-based method[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(4): 1681–1689. doi: 10.1109/TAP.2013.2287894.
[33]	EKSIOGLU E M and TANC A K. RLS algorithm with convex regularization[J]. IEEE Signal Processing Letters, 2011, 18(8): 470–473. doi: 10.1109/LSP.2011.2159373.
[34]	VOROBYOV S A, GERSHMAN A B, and LUO Zhiquan. Robust adaptive beamforming using worst-case performance optimization: A solution to the signal mismatch problem[J]. IEEE Transactions on Signal Processing, 2003, 51(2): 313–324. doi: 10.1109/TSP.2002.806865.
[35]	THAT V, MUY S, and LEE J R. Multi-UAV-aided power-up and data collection: Multi-agent DQL with genetic algorithm approach[J]. Expert Systems with Applications, 2026, 297: 129401. doi: 10.1016/j.eswa.2025.129401.
[36]	WANG Kunyu, SO A M C, CHANG T H, et al. Outage constrained robust transmit optimization for multiuser MISO downlinks: Tractable approximations by conic optimization[J]. IEEE Transactions on Signal Processing, 2014, 62(21): 5690–5705. doi: 10.1109/TSP.2014.2354312.