Multimodal Pedestrian Trajectory Prediction with Multi-Scale Spatio-Temporal Group Modeling and Diffusion
-
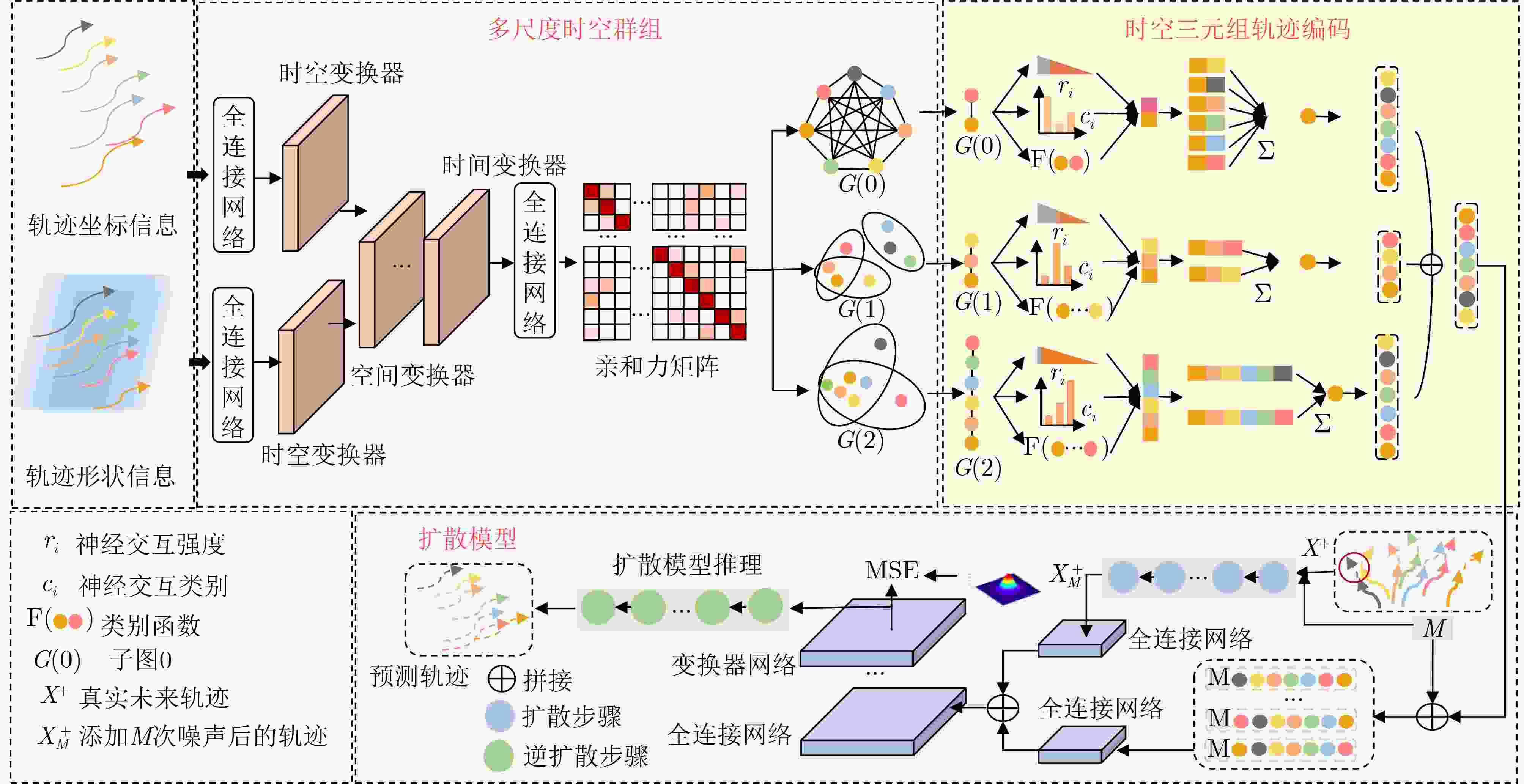
摘要: 针对行人轨迹预测中多模态特征捕捉不足及群体动态关系缺失的问题,该文提出了一种新颖的多模态行人轨迹预测框架——MSGD (Multi-Scale Spatio-Temporal Group Modeling and Diffusion),首先我们利用多尺度时空特征,准确构建多尺度时空群体;其次,设计时空交互三元组编码机制,对个体—邻居—群体的时空关系进行联合建模,兼顾局部交互细节与全局动态结构,提升对群体行为演化的表征能力。最后利用扩散模型的逆过程在生成阶段逐步减少可行区域内的不确定性,最终生成多样、合理且逼真的目标轨迹。该文在三个公开数据集(ETH、UCY和NBA数据集)上对所提出的方法进行了广泛评估,并与当前最先进的方法进行了比较。实验结果表明,MSGD框架在预测性能方面取得了显著提升,具体表现为平均偏移误差(ADE)和最终偏移误差(FDE)指标的显著改善,展现了其在建模复杂行人行为方面的有效性。Abstract:
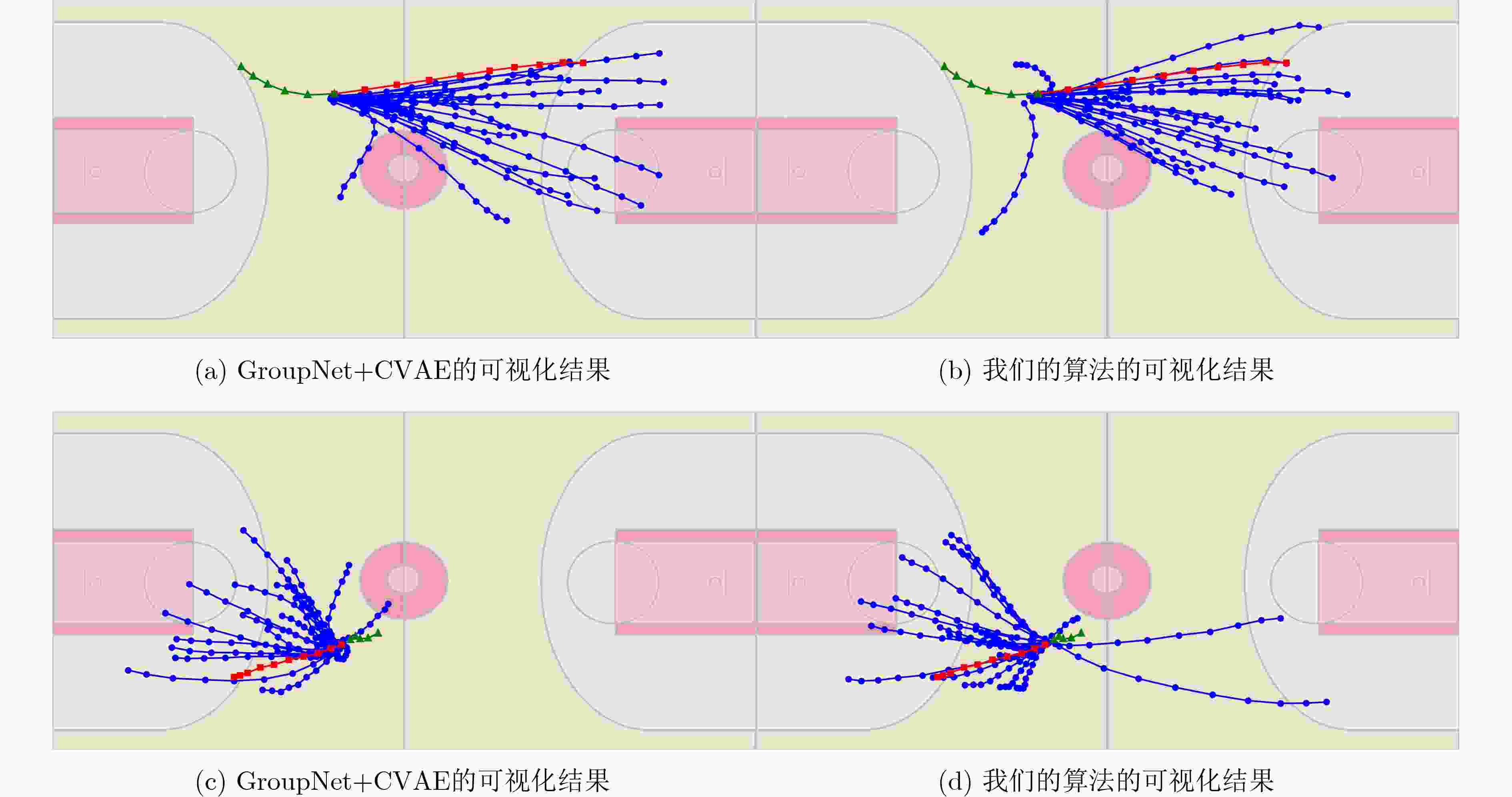
Objective With the rapid advancement of autonomous driving and social robotics, accurate pedestrian trajectory prediction has become pivotal for ensuring system safety and enhancing interaction efficiency. Existing group-based modeling approaches predominantly focus on local spatial interaction, often overlooking latent grouping characteristics across the temporal dimension. To address these challenges, this research proposes a multi-scale spatiotemporal feature construction method that achieves the decoupling of trajectory shape from absolute spatiotemporal coordinates, enabling the model to accurately capture the latent group associations over different time intervals. Simultaneously, spatiotemporal interaction three-element format encoding mechanism is introduced to deeply extract the dynamic relationships between individuals and groups. By integrating the reverse process length mechanism of diffusion models, the proposed approach incrementally mitigates prediction uncertainty. This research not only offers an intelligent solution for multi-modal trajectory prediction in complex, crowded environments but also provides robust theoretical support for improving the accuracy and robustness of long-range trajectory forecasting. Methods The proposed algorithm performs deep modeling of pedestrian trajectories through multi-scale spatiotemporal group modeling. The system is designed across three key dimensions: group construction, interaction modeling, and trajectory generation. First, to address the limitations of traditional methods that focus on local spatiotemporal relationships while overlooking cross-dimensional latent characteristics, A multi-scale trajectory grouping model is designed. Its core innovation lies in extracting trajectory offsets to represent trajectory shapes, successfully decoupling motion features from absolute positions. This enables the model to accurately capture latent group associations among agents following similar paths over different periods. Second, a coding method based on spatiotemporal interaction three-element format is proposed. By defining neural interaction strength, interaction categories, and category functions, this method deeply analyzes the complex associations between agents and groups. This not only captures fine-grained individual interactions but also effectively reveals the global dynamic evolution of collective behavior. Finally, a Diffusion Model is introduced for multimodal prediction. Through the reverse process length mechanism of the diffusion model, the model converges progressively, effectively eliminating uncertainty during the prediction process and transforming a fuzzy prediction space into clear and plausible future trajectories. Results and Discussions In this study, the proposed model was evaluated against 11 state-of-the-art baseline algorithms using the NBA dataset ( Table 1 ). Experimental results indicate that this model achieves a significant advantage in the minADE20. Notably, it demonstrates a substantial performance leap over GroupNet+CVAE in long-term prediction tasks, with minADE20 and minFDE20 improvements of 0.18 and 0.36, respectively, at the 4-second prediction horizon. Although the model slightly underperforms compared to MID in long-term trends—likely due to the frequent and intense shifts in group dynamics within NBA scenarios—it exhibits exceptional precision in instantaneous prediction. This provides strong empirical evidence for the effectiveness of multi-scale grouping strategy, based on historical trajectories, in capturing complex dynamic interactions. On the ETH/UCY datasets (Table 2 ), the MSGD method achieved consistent performance gains across all five sub-scenarios. Particularly in the pedestrian-dense and interaction-heavy UNIV scene, the proposed method surpassed all baseline models by leveraging the advantages of multi-scale modeling. While MSGD is slightly behind PPT in terms of long-distance endpoint constraints, it maintains a lead in minADE20. Furthermore, it outperforms Trajectory++ in velocity smoothness and directional coherence (std dev:0.7012 ) (Table 3 ). These results suggest that while fitting the geometric shape of trajectories, the method generates naturally smooth paths that align more closely with the physical laws of human motion. Ablation studies systematically verified the independent contributions of the diffusion model, spatiotemporal feature extraction, and multi-scale grouping modules to the overall accuracy (Table 4 ). Grouping sensitivity analysis on the NBA dataset revealed that a full-court grouping strategy (group size of 11) significantly enhances long-term stability, resulting in a further reduction of minFDE20 by 0.026–0.03 at the 4-second (Table 5 ). Simultaneously, configurations with group sizes of 5 or 2 validate the significance of team formations and “one-on-one” local offensive/defensive dynamics in trajectory prediction (Table 6 ). Additionally, sensitivity analysis of diffusion steps and training epochs revealed a “complementary” relationship: moderately increasing the number of steps (e.g., 30–40) refines the denoising process and significantly improves accuracy, whereas excessive iterations may lead to overfitting (Table 7 ). Finally, qualitative visualization intuitively demonstrates that the multimodal trajectories generated by MSGD have a high degree of overlap with ground-truth data (Fig.2 ).Conclusions This study proposes a novel trajectory prediction algorithm that enhances performance primarily in two aspects: (1) It effectively captures pedestrian interactions by extracting spatiotemporal features; (2) It strengthens the modeling of collective behavior by grouping pedestrians across multiple scales. Experimental results demonstrate that the algorithm achieves state-of-the-art (SOTA) performance on both the NBA and ETH/UCY datasets. Furthermore, ablation studies verify the effectiveness of each constituent module. Despite its superior performance and adaptability, the proposed algorithm has two primary limitations: first, the current model does not account for explicit environmental information (such as maps or obstacles); second, the diffusion model involves high computational overhead during inference. Future work will focus on improvements and research in these two directions. -
表 1 NBA数据集上minADE20和minFDE20的表现(m)。数值越低模型预测的越好。粗体表示最佳,斜体表示次优。
1s 2s 3s 4s ADE FDE ADE FDE ADE FDE ADE FDE Social-LSTM[3] 0.45 0.67 0.88 1.53 1.33 2.38 1.79 3.16 Social-GAN[22] 0.46 0.65 0.85 1.36 1.24 1.98 1.62 2.51 Social-STGCNN[23] 0.36 0.50 0.75 0.99 1.15 1.79 1.59 2.37 STGAT[24] 0.38 0.55 0.73 1.18 1.07 1.74 1.41 2.22 NRI[25] 0.45 0.64 0.84 1.44 1.24 2.18 1.62 2.84 STAR[26] 0.43 0.65 0.77 1.28 1.00 1.55 1.26 2.04 PECNet[27] 0.51 0.76 0.96 1.69 1.41 2.52 1.83 3.41 NMMP[28] 0.38 0.54 0.70 1.11 1.01 1.61 1.33 2.05 CVAE[17] 0.37 0.52 0.67 1.06 0.96 1.51 1.25 1.96 GroupNet+CVAE[17] 0.34 0.48 0.62 0.95 0.87 1.31 1.13 1.69 MID[29] 0.28 0.37 0.51 0.72 0.71 0.98 0.96 1.27 MSGD 0.23 0.32 0.47 0.72 0.70 1.03 0.94 1.33 表 2 在ETH-UCY数据集上minADE20和minFDE20的表现(m)。数值越低模型预测的越好。粗体表示最优,斜体表示次优。
ETH HOTEL UNIV ZARA1 ZARA2 AVG ADE FDE ADE FDE ADE FDE ADE FDE ADE FDE ADE FDE Social-LSTM[3] 1.09 2.35 0.79 1.76 0.67 1.40 0.47 1.00 0.56 1.17 0.72 1.54 Social-GAN[22] 0.87 1.62 0.67 1.37 0.76 1.52 0.35 0.68 0.42 0.84 0.61 1.21 Social-Attention[30] 1.39 2.39 2.51 2.91 1.25 2.54 1.01 2.17 0.88 1.75 1.41 2.35 SOPHIE[31] 0.70 1.43 0.76 1.67 0.54 1.24 0.30 0.63 0.38 0.78 0.54 1.15 STGAT[24] 0.65 1.12 0.35 0.66 0.52 1.10 0.34 0.69 0.29 0.60 0.43 0.83 NMMP[28] 0.61 1.08 0.33 0.63 0.52 1.11 0.32 0.66 0.43 0.85 0.41 0.82 STAR[26] 0.36 0.65 0.17 0.36 0.31 0.62 0.26 0.55 0.22 0.46 0.26 0.53 GroupNet+CVAE[17] 0.46 0.73 0.15 0.25 0.26 0.49 0.21 0.39 0.17 0.33 0.25 0.44 PCCSNET[32] 0.28 0.54 0.11 0.19 0.29 0.60 0.21 0.44 0.15 0.34 0.21 0.42 PCCSNET+KE loss[33] 0.26 Null 0.13 Null 0.28 Null 0.20 Null 0.16 Null 0.21 Null MID[29] 0.39 0.66 0.13 0.22 0.22 0.45 0.17 0.30 0.13 0.27 0.21 0.38 PPT[34] 0.36 0.51 0.11 0.15 0.22 0.40 0.17 0.30 0.12 0.21 0.20 0.31 MSGD 0.37 0.58 0.11 0.21 0.20 0.39 0.16 0.29 0.12 0.26 0.19 0.35 表 3 在ETH数据集上预测轨迹与真实轨迹的速度差与方向相似度的标准差。
速度差标准差 方向相似度标准差 Trajectory++[35] 0.0453 0.8054 MSGD 0.0415 0.7012 表 4 NBA数据集中的消融实验结果(ADE/FDE)(m)。粗体字表示最佳结果。
序号 组件 1 s 2 s 3 s 4 s 多尺度群组 时空特征 扩散模型 ADE FDE ADE FDE ADE FDE ADE FDE 1 √ √ 0.28 0.38 0.53 0.77 0.78 1.10 1.01 1.37 2 √ √ 0.31 0.43 0.58 0.90 0.82 1.26 1.09 1.65 3 √ √ 0.25 0.34 0.50 0.75 0.75 1.07 0.98 1.35 4 √ √ √ 0.23 0.32 0.47 0.72 0.70 1.03 0.94 1.33 表 5 NBA 数据集上不同分组规模下的性能( minADE20/minFDE20) (m)。数值越低,模型预测的越好。粗体表示最优,斜体表示次优。
1s 2s 3s 4s ADE FDE ADE FDE ADE FDE ADE FDE 2 0.230 0.327 0.472 0.736 0.710 1.049 0.947 1.360 2,3 0.229 0.326 0.471 0.734 0.709 1.045 0.946 1.355 2,3,5 0.229 0.326 0.471 0.735 0.709 1.045 0.945 1.352 2,3,5,11 0.229 0.324 0.467 0.724 0.698 1.025 0.929 1.324 表 6 NBA数据集上不同分组下的minADE20和minFDE20(m)。数值越低模型预测的越好。粗体表示最优,斜体表示次优。
1s 2s 3s 4s ADE FDE ADE FDE ADE FDE ADE FDE 2 0.2302 0.3271 0.4724 0.7364 0.7103 1.0490 0.9471 1.3598 3 0.2308 0.3282 0.4729 0.7368 0.7108 1.0498 0.9468 1.3585 4 0.2303 0.3274 0.4722 0.7367 0.7114 1.0489 0.9493 1.3570 5 0.2388 0.3253 0.4720 0.7352 0.7098 1.0467 0.9465 1.3533 11 0.2390 0.3260 0.4697 0.7299 0.7037 1.0342 0.9369 1.3375 表 7 ETH上不同扩散步骤和训练轮数下 minADE20和minFDE20(m)。数值越低模型预测的越好。粗体表示最优,斜体表示次优。
30 60 90 ADE FDE ADE FDE ADE FDE 10 0.5655 0.9261 0.5993 1.0191 0.6292 1.1002 20 0.4331 0.7096 0.4631 0.7347 0.4360 0.7086 30 0.3856 0.5445 0.3839 0.5517 0.4191 0.6262 40 0.4245 0.6646 0.3508 0.5097 0.3826 0.5866 50 0.3909 0.5774 0.3624 0.5263 0.3761 0.5807 60 0.3766 0.5395 0.3856 0.5723 0.3793 0.5570 70 0.3931 0.5820 0.3917 0.6014 0.3719 0.6061 80 0.3685 0.5244 0.3844 0.5859 0.3826 0.5755 90 0.3721 0.5233 0.3970 0.6047 0.3901 0.6006 100 0.4654 0.7959 0.3991 0.6376 0.4214 0.6927 -
[1] 李暾, 朱耀堃, 吴欣虹, 等. 基于卡口上下文和深度置信网络的车辆轨迹预测模型研究[J]. 电子与信息学报, 2021, 43(5): 1323–1330. doi: 10.11999/JEIT200137.LI Tun, ZHU Yaokun, WU Xinhong, et al. Vehicle trajectory prediction method based on intersection context and deep belief network[J]. Journal of Electronics & Information Technology, 2021, 43(5): 1323–1330. doi: 10.11999/JEIT200137. [2] THERESA W G, MADHIMITHRA R, and BHAVANA G. A hybrid RL-GNN approach for precise pedestrian trajectory prediction in autonomous navigation[C]. 8th International Conference on Trends in Electronics and Informatics, Tirunelveli, India, 2025: 1485–1490. doi: 10.1109/ICOEI65986.2025.11013272. [3] ALAHI A, GOEL K, RAMANATHAN V, et al. Social LSTM: Human trajectory prediction in crowded spaces[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 961–971. doi: 10.1109/CVPR.2016.110. [4] 余浩扬, 李艳生, 肖凌励, 等. 面向动态环境的巡检机器人轻量级语义视觉SLAM框架[J]. 电子与信息学报, 2025, 47(10): 3979–3992. doi: 10.11999/JEIT250301.YU Haoyang, LI Yansheng, XIAO Lingli, et al. A lightweight semantic visual simultaneous localization and mapping framework for inspection robots in dynamic environments[J]. Journal of Electronics & Information Technology, 2025, 47(10): 3979–3992. doi: 10.11999/JEIT250301. [5] WEI Xiaoge, LV Wei, SONG Weiguo, et al. Survey study and experimental investigation on the local behavior of pedestrian groups[J]. Complexity, 2015, 20(6): 87–97. doi: 10.1002/cplx.21633. [6] MOUSSAÏD M, PEROZO N, GARNIER S, et al. The walking behaviour of pedestrian social groups and its impact on crowd dynamics[J]. PLoS One, 2010, 5(4): e10047. doi: 10.1371/journal.pone.0010047. [7] 霍如, 吕科呈, 黄韬. 车联网中路径预测驱动的任务切分与计算资源分配方法[J]. 电子与信息学报, 2025, 47(10): 3658–3669. doi: 10.11999/JEIT250135.HUO Ru, LÜ Kecheng, and HUANG Tao. Task segmentation and computing resource allocation method driven by path prediction in internet of vehicles[J]. Journal of Electronics & Information Technology, 2025, 47(10): 3658–3669. doi: 10.11999/JEIT250135. [8] 毛琳, 解云娇, 杨大伟, 等. 行人轨迹预测条件端点局部目的地池化网络[J]. 电子与信息学报, 2022, 44(10): 3465–3475. doi: 10.11999/JEIT210716.MAO Lin, XIE Yunjiao, YANG Dawei, et al. Local destination pooling network for pedestrian trajectory prediction of condition endpoint[J]. Journal of Electronics & Information Technology, 2022, 44(10): 3465–3475. doi: 10.11999/JEIT210716. [9] LIANG Junwei, JIANG Lu, MURPHY K, et al. The garden of forking paths: Towards multi-future trajectory prediction[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, USA, 2020: 10505–10515. doi: 10.1109/CVPR42600.2020.01052. [10] 周传鑫, 简刚, 李凌书, 等. 融合兴趣点和联合损失函数的长时航迹预测模型[J]. 电子与信息学报, 2025, 47(8): 2841–2849. doi: 10.11999/JEIT250011.ZHOU Chuanxin, JIAN Gang, LI Lingshu, et al. Long-term trajectory prediction model based on points of interest and joint loss function[J]. Journal of Electronics & Information Technology, 2025, 47(8): 2841–2849. doi: 10.11999/JEIT250011. [11] HELBING D and MOLNÁR P. Social force model for pedestrian dynamics[J]. Physical Review E, 1995, 51(5): 4282–4286. doi: 10.1103/PhysRevE.51.4282. [12] SCARSELLI F, GORI M, TSOI A C, et al. The graph neural network model[J]. IEEE Transactions on Neural Networks, 2009, 20(1): 61–80. doi: 10.1109/TNN.2008.2005605. [13] WU Zonghan, PAN Shirui, CHEN Fengwen, et al. A comprehensive survey on graph neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(1): 4–24. doi: 10.1109/TNNLS.2020.2978386. [14] WANG Chenyue and WANG Dongyu. Advancing federated learning in IoV: GNN-based trajectory prediction and privacy protection[C]. 2025 IEEE Wireless Communications and Networking Conference, Milan, Italy, 2025: 1–6. doi: 10.1109/WCNC61545.2025.10978319. [15] BAE I, PARK J H, and JEON H G. Learning pedestrian group representations for multi-modal trajectory prediction[C]. 17th European Conference on Computer Vision, Tel Aviv, Israel, 2022: 270–289. doi: 10.1007/978-3-031-20047-2_16. [16] MOUSSAÏD M, PEROZO N, GARNIER S, et al. The walking behaviour of pedestrian social groups and its impact on crowd dynamics[J]. PLoS One, 2010, 5(4): e10047. doi: 10.1371/journal.pone.0010047.(查阅网上资料,本条文献与第6条文献重复,请确认). [17] XU Chenxin, LI Maosen, NI Zhenyang, et al. GroupNet: Multiscale hypergraph neural networks for trajectory prediction with relational reasoning[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, USA, 2022: 6488–6497. doi: 10.1109/CVPR52688.2022.00639. [18] ZHANG Yuzhen, SU Junning, GUO Hang, et al. S-CVAE: Stacked CVAE for trajectory prediction with incremental greedy region[J]. IEEE Transactions on Intelligent Transportation Systems, 2024, 25(12): 20351–20363. doi: 10.1109/TITS.2024.3465836. [19] YANG Jiayu, LEE J J, and ANTONIOU C. Trajectory prediction for multiple agents in dynamic environments: Factoring in traffic states and driving styles[J]. IEEE Transactions on Intelligent Transportation Systems, 2025, 26(11): 19281–19295. doi: 10.1109/TITS.2025.3595743. [20] WEI Chuheng, WU Guoyuan, BARTH M J, et al. KI-GAN: Knowledge-informed generative adversarial networks for enhanced multi-vehicle trajectory forecasting at signalized intersections[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, USA, 2024: 7115–7124. doi: 10.1109/CVPRW63382.2024.00706. [21] CHEN Yanbo, YU Huilong, and XI Junqiang. STS-GAN: Spatial-temporal attention guided social GAN for vehicle trajectory prediction[C]. 16th International Symposium on Advanced Vehicle Control, Milan, Italy, 2024: 164–170. doi: 10.1007/978-3-031-70392-8_24. [22] GUPTA A, JOHNSON J, FEI-FEI L, et al. Social GAN: Socially acceptable trajectories with generative adversarial networks[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA, 2018: 2255–2264. doi: 10.1109/CVPR.2018.00240. [23] MOHAMED A, QIAN Kun, ELHOSEINY M, et al. Social-STGCNN: A social spatio-temporal graph convolutional neural network for human trajectory prediction[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, USA, 2020: 14412–14420. doi: 10.1109/CVPR42600.2020.01443. [24] HUANG Yingfan, BI Huikun, LI Zhaoxin, et al. STGAT: Modeling spatial-temporal interactions for human trajectory prediction[C]. The IEEE/CVF International Conference on Computer Vision, Seoul, Korea (South), 2019: 6271–6280. doi: 10.1109/ICCV.2019.00637. [25] KIPF T N, FETAYA E, WANG K C, et al. Neural relational inference for interacting systems[C]. Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 2018: 2693–2702. [26] YU Cunjun, MA Xiao, REN Jiawei, et al. Spatio-temporal graph transformer networks for pedestrian trajectory prediction[C]. 16th European Conference on Computer Vision, Glasgow, UK, 2020: 507–523. doi: 10.1007/978-3-030-58610-2_30. [27] MANGALAM K, GIRASE H, AGARWAL S, et al. It is not the journey but the destination: Endpoint conditioned trajectory prediction[C]. 16th European Conference on Computer Vision, Glasgow, UK, 2020: 759–776. doi: 10.1007/978-3-030-58536-5_45. [28] HU Yue, CHEN Siheng, ZHANG Ya, et al. Collaborative motion prediction via neural motion message passing[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, USA, 2020: 6318–6327. doi: 10.1109/CVPR42600.2020.00635. [29] GU Tianpei, CHEN Guangyi, LI Junlong, et al. Stochastic trajectory prediction via motion indeterminacy diffusion[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, USA, 2022: 17092–17101. doi: 10.1109/CVPR52688.2022.01660. [30] SOHL-DICKSTEIN J, WEISS E A, MAHESWARANATHAN N, et al. Deep unsupervised learning using nonequilibrium thermodynamics[C]. Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 2015: 2256–2265. [31] SADEGHIAN A, KOSARAJU V, SADEGHIAN A, et al. SoPhie: An attentive GAN for predicting paths compliant to social and physical constraints[C]. The IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, USA, 2019: 1349–1358. doi: 10.1109/CVPR.2019.00144. [32] SUN Jianhua, LI Yuxuan, FANG Haoshu, et al. Three steps to multimodal trajectory prediction: Modality clustering, classification and synthesis[C]. Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, Canada, 2021: 13230–13239. doi: 10.1109/ICCV48922.2021.01300. [33] LIN Xiaotong, LIANG Tianming, LAI Jianhuang, et al. Progressive pretext task learning for human trajectory prediction[C]. 18th European Conference on Computer Vision, Milan, Italy, 2025: 197–214. doi: 10.1007/978-3-031-73404-5_12. [34] LI Linhui, LIN Xiaotong, HUANG Yejia, et al. Beyond minimum-of-N: Rethinking the evaluation and methods of pedestrian trajectory prediction[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2024, 34(12): 12880–12893. doi: 10.1109/TCSVT.2024.3439128. [35] SALZMANN T, IVANOVIC B, CHAKRAVARTY P, et al. Trajectron++: Dynamically-feasible trajectory forecasting with heterogeneous data[C]. 16th European Conference on Computer Vision, Glasgow, UK, 2020: 683–700. doi: 10.1007/978-3-030-58523-5_40. -





 下载:
下载:


 下载:
下载:
