多矩阵的代表性顺序统计量译码算法

王义文; 王千帆; 梁济凡; 宋林琦; 马啸

doi:10.11999/JEIT250854

多矩阵的代表性顺序统计量译码算法

doi: 10.11999/JEIT250854 cstr: 32379.14.JEIT250854

王义文^{1, 2},
王千帆^{3, 4, ,},
梁济凡^{1, 2},
宋林琦^{3, 4},
马啸^{1, 2}

1.
中山大学计算机学院广东 510006
2.
中山大学广东省信息安全重点实验室广州 510006
3.
香港城市大学香港 999077
4.
香港城市大学深圳研究院深圳 518000

基金项目: 国家重点研发计划(No.2020YFB1807100)，国家自然科学基金面上项目(62471506, 62301617, 62371411)，广东省基础与应用基础研究基金(2025A1515011650)，港澳“青年科技人才托举工程”项目(QT-025-048)

详细信息

作者简介:
王义文：男，博士生，研究方向为信道编码及其在无线通信中的应用

王千帆：男，博士后，研究方向为信道编码及其在无线通信中的应用、无线电通信技术等

梁济凡：男，博士生，研究方向为经典纠错码与量子码译码技术

宋林琦：男，副教授，博士生导师，研究方向为人工智能和信息论领域的结合等

马啸：男，教授，博士生导师，主要研究方向为信息与编码理论、编码调制技术、无线通信、光通信等

通讯作者:
王千帆　qwang742@cityu.edu.hk

中图分类号: TN92
计量
- 文章访问数: 43
- HTML全文浏览量: 15
- PDF下载量: 1
- 被引次数: 0
出版历程
- 修回日期: 2025-12-31
- 录用日期: 2025-12-31
- 网络出版日期: 2026-01-08

Multi-Matrix Representative Ordered Statistics Decoding

WANG Yiwen^{1, 2},
WANG Qianfan^{3, 4
, ,},
LIANG Jifan^{1, 2},
SONG Linqi^{3, 4},
MA Xiao^{1, 2}

1.
School of Computer Science and Engineering, Sun Yat-sen University, Guangzhou 510006, China
2.
Guangdong Key Laboratory of Information Security Technology, Sun Yat-sen University, Guangzhou 510006, China
3.
City University of Hong Kong, Hong Kong, 999077, China
4.
City University of Hong Kong Shenzhen Research Institute, Shenzhen 518000, China

Funds: The National Key R&D Program of China (No.2020YFB1807100), the National Natural Science Foundation of China (62471506, 62301617, 62371411), Guangdong Basic and Applied Basic Research Foundation (2025A1515011650), Young Talent Support Project of Guangzhou Association for Science and Technology (QT-025-048)

摘要

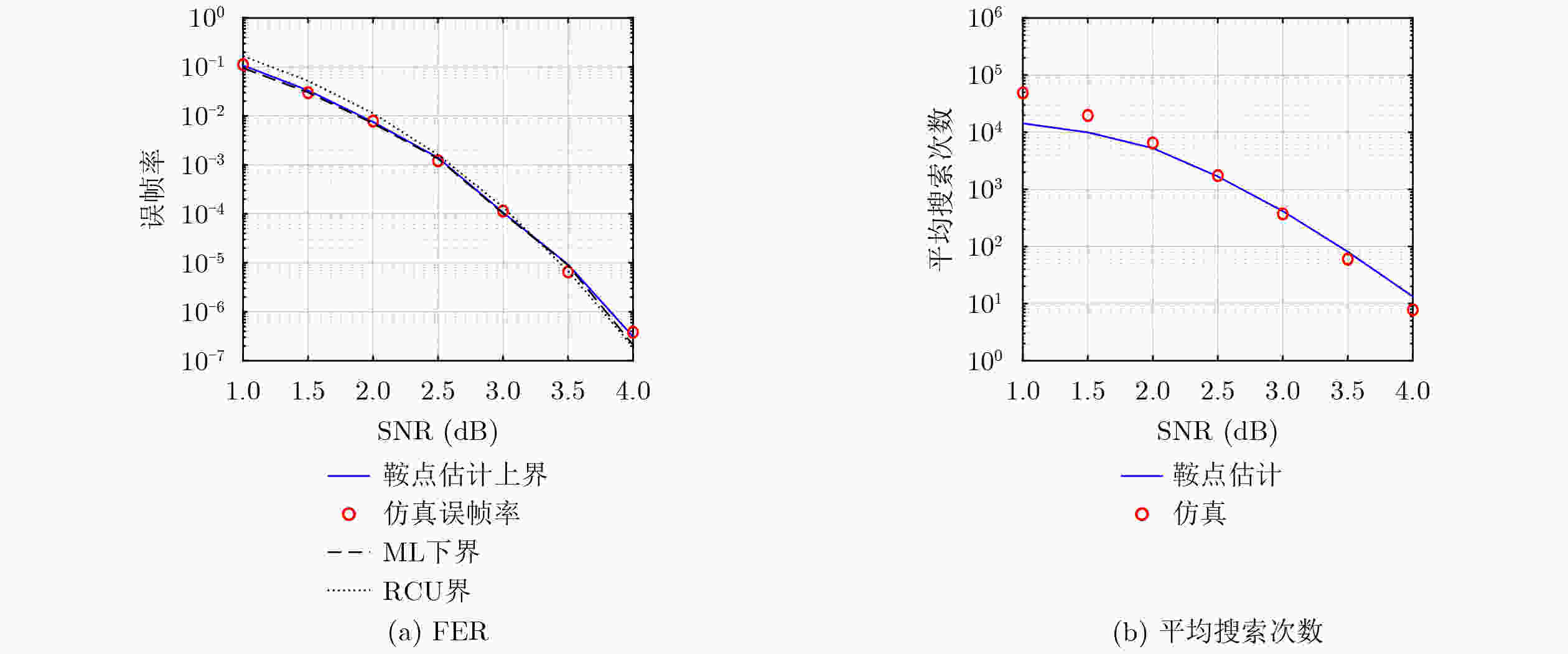
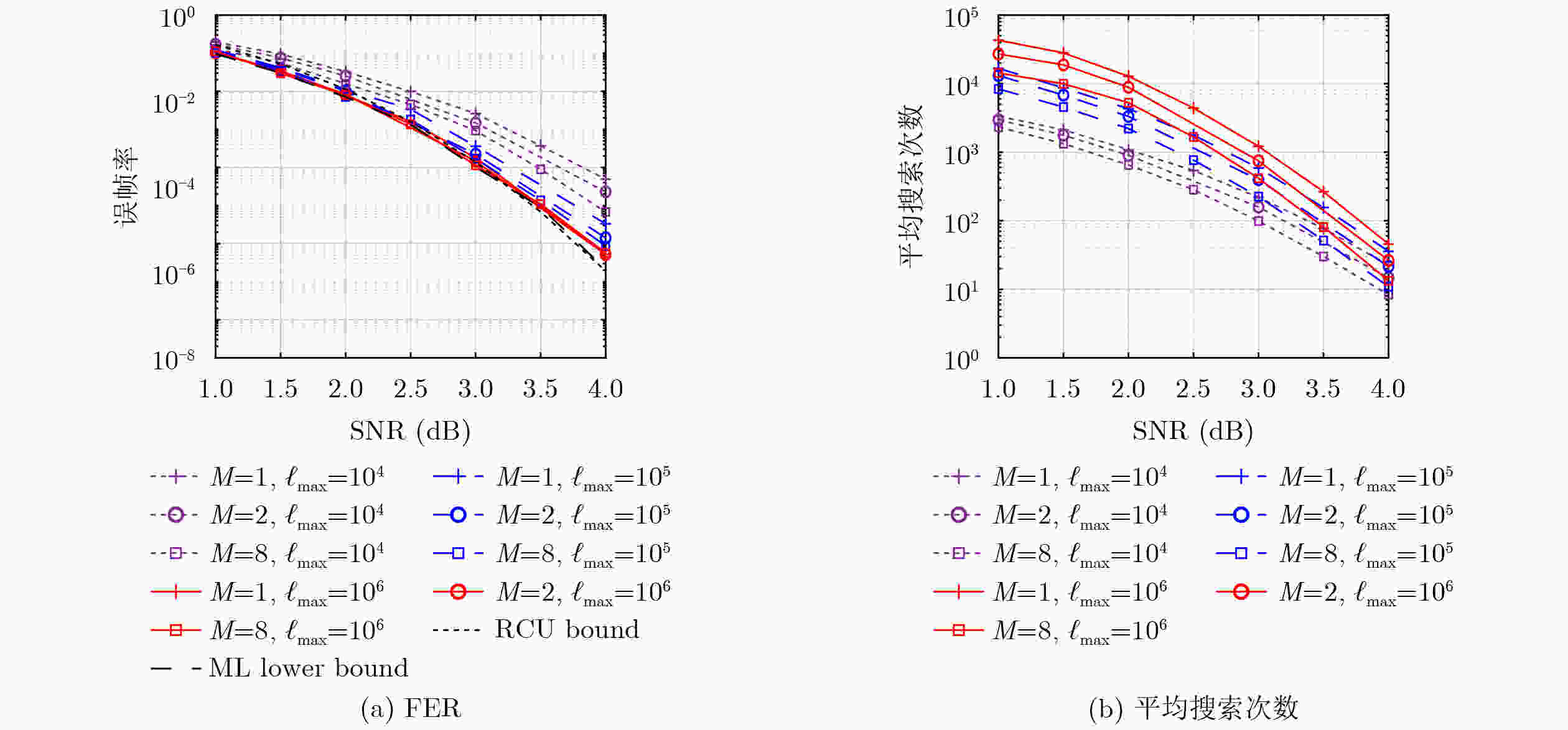
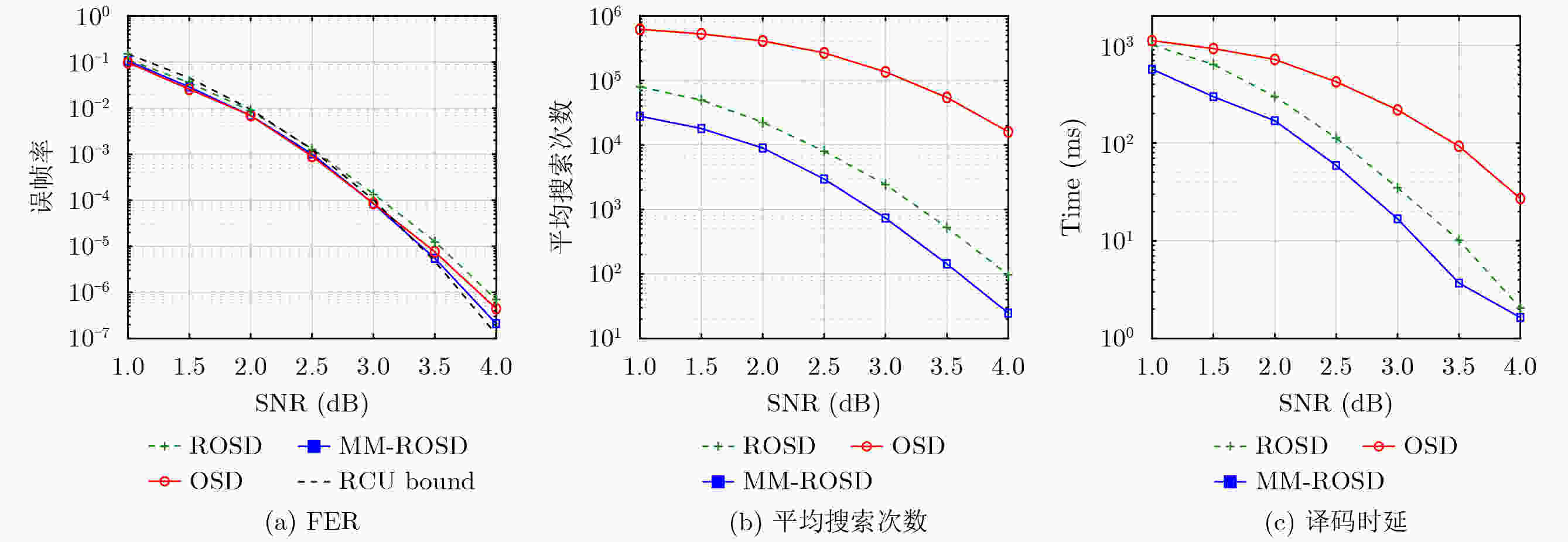
摘要: 代表性顺序统计量译码(Representative Ordered Statistics Decoding, ROSD)是一类针对阶梯矩阵码提出的能够支持并行高斯消元(Gaussian Elimination, GE)的高效译码算法。本文将ROSD推广至一般线性分组码，并利用最小重量阶梯生成矩阵(Minimum-Weight Staircase Generator Matrix, MWSGM)构造方法，为任意线性分组码生成对应的阶梯矩阵结构。在此基础上，我们特别提出了基于MWSGM的多矩阵构造与选择策略。具体而言，构造阶段在第0行(第一个阶梯)分别保留前$ M $个最小重量候选码字，并对每个给定的候选独立地搜索后续各行，最终得到$ M $个不同的阶梯生成矩阵。该多矩阵构造方法放宽了重编码基的选择约束，从而提升了其质量。译码阶段则根据各阶梯矩阵对应的可选重编码基的可靠度总和来选择一个阶梯矩阵，并针对其执行ROSD算法。在性能分析方面，本文基于鞍点近似提出了帧错误率(Frame Error Rate, FER)的上界与平均搜索次数估计。数值结果显示：(1)所提基于鞍点的FER上界能够有效预测FER性能，且所提平均搜索次数估计与实际仿真结果较为吻合；(2)相比于原始单矩阵ROSD基线算法，所提基于MWSGM的多矩阵构造与选择策略在相同最大搜索次数约束下能够显著降低FER，并有效减少平均搜索次数。
- 顺序统计量译码 /
- 多矩阵译码 /
- 并行高斯消元 /
- 阶梯矩阵码 /
- 最小重量阶梯生成矩阵
Abstract: Objective Representative ordered statistics decoding (ROSD) is a class of efficient decoding algorithms originally proposed for staircase matrix codes, which support parallel Gaussian elimination (GE) to enable low-latency implementations. In this paper, ROSD is extended to general linear block codes by utilizing the minimum-weight staircase generator matrix (MWSGM) construction, which generates staircase-structured matrices for arbitrary linear codes. Building upon this, we propose a multi-matrix representative OSD (MM-ROSD) framework that exploits the diversity of multiple candidate staircase matrices to enhance decoding performance and reduce complexity. For performance analysis, a saddlepoint-approximation-based analytical framework is developed to predict the upper bound of the frame error rate (FER) and estimate the required average number of searches. Methods The proposed MM-ROSD algorithm consists of two main components:(1) Multi-matrix construction and selection strategy: In the construction phase, the first $ M $ minimum-weight candidate codewords are retained in the first row (i.e., the first staircase), and for each candidate, the remaining rows are searched independently, yielding $ \text{M} $ staircase generator matrices with improved basis diversity. In the decoding phase, the optimal staircase matrix is selected according to the sum of reliabilities of the available re-encoding bases within each candidate matrix, and ROSD is then performed on the selected matrix.(2) Saddlepoint-based performance analysis: A saddlepoint approximation method is introduced to theoretically estimate both the FER upper bound and the required average number of searches, providing valuable guidelines for complexity-performance trade-offs and parameter tuning. Results and Discussions Extensive simulations are conducted over BPSK-modulated AWGN channels using 5G CA-polar codes $ \mathcal{C}[128{,}64] $ concatenated with an 11-bit CRC. Key findings include:Saddlepoint approximation accuracy: The predicted FER upper bound matches simulation results closely across the entire SNR range and tightly approaches both the maximum-likelihood (ML) lower bound and the random coding union (RCU) bound. Similarly, the estimated average number of searches aligns closely with simulations in both mid and high SNR regions, validating the accuracy of the analytical framework.Impact of multi-matrix diversity: Increasing the number of pre-stored staircase matrices $ M $ effectively improves basis quality and decoding performance. For example, with $ \text{M}\in \{1{,}2,8\} $ and a limited maximum number of searches $ {\ell}_{\max }\in \{{10}^{4},{10}^{5},{10}^{6}\} $, FER performance significantly improves and approaches finite-length capacity and ML lower bounds (Fig. 3(a)). Under a limited search list (e.g., $ {\ell}_{\max }={10}^{4} $), the FER and average number of searches are substantially reduced by increasing $ M $. This effect is mainly due to the improved quality of the re-encoding basis afforded by the multi-matrix strategy. Under larger budgets (e.g., $ {\ell}_{\max }={10}^{6} $), increasing $ M $ primarily reduces the average number of searches. Conclusions This work extends ROSD to general linear block codes and introduces an efficient MM-ROSD framework based on MWSGM construction. By leveraging the diversity of multiple candidate staircase matrices and the low-latency advantage of parallel GE, the proposed approach significantly improves decoding performance while reducing the average number of searches. Furthermore, the saddlepoint-based analytical framework accurately predicts both FER and the average number of searches, providing theoretical guidance for practical system design. Simulation results demonstrate that, under identical maximum search constraints, MM-ROSD achieves substantial FER gains and significant reductions in average number of searches compared with the baseline single-matrix ROSD, making it a promising decoding framework for short-block codes in ultra-reliable low-latency communication (URLLC) and hyper-reliable low-latency communication (HRLLC) scenarios.
- ordered statistics decoding /
- multi-matrix decoding /
- parallel Gaussian elimination /
- staircase matrix code /
- minimum-weight staircase generator matrix

HTML全文

图 1 鞍点近似与实际仿真得到的结果对比。所用码为 5G CA-polar $ \mathcal{C}[128{,}64] $(级联11位CRC)，译码中预存阶梯矩阵数量$ M=8 $，最大搜索次数$ {\ell}_{\max }={10}^{6} $，并采用DAI终止准则

下载: 全尺寸图片幻灯片

图 2 不同预存矩阵数量和不同最大搜索次数的性能对比。所用码为 5G CA-polar $ \mathcal{C}[128{,}64] $(级联11位CRC)，译码中预存阶梯矩阵数量$ M\in \{1{,}2,8\} $，最大搜索次数$ {\ell}_{\max }\in \{{10}^{4},{10}^{5},{10}^{6}\} $，并采用DAI终止准则

下载: 全尺寸图片幻灯片

图 3 不同译码算法在eBCH $ \mathcal{C}[128{,}64] $下的性能对比。译码算法包括ROSD、MM-ROSD($ M=8 $)以及采用提前终止策略的OSD。

下载: 全尺寸图片幻灯片

1 基于多候选第0行的最小重量阶梯生成矩阵多矩阵构造算法

输入：大小为$ k\times n $的生成矩阵$ \boldsymbol{G} $；用于码字搜索的列表译码器$ L\left(\cdot \right) $；矩阵数量$ M $。
输出：矩阵列表$ {\boldsymbol{G}}_{\boldsymbol{s}}=\{\boldsymbol{G}_{s}^{\left(0\right)},\boldsymbol{G}_{s}^{\left(1\right)},\cdots ,\boldsymbol{G}_{s}^{\left(M-1\right)}\} $
(1). 初始化：设置矩阵副本$ {\boldsymbol{G}}^{\boldsymbol{'}}\leftarrow \boldsymbol{G} $，全列索引集合$ \mathcal{P}\leftarrow \{0{,}1,\cdots ,n-1\} $，已擦除索引集合$ \mathcal{S}\leftarrow \mathcal{\varnothing } $。生成用于列表译码的初始接收序　列，并据此计算初始LLR向量 $ \boldsymbol{r} $。
(2). 第0行候选生成：
(a) 在$ ({\boldsymbol{G}}^{\boldsymbol{'}},\boldsymbol{r}) $上调用$ L\left({\boldsymbol{G}}^{\boldsymbol{'}},\boldsymbol{r}\right) $，得到候选码字集合$ \boldsymbol{C} $。
(b) 在$ \boldsymbol{C} $中按照汉明重量从小到大排序，选取前$ M $个非零码字$ \{{\boldsymbol{c}}^{\left(0{,}0\right)},{\boldsymbol{c}}^{\left(1{,}0\right)},\cdots ,{\boldsymbol{c}}^{\left(M-1{,}0\right)}\} $。
(3). 多矩阵MWSGM构造：
(a) 对于$ m=0{,}1,\cdots ,M-1 $：
① 初始化$ \boldsymbol{G}_{s}^{(m)} $为$ k\times n $零矩阵，并令$ \boldsymbol{G}_{s}^{\left(m\right)}\left(0,\colon \right)\leftarrow {\boldsymbol{c}}^{(m,0)} $。//对于一个矩阵$ \boldsymbol{A} $，我们使用$ \boldsymbol{A}\left(\ell,\colon \right) $来表示$ \boldsymbol{A} $的第$ \ell $行。
② 设置擦除集合$ {S}^{(m)}\leftarrow \left\{j\in \mathcal{P}\|\boldsymbol{c}_{\boldsymbol{j}}^{\left(m,0\right)}=1\right\} $。
③ 设置$ {{{\boldsymbol{G}}^{\boldsymbol{'}}}}^{(m)}\leftarrow {\boldsymbol{G}}^{\boldsymbol{'}} $, 令$ {\boldsymbol{r}}^{(m)}\leftarrow \boldsymbol{r} $。
④ 从$ {{{\boldsymbol{G}}^{\boldsymbol{'}}}}^{(m)} $中删除一行与$ {\boldsymbol{c}}^{(m,0)} $线性相关的行。
⑤ 对所有$ j\in {S}^{\left(m\right)} $，令$ r_{j}^{\left(m\right)}\leftarrow 0 $。
⑥ 对于$ i=1{,}2,\cdots ,k-1 $：
(i) 在$ {{{(\boldsymbol{G}}^{\boldsymbol{'}}}}^{(m)},{\boldsymbol{r}}^{(m)}) $上调用$ L\left({\boldsymbol{G}}^{\boldsymbol{'}},\boldsymbol{r}\right) $，得到候选集合$ \boldsymbol{C}_{i}^{\left(m\right)} $。
(ii) 在$ \boldsymbol{C}_{i}^{\left(m\right)} $中选择在$ \mathcal{P}\backslash {S}^{(m)} $上汉明重量最小且在$ \mathcal{P}\backslash {S}^{(m)} $上非零的码字$ {\widehat{\boldsymbol{c}}}^{(m,i)} $。
(iii) 令$ \boldsymbol{G}_{s}^{\left(m\right)}\left(i,\colon \right)\leftarrow {\widehat{\boldsymbol{c}}}^{(m,i)} $
(iv) 更新$ {S}^{(m)}\leftarrow {S}^{(m)}\cup \left\{j\in \mathcal{P}\|\widehat{\boldsymbol{c}}_{j}^{\left(m,i\right)}=1\right\} $
(v) 从$ {{{\boldsymbol{G}}^{\boldsymbol{'}}}}^{(m)} $中删除一行与$ {\widehat{\boldsymbol{c}}}^{(m,i)} $线性相关的行。
(vi) 对所有$ j\in {S}^{\left(m\right)} $，令$ r_{j}^{\left(m\right)}\leftarrow 0 $。
(4). 对每个$ \boldsymbol{G}_{s}^{(m)} $的列进必要的置换，使其成为阶梯生成矩阵。
(5). 返回$ {\boldsymbol{G}}_{\boldsymbol{s}}=\{\boldsymbol{G}_{s}^{\left(0\right)},\boldsymbol{G}_{s}^{\left(1\right)},\cdots ,\boldsymbol{G}_{s}^{\left(M-1\right)}\} $

下载: 导出CSV

参考文献(49)

[1]	3GPP. NR; Multiplexing and channel coding[S]. 3GPP TS 38.212, 2021. (查阅网上资料, 未能确认文献类型, 请确认文献类型及格式是否正确).
[2]	ITU-R. Framework and overall objectives of the future development of IMT for 2030 and beyond[S]. Recommendation ITU-R M. 2160–0, 2023. (查阅网上资料, 未能确认文献类型, 请确认文献类型及格式是否正确).
[3]	ROWSHAN M, QIU Min, XIE Yixuan, et al. Channel coding toward 6G: Technical overview and outlook[J]. IEEE Open Journal of the Communications Society, 2024, 5: 2585–2685. doi: 10.1109/OJCOMS.2024.3390000.
[4]	CHEN Qiwang, CHEN Chen, HE Yucheng, et al. Global optimization of double protograph LDPC codes for JSCC scheme[J]. Science China Information Sciences, 2024, 67(6): 169301. doi: 10.1007/s11432-023-4012-9.
[5]	XU Zhiping, WANG Lin, and CHEN Guanrong. Joint coding/decoding optimization for DC-BICM system: Collaborative design[J]. IEEE Communications Letters, 2021, 25(8): 2487–2491. doi: 10.1109/LCOMM.2021.3081678.
[6]	XU Zhiping, SONG Dan, ZHENG Jiachun, et al. Joint-decoding-complexity-oriented collaborative design for joint source-channel coding system based on double protograph-LDPC codes[J]. Science China Information Sciences, 2023, 66(8): 189301. doi: 10.1007/s11432-022-3765-2.
[7]	GAO Jian, SONG Xin, ZHANG Xiaojun, et al. Learning to decode double polar codes for joint source-channel coding[J]. IEEE Transactions on Vehicular Technology, 2025. doi: 10.1109/tvt.2025.3619411. (查阅网上资料,未找到本条文献卷期页码信息,请确认并补充).
[8]	WU Bolin, NIU Kai, DAI Jincheng, et al. Joint design of channel coding and modulation toward 6G: Probabilistically-shaped polar-coded modulation[J]. IEEE Transactions on Communications, 2025, 73(8): 5538–5553. doi: 10.1109/tcomm.2025.3535865.
[9]	LIU Sanya, WANG Lin, CHEN Jun, et al. Joint component design for the JSCC system based on DP-LDPC codes[J]. IEEE Transactions on Communications, 2020, 68(9): 5808–5818. doi: 10.1109/TCOMM.2020.3001647.
[10]	YANG Zhaojie, LI Yunye, GUAN Yongliang, et al. Source-constrained hierarchical modulation systems with protograph LDPC codes: A promising transceiver design for future 6G-enabled IoT[J]. IEEE Journal on Selected Areas in Communications, 2025, 43(4): 1103–1117. doi: 10.1109/jsac.2025.3531540.
[11]	COŞKUN M C, DURISI G, JERKOVITS T, et al. Efficient error-correcting codes in the short blocklength regime[J]. Physical Communication, 2019, 34: 66–79. doi: 10.1016/j.phycom.2019.03.004.
[12]	SHIRVANIMOGHADDAM M, MOHAMMADI M S, ABBAS R, et al. Short block-length codes for ultra-reliable low latency communications[J]. IEEE Communications Magazine, 2019, 57(2): 130–137. doi: 10.1109/mcom.2018.1800181.
[13]	YUE Chentao, MILOSLAVSKAYA V, SHIRVANIMOGHADDAM M, et al. Efficient decoders for short block length codes in 6G URLLC[J]. IEEE Communications Magazine, 2023, 61(4): 84–90. doi: 10.1109/MCOM.001.2200275.
[14]	FOSSORIER M P C and LIN Shu. Soft-decision decoding of linear block codes based on ordered statistics[J]. IEEE Transactions on Information Theory, 1995, 41(5): 1379–1396. doi: 10.1109/18.412683.
[15]	DORSCH B. A decoding algorithm for binary block codes and J-ary output channels[J]. IEEE Transactions on Information Theory, 1974, 20(3): 391–394. doi: 10.1109/TIT.1974.1055217.
[16]	WANG Qianfan, WANG Yiwen, WANG Yixin, et al. Random staircase generator matrix codes: Coding theorem, performance analysis, and code design[J]. IEEE Transactions on Information Theory, 2025, 71(5): 3497–3509. doi: 10.1109/TIT.2025.3541734.
[17]	WANG Yiwen, LIANG Jifan, WANG Qianfan, et al. Representative ordered statistics decoding of staircase matrix codes[J]. IEEE Transactions on Communications, 2025, 73(4): 2148–2158. doi: 10.1109/TCOMM.2024.3478114.
[18]	WANG Qianfan, WANG Yixin, WANG Yiwen, et al. Random staircase generator matrix codes[C]. 2024 IEEE International Symposium on Information Theory (ISIT), Athens, Greece, 2024: 2622–2627. doi: 10.1109/ISIT57864.2024.10619485.
[19]	WANG Yiwen, WANG Qianfan, LIANG Jifan, et al. Representative ordered statistics decoding of polar codes[C]. 2024 IEEE 99th Vehicular Technology Conference (VTC2024-Spring), Singapore, Singapore, 2024: 1–5. doi: 10.1109/VTC2024-Spring62846.2024.10683273.
[20]	YUE Chentao, SHIRVANIMOGHADDAM M, LI Yonghui, et al. Segmentation-discarding ordered-statistic decoding for linear block codes[C]. 2019 IEEE Global Communications Conference, Waikoloa, USA, 2019: 1–6. doi: 10.1109/GLOBECOM38437.2019.9014173.
[21]	YUE Chentao, SHIRVANIMOGHADDAM M, PARK G, et al. Linear-equation ordered-statistics decoding[J]. IEEE Transactions on Communications, 2022, 70(11): 7105–7123. doi: 10.1109/TCOMM.2022.3207206.
[22]	YUE Chentao, SHIRVANIMOGHADDAM M, PARK G, et al. Probability-based ordered-statistics decoding for short block codes[J]. IEEE Communications Letters, 2021, 25(6): 1791–1795. doi: 10.1109/LCOMM.2021.3058978.
[23]	王千帆, 郭延庚, 宋林琦, 等. 基于跳过机制的低复杂度顺序统计译码算法[J]. 电子与信息学报, 2025, 47(11): 4275–4284. doi: 10.11999/JEIT250447. WANG Qianfan, GUO Yangeng, SONG Linqi, et al. Low-complexity ordered statistic decoding algorithm based on skipping mechanisms[J]. Journal of Electronics & Information Technology, 2025, 47(11): 4275–4284. doi: 10.11999/JEIT250447.
[24]	王千帆, 郭延庚, 毕胜, 等. 面向高可靠低时延通信的顺序统计译码(OSD)关键技术综述[J]. 电子学报, 2025. 在投. (查阅网上资料, 未找到本条文献信息, 请确认). WANG Qianfan, GUO Yangeng, BI Sheng, et al. A survey of key techniques in ordered statistics decoding (OSD) for ultra-reliable low-latency communications[J]. Acta Electronica Sinica, 2025. Under review.
[25]	WANG Yiwen, LIANG Jifan, and MA Xiao. Local constraint-based ordered statistics decoding for short block codes[C]. 2022 IEEE Information Theory Workshop, Mumbai, India, 2022: 107–112. doi: 10.1109/ITW54588.2022.9965916.
[26]	LIANG Jifan, WANG Yiwen, CAI Suihua, et al. A low-complexity ordered statistic decoding of short block codes[J]. IEEE Communications Letters, 2023, 27(2): 400–403. doi: 10.1109/lcomm.2022.3222819.
[27]	王义文, 王千帆, 马啸. 强干扰环境下无速率随机码编译码方案及其性能分析[J]. 电子与信息学报, 2024, 46(10): 4017–4023. doi: 10.11999/JEIT230879. WANG Yiwen, WANG Qianfan, and MA Xiao. Rateless random coding scheme and performance analysis in strong interference environments[J]. Journal of Electronics & Information Technology, 2024, 46(10): 4017–4023. doi: 10.11999/JEIT230879.
[28]	ZHENG Xiangping, WANG Qianfan, WEI Baodian, et al. Quasi-OSD of binary image of RS codes with applications to JSCC[C]. 2024 IEEE International Symposium on Information Theory (ISIT), Athens, Greece, 2024: 3576–3581. doi: 10.1109/ISIT57864.2024.10619269.
[29]	WANG Qianfan, CHEN Yanzhi, LIANG Jifan, et al. A new joint source-channel coding in the short blocklength regime[C]. 2023 IEEE Globecom Workshops (GC Wkshps), Kuala Lumpur, Malaysia, 2023: 1566–1571. doi: 10.1109/GCWkshps58843.2023.10464813.
[30]	CHEN Yanzhi, LIANG Jifan, WANG Qianfan, et al. A new joint source-channel coding scheme with overlay spread spectrum transmission[C]. 2023 International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 2023: 239–244. doi: 10.1109/WCSP58612.2023.10404761.
[31]	WANG Qianfan, CHEN Yanzhi, LIANG Jifan, et al. A new joint source-channel coding for short-packet communications[J]. IEEE Transactions on Communications, 2024, 72(1): 28–37. doi: 10.1109/TCOMM.2023.3320699.
[32]	WANG Yiwen, WANG Qianfan, ZHENG Xiangping, et al. Reduced-complexity guessing codeword decoding of BCH codes with most reliable cyclic basis[C]. IEEE Global Communications Conference (GLOBECOM), Taipei, China, 2025.
[33]	WANG Qianfan, WANG Yiwen, ZHENG Xiangping, et al. Ordered reliability bits guessing codeword decoding of short codes[J]. IEEE Wireless Communications Letters, 2025, 14(9): 2823–2827. doi: 10.1109/LWC.2025.3580156.
[34]	ZHENG Xiangping, WANG Qianfan, and MA Xiao. SCL-GCD of short polar codes[C]. IEEE Global Communications Conference (GLOBECOM), Cape Town, South Africa, 2024: 686–691. doi: 10.1109/GLOBECOM52923.2024.10901715.
[35]	梁济凡, 王千帆, 宋林琦, 等. 参数列表化置信传播-顺序统计译码算法[J]. 电子与信息学报, 2025, 47(11): 4254–4263. doi: 10.11999/JEIT250552. LIANG Jifan, WANG Qianfan, SONG Linqi, et al. Belief propagation-ordered statistics decoding algorithm with parameterized list structures[J]. Journal of Electronics & Information Technology, 2025, 47(11): 4254–4263. doi: 10.11999/JEIT250552.
[36]	LIANG Jifan, WANG Qianfan, LI Lvzhou, et al. The BP-LCOSD algorithm for Toric codes[C]. IEEE International Symposium on Information Theory Workshops (ISIT-W), Athens, Greece, 2024: 1–6. doi: 10.1109/ISIT-W61686.2024.10591758.
[37]	LIANG Jifan, WANG Qianfan, LI Lvzhou, et al. A low-complexity BP-OSD algorithm for quantum LDPC codes[J]. The European Physical Journal Special Topics, 2025. doi: 10.1140/epjs/s11734-025-01712-x. (查阅网上资料,未找到本条文献卷期页码信息,请确认并补充).
[38]	LIANG Jifan, WANG Qianfan, LI Lvzhou, et al. A high-performance list decoding algorithm for surface codes with erroneous syndrome[Z]. arXiv: 2409.06979, 2024. doi: 10.48550/arXiv.2409.06979. (查阅网上资料,请作者核对文献类型及格式是否正确).
[39]	WANG Qianfan, LIANG Jifan, LI Lvzhou, et al. BP-LCGCD: A Gaussian-elimination-free and high-performance decoder for surface codes[J]. IEEE Communications Letters. doi: 10.1109/LCOMM.2025.3646724. (查阅网上资料,未找到本条文献卷期页码信息,请确认并补充).
[40]	YANG Lijia and CHEN Li. Low-latency ordered statistics decoding of BCH codes[C]. 2022 IEEE Information Theory Workshop (ITW), Mumbai, India, 2022: 404–409. doi: 10.1109/ITW54588.2022.9965799.
[41]	YUE Chentao, SHIRVANIMOGHADDAM M, VUCETIC B, et al. Ordered-statistics decoding with adaptive Gaussian elimination reduction for short codes[C]. 2022 IEEE Globecom Workshops (GC Wkshps), Rio de Janeiro, Brazil, 2022: 492–497. doi: 10.1109/GCWkshps56602.2022.10008654.
[42]	CHOI C and JEONG J. Fast soft decision decoding algorithm for linear block codes using permuted generator matrices[J]. IEEE Communications Letters, 2021, 25(12): 3775–3779. doi: 10.1109/LCOMM.2021.3097322.
[43]	FOSSORIER M, SHAKIBA-HERFEH M, and ZHANG Huazi. Modified OSD algorithm with reduced Gaussian elimination[J]. IEEE Communications Letters, 2024, 28(8): 1755–1759. doi: 10.1109/LCOMM.2024.3416515.
[44]	LI Xihao, CHEN Wenhao, CHEN Li, et al. Iterative basis update for ordered statistics decoding of linear block codes[J]. IEEE Communications Letters, 2024, 28(9): 1981–1985. doi: 10.1109/lcomm.2024.3425388.
[45]	DIVSALAR D. A simple tight bound on error probability of block codes with application to turbo codes[R]. TMO Progress Report 42-139, 1999.
[46]	POLYANSKIY Y, POOR H V, and VERDÚ S. Channel coding rate in the finite blocklength regime[J]. IEEE Transactions on Information Theory, 2010, 56(5): 2307–2359. doi: 10.1109/TIT.2010.2043769.
[47]	WANG Yiwen, WANG Qianfan, LIANG Jifan, et al. Representative OSD with local constraints of CA-polar codes[J]. Chinese Journal of Electronics, 2025, 34(4): 1111–1119. doi: 10.23919/cje.2024.00.220.
[48]	BUTLER R W. Saddlepoint Approximations with Applications[M]. Cambridge: Cambridge University Press, 2007. (查阅网上资料, 请补充引用页码).
[49]	FONT-SEGURA J, VAZQUEZ-VILAR G, MARTINEZ A, et al. Saddlepoint approximations of lower and upper bounds to the error probability in channel coding[C]. 2018 52nd Annual Conference on Information Sciences and Systems (CISS), Princeton, USA, 2018: 1–6. doi: 10.1109/CISS.2018.8362304.