Dynamic State Estimation of Distribution Network by Integrating High-degree Cubature Kalman Filter and Long Short-Term Memory Under False Data Injection Attack
-
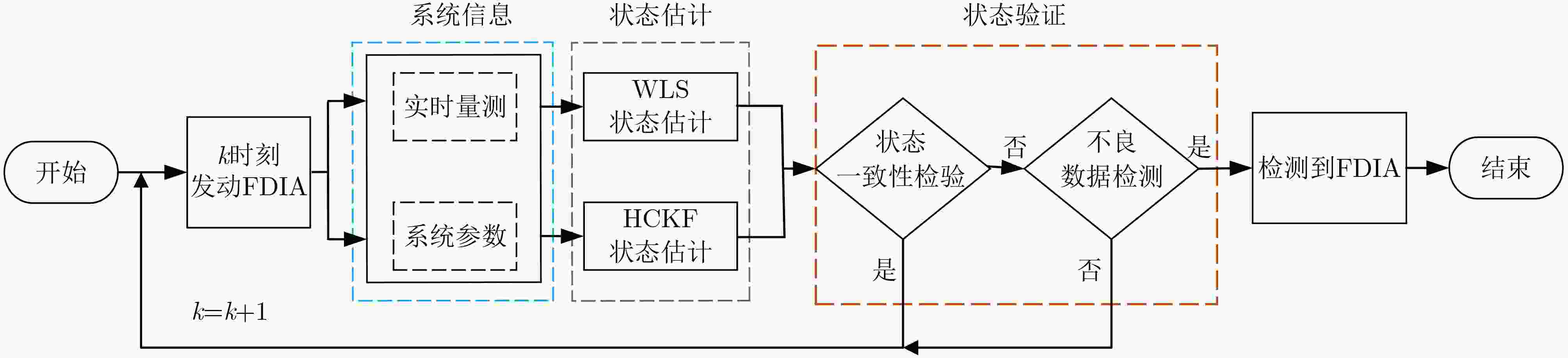
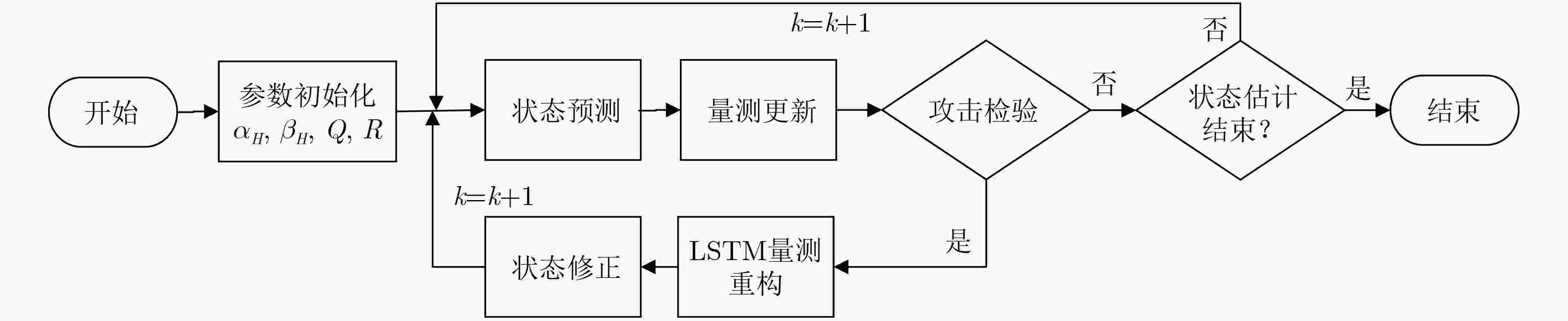
摘要: 配电网动态状态估计是保障电力物理信息系统安全稳定运行的关键技术,但系统的强非线性、高维特性及虚假数据注入攻击(FDIA)严重制约了其精度与安全。针对上述问题,该文提出一种融合高阶容积卡尔曼滤波(HCKF)与长短期记忆网络(LSTM)的动态状态估计方法。首先,建立基于混合量测的配电系统状态估计模型,并利用HCKF通过高阶容积点生成策略提升对强非线性高维配电网的状态估计精度;其次,结合加权最小二乘法(WLS)与HCKF的状态估计值,基于残差分析实现FDIA的快速检测;最后,当检测到FDIA时,利用LSTM模型对受攻击节点的量测数据进行时序预测与重构,修正状态估计结果。在IEEE33节点配电系统上的实验表明,在无FDIA时基于HCKF的动态状态估计算法对电压幅值和相角的估计精度高于现有方法。在FDIA场景下,验证了基于残差分析的攻击检测方法、基于LSTM的量测数据预测,以及所提动态状态估计算法的有效性。Abstract:
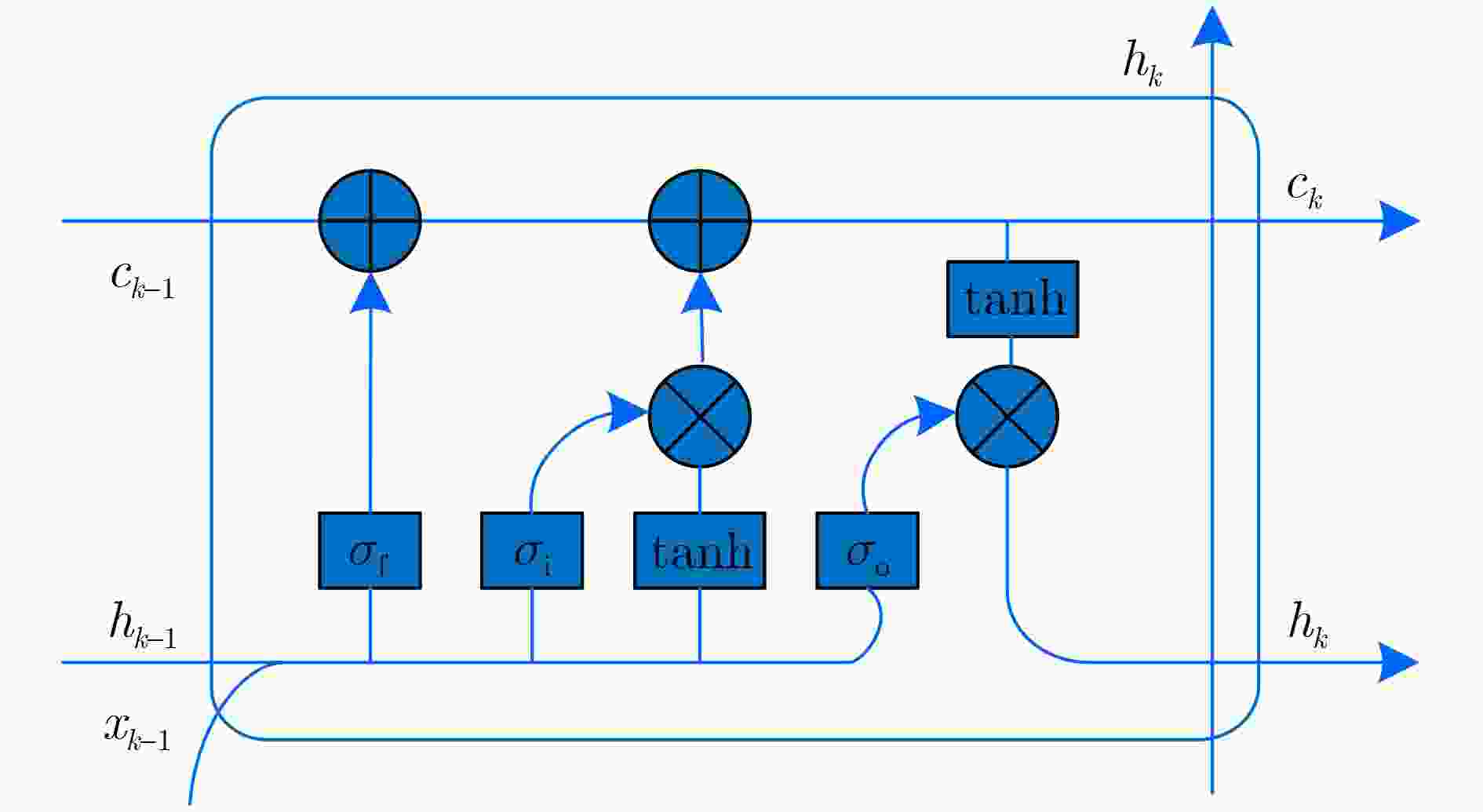
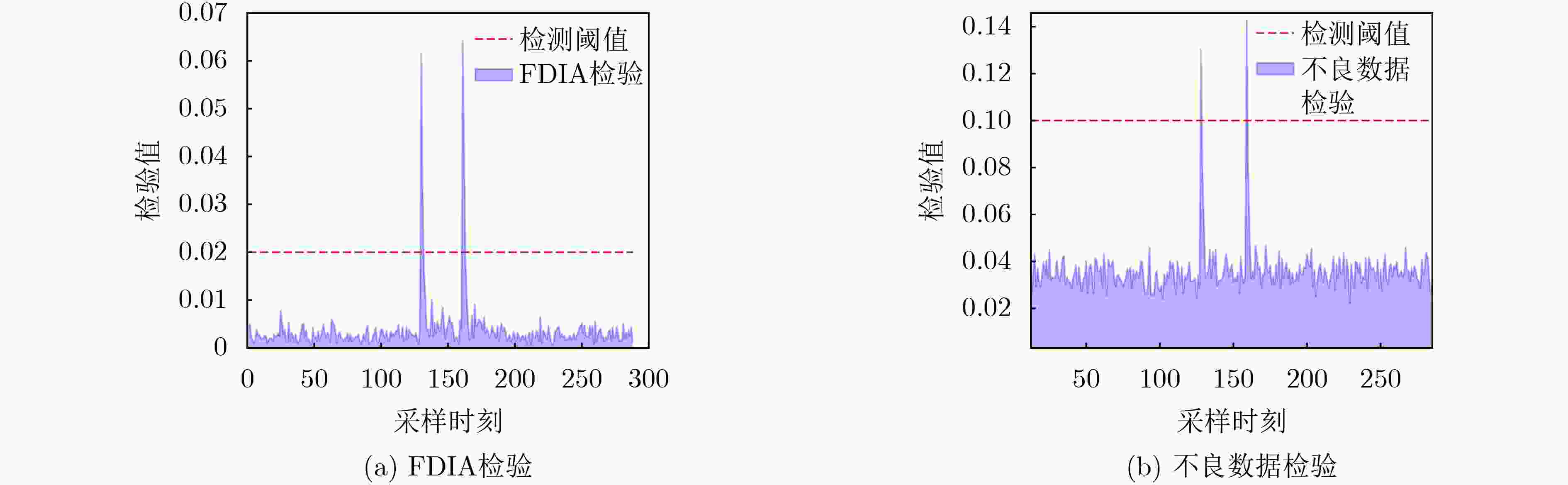
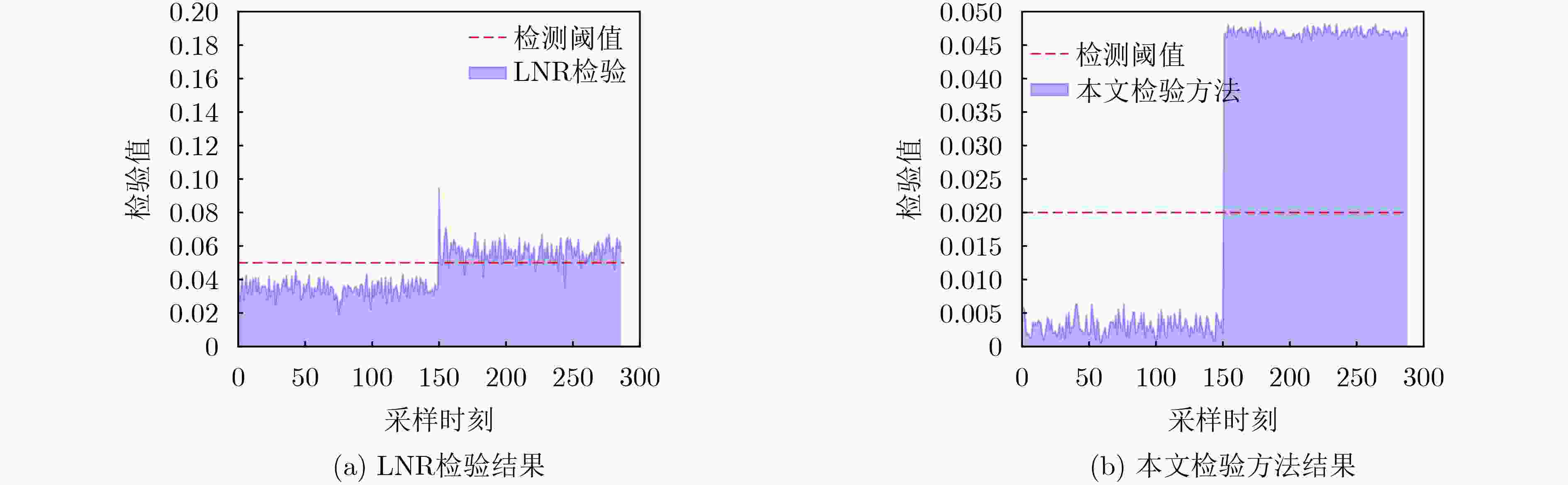
Objective Dynamic state estimation of distribution networks is presented as a core technique for maintaining secure and stable operation in cyber-physical power systems. Its practical performance is limited by strong system nonlinearity, high-dimensional state characteristics, and the threat posed by False Data Injection Attack (FDIA). A method that integrates High-degree Cubature Kalman Filter (HCKF) with Long Short-Term Memory network (LSTM) is proposed. HCKF is applied to enhance estimation precision in nonlinear high-dimensional scenarios. The estimation outputs from HCKF and Weighted Least Squares (WLS) are combined for rapid FDIA identification using residual-based analysis. The LSTM model is then employed to reconstruct measurement data of compromised nodes and refine state estimation results. The approach is validated on the IEEE 33-bus distribution system, demonstrating reliable accuracy enhancement and effective attack resilience. Methods The strong nonlinearity of distribution networks limits the estimation accuracy of dynamic methods based on the Cubature Kalman Filter (CKF). A hybrid measurement state estimation model that combines data from Phasor Measurement Unit (PMU) and Supervisory Control And Data Acquisition (SCADA) is established. HCKF is applied to enhance estimation performance in nonlinear, high-dimensional scenarios by generating higher-order cubature points. Under FDIA, the estimation outputs from WLS and HCKF are jointly assessed, allowing rapid intrusion detection through residual evaluation and state consistency checking. Once an attack is identified, an LSTM model performs time-series prediction to reconstruct the measurement data of compromised nodes. The reconstructed data replace abnormal values, enabling correction of the final state estimation. Results and Discussions Experiments on the IEEE 33-bus distribution system show that without FDIA, HCKF achieves higher estimation accuracy for voltage magnitude and phase angle than CKF. The Average voltage Relative Error (ARE) of voltage magnitude decreases by 57.9%, and the corresponding phase-angle error decreases by 28.9%, confirming the superiority of the method for strongly nonlinear and high-dimensional state estimation. Under FDIA, residual-based detection effectively identifies cyber attacks and avoids false alarms and missed detections. The prediction error of LSTM for the measurement data of compromised nodes and their associated branches remains on the order of 10–6, indicating high reconstruction fidelity. The combined HCKF and LSTM maintains stable state tracking after intrusion, and its performance exceeds that of WLS and adaptive Unscented Kalman Filter. Conclusions The dynamic state estimation method that integrates HCKF and LSTM enhances adaptability to strong nonlinearity and high-dimensional characteristics of distribution networks. Rapid and accurate FDIA identification is achieved through residual evaluation, and LSTM reconstructs the measurement data of compromised nodes with high reliability. The method maintains high estimation accuracy under normal operation and preserves stability and precision under cyber intrusion. It offers technical support for secure and stable operation of distribution networks in the presence of malicious attacks. -
表 1 不同量测装置的测量标准差
测量方式 注入功率 支路功率 电压幅值 电压相角 PMU $ {10}^{-5} $ $ {10}^{-5} $ 0.005 0.002 SCADA $ {10}^{-4} $ $ {10}^{-4} $ 0.02 - 表 2 LSTM预测性能
性能指标 第18号节点 第17号支路 有功功率 无功功率 有功功率 无功功率 RMSE 4.89e–06 2.06e–06 1.17e–05 2.22e–06 MAE 3.89e–06 1.58e–06 9.25e–06 1.78e–06 -
[1] 方洁, 张少辉, 江泳. 基于改进自适应协同控制方法的电力系统混沌控制[J]. 电子与信息学报, 2024, 46(2): 728–737. doi: 10.11999/JEIT230075.FANG Jie, ZHANG Shaohui, and JIANG Yong. Chaotic power system control based on improved adaptive synergetic control method[J]. Journal of Electronics & Information Technology, 2024, 46(2): 728–737. doi: 10.11999/JEIT230075. [2] 邓洪高, 余润华, 纪元法, 等. 偏差未补偿自适应边缘化容积卡尔曼滤波跟踪方法[J]. 电子与信息学报, 2025, 47(1): 156–166. doi: 10.11999/JEIT240469.DENG Honggao, YU Runhua, JI Yuanfa, et al. An adaptive target tracking method utilizing marginalized cubature Kalman filter with uncompensated biases[J]. Journal of Electronics & Information Technology, 2025, 47(1): 156–166. doi: 10.11999/JEIT240469. [3] TIAN Jiwei, SHEN Chao, WANG Buhong, et al. LESSON: Multi-label adversarial false data injection attack for deep learning locational detection[J]. IEEE Transactions on Dependable and Secure Computing, 2024, 21(5): 4418–4432. doi: 10.1109/TDSC.2024.3353302. [4] XIAO Liang, CHEN Haoyu, XU Shiyu, et al. Reinforcement learning-based false data injection attacks in smart grids[J]. IEEE Transactions on Industrial Informatics, 2025, 21(4): 3475–3484. doi: 10.1109/TII.2025.3528571. [5] GUO Mengmeng, HAO Yongsheng, LEE K. Y, et al. Extended-state Kalman filter-based model predictive control and energy-saving performance analysis of a coal-fired power plant[J]. Energy, 2025, 314: 134169. doi: 10.1016/j.energy.2024.134169. [6] NGUYEN D V, ZHAO Haiquan, HU Jinhui, et al. Adaptive robust unscented Kalman filter for dynamic state estimation of power system[J]. IEEE Transactions on Industrial Informatics, 2025, 21(7): 5081–5092. doi: 10.1109/TII.2025.3545093. [7] SHARMA A, SRIVASTAVA S C, and CHAKRABARTI S. A cubature Kalman filter based power system dynamic state estimator[J]. IEEE Transactions on Instrumentation and Measurement, 2017, 66(8): 2036–2045. doi: 10.1109/TIM.2017.2677698. [8] BASETTI V, CHANDEL A K, and SHIVA C K. Square-root cubature Kalman filter based power system dynamic state estimation[J]. Sustainable Energy, Grids and Networks, 2022, 31: 100712. doi: 10.1016/j.segan.2022.100712. [9] LIU Bo and WU Hongyu. Low-rank false data injection attacks with incomplete network information against machine-learning detectors[J]. IEEE Transactions on Industrial Informatics, 2025, 21(4): 2868–2877. doi: 10.1109/TII.2024.3513481. [10] LIU Yifa, CHENG Long, and YE Dan. Stealthy false data injection attacks against the summation detector in cyber-physical systems[J]. IEEE Transactions on Industrial Cyber-Physical Systems, 2024, 2: 391–403. doi: 10.1109/TICPS.2024.3446469. [11] RAGHUVAMSI Y and TEEPARTHI K. Detection and reconstruction of measurements against false data injection and DoS attacks in distribution system state estimation: A deep learning approach[J]. Measurement, 2023, 210: 112565. doi: 10.1016/j.measurement.2023.112565. [12] 黄崇鑫, 洪明磊, 伏帅, 等. 考虑虚假数据注入攻击的有源配电网分布式状态估计[J]. 电力工程技术, 2022, 41(3): 22–31. doi: 10.12158/j.2096-3203.2022.03.003.HUANG Chongxin, HONG Minglei, FU Shuai, et al. Distributed state estimation of active distribution network considering false data injection attack[J]. Electric Power Engineering Technology, 2022, 41(3): 22–31. doi: 10.12158/j.2096-3203.2022.03.003. [13] XU Junjun, ZHANG Sheng, LIN Tong, et al. A distributed secure state estimation framework for unbalanced active distribution systems[J]. IEEE Transactions on Smart Grid, 2025, 16(5): 3714–3727. doi: 10.1109/TSG.2025.3587483. [14] DONG Lewei, XU Huiling, PARK J H, et al. Intermediate-variable-based robust state estimation for cyber–physical systems against FDI attacks[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2024, 71(5): 2719–2723. doi: 10.1109/TCSII.2024.3351159. [15] MIAO Kelei, ZHANG Wen’an, and QIU Xiang. An adaptive unscented Kalman filter approach to secure state estimation for wireless sensor networks[J]. Asian Journal of Control, 2023, 25(1): 629–636. doi: 10.1002/asjc.2783. -





 下载:
下载:





 下载:
下载:
