Considering Workload Uncertainty in Strategy Gradient-Based Hyper-Heuristic Scheduling for Software Projects
-
摘要: 围绕软件项目开发过程中存在的不确定因素，建立一种考虑任务工作量不确定性的多目标软件项目调度模型。该模型采用非对称三角区间二型模糊数描述工作量的不确定性。为了提高不确定环境下的决策质量，提出一种基于策略梯度的超启发式算法求解该模型。该算法将强化学习中的一种策略梯度算法(即Actor-Critic算法)作为高层策略，根据算法的当前运行状态选择合适的低层启发式策略。同时引入优先经验回放法，以利用历史经验信息更新网络参数，加快收敛速度并降低学习成本。将所提算法与6种代表性算法在12个人工合成算例和3个实例上进行了对比。实验结果表明，所提算法在不确定调度环境中能够搜索到一组收敛性和多样性更好的非支配解。Abstract:
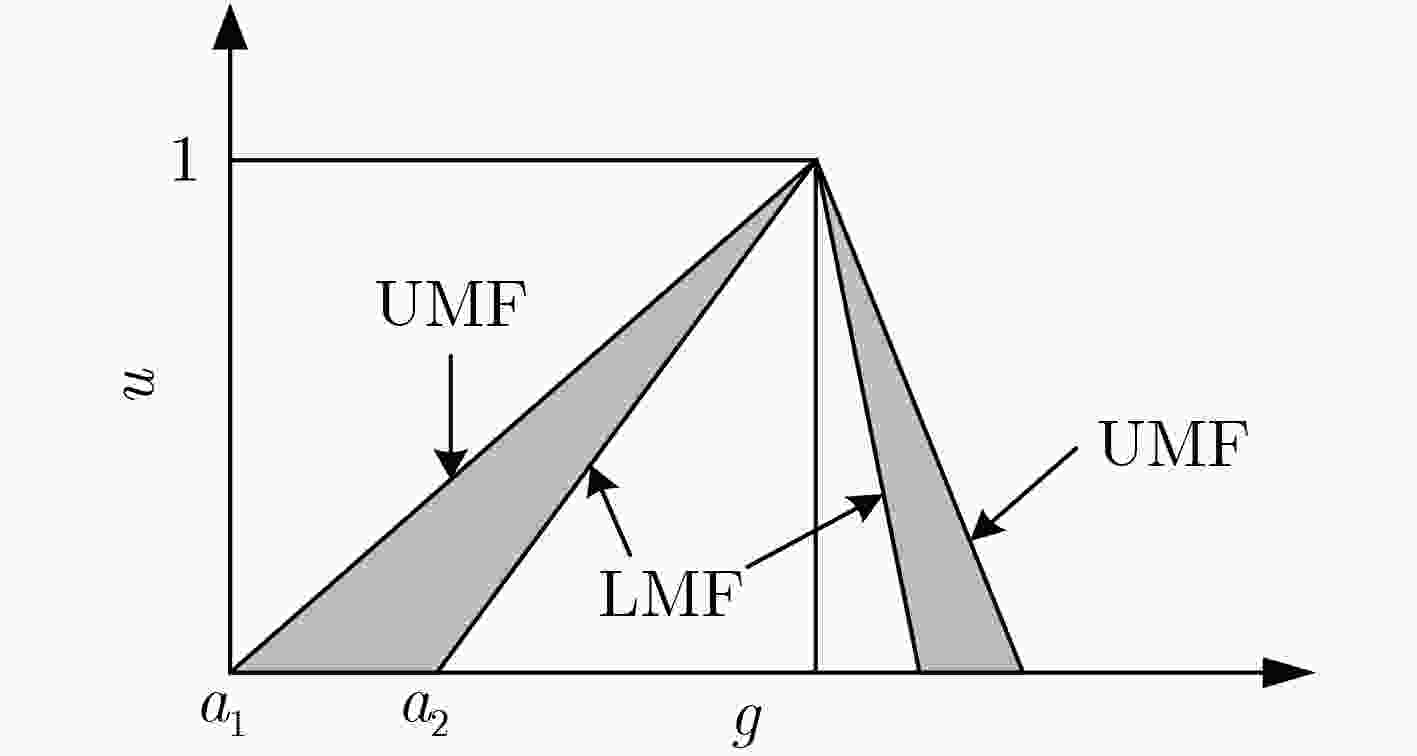
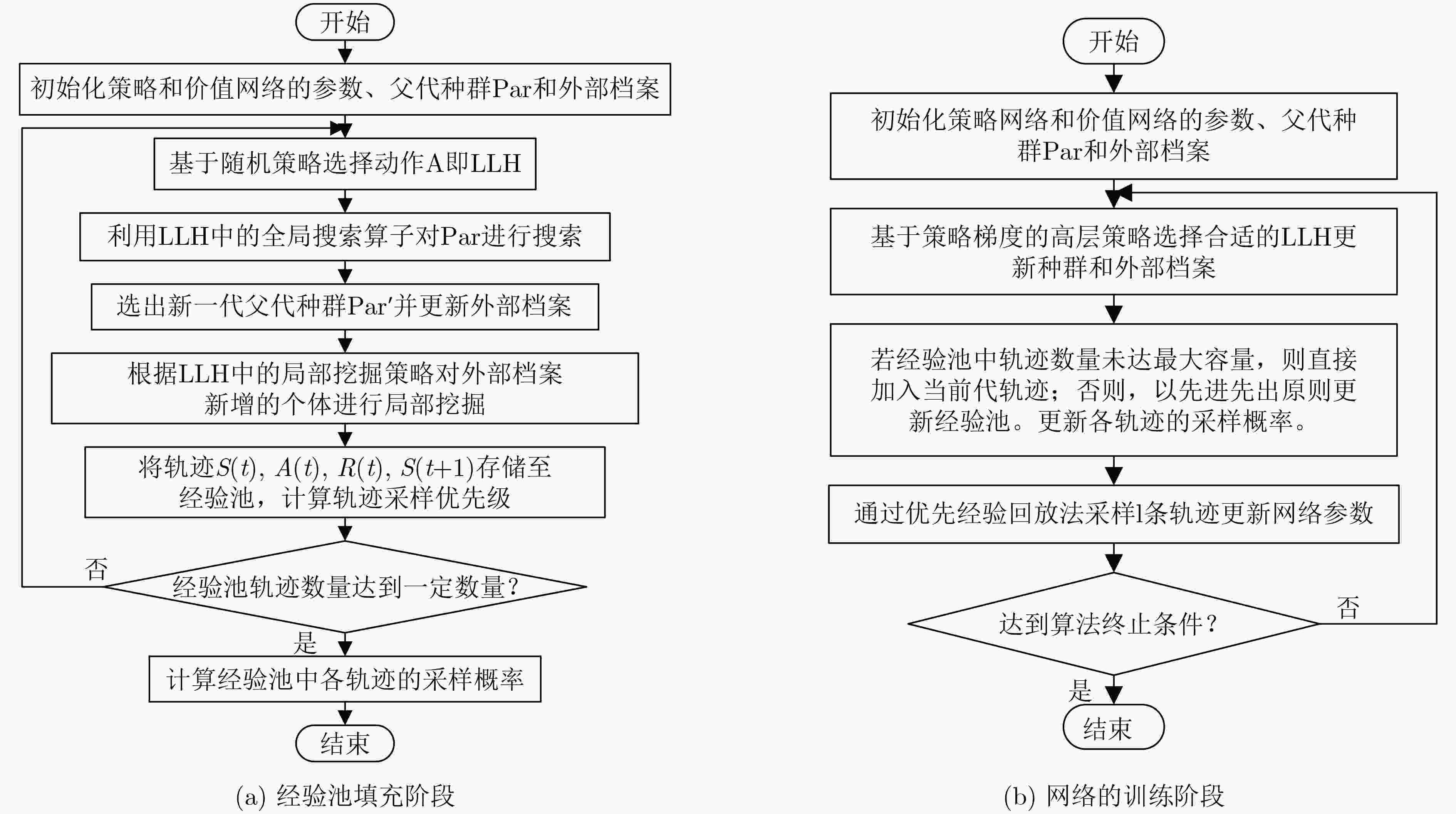
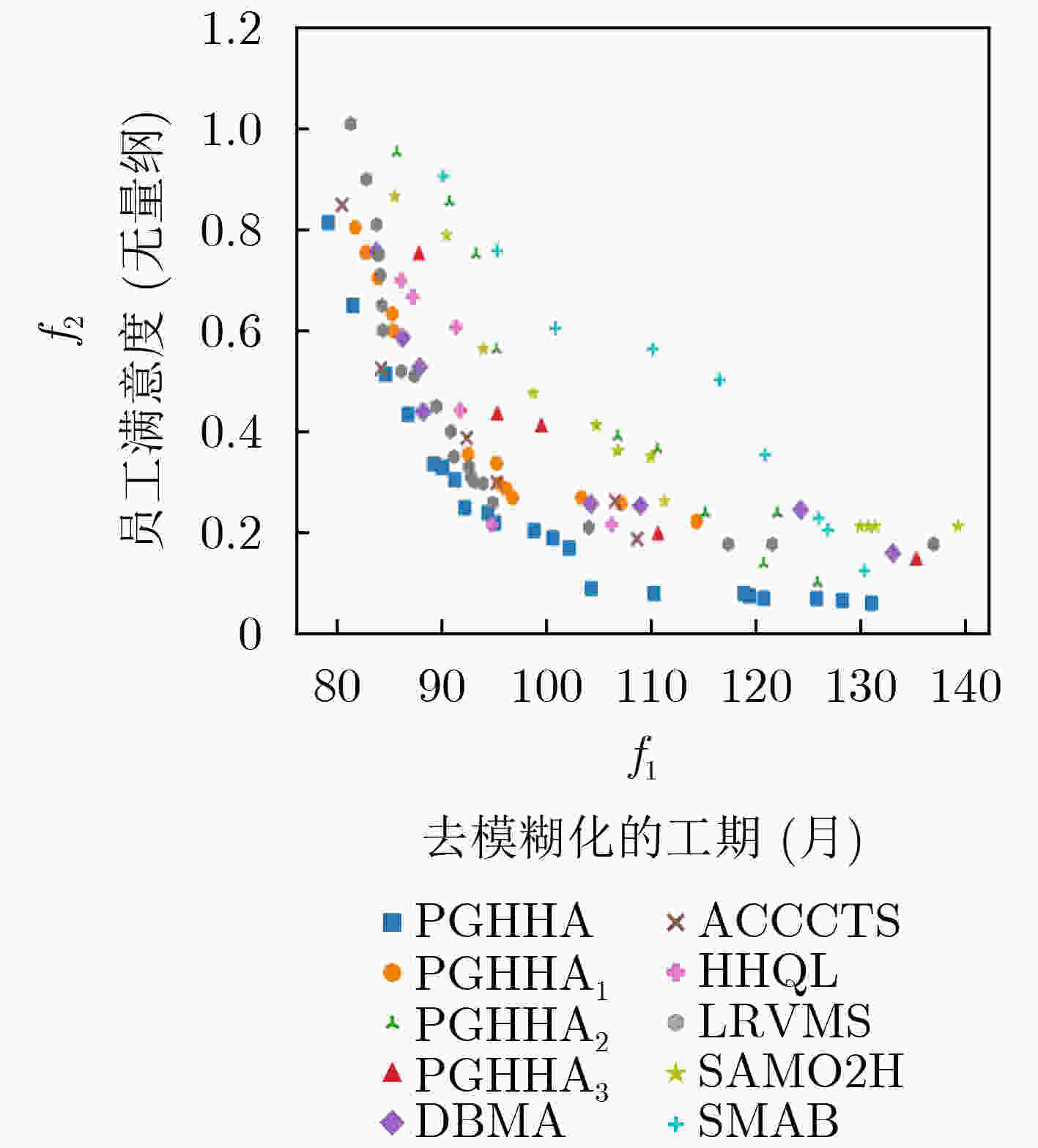
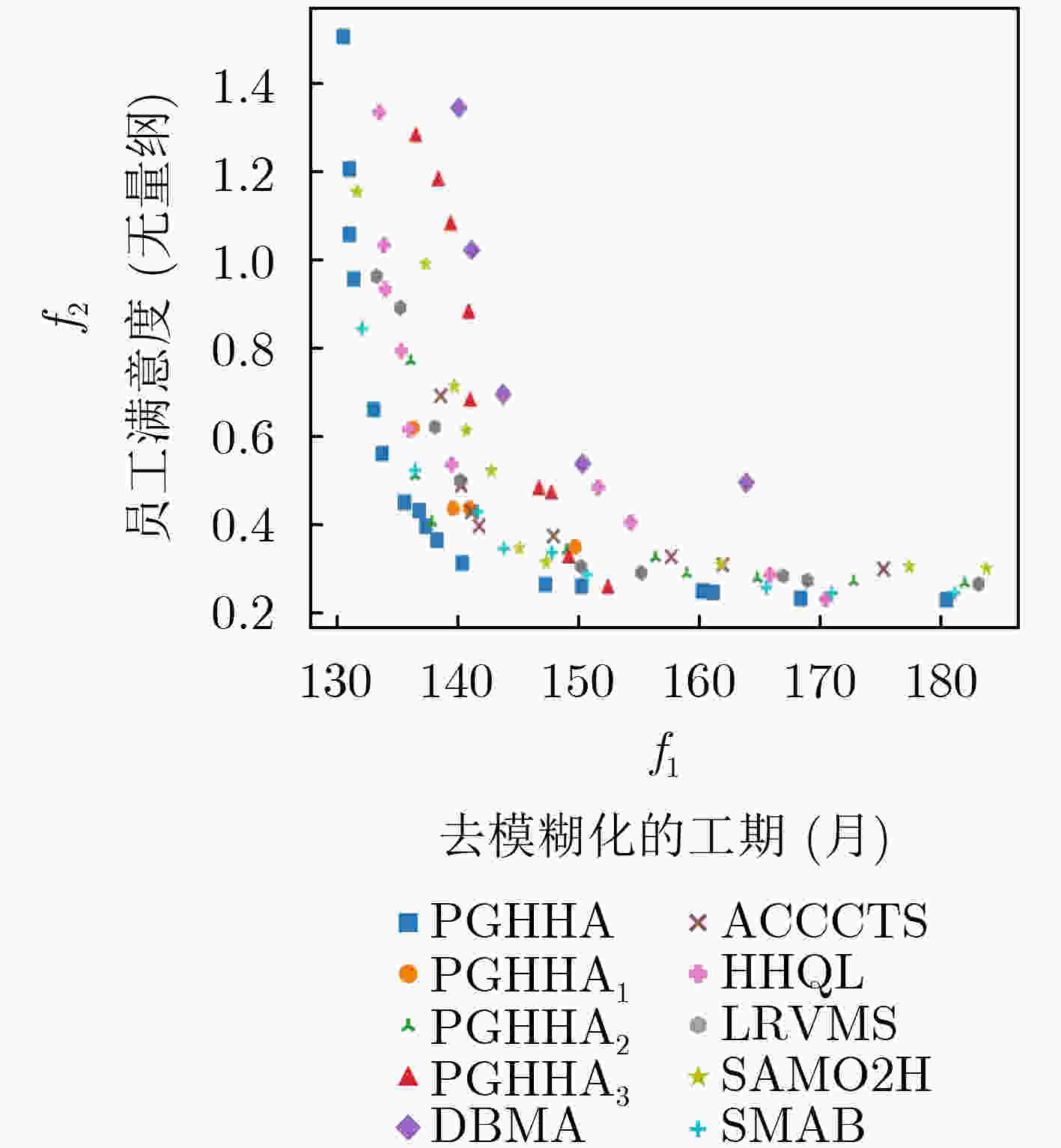
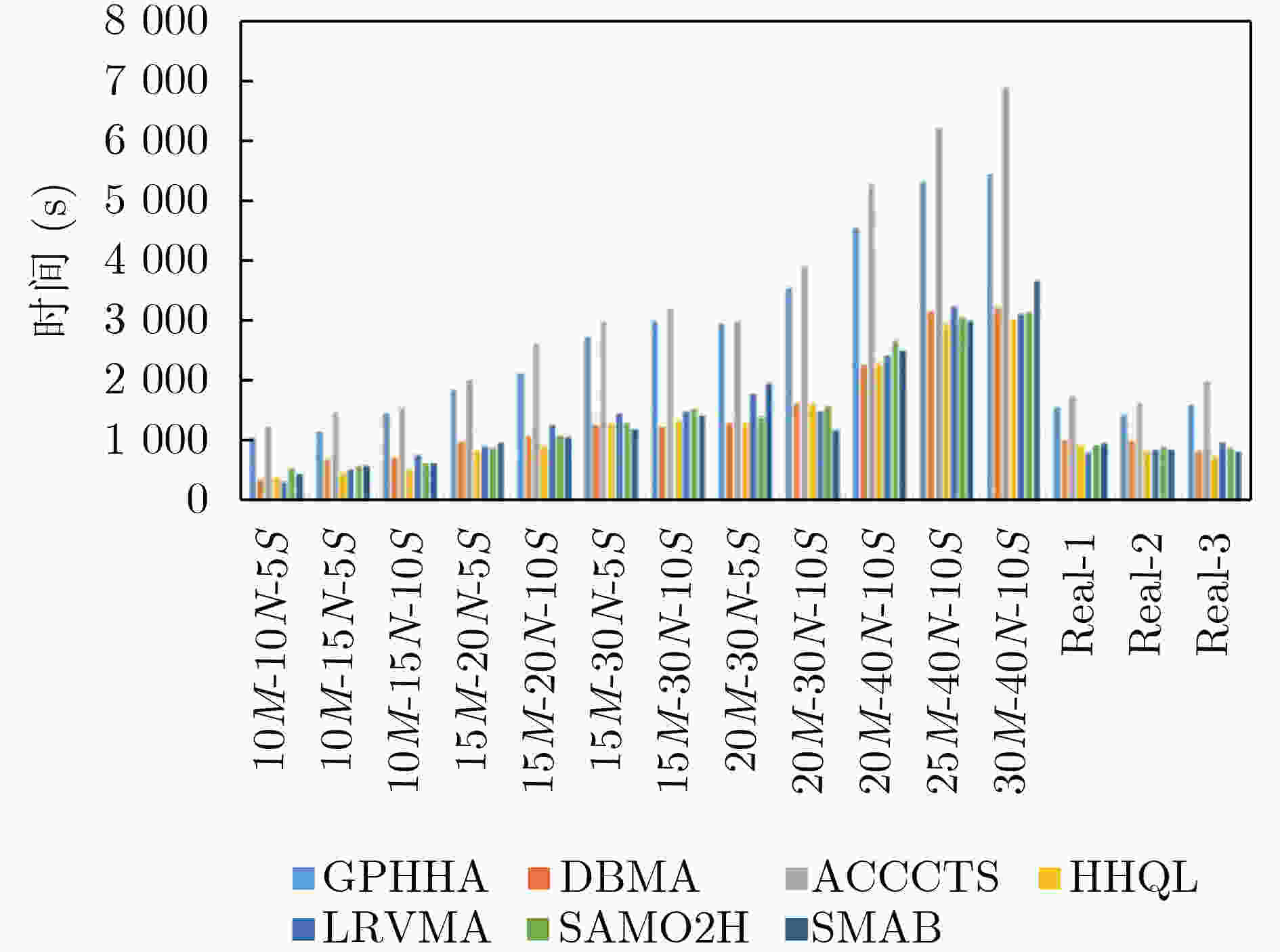
Objective The Software Project Scheduling Problem (SPSP) is critical for optimizing resource allocation and task sequencing in software development, directly impacting economic efficiency and market competitiveness. However, traditional SPSP models assume deterministic task attributes, ignoring pervasive uncertainties such as fluctuating efforts due to demand changes or estimation inaccuracies. These limitations often lead to infeasible or suboptimal scheduling solutions in real-world dynamic environments. To address this gap, this study establishes a novel multi-objective software project scheduling model that explicitly incorporates task effort uncertainty. The model employs asymmetric triangular interval type-2 fuzzy numbers to robustly characterize effort variability, ensuring a realistic representation of complex software development environments. The primary objective is to enhance decision-making quality under uncertainty by developing an efficient optimization algorithm that minimizes project duration while maximizing employee satisfaction, thereby improving scheduling robustness and adaptability in dynamic software projects. Methods A Policy Gradient-based Hyper-Heuristic Algorithm (PGHHA) is developed to address the formulated model. The algorithm framework consists of a High Level Strategy (HLS) and a set of Low Level Heuristics (LLHs). HLS employs an Actor-Critic reinforcement learning architecture, where the Actor network selects appropriate LLHs based on real-time evolutionary states characterized by population convergence and diversity, while the Critic network evaluates the quality of the selected actions. Eight LLHs are designed by combining two global search operators (the matrix crossover operator and the Jaya operator with random Jitter) with two local mining strategies (duration-based local search and satisfaction-based local search). Each LLH is further configured with two levels of neighborhood search depth (V1=5, V2=20), whose values are determined through Taguchi orthogonal experiments. Each individual is encoded as a real-valued task-employee effort matrix, and constraints such as skill coverage, the maximum dedication and the maximum participant limit are enforced during optimization. To accelerate convergence, a prioritized experience replay mechanism is integrated to sample and learn from historical interaction trajectories, thereby efficiently updating network parameters. Results and Discussions Experimental evaluations were conducted on 12 synthetic instances and three real-world software projects. The proposed strategies were validated and our algorithm PGHHA was compared with six state-of-the-art ones. Performance was measured using Hypervolume Ratio (HVR) and Inverted Generational Distance (IGD), with statistical significance assessed via Wilcoxon rank-sum tests at a significance level of 0.05. Results demonstrate that PGHHA significantly outperforms all comparison algorithms in both convergence and diversity across most test instances ( Table 5 ,Table 6 ). Visual comparisons of Pareto fronts (Fig. 4 ,Fig. 5 ) further confirm that solutions obtained by PGHHA are located below those of other algorithms, reflecting enhanced convergence precision, while also exhibiting better spread and uniformity. Although PGHHA requires longer computational time due to the neural network training and experience replay mechanism (Fig. 6 ), the significant improvement in solution quality is considered acceptable given the typically longer cycles of software development projects. The incorporation of asymmetric triangular interval type-2 fuzzy numbers effectively handles task effort uncertainty, and the dynamic selection of LLH via the Actor-Critic framework, combined with prioritized experience replay, contributes to the algorithm’s robust performance in uncertain environments. These results validate that PGHHA provides a more effective scheduling support tool, balancing multiple objectives under uncertainty without compromising solution diversity.Conclusions This paper establishes a multi-objective software project scheduling model that incorporates task effort uncertainty using asymmetric triangular interval type-2 fuzzy numbers. To solve this model, a policy gradient-based hyper-heuristic algorithm is proposed, which employs an Actor-Critic reinforcement learning framework as the high-level strategy to dynamically select low-level heuristics according to the evolutionary state of the population. A prioritized experience replay mechanism is integrated to improve learning efficiency and convergence speed. Experimental results on synthetic and real-world instances demonstrate that: (1) The proposed algorithm achieves significantly better convergence and diversity in uncertain environments compared to six state-of-the-art algorithms; (2) The combination of global search operators and local mining strategies effectively balances exploration and exploitation during evolution; (3) The use of type-2 fuzzy numbers provides a more robust representation of effort uncertainty than type-1 fuzzy numbers. However, the current model is limited to single-project scenarios. In future research, the model will be extended to multi-project scheduling environments with shared resources and cross-project dependencies. Furthermore, the integration of more adaptive reward mechanisms and lightweight neural architectures will be explored to reduce computational cost while maintaining solution quality. -
表 1 员工和任务属性
符号 定义 $ {E_i} $ 第i个员工，i=1,2,···,M，M为员工总数 $ E_i^{{\text{maxded}}} $ $ {E_i} $对项目的最大投入度 $ v_i^k $ 员工$ {E_i} $在技能k上的等级，技能等级分为5级，$ v_i^k \in \left\{ {1,2,3,4,5} \right\} $ $ {o_i} $ $ {E_i} $已掌握的技能集合 $ p_i^k $ $ {E_i} $对技能k的熟练度，$ p_i^k \in [0,C] $，C=5 $ {\text{c}}{{\text{o}}_{il}} $ 员工$ {E_i} $和员工$ {E_l} $的合作次数 $ {T_j} $ 第j个任务，j=1,2,…,N，N为任务总数 $ \tilde T_j^{{\text{eff}}} $ $ {T_j} $所需要的模糊工作量，单位是人·月 $ {\text{T\_li}}{{\text{m}}_j} $ $ {T_j} $的最大参与人数 $ T_j^{{\text{ext}}} $ 任务$ {T_j} $的重要程度，$ T_j^{{\text{ext}}} \in \left\{ {1,2,3,4,5} \right\} $ $ {T^{{\text{im}}}} $ 重要任务的集合，由重要程度为5级的任务构成，即$ {T^{{\text{im}}}} = \left\{ {{T_j}|T_j^{{\text{ext}}} = 5,j = 1,2,\cdots,N} \right\} $ $ {\text{re}}{{\text{q}}_j} $ $ {T_j} $所需要的技能集合 $ {H^k} $ 在技能k上骨干员工的集合，由技能等级为4级或5级的员工构成，即$ {H}^{k}=\left\{{E}_{i}|{v}_{i}^{k}=4\text{ }，或{\text{ v}}_{i}^{k}=5,i=1,2,\cdots ,M\right\} $ 
下载: 导出CSV
表 2 4种种群状态的划分
$ {S_1} $ $ {S_2} $ $ {S_3} $ $ {S_4} $ $ \Delta {\text{HV}} > 0 $ $ \Delta {\text{HV}} < 0 $ $ \Delta {\text{HV}} > 0 $ $ \Delta {\text{HV}} \leqslant 0 $ $ \Delta {\text{DV}} > 0 $ $ \Delta {\text{DV}} > 0 $ $ \Delta {\text{DV}} < 0 $ $ \Delta {\text{DV}} \leqslant 0 $
下载: 导出CSV
表 3 8种低层启发式策略
LLH1 LLH2 LLH3 LLH4 MCO+SLSS+V1 MCO+SLSS+V2 MCO+DLSS+V1 MCO+DLSS+V2 LLH5 LLH6 LLH7 LLH8 JORJ+SLSS+V1 JORJ+SLSS+V2 JORJ+DLSS+V1 JORJ+DLSS+V2
下载: 导出CSV
表 4 20M-40N-10S算例上不同参数的取值结果对比
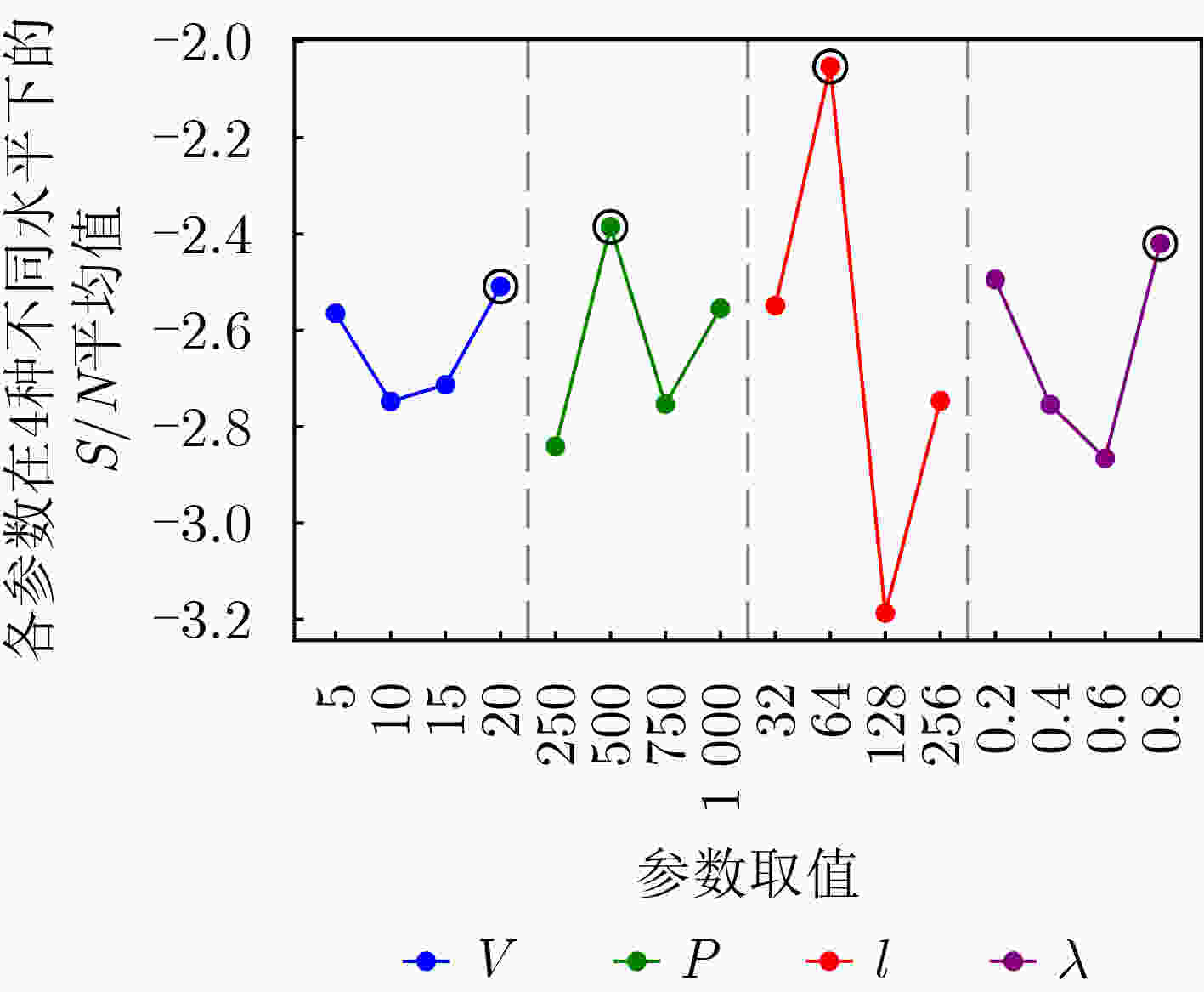
组别 参数 结果 V L l $ \lambda $ S/N 1 5 250 32 0.2 – 2.3655 2 5 500 64 0.4 – 1.7542 3 5 750 128 0.6 – 3.6635 4 5 1000 256 0.8 – 2.4745 5 10 250 64 0.6 – 2.6962 6 10 500 32 0.8 – 2.3946 7 10 750 256 0.2 – 2.7389 8 10 1000 128 0.4 – 3.1599 9 15 250 128 0.8 – 3.1577 10 15 500 256 0.6 – 2.6271 11 15 750 32 0.4 – 2.9583 12 15 1000 64 0.2 – 2.1076 13 20 250 256 0.4 – 3.1444 14 20 500 128 0.2 – 2.7643 15 20 750 64 0.8 – 1.6519 16 20 1000 32 0.6 – 2.4745
下载: 导出CSV
表 5 所提算法PGHHA和替换单一策略算法的对比结果
算例 PGHHA PGHHA1 PGHHA2 PGHHA3 HVR IGD HVR IGD HVR IGD HVR IGD 10M-10N-5S 0.99250 0.09220 0.98400 =0.12346 +0.96899 +0.21161 +0.97471 +0.14761 +10M-15N-5S 0.95844 0.05834 0.89655 +0.20335 +0.93145 +0.17469 +0.81489 +0.29439 +10M-15N-10S 0.94790 0.11968 0.87704 +0.26172 +0.92149 +0.18779 +0.80562 +0.29297 +15M-20N-5S 0.98163 0.08262 0.79431 +0.38438 +0.90486 +0.15519 +0.77907 +0.38811 +15M-20N-10S 0.97927 0.11605 0.74462 +0.29048 +0.77350 +0.23512 +0.76558 +0.27590 +15M-30N-5S 0.96563 0.09172 0.74232 +0.23335 +0.79543 +0.24815 +0.69608 +0.31365 +15M-30N-10S 0.97375 0.08377 0.41407 +0.45349 +0.86138 +0.17924 +0.78636 +0.29754 +20M-30N-5S 0.99449 0.04014 0.76834 +0.23783 +0.79635 +0.18083 +0.76224 +0.26607 +20M-30N-10S 0.97315 0.17456 0.49679 +0.46848 +0.57295 +0.37948 +0.76702 +0.24577 +20M-40N-10S 0.87440 0.07848 0.71880 +0.15870 +0.63450 +0.12640 +0.70570 +0.12980 +25M-40N-10S 0.95382 0.09408 0.89277 +0.15278 +0.84310 +0.13515 +0.87307 +0.19490 +30M-40N-10S 0.94910 0.10911 0.89051 +0.18086 +0.86931 +0.17546 +0.89889 +0.18816 +Real-1 0.98426 0.10089 0.78669 +0.31839 +0.79828 +0.30680 +0.76297 +0.35578 +Real-2 0.96564 0.05132 0.84702 +0.12234 +0.86167 +0.09253 +0.83655 +0.17651 +Real-3 0.97003 0.22431 0.94249 +0.37577 +0.96009 =0.32971 +0.92067 +0.29233 ++/-/= 14/0/1 15/0/0 14/0/1 15/0/0 15/0/0 15/0/0
下载: 导出CSV
表 6 所提算法的性能验证实验中六种算法的对比结果
算例 PGHHA DBMA ACCCTS HHQL HVR IGD HVR IGD HVR IGD HVR IGD 10M-10N-5S 0.99258 0.09220 0.97294 +0.15199 +0.98768 =0.10607 +0.98235 +0.12064 +10M-15N-5S 0.95844 0.05834 0.82412 +0.22569 +0.88027 +0.16973 +0.84688 +0.20773 +10M-15N-10S 0.94790 0.11968 0.84145 +0.26447 +0.89963 +0.20285 +0.87447 +0.25913 +15M-20N-5S 0.98163 0.08262 0.79265 +0.36254 +0.80773 +0.23642 +0.79295 +0.33822 +15M-20N-10S 0.97927 0.11605 0.74482 +0.31588 +0.77390 +0.23932 +0.75041 +0.24309 +15M-30N-5S 0.96563 0.09172 0.72179 +0.30118 +0.76937 +0.13433 +0.71657 +0.25633 +15M-30N-10S 0.97375 0.08377 0.82710 +0.26013 +0.86548 +0.20556 +0.82900 +0.23633 +20M-30N-5S 0.99449 0.04014 0.77301 +0.23358 +0.80215 +0.17489 +0.79327 +0.18709 +20M-30N-10S 0.97315 0.17456 0.51097 +0.52757 +0.84647 +0.36461 +0.74630 +0.48835 +20M-40N-10S 0.87440 0.07848 0.73501 +0.12918 +0.80785 +0.12685 +0.79785 +0.14953 +25M-40N-10S 0.95382 0.09408 0.89869 +0.14658 +0.93671 +0.10052 =0.90224 +0.09777 =30M-40N-10S 0.94910 0.10911 0.93293 +0.16346 +0.94881 =0.11868 +0.94190 +0.14346 +Real-1 0.98426 0.10089 0.77856 +0.29865 +0.79490 +0.30287 +0.78771 +0.25761 +Real-2 0.96564 0.05132 0.87619 +0.16981 +0.90169 +0.09354 +0.85187 +0.15740 +Real-3 0.97003 0.22431 0.92007 +0.35695 +0.93587 +0.33432 +0.96637 =0.22856 ++/-/= 15/0/0 15/0/0 13/0/2 14/0/1 14/0/1 14/0/1 10M-10N-5S 0.98428 +0.10658 +0.98795 =0.11816 +0.99009 =0.11218 +10M-15N-5S 0.87415 +0.16099 +0.86120 +0.16605 +0.87402 +0.12515 +10M-15N-10S 0.87242 +0.23220 +0.86701 +0.22302 +0.85549 +0.25300 +15M-20N-5S 0.80580 +0.35287 +0.80364 +0.35751 +0.80681 +0.32411 +15M-20N-10S 0.90308 +0.15268 +0.80479 +0.25375 +0.76270 +0.19806 +15M-30N-5S 0.74572 +0.23613 +0.74964 +0.21988 +0.74641 +0.16522 +15M-30N-10S 0.82229 +0.26220 +0.85177 +0.16454 +0.85042 +0.16622 +20M-30N-5S 0.78010 +0.22599 +0.79598 +0.14746 +0.79434 +0.17365 +20M-30N-10S 0.52278 +0.45390 +0.54351 +0.40593 +0.57787 +0.39774 +20M-40N-10S 0.69624 +0.16358 +0.78799 +0.11185 +0.80452 +0.11378 +25M-40N-10S 0.90800 +0.13031 +0.92778 +0.09934 =0.92141 +0.15109 +30M-40N-10S 0.91817 +0.15803 +0.94147 +0.14479 +0.94544 =0.12199 +Real-1 0.78399 +0.28787 +0.79216 +0.29067 +0.80337 +0.25183 +Real-2 0.85814 +0.17055 +0.85469 +0.11839 +0.86265 +0.04942 =Real-3 0.95563 +0.23613 +0.94699 +0.25314 +0.92067 +0.29233 ++/-/= 15/0/0 15/0/0 14/0/1 14/0/1 13/0/2 14/0/1
下载: 导出CSV
-
[1] HASTIE S. Standish group 2023 chaos report[R]. 2023. (查阅网上资料, 未找到本条文献信息, 请确认并补充报告编号). [2] CRAWFORD B, SOTO R, JOHNSON F, et al. A max–min ant system algorithm to solve the software project scheduling problem[J]. Expert Systems with Applications, 2014, 41(15): 6634–6645. doi: 10.1016/j.eswa.2014.05.003. [3] ALBA E and CHICANO J F. Software project management with GAs[J]. Information Sciences, 2007, 177(11): 2380–2401. doi: 10.1016/j.ins.2006.12.020. [4] LI Hongbo, ZHU Hanyu, ZHENG Linwen, et al. Software project scheduling with multitasking[J]. Economic Computation and Economic Cybernetics Studies and Research, 2023, 57(1): 153–170. doi: 10.24818/18423264/57.1.23.10. [5] LI Hongbo, ZHU Hanyu, ZHENG Linwen, et al. Software project scheduling under activity duration uncertainty[J]. Annals of Operations Research, 2024, 338(1): 477–512. doi: 10.1007/s10479-023-05343-0. [6] MASMOUDI M and HAÏT A. Project scheduling under uncertainty using fuzzy modelling and solving techniques[J]. Engineering Applications of Artificial Intelligence, 2013, 26(1): 135–149. doi: 10.1016/j.engappai.2012.07.012. [7] YU Hui, GAO Kaizhou, WU Naiqi, et al. Scheduling multiobjective dynamic surgery problems via Q-learning-based meta-heuristics[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2024, 54(6): 3321–3333. doi: 10.1109/TSMC.2024.3352522. [8] MAHDAVI A, SHIRAZI B, and REZAEIAN J. Toward a scalable type-2 fuzzy model for resource-constrained project scheduling problem[J]. Applied Soft Computing, 2021, 100: 106988. doi: 10.1016/j.asoc.2020.106988. [9] LI Junqing, LIU Zhengmin, LI Chengdong, et al. Improved artificial immune system algorithm for type-2 fuzzy flexible job shop scheduling problem[J]. IEEE Transactions on Fuzzy Systems, 2021, 29(11): 3234–3248. doi: 10.1109/TFUZZ.2020.3016225. [10] JI Jianjiao, GUO Yinan, GAO Xiaozhi, et al. Q-Learning-Based hyperheuristic evolutionary algorithm for dynamic task allocation of crowdsensing[J]. IEEE Transactions on Cybernetics, 2023, 53(4): 2211–2224. doi: 10.1109/TCYB.2021.3112675. [11] HUANG Yao, GUO Yinan, CHEN Guoyu, et al. Q-learning assisted multi-objective evolutionary optimization for low-carbon scheduling of open-pit mine trucks[J]. Swarm and Evolutionary Computation, 2025, 92: 101778. doi: 10.1016/j.swevo.2024.101778. [12] 杨潇, 郭一楠, 吉建娇, 等. 异构群智感知PPO多目标任务指派方法[J]. 控制理论与应用, 2024, 41(6): 1056–1066. doi: 10.7641/CTA.2023.20950.YANG Xiao, GUO Yinan, JI Jianjiao, et al. PPO multi-objective task allocation method for heterogeneous crowd sensing[J]. Control Theory & Applications, 2024, 41(6): 1056–1066. doi: 10.7641/CTA.2023.20950. [13] CHEN Mengjiao, XU Jiyuan, ZHANG Wenyu, et al. A new customer-oriented multi-task scheduling model for cloud manufacturing considering available periods of services using an improved hyper-heuristic algorithm[J]. Expert Systems with Applications, 2025, 269: 126419. doi: 10.1016/j.eswa.2025.126419. [14] YANG Jinfeng, XU Hua, CHENG Jinhai, et al. A decomposition-based memetic algorithm to solve the biobjective green flexible job shop scheduling problem with interval type-2 fuzzy processing time[J]. Computers & Industrial Engineering, 2023, 183: 109513. doi: 10.1016/j.cie.2023.109513. [15] 杨和林, 郑梦婷, 刘帅, 等. 恶意干扰下的无人机辅助边缘计算加权能耗与时延智能优化[J]. 电子与信息学报, 2024, 46(7): 2879–2887. doi: 10.11999/JEIT230986.YANG Helin, ZHENG Mengting, LIU Shuai, et al. Intelligent weighted energy consumption and delay optimization for UAV-assisted MEC under malicious jamming[J]. Journal of Electronics & Information Technology, 2024, 46(7): 2879–2887. doi: 10.11999/JEIT230986. [16] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182–197. doi: 10.1109/4235.996017. [17] MINKU L L, SUDHOLT D, and YAO Xin. Improved evolutionary algorithm design for the project scheduling problem based on runtime analysis[J]. IEEE Transactions on Software Engineering, 2014, 40(1): 83–102. doi: 10.1109/TSE.2013.52. [18] CHEN Weineng and ZHANG Jun. Ant colony optimization for software project scheduling and staffing with an event-based scheduler[J]. IEEE Transactions on Software Engineering, 2013, 39(1): 1–17. doi: 10.1109/TSE.2012.17. [19] CHANG C K, JIANG H Y, DI Yu, et al. Time-line based model for software project scheduling with genetic algorithms[J]. Information and Software Technology, 2008, 50(11): 1142–1154. doi: 10.1016/j.infsof.2008.03.002. [20] SHEN Xiaoning, MINKU L L, MARTURI N, et al. A Q-learning-based memetic algorithm for multi-objective dynamic software project scheduling[J]. Information Sciences, 2018, 428: 1–29. doi: 10.1016/j.ins.2017.10.041. [21] MAHMUD S, ABBASI A, CHAKRABORTTY R K, et al. A self-adaptive hyper-heuristic based multi-objective optimisation approach for integrated supply chain scheduling problems[J]. Knowledge-Based Systems, 2022, 251: 109190. doi: 10.1016/j.knosys.2022.109190. [22] CIMBALA J M. Taguchi orthogonal arrays[EB/OL]. https://www.me.psu.edu/cimbala/me345web_Fall_2014/Lectures/Taguchi_orthogonal_arrays.pdf, 2025. [23] ZHAO Fuqing, DI Shilu, and WANG Ling. A hyperheuristic with Q-learning for the multiobjective energy-efficient distributed blocking flow shop scheduling problem[J]. IEEE Transactions on Cybernetics, 2023, 53(5): 3337–3350. doi: 10.1109/TCYB.2022.3192112. [24] SHAO Zhongshi, SHAO Weishi, CHEN Jianrui, et al. A feedback learning-based selection hyper-heuristic for distributed heterogeneous hybrid blocking flow-shop scheduling problem with flexible assembly and setup time[J]. Engineering Applications of Artificial Intelligence, 2024, 131: 107818. doi: 10.1016/j.engappai.2023.107818. [25] WU Xiuli, CONSOLI P, MINKU L, et al. An evolutionary hyper-heuristic for the software project scheduling problem[C]. Proceedings of the 14th International Conference on Parallel Problem Solving from Nature–PPSN XIV, Edinburgh, UK, 2016: 37–47. doi: 10.1007/978-3-319-45823-6_4. [26] LI Rui, GONG Wenyin, LU Chao, et al. A learning-based memetic algorithm for energy-efficient flexible job-shop scheduling with type-2 fuzzy processing time[J]. IEEE Transactions on Evolutionary Computation, 2023, 27(3): 610–620. doi: 10.1109/TEVC.2022.3175832. [27] ZHU Lilu, WU Feng, HU Yanfeng, et al. A heuristic multi-objective task scheduling framework for container-based clouds via actor-critic reinforcement learning[J]. Neural Computing and Applications, 2023, 35(13): 9687–9710. doi: 10.1007/s00521-023-08208-6. -
图(6) / 表(6)
计量
- 文章访问数: 25
- HTML全文浏览量: 10
- PDF下载量: 0
- 被引次数: 0
下载:
