车联网中采用混合分层DRL的无人机辅助移动边缘计算

杨淼焱; 方旭明

doi:10.11999/JEIT250743

车联网中采用混合分层DRL的无人机辅助移动边缘计算

doi: 10.11999/JEIT250743 cstr: 32379.14.JEIT250743

西南交通大学信息科学与技术学院成都 610031

详细信息

作者简介:
杨淼焱：男，博士生，研究方向为移动边缘计算

方旭明：男，教授，研究方向为无线与移动通信网络、交通通信与信息系统等

中图分类号: TN929
计量
- 文章访问数: 10
- HTML全文浏览量: 3
- PDF下载量: 0
- 被引次数: 0
出版历程
- 修回日期: 2026-01-22
- 录用日期: 2026-01-22
- 网络出版日期: 2026-02-12

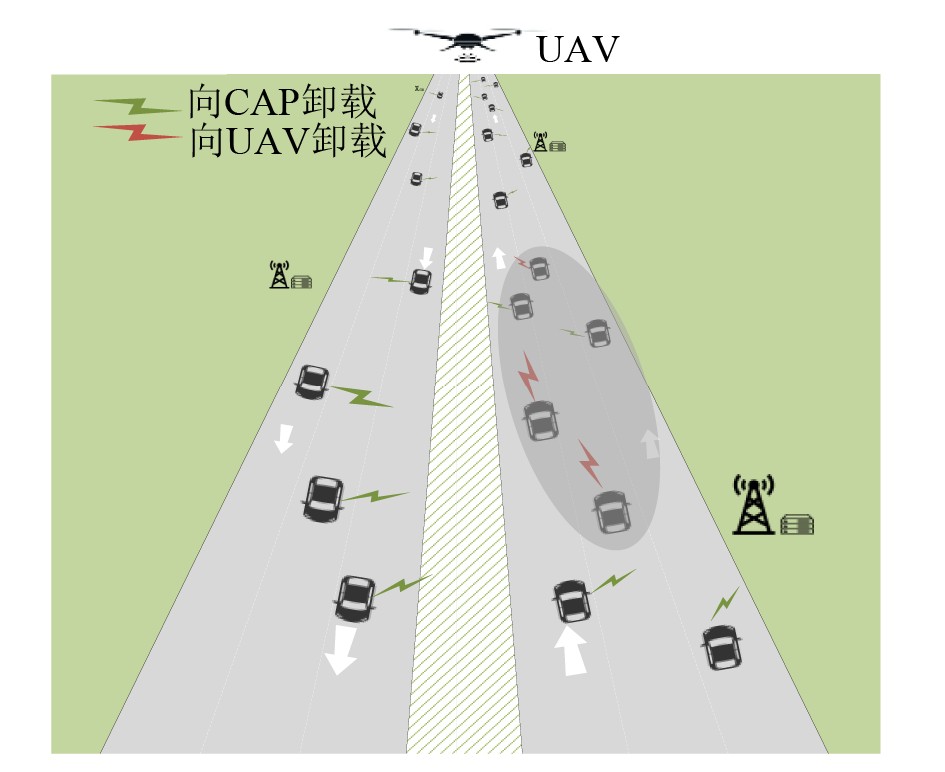
UAV-assisted Mobile Edge Computing based on Hybrid Hierarchical DRL in the Internet of Vehicular

School of Information Science and Technology, Southwest Jiaotong University, Chengdu 610031, China

摘要

摘要: 针对车联网中无人机辅助移动边缘计算场景下，基于深度强化学习的时延优化方法因车辆规模增大导致动作空间维度爆炸、训练效率低的问题，该文提出一种无人机辅助移动边缘计算的双层混合优化方案。首先，通过联合优化任务卸载、计算与通信资源分配以及无人机飞行控制，构建满足飞行与能耗约束条件下最小化系统计算任务总时延的模型。其次，该文通过双层算法结构将深度强化学习与贪婪算法相结合，提出混合分层深度强化学习(Hybrid Hierarchical Deep Reinforcement Learning, HHDRL)算法对问题求解，以降低训练复杂度并加快收敛。仿真结果表明，该算法在保持时延性能接近传统深度强化学习算法的同时，提升了收敛速度。
- 无人机 /
- 移动边缘计算 /
- 混合算法 /
- 资源分配 /
- 深度强化学习
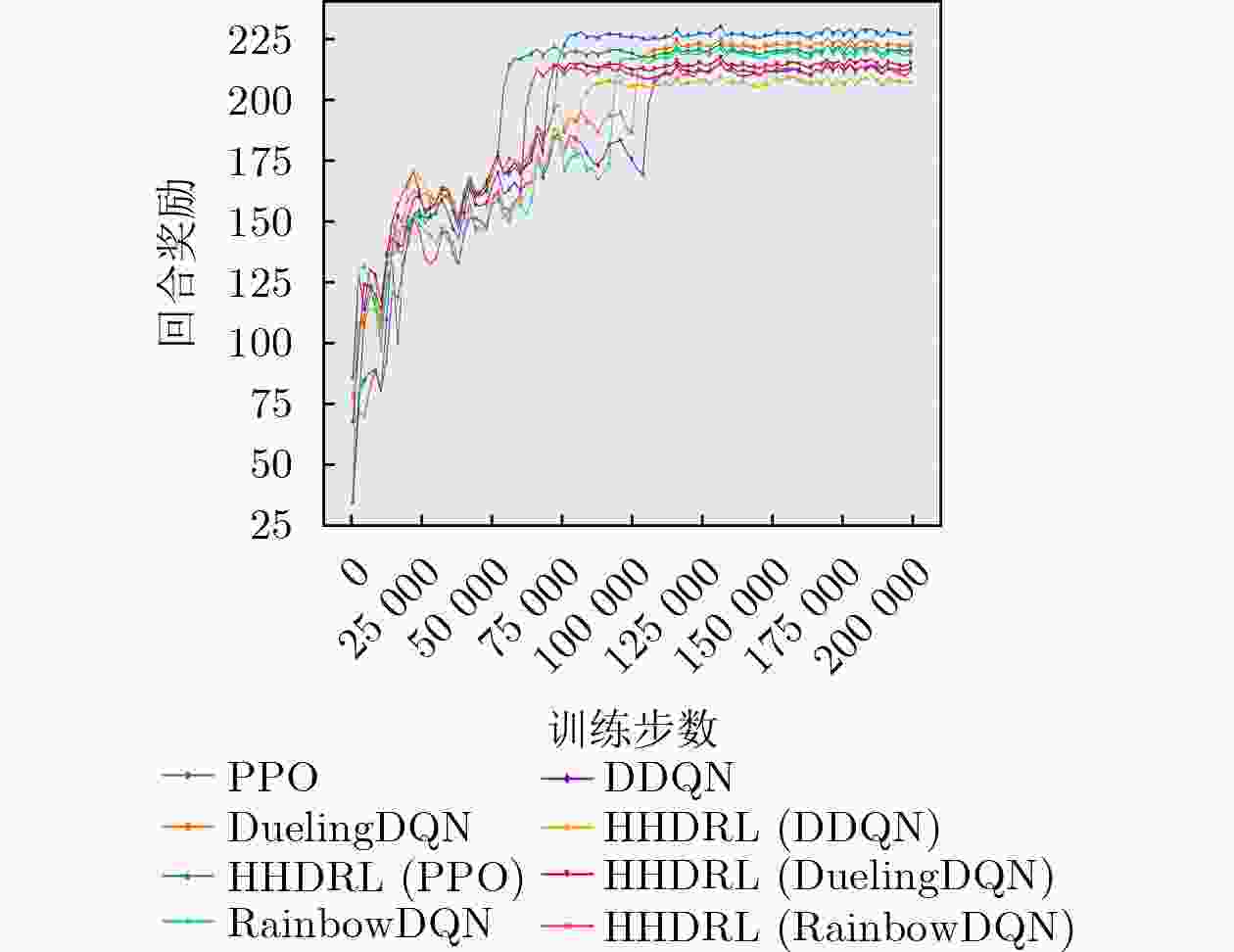
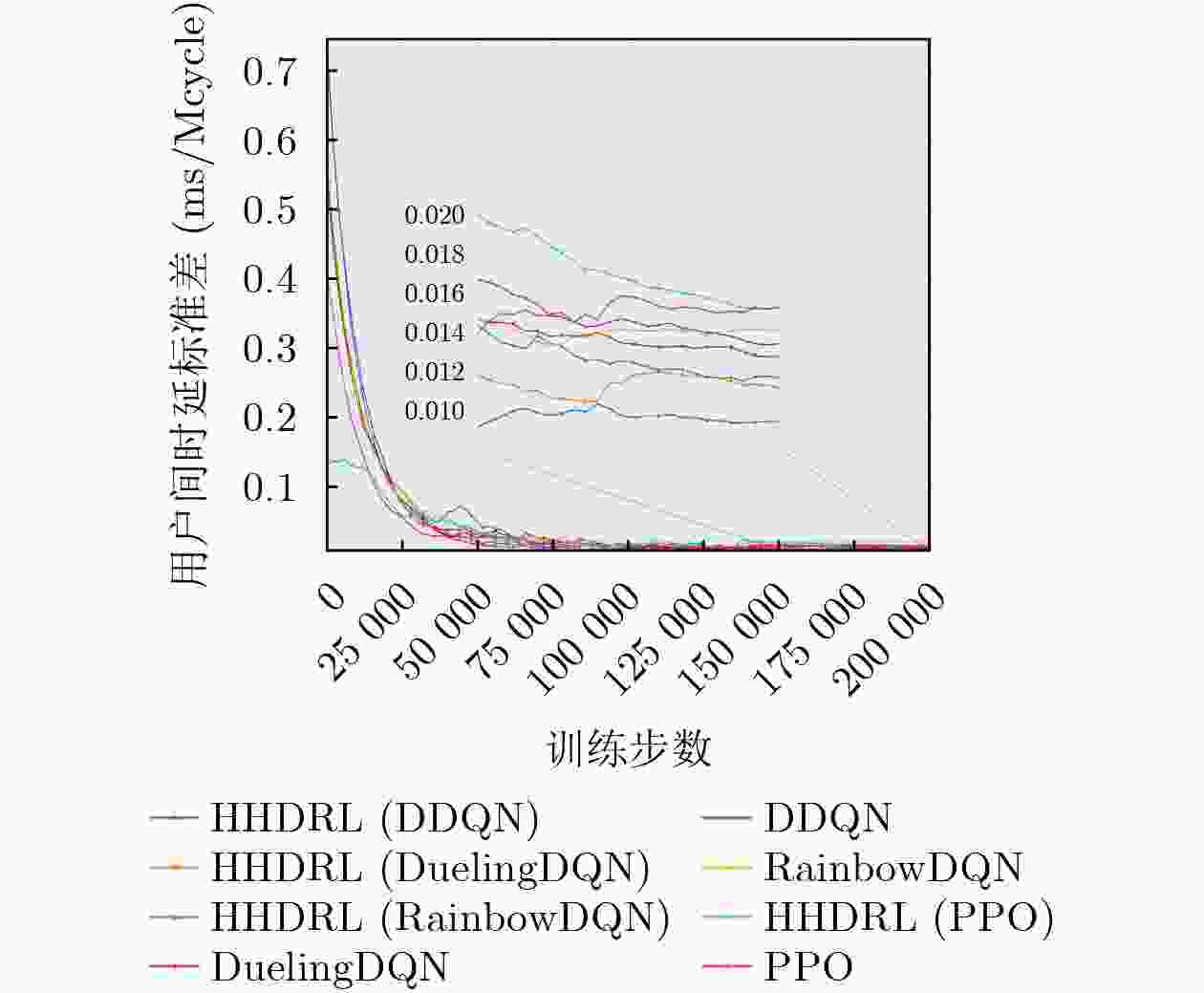
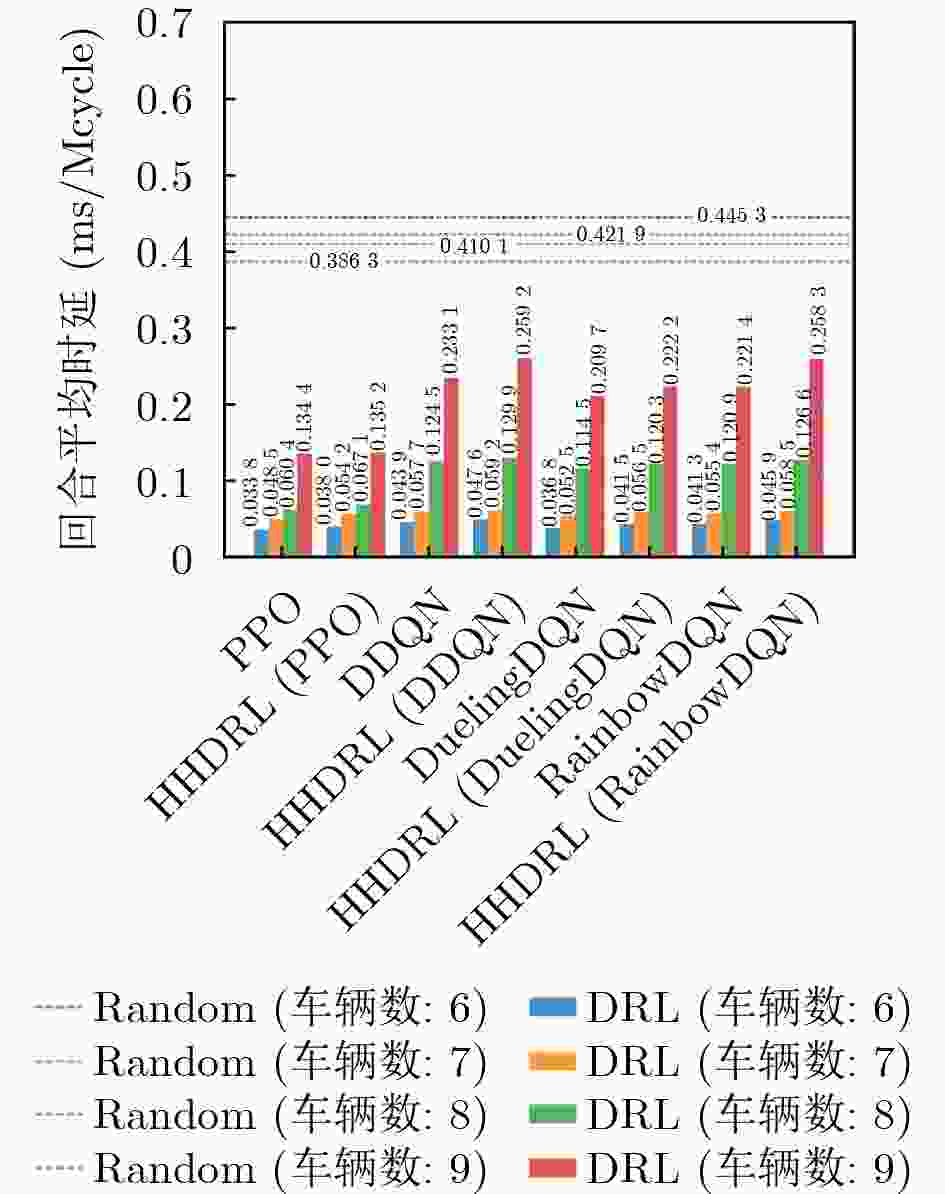
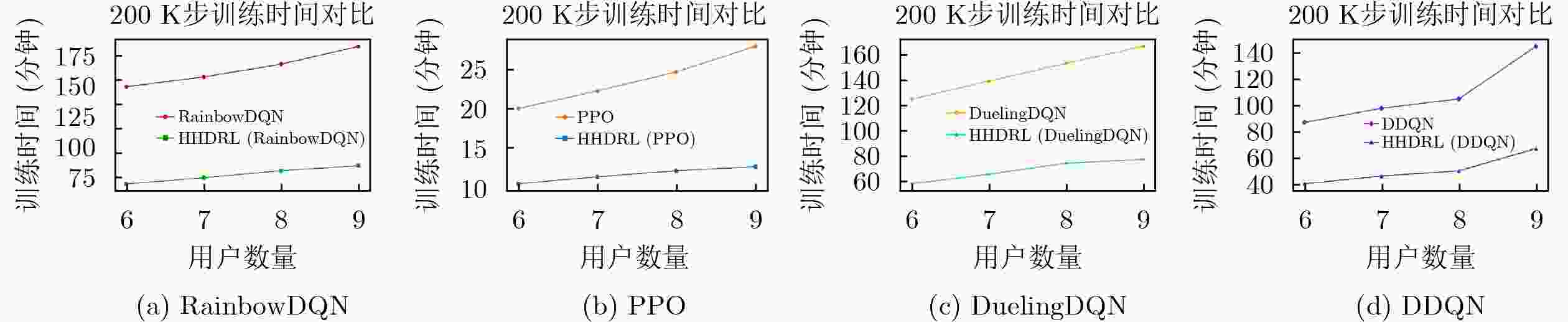
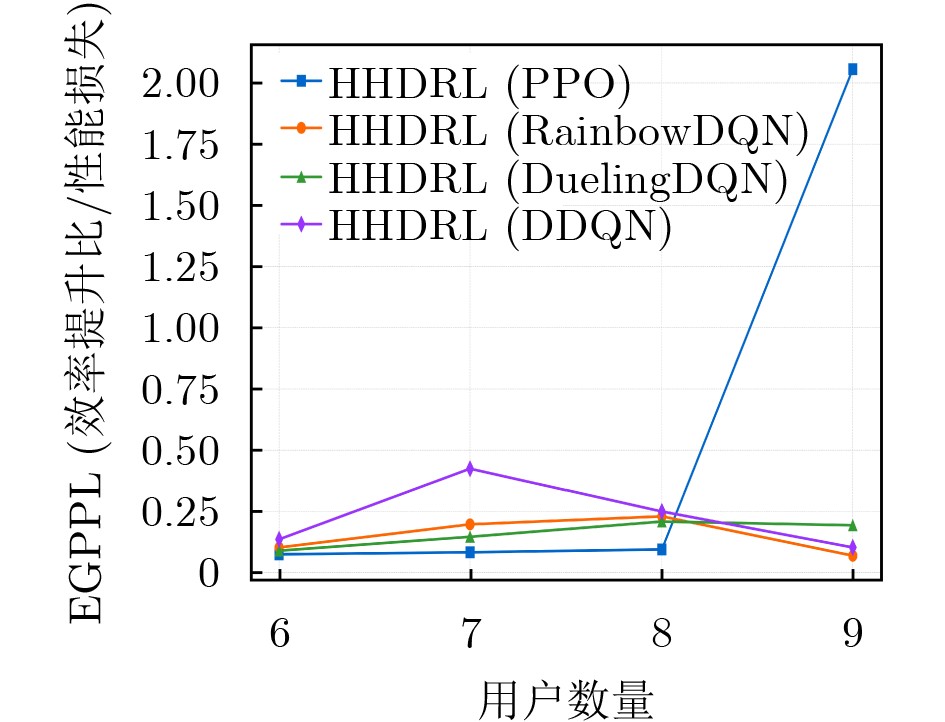
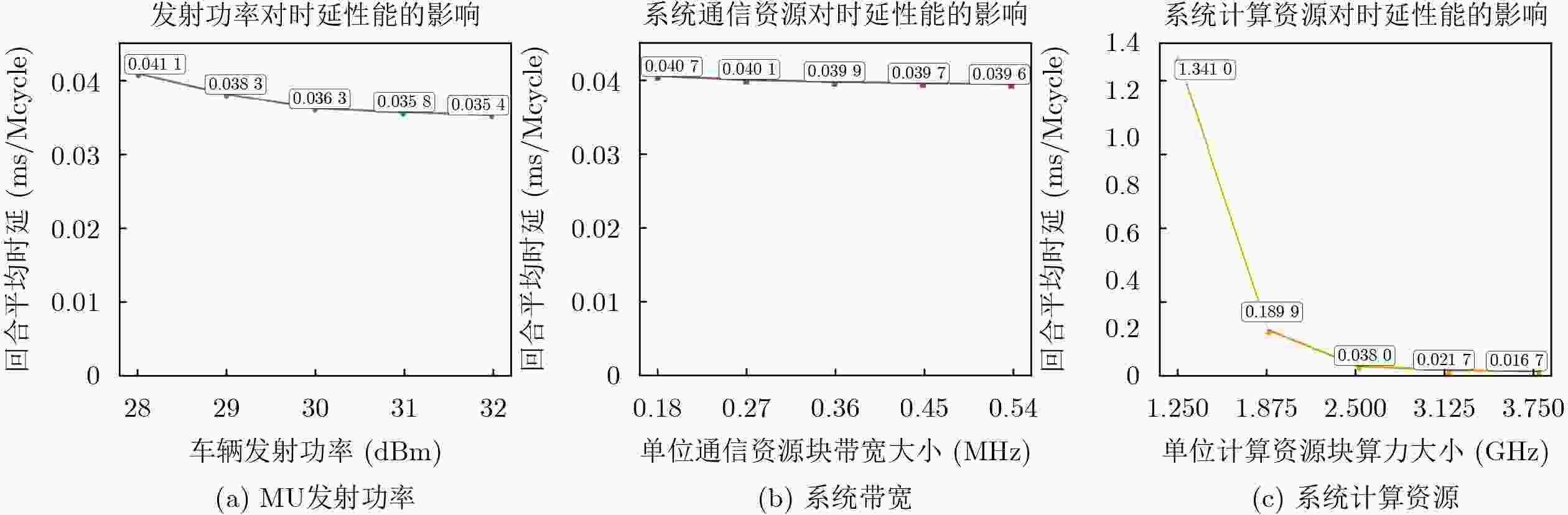
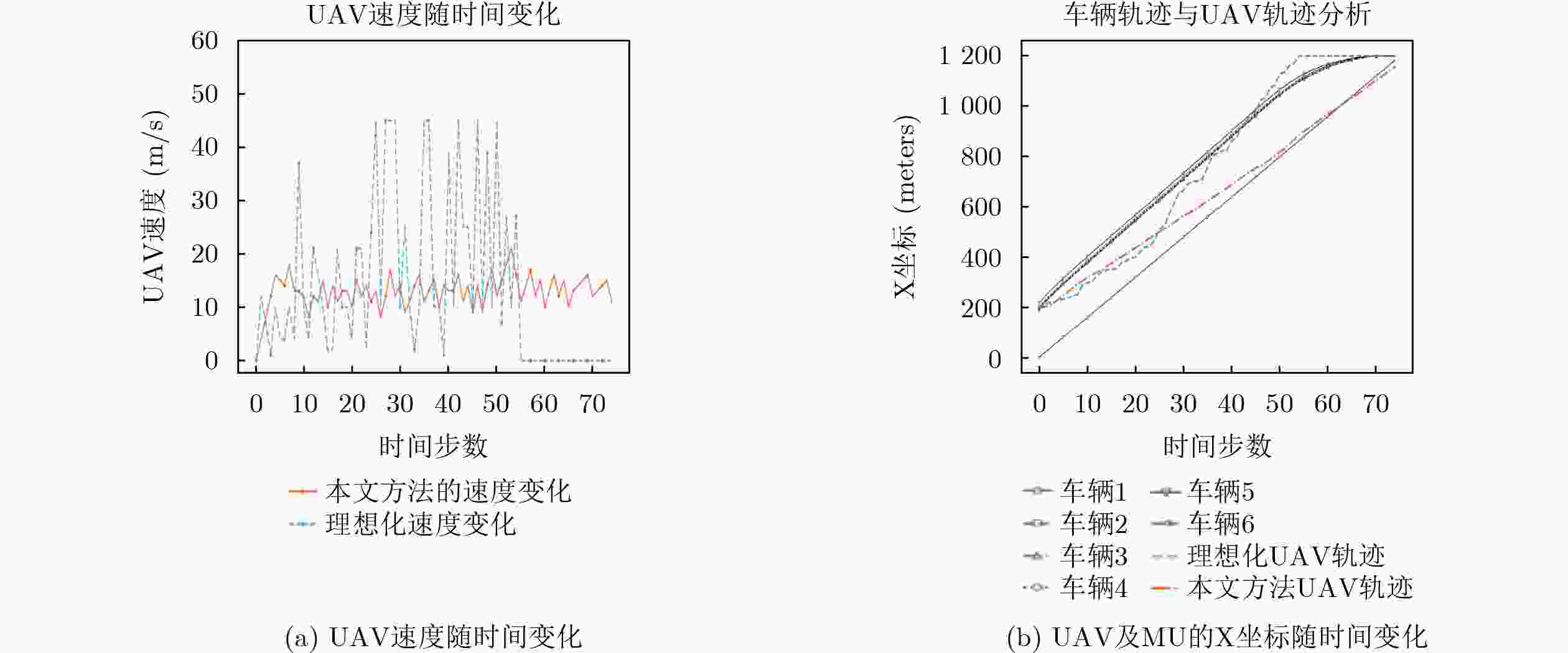
Abstract: Objective In the internet of vehicle (IoV), utilizing unmanned aerial vehicle (UAV) to address the tidal wave of edge computing has become a key technology in the 6G field in recent years. However, when using deep reinforcement learning (DRL) to optimize system latency, the action space dimension grows exponentially with the number of vehicles, leading to training difficulties and slow convergence. Therefore, this paper proposes a two-layer hybrid solution for UAV-assisted mobile edge computing (MEC) based on DRL which called hybrid hierarchical deep reinforcement learning(HHDRL). Methods The proposed HHDRL algorithm employs a two-layer architecture to hierarchically solve complex optimization problems. The upper layer employs an agent based on proximal policy optimization (PPO) combined with a multi-head actor network to manage user offloading policy and UAV control policy. The N heads in this network handle offloading decisions for the N users (local processing, offloadi- -ng to associated CAPs or UAV). A UAV flight control head is responsible for selecting from a set of discrete acceleration actions to reflect actual control constraints. The lower layer employs a computation- -ally efficient greedy algorithm to prioritize resources based on task characteristics. This hybrid hierarchi- -cal approach avoids the high computational cost of resource allocation schemes based solely on DRL. Results and Discussions The performance of the proposed HHDRL scheme was verified through numerical simulations. The parameters used in the simulation include parameters related to the specific Rician fading channel, parameters related to the UAV flight energy consumption model, and system parameters(e.g., mission data size of 9-18 Mbits and mission complexity of 2000-3000 cycles/bit). Figure 3 shows a training convergence comparison between the HHDRL scheme and the original DRL algorithm, demonstrating that HHDRL consistently converges faster than the DRL scheme, despite achieving slightly lower final rewards compared to the pure DRL approach. Figure 4 illustrates the impact of the HHDRL architecture on user delay fairness; the comparison reveals that the introduction of the HHDRL framework does not compromise the user fairness performance inherent to the DRL method. The performance evaluation in Figure 5 shows that the proposed scheme reduces system latency by approximately 71%-91% compared to a random baseline, and 1%-12% compared to the original DRL algorithm. Figure 6 shows a training time analysis for different numbers of users. Across different numbers of users, the HHDRL scheme consistently has shorter training times than the DRL scheme. Furthermore, as the number of users increases, the HHDRL scheme's training time increases more slowly. This is attributed to the hybrid hierarchical algorithm network architecture, which simplifies the DRL output action space. When we replace the upper-layer algorithm from PPO with other DRL algorithm, we still outperform the random baseline, and achieve comparable performance to the non-hybrid-hierarchical approach. This demonstrates the effectiveness and universality of the hybrid hierarchical architecture in achieving significant training acceleration while maintaining performance. The system parameter sensitivity analysis in Figure 8 shows that computational resources have the most significant impact on latency performance, compared to user transmission power and system bandwidth. This is because computational latency typically accounts for a larger proportion than communication latency in task processing. Figure 9 shows the results of the UAV trajectory optimization. Figure 9(a) shows the change in the UAV's velocity over time, demonstrating that discrete acceleration control reflects actual control accuracy and response delay considerations rather than idealized instantaneous velocity changes. Figure 9(b) shows the X-coordinates of the UAV and user over time, illustrating that the UAV adaptively adjusts its position to match the changing user distribution while maintaining flight stability. Conclusions This paper proposes a HHDRL algorithm that integrates DRL with a greedy algorithm in a hierarchical framework to address the difficulty of training UAV-assisted MEC systems in IoV. Simulation results confirm that: (1) Compared with the DRL method, the proposed method significantly accelerates the training convergence speed and shortens the training time. (2) The system latency performance of the proposed algorithm is almost comparable to that of the pure DRL method, while significantly outperforming the heuristic baseline and random baseline algorithms. (3) The HHDRL framework is able to effectively manage user task offloading, computing node resource allocation, and joint optimization of UAV trajectories under practical operational constraints. Future work will extend the framework to apply to multi-UAV collaboration and consider more complex environments.
- UAV /
- Mobile Edge Computing (MEC) /
- Hybrid algorithm /
- Resource allocation /
- Deep Reinforcement Learning (DRL)

HTML全文

图 1 场景示意图

下载: 全尺寸图片幻灯片

图 2 HHDRL算法网络结构示意图

下载: 全尺寸图片幻灯片

图 3 训练收敛性对比

下载: 全尺寸图片幻灯片

图 4 用户间时延均衡性随训练步长变化

下载: 全尺寸图片幻灯片

图 5 所提方案和基线方案在不同车辆环境下的性能对比图

下载: 全尺寸图片幻灯片

图 6 EGPPL随用户数变化

下载: 全尺寸图片幻灯片

图 76 HHDRL和DRL的训练时长随用户数变化

下载: 全尺寸图片幻灯片

图 8 不同系统参数对时延性能的影响

下载: 全尺寸图片幻灯片

图 9 所提出算法的UAV轨迹示意图

下载: 全尺寸图片幻灯片

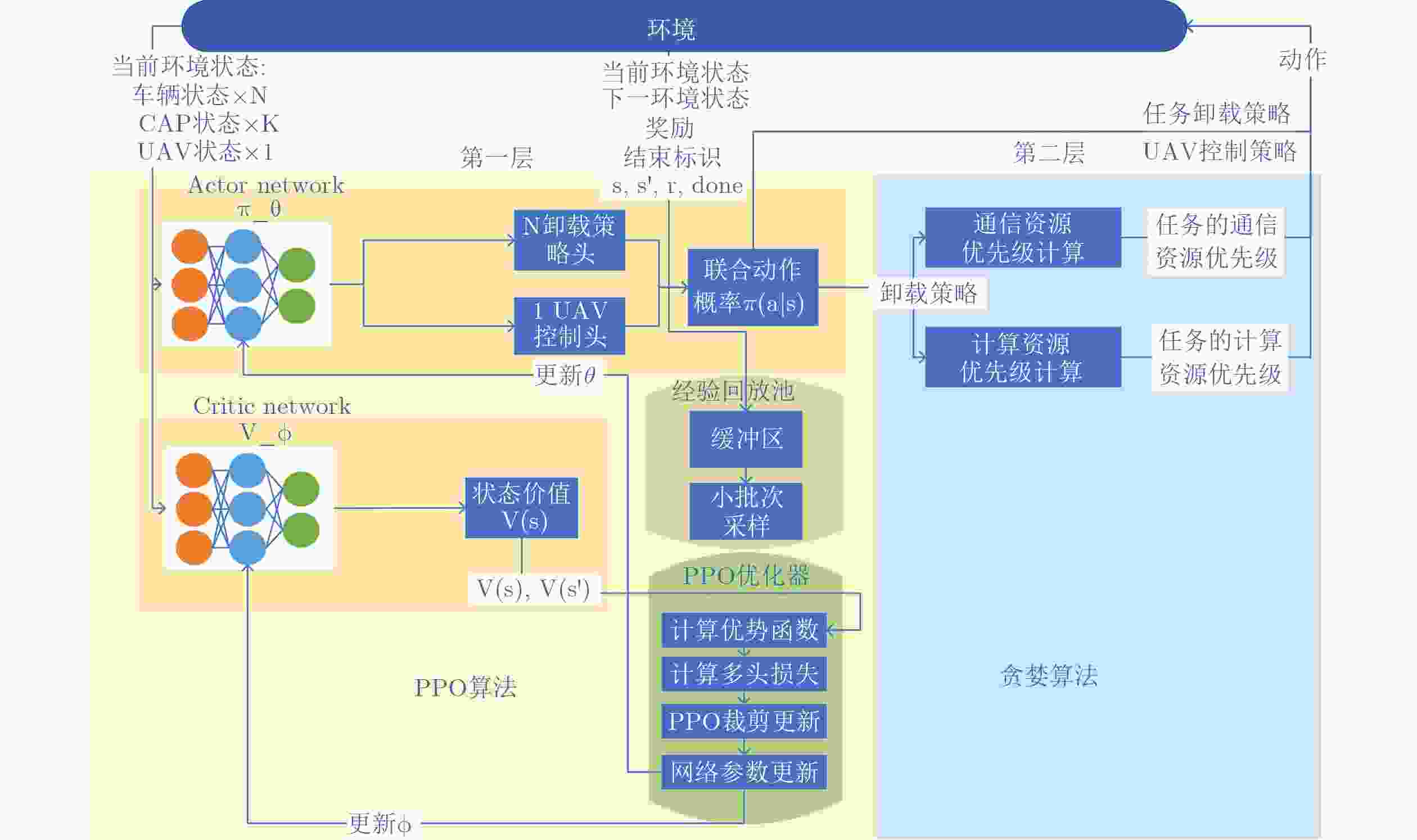
1 计算任务卸载和UAV控制决策

1. 输入：当前时隙系统状态$ S\left(m\right) $，车辆数量$ N $，CAP数量 $ K $，多头Actor网络$ {\text{π} }_{\theta } $，Critic网络$ {V}_{\phi } $
2. 输出：计算任务卸载策略$ OP(m) $和UAV控制策略 $ F(m) $
3. 状态获取：从环境获取当前时隙状态$ S\left(m\right) $：$ N $个用户状态、$ C $个CAP状态、1个UAV状态
4. 状态输入：状态$ S\left(m\right) $同时输入到Actor网络$ {\text{π} }_{\theta } $和Critic网络$ {V}_{\phi } $
5. 多头Actor网络推理：
6. 　任务卸载策略头($ N $个)：$ O{P}_{i}(m)=\text{π} _{\theta }^{{\mathrm{task}}_{i}}(S(m))\in \{0,1,2\},i=1,2,\cdots ,N $
7. 　UAV控制头(1个)：$ d(m)=\text{π} _{\theta }^{\mathrm{UAV}}(S(m))\in \{0,1,2,\cdots ,10\} $(加速度档位选择)
8. Critic网络推理：状态价值评估$ {V}_{\phi }(S(m)) $
9. 策略输出：
10. 卸载策略：$ OP(m)=[O{P}_{1}(m),O{P}_{2}(m),\cdots ,O{P}_{N}(m)] $
11. UAV控制策略：$ F(m)=d(m) $
12. Return $ OP(m) $，$ F(m) $

下载: 导出CSV

2 计算任务的计算资源和通信资源优先级计算

1. 输入：当前时隙系统状态$ S\left(m\right) $，计算任务卸载策略　$ OP(m) $，计算任务数据量$ \{{D}_{i}(m)\}_{i=1}^{N} $，计算任务复杂度　$ \{{\kappa }_{i}(m)\}_{i=1}^{N} $
2. 输出：通信资源优先级$ {P}_{\mathrm{comm}}(m) $，计算资源优先级$ {P}_{\mathrm{comp}}(m) $
3. 初始化：本地处理任务列表$ {L}_{\mathrm{local}}(m)=\varnothing $，卸载任务列表　$ {L}_{\mathrm{offload}}(m)=\varnothing $
4. 任务分类：
5. 　for 车辆$ i=1 $ to$ N $ do
6. 　　if $ O{P}_{i}(m)=0 $then
7. 　　　$ {L}_{\mathrm{local}}(m)={L}_{\mathrm{local}}(m)\cup \{i\} $//本地计算
8. 　　else
9. 　　　$ {L}_{\mathrm{offload}}(m)={L}_{\mathrm{offload}}(m)\cup \{i\} $//卸载处理
10. 　 endif
11. endfor
12. 通信资源优先级计算：
13. 　 for 任务$ i\in {L}_{\mathrm{offload}}(m) $do
14. 　　通信资源优先级权重：$ W_{i}^{\mathrm{comm}}(m)={D}_{i}(m) $
15. 　 endfor
16. $ {P}_{\mathrm{comm}}(m)=\mathrm{sort}({L}_{\mathrm{offload}}(m),W_{i}^{\mathrm{comm}}(m)) $//按权重降序排列
17. 计算资源优先级计算：
18. 　 for 任务$ i\in {L}_{\mathrm{offload}}(m) $do
19. 　　计算资源优先级权重：$ W_{i}^{\mathrm{comp}}(m)={D}_{i}(m)\times {\kappa }_{i}(m) $
20. 　 endfor
21. $ {P}_{\mathrm{comp}}(m)=\mathrm{sort}({L}_{\mathrm{offload}}(m),W_{i}^{\mathrm{comp}}(m)) $//按权重降序排列
22. Return $ {P}_{\mathrm{comm}}(m) $，$ {P}_{\mathrm{comp}}(m) $

下载: 导出CSV

3 基于HHDRL的联合优化方案

1. 输入：系统时隙$ m $，车辆数量$ N $，CAP数量$ K $，最大时隙　$ {T}_{\max } $
2. 输出：最小化累计系统时延的联合优化结果
3. 初始化：BSC基站控制器，系统参数，网络参数，经验回放　缓冲区$ B $
4. while $ m\leq {T}_{\max } $ do
5. 　高层决策：执行算法1
6. 　　输入当前系统状态$ S\left(m\right) $，获取卸载策略$ OP\left(m\right) $和　　　　UAV控制策略$ F\left(m\right) $
7. 　低层决策：执行算法2
8. 　　输入$ OP\left(m\right) $，$ F\left(m\right) $获取资源优先级$ {P}_{\mathrm{comm}}(m) $，　　　　$ {P}_{\mathrm{comp}}(m) $
9. 　形成完整动作：组合高层策略$ OP\left(m\right) $，$ F\left(m\right) $和低层优先　　　级$ {P}_{\mathrm{comm}}(m) $，$ {P}_{\mathrm{comp}}(m) $
10. 环境交互：执行完整动作，获取环境反馈$ S\left(m+1\right) $，　　　$ R\left(m\right) $
11. 高层策略优化(PPO网络参数$ \theta $和$ \phi $更新)：
12. 　存储经验元组到缓冲区$ B $
13. 　if 缓冲区满 then 执行PPO网络参数更新
14. 　$ m\leftarrow m+1 $
15. endwhile
16. return 累计系统时延最小化的联合优化结果

下载: 导出CSV

表 1 仿真参数说明

参数	数值	描述	参数	数值	描述
l	2	路径损耗指数	$ R_{\text{CAP}}^{\text{comm}} $	277	每个CAP最大通信资源块数
$ {P}_{0} $	-50 dB	参考距离信道功率增益	$ R_{\text{UAV}}^{comm} $	277	UAV最大通信资源块数
$ {d}_{0} $	1 m	参考距离	Lanes	3	观测车道数
$ {N}_{0} $	-169 dBm/Hz	噪声功率密度	Length	1200 m	观测车道以及UAV准飞区域长度
f	2.5 GHz	单位计算资源块算力	Width	3.75 m	观测车道以及UAV准飞区域宽度
$ {p}_{n} $	30 dBm	MU发射功率	H	100 m	UAV飞行高度
$ {b}^{sub} $	30 kHz	单位通信资源块带宽	$ E_{\text{UAV}}^{\max } $	500 kJ	UAV最大电池容量
$ D $	9 ～18 Mbits	MU计算任务大小	$ E_{\text{UAV}}^{\text{back}} $	100 kJ	UAV安全电量水平
$ \kappa $	2000～3000 cycle/bit	MU计算任务复杂度	$ {P}_{1} $	200 W	悬停桨叶轮廓功率常数
$ {\varepsilon }_{\text{UAV}} $	10^(–27) W·s³/cycle³	UAV计算功耗系数	$ {P}_{2} $	4340 W	悬停诱导功率常数
$ R_{\text{CAP}}^{\text{comp}} $	50	每个CAP最大计算资源块数	$ {v}_{0} $	8.92 m/s	悬停平均诱导速度
$ R_{\text{UAV}}^{\text{comp}} $	50	UAV最大计算资源块数	$ {v}^{\max } $	30 m/s	UAV最大飞行速度
$ R_{\text{MU}}^{\text{comp}} $	8	每个MU最大计算资源块数	A	$ \left[-5,-4,\ldots ,5\right]\mathrm{m}/{\mathrm{s}}^{2} $	UAV加速度

下载: 导出CSV

参考文献(19)

[1]	CHENG Kaijun and FANG Xuming. A cost efficient edge computing scheme in dual-band cooperative vehicular network[C]. Proceedings of 2023 IEEE Wireless Communications and Networking Conference (WCNC), Glasgow, United Kingdom, 2023: 1–6. doi: 10.1109/WCNC55385.2023.10118669.
[2]	王汝言, 杨安琪, 吴大鹏, 等. 异步移动边缘计算网络中的联合任务调度与计算资源分配优化策略[J]. 电子与信息学报, 2025, 47(2): 470–479. doi: 10.11999/JEIT240685. WANG Ruyan, YANG Anqi, WU Dapeng, et al. Joint task scheduling and computing resource allocation optimization strategy in asynchronous mobile edge computing networks[J]. Journal of Electronics & Information Technology, 2025, 47(2): 470–479. doi: 10.11999/JEIT240685.
[3]	LIU Yanping, FANG Xuming, XIAO Ming, et al. Latency optimization for multi-UAV-assisted task offloading in air-ground integrated millimeter-wave networks[J]. IEEE Transactions on Wireless Communications, 2024, 23(10): 13359–13376. doi: 10.1109/TWC.2024.3400843.
[4]	WU Yu, FANG Xuming, MIN Geyong, et al. Intelligent offloading balance for vehicular edge computing and networks[J]. IEEE Transactions on Intelligent Transportation Systems, 2025, 26(5): 5792–5803. doi: 10.1109/TITS.2025.3549493.
[5]	杨守义, 成昊泽, 党亚萍. 基于集群协作的云雾混合计算资源分配和负载均衡策略[J]. 电子与信息学报, 2023, 45(7): 2423–2431. doi: 10.11999/JEIT220719. YANG Shouyi, CHENG Haoze, and DANG Yaping. Resource allocation and load balancing strategy in cloud-fog hybrid computing based on cluster-collaboration[J]. Journal of Electronics & Information Technology, 2023, 45(7): 2423–2431. doi: 10.11999/JEIT220719.
[6]	DENG Cailian, FANG Xuming, and WANG Xianbin. UAV-enabled mobile-edge computing for AI applications: Joint model decision, resource allocation, and trajectory optimization[J]. IEEE Internet of Things Journal, 2023, 10(7): 5662–5675. doi: 10.1109/JIOT.2022.3151619.
[7]	YAN Xuezhen, FANG Xuming, DENG Cailian, et al. Joint optimization of resource allocation and trajectory control for mobile group users in fixed-wing UAV-enabled wireless network[J]. IEEE Transactions on Wireless Communications, 2024, 23(2): 1608–1621. doi: 10.1109/TWC.2023.3290748.
[8]	HE Long, SUN Geng, SUN Zemin, et al. An online joint optimization approach for QoE maximization in UAV-enabled mobile edge computing[C]. Proceedings of the IEEE INFOCOM 2024-IEEE Conference on Computer Communications, Vancouver, Canada, 2024: 101–110. doi: 10.1109/INFOCOM52122.2024.10621306.
[9]	李斌, 蔡海晨, 赵传信, 等. 基于计算重用的无人机辅助边缘计算系统能耗优化[J]. 电子与信息学报, 2024, 46(7): 2740–2747. doi: 10.11999/JEIT231061. LI Bin, CAI Haichen, ZHAO Chuanxin, et al. Energy optimization for computing reuse in unmanned aerial vehicle-assisted edge computing systems[J]. Journal of Electronics & Information Technology, 2024, 46(7): 2740–2747. doi: 10.11999/JEIT231061.
[10]	ZHANG You and MAO Zhengchong. Computation offloading service in UAV-assisted mobile edge computing: A soft actor-critic approach[C]. Proceedings of 2023 International Conference on Ubiquitous Communication (Ucom), Xi’an, China, 2023: 373–378. doi: 10.1109/Ucom59132.2023.10257660.
[11]	GAO Yuan, DING Yu, WANG Ye, et al. Deep reinforcement learning-based trajectory optimization and resource allocation for secure UAV-enabled MEC networks[C]. Proceedings of the IEEE INFOCOM 2024-IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Vancouver, Canada, 2024: 01–05. doi: 10.1109/INFOCOMWKSHPS61880.2024.10620895.
[12]	CHEN Ying, YANG Yaozong, WU Yuan, et al. Joint trajectory optimization and resource allocation in UAV-MEC systems: A Lyapunov-assisted DRL approach[J]. IEEE Transactions on Services Computing, 2025, 18(2): 854–867. doi: 10.1109/TSC.2025.3544124.
[13]	YIN Baolin, FANG Xuming, and WANG Xianbin. Joint optimization of trajectory control, resource allocation, and user association based on DRL for multi-fixed-wing UAV networks[J]. IEEE Transactions on Wireless Communications, 2024, 23(10): 13330–13343. doi: 10.1109/TWC.2024.3400821.
[14]	YANG M, JEON S W, and KIM D K. Optimal trajectory for curvature-constrained UAV mobile base stations[J]. IEEE Wireless Communications Letters, 2020, 9(7): 1056–1059. doi: 10.1109/LWC.2020.2980281.
[15]	ICAO. Unmanned Aircraft Systems (UAS) Traffic Management (UTM). Doc 10049, 2023. (查阅网上资料, 未找到本条文献信息, 请核对).
[16]	YOU Changsheng and ZHANG Rui. 3D trajectory optimization in Rician fading for UAV-enabled data harvesting[J]. IEEE Transactions on Wireless Communications, 2019, 18(6): 3192–3207. doi: 10.1109/TWC.2019.2911939.
[17]	XU Yanke, GENG Qingbo, FEI Qing, et al. Research on UAV-assisted computation offloading based on PER-SAC[C]. Proceedings of 2024 China Automation Congress (CAC), Qingdao, China, 2024: 5672–5677. doi: 10.1109/CAC63892.2024.10865625.
[18]	ZENG Yong, XU Jie, and ZHANG Rui. Energy minimization for wireless communication with rotary-wing UAV[J]. IEEE Transactions on Wireless Communications, 2019, 18(4): 2329–2345. doi: 10.1109/TWC.2019.2902559.
[19]	CHEN Juan, XING Huanlai, XIAO Zhiwen, et al. A DRL agent for jointly optimizing computation offloading and resource allocation in MEC[J]. IEEE Internet of Things Journal, 2021, 8(24): 17508–17524. doi: 10.1109/JIOT.2021.3081694.