Minimax Robust Kalman Filtering under Multistep Random Measurement Delays and Packet Dropouts
-
摘要: 该文研究了多步随机观测滞后和丢包系统的极大极小鲁棒Kalman滤波问题。系统噪声方差不确定但有已知保守上界,传感器到估值器的多步随机观测滞后和丢包通过一组概率已知的伯努利分布随机变量描述。利用哈达玛乘积改进模型转换方法,设计了极大极小鲁棒时变Kalman估值器。利用矩阵初等变换、盖尔圆盘定理和哈达玛乘积定理证明了广义李雅普诺夫方程解的半正定性,进而应用矩阵分解和李雅普诺夫方程方法证明了所设计估值器的鲁棒性,即对所有容许的不确定性,确保实际估计误差方差有最小上界。给出时变广义李雅普诺夫方程存在稳态唯一半正定解的条件,进而设计了鲁棒稳态估值器。证明了时变和稳态估值器的按实现收敛性。仿真实例验证了其有效性。Abstract:
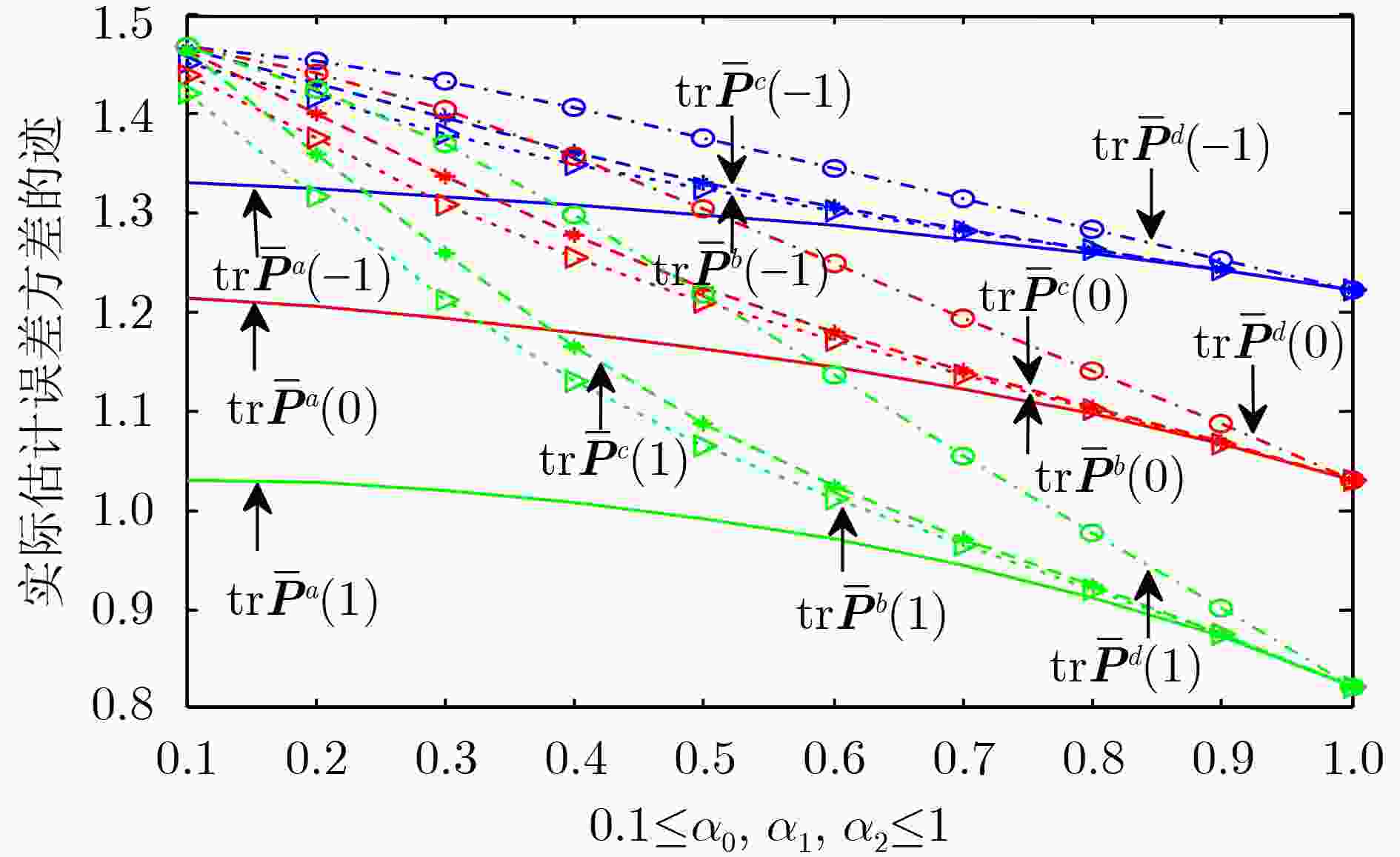
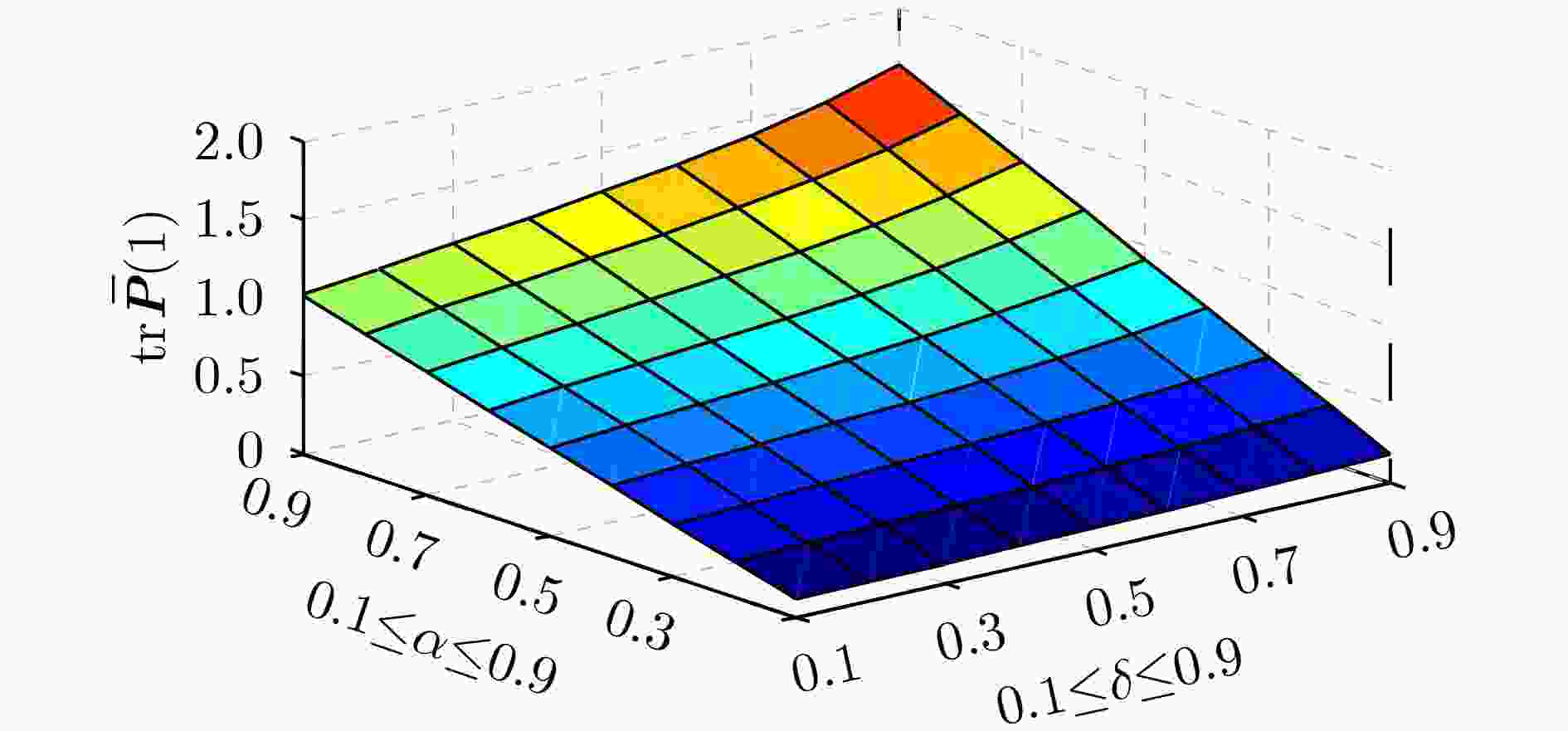
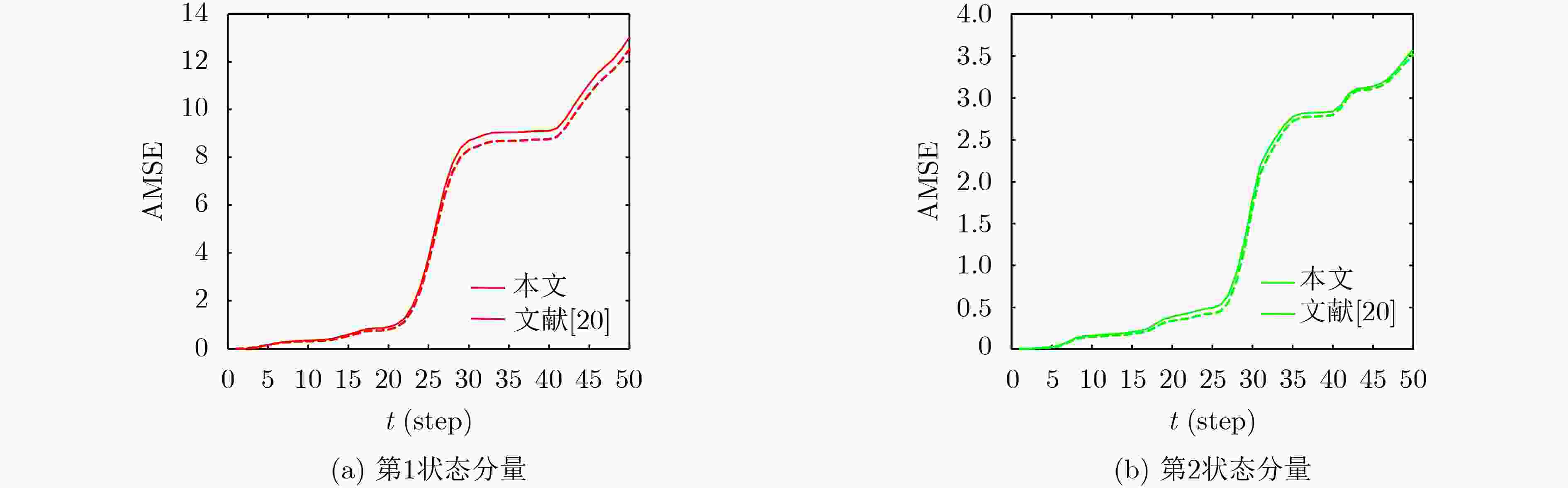
Objective Networked Control Systems (NCSs) provide advantages such as flexible installation, convenient maintenance, and reduced cost, but they also present challenges arising from random measurement delays and packet dropouts caused by communication network unreliability and limited bandwidth. Moreover, system noise variance may fluctuate significantly under strong electromagnetic interference. In NCSs, time delays are random and uncertain. When a set of Bernoulli-distributed random variables is used to describe multistep random measurement delays and packet dropouts, the fictitious noise method in existing studies introduces autocorrelation among different components, which complicates the computation of fictitious noise variances and makes it difficult to establish robustness. This study presents a solution for minimax robust Kalman filtering in systems characterized by uncertain noise variance, multistep random measurement delays, and packet dropouts. Methods The main challenges lie in model transformation and robustness verification. When a set of Bernoulli-distributed random variables is employed to represent multistep random measurement delays and packet dropouts, a series of strategies are applied to address the minimax robust Kalman filtering problem. First, a new model transformation method is proposed based on the flexibility of the Hadamard product in multidimensional data processing, after which a robust time-varying Kalman estimator is designed in a unified framework following the minimax robust filtering principle. Second, the robustness proof is established using matrix elementary transformation, strictly diagonally dominant matrices, the Gerŝgorin circle theorem, and the Hadamard product theorem within the framework of the generalized Lyapunov equation method. Additionally, by converting the Hadamard product into a matrix product through matrix factorization, a sufficient condition for the existence of a steady-state estimator is derived, and the robust steady-state Kalman estimator is subsequently designed. Results and Discussions The proposed minimax robust Kalman filter extends the robust Kalman filtering framework and provides new theoretical support for addressing the robust fusion filtering problem in complex NCSs. The curves ( Fig. 5 ) present the actual accuracy ${\text{tr}}{{\mathbf{\bar P}}^l}(N)$, $l = a,b,c,d$ as a function of $ 0.1 \le {\alpha _0} $, ${\alpha _1} $, ${\alpha _2} \le 1 $. It is observed that situation (1) achieves the highest robust accuracy, followed by situations (2) and (3), whereas situation (4) exhibits poorer accuracy. This difference arises because the estimators in situation (1) receive measurements with one-step random delay, whereas situation (4) experiences a higher packet loss rate. The curves (Fig. 5 ) confirm the validity and effectiveness of the proposed method. Another simulation is conducted for a mass-spring-damper system. The comparison between the proposed approach and the optimal robust filtering method (Table 2 ,Fig. 7 ) indicates that although the proposed method ensures that the actual prediction error variance attains the minimum upper bound, its actual accuracy is slightly lower than the optimal prediction accuracy.Conclusions The minimax robust Kalman filtering problem is investigated for systems characterized by uncertain noise variance, multistep random measurement delays, and packet dropouts. The system noise variance is uncertain but bounded by known conservative upper limits, and a set of Bernoulli-distributed random variables with known probabilities is used to represent the multistep random measurement delays and packet dropouts between the sensor and the estimator. The Hadamard product is used to enhance the model transformation method, followed by the design of a minimax robust time-varying Kalman estimator. Robustness is demonstrated through matrix elementary transformation, the Gerschgorin circle theorem, the Hadamard product theorem, matrix factorization, and the Lyapunov equation method. A sufficient condition is established for the time-varying generalized Lyapunov equation to possess a unique steady-state positive semidefinite solution, based on which a robust steady-state estimator is constructed. The convergence between the time-varying and steady-state estimators is also proven. Two simulation examples verify the effectiveness of the proposed approach. The presented methods overcome the limitations of existing techniques and provide theoretical support for solving the robust fusion filtering problem in complex NCSs. -
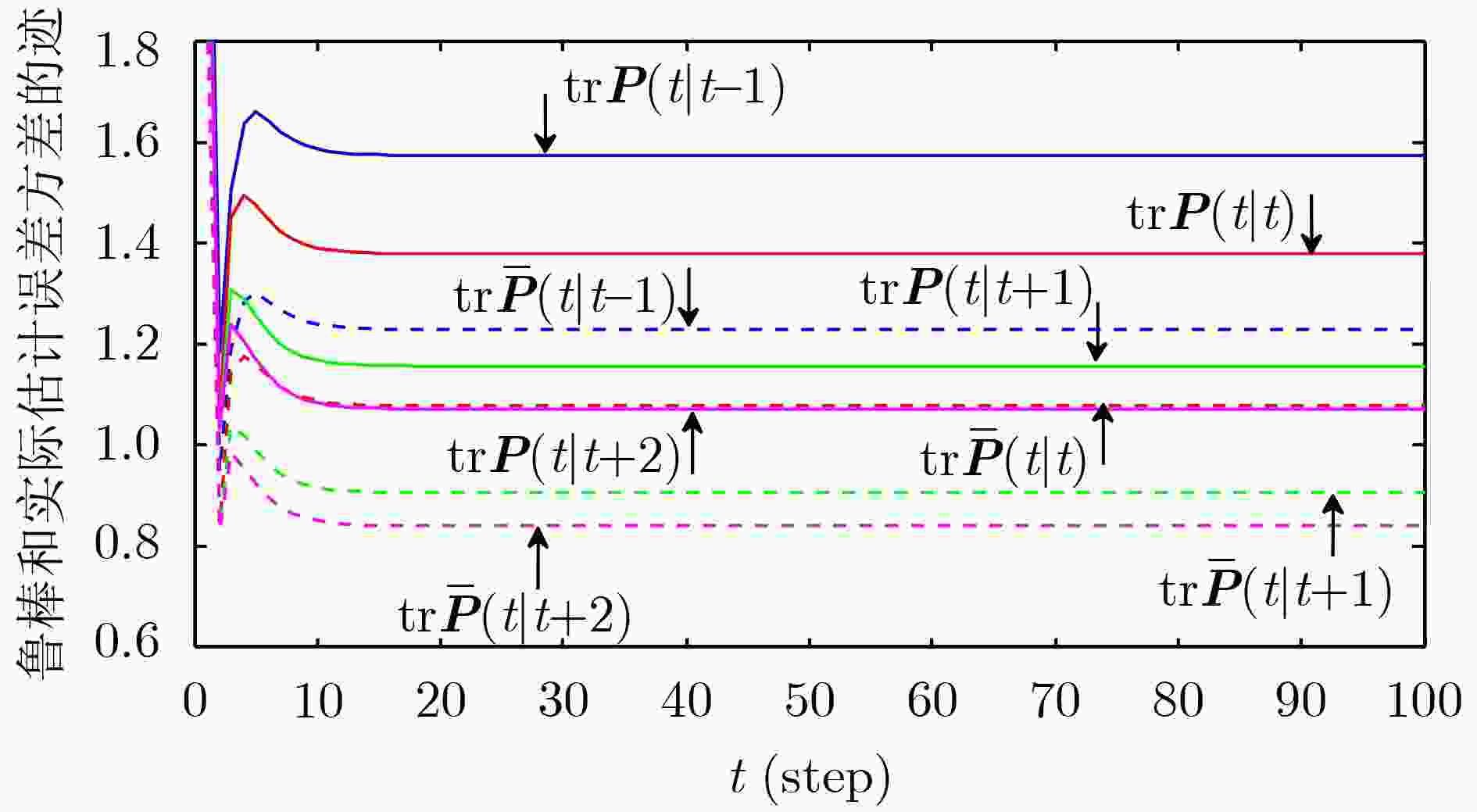
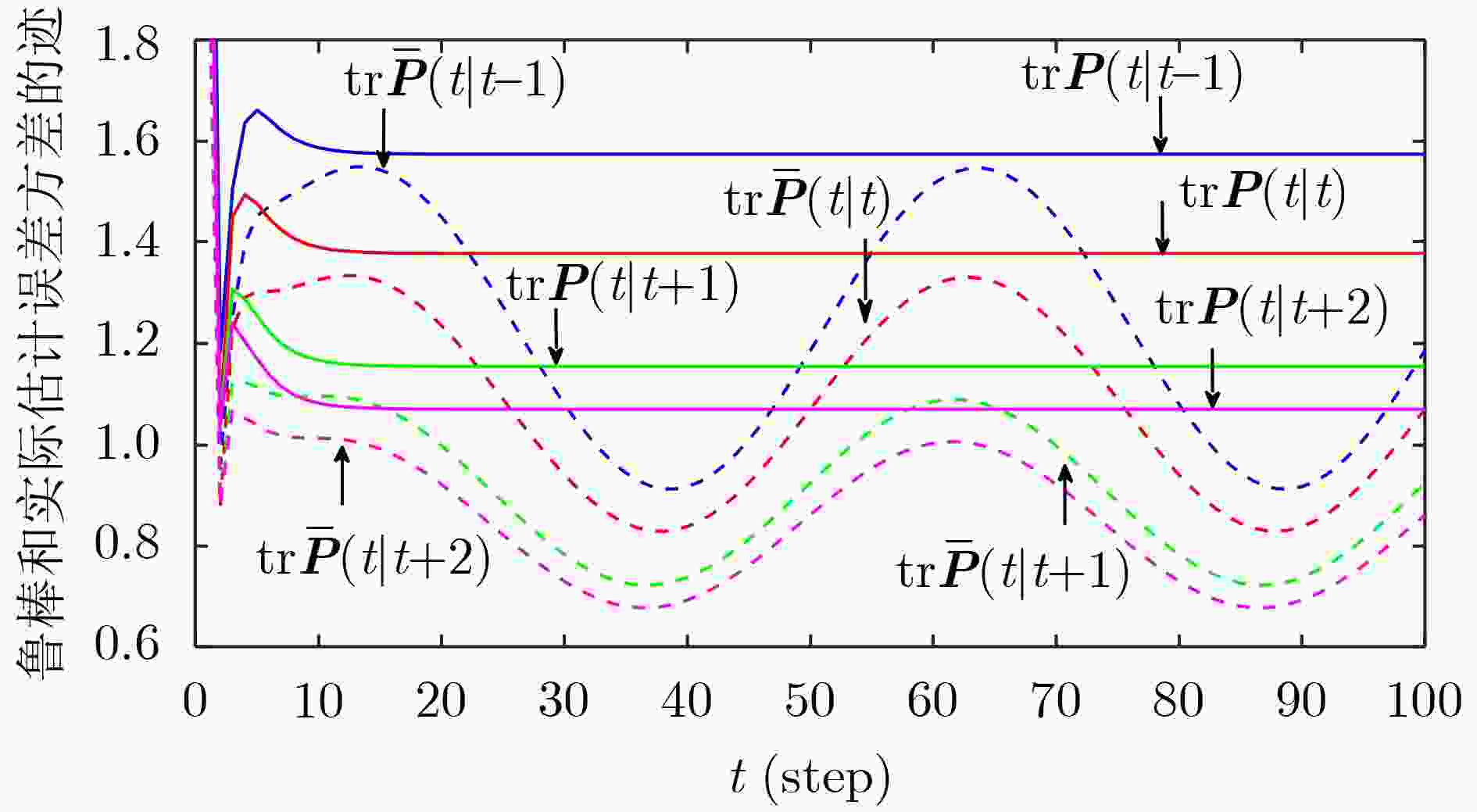
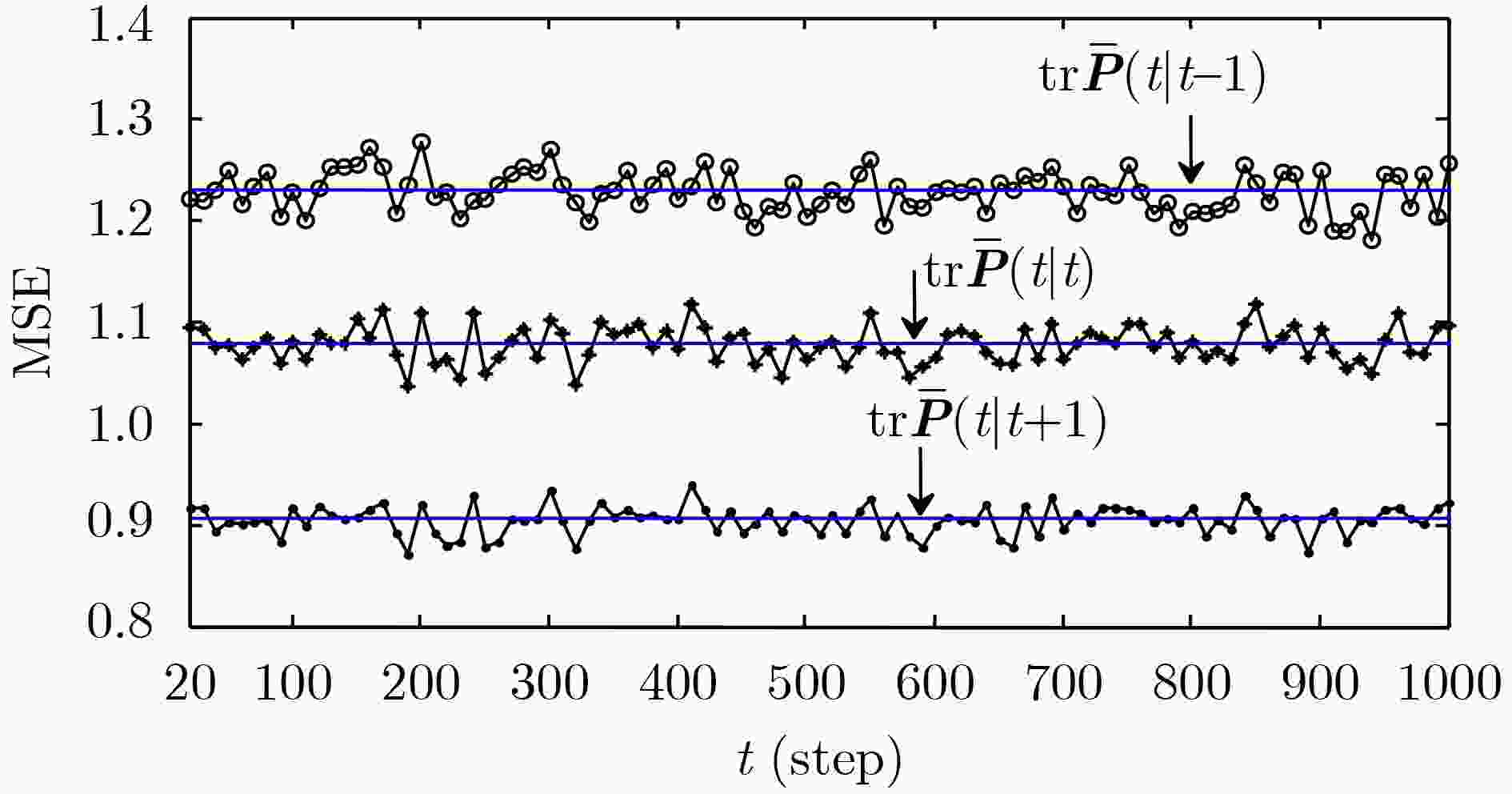
表 1 鲁棒稳态Kalman估值器的实际和鲁棒精度
${\text{tr}}{\boldsymbol{P}}( - 1)$ ${\text{tr}}{\boldsymbol{P}}(0)$ ${\text{tr}}{\boldsymbol{P}}(1)$ ${\text{tr}}{\boldsymbol{P}}(2)$ 1.5742 1.3780 1.1550 1.0702 ${\text{tr}}{\boldsymbol{\bar P}}( - 1)$ ${\text{tr}}{\boldsymbol{\bar P}}(0)$ ${\text{tr}}{\boldsymbol{\bar P}}(1)$ ${\text{tr}}{\boldsymbol{\bar P}}(2)$ 1.2292 1.0779 0.9043 0.8381 表 2 2种方法的精度比较
2种方法的精度 本文实际精度 文献[20]最优精度 预报器 0.1496 0.1491 滤波器 0.1474 0.1468 一步平滑器 0.1447 0.1440 二步平滑器 0.1418 0.1409 -
[1] 徐心宇, 陈建. 无人机状态检测Kalman滤波空地目标跟踪算法[J]. 航空学报, 2024, 45(16): 329834. doi: 10.7527/S1000-6893.2024.29834.XU Xinyu and CHEN Jian. UAV object tracking for air-ground targets based on status detection and Kalman filter[J]. Acta Aeronautica et Astronautica Sinica, 2024, 45(16): 329834. doi: 10.7527/S1000-6893.2024.29834. [2] 秦家虎, 马麒超, 李曼, 等. 多智能体协同研究进展综述: 博弈和控制交叉视角[J]. 自动化学报, 2025, 51(3): 489–509. doi: 10.16383/j.aas.c240508.QIN Jiahu, MA Qichao, LI Man, et al. Recent advances on multi-agent collaboration: A cross-perspective of game and control theory[J]. Acta Automatica Sinica, 2025, 51(3): 489–509. doi: 10.16383/j.aas.c240508. [3] 邓洪高, 余润华, 纪元法, 等. 偏差未补偿自适应边缘化容积卡尔曼滤波跟踪方法[J]. 电子与信息学报, 2025, 47(1): 156–166. doi: 10.11999/JEIT240469.DENG Honggao, YU Runhua, JI Yuanfa, et al. An adaptive target tracking method utilizing marginalized cubature Kalman filter with uncompensated biases[J]. Journal of Electronics & Information Technology, 2025, 47(1): 156–166. doi: 10.11999/JEIT240469. [4] 孙小君, 周晗, 闫广明. 基于新息的自适应增量Kalman滤波器[J]. 电子与信息学报, 2020, 42(9): 2223–2230. doi: 10.11999/JEIT190493.SUN Xiaojun, ZHOU Han, and YAN Guangming. Adaptive incremental Kalman filter based on innovation[J]. Journal of Electronics & Information Technology, 2020, 42(9): 2223–2230. doi: 10.11999/JEIT190493. [5] ZHOU Zebo, ZHANG Zeliang, and ZHU Shuai. Adaptive Kalman filtering with uncertain system noises based on variance component estimation theory[J]. IEEE Sensors Journal, 2024, 24(11): 17896–17906. doi: 10.1109/JSEN.2024.3386683. [6] 林爽, 张依恋, 丁宗贺, 等. 基于改进集员滤波的港口自动跨运车状态估计方法[J]. 控制与决策, 2024, 39(1): 129–136. doi: 10.13195/j.kzyjc.2022.0501.LIN Shuang, ZHANG Yilian, DING Zonghe, et al. State estimation of automated straddle carriers via improved set-membership filtering approach[J]. Control and Decision, 2024, 39(1): 129–136. doi: 10.13195/j.kzyjc.2022.0501. [7] SUN Shiyu, CHEN Dongyan, HU Jun, et al. Event-triggered set-membership state estimation for discrete delayed linear systems over sensor networks[J]. Circuits, Systems, and Signal Processing, 2024, 43(8): 4813–4835. doi: 10.1007/s00034-024-02689-z. [8] ZHANG Huanshui, ZHANG D, XIE Lihua, et al. Robust filtering under stochastic parametric uncertainties[J]. Automatica, 2004, 40(9): 1583–1589. doi: 10.1016/j.automatica.2004.04.002. [9] WANG Rusheng, CHEN Bo, and YU Li. Distributed nonlinear fusion estimation without knowledge of noise statistical information: A robust design approach[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(5): 3107–3117. doi: 10.1109/TAES.2021.3069270. [10] QI Wenjuan, ZHANG Peng, and DENG Zili. Robust weighted fusion Kalman filters for multisensor time-varying systems with uncertain noise variances[J]. Signal Processing, 2014, 99: 185–200. doi: 10.1016/j.sigpro.2013.12.013. [11] GAO Yuan and DENG Zili. Robust weighted fusion Kalman estimators for networked multisensor mixed uncertain systems with random one-step sensor delays, uncertain-variance multiplicative, and additive white noises[J]. IEEE Sensors Journal, 2019, 19(22): 10935–10946. doi: 10.1109/JSEN.2019.2935163. [12] 杨春山, 经本钦, 刘政, 等. 具有噪声方差及多种网络诱导不确定系统鲁棒Kalman估计[J]. 控制理论与应用, 2021, 38(10): 1607–1618. doi: 10.7641/CTA.2021.00598.YANG Chunshan, JING Benqin, LIU Zheng, et al. Robust Kalman estimation for system with uncertainties of noise variances and multiple networked inducements[J]. Control Theory & Applications, 2021, 38(10): 1607–1618. doi: 10.7641/CTA.2021.00598. [13] GAO Yuan and DENG Zili. Robust integrated sequential covariance intersection fusion Kalman filters and their convergence and stability for networked sensor systems with five uncertainties[J]. International Journal of Robust and Nonlinear Control, 2023, 33(2): 1371–1406. doi: 10.1002/rnc.6465. [14] YANG Chunshan, ZHAO Ying, and LIU Zheng. Robust weighted fusion Kalman filters under linearly correlated noise and mixed uncertainties of noise variances, multiplicative noises, and multiple networked inducements[J]. Asian Journal of Control, 2024, 26(1): 205–226. doi: 10.1002/asjc.3195. [15] YANG Chunshan, ZHAO Ying, LIU Zheng, et al. Robust weighted fusion Kalman estimators for systems with uncertain noise variances, multiplicative noises, missing measurements, packets dropouts and two-step random measurement delays[J]. Optimal Control Applications and Methods, 2023, 44(5): 2744–2774. doi: 10.1002/oca.3002. [16] HU Jun, WANG Zidong, LIU S, et al. A variance-constrained approach to recursive state estimation for time-varying complex networks with missing measurements[J]. Automatica, 2016, 64: 155–162. doi: 10.1016/j.automatica.2015.11.008. [17] HORN R A and JOHNSON C R. Matrix Analysis[M]. 2nd ed. New York: Cambridge University Press, 2012: 387–485. [18] SUN Shuli and XIAO Wendong. Optimal linear estimators for systems with multiple random measurement delays and packet dropouts[J]. International Journal of Systems Science, 2013, 44(2): 358–370. doi: 10.1080/00207721.2011.601347. [19] LIU Ming, ZHANG Lixian, SHI Peng, et al. Sliding mode control of continuous-time Markovian jump systems with digital data transmission[J]. Automatica, 2017, 80: 200–209. doi: 10.1016/j.automatica.2017.02.002. [20] MA Jing and SUN Shuli. Optimal linear estimators for multi-sensor stochastic uncertain systems with packet losses of both sides[J]. Digital Signal Processing, 2015, 37: 24–34. doi: 10.1016/j.dsp.2014.11.005. -





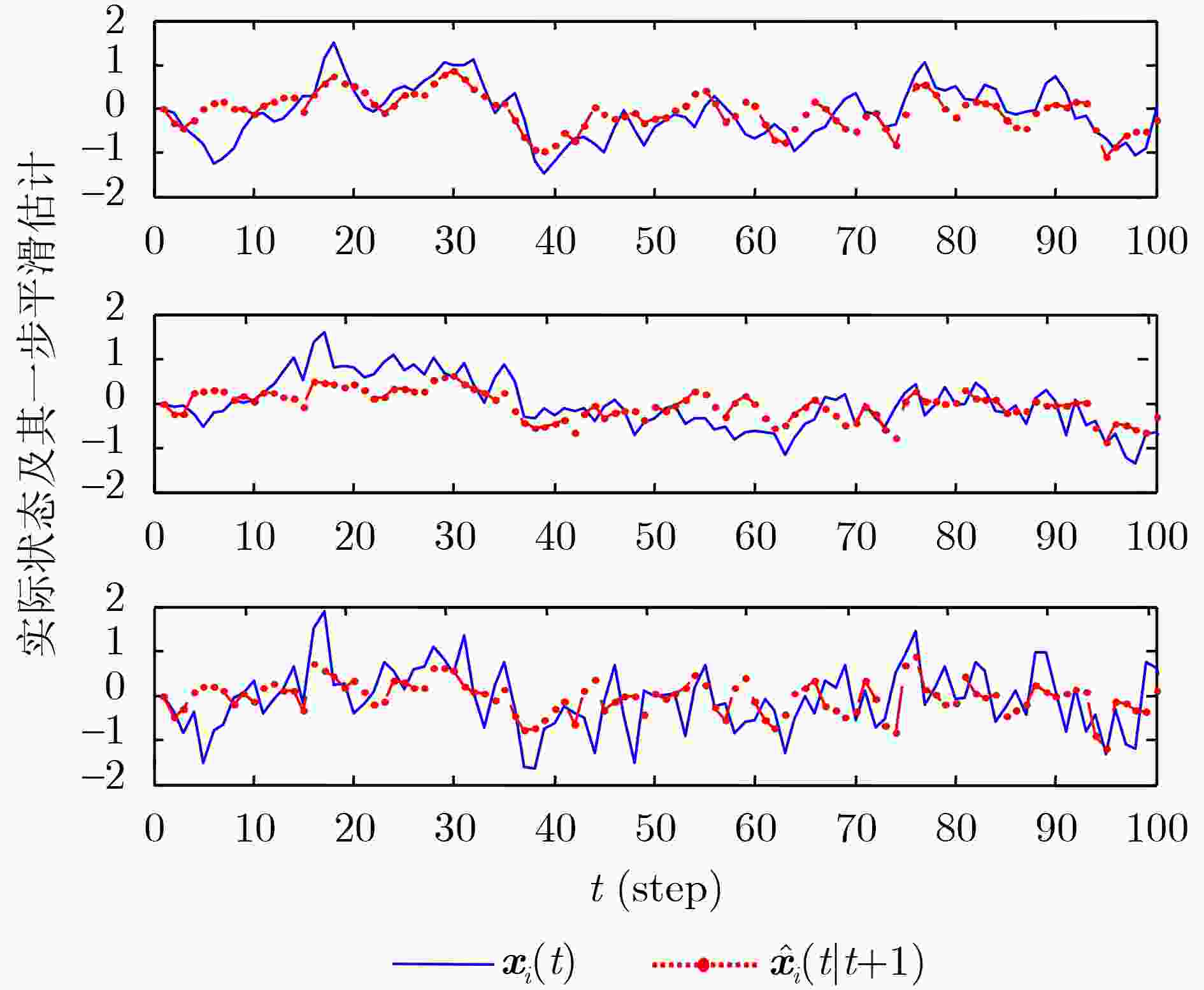
 下载:
下载:


 下载:
下载:
