基于非均匀四线性自相关函数的二次调频信号检测与参数估计

杨宇超; 方刚

doi:10.11999/JEIT250723

基于非均匀四线性自相关函数的二次调频信号检测与参数估计

doi: 10.11999/JEIT250723 cstr: 32379.14.JEIT250723

杨宇超^,,
方刚

上海航天电子技术研究所上海 201109

基金项目: 无

详细信息

作者简介:
杨宇超：男，工程师，研究方向为雷达信号处理

方刚：男，高级工程师，研究方向为雷达数据处理和资源调度

通讯作者:
杨宇超　849282170@qq.com

中图分类号: TN958.2
计量
- 文章访问数: 14
- HTML全文浏览量: 7
- PDF下载量: 1
- 被引次数: 0
出版历程
- 修回日期: 2026-01-12
- 录用日期: 2026-01-12
- 网络出版日期: 2026-01-27

Detection and parameter estimation of quadratic frequency modulated signal based on non-uniform quadrilinear autocorrelation function

YANG Yuchao^,,
FANG Gang

Shanghai Aerospace Electronic Technology Institute, Shanghai 201109, China

Funds: 无

摘要

摘要: 该文提出了一种新颖的集成式时频分析技术，即非均匀四线性自相关函数(Non-uniform quadrilinear autocorrelation function, NQAF)，用于针对高斯白噪声背景下二次调频(Quadratic frequency modulated, QFM)信号的检测与参数估计。该文所提方法的核心思路在于利用非均匀采样技术构建高阶自相关函数实现信号在时间-延迟时间域的相参积累与检测，并利用de-chirp技术分步完成信号的参数估计。该方法扩展了自相关处理的框架，降低了核函数的非线性度。理论分析与数值模拟表明，与主流先进算法相比，该文所提方法对于采样样本的处理方法更为灵活，在性能方面拥有较低的计算复杂度与信噪比阈值。
- 时频分析 /
- 二次调频信号 /
- 非均匀采样技术 /
- 自相关函数
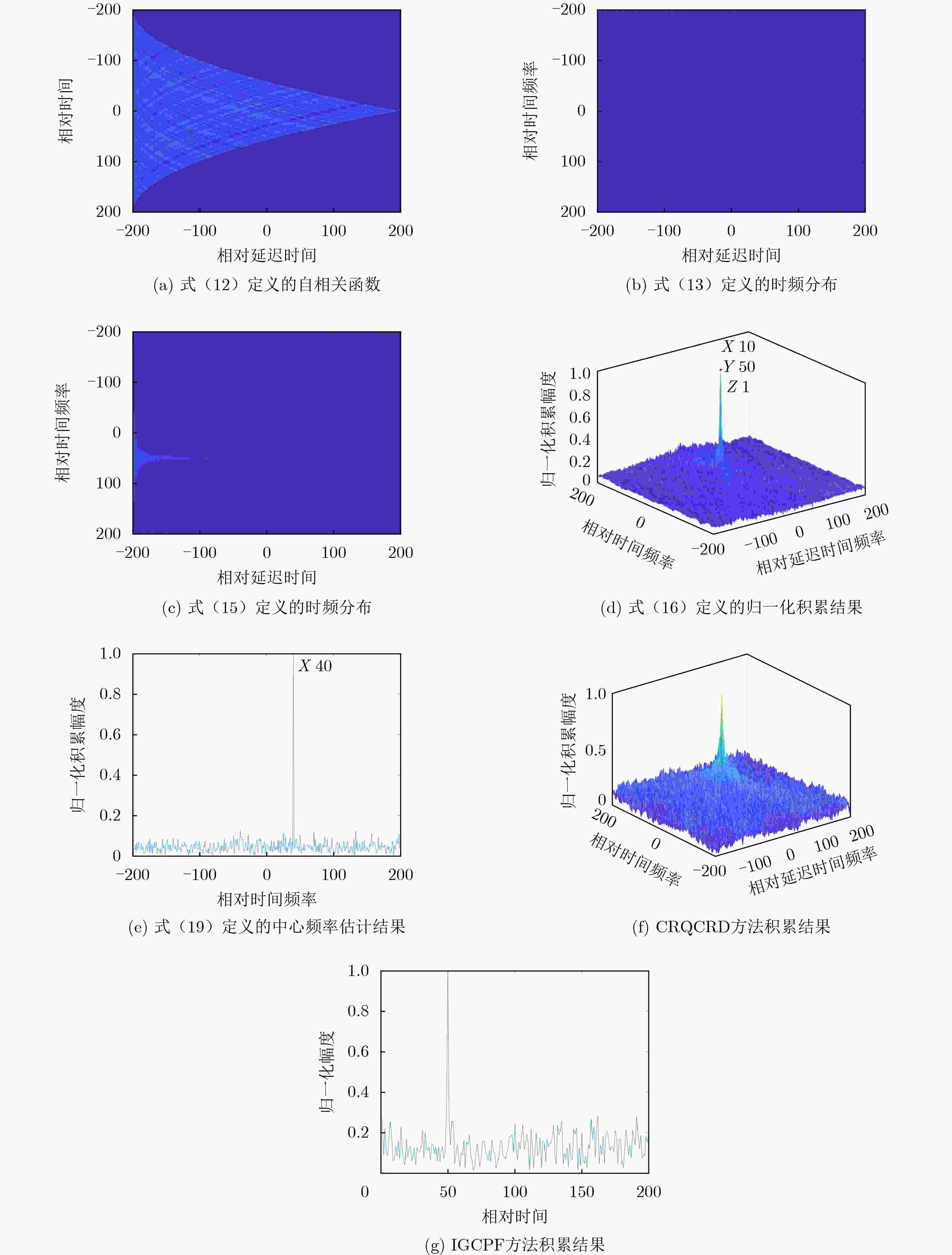
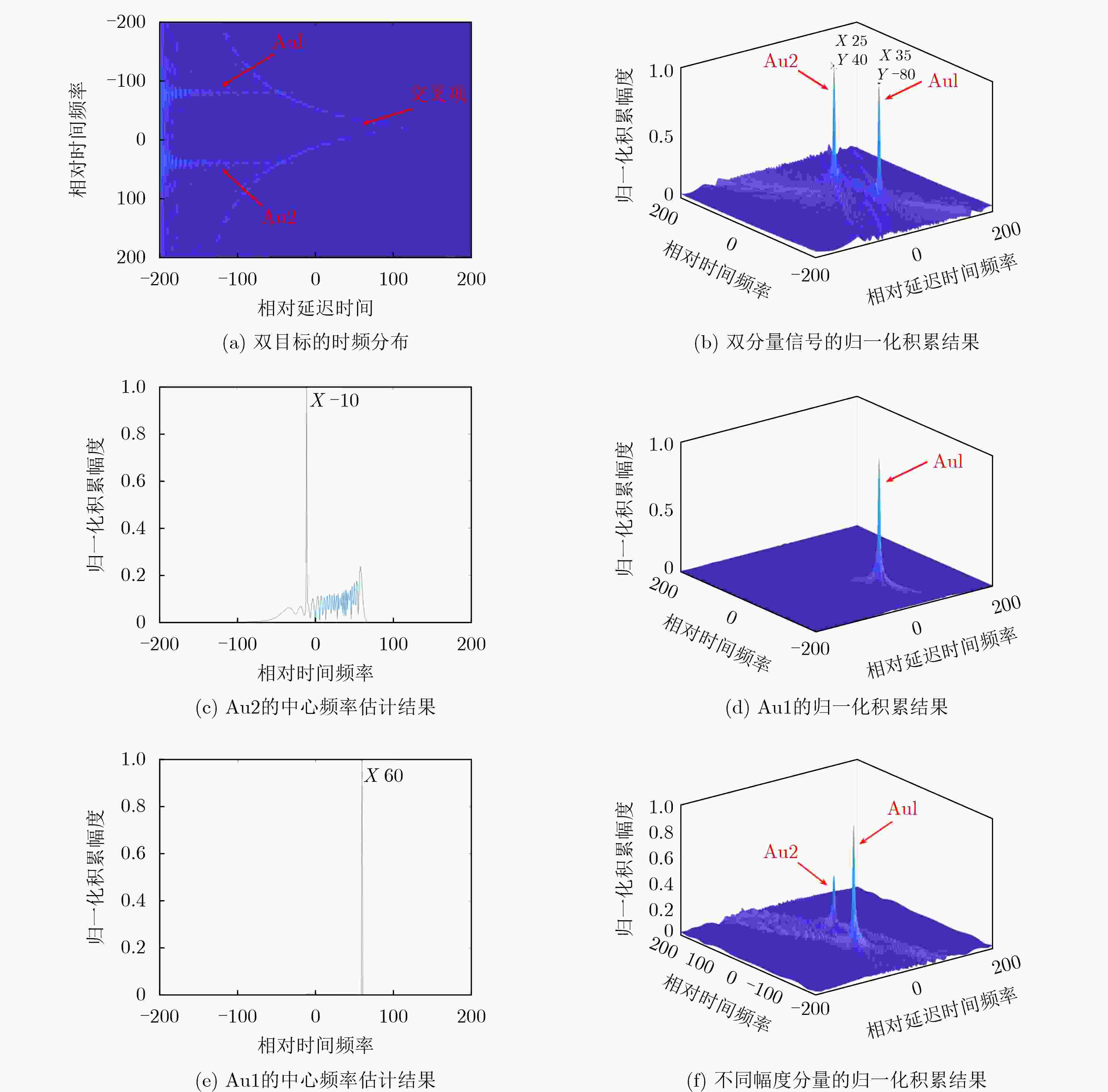
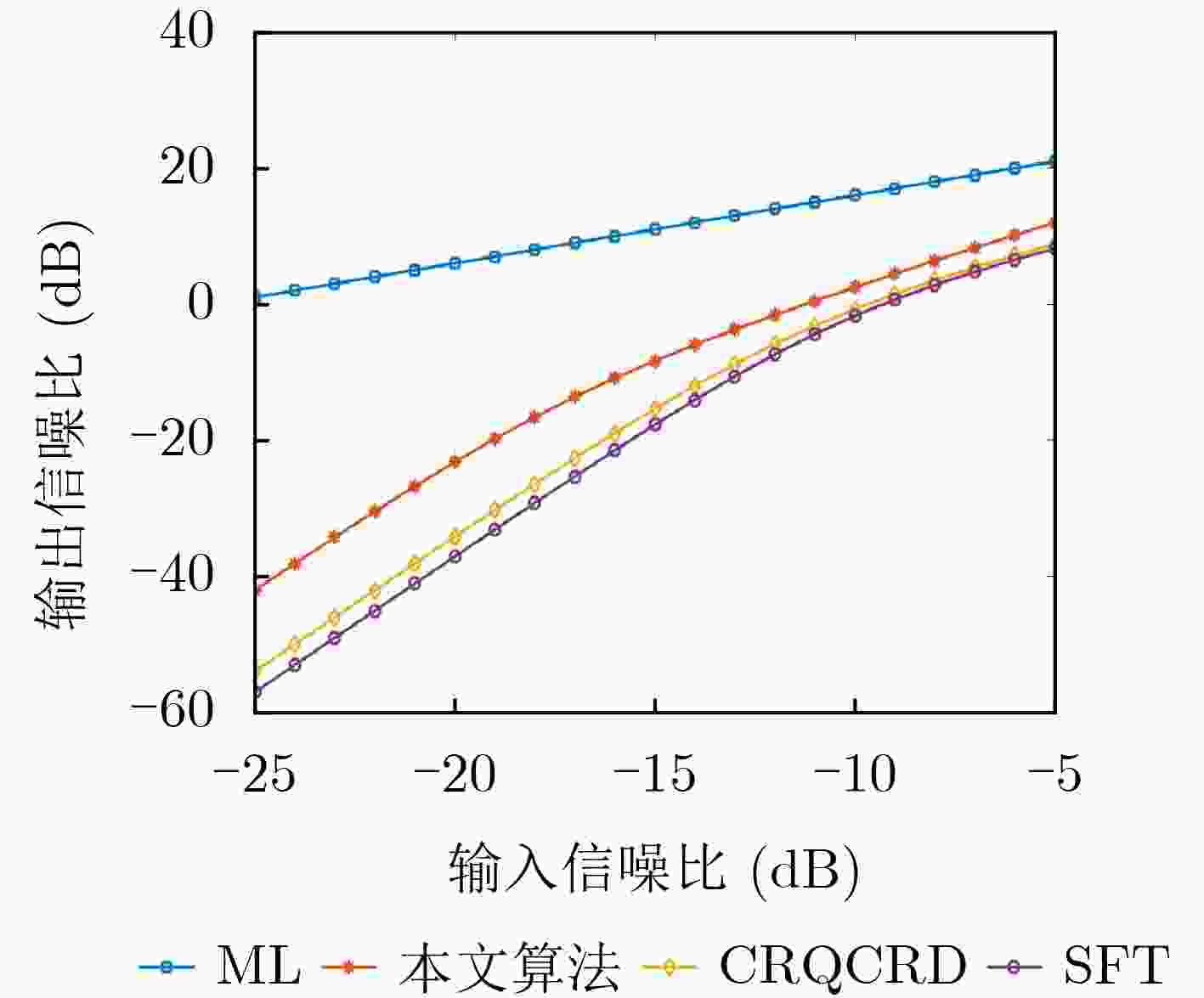
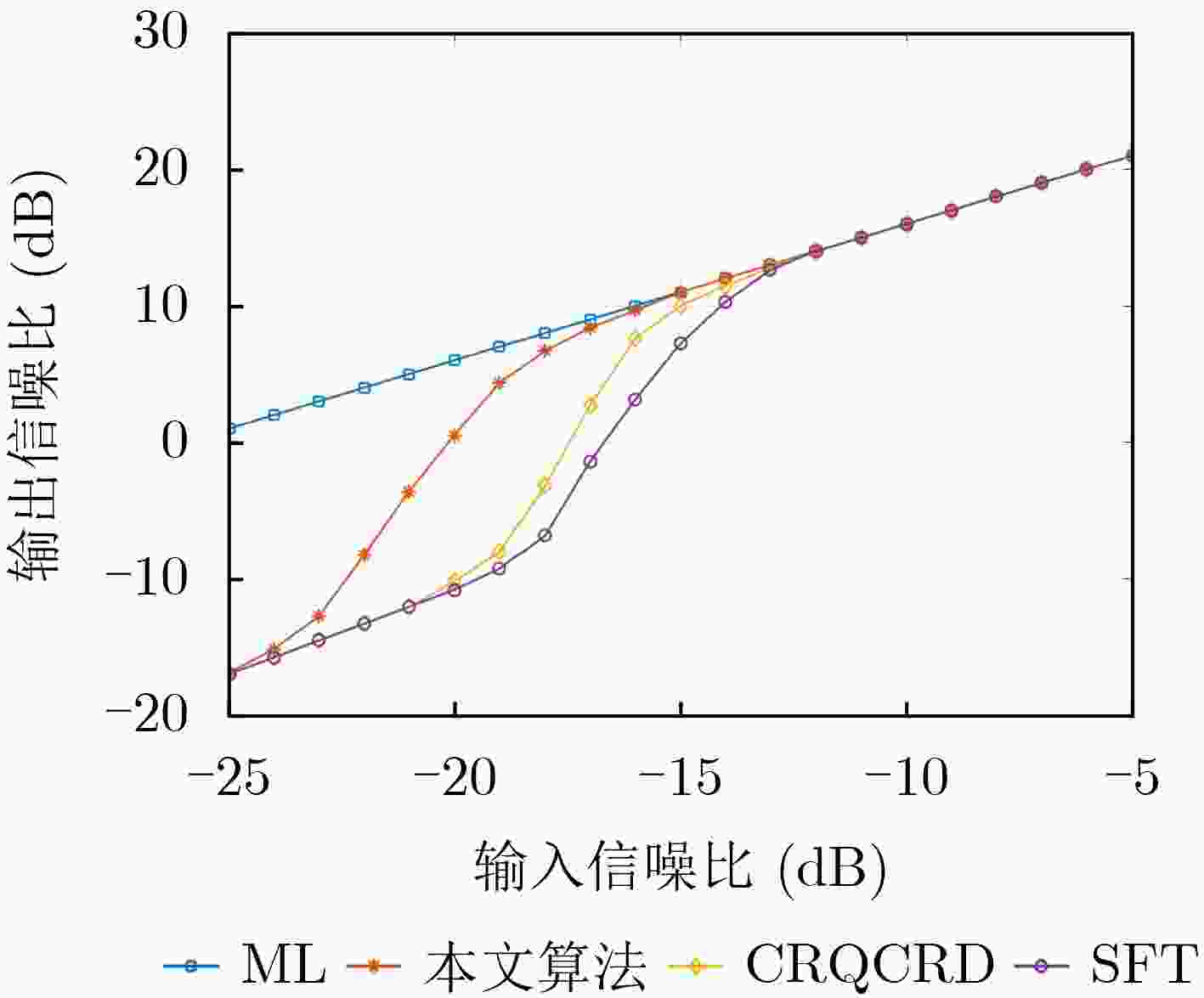
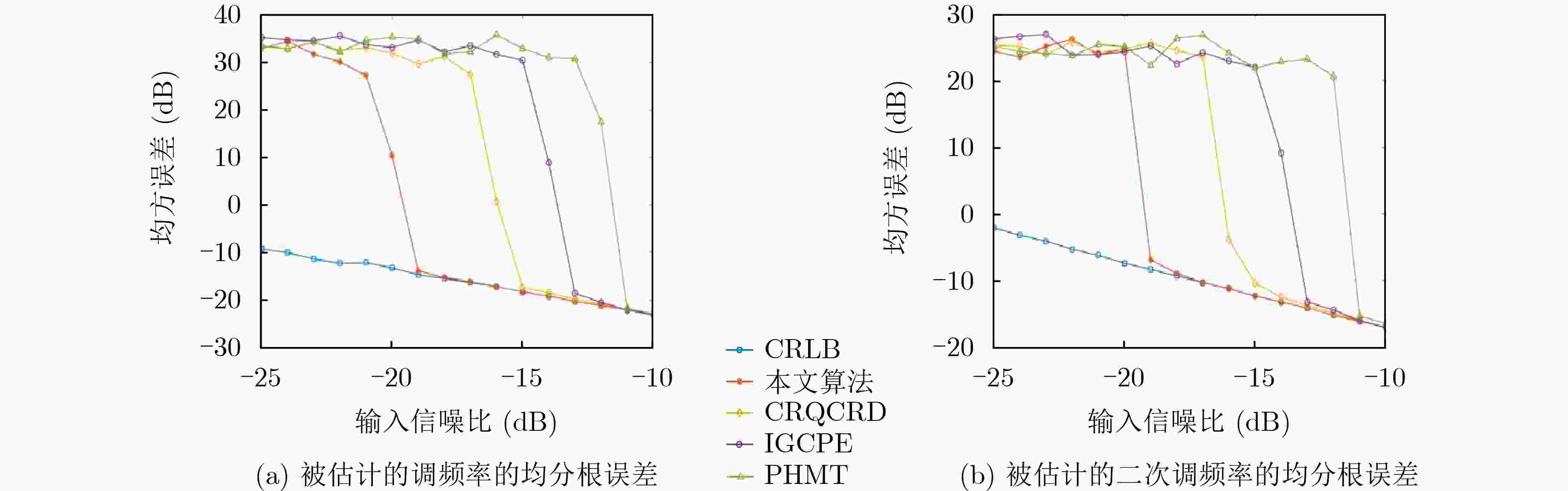
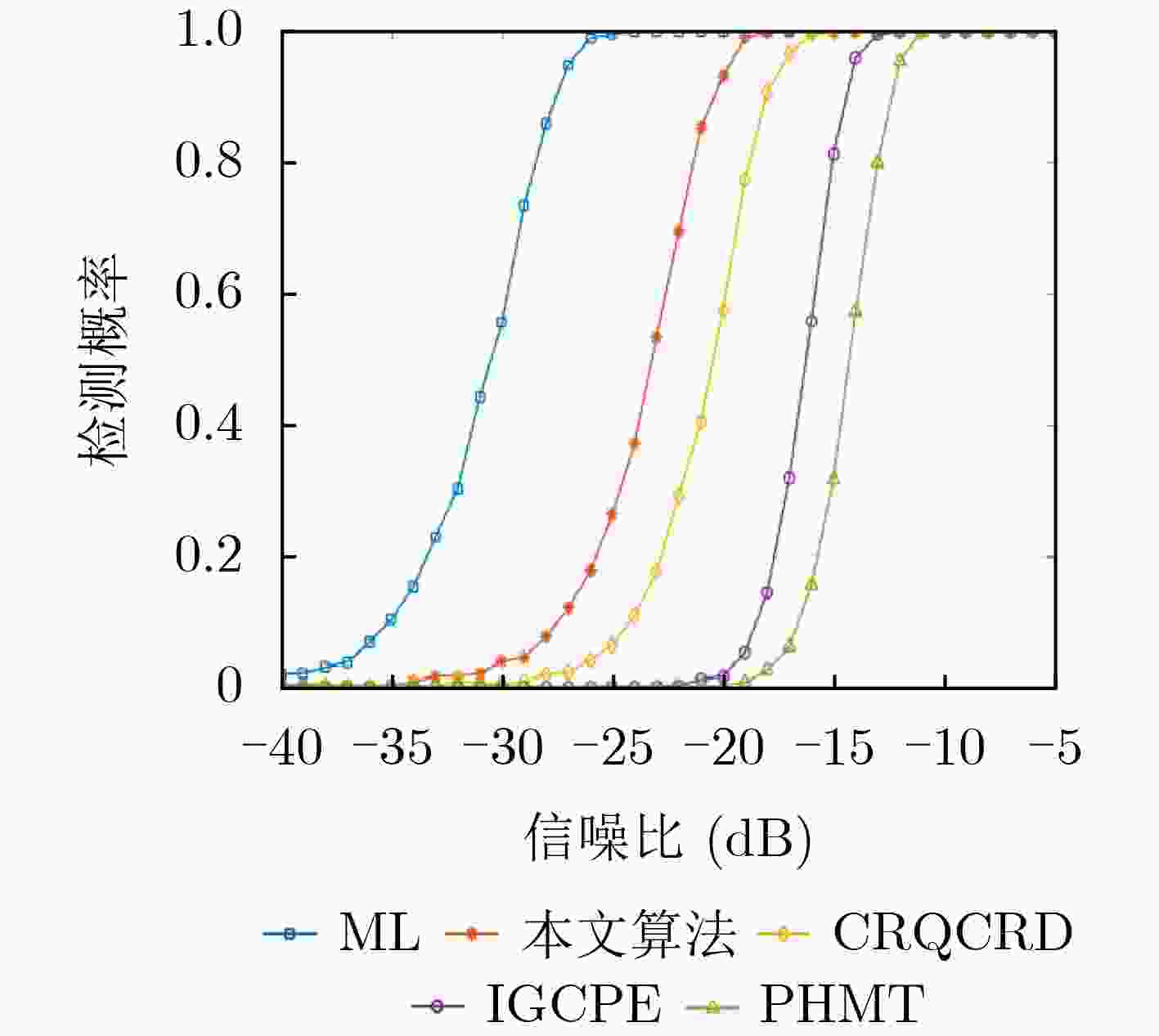
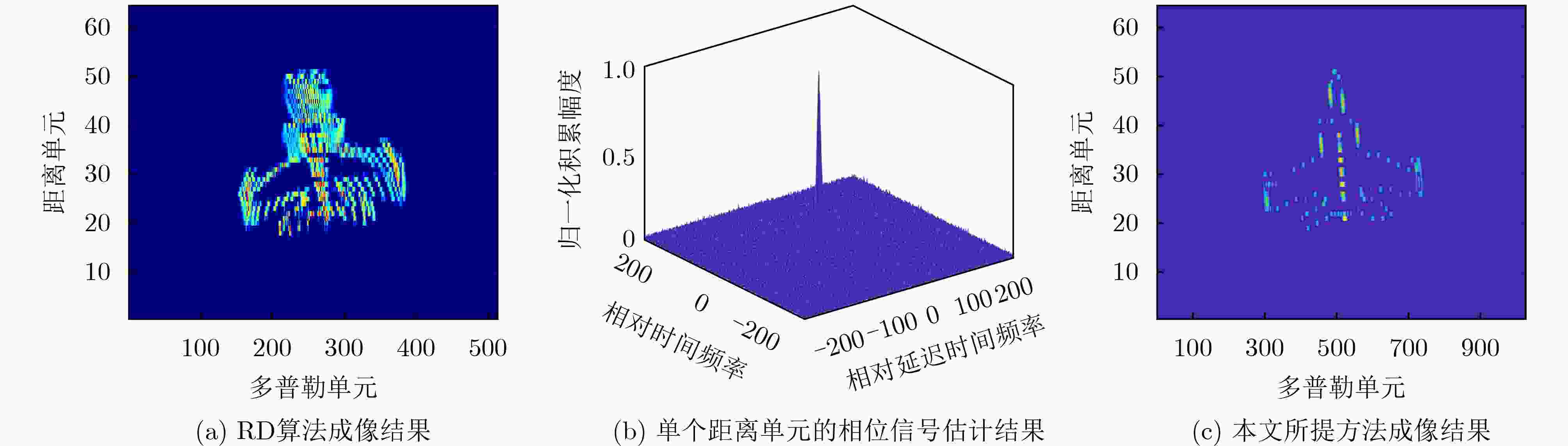
Abstract: Objective Polynomial phase signal (PPS) analysis has been a research field of interest in recent decades due to the fact that many signals in radar, sonar, and seismic are usually modeled as a PPS of different orders based on research needs. First-order PPS can be quickly focused to a frequency bin through Fourier transform, thereby obtaining the estimation of center frequency. However, for high-order PPS, e.g., quadratic frequency modulated signal, due to its non-coherent characteristic, conventional Fourier transform is insufficient for energy integration. Existing time-frequency distribution method, e.g., short-time Fourier transform and Wigner-Ville distribution fail to effectively address the conflicts between auto-terms and cross terms, as well as time-domain resolution and frequency-domain resolution. Furthermore, existing algorithms struggle to strike a balance between computational complexity and signal detection performance. These issues result in poor parameter estimation performance of existing methods. This research proposes a QFM signal detection methods based on non-uniform sampling autocorrelation function, aiming to provide a balanced solution in the application of parameter estimation of QFM signal, considering both computational cost and detection performance. Methods This research presents a time-frequency distribution method for the QFM signal detection and parameter estimation. This method utilizes non-uniform sampling technology and maps one-dimensional signal into a two-dimensional time domain through a novel forth-order autocorrelation function. Subsequently, non-uniform fast Fourier transform is employed to resolve the time variable, and integrates the signal energy into a vertical line on a two-dimensional plane. Then, through FFT along this line, the signal is focused into a peak, and the estimation of chirp rate and quadratic chirp rate can be obtained based on peak position. Finally, de-chirp processing compensates the high-order phase terms of the original signal, and the center frequency parameter estimation is obtained through FFT. Results and Discussions Theoretical analysis and simulation data demonstrate that the proposed method achieves a balance between computational complexity and signal detection performance. In low signal-to-noise ratio scenario, the proposed method can effectively distinguish targets and achieve accurate parameter estimation (Fig. 1). For multi-component signal with significant amplitude differences, the proposed method can accomplish detection and estimation by steps (Fig. 2). Comparative experiments with mainstream state-of-the-art algorithms show that the proposed method is quasi-optimal in terms of estimation accuracy and integration gain (Fig. 3, Fig. 4, Fig. 5 and Fig. 6). However, compared to the ML best estimator, the proposed method significantly improves computational efficiency. Conclusions This paper proposes a method based on non-uniform sampling autocorrelation functions for QFM signal detection and parameter estimation. The method maps QFM signal into a two-dimensional time domain through a novel autocorrelation kernel function and achieves coherent integration through scaling and FFT. Mathematical analysis and simulation experiments demonstrate that, compared to ML method with optimal detection capabilities, the proposed method sacrifices a portion of detection performance to significantly reduce computational complexity. Furthermore, when computational efficiency is similar, the proposed method outperforms other classical methods in terms of signal detection and parameter estimation performance. Overall, this paper provides a balanced solution for QFM signal detection and parameter estimation.
- time-frequency analysis /
- quadratic frequency modulated signal /
- non-uniform sampling technology /
- autocorrelation function

HTML全文

图 1 NQAF方法及其同类方法的单分量仿真结果

下载: 全尺寸图片幻灯片

图 2 NQAF方法的多分量仿真结果

下载: 全尺寸图片幻灯片

图 3 实例3的仿真结果

下载: 全尺寸图片幻灯片

图 4 积累增益的仿真验证

下载: 全尺寸图片幻灯片

图 5 估计精度的验证

下载: 全尺寸图片幻灯片

图 6 检测性能的验证

下载: 全尺寸图片幻灯片

图 7 雷达实测数据的验证

下载: 全尺寸图片幻灯片

表 1 不同方法运行时间对比

方法 ML 本文方法 CRQCRD PHMT CPF

运行时间(秒) 31.4 4.4 4.3 4.1 0.9

下载: 导出CSV

参考文献(28)

[1]	LI Suqi, WANG Yihan, LIANG Yanfeng, et al. Long-time coherent integration for the spatial-based bistatic radar based on dual-scale decomposition and conditioned CPF[J]. Remote Sensing, 2024, 16(10): 1798. doi: 10.3390/rs16101798.
[2]	NIU Zhiyong, ZHENG Jibin, and SU Tao. Novel motion parameter estimation and coherent integration algorithm for high maneuvering target with jerk motion[J]. Signal Processing, 2024, 221: 109467. doi: 10.1016/j.sigpro.2024.109467.
[3]	XU Wenwen, WANG Yuhang, Huang Jidan, et al. SAF-SFT-SRAF-based signal coherent integration method for high-speed target detecting in airborne radar[J]. Progress in Electromagnetics Research C Pier C, 2025, 154(3): 183–190. doi: 10.2528/PIERC25012202.
[4]	MA Jingtao, XIA Xianggen, HUANG Penghui, et al. An efficient parameter estimation and imaging approach for ground maneuvering targets by mixed symmetric function in SAR imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2025, 63: 5206520. doi: 10.1109/TGRS.2025.3548873.
[5]	MA Jingtao, XIA Xianggen, WANG Jiannan, et al. An efficient refocusing method for ground moving targets in multichannel SAR imagery[J]. IEEE Geoscience and Remote Sensing Letters, 2024, 21: 4014105. doi: 10.1109/LGRS.2024.3437429.
[6]	MA Jingtao, WANG Jiannan, XIA Xianggen, et al. A novel ISAR imaging algorithm for a maneuvering target based on generalized second-order time-scaled transform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2025, 63: 5102419. doi: 10.1109/TGRS.2025.3540457.
[7]	DING Jiabao, WANG Jiadong, LI Yachao, et al. An efficient ISAR imaging and scaling method for highly maneuvering targets based on ICPF-PSVA[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 5923409. doi: 10.1109/TGRS.2024.3440839.
[8]	XU Wenwen, WANG Yuhang, CAO Jianyin, et al. KT-SRAF-LVD-based signal coherent integration method for high-speed target detecting in airborne radar[J]. Sensors, 2025, 25(7): 2128. doi: 10.3390/s25072128.
[9]	MEIGNEN S, OBERLIN T, and MCLAUGHLIN S. A new algorithm for multicomponent signals analysis based on synchrosqueezing: With an application to signal sampling and denoising[J]. IEEE Transactions on Signal Processing, 2012, 60(11): 5787–5798. doi: 10.1109/TSP.2012.2212891.
[10]	XIA Xianggen, WANG Genyuan, and CHEN V C. Quantitative SNR analysis for ISAR imaging using joint time-frequency analysis-short time Fourier transform[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(2): 649–649. doi: 10.1109/TAES.2002.1008993.
[11]	KATKOVNIK V. A new form of the Fourier transform for time-varying frequency estimation[C]. Proceedings of ISSE'95 - International Symposium on Signals, Systems and Electronics, San Francisco, USA, 1995: 179–182. doi: 10.1109/ISSSE.1995.497962.
[12]	SONG Yu’e, ZHANG Xiaoyan, SHANG Chunheng, et al. The Wigner-Ville distribution based on the linear canonical transform and its applications for QFM signal parameters estimation[J]. Journal of Applied Mathematics, 2014, 2014: 516557. doi: 10.1155/2014/516457.
[13]	ZHANG Liang, ZHOU Bilei, SONG Rongguo, et al. Wideband Lv’s distribution: A signal processing tool for hyperbolic frequency-modulated signal analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 2024, 60(5): 6061–6074. doi: 10.1109/TAES.2024.3398611.
[14]	AMAR A. Efficient estimation of a narrow-band polynomial phase signal impinging on a sensor array[J]. IEEE Transactions on Signal Processing, 2010, 58(2): 923–927. doi: 10.1109/TSP.2009.2030608.
[15]	LI Yanyan, SU Tao, ZHENG Jibin, et al. ISAR imaging of targets with complex motions based on modified Lv’s distribution for cubic phase signal[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(10): 4775–4784. doi: 10.1109/JSTARS.2015.2460734.
[16]	SU Jia, TAO Haihong, RAO Xuan, et al. Coherently integrated cubic phase function for multiple LFM signals analysis[J]. Electronics Letters, 2015, 51(5): 411–413. doi: 10.1049/el.2014.4164.
[17]	RHEE K, BAIK J, SONG C, et al. LPI radar waveform recognition based on hierarchical classification approach and maximum likelihood estimation[J]. Entropy, 2024, 26(11): 915. doi: 10.3390/e26110915.
[18]	WU Liang, WEI Xizhang, YANG Degui, et al. ISAR imaging of targets with complex motion based on discrete chirp Fourier transform for cubic chirps[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(10): 4201–4212. doi: 10.1109/TGRS.2012.2189220.
[19]	WANG Yong, KANG Jian, and JIANG Yicheng. ISAR imaging of maneuvering target based on the local polynomial Wigner distribution and integrated high-order ambiguity function for cubic phase signal model[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(7): 2971–2991. doi: 10.1109/JSTARS.2014.2301158.
[20]	BARBAROSSA S, SCAGLIONE A, and GIANNAKIS G B. Product high-order ambiguity function for multicomponent polynomial-phase signal modeling[J]. IEEE Transactions on Signal Processing, 1998, 46(3): 691–708. doi: 10.1109/78.661336.
[21]	WANG Pu, LI Hongbin, DJUROVIĆ I, et al. Integrated cubic phase function for linear FM signal analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(3): 963–977. doi: 10.1109/TAES.2010.5545167.
[22]	WANG Yong and JIANG Yicheng. ISAR imaging of a ship target using product high-order matched-phase transform[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(4): 658–661. doi: 10.1109/LGRS.2009.2013876.
[23]	ZHENG Jibin, SU Tao, ZHANG Long, et al. ISAR imaging of targets with complex motion based on the chirp rate–quadratic chirp rate distribution[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(11): 7276–7289. doi: 10.1109/TGRS.2014.2310474.
[24]	EI-DEN B M and RASLAN W. A reversible and robust hybrid image steganography framework using radon transform and integer lifting wavelet transform[J]. Scientific Reports, 2025, 15(1): 15687. doi: 10.1038/s41598-025-98539-2.
[25]	SONG Hengli, XIONG Yixiang, and ZHAO Qingpu. Topological image reconstruction of regular grounding network based on Hough transform[J]. IEEE Sensors Journal, 2024, 24(17): 27587–27596. doi: 10.1109/JSEN.2024.3428574.
[26]	ZHAN Muyang, ZHAO Chanjuan, QIN Kun, et al. Subaperture keystone transform matched filtering algorithm and its application for air moving target detection in an SBEWR system[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2023, 16: 2262–2274. doi: 10.1109/JSTARS.2023.3245295.
[27]	ZHANG Jiancheng, LI Yanyan, SU Tao, et al. Quadratic FM signal detection and parameter estimation using coherently integrated trilinear autocorrelation function[J]. IEEE Transactions on Signal Processing, 2020, 68: 621–633. doi: 10.1109/tsp.2020.2965279.
[28]	LI Yanyan, ZHANG Jiancheng, ZHOU Yan, et al. ISAR imaging of nonuniformly rotating targets with low SNR based on coherently integrated nonuniform trilinear autocorrelation function[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(6): 1074–1078. doi: 10.1109/LGRS.2020.2992513.