基于带限信号压缩的高效软件无线电卫星双向时间比对

程龙; 董绍武; 武文俊; 弓剑军; 王威雄; 高喆

doi:10.11999/JEIT250705

基于带限信号压缩的高效软件无线电卫星双向时间比对

doi: 10.11999/JEIT250705 cstr: 32379.14.JEIT250705

程龙^{1, 2,},
董绍武^{1, 3, 4, ,},
武文俊^{1, 3, 4},
弓剑军^{1, 3},
王威雄^{1, 3},
高喆^{1, 3}

1.
中国科学院国家授时中心西安 710600
2.
中国科学院大学北京 100049
3.
中国科学院时间基准及应用重点实验室西安 710600
4.
中国科学院大学天文与空间科学学院北京 100049

详细信息

作者简介:
程龙：男，博士生，研究方向为高精度时间频率传递

董绍武：男，研究员，研究方向为守时技术、卫星导航系统时间

武文俊：男，研究员，研究方向为时间与频率、卫星导航

弓剑军：男，工程师，研究方向为守时技术

王威雄：男，助理研究员，研究方向为守时技术、高精度时间频率传递

高喆：女，助理研究员，研究方向为高精度时间频率传递

通讯作者:
董绍武　sdong@ntsc.ac.cn

中图分类号: TN927
计量
- 文章访问数: 97
- HTML全文浏览量: 38
- PDF下载量: 13
- 被引次数: 0
出版历程
- 收稿日期: 2025-07-28
- 修回日期: 2025-12-06
- 录用日期: 2025-12-06
- 网络出版日期: 2025-12-15

Band-Limited Signal Compression Enabled Computationally Efficient Software-Defined Radio for Two-Way Satellite Time and Frequency Transfer

CHENG Long^{1, 2
,},
DONG Shaowu^{1, 3, 4
, ,},
WU Wenjun^{1, 3, 4},
GONG Jianjun^{1, 3},
WANG Weixiong^{1, 3},
GAO Zhe^{1, 3}

1.
National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China
2.
University of Chinese Academy of Sciences, Beijing 100049, China
3.
Key Laboratory of Time Reference and Applications, Chinese Academy of Sciences, Xi’an 710600, China
4.
School of Astronomy and Space Science, University of Chinese Academy of Sciences, Beijing 100049, China

摘要

摘要: 卫星双向时间比对(TWSTFT)技术因其高精度特性在时间同步领域具有重要应用价值，其中实时性是衡量系统性能的关键指标。传统硬件实现的TWSTFT存在显著的周日效应问题，而基于开环架构和高分辨率多相关器的软件定义无线电(SDR)实现方法虽能有效抑制该效应，却因计算复杂度高而面临实时性挑战。为提升SDR接收机的运算效率并改善其短期稳定性，该研究在传统信号压缩法基础上提出了一种基于带限信号压缩的高效SDR实现方法。该方法创新性地采用伪随机噪声(PRN)码整数倍抽取序列与接收信号进行相关运算以获得压缩值，并通过建立抽取序列采样频率与信号带宽的定量关系实现相关结果的高效重构。该机制通过消除传统算法的冗余计算环节，在保证测量精度的同时显著提升了运算效率并降低了系统资源开销。为验证方法有效性，该文设计了不同带宽和基线长度的对比实验，结果表明：相较于TWSTFT SDR中常用的多相关器法，该方法的运算速度提升了7～8倍，资源消耗量降低了85～90%，且信号预处理阶段的滤波操作能有效抑制带外噪声干扰。这种效率提升不仅增加了单位拟合周期内的有效测量数据量，通过统计平均效应降低了随机噪声影响，还显著提高了比对结果的短期稳定性，为高精度时间比对提供了新的技术途径。
- 卫星双向时间比对 /
- 软件定义无线电 /
- 信号压缩 /
- 多相关器 /
- 伪随机噪声码
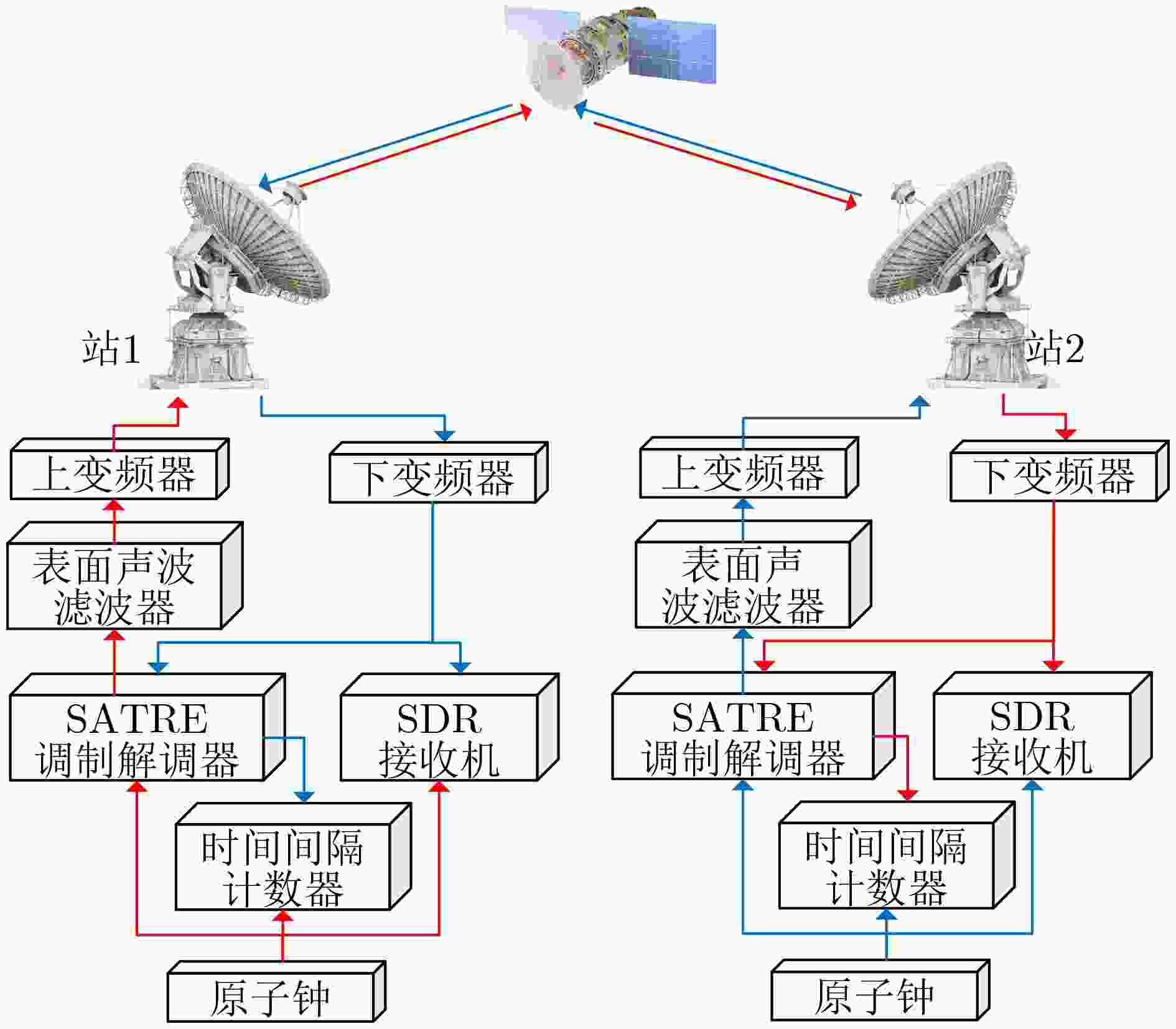
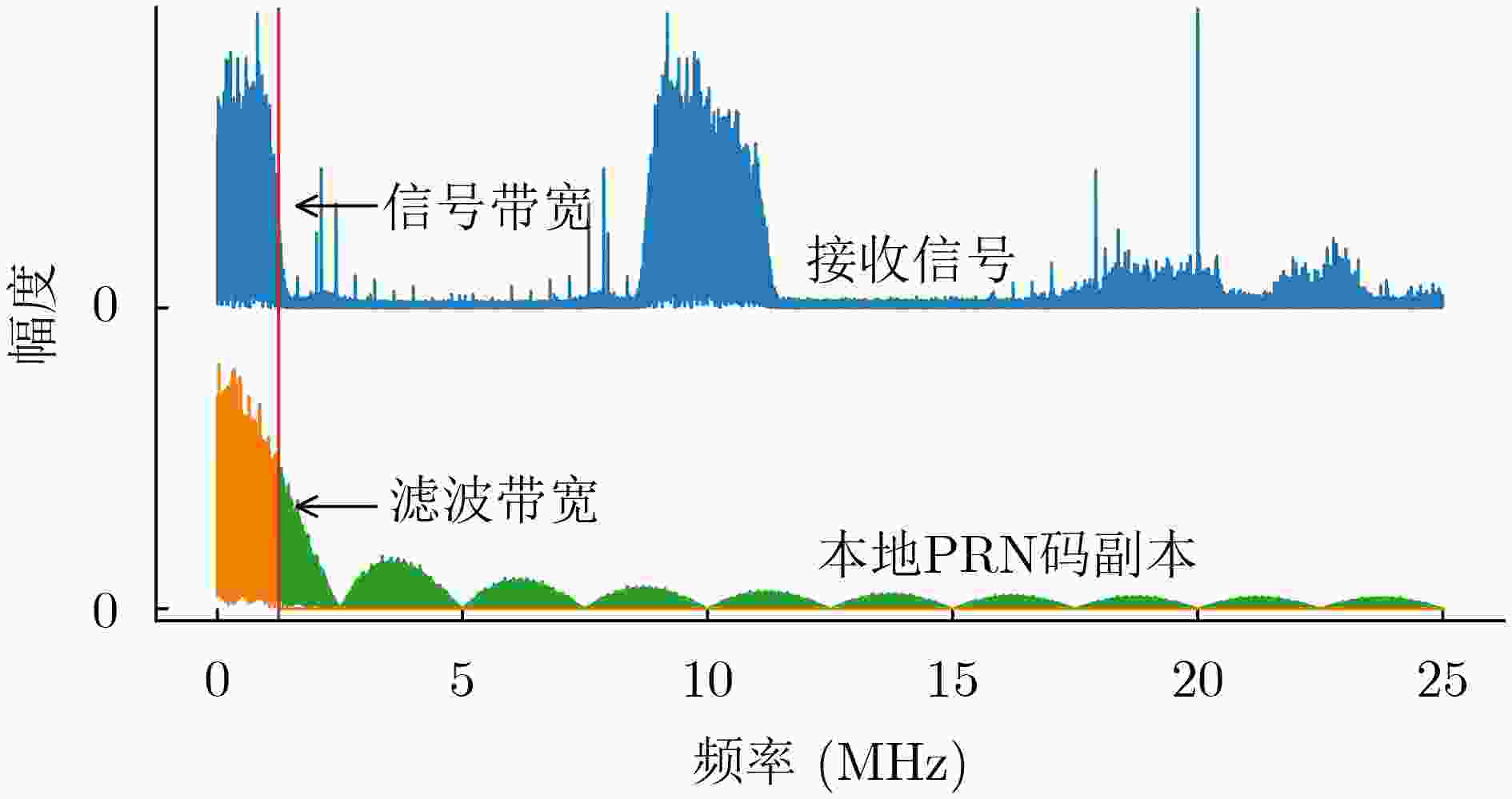
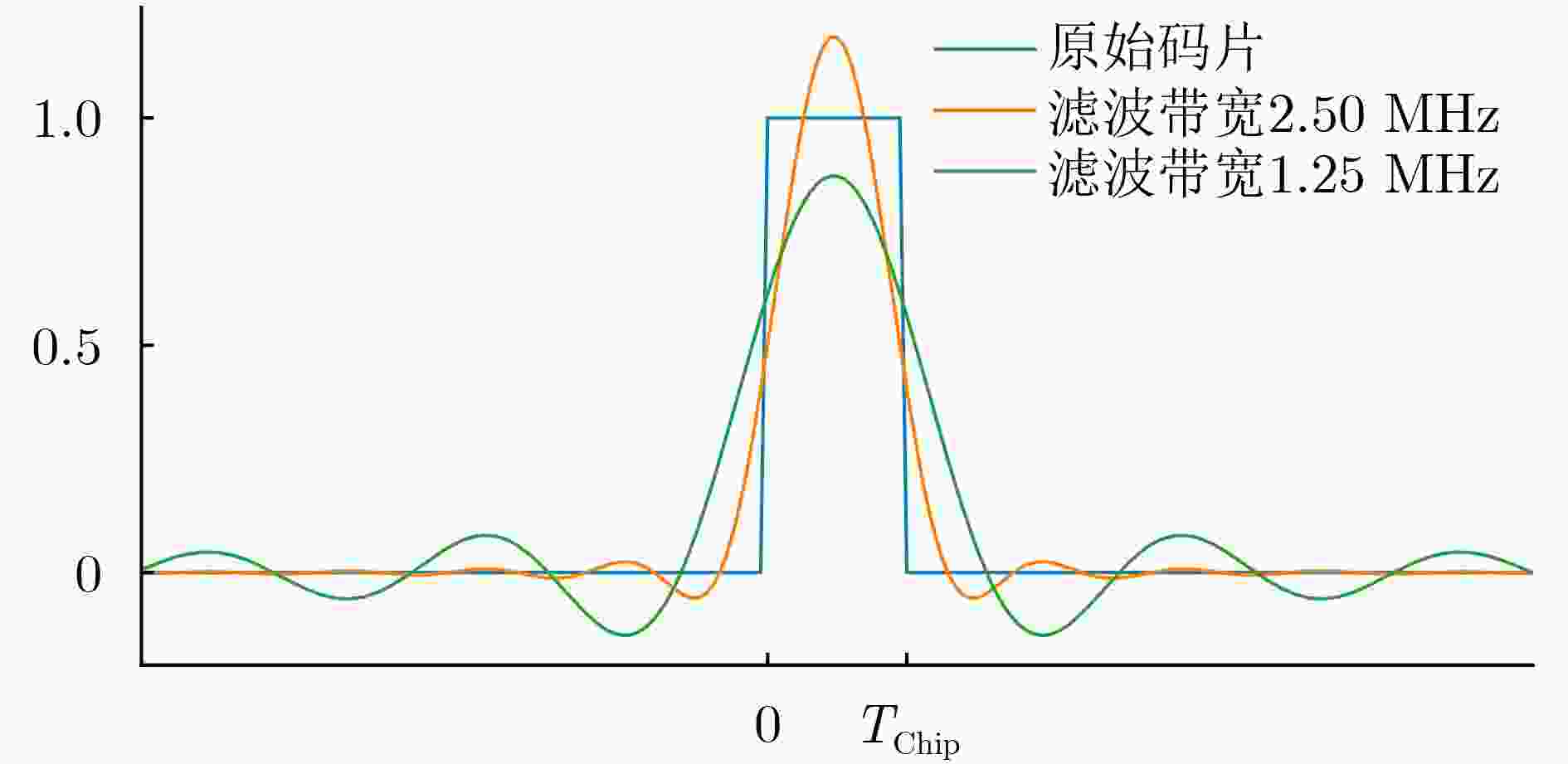
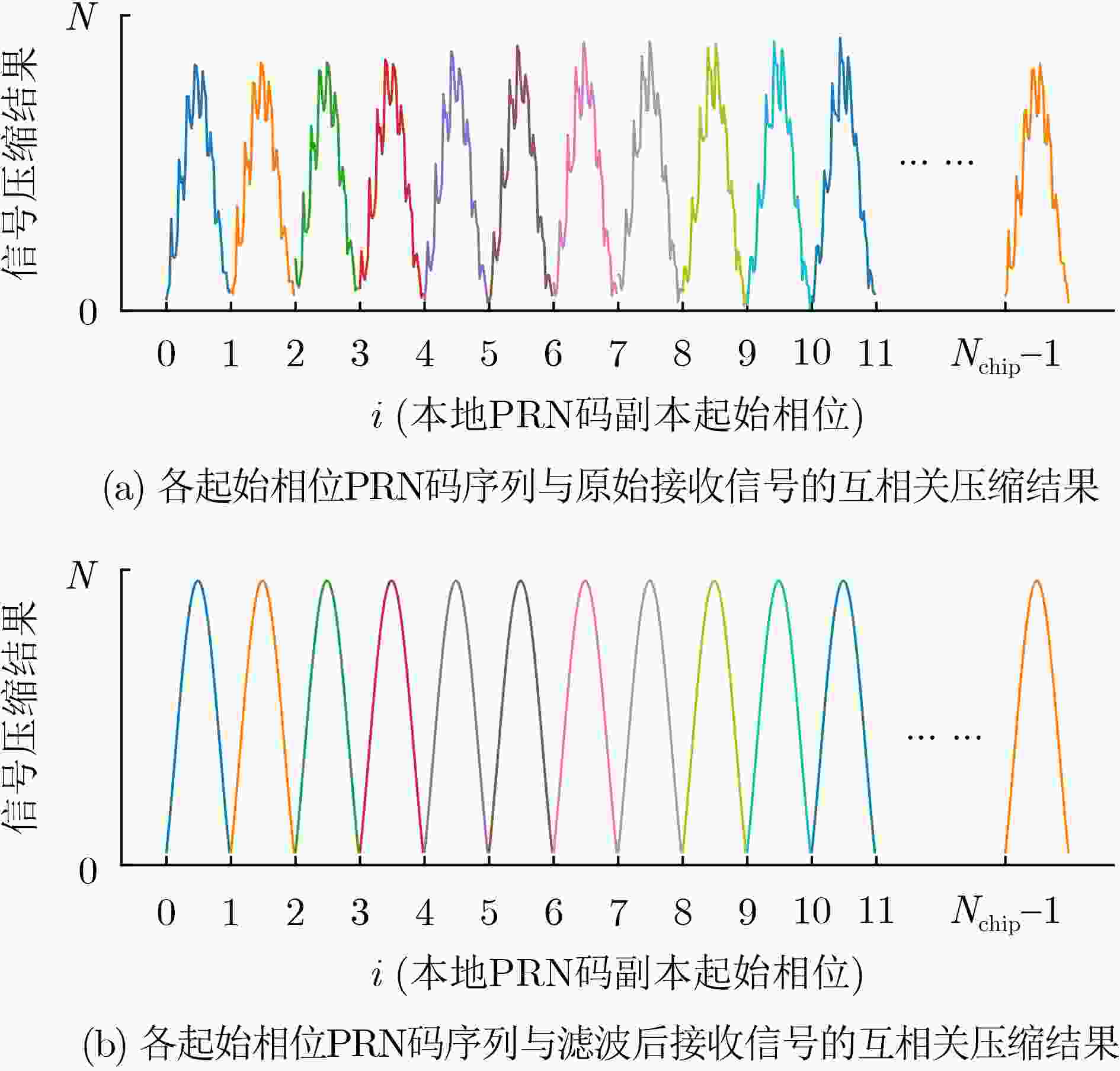
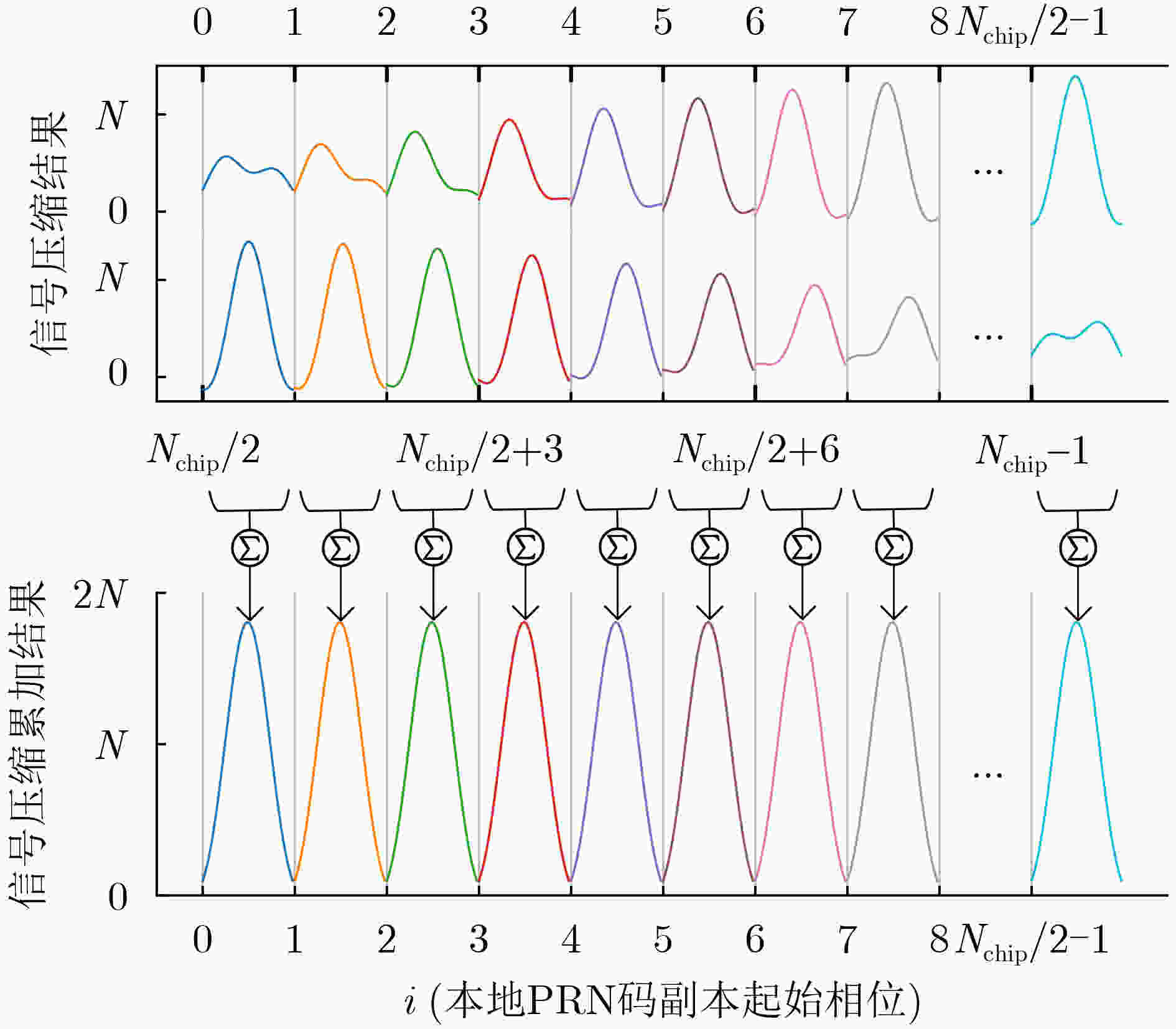
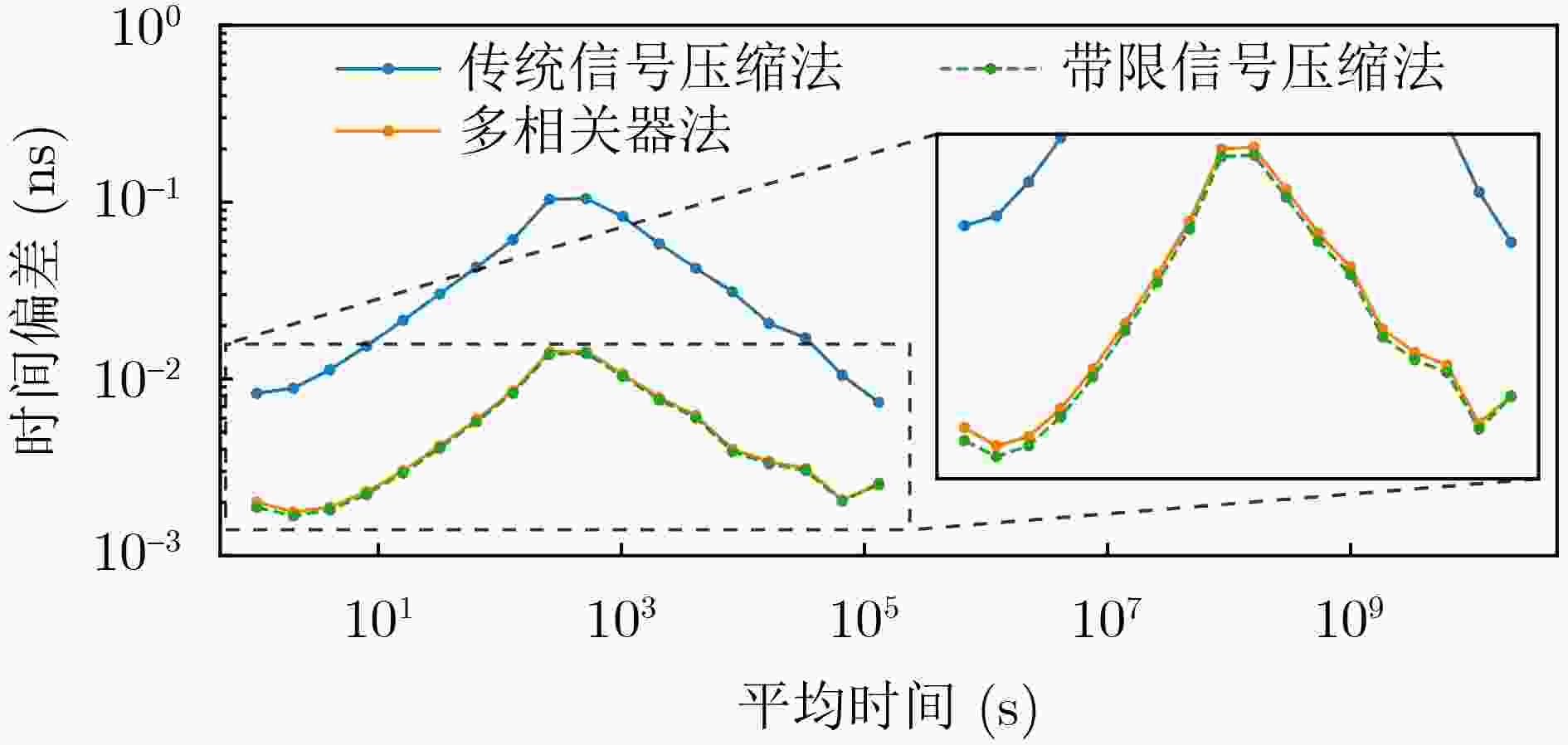
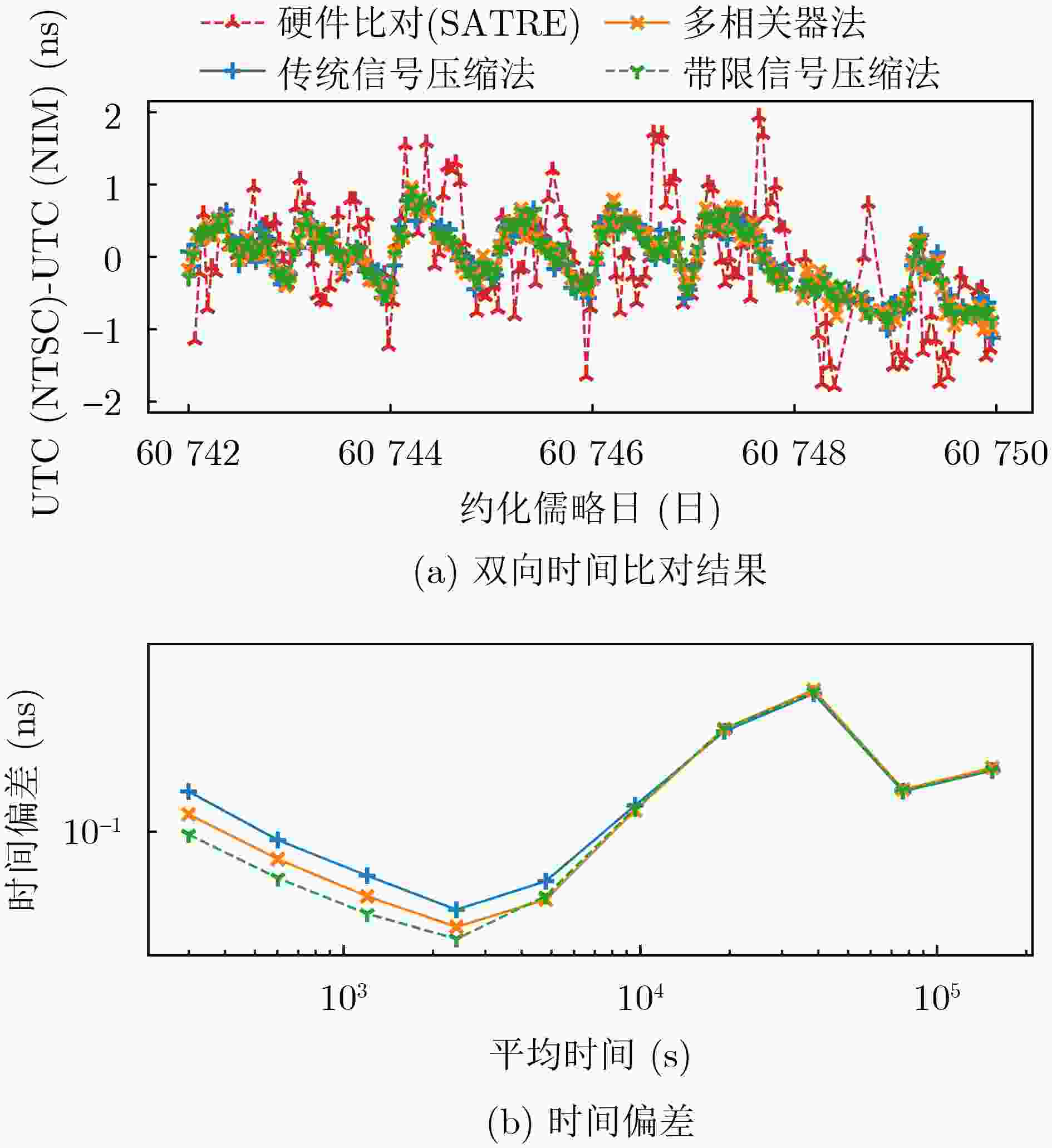
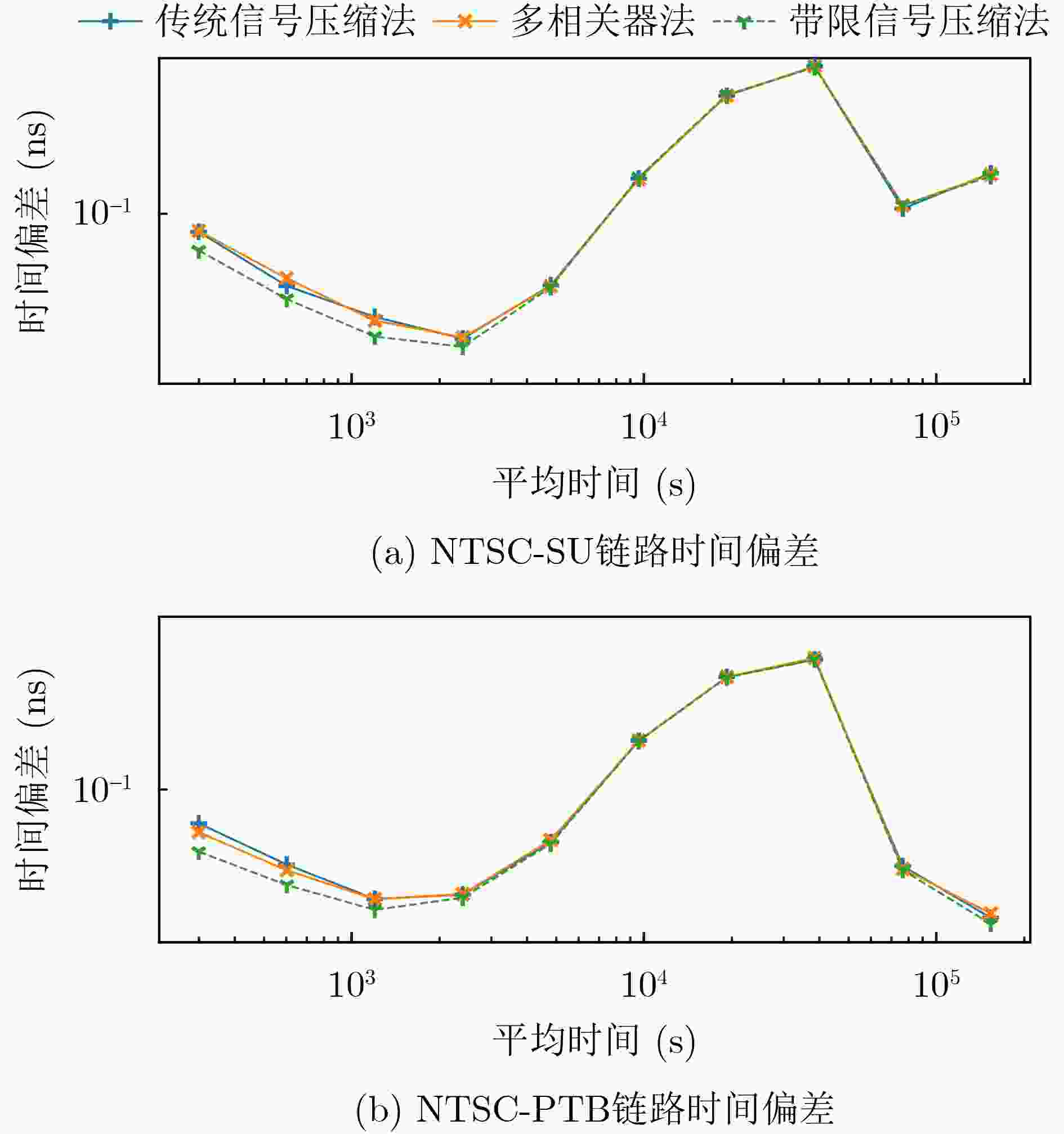
Abstract: Objective This study addresses key challenges in Two-Way Satellite Time and Frequency Transfer (TWSTFT) systems, with emphasis on the computational inefficiency and high resource consumption of Software-Defined Radio (SDR) receivers. Although TWSTFT provides excellent long-term stability and time-transfer precision, conventional hardware implementations exhibit significant diurnal effects. Existing mitigation approaches, such as fusion with GPS Precise Point Positioning, depend on auxiliary link quality and lack unified algorithms across international networks. SDR receivers reduce diurnal effects and improve accuracy; however, high sampling rates and multi-correlator processing impose excessive computational burdens that limit real-time multi-station operation. The objective is to develop a band-limited signal compression approach that preserves measurement resolution while substantially improving computational efficiency, thereby enabling scalable and high-performance time transfer across international timing laboratories. Methods A band-limited signal compression method tailored to TWSTFT is proposed by accounting for the distortion of Pseudo-Random Noise (PRN) code square-wave characteristics under bandwidth constraints. Bandwidth-matched filtering is first applied to the local PRN code replica to align its spectrum with the effective bandwidth of the received signal and suppress out-of-band noise. For received signals with different bandwidths, n groups (e.g., n = 1, 2, or 20) of phase-diversified, equally spaced PRN code subsequences are generated. The number of subsequence groups n satisfies n × R_chip≥ 2 × Band_signal, where R_chip denotes the sampling rate of the subsequences and Band_signal represents the signal bandwidth. After bandpass filtering, the received signal undergoes parallel correlation with the phase-diversified PRN subsequences. The full correlation function is reconstructed by a linear combination of the n independent correlation outputs, each scaled by N_chip/n, where N_chip is the number of samples per PRN chip. Adaptive sampling-rate adjustment and resource-allocation strategies are applied to achieve efficient processing with preserved accuracy. Results and Discussions Experimental validation is performed on a TWSTFT platform at the National Time Service Center using TWSTFT links (NTSC–NIM, NTSC–SU, NTSC–PTB) and SATRE local-loop tests. Data from MJD 60 742 to MJD 60 749 are collected in accordance with ITU-R TF.1153.4. In local-loop tests, the proposed method provides the most stable Time of Arrival measurements while maintaining a high signal-to-noise ratio (Table 2). Time deviation outperforms traditional multi-correlator and conventional compression methods over all averaging times (Fig. 9). For operational links, superior short-term stability is observed across different baseline lengths (Fig. 10 and Fig. 11). With n = 1 and n = 2, processing speed increases by 795% and 707%, respectively, while GPU memory usage decreases by 89.77% and 84.65% (Table 4). The method supports up to 102 concurrent channels (n = 1), exceeding the 11-channel capacity of conventional approaches (Table 5). Increasing n beyond these values yields no further precision improvement but increases resource consumption, confirming an optimal trade-off between accuracy and efficiency. Conclusions A band-limited signal compression method is presented to address the computational constraints of TWSTFT SDR receivers. Parallel short-correlation processing combined with bandwidth-aware sampling achieves substantial gains in precision and efficiency. Experimental results confirm improved short-term stability across signal bandwidths and baseline lengths relative to conventional multi-correlator methods. The approach delivers large efficiency gains, with processing speed increases of 795% (n = 1) and 707% (n = 2) and GPU memory reductions of 89.77% and 84.65%, respectively. System scalability is markedly enhanced, supporting up to 102 concurrent channels. These results demonstrate an effective balance between performance and resource utilization for TWSTFT applications.
- Two-Way Satellite Time and Frequency Transfer (TWSTFT) /
- Software-Defined Radio (SDR) /
- Signal compression /
- Multi-correlator /
- Pseudo-Random Noise (PRN) code

HTML全文

图 1 TWSTFT SDR比对原理其中红色箭头为站点1的上行链路，蓝色箭头为站点2的上行链路。

下载: 全尺寸图片幻灯片

图 2 信号压缩中的本地PRN码副本

下载: 全尺寸图片幻灯片

图 3 传统信号压缩法相关结果计算原理

下载: 全尺寸图片幻灯片

图 4 接收信号与本地PRN码副本频谱

下载: 全尺寸图片幻灯片

图 5 不同滤波带宽时本地PRN码副本的码片形状

下载: 全尺寸图片幻灯片

图 6 各起始相位ε_i,k与接收信号的互相关压缩结果

下载: 全尺寸图片幻灯片

图 7 ε_i,k等效采样率等于信号带宽时(n=2)相关值的计算过程

下载: 全尺寸图片幻灯片

图 8 实验平台接收设备

下载: 全尺寸图片幻灯片

图 9 本地回路中传统信号压缩法、多相关器法以及带限信号压缩法的时间偏差

下载: 全尺寸图片幻灯片

图 10 NTSC-NIM链路卫星双向比对结果及时间偏差

下载: 全尺寸图片幻灯片

图 11 NTSC-SU和NTSC-PTB链路的时间偏差

下载: 全尺寸图片幻灯片

表 1 实验参数配置表

接收机通道	有效信号带宽（MHz）	比对方法	压缩信号组数	动态范围(码片)	本地PRN码副本滤波带宽(MHz)	接收信号是否滤波	接收信号滤波带宽/ 中心频率(MHz)
R0	1.25	多相关器法	-	±0.7	1.25	否	-
R0	1.25	传统信号压缩法	-	±1.0	-	否	-
R0	1.25	带限信号压缩法	20, 2, 1	±1.0	1.25	是	1.25/ 70.00
R1	2.5	多相关器法	-	±0.7	2.50	否	-
R1	2.5	传统信号压缩法	-	±1.0	-	否	-
R1	2.5	带限信号压缩法	20, 2	±1.0	2.50	是	2.50/ 70.02

下载: 导出CSV

表 2 本地回路中到达时间以及信噪比的统计

方法	到达时间		信噪比
方法	均值(ns)	标准差(ps)	均值(dB)	标准差(dB)
传统信号压缩	1453.37	162.56	9.702	0.0186
多相关器	1441.45	22.57	14.308	0.0229
带限信号压缩(n=20)	1441.44	21.98	14.274	0.0309
带限信号压缩(n=2)	1441.45	22.03	14.276	0.0313

下载: 导出CSV

表 3 NTSC-NIM、NTSC-SU和NTSC-PTB链路中传统信号压缩法、多相关器法和带限信号压缩法单向结果统计(ps)

方法	NTSC-NIM	NTSC-SU	NTSC-PTB
传统信号压缩	14.57	10.66	8.40
多相关器	13.56	10.41	7.98
带限信号压缩(n=20)	12.84	9.89	7.36
带限信号压缩(n=2)	12.84	9.91	7.33
带限信号压缩(n=1)	12.82	9.90	7.36

下载: 导出CSV

表 4 SATRE本地回路和TWSTFT链路中多相关器法和带限信号压缩法的时间以及资源消耗统计情况

方法	SATRE本地回路 (ms)	NTSC-NIM (ms)	NTSC-SU (ms)	NTSC-PTB (ms)	平均时耗 (ms)	加速比	资源占用 (MiB)
多相关器	81.99	80.54	81.90	85.32	82.43	1	430
带限信号压缩(n=20)	32.94	28.21	32.82	27.47	30.36	2.72	410
带限信号压缩(n=2)	8.21	8.65	8.07	15.95	10.22	8.07	66
带限信号压缩(n=1)	-	14.91	6.37	6.32	9.20	8.95	44

下载: 导出CSV

表 5 多相关器法和带限信号压缩法所支持的最大比对通道数的统计结果

方法		时间限制比对通道数	GPU内存限制比对通道数	最大比对通道数
信号未经滤波操作	多相关器	11.8	16.3	11
信号未经滤波操作	带限信号压缩(n=20)	31.9	17.1	17
信号经过滤波操作	带限信号压缩(n=20)	30.9	15.3	15
	带限信号压缩(n=2)	91.9	95.3	91
	带限信号压缩(n=1)	102.2	143.0	102

下载: 导出CSV

参考文献(21)

[1]	WANG Weixiong, DONG Shaowu, WU Wenjun, et al. Evaluation of Asia-Europe TWSTFT Links using the express-80 satellite[J]. IEEE Instrumentation & Measurement Magazine, 2022, 25(6): 19–24. doi: 10.1109/MIM.2022.9847188.
[2]	JIANG Zhiheng, KONATÉ H, and LEWANDOWSKI W. Review and preview of two-way time transfer for UTC generation - from TWSTFT to TWOTFT[C]. Joint European Frequency and Time Forum & International Frequency Control Symposium (EFTF/IFC), Prague, Czech Republic, 2013: 501–504. doi: 10.1109/EFTF-IFC.2013.6702103.
[3]	王威雄, 董绍武, 武文俊, 等. 基于软件接收机和间接链路的卫星双向时间比对性能分析[J]. 仪器仪表学报, 2019, 40(10): 152–160. doi: 10.19650/j.cnki.cjsi.J1905616. WANG Weixiong, DONG Shaowu, WU Wenjun, et al. Performance analysis of two-way satellite time and frequency transfer based on SDR receivers and indirect links[J]. Chinese Journal of Scientific Instrument, 2019, 40(10): 152–160. doi: 10.19650/j.cnki.cjsi.J1905616.
[4]	WANG Xiang, DONG Shaowu, SONG Huijie, et al. Time Transfer Link fusion algorithm based on wavelet multi-resolution analysis[J]. Measurement, 2024, 232: 114599. doi: 10.1016/j.measurement.2024.114599.
[5]	刘强, 孙浩冉, 胡邓华, 等. 基于Vondrak-Cepek组合滤波和注意力机制加权的时间比对融合算法[J]. 系统工程与电子技术, 2025, 47(2): 673–679. doi: 10.12305/j.issn.1001-506X.2025.02.34. LIU Qiang, SUN Haoran, HU Denghua, et al. Time alignment fusion algorithm based on Vondrak-Cepek combined filtering and attention mechanism weighting[J]. Systems Engineering and Electronics, 2025, 47(2): 673–679. doi: 10.12305/j.issn.1001-506X.2025.02.34.
[6]	PANFILO G and ARIAS F. The coordinated universal time (UTC)[J]. Metrologia, 2019, 56(4): 042001. doi: 10.1088/1681-7575/ab1e68.
[7]	BIPM. Two-way satellite time and frequency transfer: First use of a software defined radio receiver in UTC calculation[EB/OL]. https://www.bipm.org/en/-/2020-twstft-sdr, 2025.
[8]	SICCARDI M, THAI T T, ROVERA D G, et al. A TWSTFT transmitter prototype compatible with SDR receivers and SATRE modems[C]. Joint Conference of the IEEE International Frequency Control Symposium and International Symposium on Applications of Ferroelectrics (IFCS-ISAF), Keystone, USA, 2020: 1–3. doi: 10.1109/IFCS-ISAF41089.2020.9234873.
[9]	FRIEDT J M, LOURS M, GOAVEC-MEROU G, et al. Development of an opensource, Openhardware, software-defined radio platform for two-way satellite time and frequency transfer[C]. 2023 Joint Conference of the European Frequency and Time Forum and IEEE International Frequency Control Symposium (EFTF/IFCS), Toyama, Japan, 2023: 1–4. doi: 10.1109/EFTF/IFCS57587.2023.10272067.
[10]	ACHKAR J, MEYER É, CHUPIN B, et al. Two-way satellite time and frequency transfer using an opensource, Openhardware software-defined radio platform[C]. 4th URSI Atlantic Radio Science Meeting (AT-RASC), Gran Canaria, Spain, 2024: 1–4. doi: 10.46620/URSIATRASC24/ZXOX6507.
[11]	LEE J, OH J I, CHOI G W, et al. Truncated M-sequence and BOC modulation based ranging signal design for TWSTFT[C]. Conference on Precision Electromagnetic Measurements (CPEM), Denver, USA, 2024: 1–2. doi: 10.1109/CPEM61406.2024.10646003.
[12]	WEILL L R. Theory and applications of signal compression in GNSS receivers[C]. The 20th International Technical Meeting of the Satellite Division of The Institute of Navigation, Fort Worth, USA, 2007: 708–719.
[13]	WANG Xiang, GAO Yang, CUI Xiaowei, et al. A signal quality monitoring algorithm based on chip domain observables for BDS B1C signal[C]. International Technical Meeting of the Institute of Navigation, San Diego, USA, 2021: 149–161. doi: 10.33012/2021.17810.
[14]	WANG Xiang, CUI Xiaowei, LIU Gang, et al. Signal quality monitoring based on chip domain observables: Theory, design, and implementation[J]. NAVIGATION: Journal of the Institute of Navigation, 2022, 69(4): navi. 543. doi: 10.33012/navi.543.
[15]	WANG Chuanrui, WANG Xiang, CUI Xiaowei, et al. Efficient chip-shape correlator implementation on a GPU-based real-time GNSS SDR receiver[J]. GPS Solutions, 2022, 26(4): 143. doi: 10.1007/s10291-022-01332-1.
[16]	JIANG Zhiheng, ZHANG V, HUANG Y J, et al. Use of software-defined radio receivers in two-way satellite time and frequency transfers for UTC computation[J]. Metrologia, 2018, 55(5): 685–698. doi: 10.1088/1681-7575/aacbe6.
[17]	王威雄, 董绍武, 武文俊, 等. 卫星双向时间传递链路校准及其不确定度分析[J]. 仪器仪表学报, 2018, 39(12): 64–72. doi: 10.19650/j.cnki.cjsi.J1803688. WANG Weixiong, DONG Shaowu, WU Wenjun, et al. Link calibration of two-way satellite time and frequency transfer and its uncertainty analysis[J]. Chinese Journal of Scientific Instrument, 2018, 39(12): 64–72. doi: 10.19650/j.cnki.cjsi.J1803688.
[18]	HUANG Y J, FUJIEDA M, TAKIGUCHI H, et al. Stability improvement of an operational two-way satellite time and frequency transfer system[J]. Metrologia, 2016, 53(2): 881–890. doi: 10.1088/0026-1394/53/2/881.
[19]	QI Yunhan, YAO Zheng, and LU Mingquan. General design methodology of code multi-correlator discriminator for GNSS multi-path mitigation[J]. IET Radar, Sonar & Navigation, 2021, 15(9): 969–984. doi: 10.1049/rsn2.12088.
[20]	SIEBERT C, KONOVALTSEV A, and MEURER M. Development and validation of a multipath mitigation technique using multi-correlator structures[J]. NAVIGATION: Journal of the Institute of Navigation, 2023, 70(4): navi. 609. doi: 10.33012/navi.609.
[21]	GAO Zhe, WANG Weixiong, WU Wenjun, et al. Experiment of Asia-Europe TWSTFT Link using new satellite express-80[C]. 2024 IEEE Ultrasonics, Ferroelectrics, and Frequency Control Joint Symposium, Taipei, China, 2024: 1–4. doi: 10.1109/UFFC-JS60046.2024.10793506.