ISAR Sequence Motion Modeling and Fuzzy Attitude Classification Method for Small Sample Space Target
-
摘要: 空间目标姿态分类是空间态势感知中的关键环节，针对现有方法存在计算复杂度高、训练数据依赖性强、分类粒度粗糙，以及时序运动建模和小样本分类能力不足等问题，该文提出一种面向小样本、融合运动建模与模糊理论的姿态模糊分类方法。所提方法依托地基逆合成孔径雷达成像与图像解译技术，构建融合地平坐标系、UNW轨道坐标系和机体坐标系的映射模型，从姿态与特征间映射关系出发，结合傅里叶级数深入目标时序运动建模，利用特征设计细化分类粒度，并引入模糊理论实现小样本下线性阶计算复杂度姿态模糊分类。仿真实验验证了该方法小样本场景不同成像角度与异常干扰下的稳健性。横向对比显示所提方法无需训练，并在实时性和小样本处理能力等方面具有性能提升。Abstract:
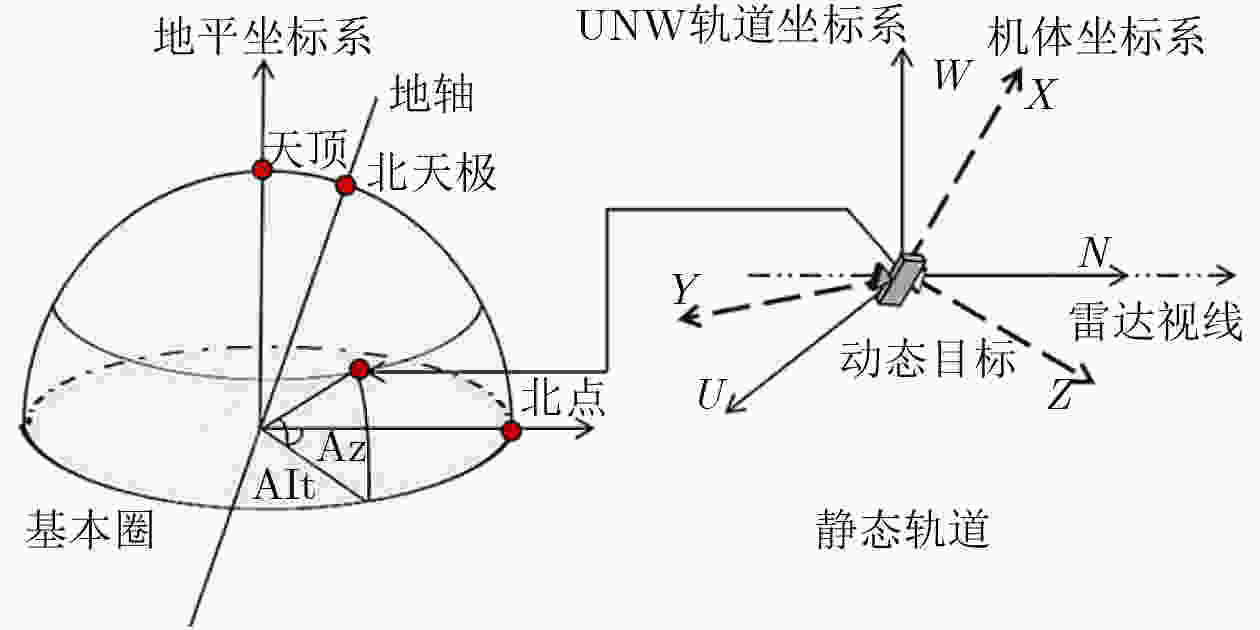
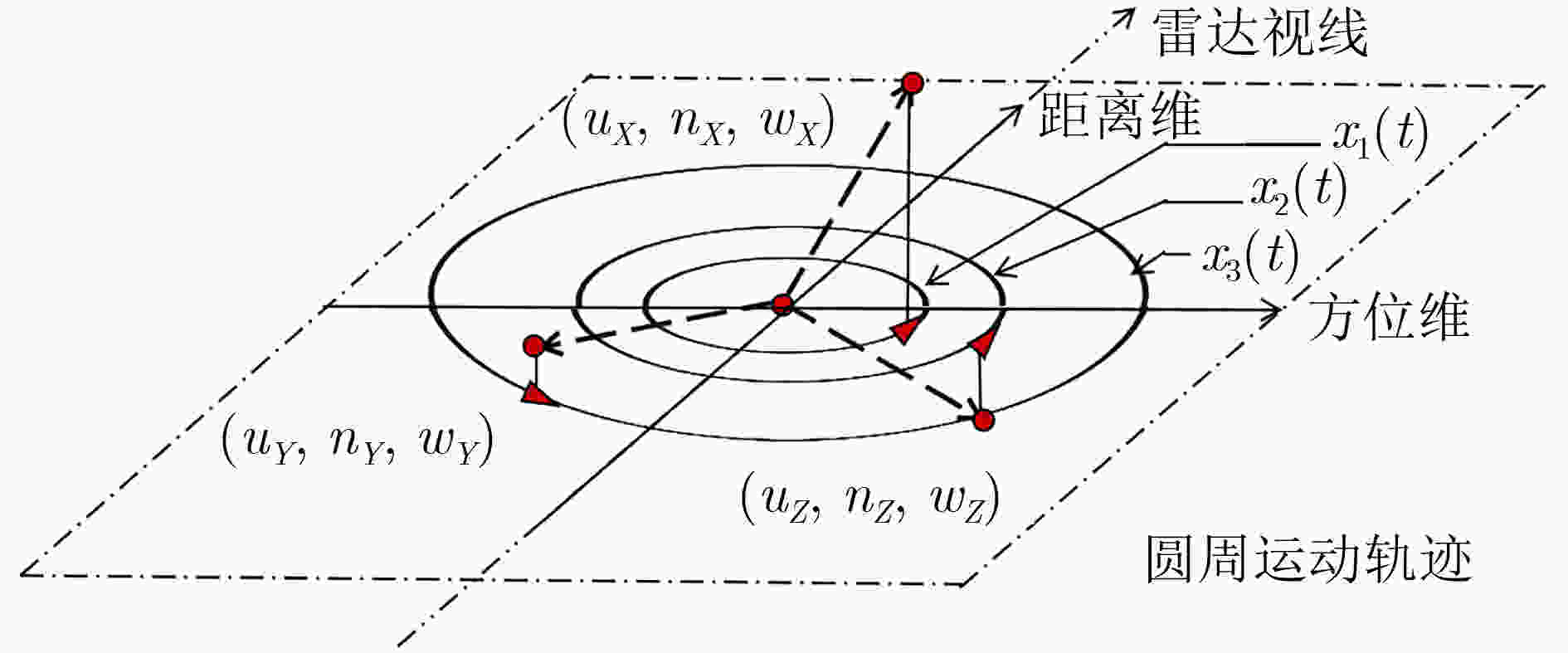
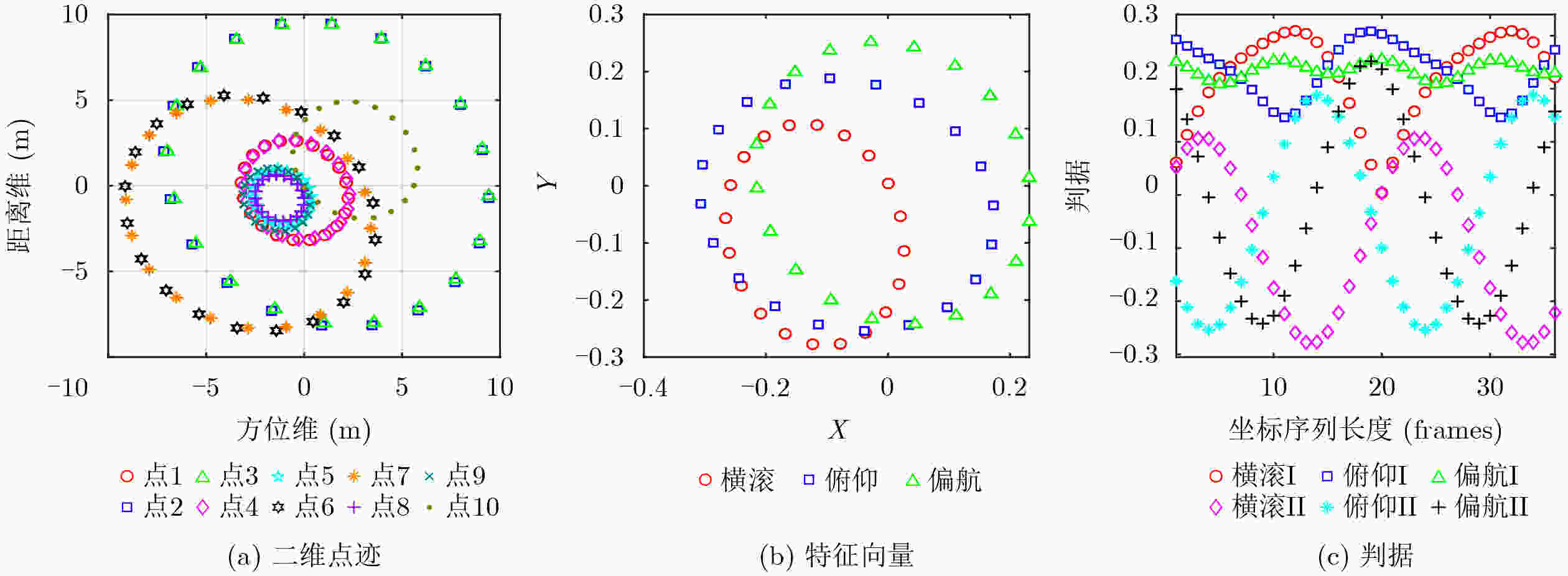
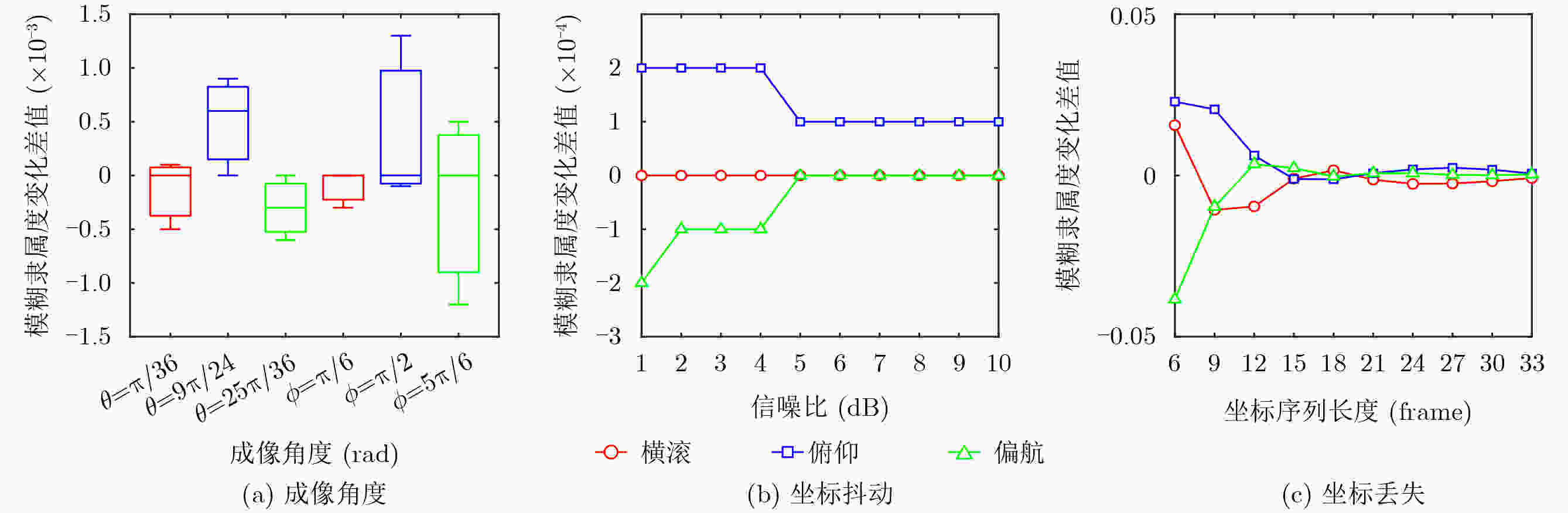
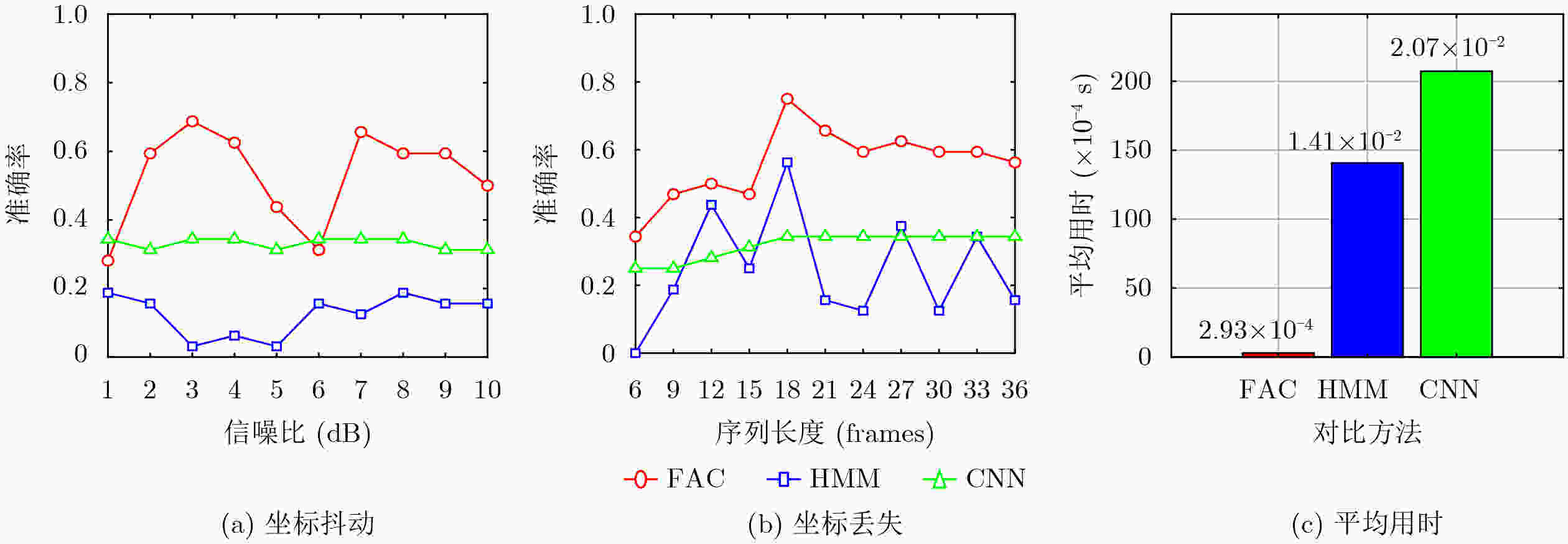
Objective With the intensification of space activities, Space Situational Awareness (SSA) is required to ensure national security and collision avoidance. A key task is the classification of space target attitudes to interpret states and predict behavior. Current approaches mainly rely on Ground-Based Inverse Synthetic Aperture Radar (GBISAR), which exhibit certain limitations. Model-driven methods rely on accurate prior models and involve high computational costs, while data-driven methods such as deep learning depend on large annotated datasets, which are difficult to obtain for space targets, and thus perform poorly in small-sample scenarios. To address this, a fuzzy attitude classification (FAC) method is proposed, which integrates temporal motion modeling with fuzzy set theory. The method is designed as a training-free and real-time classifier for rapid deployment under data-constrained conditions. Methods The method establishes a mapping between three-dimensional (3D) attitude dynamics and two-dimensional (2D) ISAR features through a framework combining the Horizon Coordinate System (HCS), the UNW orbital system, and the Body-Fixed Reference Frame (BFRF). Attitude changes are modeled as Euler rotations of BFRF relative to UNW. The periodic 3D rotation is projected onto the 2D Range-Doppler plane as circular keypoint trajectories. Fourier series analysis is then used to decompose the motion into one-dimensional (1D) cosine features, where phase encodes angular velocity and amplitude indicates motion magnitude. A 10-point annotation model is employed to represent targets, and dimensionless roll, pitch, and yaw feature vectors are derived. For classification, magnitude- and angle-based criteria are defined and processed by a softmax membership function, which incorporates variance across the sequence to compute fuzzy membership degrees. The algorithm operates directly on keypoint sequences, avoids training, and maintains linear computational complexity O(n), enabling real-time application. Results and Discussions The FAC method is evaluated on a Ku-band GBISAR simulated dataset of a spinning target. The dataset consists of 36 sequences, each with 36 frames of 512×512 images, devided as reference set as well as testing set. While raw keypoint tracks appear disordered ( Fig. 4(a) ), the engineered features form clustered patterns (Fig. 4(b) ). The variance of the criteria effectively represents motion significance (Fig. 4(c) ). Robustness is demonstrated: across nine imaging angles, classification consistency remains 100% within a 0.04 tolerance (Fig. 5(a) ). Under noise, consistency is preserved from 10 dB to 1 dB SNR (Fig. 5(b) ). With frame loss, 90% consistency is sustained at a 0.1 threshold, with six frames being the minimum for effective classification (Fig. 5(c) ). Benchmark comparisons show that FAC outperforms HMM and CNN, maintaining accuracy under noise (Fig. 6(a) ), stability under frame loss where HMM degrades to random behavior (Fig. 6(b) ), and achieving much lower processing time than both HMM and CNN (Fig. 6(c) ).Conclusions A fuzzy attitude classification method combining motion modeling and fuzzy reasoning is presented for small-sample space target classification. By mapping multi-coordinate kinematics into interpretable cosine features, the method reduces dependence on prior models and large datasets, while achieving training-free, linear-time operation. Simulations verify robustness across observation angles, SNR levels, and frame availability. Benchmark results confirm superior accuracy, stability, and efficiency compared with HMM and CNN. The FAC method therefore provides a practical solution for real-time, small-sample attitude classification. Future work will extend the framework to multi-axis tumbling and validation using measured data, with potential integration of multi-modal observations to further enhance adaptability. -
表 1 特征向量定义(-)
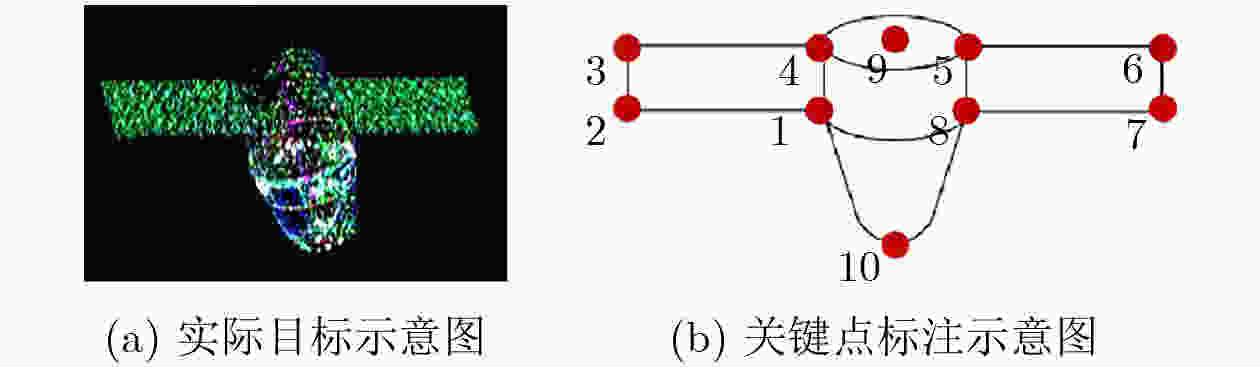
序号 命名 符号 定义 1 等多普勒线特征向量 $ {{\boldsymbol{c}}_2} $ $ (0,1) $ 2 横滚特征向量 $ {{\boldsymbol{c}}_1} $ $ \dfrac{{{p_9} - {p_{10}}}}{{\left\| {{p_9} - {p_{10}}} \right\|}} $ 3 俯仰特征向量 $ {{\boldsymbol{c}}_3} $ $ \dfrac{{{p_6} - {p_3}}}{{\left\| {{p_6} - {p_3}} \right\|}} $ 4 偏航特征向量 $ {{\boldsymbol{c}}_4} $ $ \dfrac{{{{\boldsymbol{c}}_2} \times {{\boldsymbol{c}}_3}}}{{\left\| {{{\boldsymbol{c}}_2} \times {{\boldsymbol{c}}_3}} \right\|}} $ 
下载: 导出CSV
表 2 判据定义(-)
序号 判据命名 设计特点 定义 1 横滚I 基于模值 $ \left\| {{{\boldsymbol{c}}_2}} \right\| $ 2 俯仰I 基于模值 $ \left\| {{{\boldsymbol{c}}_3}} \right\| $ 3 偏航I 基于模值 $ \left\| {{{\boldsymbol{c}}_4}} \right\| $ 4 横滚II 基于角度 $ {{\boldsymbol{c}}_1} \cdot {{\boldsymbol{c}}_2} $ 5 俯仰II 基于角度 $ {{\boldsymbol{c}}_1} \cdot {{\boldsymbol{c}}_3} $ 6 偏航II 基于角度 $ {{\boldsymbol{c}}_1} \cdot {{\boldsymbol{c}}_4} $
下载: 导出CSV
表 3 空间目标姿态模糊分类算法表
算法1：空间目标姿态模糊分类算法 输入：GBISAR空间目标关键点坐标序列$ {\boldsymbol{p}} $ 输出：空间目标姿态模糊分类结果$ A $ 1读取坐标$ {({\boldsymbol{x}},{\boldsymbol{y}},{\boldsymbol{z}})^T} $ 2显示空间目标二维点迹$ (r,d) $ 3计算特征向量$ {{\boldsymbol{c}}_i} $ 4展开特征空间 5计算判据 6计算模糊隶属度$ {\mu _A}(x) $ 7生成模糊集合$ A $
下载: 导出CSV
表 4 空间目标姿态分类方法横向对比
对比方面 模糊分类 反演还原 特征匹配 训练数据依赖性 无需训练 需训练 需训练 适合样本规模 小样本 中等样本 大规模数据库 适用环境复杂度 中 中 高 平均计算复杂度 $ o(n) $ $ o({n^3}) $ $ o({n^3}) $ 波动程度 低 高 低 分类粒度 精细 精细 粗略 目标自旋角速度 能估计 能估计 能估计 分类侧重 姿态类别 三维结构 目标型号 适用范围 仅地基 地基天基 地基天基
下载: 导出CSV
-
[1] ESA Space Debris Office. ESA’s space environment report 2022[R]. 2022. (查阅网上资料, 未找到本条文献报告编号信息, 请确认并补充). [2] JIA Qianlei, XIAO Jiaping, BAI Lu, et al. Space situational awareness systems: Bridging traditional methods and artificial intelligence[J]. Acta Astronautica, 2025, 228: 321–330. doi: 10.1016/j.actaastro.2024.11.025. [3] WALKER J L. Range-Doppler imaging of rotating objects[J]. IEEE Transactions on Aerospace and Electronic Systems, 1980, AES-16(1): 23–52. doi: 10.1109/TAES.1980.308875. [4] XU Gang, ZHANG Bangjie, CHEN Jianlai, et al. Sparse inverse synthetic aperture radar imaging using structured low-rank method[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5213712. doi: 10.1109/TGRS.2021.3118083. [5] ZHU Xiaoxiu, LIU Limin, GUO Baofeng, et al. Coherent compensation and high-resolution technology of multi-band inverse synthetic aperture radar fusion imaging[J]. IET Radar, Sonar & Navigation, 2021, 15(2): 167–180. doi: 10.1049/rsn2.12030. [6] 保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005: 244–291.BAO Zheng, XING Mengdao, and WANG Tong. Radar Imaging Technology[M]. Beijing: Publishing House of Electronics Industry, 2005: 244–291. (查阅网上资料, 未找到本条文献英文翻译, 请确认). [7] TAN Yunxin, LI Guangju, ZHANG Chun, et al. An efficient and accurate ground-based synthetic aperture radar (GB-SAR) real-time imaging scheme based on parallel processing mode and architecture[J]. Electronics, 2024, 13(16): 3138. doi: 10.3390/electronics13163138. [8] GOODMAN N A. Dynamic management of digital array resources for radar target tracking[C]. 2024 IEEE Wireless and Microwave Technology Conference (WAMICON), Clearwater, USA, 2024: 1–4. doi: 10.1109/WAMICON60123.2024.10522872. [9] 周叶剑. 基于ISAR序列成像的空间目标状态估计方法研究[D]. [博士论文], 西安电子科技大学, 2020. doi: 10.27389/d.cnki.gxadu.2020.003406.ZHOU Yejian. Study on state estimation techniques of space targets based on ISAR sequential imaging[D]. [Ph. D. dissertation], Xidian University, 2020. doi: 10.27389/d.cnki.gxadu.2020.003406. [10] ZHOU Yejian, WEI Shaopeng, ZHANG Lei, et al. Dynamic estimation of spin satellite from the single-station ISAR image sequence with the hidden Markov model[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(5): 4626–4638. doi: 10.1109/TAES.2022.3164015. [11] ZHANG Yunze, HE Yonghua, and LI Yonggang. Comparison of HRRP-based satellite target identification methods[C]. 2022 IEEE 6th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Beijing, China, 2022: 125–131. doi: 10.1109/IAEAC54830.2022.9929705. [12] LIN Hua, ZENG Chao, ZHANG Hai, et al. Motion parameter estimation of high-speed manoeuvering targets based on hybrid integration and synchrosqueezing transform[J]. IET Radar, Sonar & Navigation, 2022, 16(5): 852–868. doi: 10.1049/rsn2.12225. [13] 周叶剑, 马岩, 张磊, 等. 空间目标在轨状态雷达成像估计技术综述[J]. 雷达学报, 2021, 10(4): 607–621. doi: 10.12000/JR21086.ZHOU Yejian, MA Yan, ZHANG Lei, et al. Review of on-orbit state estimation of space targets with radar imagery[J]. Journal of Radars, 2021, 10(4): 607–621. doi: 10.12000/JR21086. [14] 谢朋飞. 空间目标序列成像的运动几何重建技术研究[D]. 中山大学, 2023. (查阅网上资料, 未找到本条文献信息, 请确认).XIE Pengfei. Research on motion geometric reconstruction technology of space target sequence imaging[D]. Sun Yat-sen University, 2023. [15] XUE Ruihang, BAI Xueru, CAO Xiangyong, et al. Sequential ISAR target classification based on hybrid transformer[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5111411. doi: 10.1109/TGRS.2022.3155246. [16] ZHOU Xuening, BAI Xueru, WANG Li, et al. Robust ISAR target recognition based on ADRISAR-Net[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(6): 5494–5505. doi: 10.1109/TAES.2022.3174826. [17] XUE Ruihang, BAI Xueru, and ZHOU Feng. SAISAR-Net: A robust sequential adjustment ISAR image classification network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5214715. doi: 10.1109/TGRS.2021.3113655. [18] YANG Hong, ZHANG Yasheng, and DING Wenzhe. Multiple heterogeneous P-DCNNs ensemble with stacking algorithm: A novel recognition method of space target ISAR images under the condition of small sample set[J]. IEEE Access, 2020, 8: 75543–75570. doi: 10.1109/ACCESS.2020.2989162. [19] ZHOU Xuening and BAI Xueru. Robust ISAR target recognition based on IC-STNs[C]. 2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 2019: 1–5. doi: 10.1109/APSAR46974.2019.9048576. [20] LI Xiaobo, YAN Lei, QI Pengfei, et al. Polarimetric imaging via deep learning: A review[J]. Remote Sensing, 2023, 15(6): 1540. doi: 10.3390/rs15061540. [21] VOROBEV A V and VOROBEVA G R. Web-based approach to transforming geocentric coordinate systems[J]. Geodesy and Cartography, 2024, 85(3): 30–41. doi: 10.22389/0016-7126-2024-1005-3-30-41. (查阅网上资料,请核对卷号信息). [22] 张炜, 张荣之, 王秀红, 等. 星链卫星碰撞威胁及预警策略研究[J]. 载人航天, 2022, 28(5): 606–612. doi: 10.3969/j.issn.1674-5825.2022.05.006.ZHANG Wei, ZHANG Rongzhi, WANG Xiuhong, et al. Analysis of collision threat and collision detection strategy of Starlink constellation[J]. Manned Spaceflight, 2022, 28(5): 606–612. doi: 10.3969/j.issn.1674-5825.2022.05.006. [23] 蔡立锋, 吴凌九, 张国云, 等. 航天器碰撞规避单脉冲切向控制最优策略[J]. 航天控制, 2023, 41(2): 10–16. doi: 10.3969/j.issn.1006-3242.2023.02.002.CAI Lifeng, WU Lingjiu, ZHANG Guoyun, et al. Optimal control strategy of spacecraft tangential collision avoidance with single pulse[J]. Aerospace Control, 2023, 41(2): 10–16. doi: 10.3969/j.issn.1006-3242.2023.02.002. [24] GULISTAN M and PEDRYCZ W. Introduction to q-fractional fuzzy set[J]. International Journal of Fuzzy Systems, 2024, 26(5): 1399–1416. doi: 10.1007/s40815-023-01633-8. [25] REZAEI A, TALAEIZADEH A, and ALASTY A. Comparing the performance of quaternion, rotation matrix, and Euler Angles based attitude PID controllers for quadrotors[C]. 2024 12th RSI International Conference on Robotics and Mechatronics (ICRoM), Tehran, Iran, 2024: 492–497. doi: 10.1109/ICRoM64545.2024.10903617. -
图(6) / 表(4)
计量
- 文章访问数: 46
- HTML全文浏览量: 25
- PDF下载量: 3
- 被引次数: 0
下载:
