High Area-efficiency Radix-4 Number Theoretic Transform Hardware Architecture with Conflict-free Memory Access Optimization for Lattice-based Cryptography
-
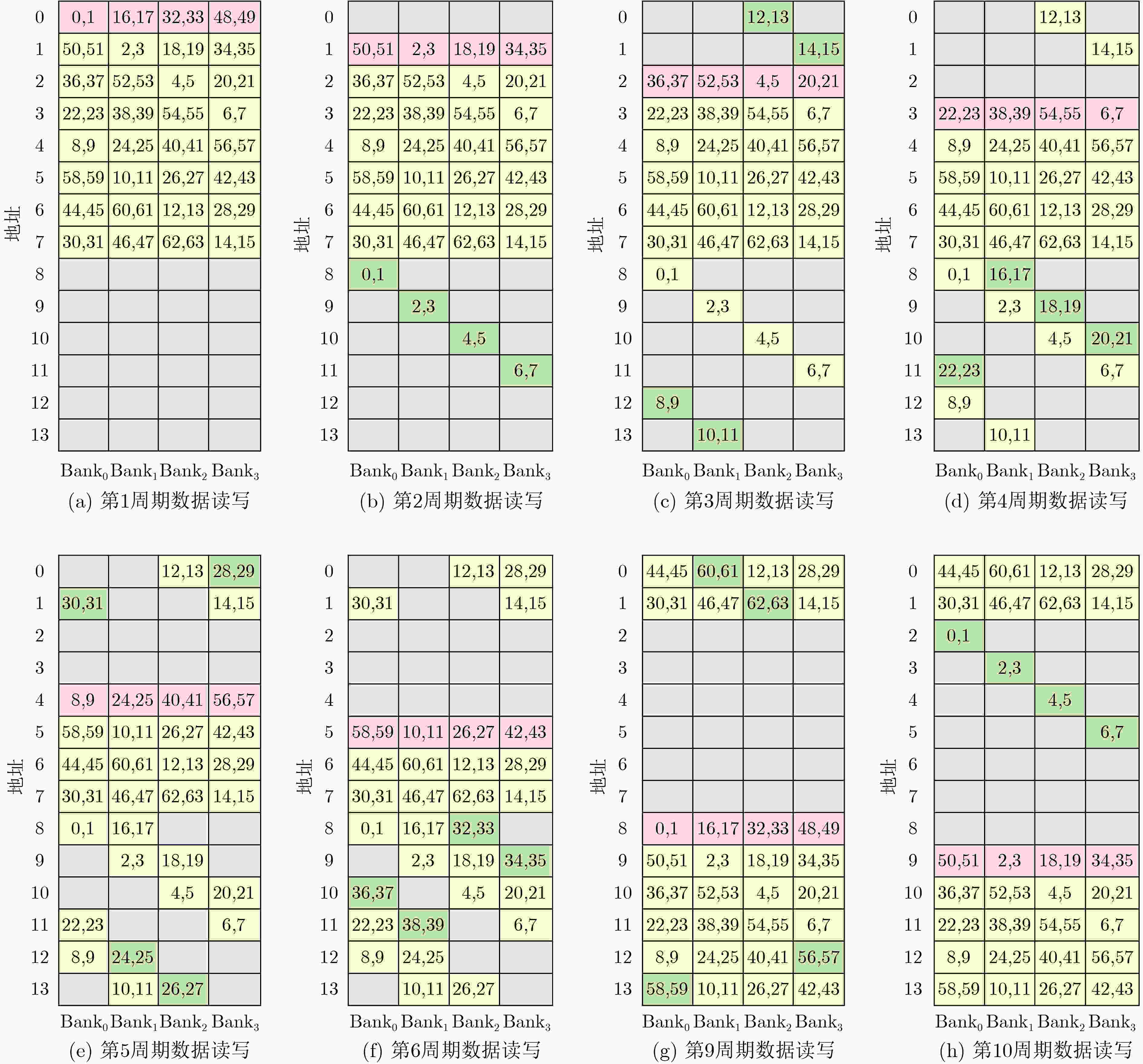
摘要: 针对格基后量子密码(PQC)算法中基-2数论变换(NTT)计算效率较低以及原位计算内存访问模式复杂的问题,该文提出一种高面积效率的基-4 NTT硬件设计。首先,介绍了负包裹卷积方法的运算流程及适用条件,在此基础上提出了一种恒定几何(CG)结构的低计算复杂度基-4 NTT/INTT算法。其次,深入分析不同PQC算法中模数的共性特征,设计了基于K2-RED约简的可扩展模乘单元。最后,通过优化存储器与蝶形单元之间的数据分解与重组,提出一种基于顺序循环和阶梯循环访存的读写地址生成方案,实现了高效的无访存冲突。与传统的乒乓存储模式相比,该方案可减少12.5%的存储空间。实验结果表明,在(项数,模数位宽)分别为(256, 13),(256, 23)和(
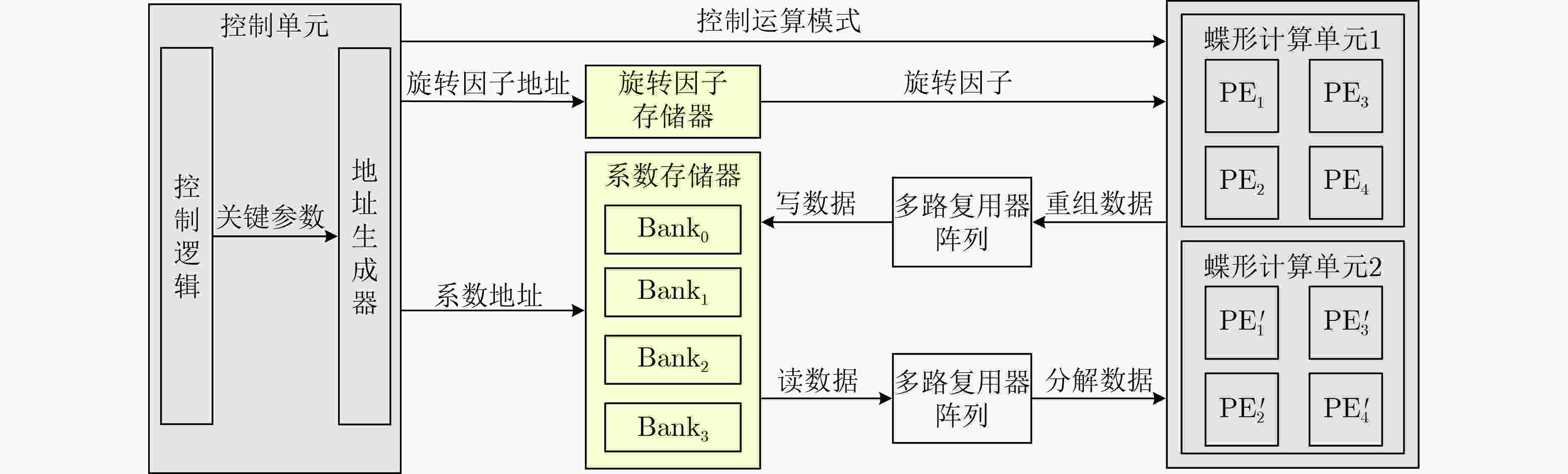
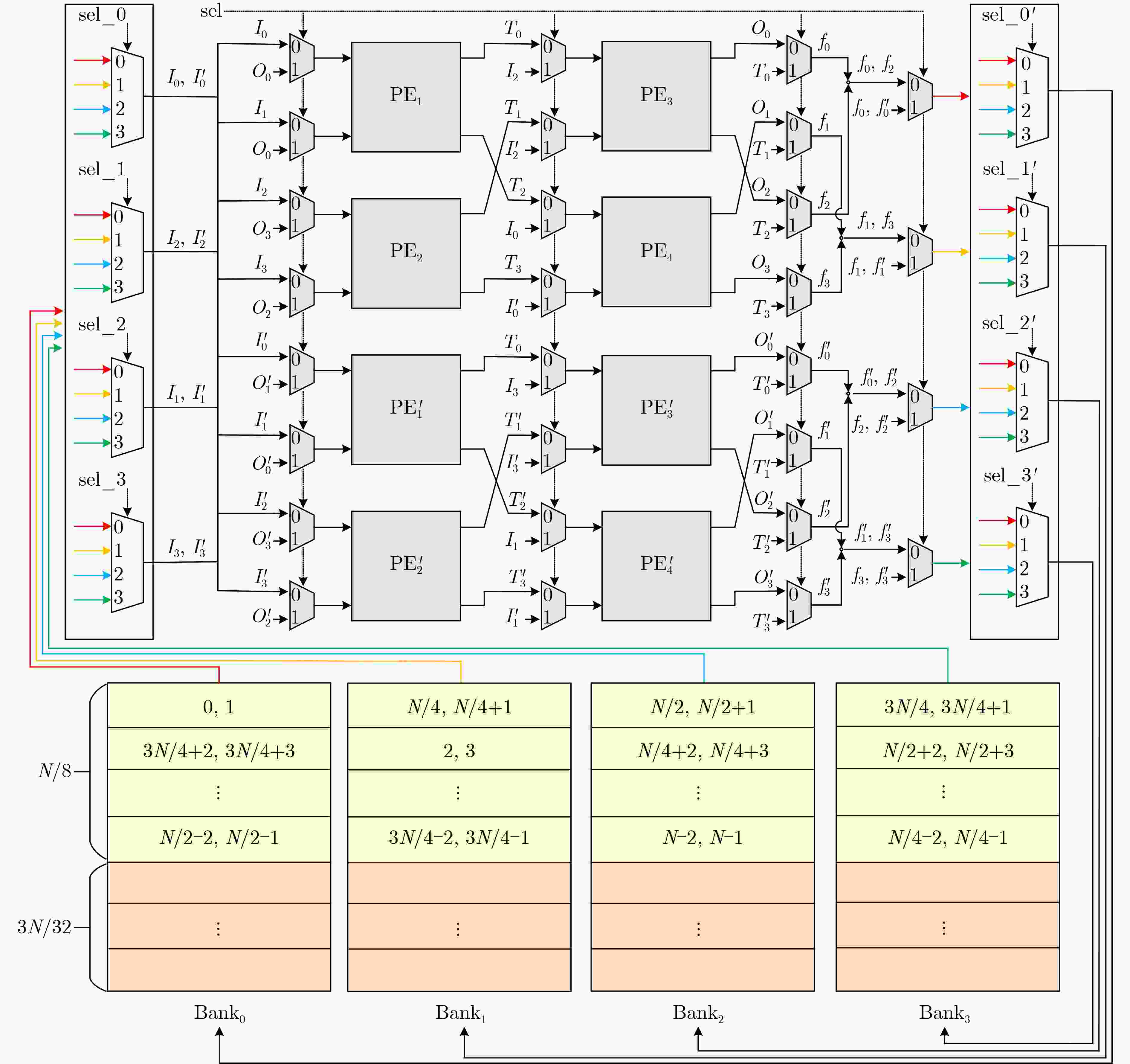
1024 , 14)的3种配置下,该设计的面积-时间积(ATP)较现有方案分别降低56.4%,69.8%和50.3%以上,具有更高的面积效率。Abstract:Objective The advancement of Post-Quantum Cryptography (PQC) standardization increases the demand for efficient Number Theoretic Transform (NTT) hardware modules. Existing high-radix NTT studies primarily optimize in-place computation and configurability, yet the performance is constrained by complex memory access behavior and a lack of designs tailored to the parameter characteristics of lattice-based schemes. To address these limitations, a high area-efficiency radix-4 NTT design with a Constant-Geometry (CG) structure is proposed. The modular multiplication unit is optimized through an analysis of common modulus properties and the integration of multi-level operations, while memory allocation and address-generation strategies are refined to reduce capacity requirements and improve data-access efficiency. The design supports out-of-place storage and achieves conflict-free memory access, providing an effective hardware solution for radix-4 CG NTT implementation. Methods At the algorithmic level, the proposed radix-4 CG NTT/INTT employs a low-complexity design and removes the bit-reversal step to reduce multiplication count and computation cycles, with a redesigned twiddle-factor access scheme. For the modular multiplication step, which is the most time-consuming stage in the radix-4 butterfly, the critical path is shortened by integrating the multiplication with the first-stage K−RED reduction and simplifying the correction logic. To support three parameter configurations, a scalable modular-multiplication method is developed through an analysis of the shared properties of the moduli. At the architectural level, two coefficients are concatenated and stored at the same memory address. A data-decomposition and reorganization scheme is designed to coordinate memory interaction with the dual-butterfly units efficiently. To achieve conflict-free memory access, a cyclic memory-reuse strategy is employed, and read and write address-generation schemes using sequential and stepped access patterns are designed, which reduces required memory capacity and lowers control-logic complexity. Results and Discussions Experimental results on Field Programmable Gate Arrays demonstrate that the proposed NTT architecture achieves high operating frequency and low resource consumption under three parameter configurations, together with notable improvement in the Area-Time Product (ATP) compared with existing designs ( Table 1 ). For the configuration with 256 terms and a modulus of 7 681, the design uses 2 397 slices, 4 BRAMs, and 16 DSPs, achieves an operating frequency of 363 MHz, and yields at least a 56.4% improvement in ATP. For the configuration with 256 terms and a modulus of 8 380 417, it uses 3 760 slices, 6 BRAMs, and 16 DSPs, achieves an operating frequency of 338 MHz, and yields at least a 69.8% improvement in ATP. For the configuration with 1 024 terms and a modulus of 12 289, it uses 2 379 slices, 4 BRAMs, and 16 DSPs, achieves an operating frequency of 357 MHz, and yields at least a 50.3% improvement in ATP.Conclusions A high area-efficiency radix-4 NTT hardware architecture for lattice-based PQC is proposed. The use of a low-complexity radix-4 CG NTT/INTT and the removal of the bit-reversal step reduce latency. Through an analysis of shared characteristics among three moduli and the merging of partial computations, a scalable modular-multiplication architecture based on K²−RED reduction is designed. The challenges of increased storage requirements and complex address-generation logic are addressed by reusing memory efficiently and designing sequential and stepped address-generation schemes. Experimental results show that the proposed design increases operating frequency and reduces resource consumption, yielding lower ATP under all three parameter configurations. As the present work focuses on a dual-butterfly architecture, future research may examine higher-parallelism designs to meet broader performance requirements. -
1 基-4 CG NTT算法
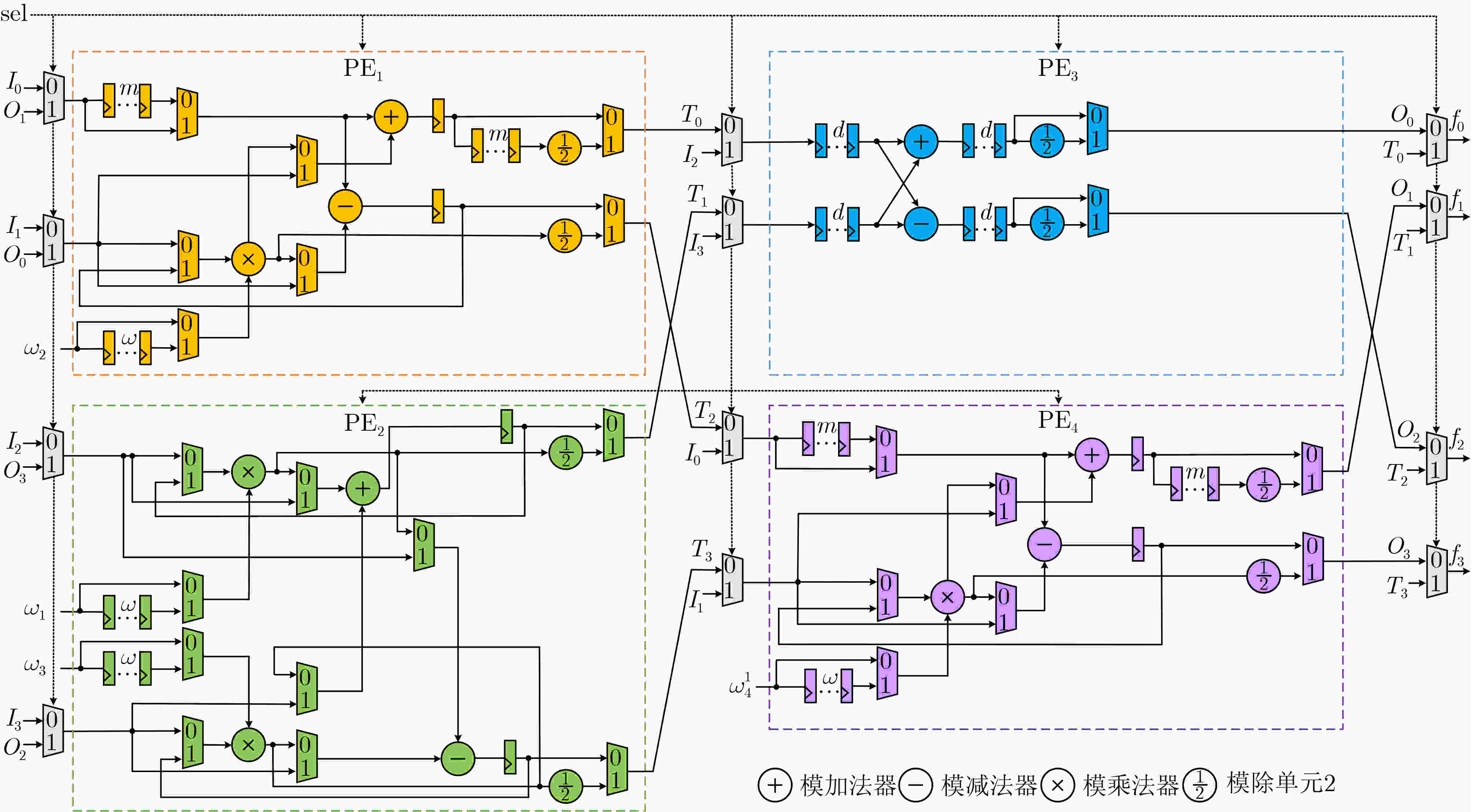
输入:$ \mathrm{ } $$a(x) \in {R_p}$,${\varphi _{2N}} \in {\mathbb{Z}_p}$,$\omega _4^1$ 输出:$ A(x)=\mathrm{NTT}(a(x)) $ (a)存储预计算的旋转因子 1. for $s = 1$ to ${\log _4}N$ do 2. $l = N{\text{/}}{4^s}$ 3. ${\omega _m} = \varphi _{2N}^l$ 4. for $j = 0$ to ${4^{s - 1}} - 1$ do 5. ROM_1.append$ [\omega _m^{2{\text{bit}} - {\text{reversed(}}j) + 1}] $ 6. ROM_2.append$[\omega _m^{2 \cdot (2{\text{bit}} - {\text{reversed(}}j) + 1)}]$ 7. ROM_3.append$[\omega _m^{3 \cdot (2{\text{bit}} - {\text{reversed(}}j) + 1)}]$ 8. end for 9. end for (b)基-4 CG NTT运算 1. for $s = 1$ to ${\log _4}N$ do 2. for $i = 0$ to $N{\text{/}}4 - 1$ do 3. ${r^{'}} = i{\rm{mod}} {4^{s - 1}}$ 4. $r = {\text{convert(}}{r^{'}}) + ({4^{s - 1}} - 1)/3$ 5. ${\omega _1} = {\text{ROM\_1[}}r{\text{]}}$ 6. ${\omega _2} = {\text{ROM}}\_2[r]$ 7. ${\omega _3} = {\text{ROM\_3[}}r{\text{]}}$ 8. ${T_0} = (a[i] + a[i + 2N/4] \cdot {\omega _2}){\rm{mod}} p$ 9. ${T_1} = (a[i] - a[i + 2N/4] \cdot {\omega _2}){\rm{mod}} p$ 10. ${T_2} = (a[i + N/4] \cdot {\omega _1} + a[i + 3N/4] \cdot {\omega _3}){\rm{mod}} p$ 11. ${T_3} = (a[i + N/4] \cdot {\omega _1} - a[i + 3N/4] \cdot {\omega _3}){\rm{mod}} p$ 12. $A[4i] = ({T_0} + {T_2}){\rm{mod}} p$ 13. $A[4i + 1] = ({T_1} + {T_3} \cdot \omega _4^1){\rm{mod}} p$ 14. $A[4i + 2] = ({T_0} - {T_2}){\rm{mod}} p$ 15. $A[4i + 3] = ({T_1} - {T_3} \cdot \omega _4^1){\rm{mod}} p$ 16. end for 17.end for 2 基-4 CG INTT算法
输入:$ \mathrm{ } $$A(x) \in {R_P}$,${\varphi _{2N}} \in {\mathbb{Z}_p}$,$\omega _4^1$ 输出:$ a(x)=\mathrm{INTT}(A(x)) $ 1. for $s = {\log _4}N$ to 1 do 2. for $i = 0$ to $N{\text{/}}4 - 1$ do 3. ${i^{'}} = N{\text{/}}4 - 1 - i$ 4. ${r^{'}} = {i^{'}}{\rm{mod}} {4^{s - 1}}$ 5. $r = {\text{convert(}}{r^{'}}) + ({4^{s - 1}} - 1)/3$ 6. ${\omega _1} = {\text{ROM\_1}}[r]$ 7. ${\omega _2} = {\text{ROM\_2[}}r]$ 8. ${\omega _3} = {\text{ROM\_3}}[r]$ 9. ${T_0} = {2^{ - 1}} \cdot (A[4i] + A[4i + 2]){\rm{mod}} p$ 10. $ T_1=2^{-1}\cdot(A[4i+2]-A[4i])\cdot\omega_4^1\rm{mod}p $ 11. ${T_2} = {2^{ - 1}} \cdot (A[4i + 1] + A[4i + 3]){\rm{mod}} p$ 12. ${T_3} = {2^{ - 1}} \cdot (A[4i + 3] - A[4i + 1]){\rm{mod}} p$ 13. $a[i] = {2^{ - 1}} \cdot ({T_0} + {T_2}){\rm{mod}} p$ 14. $a[i + N/4] = {2^{ - 1}} \cdot ({T_1} + {T_3}) \cdot {\omega _1}{\rm{mod}} p$ 15. $a[i + 2N/4] = {2^{ - 1}} \cdot ({T_2} - {T_0}) \cdot {\omega _2}{\rm{mod}} p$ 16. $a[i + 3N/4] = {2^{ - 1}} \cdot ({T_3} - {T_1}) \cdot {\omega _3}{\rm{mod}} p$ 17. end for 18.end for 3 K2-RED约简算法
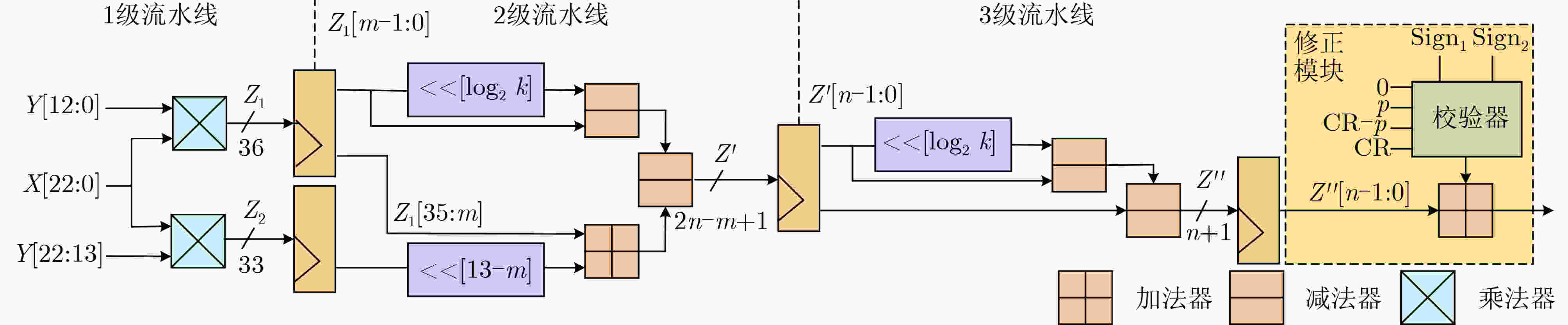
输入:$Z \in [0,{p^2})$, $p = k \cdot {2^m} + 1$, $n = \left\lfloor {{{\log }_2}p} \right\rfloor $ 输出:${Z^{''}} = {k^2} \cdot Z{\rm{mod}} p$ 1: ${Z_l} = Z[m - 1:0]$ $ {{Z}}_{\mathrm{l}}={Z}\mathrm{ }\left(\mathrm{m}\mathrm{o}\mathrm{d}{2}^{{m}}\right) $ 2: ${Z_h} = Z[2n - 1:m]$ 3: ${Z^{'}} = k{Z_l} - {Z_h}$ 4: ${Z_l}^{'} = {Z^{'}}[m - 1:0]$ 5: ${Z_h}^{'} = {Z^{'}}[2n - m - 1:m]$ 6: ${Z^{''}} = k{Z_l}^{'} - {Z_h}^{'}$ 7: return ${Z^{''}}$ 表 1 格基PQC方案中模乘核心步骤的定量比较
Kyber v1算法 Dilithium算法 Falcon算法 $(m,k,n)$ (9,15,13) (13, 1023 ,23)(12,3,14) 2阶段K-RED约简 ${Z^{'}} = ({Z_l} \lt \lt 4) - {Z_l} - {Z_h}$
${Z^{''}} = (Z_l^{\prime} \lt \lt 4) - Z_l^{\prime} - Z_h^{\prime}$${Z^{'}} = ({Z_l} \lt \lt 10) - {Z_l} - {Z_h}$
${Z^{''}} = (Z_l^{\prime} \lt \lt 10) - Z_l^{\prime} - Z_h^{\prime}$${Z^{'}} = ({Z_l} \lt \lt 2) - {Z_l} - {Z_h}$
${Z^{''}} = (Z_l^{\prime} \lt \lt 2) - Z_l^{\prime} - Z_h^{\prime}$修正值 ${\text{Sig}}{{\text{n}}_1}{\text{Sig}}{{\text{n}}_2} = 01$ 7 681 8380417 12289 ${\text{Sig}}{{\text{n}}_1}{\text{Sig}}{{\text{n}}_2} = 10$① – 7425 – 7331841 – 12273 ${\text{Sig}}{{\text{n}}_1}{\text{Sig}}{{\text{n}}_2} = 10$② 256 1048576 16 ${\text{Sig}}{{\text{n}}_1}{\text{Sig}}{{\text{n}}_2} = 11$ 表 2 时间性能及资源消耗对比
(N,l) 方案 平台 周期 频率(MHz) 时延(μs) 资源消耗(LUT/FF/BRAM/DSP) ATP(×103) (256,13) 文献[7] Virtex-7 151 329 0.5 2800 2500 20 24 5.6 文献[9] Virtex-7 160 125 1.28 2371 - 12 24 10.71 文献[22] Virtex-7 135 256 0.5 6245 1 864 12 24 6.12 文献[23] Virtex-7 91 195 0.47 14758 8745 24 64 13.33 本文 Virtex-7 172 363 0.47 2397 1 904 4 16 2.44 (256,23) 文献[9] Virtex-7 200 125 1.6 5071 - 12 56 22.83 文献[21] UltraScale 156 220 0.71 11006 8791 12 24 12.07 文献[23] Virtex-7 107 195 0.55 14758 8745 24 64 15.60 本文 Virtex-7 172 338 0.51 3760 3331 6 16 3.65 ( 1024 ,14)文献[7] Virtex-7 649 307 2.1 2900 2600 20 24 23.73 文献[8] Virtex-7 668 250 2.7 2953 1 875 5.5 27 19.72 文献[9] Virtex-7 680 125 5.4 2584 - 16 24 52.83 文献[16] Virtex-7 650 292 2.22 3400 2300 12 16 19.09 文献[22] Virtex-7 654 179 3.7 3472 1789 7.5 25 30.42 文献[23] Virtex-7 343 225 1.52 12836 7213 28 64 42.01 本文 Virtex-7 654 357 1.83 2379 2219 4 16 9.48 -
[1] SHOR P W. Algorithms for quantum computation: Discrete logarithms and factoring[C]. The 35th Annual Symposium on Foundations of Computer Science, Santa Fe, USA, 1994: 124–134. doi: 10.1109/SFCS.1994.365700. [2] MOODY D. Post-quantum cryptography: NIST’s plan for the future[C]. The Seventh International Conference on Post-Quntum Cryptography, Fukuoka, Japan, 2016. [3] GUO Wenbo and LI Shuguo. Split-radix based compact hardware architecture for CRYSTALS-Kyber[J]. IEEE Transactions on Computers, 2024, 73(1): 97–108. doi: 10.1109/TC.2023.3320040. [4] LI Guangyan, CHEN Donglong, MAO Gaoyu, et al. Algorithm-hardware co-design of split-radix discrete Galois transformation for KyberKEM[J]. IEEE Transactions on Emerging Topics in Computing, 2023, 11(4): 824–838. doi: 10.1109/TETC.2023.3270971. [5] ZHANG Neng, YANG Bohan, CHEN Chen, et al. Highly efficient architecture of NewHope-NIST on FPGA using low-complexity NTT/INTT[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2020, 2020(2): 49–72. doi: 10.13154/tches.v2020.i2.49-72. [6] XING Yufei and LI Shuguo. A compact hardware implementation of CCA-secure key exchange mechanism CRYSTALS-Kyber on FPGA[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2021, 2021(2): 328–356. doi: 10.46586/tches.v2021.i2.328-356. [7] LIU Sihuang, KUO C Y, MO Yannan, et al. An area-efficient, conflict-free, and configurable architecture for accelerating NTT/INTT[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2024, 32(3): 519–529. doi: 10.1109/TVLSI.2023.3336951. [8] CHEN Xiangren, YANG Bohan, YIN Shouyi, et al. CFNTT: Scalable radix-2/4 NTT multiplication architecture with an efficient conflict-free memory mapping scheme[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2021, 2022(1): 94–126. doi: 10.46586/tches.v2022.i1.94-126. [9] MERT A C, KARABULUT E, ÖZTÜRK E, et al. An extensive study of flexible design methods for the number theoretic transform[J]. IEEE Transactions on Computers, 2022, 71(11): 2829–2843. doi: 10.1109/TC.2020.3017930. [10] ZHAO Yanrui, LIU Xiaofan, HU Yue, et al. Design of an efficient NTT/INTT architecture with low-complex memory mapping scheme[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2024, 71(1): 400–404. doi: 10.1109/TCSII.2023.3296492. [11] 付秋兴, 李伟, 别梦妮, 等. 格基后量子密码的可重构NTT运算单元与高效调度算法研究[J]. 电子学报, 2025, 53(4): 1182–1191. doi: 10.12263/DZXB.20240788.FU Qiuxing, LI Wei, BIE Mengni, et al. Research on reconfigurable NTT arithmetic unit and efficient scheduling algorithm for lattice post-quantum cryptography[J]. Acta Electronica Sinica, 2025, 53(4): 1182–1191. doi: 10.12263/DZXB.20240788. [12] BANERJEE U, UKYAB T S, and CHANDRAKASAN A P. Sapphire: A configurable crypto-processor for post-quantum lattice-based protocols[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2019, 2019(4): 17–61. doi: 10.13154/tches.v2019.i4.17-61. [13] SU Yang, YANG Bailong, YANG Chen, et al. A highly unified reconfigurable multicore architecture to speed up NTT/INTT for homomorphic polynomial multiplication[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2022, 30(8): 993–1006. doi: 10.1109/TVLSI.2022.3166355. [14] WANG Jianfei, YANG Chen, MENG Yishuo, et al. A reconfigurable and area-efficient polynomial multiplier using a novel in-place constant-geometry NTT/INTT and conflict-free memory mapping scheme[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2025, 72(3): 1358–1371. doi: 10.1109/TCSI.2024.3483229. [15] SUN Junyan and BAI Xuefei. A high-speed hardware architecture of an NTT accelerator for CRYSTALS-Kyber[J]. Integrated Circuits and Systems, 2024, 1(2): 92–102. doi: 10.23919/ICS.2024.3419562. [16] GENG Yue, HU Xiao, LI Minghao, et al. Rethinking parallel memory access pattern in number theoretic transform design[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2023, 70(5): 1689–1693. doi: 10.1109/TCSII.2023.3260811. [17] ALHASSANI A and BENAISSA M. High-speed polynomials multiplication HW accelerator for CRYSTALS-Kyber[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2024, 71(12): 6105–6113. doi: 10.1109/TCSI.2024.3427011. [18] AIKATA A, MERT A C, IMRAN M, et al. KaLi: A crystal for post-quantum security using Kyber and Dilithium[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2023, 70(2): 747–758. doi: 10.1109/TCSI.2022.3219555. [19] HU Xiao, TIAN Jing, LI Minghao, et al. AC-PM: An area-efficient and configurable polynomial multiplier for lattice based cryptography[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2023, 70(2): 719–732. doi: 10.1109/TCSI.2022.3218192. [20] BISHEH-NIASAR M, AZARDERAKHSH R, and MOZAFFARI-KERMANI M. High-speed NTT-based polynomial multiplication accelerator for post-quantum cryptography[C]. 2021 IEEE 28th Symposium on Computer Arithmetic (ARITH), Lyngby, Denmark, 2021: 94–101. doi: 10.1109/ARITH51176.2021.00028. [21] LI Bin, YAN Yunfei, WEI Yuanxin, et al. Scalable and parallel optimization of the number theoretic transform based on FPGA[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2024, 32(2): 291–304. doi: 10.1109/TVLSI.2023.3312423. [22] MU Jianan, REN Yi, WANG Wen, et al. Scalable and conflict-free NTT hardware accelerator design: Methodology, proof, and implementation[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2023, 42(5): 1504–1517. doi: 10.1109/TCAD.2022.3205552. [23] 周清雷, 韩贺茹, 李斌, 等. 面向格密码的可配置基-4 NTT硬件优化与实现[J]. 通信学报, 2024, 45(10): 163–179. doi: 10.11959/j.issn.1000-436x.2024188.ZHOU Qinglei, HAN Heru, LI Bin, et al. Configurable radix-4 NTT hardware optimization and implementation for lattice-based cryptography[J]. Journal on Communications, 2024, 45(10): 163–179. doi: 10.11959/j.issn.1000-436x.2024188. -





 下载:
下载:


 下载:
下载:
