局部有源忆阻器电路的类生物神经网络存算研究

李付鹏; 王光义; 刘敬彪; 应佳捷

doi:10.11999/JEIT250631

局部有源忆阻器电路的类生物神经网络存算研究

doi: 10.11999/JEIT250631 cstr: 32379.14.JEIT250631

1.
杭州电子科技大学电子信息学院杭州 30018
2.
南京师范大学计算机与人工智能学院南京 210016

基金项目: 国家自然科学基金(61771176, 61801154)

详细信息

作者简介:
李付鹏：男，博士生，研究方向为忆阻器振荡电路、混沌密码理论及应用

王光义：男，教授，研究方向为新型纳米记忆器件理论及应用，混沌密码、信息加密与保密通信

刘敬彪：男，教授，研究方向为海洋探测、海底视频监控、电能与数据信息混合传输

应佳捷：女，讲师，研究方向为忆阻混沌动力学、忆阻神经元及神经形态机理和忆阻神经网络

通讯作者:
王光义　wanggy@163.com

中图分类号: TP301.1
计量
- 文章访问数: 53
- HTML全文浏览量: 11
- PDF下载量: 5
- 被引次数: 0
出版历程
- 收稿日期: 2025-07-04
- 修回日期: 2025-11-03
- 录用日期: 2025-11-03
- 网络出版日期: 2025-11-12

The Storage and Calculation of Biological-like Neural Networks for Locally Active Memristor Circuits

1.
School of Electronics and Information Engineering, Hangzhou Dianzi University, Hangzhou 310018, China
2.
School of Computer and Electronic Information/School of Artificial Intelligence, Nanjing Normal University, Nanjing 210016, China

Funds: The National Natural Science Foundation of China(61771176, 61801154)

摘要

摘要: 生物神经系统在低功耗计算、动态存储方面具有显著的优势，这与神经元通过定向分泌递质来传递神经信号的工作机制密切相关。神经信号的产生涉及刺激信号的放大和运算，其工作机制可以利用忆阻器容控混沌振荡器实现。本文利用局部有源忆阻器随外接电容改变形成稳定的倍周期分叉的电压信号振荡，获得了电路中电容与忆阻器两端电压信号之间稳定的映射关系，电路中电容的改变使得忆阻器两端串行输出不同形态的电信号，其电压幅值稳定的周期改变。使得改变的电容与输出的电压信号之间形成稳定的多状态映射关系，从而构成存算单元。结合蔡氏结型忆阻器模型建立了三阶忆阻器电路，当忆阻器工作在局部有源区其三阶电路构成的振荡器能够同时完成信号放大、运算和存储。
- 局部有源 /
- 忆阻器 /
- 混沌 /
- 神经网络
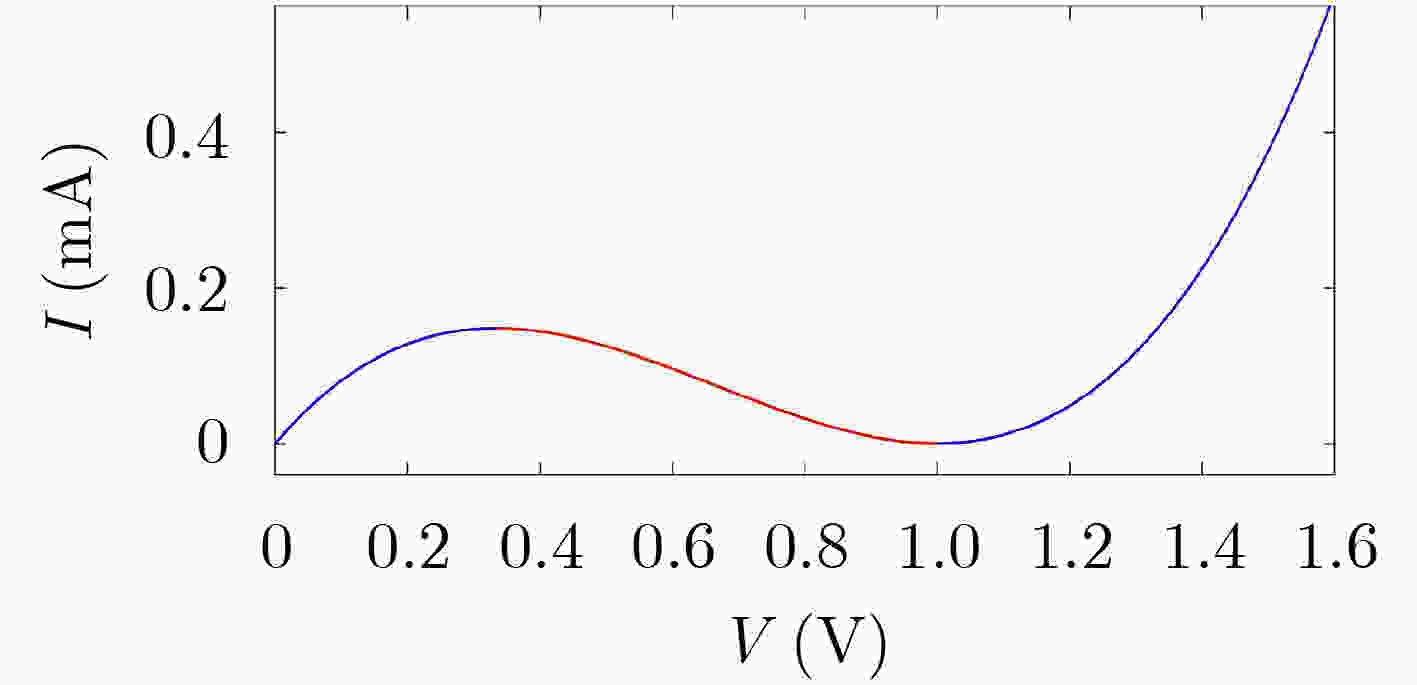
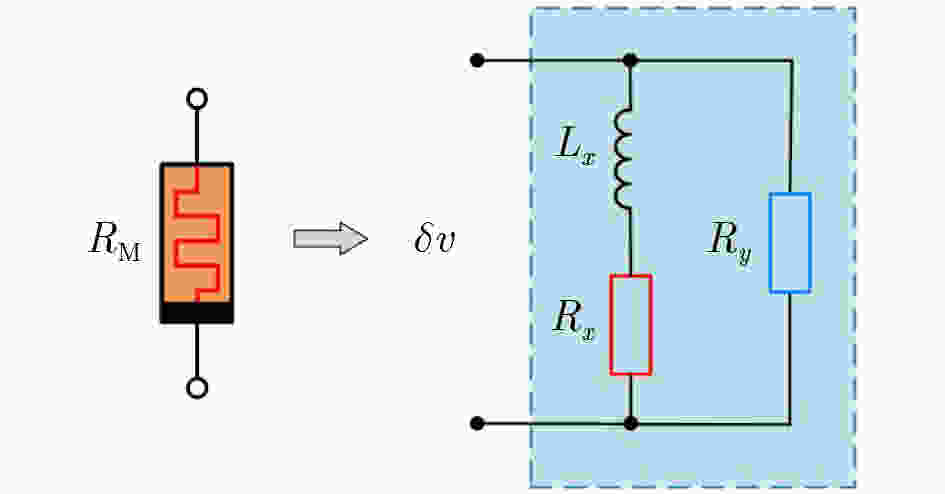
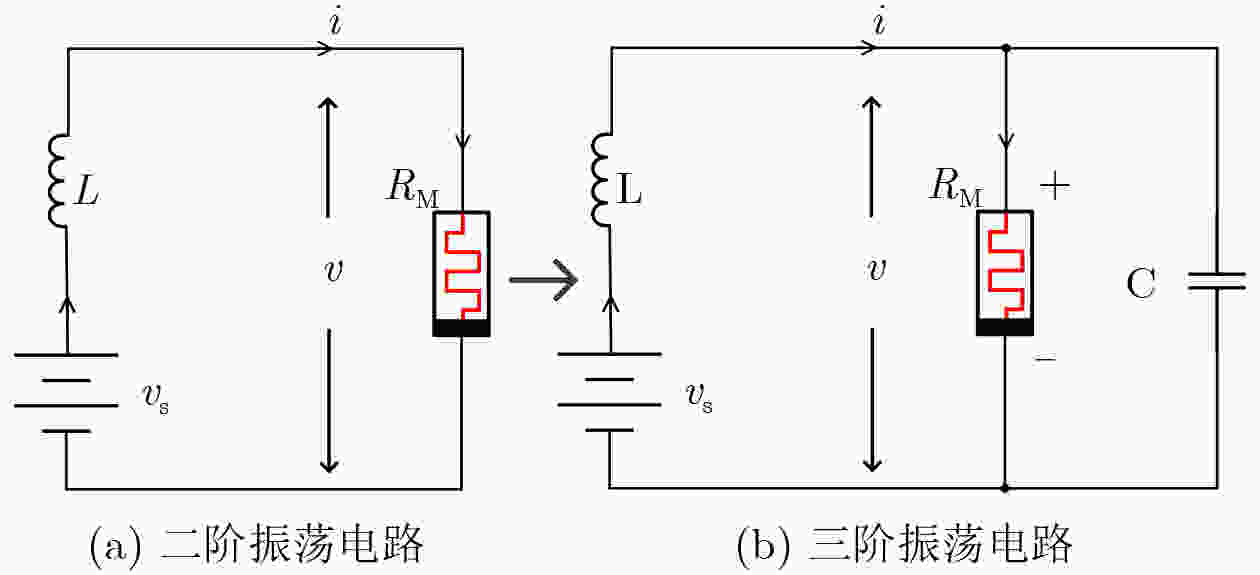
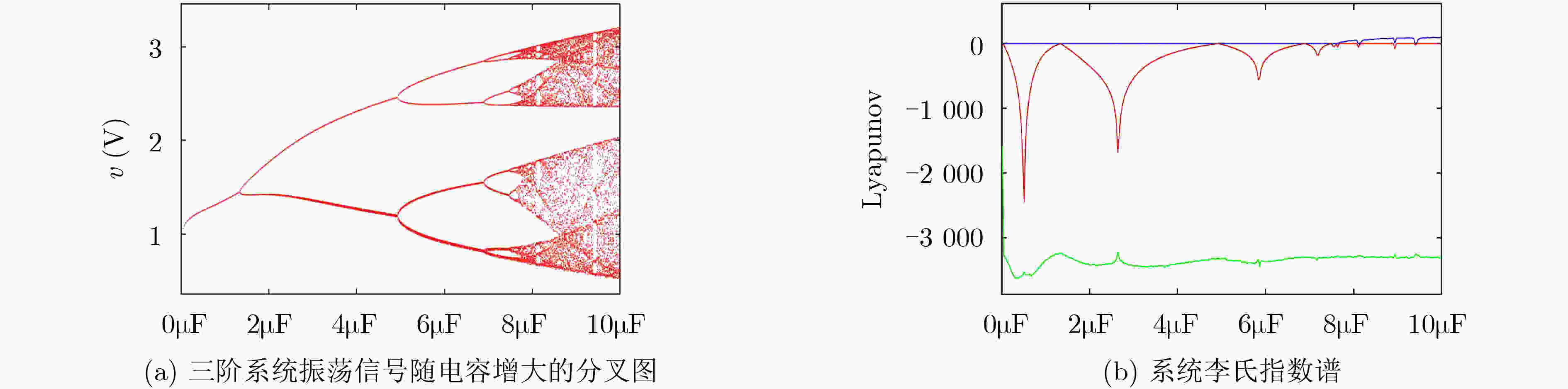
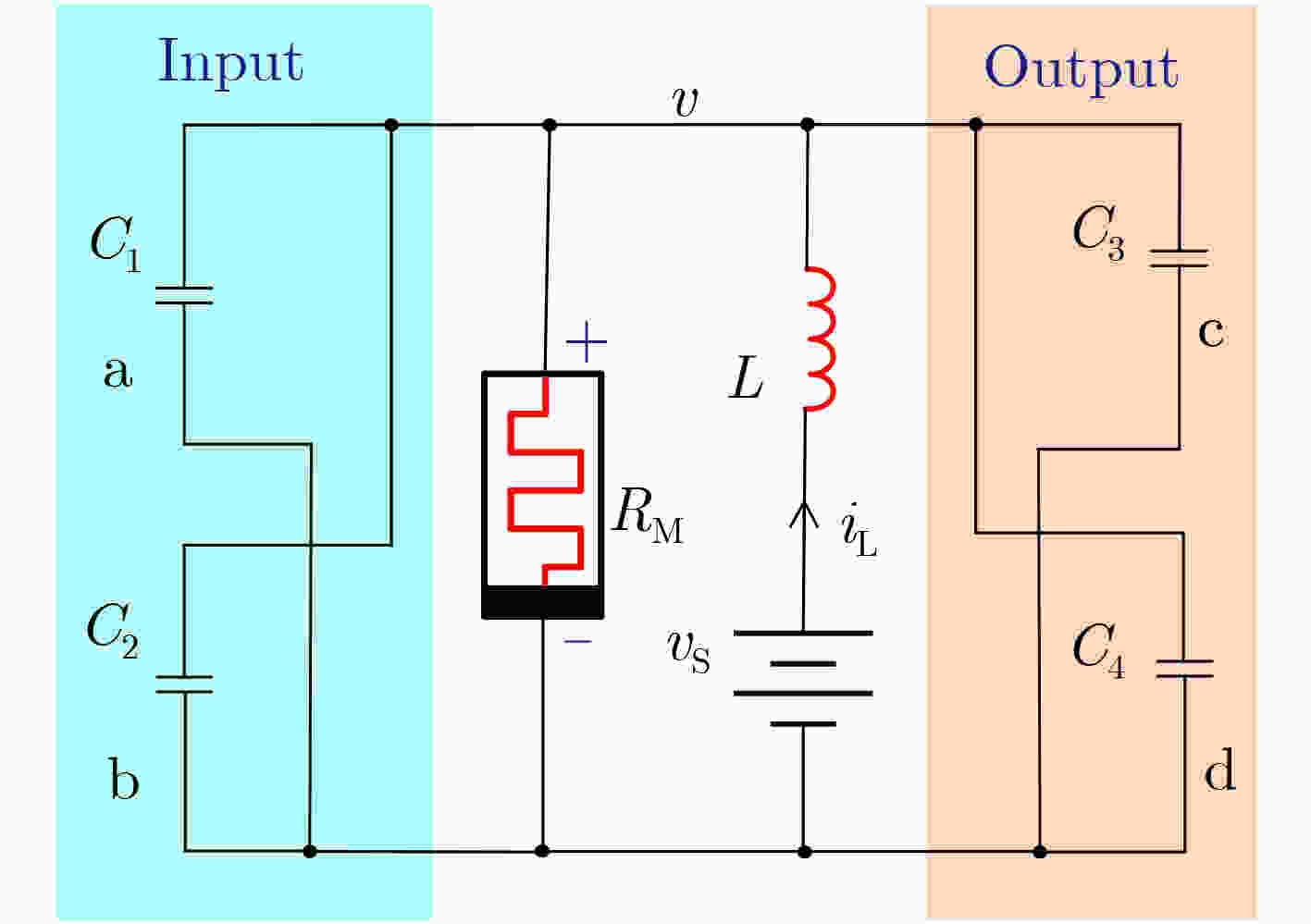
Abstract: Objective At present, binary computing systems have encountered bottlenecks in terms of power consumption, operation speed and storage capacity. In contrast, the biological nervous system seems to have unlimited capacity. The biological nervous system has significant advantages in low-power computing and dynamic storage capability, which is closely related to the working mechanism of neurons transmitting neural signals through directional secretion of neurotransmitters. After analyzing the Hodgkin-Huxley model of squid giant axon, Professor Leon Chua proposed that synapses could be composed of locally passive memristors, and neurons could be made up of locally active memristors. The two types of memristors share similar electrical characteristics with nerve fibers. Since the memristors was claimed to be found, locally active memristive devices have been identified in the research of devices with layered structures. The circuits constructed from those devices exhibit different types of neuromorphic_dynamics under different excitations, However, a single two-terminal device capable of achieving multi-state storage has not yet been reported. Locally active memristors have advantages in generating biologically-inspired neural signals. Various forms of locally active memristor models can produce neural morphological signals based on spike pulses. The generation of neural signals involves the amplification and computation of stimulus signals, and its working mechanism can be realized using capacitance-controlled memristor oscillators. When a memristor operates in the locally active domian, the output voltage of its third-order circuit undergoes a period-doubling bifurcation as the capacitance in the circuit changes regularly, forming a multi-state mapping between capacitance values and oscillating voltages. In this paper, the local active memristor-based third-order circuitis used as a unit to generate neuromorphic signals, thereby forming a biologically-inspired neural operation unit, and an operation network can be formed based on the operation unit. Methods The mathematical model of the Chua Corsage Memristor proposed by Leon Chua was selected for analysis. The characteristics of the partial local active domain were examined, and an appropriate operating point and external components were chosen to establish a third-order memristor chaotic circuit. Circuit simulation and analysis were then conducted on this circuit. When the memristor operates in the locally active domain, the oscillator formed by its third-order circuit can simultaneously perform the functions of signal amplification, computation, and storage. In this way, the third-order circuit can be perform as the nerve cell and the variable capacitors as cynapses. Enables the electrical signal and the dielectric capacitor to work in succession, allowing the third-order oscillation circuit of the memristor to function like a neuron, with alternating electrical fields and neurotransmitters forming a brain-like computing and storage system. The secretion of biological neurotransmitters has a threshold characteristic, and the membrane threshold voltage controls the secretion of neurotransmitters to the postsynaptic membrane, thereby forming the transmission of neural signals. The step peak value of the oscillation circuit can serve as the trigger voltage for the transfer of the capacity electrolyte. Results and Discussions This study utilizes the third-order circuit of a local active memristor to generate stable period-doubling bifurcation voltage signal oscillations as the external capacitance changes. The variation of capacitance in the circuit causes different forms of electrical signals to be serially output at the terminals of the memristor, and the voltage amplitude of these signals changes stably in a periodic manner. This results in a stable multi-state mapping relationship between the changed capacitance and the output voltage signal, thereby forming a storage and computing unit, and subsequently a storage and computing network. Currently, a structure that enables the dielectric to transfer and change the capacitance value to the next stage under the control of the modulated voltage threshold needs to be realized. It is similar to the function of neurotransmitter secretion. The feasibility of using the third-order oscillation circuit of the memristor as a storage and computing unit is expounded, and a storage and computing structure based on the change of capacitance value is obtained. Conclusions When the Chua Corsage Memristor operates in its locally active domain, its third order circuit–powered solely by a voltage-stabilized source generates stable period-doubling bifurcation oscillations as external capacitance changes. The serially output oscillating signals exhibit stable voltage amplitudes/periods and has threshold characteristics. The change of the capacitance in the circuit causes different forms of electrical signals to be serially output at the terminals of the memristor, and the voltage amplitude of these signals changes stably in a periodic manner. This results in a stable multi-state mapping relationship between the changed capacitance and the output voltage signal, thereby forming a storage and computing unit, and subsequently a storage and computing network. Currently, a structure is need to realize the transfer of the dielectric to the subordinate under the control of the modulated voltage threshold, similar to the function of neurotransmitter secretion. The feasibility of using the third-order oscillation circuit of the memristor as a storage and computing unit is obtained, and a storage and computing structure based on the variation of capacitance value is described.
- Locally /
- active memristor /
- Chaos /
- Neural network

HTML全文

图 1 忆阻器DC V-I图局部有源区部分

下载: 全尺寸图片幻灯片

图 2 忆阻器电导函数等效模型

下载: 全尺寸图片幻灯片

图 3 忆阻器三阶电路 (a)忆阻器串联电感后构成二阶振荡电路，(b) 忆阻器三阶振荡电路

下载: 全尺寸图片幻灯片

图 4 电路振荡输出随电容增大发生倍周期分叉

下载: 全尺寸图片幻灯片

图 5 忆阻器两端荡信号随电容变化的时序图

下载: 全尺寸图片幻灯片

图 6 忆阻器两端荡信号随电容变化的V-I相图

下载: 全尺寸图片幻灯片

图 7 多输入多输出忆阻器三阶电路

下载: 全尺寸图片幻灯片

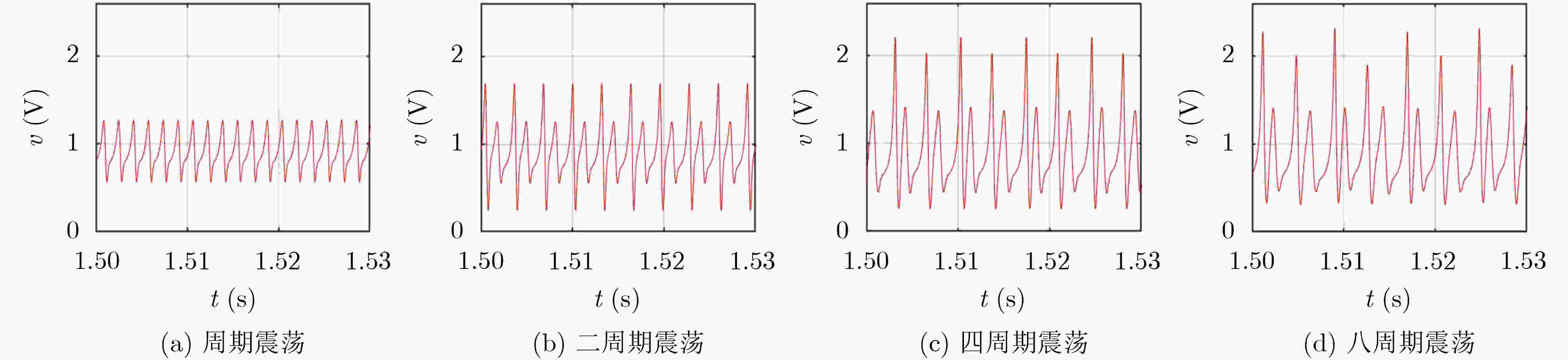
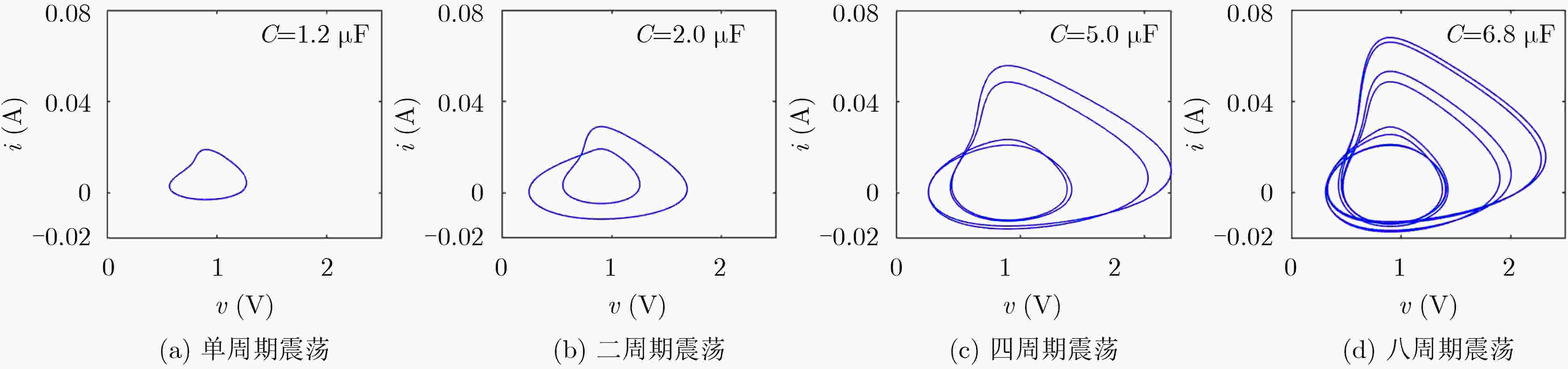
表 1 忆阻器三阶电路振荡输出与电容值之间的映射关系。

忆阻器振荡V-I图 C₁=0.5 μF C₁=2.0 μF C₁=4.0 μF

C₂=0.5 μF

C₂=2.0 μF

C₂=4.0 μF

下载: 导出CSV

参考文献(22)

[1]	DRUKARCH B, HOLLAND H A, VELICHKOV M, et al. Thinking about the nerve impulse: A critical analysis of the electricity-centered conception of nerve excitability[J]. Progress in Neurobiology, 2018, 169: 172–185. doi: 10.1016/j.pneurobio.2018.06.009.
[2]	DEBANNE D, BIALOWAS A, and RAMA S. What are the mechanisms for analogue and digital signalling in the brain?[J]. Nature Reviews Neuroscience, 2013, 14(1): 63–69. doi: 10.1038/nrn3361.
[3]	HODGKIN A and HUXLEY A F. A quantitative description of membrane current and its application to conduction and excitation in nerve[J]. Bulletin of Mathematical Biology, 1990, 52(1): 25–71. doi: 10.1007/BF02459568.
[4]	PICCOLINO M. Animal electricity and the birth of electrophysiology: The legacy of Luigi Galvani[J]. Brain Research Bulletin, 1998, 46(5): 381–407. doi: 10.1016/S0361-9230(98)00026-4.
[5]	MCCULLOCH W and PITTS W. A logical calculus of the ideas immanent in nervous activity[J]. Bulletin of Mathematical Biophysics, 1990, 52(1/2): 99–115. doi: 10.1016/S0092-8240(05)80006-0.
[6]	BALUŠKA F and LEVIN M. On having no head: Cognition throughout biological systems[J]. Frontiers in Psychology, 2016, 7: 902. doi: 10.3389/fpsyg.2016.00902.
[7]	NIYONAMBAZA S D, KUMAR P, XING P, et al. A review of neurotransmitters sensing methods for neuro-engineering research[J]. Applied Sciences, 2019, 9(21): 4719. doi: 10.3390/app9214719.
[8]	DRACHMAN D A. Do we have brain to spare?[J]. Neurology, 2005, 64(12): 2004–2005. doi: 10.1212/01.WNL.0000166914.38327.BB.
[9]	SAH M P, KIM H, and CHUA L O. Brains are made of memristors[J]. IEEE Circuits and Systems Magazine, 2014, 14(1): 12–36. doi: 10.1109/MCAS.2013.2296414.
[10]	STRUKOV D B, SNIDER G S, STEWART D R, et al. The missing memristor found[J]. Nature, 2008, 453(7191): 80–83. doi: 10.1038/nature06932.
[11]	WEIHER M, HERZIG M, TETZLAFF R, et al. Improved vertex coloring with NbOₓ memristor-based oscillatory networks[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2021, 68(5): 2082–2095. doi: 10.1109/TCSI.2021.3061973.
[12]	YI Wei, TSANG K, LAM S K, et al. Biological plausibility and stochasticity in scalable VO₂ active memristor neurons[J]. Nature Communications, 2018, 9(1): 4661. doi: 10.1038/s41467-018-07052-w.
[13]	CHUA L. Hodgkin-Huxley equations implies edge of chaos kernel[J]. Japanese Journal of Applied Physics, 2022, 61(SM): SM0805. doi: 10.35848/1347-4065/ac64e1.
[14]	YING Jiajie, LIANG Yian, WANG Guangyi, et al. Action potential and chaos near the edge of chaos in memristive circuits[J]. Chaos, 2022, 32(9): 093101. doi: 10.1063/5.0097075.
[15]	JIN Peipei, WANG Guangyi, LIANG Yian, et al. Neuromorphic dynamics of Chua corsage memristor[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2021, 68(11): 4419–4432. doi: 10.1109/TCSI.2021.3121676.
[16]	YING Jiajie, LIANG Yian, LI Fupeng, et al. Complex oscillations of Chua corsage memristor with two symmetrical locally active domains[J]. Electronics, 2022, 11(4): 665. doi: 10.3390/electronics11040665.
[17]	JIN Peipei, HAN Ningna, ZHANG Xianfei, et al. Edge of Chaos Kernel and neuromorphic dynamics of a locally-active memristor[J]. Communications in Nonlinear Science and Numerical Simulation, 2023, 117: 106961. doi: 10.1016/j.cnsns.2022.106961.
[18]	KOCH C and SEGEV I. The role of single neurons in information processing[J]. Nature Neuroscience, 2000, 3(11): 1171–1177. doi: 10.1038/81444.
[19]	YOON J, WANG Zhongrui, KIM K M, et al. An artificial nociceptor based on a diffusive memristor[J]. Nature Communications, 2018, 9(1): 417. doi: 10.1038/s41467-017-02572-3.
[20]	ZHAO Han, LIU Zhengwu, TANG Jianshi, et al. Memristor-based signal processing for edge computing[J]. Tsinghua Science and Technology, 2022, 27(3): 455–471. doi: 10.26599/TST.2021.9010043.
[21]	XIE Ying, YE Zhiqiu, LI Xueming, et al. A novel memristive neuron model and its energy characteristics[J]. Cognitive Neurodynamics, 2024, 18(4): 1989–2001. doi: 10.1007/s11571-024-10065-5.
[22]	WANG Tianshi. Novel computing paradigms using oscillators[D]. [Ph. D. dissertation], Uiniversity of California, 2019.