Research on Optimization Methods for Static Random-Access Memory-Physical Unclonable Function Key Extraction
-
摘要: 该文提出一种适应于比特筛选的静态随机存取存储器物理不可克隆功能(SRAM PUF)密钥提取新方案,使用SRAM的噪声单元生成密钥,使用SRAM的稳定单元重建PUF。该方案利用噪声单元的高熵特性,提高密钥熵值;基于稳定单元的低误码率优势,构建轻量级编解码体系,该方案的运算复杂度比方案2减少40%,比方案3减少98.9%,比方案4减少99.12%;通过实验数据统计出PUF单元变化率,并推导出PUF单元变化率与密钥重构成功率的关系,该方案密钥重构失败概率极低(1.4876E–9),比方案2和方案3降低4个数量级,比方案5降低1个数量级。最后,实验数据表明1 024字节的SRAM空间可提取128位满熵值密钥。Abstract:
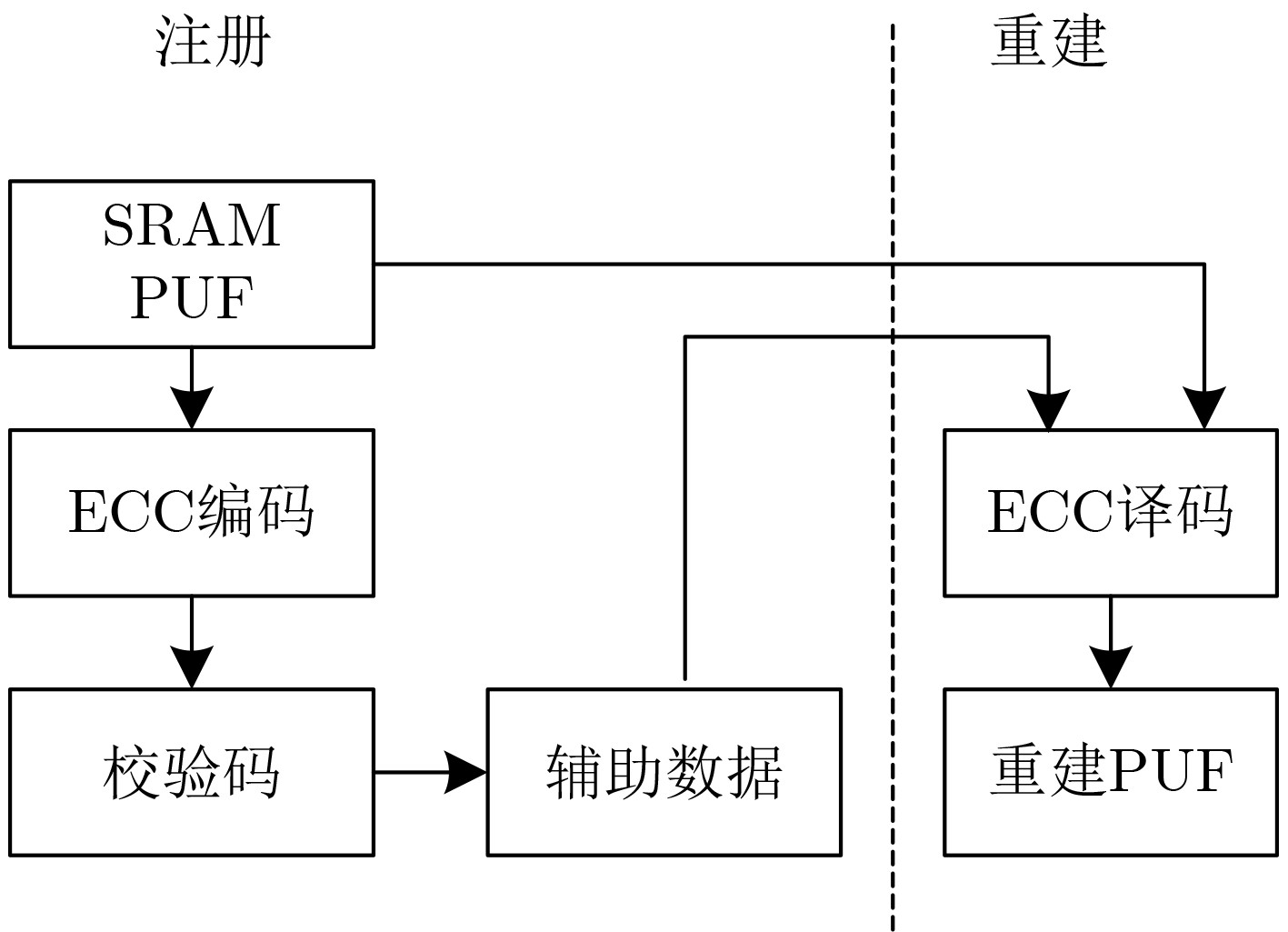
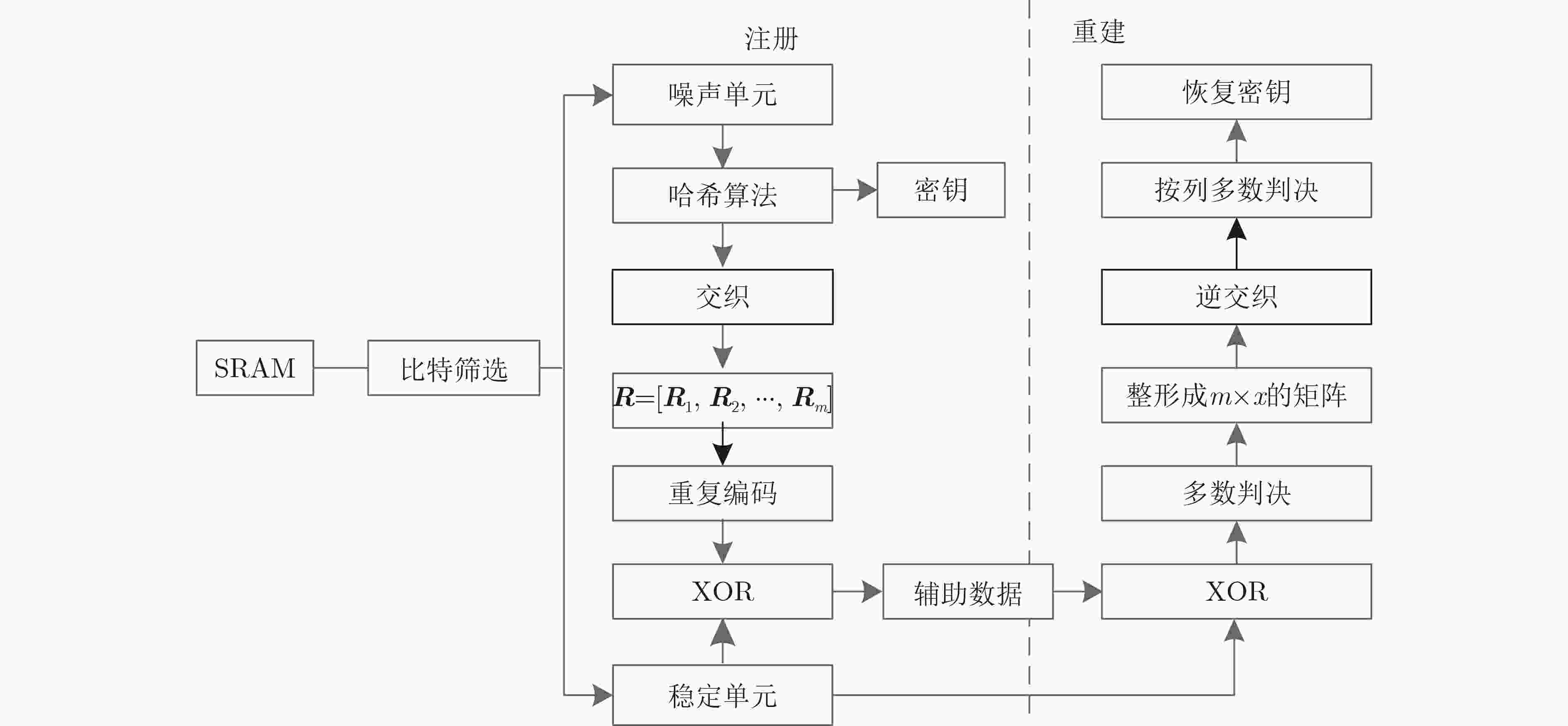
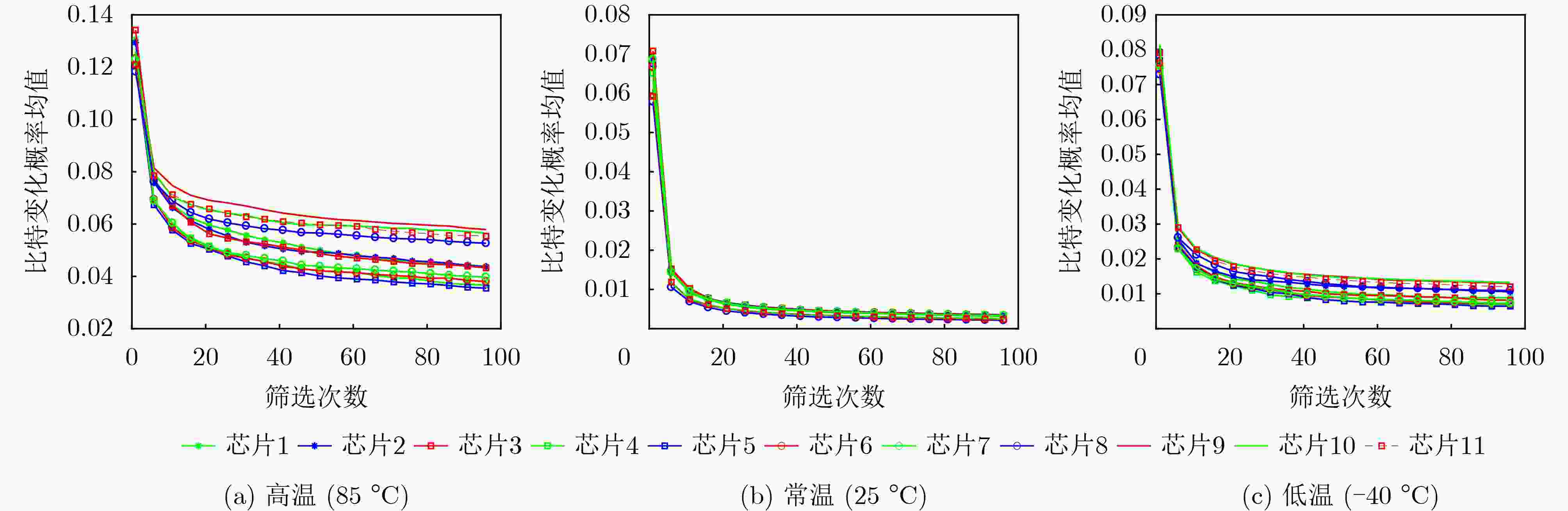
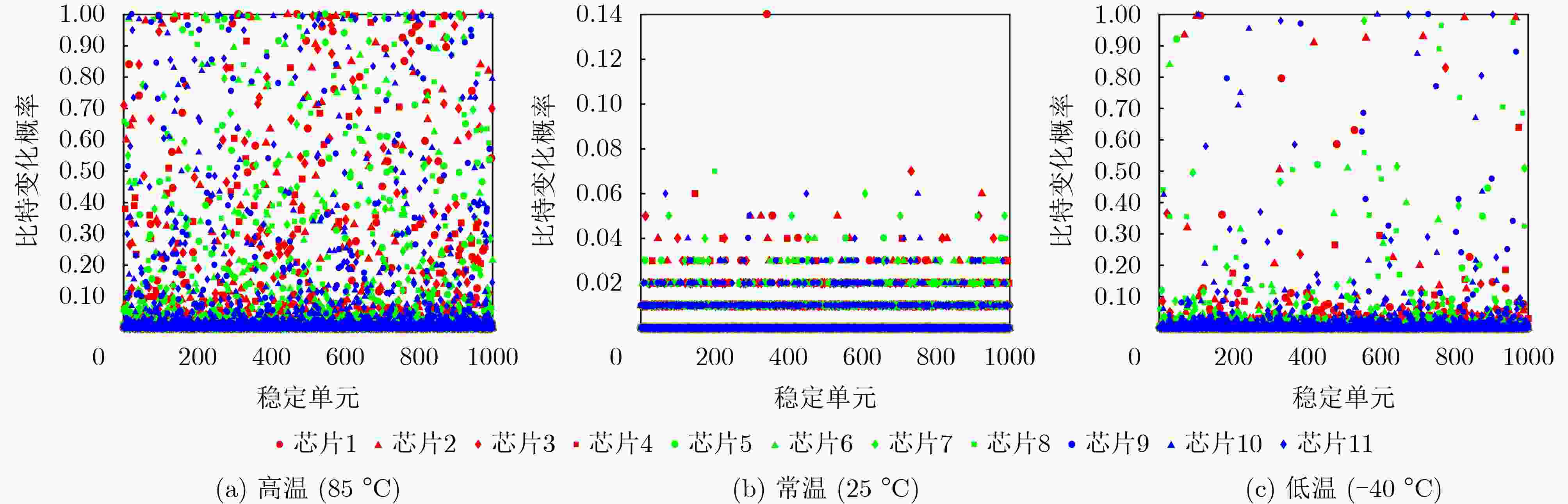
Objective Non-Volatile Memory (NVM) storage keys are exposed to physical attacks, and most lightweight Internet-of-Things (IoT) devices cannot deploy costly protection. A Physical Unclonable Function (PUF) offers a practical defense. However, Static Random-Access Memory PUFs (SRAM-PUFs) used as key generators exhibit environmental sensitivity that degrades stability. Therefore, optimization methods for SRAM-PUF–based key extraction fall into three main categories: (1) circuit-level enhancements that modify the SRAM cell to strengthen its inherent 0/1 bias; (2) cell selection methods that identify and retain only stable cells through dedicated algorithms; and (3) fuzzy-extractor schemes tailored to SRAM-PUFs that correct residual noise to yield reproducible cryptographic keys. Methods The selection of SRAM cells can markedly enhance bit stability. However, although reducing the complexity of Error-Correcting Code (ECC) encoding and decoding, this approach requires consuming a large number of stable cells to satisfy key entropy requirements, which in turn increases ECC code length. To address this contradiction, this paper proposes a new key extraction scheme ( Figure 2 ). In the proposed method, SRAM bits are divided into stable and noisy categories. The high entropy of noisy bits is leveraged for key generation: noisy bits are hashed to produce entropy-rich values, whereas stable bits with a low bit error rate are used to generate PUF responses. In the registration stage, the synthesized key is rearranged to form m vectors ( R 1, R 2,···, R m) according to m different rules. These m vectors are then combined into a new vector R . A repetition code of length 2t+1 (able to correct t errors) is applied to R to generate a codeword C . The codeword C is XORed with the PUF response to obtain helper data w, which is stored in NVM. In the reconstruction stage, w is XORed with a new PUF response to obtain C ′. Due to the repetition coding applied during registration, decoding is performed using a majority decision rule with a threshold of t+1. The decoding result R ' is reshaped into a matrix D with m rows and x columns, followed by reverse interleaving based on the rules used in registration. A majority decision is then executed independently for each column, with a decision threshold of m/2+1. The recovered key is output as the final result.Results and Discussions SRAM. Tests at –40 °C, 25 °C, and 85 °C show that the proposed bit-selection algorithm reduces the bit-change rate of SRAM-PUFs, with the number of screenings inversely proportional to the average change rate. The bit-change rate is highest at elevated temperatures. After 20 screenings, the average change rate at 85 °C decreases from 0.14 to 0.07, and after 80 screenings, it further decreases to 0.06. A quantitative analysis of error-correction capability is also performed. Based on the measured bit-change rates at high temperatures, the probability of key reconstruction failure is derived as low as 1.487 6E–9. In addition, 1 024 byte of SRAM cells are shown to yield entropy keys of 128 bit. Conclusions This paper proposes a novel SRAM-PUF key extraction scheme that resolves the trade-off between stability requirements and high entropy demands by employing a bit-selection algorithm. The scheme simplifies error-correction encoding and decoding while enhancing the entropy of the generated keys. Compared with existing approaches, the computational complexity is reduced by 40% relative to Scheme 2, by 98.9% relative to Scheme 3, and by 99.12% relative to Scheme 4. Furthermore, the method provides an integrated solution for screening stable SRAM cells, highlighting its practical application potential. Based on the bit error rate of 28 nm SRAM-PUFs, the key reconstruction success rate is calculated as (1–1.4876E–9). In tests conducted at –40 °C, 25 °C, and 85 °C, with 200 key reconstruction attempts per condition, all 11 chips achieved successful reconstruction. Considering variations across different fabrication processes, the number of screening cycles as well as parameters m and t can be adjusted to accommodate other process nodes. -
表 1 不同方法SRAM PUF稳定性对比
1 译码成功概率评估算法
(1)初始化PMF,其中p为各次试验成功概率向量。 n=length(p); pmf = zeros(1, n+1); pmf(1) = 1;% 0次成功的概率为1 (2)逐步更新PMF。 for i = 1:n %递归更新:前i–1次成功k–1次且第i次成功或者前i–1次成功k次且第i次失败 Pmf=[pmf(1)·(1–p(i)),pmf(2:end)·(1–p(i))+pmf(1:end–1)·
p(i)];End (3)k次成功的概率为pmf(k+1),Puf 重建成功概率计算过程如下。 For j=1: x For i=1:m pmf1=PMF_func(e(((i–1)·x+(j–1))·(2t+1)+1:((i–1)·x+j)
(2t+1)))${{\boldsymbol{p}}}{{(i,j)}} = {{\textit{1}}} - \displaystyle\sum\limits_{k = t + 2}^{2t + 2} {{\bf{pm}}{{\bf{f}}_{1}}} (k)$ end end (4)根据解交织规律,重排p,得到p'。 p3 = 1; for j=1:x pmf2 = PMF_func(p'(:,j)) ${\boldsymbol{\gamma }}{{(j) = }}\displaystyle\sum\limits_{k = m/2 + 2}^{m + 1} {{\bf{pm}}{{\bf{f}}_2}(k)} $ p3=p3·${\boldsymbol{\gamma }}\left( j \right) $ end 表 2 高温下PUF重建成功概率
编号 x=128, t=2, m=5 x=128, t=2, m=7 x=128, t=2, m=9 1 1–6.0390E–8 1–2.9159E–11 1– 6.2172E–15 2 1–4.3533E–7 1–1.5952E–10 1– 1.7542E–14 3 1–1.2722E–8 1–1.7840E–10 1– 4.7740E–15 4 1–3.7780E–8 1–2.8923E–11 1– 1.0769E–14 5 1–2.2309E–7 1–9.7857E–12 1– 1.2212E–15 6 1–4.4398E–6 1–7.5267E–10 1– 1.5432E–14 7 1–7.5811E–8 1–3.5191E–12 1–3.7748E–15 8 1–1.0748E–7 1–8.4819E–10 1– 1.4299E–12 9 1–8.8959E–7 1–1.4876E–9 1– 9.7844E–13 10 1–5.4529E–6 1–3.0186E–10 1– 3.6240E–12 11 1–5.8480E–8 1–3.0397E–9 1– 7.1021E–13 表 3 运算量和密钥重建失败概率对比
方案 内码 外码 长度 失败概率 运算量 1 CREP(5,1,2) Cour(896,128,384) 4 480 1.4876E–9 5 376次加法、1 024次比较和56次置换 4 480次加法、896次比较 56次置位、896次加法、128次比较 2 CREP(3,1,1) RM(2,7) = CRM(128,29,15) 5 376 3E–5 8 764次小数加法、5 124次小数比较和
3 332次除2运算5 376次小数加法、1 792次小数比较 3 332次小数比较、3 332次除2、
3 388次小数加法。3 CREP(7,1,3) BCH(1 754,742,105) 12 278 5E–5 480 368次加法和574 560次乘法
和1 754次比较12 278次加法、1 754次比较 468 090次加法、574 560次乘法 4 无 BCH(2 236,1 024,106) 2 236 无 604 836次加法和733 520次乘法 604 836次加法、733 520次乘法 5 无 CREP(5,1,2) 640 6.07E–8 640次加法和128次比较 640次加法、128次比较 表 4 3温度下200次上电密钥成功重建次数
编号 重建成功次数 –45 °C 25 °C 85 °C 1 200 200 200 2 200 200 200 3 200 200 200 4 200 200 200 5 200 200 200 6 200 200 200 7 200 200 200 8 200 200 200 9 200 200 200 10 200 200 200 11 200 200 200 表 5 1 664个噪声单元在常温下的熵值
编号 熵值 1 465.02 2 448.95 3 462.32 4 440.70 5 467.76 6 472.85 7 479.55 8 416.86 9 425.08 10 430.57 11 416.96 表 6 6 528个PUF单元在常温下的熵值
编号 熵值 1 58.89 2 60.22 3 59.70 4 58.77 5 59.99 6 59.68 7 27.76 8 43.40 9 43.26 10 46.27 11 48.30 -
[1] 张源, 罗静茹, 张吉良. SDL PUF: 高可靠自适应偏差锁定PUF电路[J]. 电子与信息学报, 2024, 46(5): 2274–2280. doi: 10.11999/JEIT231313.ZHANG Yuan, LUO Jingru, and ZHANG Jiliang. SDL PUF: A high reliability self-adaption deviation locking PUF[J]. Journal of Electronics & Information Technology, 2024, 46(5): 2274–2280. doi: 10.11999/JEIT231313. [2] HOLCOMB D E, BURLESON W P, and FU K. Power-up SRAM state as an identifying fingerprint and source of true random numbers[J]. IEEE Transactions on Computers, 2009, 58(9): 1198–1210. doi: 10.1109/TC.2008.212. [3] 陈帅, 蔡敏, 杨志勇, 等. 嵌入式系统中的内生存储器PUF研究综述[J]. 集成电路与嵌入式系统, 2024, 24(9): 7–16. doi: 10.20193/j.ices2097-4191.2024.0005.CHEN Shuai, CAI Min, YANG Zhiyong, et al. Review of extracting intrinsic PUF from embedded memory[J]. Integrated Circuits and Embedded Systems, 2024, 24(9): 7–16. doi: 10.20193/j.ices2097-4191.2024.0005. [4] RAIKWAL P, GUPTA N, AGARWAL N, et al. Security key generation in SRAM based PUF for cryptographic applications[C]. 2025 Fifth International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies, Bhilai, India, 2025. doi: 10.1109/ICAECT63952.2025.10958966. [5] TIMOTIUS S I, WANG Yilun, and CHEN H S. An SRAM-based PUF with high native-stability using alternative configuration technique[C]. 2025 IEEE International Conference on Consumer Electronics, Las Vegas, USA, 2025. doi: 10.1109/ICCE63647.2025.10929913. [6] LIU Kunyang, PU Hongliang, and SHINOHARA H. A 0.5-V 2.07-fJ/b 497-F2 EE/CMOS hybrid SRAM physically unclonable function with < 1E–7 bit error rate achieved through hot carrier injection burn-in[C]. 2020 IEEE Custom Integrated Circuits Conference, Boston, USA, 2020. doi: 10.1109/CICC48029.2020.9075875. [7] BATURONE I, PRADA-DELGADO M A, and EIROA S. Improved generation of identifiers, secret keys, and random numbers from SRAMs[J]. IEEE Transactions on Information Forensics and Security, 2015, 10(12): 2653–2668. doi: 10.1109/TIFS.2015.2471279. [8] 陈泽亮, 孔德珠, 尹爱国, 等. 基于数据残留时间的SRAM-PUF预选算法[J]. 电子学报, 2024, 52(5): 1478–1487. doi: 10.12263/DZXB.20221413.CHEN Zeliang, KONG Dezhu, YIN Aiguo, et al. SRAM-PUF preselection algorithm based on data remanence time[J]. Acta Electronica Sinica, 2024, 52(5): 1478–1487. doi: 10.12263/DZXB.20221413. [9] WANG Wendong, SINGH A, GUIN U, et al. Exploiting power supply ramp rate for calibrating cell strength in SRAM PUFs[C]. The 19th Latin-American Test Symposium, Sao Paulo, Brazil, 2018: 1–6. doi: 10.1109/LATW.2018.8349685. [10] SARAZA-CANFLANCA P, CARRASCO-LOPEZ H, SANTANA-ANDREO A, et al. Improving the reliability of SRAM-based PUFs under varying operation conditions and aging degradation[J]. Microelectronics Reliability, 2021, 118: 114049. doi: 10.1016/j.microrel.2021.114049. [11] SANTANA-ANDREO A, SARAZA-CANFLANCA P, CASTRO-LOPEZ R, et al. Reliability improvement of SRAM PUFs based on a detailed experimental study into the stochastic effects of aging[J]. AEU-International Journal of Electronics and Communications, 2024, 176: 155147. doi: 10.1016/j.aeue.2024.155147. [12] HE Ze and LI Shaoqing. A design of key generation unit based on SRAM PUF[C]. The 2nd International Conference on Frontiers of Electronics, Information and Computation Technologies, Wuhan, China, 2022. doi: 10.1109/ICFEICT57213.2022.00032. [13] 张亮亮, 张维, 孙瑞一, 等. 可用于SRAM PUF的密钥提取方案[J]. 北京大学学报: 自然科学版, 2017, 53(6): 997–1002. doi: 10.13209/j.0479-8023.2017.059.ZHANG Liangliang, ZHANG Wei, SUN Ruiyi, et al. Key extraction schemes for SRAM PUF[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2017, 53(6): 997–1002. doi: 10.13209/j.0479-8023.2017.059. [14] 李冰, 涂云晶, 陈帅, 等. 基于SRAM物理不可克隆函数的高效真随机种子发生器设计[J]. 电子与信息学报, 2017, 39(6): 1458–1563. doi: 10.11999/JEIT160835.LI Bing, TU Yunjing, CHEN Shuai, et al. Efficient design of truly random seed generator based on SRAM physical unclonable functions[J]. Journal of Electronics & Information Technology, 2017, 39(6): 1458–1463. doi: 10.11999/JEIT160835. [15] ARM Limited. Arm artisan 28nm SMIC 28HKCP memory power management application[EB/OL]. http://infocenter.arm.com, 2024. [16] WANG Y H. On the number of successes in independent trials[J]. Statistica Sinica, 1993, 3(2): 295–312. [17] 周昱, 于宗光. 基于RS和BCH码的SRAM-PUF密钥提取方法及性能分析[J]. 计算机工程, 2024, 50(7): 187–193. doi: 10.19678/j.issn.1000-3428.0068443.ZHOU Yu and YU Zongguang. SRAM-PUF key extraction method and performance analysis based on RS and BCH codes[J]. Computer Engineering, 2024, 50(7): 187–193. doi: 10.19678/j.issn.1000-3428.0068443. [18] SANTANA-ANDREO A, SARAZA-CANFLANCA P, CARRASCO-LOPEZ H, et al. A DRV-based bit selection method for SRAM PUF key generation and its impact on ECCs[J]. Integration, 2022, 85: 1–9. doi: 10.1016/J.VLSI.2022.02.008. [19] 王新梅, 肖国镇. 纠错码——原理与方法[M]. 西安: 西安电子科技大学出版社, 2001: 242–290.WANG Xinmei and XIAO Guozhen. Town Error Correction Coding - Principles and Methods[M]. Xi’an: Xidian University Press, 2001: 242–290. -





 下载:
下载:


 下载:
下载:
