Multi-Channel Switching Array DOA Estimation Algorithm Based on FRIDA
-
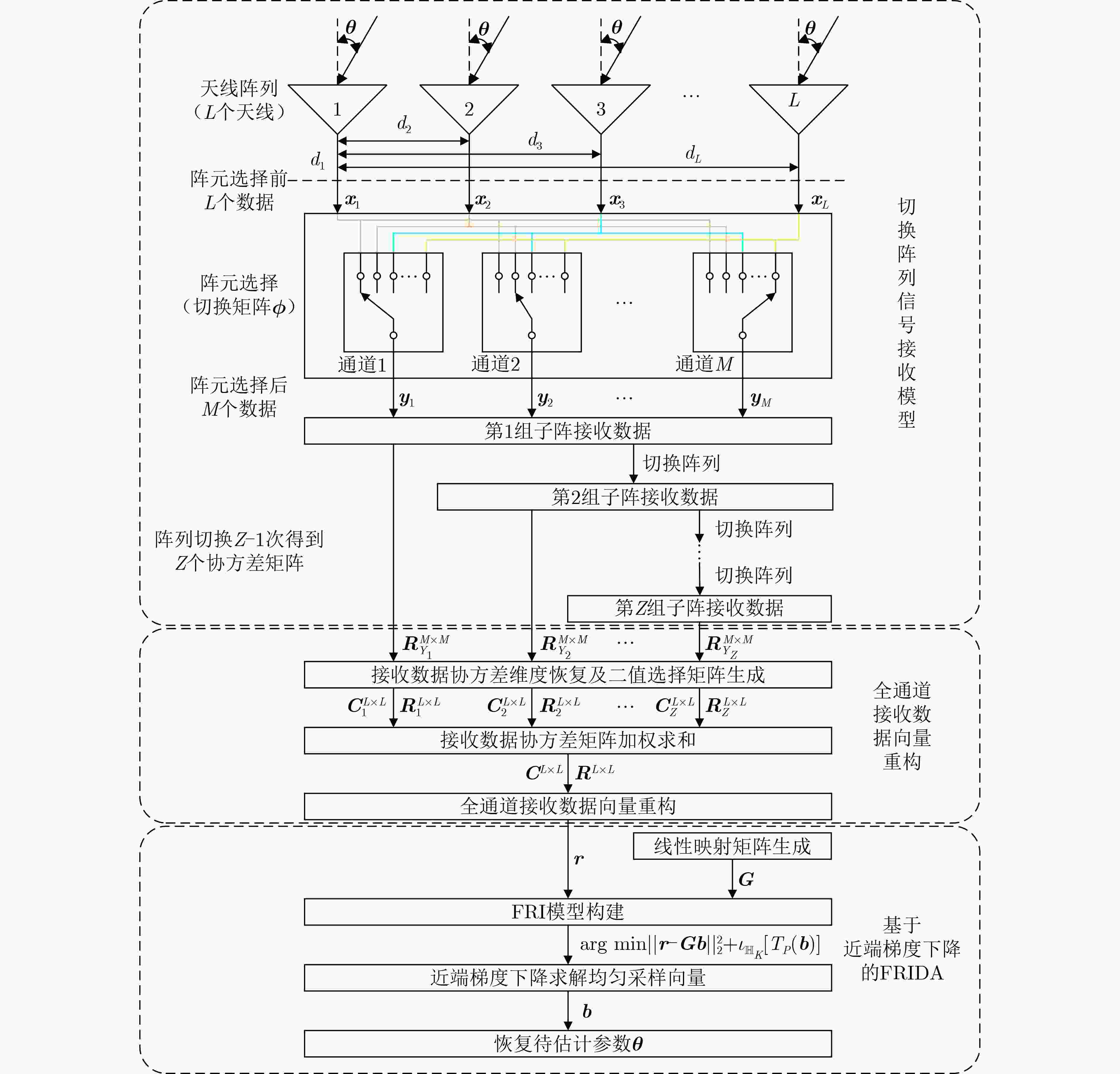
摘要: 针对波达方向(Direction Of Arrival, DOA)估计在实际测向系统中系统复杂度受接收通道数目影响的问题，该文提出了一种基于FRIDA(Finite Rate of Innovation Direction-of-Arrival)的多通道切换阵列DOA估计算法。该算法首先利用开关将特定子阵接收的数据传输至通道从而减少测向系统中使用的通道数目，然后通过切换不同的子阵接入通道并采样得到多个少通道接收数据协方差矩阵，利用这些协方差矩阵重构出全通道接收数据向量，以此来构建基于有限新息率(Finite Rate of Innovation, FRI)的DOA估计模型，最后通过近端梯度下降算法获得信号入射方向的估计结果。仿真实验与对实测数据的实验验证了该算法优于同等条件下的其它算法。Abstract:
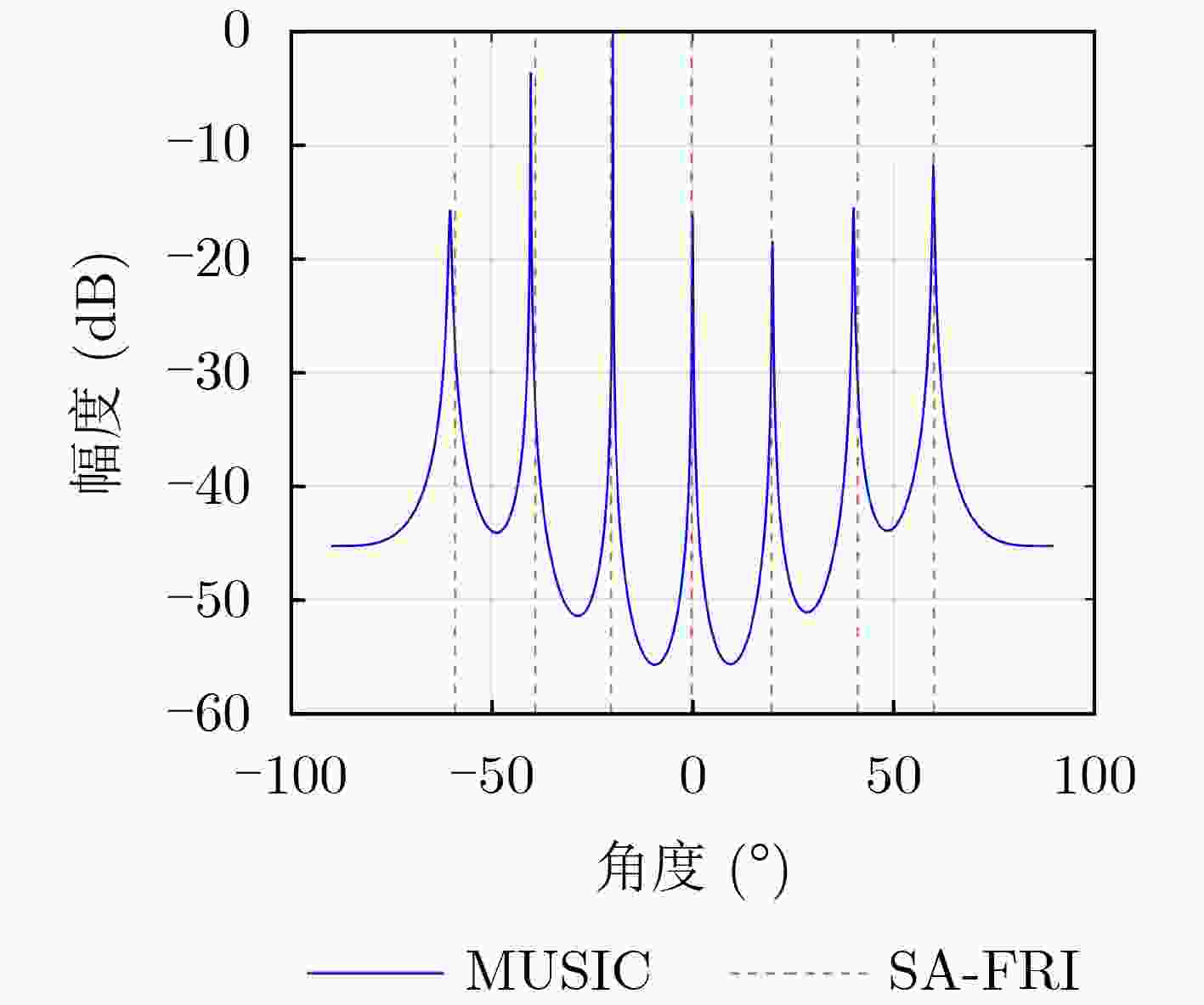
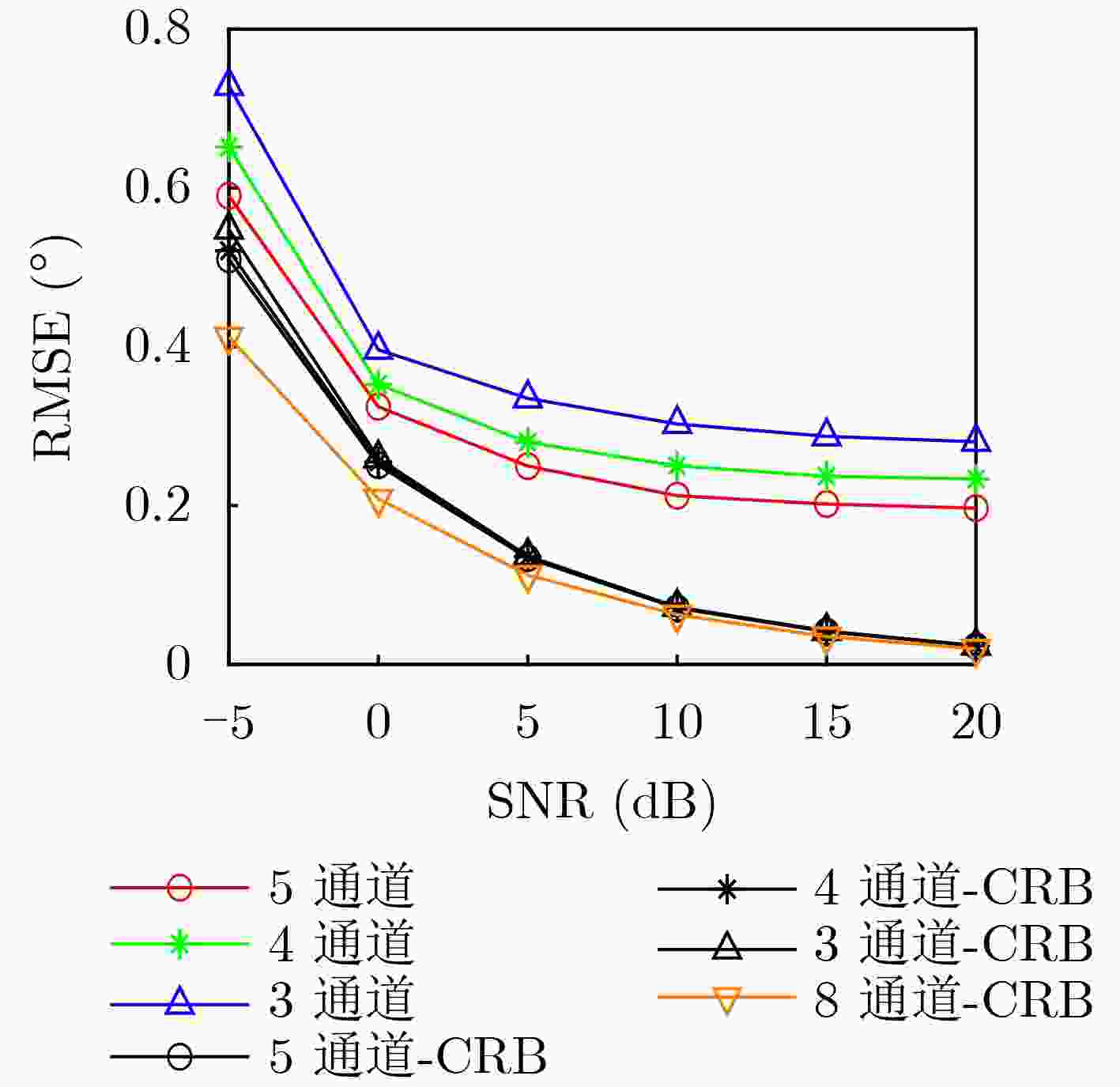
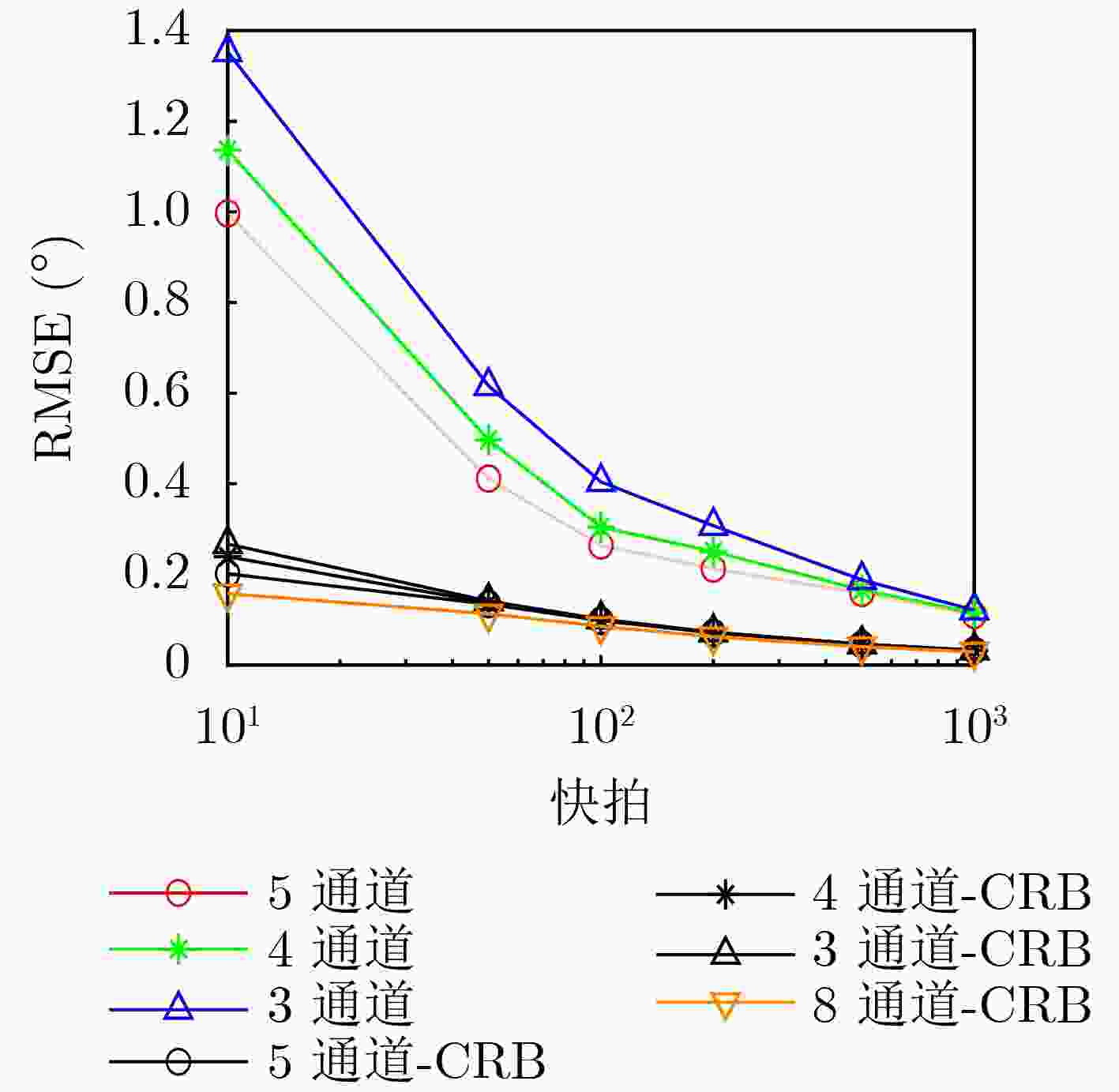
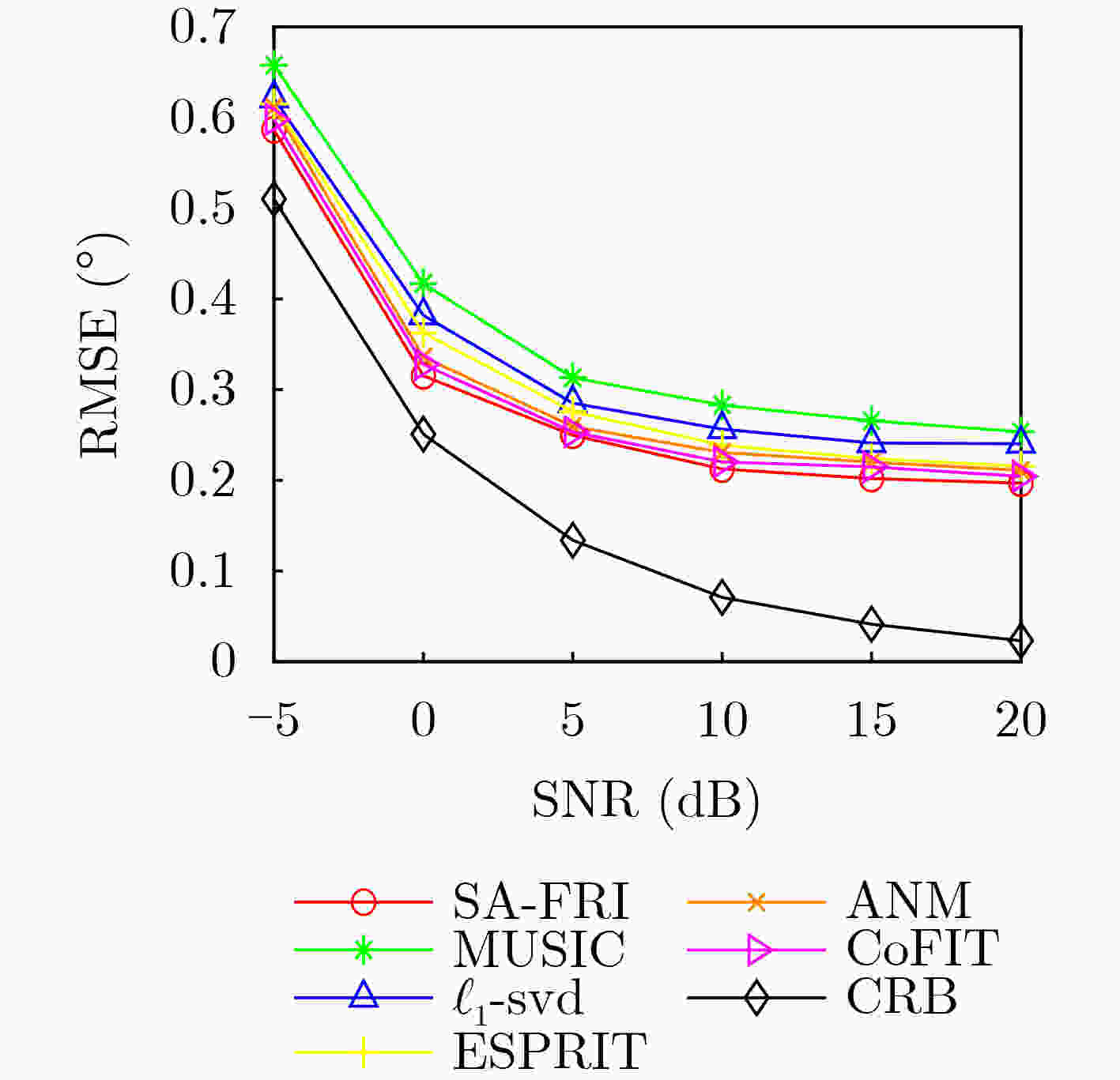
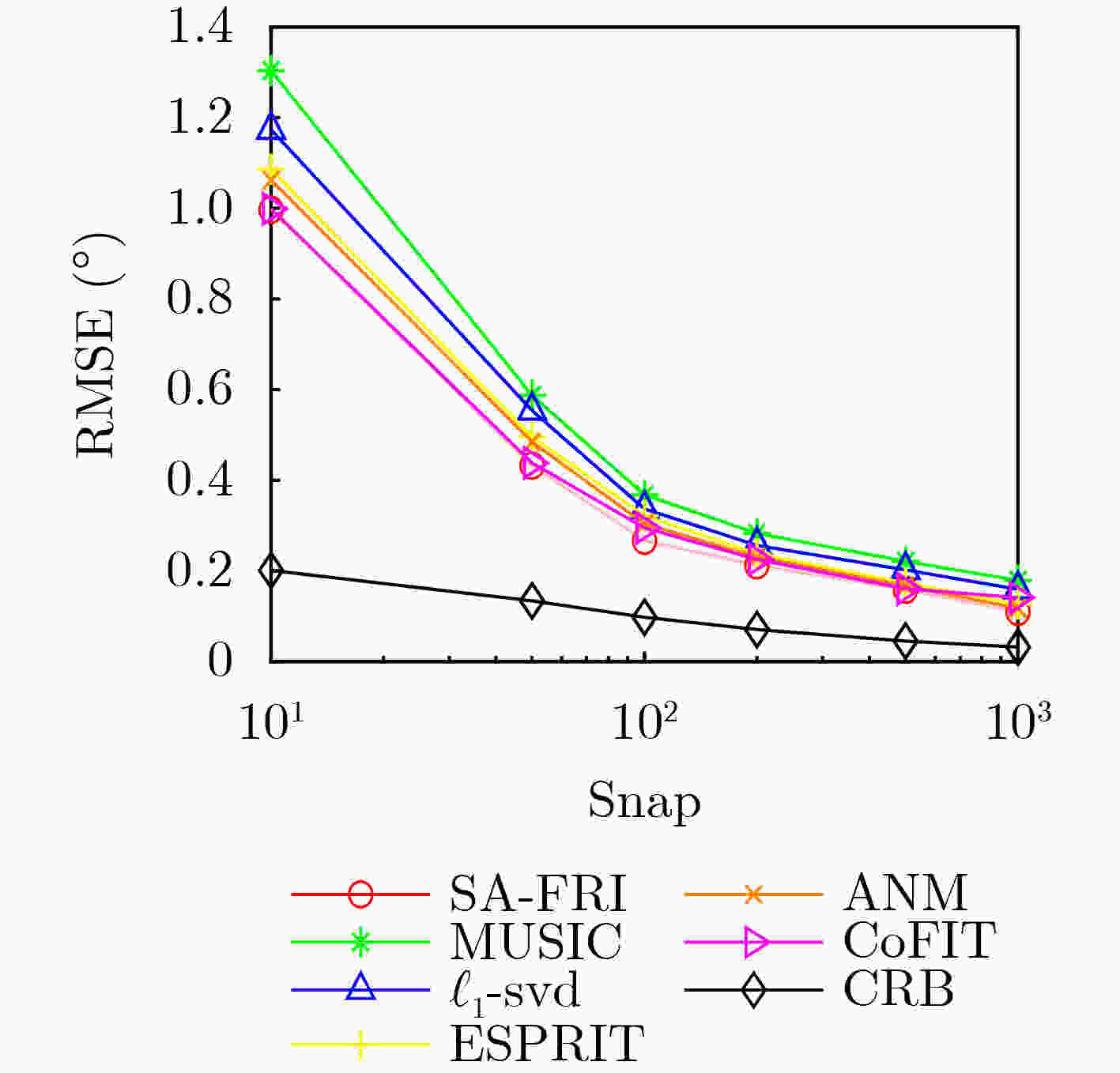
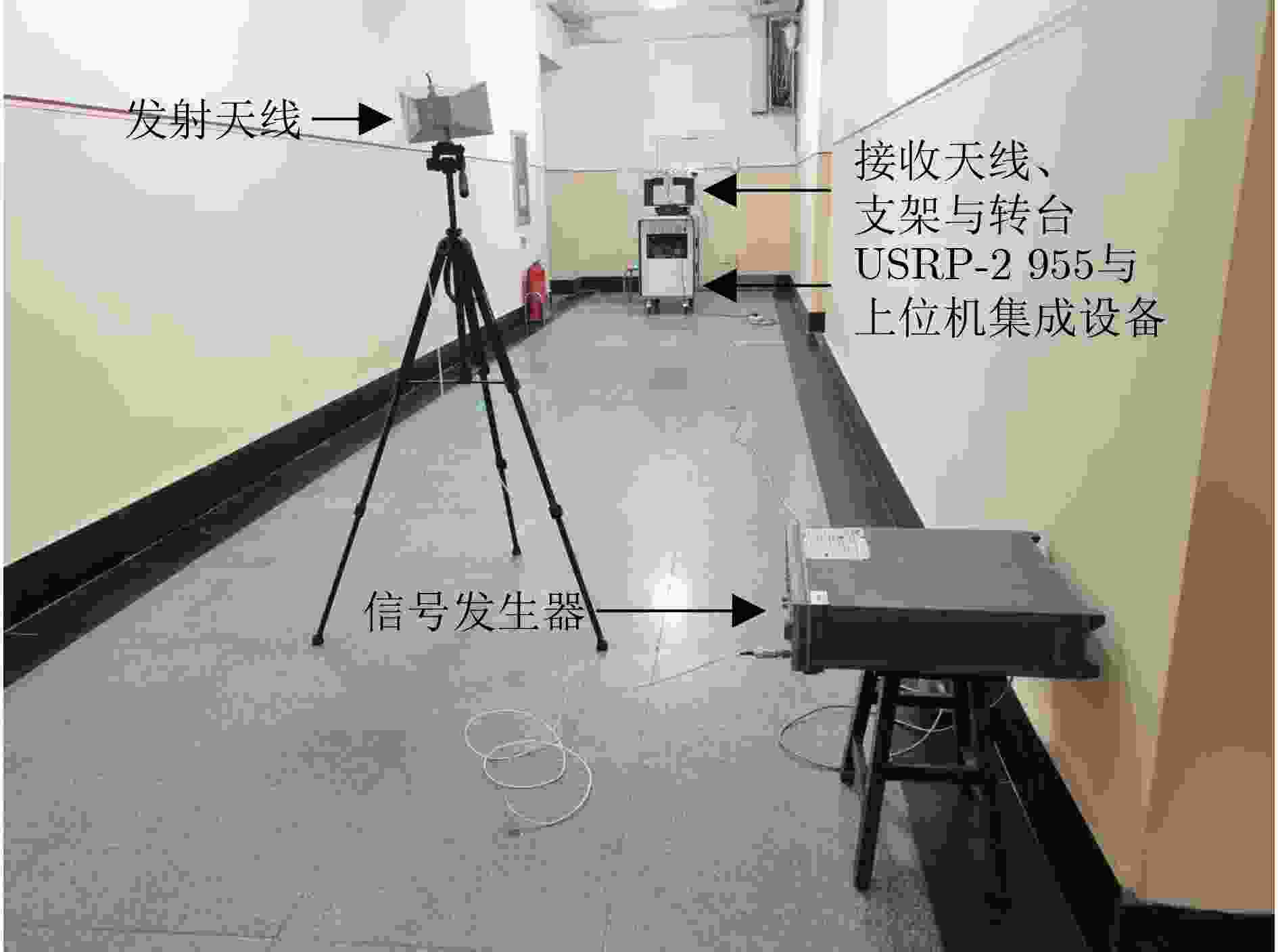
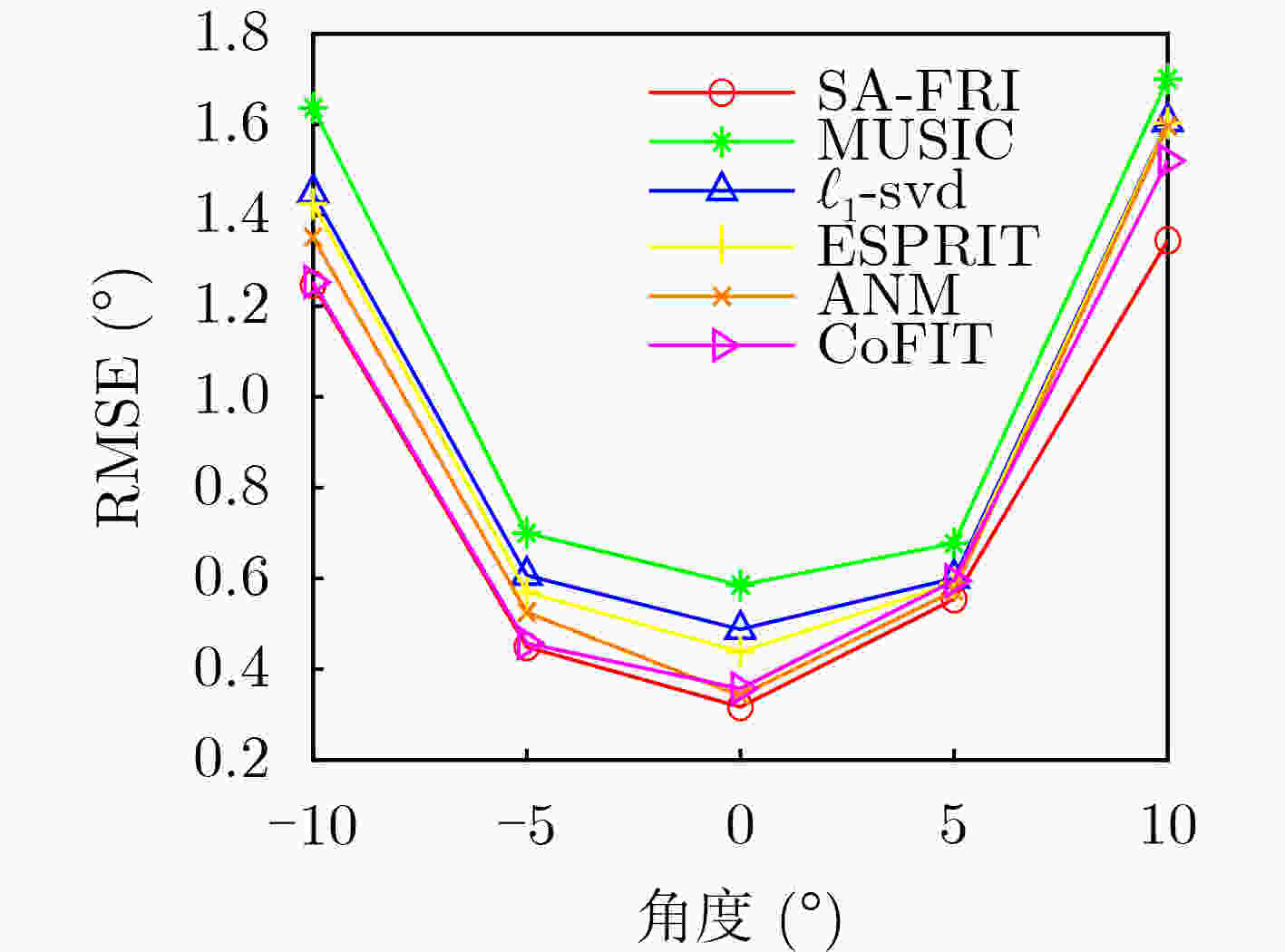
Objective With the increasing complexity of the electromagnetic environment, the requirements for estimation accuracy in practical direction finding systems are rising. Increasing the size of the antenna array is an effective means of improving the estimation accuracy of the actual direction finding system, but increasing the size of the antenna significantly increases the complexity of the actual direction finding system. This paper aims to reduce the number of channels used while maintaining the performance of DOA estimation for full-channel data. By combining the advantages of the channel compression algorithm in reducing the number of channels used with the structure of time-modulated arrays that incorporate switches in the RF front-end, This paper proposes a Multi-Channel Switching Array DOA Estimation Algorithm Based on FRIDA. Methods The algorithm first introduces a selection matrix consisting of switches between the antenna array and the channel, which is responsible for passing the signal data received by the particular antenna selected into the channel, i.e., a particular subarray is selected to receive the data through the selection matrix. Switching different subarrays to collect different less channel received data covariance matrix, by stipulating the common array elements in each subarray to ensure the phase consistency in the covariance matrix, these covariance matrices recover the dimensionality of the covariance matrix after the weighted summation to obtain the total covariance matrix. The total covariance matrix is weighted and summed to obtain the full-channel received data vector after weighting and summing the elements of the total covariance matrix that correspond to the same spacing of the array elements. The FRI reconstruction model is then constructed using the full-channel received data vector, and finally the estimated incident angle is obtained by using the proximal gradient descent algorithm together with the parameter recovery algorithm. Results and Discussions Simulation results of DOA estimation for SA-FRI at multiple source incidence show that: the full-channel received data vectors constructed using multiple covariance matrices of the less-channeled received data are able to discriminate multi-source incident signals, and their performance in this aspect is approximately the same as that of the full-channeled received data( Fig 2 ). Simulation results of the estimation accuracy with the number of snapshots and SNR under different channel numbers show that the estimation accuracy of the algorithm proposed in this paper with different channel numbers increases with the number of snapshots and SNR, and the more channels are used, the higher the DOA estimation accuracy is under the same SNR and the number of snapshots (Fig 3 ,Fig 4 ). Simulation results of DOA estimation accuracy of four different algorithms under different SNR and number of snapshots show that the DOA estimation accuracy of the four algorithms increases with the increase of SNR and number of snapshots, and the algorithms proposed in this paper outperform the other algorithms under the same conditions(Fig 5 ,Fig 6 ). Meanwhile, the same results were obtained by verifying the actual measured data(Fig 9 ), which further proved the effectiveness of the algorithm proposed in this paper.Conclusions Aiming at the problem of how to reduce the number of channels used in the actual DOA estimation system, this paper proposes an array switching DOA estimation based on proximal gradient descent. The algorithm firstly reduces the number of channels using the switching matrix, and then obtains multiple covariance matrices by switching different subarray access channels for multiple acquisitions, uses these covariance matrices to recover and complete the covariance matrix of the full-channel received data, and uses the matrix, and finally obtains the estimation of the DOA parameter of the incident signal by using the proximal gradient descent algorithm. At the same time, the simulation verifies that the proposed algorithm can reduce the use of channels under the premise of guaranteeing certain estimation accuracy. In addition, the effectiveness of the algorithm is further verified by the DOA estimation of the measured data collected through the actual DOA estimation system, which obtains results similar to those of the simulation. -
1 基于FRIDA的多通道切换阵列DOA估计算法流程
输入： 接收数据$ {Y_1},{Y_2}, \cdots ,{Y_Z} $。 输出： 入射信号的DOA估计结果${\widehat \theta _k}$，$k = 1,2,\cdots,K$。 初始化：Toeplitz算子维度参数$P$，正则化参数$\tau > 0$，参数$n \in {\mathbb{Z}_{ + + }}$，迭代停止阈值$\varepsilon \geqslant 0$， 一类Bessel函数最大阶数参数$Q$，线性映射矩阵$G$，迭代次数$k = 0$，以及初始化向量${b^{\left( 0 \right)}} \in {\mathbb{C}^{2Q + 1}}$； 步骤1：根据${R_{{Y_z}}} = \displaystyle\sum\nolimits_{u = 1}^u {y(u)y{{(u)}^{\rm H}}/U} $计算各接受数据协方差矩阵${R_{{Y_1}}},{R_{{Y_2}}}, \cdots ,{R_{{Y_Z}}}$； 步骤2：根据公式(5)将计算出的$M \times M$维矩阵${R_{{Y_1}}},{R_{{Y_2}}}, \cdots ,{R_{{Y_Z}}}$转化为$L \times L$维矩阵${R_1},{R_2}, \cdots ,{R_Z}$， 根据公式(6)(7)计算出二值选择矩阵$C$； 步骤3：根据公式(8)将矩阵${R_1},{R_2}, \cdots ,{R_Z}$加权求和为$ R $，根据公式(9)(10)(11)计算全通道接收数据向量$r$； 步骤4：根据公式(20)计算$ {b^{\left( {k + 1} \right)}} = pro{x_{\tau H}}\left( {{b^{\left( k \right)}} - 2\tau {G^{\rm H}}\left( {G{b^{\left( k \right)}} - r} \right)} \right) $； 步骤5：判断$\left\| {{b^{\left( {k + 1} \right)}} - {b^{\left( k \right)}}} \right\|_2^2$与$\varepsilon $的大小关系，若$\left\| {{b^{\left( {k + 1} \right)}} - {b^{\left( k \right)}}} \right\|_2^2 \le \varepsilon $，停止迭代，进入步骤6，否则$k = k + 1$，返回步骤4； 步骤6：对得到的${b^{\left( {k + 1} \right)}}$计算$ {T_P}\left( {{b^{(k + 1)}}} \right) $并计算其SVD分解结果$ {T_P}\left( {{b^{(k + 1)}}} \right) = {U_b}{S_b}V_b^{\rm H} $； 步骤7：以矩阵$V$的最后一列为系数，构造多项式$ F $，并计算其零点，记为${\lambda _k}$； 步骤8：计算信号的DOA参数$ {\theta _k} = - angle\left( {{\lambda _k}} \right) $，其中$angle\left( \cdot \right)$表示复数的幅角。 
下载: 导出CSV
表 1 各算法计算复杂度比较
算法 复杂度 SA-FRI $o\left( {n{T_{SA - FRI}}{{(2Q + 1 - P)}^2}P} \right)$ MUSIC $o\left( {{L^3} + {L^2}U + {N_{grid}}{L^2}} \right)$ ${\ell _1}$-svd $o\left( {{L^3}N_{grid}^3} \right)$ ESPRIT $o\left( {{L^3} + {L^2}U} \right)$ ANM $o\left( {{L^3}\log \left( {{1 \mathord{\left/ {\vphantom {1 \varepsilon }} \right. } \varepsilon }} \right)} \right)$ CoFIT $o\left( {{T_{SBL}}\left( {{N_{grid}}{L^2} + {L^3}} \right) + {T_{iter}}{L^3}} \right)$
下载: 导出CSV
表 2 各算法运行时间比较
算法 SA-FRI MUSIC ${\ell _1}$-svd ESPRIT ANM CoFIT 运行时间(秒) 52.79 2.62 140.81 0.13 169.77 179.37
下载: 导出CSV
-
[1] 马健钧, 魏少鹏, 马晖, 等. 基于ADMM的低仰角目标二维DOA估计算法[J]. 电子与信息学报, 2022, 44(8): 2859–2866. doi: 10.11999/JEIT210582.MA Jianjun, WEI Shaopeng, MA Hui, et al. Two-dimensional DOA estimation for low-angle target based on ADMM[J]. Journal of Electronics & Information Technology, 2022, 44(8): 2859–2866. doi: 10.11999/JEIT210582. [2] WANG Zhuying, YAN Yongsheng, HE Ke, et al. Augmented matrix construction based DOA estimation of coherent underwater acoustic signals[C]. 2023 IEEE International Conference on Signal Processing, Communications and Computing, Zhengzhou, China, 2023: 1–5. doi: 10.1109/ICSPCC59353.2023.10400250. [3] WEN Fangqing, WANG Han, GUI Guan, et al. Polarized intelligent reflecting surface aided 2D-DOA estimation for NLoS sources[J]. IEEE Transactions on Wireless Communications, 2024, 23(7): 8085–8098. doi: 10.1109/TWC.2023.3348520. [4] SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276–280. doi: 10.1109/TAP.1986.1143830. [5] ROY R, PAULRAJ A, and KAILATH T. ESPRIT--A subspace rotation approach to estimation of parameters of cisoids in noise[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1986, 34(5): 1340–1342. doi: 10.1109/TASSP.1986.1164935. [6] LIU Liang, LI Zhouchen, AN Jiancheng, et al. DOA estimation for switch-element arrays based on sparse representation[C]. 2024 IEEE International Conference on Acoustics, Speech and Signal Processing, Seoul, Korea, 2024: 8506–8510. doi: 10.1109/ICASSP48485.2024.10446599. [7] ALLMANN C, SPRINGER J, OISPUU M, et al. Experimental direction finding results using a time-multiplexed co-array approach[C]. 2023 IEEE 9th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, Herradura, Costa Rica, 2023: 336–340. doi: 10.1109/CAMSAP58249.2023.10403472. [8] 陈涛, 申梦雨, 史林, 等. 基于通道压缩的原子范数最小化DOA估计算法[J]. 仪器仪表学报, 2022, 43(4): 246–253. doi: 10.19650/j.cnki.cjsi.J2108691.CHEN Tao, SHEN Mengyu, SHI Lin, et al. A channel compression DOA estimation algorithm based on atomic norm minimization[J]. Chinese Journal of Scientific Instrument, 2022, 43(4): 246–253. doi: 10.19650/j.cnki.cjsi.J2108691. [9] IBRAHIM M, RAMIREDDY V, LAVRENKO A, et al. Design and analysis of compressive antenna arrays for direction of arrival estimation[J]. Signal Processing, 2017, 138: 35–47. doi: 10.1016/j.sigpro.2017.03.013. [10] GU Yujie, ZHANG Y D, and GOODMAN N A. Optimized compressive sensing-based direction-of-arrival estimation in massive MIMO[C]. 2017 IEEE International Conference on Acoustics, Speech and Signal Processing, New Orleans, USA, 2017: 3181–3185. doi: 10.1109/ICASSP.2017.7952743. [11] JING Zhehan, CAO Bingxia, MENG Xiangtian, et al. Noniterative DOA Estimation in time-modulated array under unidirectional phase center motion[J]. IEEE Antennas and Wireless Propagation Letters, 2024, 23(8): 2416–2420. doi: 10.1109/LAWP.2024.3394610. [12] KIM G U and KIM J P. Measurement of phase difference and direction of arrival using time-modulated array with general modulation parameters[J]. IEEE Antennas and Wireless Propagation Letters, 2023, 22(7): 1557–1561. doi: 10.1109/LAWP.2023.3251322. [13] NIU C, LV Tingting, LIU Yulong, et al. A DOA estimation method for coherent signals based on weighted l1-SVD[C]. 2023 IEEE 6th International Conference on Electronic Information and Communication Technology, Qingdao, China, 2023: 694–699. doi: 10.1109/ICEICT57916.2023.10245436. [14] CHEN Zhimin and CHEN Peng. Compressed sensing-based DOA and DOD estimation in bistatic co-prime MIMO arrays[C]. 2017 IEEE Conference on Antenna Measurements & Applications, Tsukuba, Japan, 2017: 297–300. doi: 10.1109/CAMA.2017.8273431. [15] 陈涛, 李敏行, 郭立民, 等. 基于原子范数最小化的极化敏感阵列DOA估计[J]. 电子学报, 2023, 51(4): 835–842. doi: 10.12263/DZXB.20220429.CHEN Tao, LI Minxing, GUO Limin, et al. DOA estimation of polarization sensitive array based on atomic norm minimization[J]. Acta Electronica Sinica, 2023, 51(4): 835–842. doi: 10.12263/DZXB.20220429. [16] 陈涛, 史林, 黄桂根, 等. 适用于任意几何结构平面阵列的无网格DOA估计算法[J]. 电子与信息学报, 2022, 44(3): 1052–1058. doi: 10.11999/JEIT210038.CHEN Tao, SHI Lin, HUANG Guigen, et al. Gridless DOA estimation algorithm for planar arrays with arbitrary geometry[J]. Journal of Electronics & Information Technology, 2022, 44(3): 1052–1058. doi: 10.11999/JEIT210038. [17] 陈涛, 赵立鹏, 史林, 等. 基于有限新息率的正交偶极子阵列信号参数估计算法[J]. 电子与信息学报, 2022, 44(7): 2469–2477. doi: 10.11999/JEIT210357.CHEN Tao, ZHAO Lipeng, SHI Lin, et al. Signal parameter estimation algorithm for orthogonal dipole array based on finite rate of innovation[J]. Journal of Electronics & Information Technology, 2022, 44(7): 2469–2477. doi: 10.11999/JEIT210357. [18] FU Ning, YUN Shuangxing, and QIAO Liyan. An efficient estimation method for the model order of FRI signal based on sub-Nyquist sampling[J]. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 6505513. doi: 10.1109/TIM.2023.3320730. [19] PAN Hanjie, SCHEIBLER R, BEZZAM E, et al. FRIDA: FRI-based DOA estimation for arbitrary array layouts[C]. 2017 IEEE International Conference on Acoustics, Speech and Signal Processing, New Orleans, USA, 2017: 3186–3190. doi: 10.1109/ICASSP.2017.7952744. [20] SIMEONI M, BESSON A, HURLEY P, et al. CPGD: Cadzow plug-and-play gradient descent for generalised FRI[J]. IEEE Transactions on Signal Processing, 2021, 69: 42–57. doi: 10.1109/TSP.2020.3041089. [21] WEISS A J and FRIEDLANDER B. Performance analysis of diversely polarized antenna arrays[J]. IEEE Transactions on Signal Processing, 1991, 39(7): 1589–1603. doi: 10.1109/78.134397. [22] PARK Y, GERSTOFT P, and MECKLENBRÄUKER C F. Atom-constrained gridless DOA refinement with wirtinger gradients[J]. IEEE Open Journal of Signal Processing, 2024, 5: 1134–1146. doi: 10.1109/OJSP.2024.3496815. -
图(9) / 表(3)
计量
- 文章访问数: 22
- HTML全文浏览量: 16
- PDF下载量: 1
- 被引次数: 0
下载:
