信息熵驱动的图神经网络黑盒迁移对抗攻击方法

吴涛; 纪琼辉; 先兴平; 乔少杰; 王超; 崔灿一星

doi:10.11999/JEIT250303

信息熵驱动的图神经网络黑盒迁移对抗攻击方法

doi: 10.11999/JEIT250303 cstr: 32379.14.JEIT250303

1.
重庆邮电大学网络空间安全与信息法学院重庆 400065
2.
成都信息工程大学软件工程学院成都 610225
3.
重庆师范大学计算机与信息科学学院重庆 401331

基金项目: 国家自然科学基金(62376047, 62106030)，重庆市自然科学基金创新发展联合基金重点项目(CSTB2023NSCQ-LZX0003)，重庆市教委科学技术研究计划重点项目(KJZD-K202300603, KJZD-K202500604)

详细信息

作者简介:
吴涛：男，教授，博士生导师，研究方向为图神经网络、知识图谱、人工智能安全、图数据挖掘等

纪琼辉：男，硕士生，研究方向为图神经网络、知识图谱、人工智能安全等

先兴平：女，副教授，硕士生导师，研究方向为图数据挖掘、数据隐私保护、智能算法安全等

乔少杰：男，教授，博士生导师，研究方向为大数据技术与应用、领域大数据分析、空间人工智能等

王超：男，副教授，硕士生导师，研究方向为时序数据和图数据表征、自然语言处理及其应用等

崔灿一星：女，博士生，研究方向为图神经网络、知识图谱、人工智能安全等

通讯作者:
先兴平　xianxp@cqupt.edu.cn

中图分类号: TN915.08; TP393
计量
- 文章访问数: 25
- HTML全文浏览量: 13
- PDF下载量: 3
- 被引次数: 0
出版历程
- 收稿日期: 2025-04-25
- 修回日期: 2025-09-10
- 网络出版日期: 2025-09-16

Entropy-Driven Black-box Transferable Adversarial Attack Method for Graph Neural Networks

1.
School of Cyber Security and Information Law, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
2.
School of Software Engineering, Chengdu University of Information Technology, Chengdu 610225, China
3.
School of Computer and Information Science, Chongqing Normal University, Chongqing 401331, China

Funds: The National Natural Science Foundation of China (62376047, 62106030), Key Project of Innovation and Development Fund of Chongqing Natural Science Foundation (CSTB2023NSCQ-LZX0003), Key Project of Science and Technology Program of Chongqing Education Commission (KJZD-K202300603, KJZD-K202500604)

摘要

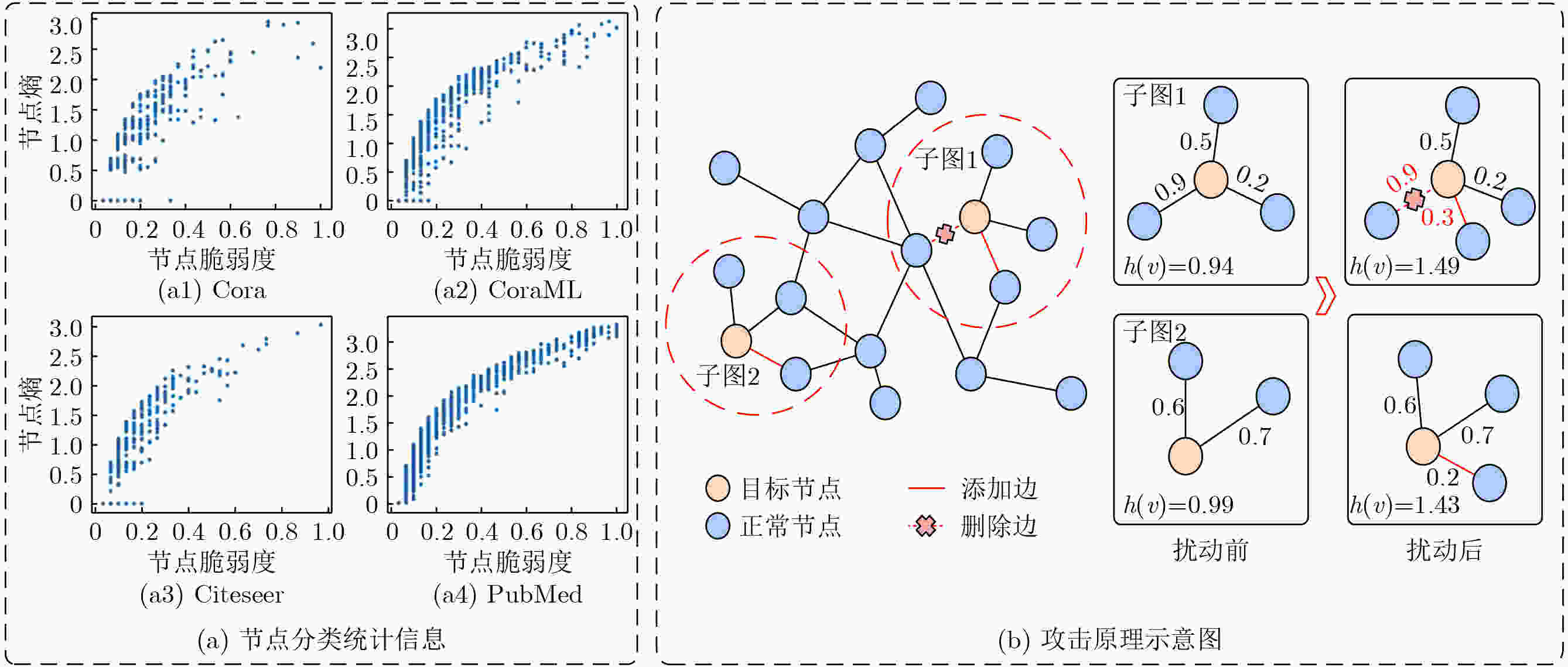
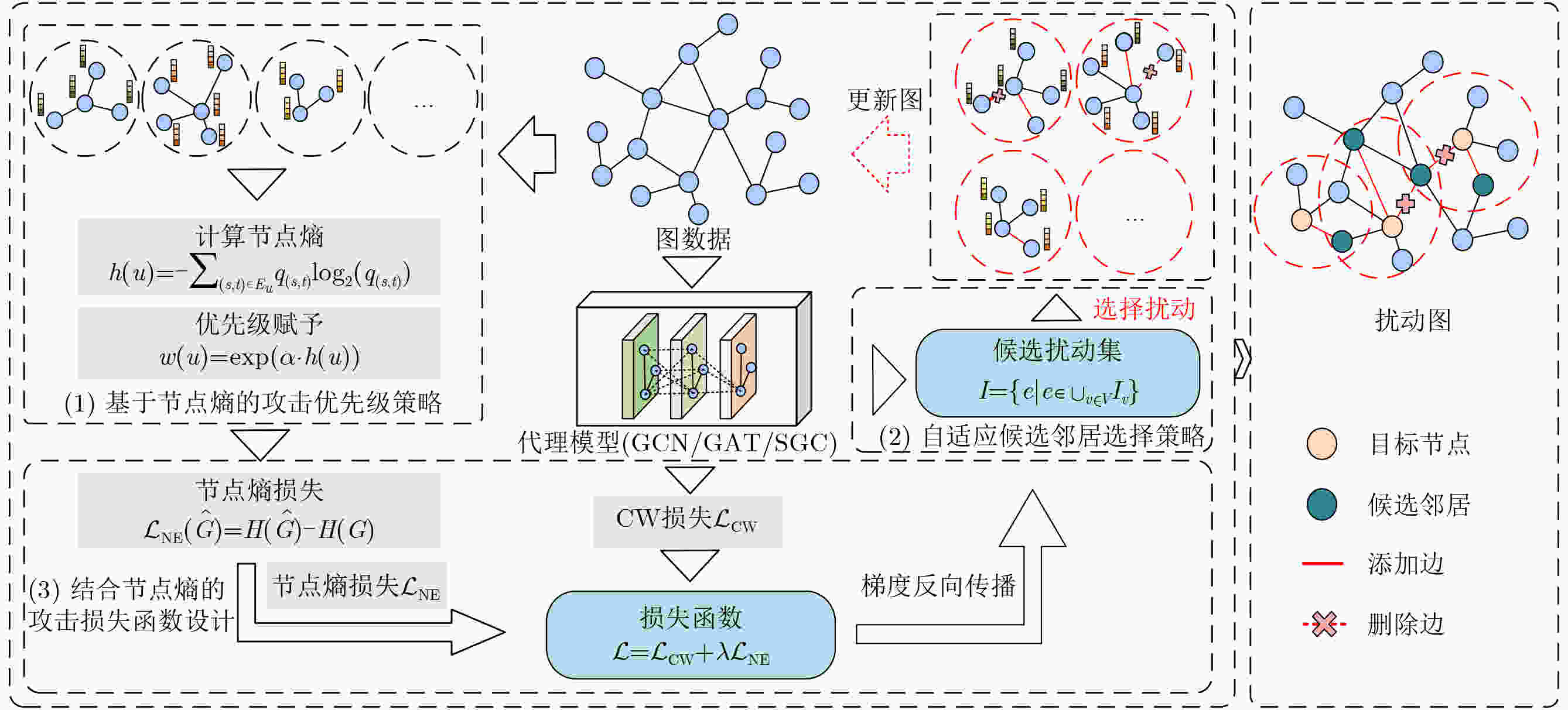
摘要: 图神经网络(GNNs)的对抗鲁棒性对其在安全关键场景中的应用具有重要意义。近年来，对抗攻击尤其是基于迁移的黑盒攻击引起了研究人员的广泛关注，但这些方法过度依赖代理模型的梯度信息导致生成的对抗样本迁移性较差。此外，现有方法多从全局视角出发选择扰动策略导致攻击效率低下。为了解决以上问题，该文探索熵与节点脆弱性之间的关联，并创新性地提出一种全新的对抗攻击思路。具体而言，针对同构图神经网络，利用节点熵来捕获节点的邻居子图的特征平滑性，提出基于节点熵的图神经网络迁移对抗攻击方法(NEAttack)。在此基础上，提出基于图熵的异构图神经网络对抗攻击方法(GEHAttack)。通过在多个模型和数据集上的大量实验，验证了所提方法的有效性，揭示了节点熵与节点脆弱性之间的关联关系在提升对抗攻击性能中的重要作用。
- 图神经网络 /
- 对抗攻击 /
- 黑盒攻击 /
- 信息熵 /
- 模型鲁棒性
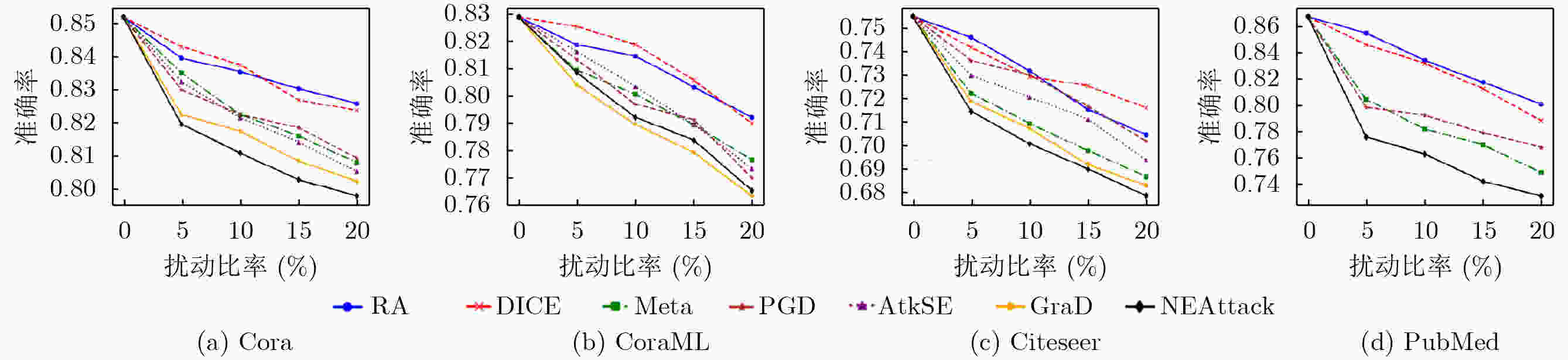
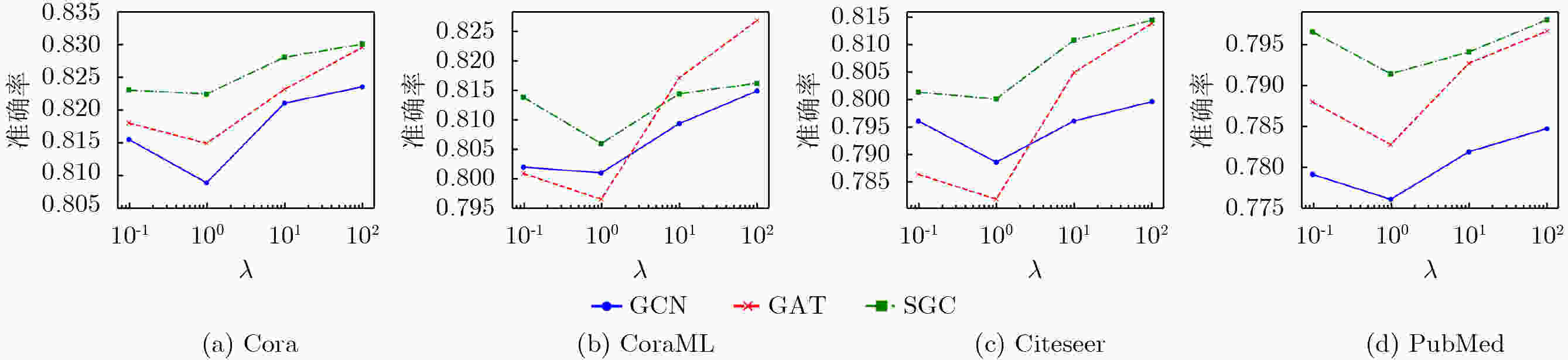
Abstract: Objective Graph Neural Networks (GNNs) achieve state-of-the-art performance in modeling complex graph-structured data and are increasingly applied in diverse domains. However, their vulnerability to adversarial attacks raises significant concerns for deployment in security-critical applications. Understanding and improving GNN robustness under adversarial conditions is therefore crucial to ensuring safe and reliable use. Among adversarial strategies, transfer-based black-box attacks have attracted considerable attention. Yet existing approaches face inherent limitations. First, they rely heavily on gradient information derived from surrogate models, while insufficiently exploiting critical structural cues embedded in graphs. This reliance often leads to overfitting to the surrogate, thereby reducing the transferability of adversarial samples. Second, most methods adopt a global perspective in perturbation selection, which hinders their ability to identify local substructures that decisively influence model predictions, ultimately resulting in suboptimal attack efficiency. Methods Motivated by the intrinsic structural characteristics of graph data, the latent association between information entropy and node vulnerability is investigated, and an entropy-guided adversarial attack framework is proposed. For homogeneous GNNs, a transferable black-box attack method, termed NEAttack, is designed. This method exploits node entropy to capture the structural complexity of node-level neighborhood subgraphs. By measuring neighborhood entropy, reliance on surrogate model gradients is reduced and perturbation selection is made more efficient. Based on this framework, the approach is further extended to heterogeneous graphs, leading to the development of GEHAttack, an entropy-based adversarial method that employs graph-level entropy to account for the semantic and relational diversity inherent in heterogeneous graph data. Results and Discussions The effectiveness and generalizability of the proposed methods are evaluated through extensive experiments on multiple datasets and model architectures. For homogeneous GNNs, NEAttack is assessed against six representative baselines on four datasets (Cora, CoraML, Citeseer, and PubMed) and three GNN models (Graph Convolutional Network (GCN), Graph Attention Network (GAT), Simplified Graph Convolution (SGC)). As reported in (Table 3) and (Table 4), NEAttack consistently outperforms existing approaches. In terms of accuracy, average improvements of 10.25%, 17.89%, 6.68%, and 12.6% are achieved on Cora, CoraML, Citeseer, and PubMed, respectively. For the F1-score, the corresponding gains are 9.41%, 16.83%, 6.21%, and 17.24%. Random Attack and Delete Internal, Connect External (DICE), which rely on randomness, exhibit stable but weak transferability, leading to only minor reductions in model performance. Meta-Self and Projected Gradient Descent (PGD) generate effective adversarial samples in white-box scenarios but show poor transfer performance due to overfitting to surrogate models. AtkSE and GraD perform better but remain affected by overfitting, while their computational cost increases sharply with data scale. For heterogeneous GNNs, GEHAttack is compared with four baselines on three datasets (ACM, IMDB, and DBLP) and six Heterogeneous Graph Neural Network (HGNN) models (Heterogeneous Graph Attention Network (HAN), Heterogeneous Graph Transformer (HGT), Simple Heterogeneous Graph Neural Network (SimpleHGN), Relational Graph Convolutional Network (RGCN), Robust Heterogeneous (RoHe), and Fast Robust Heterogeneous Graph Convolutional Network (FastRo-HGCN)). As shown in (Table 5 and Table 6), GEHAttack exhibits clear advantages. On the ACM dataset, compared with the HG Baseline, GEHAttack improves the average Micro-F1 and Macro-F1 scores of HAN, HGT, SimpleHGN, and RGCN by 3.93% and 3.46%, respectively. On the more robust RoHe and FastRo models, the corresponding improvements are 2.75% and 1.65%. Similar improvements are also observed on the IMDB and DBLP datasets, confirming the robustness and transferability of GEHAttack. Conclusions This study presents a unified entropy-oriented adversarial attack framework for both homogeneous and heterogeneous GNNs in black-box transfer settings. By leveraging the relationship between entropy and structural vulnerability, the proposed NEAttack and GEHAttack methods address the key limitations of gradient-dependent approaches and enable more efficient perturbation generation. Extensive evaluations across diverse datasets and models demonstrate their superiority in both performance and adaptability, providing new insights into advancing adversarial robustness research on graph-structured data.
- Graph Neural Networks (GNNs) /
- Adversarial attacks /
- Black-box attacks /
- Information entropy /
- Model robustness

HTML全文

图 1 节点相关子图特征平滑性与其脆弱性之间的内在联系

下载: 全尺寸图片幻灯片

图 2 基于节点熵的图神经网络迁移对抗攻击方法框架

下载: 全尺寸图片幻灯片

图 3 扰动预算对攻击性能的影响

下载: 全尺寸图片幻灯片

图 4 超参数$\lambda $对攻击性能的影响

下载: 全尺寸图片幻灯片

图 5 节点熵在生成扰动时随迭代轮次变化曲线

下载: 全尺寸图片幻灯片

图 6 不同攻击方法的攻击效果比较

下载: 全尺寸图片幻灯片

表 1 同构图场景下准确率实验结果

方法		Cora			CoraML			Citeseer			PubMed
Sur_Mod	Vic_Mod	GCN	GAT	SGC	GCN	GAT	SGC	GCN	GAT	SGC	GCN	GAT	SGC
Sur_Mod	Clean	0.852 1	0.859 7	0.849 1	0.849 0	0.853 4	0.827 0	0.754 7	0.769 9	0.750 6	0.867 3	0.857 9	0.791 5
GCN	RA	0.848 6	0.840 4	0.843 6	0.838 7	0.837 6	0.814 0	0.735 6	0.742 6	0.747 5	0.857 7	0.843 2	0.764 2
	DICE	0.844 1	0.843 6	0.836 5	0.825 4	0.837 2	0.807 8	0.731 3	0.754 6	0.733 4	0.856 1	0.848 7	0.761 4
	Mettack	0.839 0	0.850 6	0.820 1	0.807 9	0.840 3	0.792 3	0.721 9	0.721 0	0.729 9	0.803 1	0.806 2	0.720 2
	PGD	0.839 5	0.838 5	0.827 0	0.813 2	0.848 1	0.775 8	0.735 8	0.731 0	0.731 0	0.800 5	0.817 0	0.721 5
	AtkSE	0.821 5	0.831 1	0.794 7	0.816 1	0.825 8	0.790 5	0.719 6	0.729 3	0.719 8	OOM	OOM	OOM
	GraD	0.827 5	0.822 1	0.806 7	0.804 0	0.830 6	0.765 2	0.718 1	0.730 5	0.713 3	OOM	OOM	OOM
	NEAttack	0.808 9	0.813 4	0.792 0	0.805 2	0.809 2	0.755 3	0.714 2	0.706 8	0.703 9	0.776 2	0.782 6	0.700 6
GAT	RA	0.838 0	0.838 0	0.839 0	0.835 6	0.843 4	0.816 2	0.748 1	0.754 1	0.730 9	0.861 7	0.844 3	0.764 8
	DICE	0.845 6	0.842 6	0.834 3	0.837 2	0.833 6	0.813 6	0.746 3	0.745 9	0.724 3	0.857 9	0.837 1	0.753 6
	Mettack	0.843 6	0.840 1	0.832 5	0.812 3	0.840 3	0.755 8	0.732 8	0.735 8	0.684 8	0.814 0	0.812 3	0.722 5
	PGD	0.838 0	0.847 0	0.821 3	0.808 1	0.837 6	0.728 6	0.735 2	0.738 7	0.705 0	0.821 3	0.826 4	0.720 6
	AtkSE	0.830 2	0.812 5	0.839 5	0.810 7	0.805 8	0.790 9	0.742 9	0.717 6	0.744 7	OOM	OOM	OOM
	GraD	0.844 6	0.801 5	0.829 0	0.813 4	0.804 1	0.789 1	0.729 3	0.728 2	0.705 6	OOM	OOM	OOM
	NEAttack	0.814 9	0.804 8	0.801 3	0.796 3	0.767 3	0.688 6	0.707 5	0.725 2	0.675 4	0.782 9	0.790 4	0.686 1
SGC	RA	0.835 5	0.843 6	0.823 9	0.834 9	0.838 1	0.811 6	0.730 7	0.742 1	0.733 9	0.857 7	0.841 7	0.769 1
	DICE	0.838 4	0.845 4	0.826 5	0.821 4	0.827 7	0.805 2	0.734 6	0.738 8	0.743 8	0.854 3	0.837 2	0.764 6
	Mettack	0.841 6	0.843 1	0.823 9	0.820 3	0.838 1	0.786 9	0.747 0	0.731 8	0.726 9	0.799 5	0.800 3	0.701 0
	PGD	0.837 1	0.834 0	0.814 9	0.821 4	0.846 5	0.738 9	0.733 4	0.726 4	0.737 6	0.813 7	0.794 6	0.717 0
	AtkSE	0.845 6	0.826 5	0.810 5	0.800 3	0.811 4	0.774 5	0.724 7	0.742 3	0.719 3	OOM	OOM	OOM
	GraD	0.838 5	0.823 4	0.827 0	0.812 3	0.839 0	0.771 8	0.738 8	0.740 5	0.702 6	OOM	OOM	OOM
	NEAttack	0.822 4	0.794 8	0.805 3	0.784 6	0.787 8	0.718 0	0.725 7	0.712 3	0.669 4	0.791 7	0.799 6	0.674 7
*Sur_Mod,Vic_Mod分别表示代理模型和目标模型；Clean表示无扰动，RA表示Random Attack；最优结果以黑体标出；OOM表示超出内存

下载: 导出CSV

表 2 同构图场景下F1分数实验结果

方法		Cora			CoraML			Citeseer			PubMed
Sur_Mod	Vic_Mod	GCN	GAT	SGC	GCN	GAT	SGC	GCN	GAT	SGC	GCN	GAT	SGC
Sur_Mod	Clean	0.842 3	0.843 7	0.846 1	0.857 3	0.827 1	0.795 3	0.703 9	0.689 4	0.682 2	0.855 2	0.852 0	0.772 3
GCN	RA	0.824 3	0.836 6	0.837 1	0.848 9	0.819 3	0.751 4	0.685 6	0.658 5	0.675 7	0.851 0	0.836 6	0.742 3
	DICE	0.833 6	0.838 4	0.838 8	0.843 2	0.824 1	0.788 3	0.690 6	0.643 4	0.673 6	0.843 0	0.832 4	0.742 2
	Mettack	0.823 1	0.826 5	0.813 2	0.833 6	0.813 8	0.732 8	0.655 5	0.635 7	0.630 5	0.823 0	0.816 2	0.709 1
	PGD	0.824 5	0.820 6	0.819 2	0.827 8	0.805 3	0.754 6	0.663 5	0.639 6	0.639 4	0.816 2	0.820 0	0.711 6
	AtkSE	0.816 3	0.829 4	0.813 0	0.808 6	0.815 2	0.737 4	0.648 2	0.644 0	0.637 7	OOM	OOM	OOM
	GraD	0.802 4	0.810 4	0.814 3	0.786 6	0.811 5	0.738 0	0.629 9	0.638 1	0.624 5	OOM	OOM	OOM
	NEAttack	0.786 5	0.803 2	0.783 0	0.792 3	0.786 0	0.700 2	0.632 6	0.623 2	0.603 7	0.778 2	0.792 8	0.665 5
GAT	RA	0.827 9	0.834 3	0.830 7	0.826 2	0.818 4	0.735 5	0.699 8	0.650 6	0.659 8	0.849 7	0.831 0	0.746 8
	DICE	0.838 5	0.833 8	0.837 3	0.818 3	0.811 4	0.760 1	0.687 4	0.654 0	0.666 8	0.852 5	0.829 9	0.745 3
	Mettack	0.811 8	0.810 8	0.820 2	0.838 3	0.795 7	0.733 4	0.670 5	0.649 7	0.658 3	0.818 2	0.811 0	0.705 0
	PGD	0.826 4	0.815 2	0.807 9	0.831 7	0.787 6	0.689 5	0.664 4	0.637 5	0.646 2	0.826 1	0.822 5	0.716 5
	AtkSE	0.823 2	0.827 1	0.815 3	0.823 1	0.804 2	0.733 3	0.654 5	0.624 8	0.669 4	OOM	OOM	OOM
	GraD	0.811 9	0.795 3	0.812 7	0.825 4	0.803 5	0.743 7	0.645 7	0.629 1	0.653 3	OOM	OOM	OOM
	NEAttack	0.798 5	0.808 6	0.788 5	0.800 9	0.780 0	0.643 8	0.627 4	0.602 4	0.613 6	0.799 5	0.767 3	0.659 9
SGC	RA	0.787 9	0.828 3	0.823 8	0.834 2	0.821 2	0.751 2	0.693 2	0.676 4	0.679 9	0.847 6	0.833 6	0.743 7
	DICE	0.791 1	0.836 2	0.836 7	0.838 5	0.812 1	0.767 3	0.696 0	0.662 3	0.669 4	0.842 5	0.839 1	0.741 0
	Mettack	0.825 4	0.815 1	0.800 9	0.827 5	0.812 4	0.733 1	0.669 9	0.642 6	0.648 1	0.811 7	0.806 8	0.710 2
	PGD	0.811 9	0.818 0	0.792 7	0.822 3	0.784 0	0.700 3	0.657 5	0.639 1	0.650 5	0.809 4	0.820 4	0.695 5
	AtkSE	0.824 5	0.819 2	0.816 4	0.817 8	0.809 7	0.730 0	0.648 4	0.646 3	0.643 7	OOM	OOM	OOM
	GraD	0.806 2	0.809 6	0.809 6	0.825 9	0.800 5	0.736 3	0.655 2	0.635 4	0.632 0	OOM	OOM	OOM
	NEAttack	0.785 2	0.791 6	0.775 1	0.816 5	0.775 6	0.651 0	0.625 7	0.613 9	0.600 1	0.787 9	0.774 3	0.643 5
*Sur_Mod,Vic_Mod分别表示代理模型和目标模型；Clean表示无扰动，RA表示Random Attack；最优结果以黑体标出；OOM表示超出内存

下载: 导出CSV

表 3 异构图场景下Micro-F1实验结果

数据集	攻击方法	HAN	HGT	SimpleHGN	RGCN	RoHe	FastRo-HGCN
ACM	Clean	0.916 8	0.924 0	0.901 5	0.921 9	0.911 7	0.927 1
	RA	0.855 0	0.846 3	0.856 1	0.880 0	0.878 7	0.905 0
	HGB	0.800 8	0.844 0	0.719 5	0.836 1	0.905 7	0.921 5
	CLGA	0.862 6	0.892 5	0.861 3	0.843 1	0.893 2	0.911 9
	GHAC	0.746 2	0.847 2	0.819 5	0.827 5	0.887 7	0.909 6
	GEHA	0.713 4	0.802 3	0.749 2	0.818 4	0.878 5	0.893 6
IMDB	Clean	0.604 3	0.613 7	0.592 6	0.603 7	0.512 0	0.602 9
	RA	0.595 6	0.609 2	0.586 5	0.581 4	0.505 9	0.595 3
	HGB	0.452 3	0.477 7	0.488 6	0.559 4	0.498 5	0.589 1
	CLGA	0.571 2	0.600 7	0.577 7	0.578 0	0.500 4	0.595 5
	GHAC	0.485 0	0.468 2	0.538 4	0.555 1	0.497 5	0.579 8
	GEHA	0.424 7	0.461 7	0.454 6	0.548 4	0.487 0	0.575 0
DBLP	Clean	0.934 9	0.941 5	0.940 0	0.935 1	0.928 0	0.935 7
	RA	0.902 6	0.922 1	0.927 7	0.915 0	0.917 3	0.930 8
	HGB	0.720 6	0.801 5	0.812 0	0.877 1	0.921 2	0.924 8
	CLGA	0.892 9	0.916 3	0.924 3	0.916 6	0.922 7	0.932 0
	GHAC	0.809 6	0.847 6	0.885 2	0.910 5	0.917 0	0.922 6
	GEHA	0.678 8	0.747 5	0.796 8	0.861 9	0.912 0	0.911 5
* Clean：无扰动；RA：Random Attack；GEHA：GEHAttack

下载: 导出CSV

表 4 异构图场景下Macro-F1实验结果

数据集	攻击方法	HAN	HGT	SimpleHGN	RGCN	RoHe	FastRo-HGCN
ACM	Clean	0.920 6	0.925 7	0.903 5	0.921 9	0.910 3	0.914 1
	RA	0.848 8	0.838 0	0.854 1	0.885 0	0.884 5	0.882 0
	HGB	0.799 6	0.845 7	0.741 5	0.836 1	0.904 3	0.908 5
	CLGA	0.860 8	0.884 2	0.833 3	0.863 1	0.891 8	0.898 9
	GHAC	0.755 2	0.848 9	0.821 5	0.817 5	0.886 3	0.896 6
	GEHA	0.737 0	0.804 0	0.762 2	0.808 4	0.877 1	0.880 6
IMDB	Clean	0.582 8	0.591 4	0.573 6	0.613 1	0.536 4	0.612 1
	RA	0.569 2	0.578 9	0.567 5	0.590 8	0.530 3	0.604 5
	HGB	0.440 4	0.466 7	0.416 8	0.526 7	0.522 9	0.598 3
	CLGA	0.529 5	0.548 3	0.498 2	0.577 5	0.523 8	0.604 7
	GHAC	0.443 4	0.440 3	0.490 5	0.528 6	0.521 9	0.589 0
	GEHA	0.398 1	0.429 4	0.389 3	0.507 8	0.511 4	0.584 2
DBLP	Clean	0.918 5	0.929 3	0.921 7	0.923 4	0.917 8	0.926 1
	RA	0.882 8	0.909 9	0.909 4	0.903 3	0.907 1	0.921 2
	HGB	0.731 8	0.789 3	0.793 7	0.785 4	0.911 0	0.915 2
	CLGA	0.876 5	0.893 6	0.896 0	0.905 8	0.912 2	0.914 8
	GHAC	0.792 6	0.866 2	0.887 4	0.868 7	0.906 2	0.911 9
	GEHA	0.697 2	0.775 3	0.778 5	0.774 2	0.901 8	0.901 9
* Clean：无扰动；RA：Random Attack；GEHA：GEHAttack

下载: 导出CSV

参考文献(34)

[1]	吴涛, 曹新汶, 先兴平, 等. 图神经网络对抗攻击与鲁棒性评测前沿进展[J]. 计算机科学与探索, 2024, 18(8): 1935–1959. doi: 10.3778/j.issn.1673-9418.2311117. WU Tao, CAO Xinwen, XIAN Xingping, et al. Advances of adversarial attacks and robustness evaluation for graph neural networks[J]. Journal of Frontiers of Computer Science & Technology, 2024, 18(8): 1935–1959. doi: 10.3778/j.issn.1673-9418.2311117.
[2]	MU Jiaming, WANG Binghui, LI Qi, et al. A hard label black-box adversarial attack against graph neural networks[C]. Proceedings of the 2021 ACM SIGSAC Conference on Computer and Communications Security, Virtual Event, 2021: 108–125. doi: 10.1145/3460120.3484796. (查阅网上资料,未找到本条文献出版地信息,请确认).
[3]	ZÜGNER D, AKBARNEJAD A, and GÜNNEMANN S. Adversarial attacks on neural networks for graph data[C]. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 2018: 2847–2856. doi: 10.1145/3219819.3220078.
[4]	ZÜGNER D and GÜNNEMANN S. Adversarial attacks on graph neural networks via meta learning[C]. 7th International Conference on Learning Representations, New Orleans, USA, 2019.
[5]	SHANG Yu, ZHANG Yudong, CHEN Jiansheng, et al. Transferable structure-based adversarial attack of heterogeneous graph neural network[C]. Proceedings of the 32nd ACM International Conference on Information and Knowledge Management, Birmingham, UK, 2023: 2188–2197. doi: 10.1145/3583780.3615095.
[6]	XU Kaidi, CHEN Hongge, LIU Sijia, et al. Topology attack and defense for graph neural networks: An optimization perspective[C]. Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 2019: 3961–3967. doi: 10.24963/ijcai.2019/550.
[7]	ZHANG Jianping, WU Weibin, HUANG J T, et al. Improving adversarial transferability via neuron attribution-based attacks[C]. Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, USA, 2022: 14973–14982. doi: 10.1109/CVPR52688.2022.01457.
[8]	WU Jun, TAN Yuejin, DENG Hongzhong, et al. Heterogeneity of scale-free networks[J]. Systems Engineering-Theory & Practice, 2007, 27(5): 101–105. doi: 10.1016/S1874-8651(08)60036-8.
[9]	WANG Bing, TANG Huanwen, GUO Chonghui, et al. Entropy optimization of scale-free networks’ robustness to random failures[J]. Physica A: Statistical Mechanics and its Applications, 2006, 363(2): 591–596. doi: 10.1016/j.physa.2005.08.025.
[10]	蔡萌, 杜海峰, 费尔德曼. 一种基于最大流的网络结构熵[J]. 物理学报, 2014, 63(6): 060504. doi: 10.7498/aps.63.060504. CAI Meng, DU Haifeng, and FELDMAN M W. A new network structure entropy based on maximum flow[J]. Acta Physica Sinica, 2014, 63(6): 060504. doi: 10.7498/aps.63.060504.
[11]	黄丽亚, 霍宥良, 王青, 等. 基于K-阶结构熵的网络异构性研究[J]. 物理学报, 2019, 68(1): 018901. doi: 10.7498/aps.68.20181388. HUANG Liya, HUO Youliang, WANG Qing, et al. Network heterogeneity based on K-order structure entropy[J]. Acta Physica Sinica, 2019, 68(1): 018901. doi: 10.7498/aps.68.20181388.
[12]	CARLINI N and WAGNER D. Towards evaluating the robustness of neural networks[C]. 2017 IEEE Symposium on Security and Privacy, San Jose, USA, 2017: 39–57. doi: 10.1109/SP.2017.49.
[13]	WU Tao, YANG Nan, CHEN Long, et al. ERGCN: Data enhancement-based robust graph convolutional network against adversarial attacks[J]. Information Sciences, 2022, 617: 234–253. doi: 10.1016/j.ins.2022.10.115.
[14]	MCCALLUM A K, NIGAM K, RENNIE J, et al. Automating the construction of internet portals with machine learning[J]. Information Retrieval, 2000, 3(2): 127–163. doi: 10.1023/A:1009953814988.
[15]	GILES C L, BOLLACKER K D, and LAWRENCE S. CiteSeer: An automatic citation indexing system[C]. Proceedings of the Third ACM Conference on Digital Libraries, Pittsburgh, USA, 1998: 89–98. doi: 10.1145/276675.276685.
[16]	SEN P, NAMATA G, BILGIC M, et al. Collective classification in network data[J]. AI Magazine, 2008, 29(3): 93–106. doi: 10.1609/aimag.v29i3.2157.
[17]	WANG Xiao, LIU Nian, HAN Hui, et al. Self-supervised heterogeneous graph neural network with co-contrastive learning[C]. Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Virtual Event, Singapore, 2021: 1726–1736. doi: 10.1145/3447548.3467415. (查阅网上资料,未找到本条文献出版地信息,请确认).
[18]	FU Xinyu, ZHANG Jiani, MENG Ziqiao, et al. MAGNN: Metapath aggregated graph neural network for heterogeneous graph embedding[C]. Proceedings of The Web Conference 2020, Taipei, China, 2020: 2331–2341. doi: 10.1145/3366423.3380297.
[19]	HAN Hui, ZHAO Tianyu, YANG Cheng, et al. OpenHGNN: An open source toolkit for heterogeneous graph neural network[C]. Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, USA, 2022: 3993–3997. doi: 10.1145/3511808.3557664.
[20]	MALIK H A M, ABID F, WAHIDDIN M R, et al. Robustness of dengue complex network under targeted versus random attack[J]. Complexity, 2017, 2017(1): 2515928. doi: 10.1155/2017/2515928.
[21]	WANIEK M, MICHALAK T P, WOOLDRIDGE M J, et al. Hiding individuals and communities in a social network[J]. Nature Human Behaviour, 2018, 2(2): 139–147. doi: 10.1038/s41562-017-0290-3.
[22]	LIU Zihan, LUO Yun, WU Lirong, et al. Are gradients on graph structure reliable in gray-box attacks?[C]. Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, USA, 2022: 1360–1368. doi: 10.1145/3511808.3557238.
[23]	LIU Zihan, LUO Yun, WU Lirong, et al. Towards reasonable budget allocation in untargeted graph structure attacks via gradient debias[C]. Proceedings of the 36th International Conference on Neural Information Processing Systems, New Orleans, USA, 2022: 2028.
[24]	ZHANG Mengmei, WANG Xiao, ZHU Meiqi, et al. Robust heterogeneous graph neural networks against adversarial attacks[C]. Proceedings of the 36th AAAI Conference on Artificial Intelligence, Virtual Event, 2022: 4363–4370. doi: 10.1609/aaai.v36i4.20357. (查阅网上资料,未找到本条文献出版地信息,请确认).
[25]	ZHANG Sixiao, CHEN Hongxu, SUN Xiangguo, et al. Unsupervised graph poisoning attack via contrastive loss back-propagation[C]. Proceedings of the ACM Web Conference 2022, Virtual Event, France, 2022: 1322–1330. doi: 10.1145/3485447.3512179. (查阅网上资料,未找到本条文献出版地信息,请确认).
[26]	WANG Haosen, XU Can, SHI Chenglong, et al. Unsupervised heterogeneous graph rewriting attack via node clustering[C]. Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Barcelona, Spain, 2024: 3057–3068. doi: 10.1145/3637528.3671716.
[27]	KIPF T N and WELLING M. Semi-supervised classification with graph convolutional networks[C]. 5th International Conference on Learning Representations, Toulon, France, 2017.
[28]	VELIČKOVIĆ P, CUCURULL G, CASANOVA A, et al. Graph attention networks[J]. arXiv preprint arXiv: 1710.10903, 2017. doi: 10.48550/arXiv.1710.10903. (查阅网上资料,请作者核对文献类型及格式是否正确).
[29]	WU F, SOUZA A, ZHANG Tianyi, et al. Simplifying graph convolutional networks[C]. Proceedings of the 36th International Conference on Machine Learning, Long Beach, USA, 2019: 6861–6871.
[30]	WANG Xiao, JI Houye, SHI Chuan, et al. Heterogeneous graph attention network[C]. The World Wide Web Conference, San Francisco, USA, 2019: 2022–2032. doi: 10.1145/3308558.3313562.
[31]	HU Ziniu, DONG Yuxiao, WANG Kuansan, et al. Heterogeneous graph transformer[C]. Proceedings of The Web Conference 2020, Taipei, China, 2020: 2704–2710. doi: 10.1145/3366423.3380027.
[32]	LV Qingsong, DING Ming, LIU Qiang, et al. Are we really making much progress? Revisiting, benchmarking and refining heterogeneous graph neural networks[C]. Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Singapore, Singapore, 2021: 1150–1160. doi: 10.1145/3447548.3467350.
[33]	SCHLICHTKRULL M, KIPF T N, BLOEM P, et al. Modeling relational data with graph convolutional networks[C]. 15th International Conference on The Semantic Web, Heraklion, Greece, 2018: 593–607. doi: 10.1007/978-3-319-93417-4_38.
[34]	YAN Yeyu, ZHAO Zhongying, YANG Zhan, et al. A fast and robust attention-free heterogeneous graph convolutional network[J]. IEEE Transactions on Big Data, 2024, 10(5): 669–681. doi: 10.1109/TBDATA.2024.3375152.