Dynamic Adaptive Partitioning of Deep Neural Networks Based on Early Exit Mechanism under Edge-End Collaboration
-
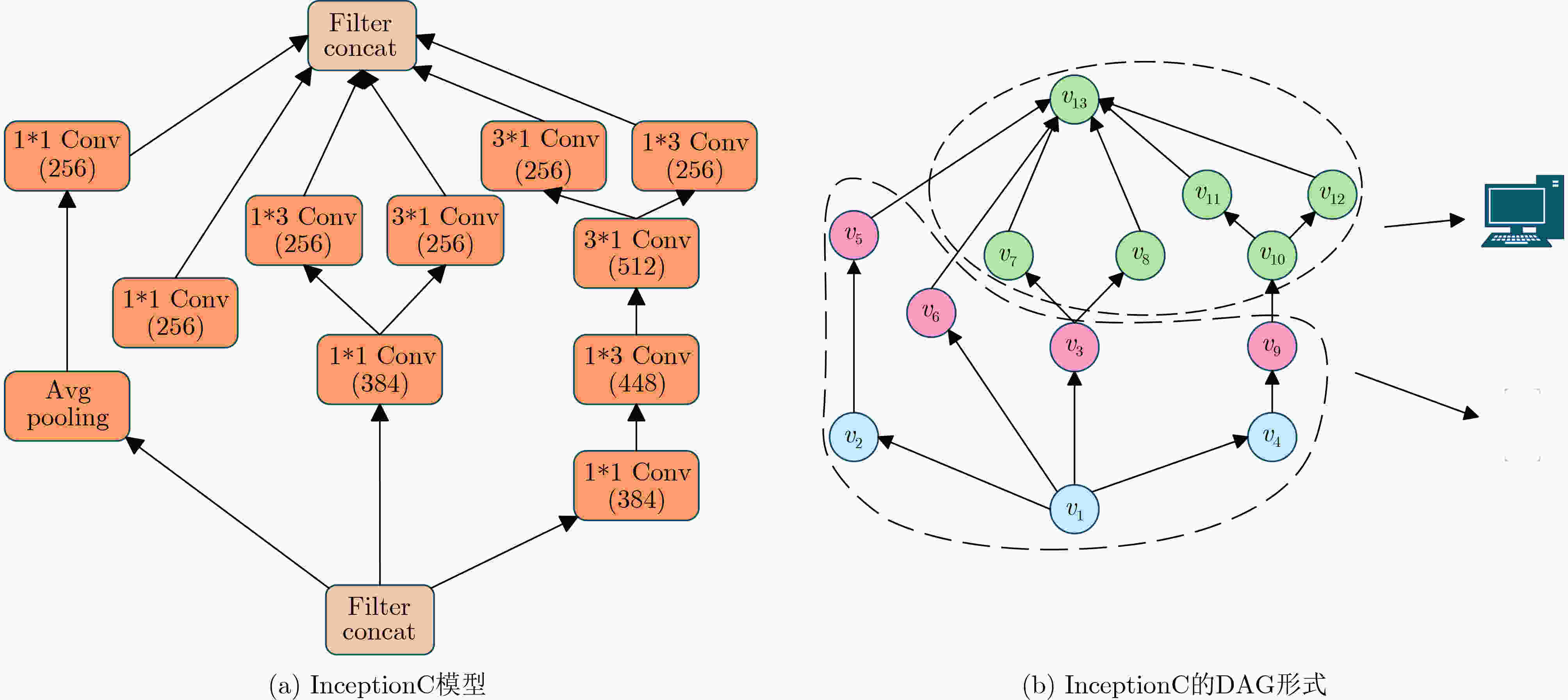
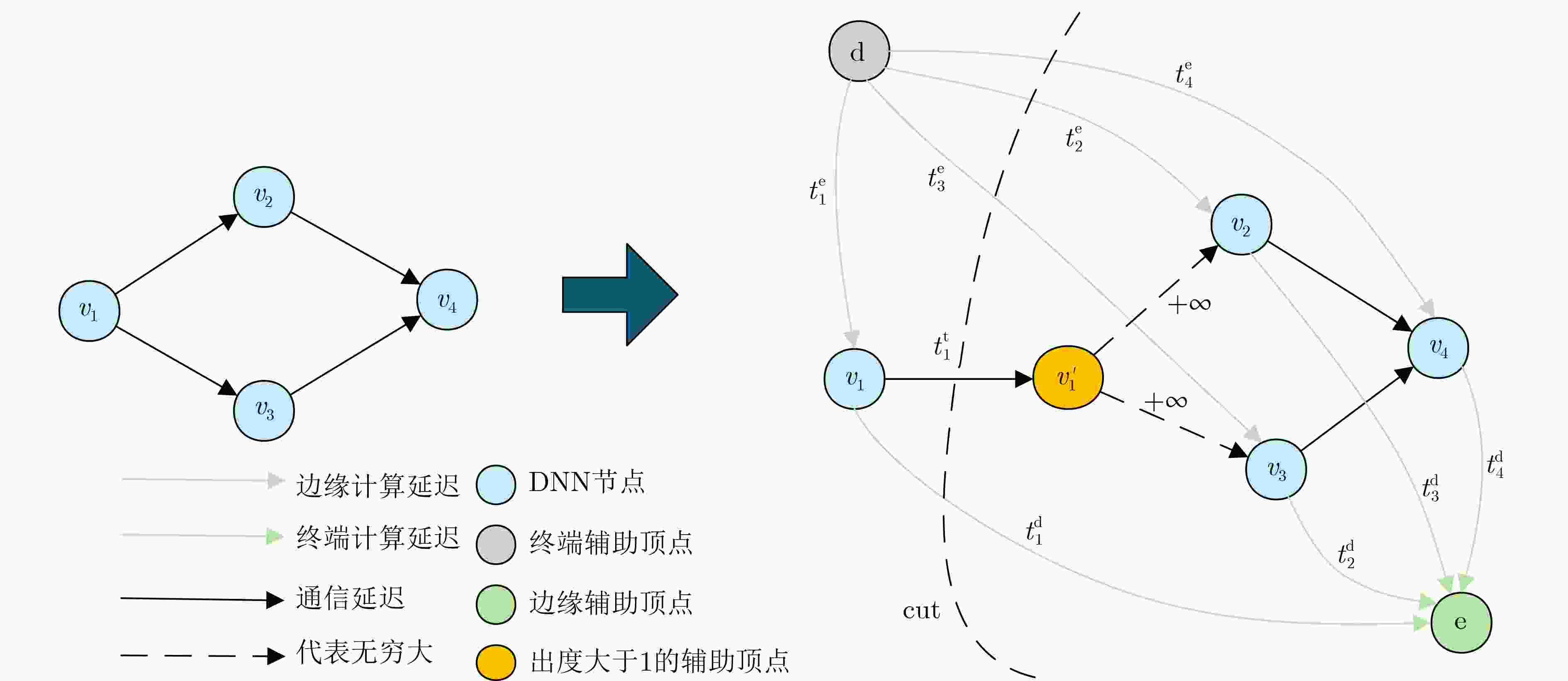
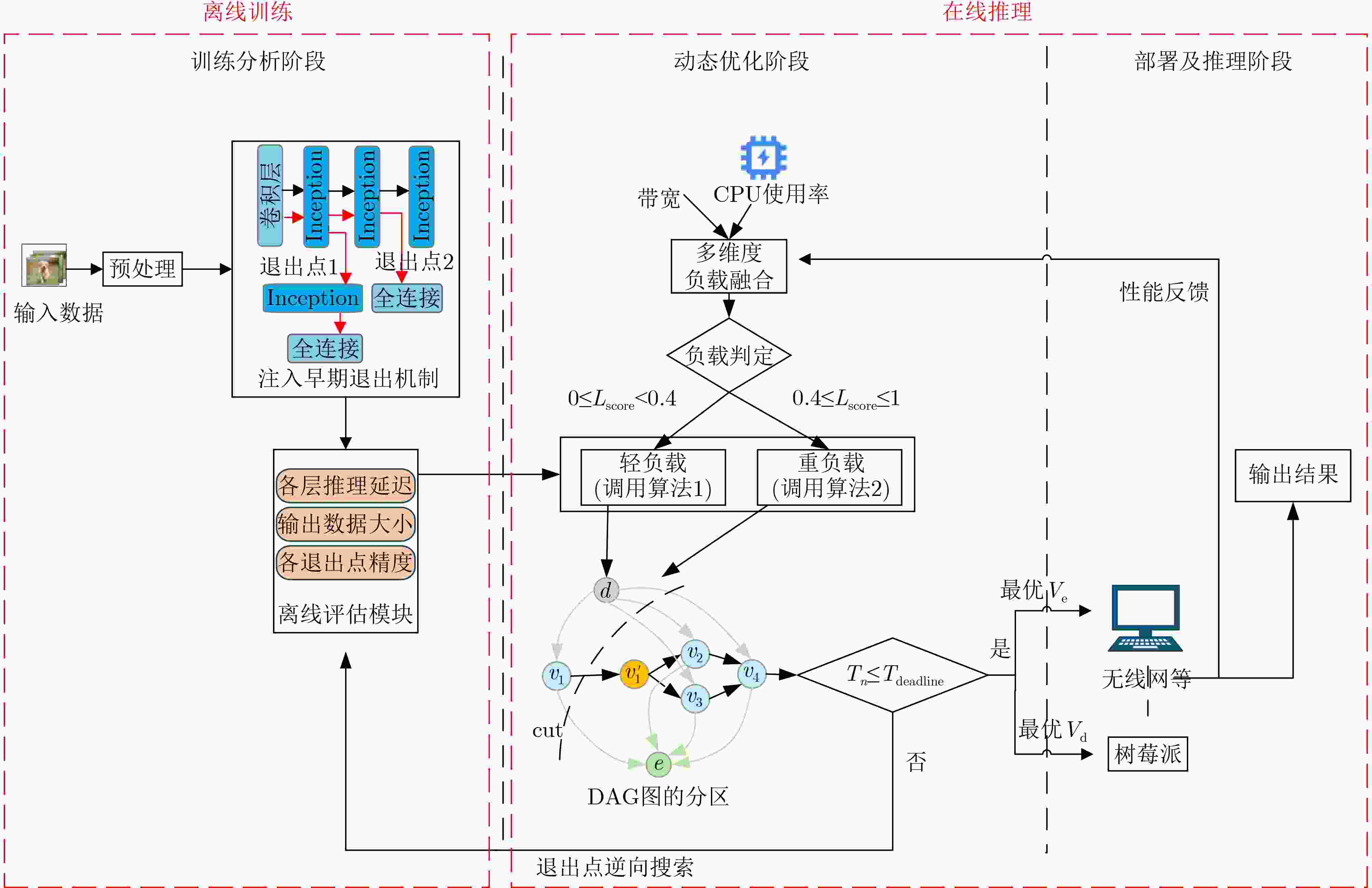
摘要: 在工业智能化场景中,深度神经网络(DNN)的推理任务因有向无环图(DAG)复杂结构特性与动态资源约束,面临延迟与精度难以协同优化的挑战。现有方法多局限于链式DNN,且缺乏对网络波动与异构计算资源的自适应支持。为此,该文提出一种边-端协作下基于早期退出机制的DNN动态自适应分区框架(DAPDEE),通过边-端协作实现高精度低延迟推理。其核心创新如下:将链式与复杂DNN统一表征为DAG结构,为分区优化提供通用拓扑基础;基于多任务学习离线优化各层早期退出分类器,部署时仅需加载预训练模型参数,结合实时网络带宽、终端计算负载等指标,动态选择最优退出点与分区策略;通过逆向搜索机制联合优化延迟与精度,轻负载下最小化单帧端到端延迟,重负载下最大化系统吞吐量。实验表明,在CIFAR-10数据集与VGG16和AlexNet模型上,DAPDEE在CAT1/3G/4G网络中较Device-Only方法降低延迟达7.7%(重负载)与7.5%(轻负载),吞吐量提升9.9倍,且精度损失始终低于1.2%。该框架为智能制造、自动驾驶等时敏场景中DAG结构DNN的高效推理提供了理论与技术支撑。Abstract:
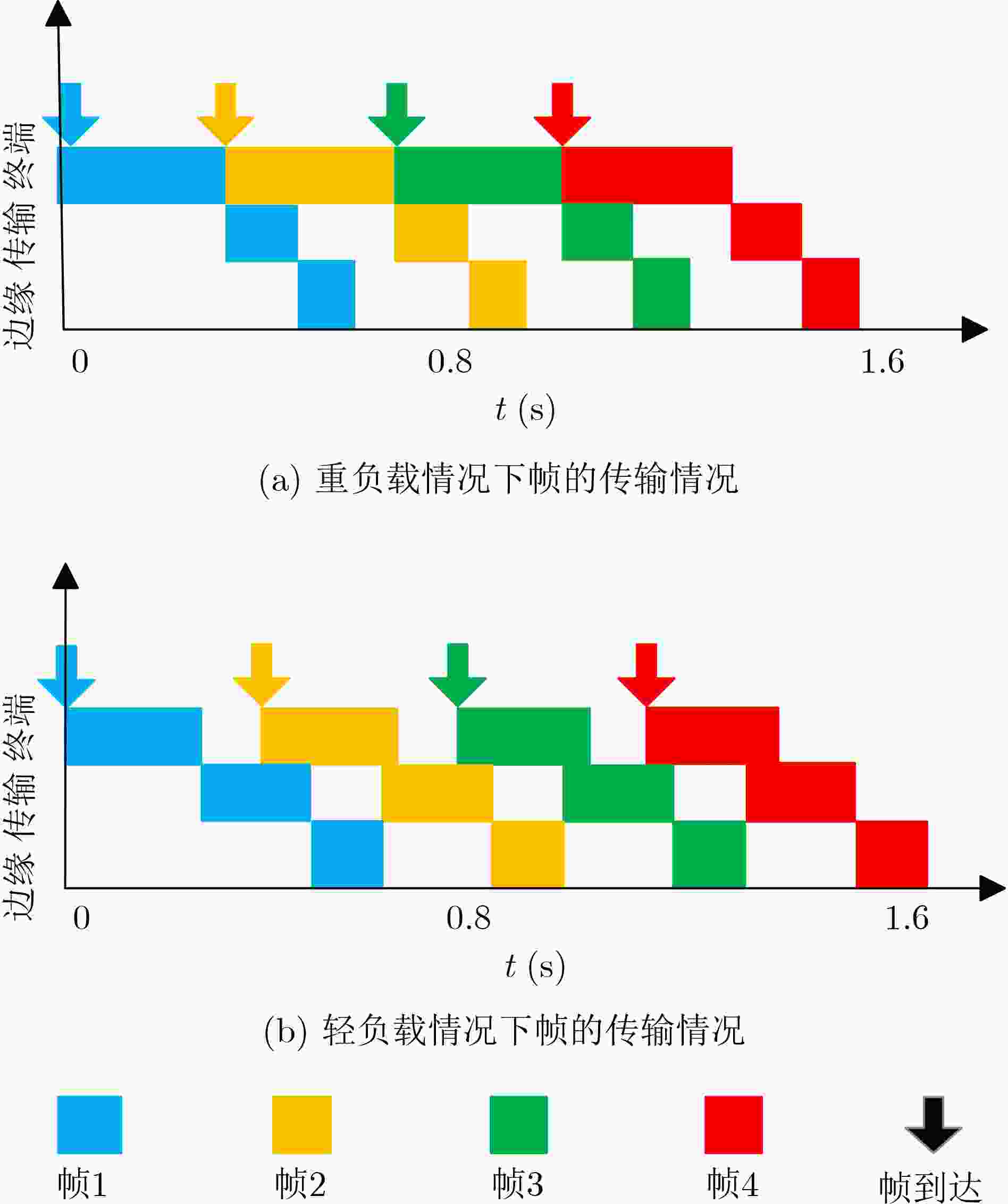
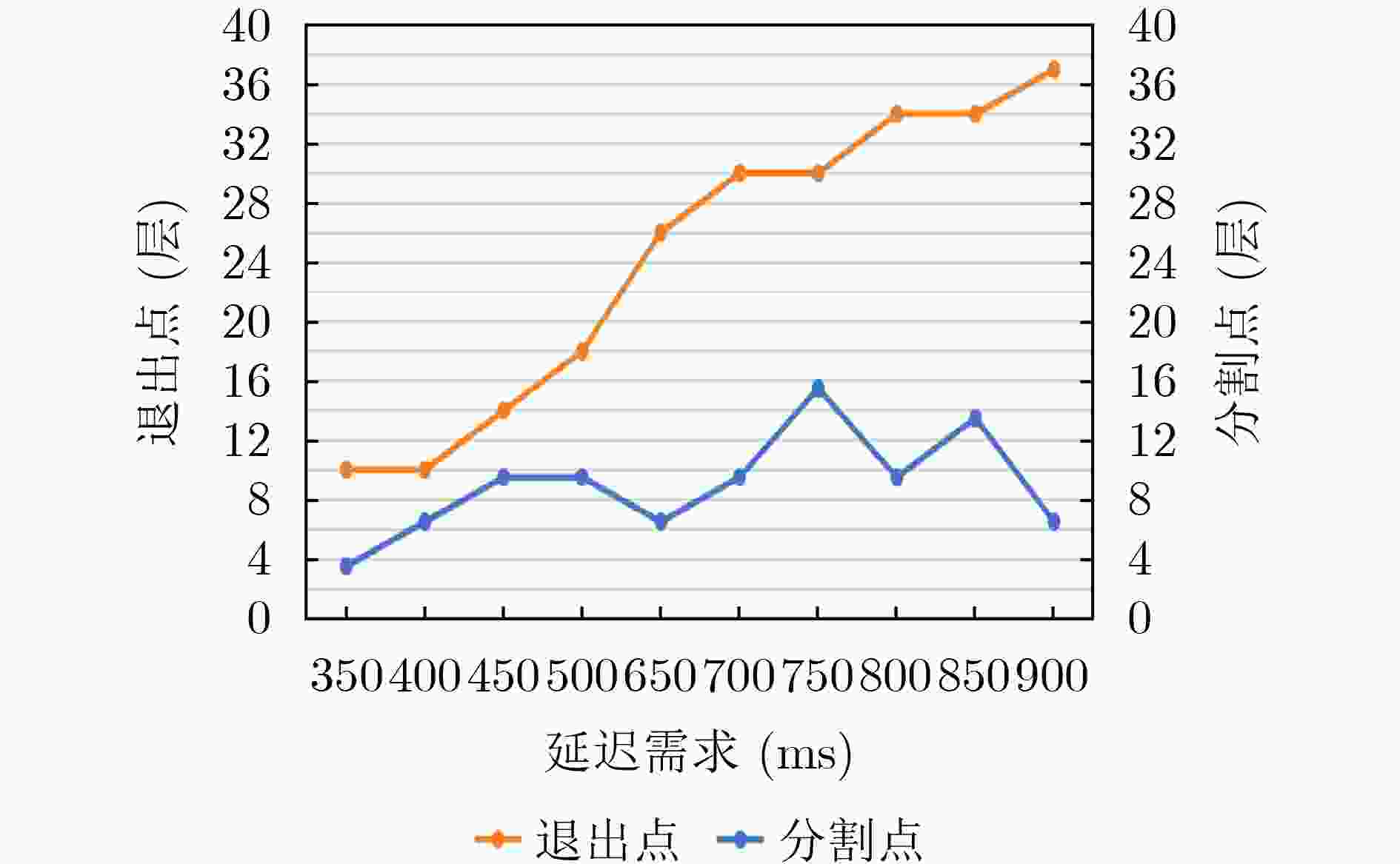
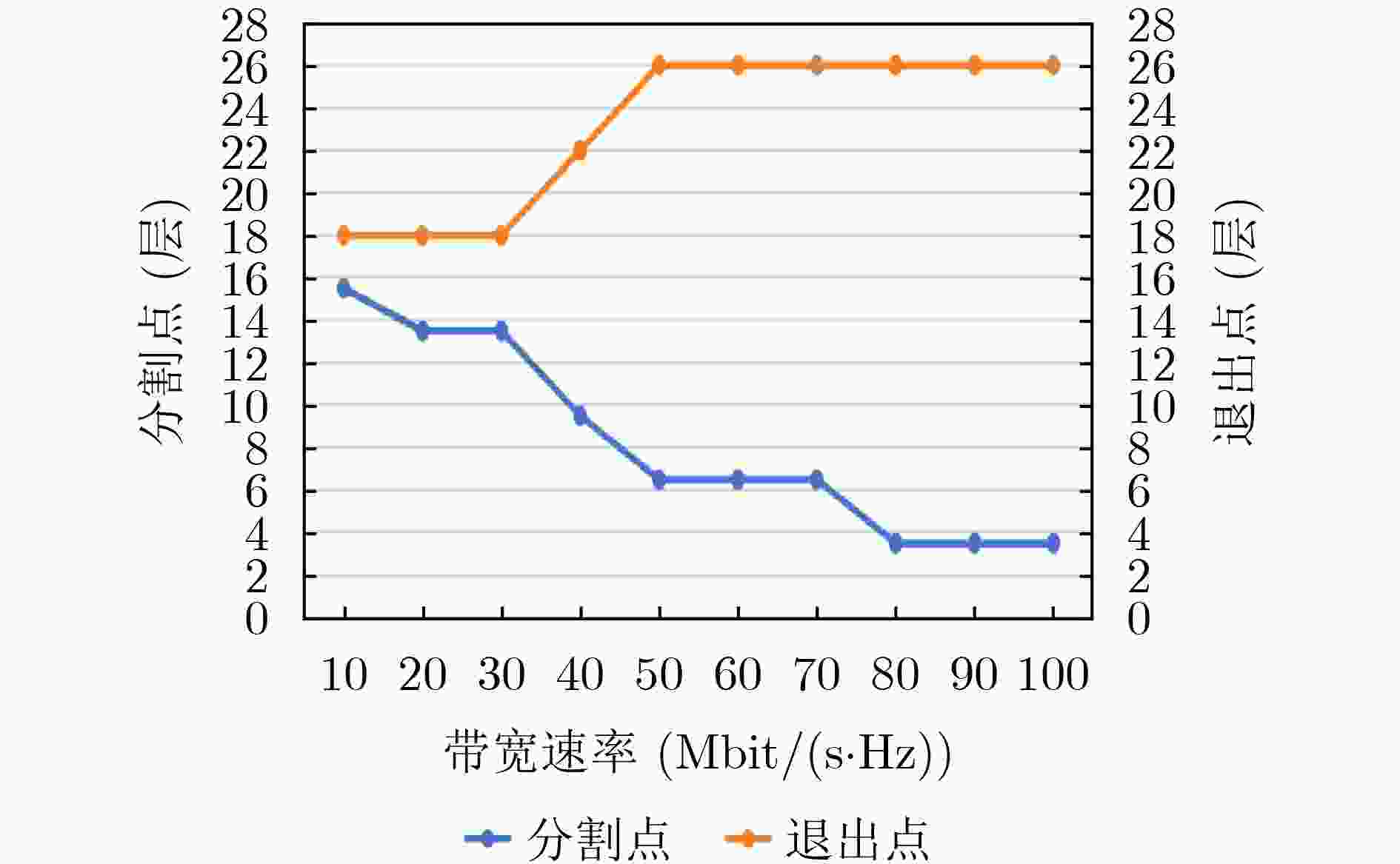
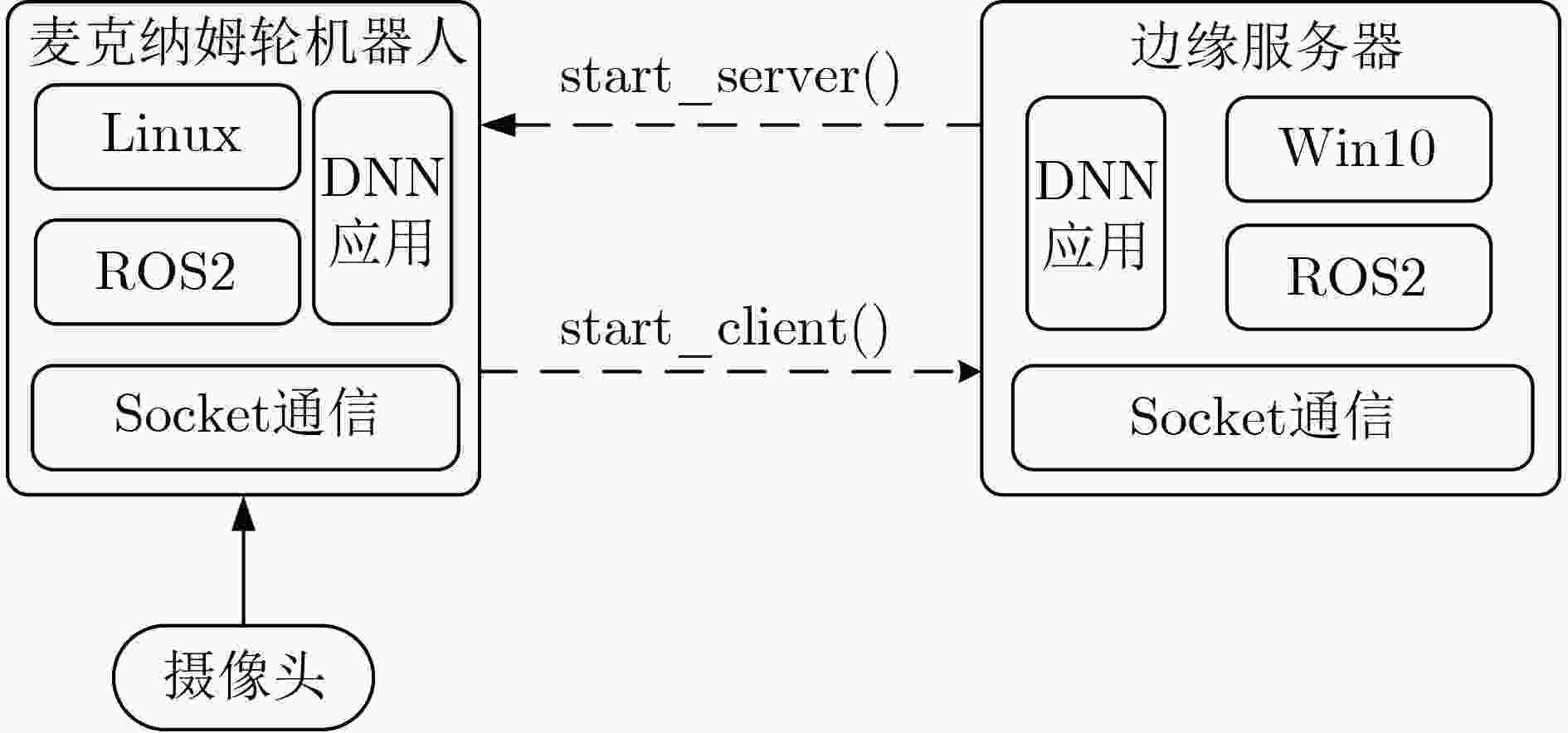
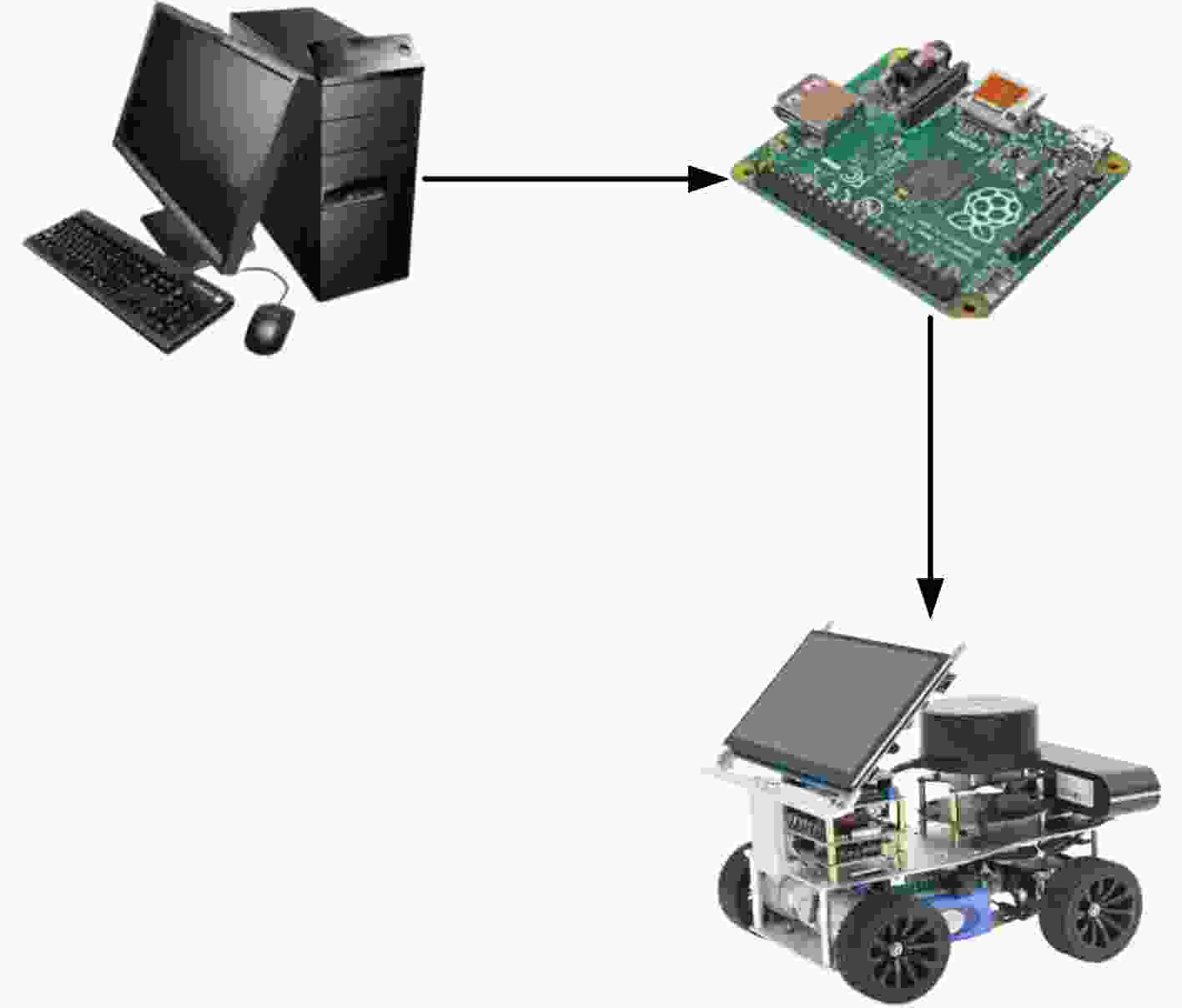
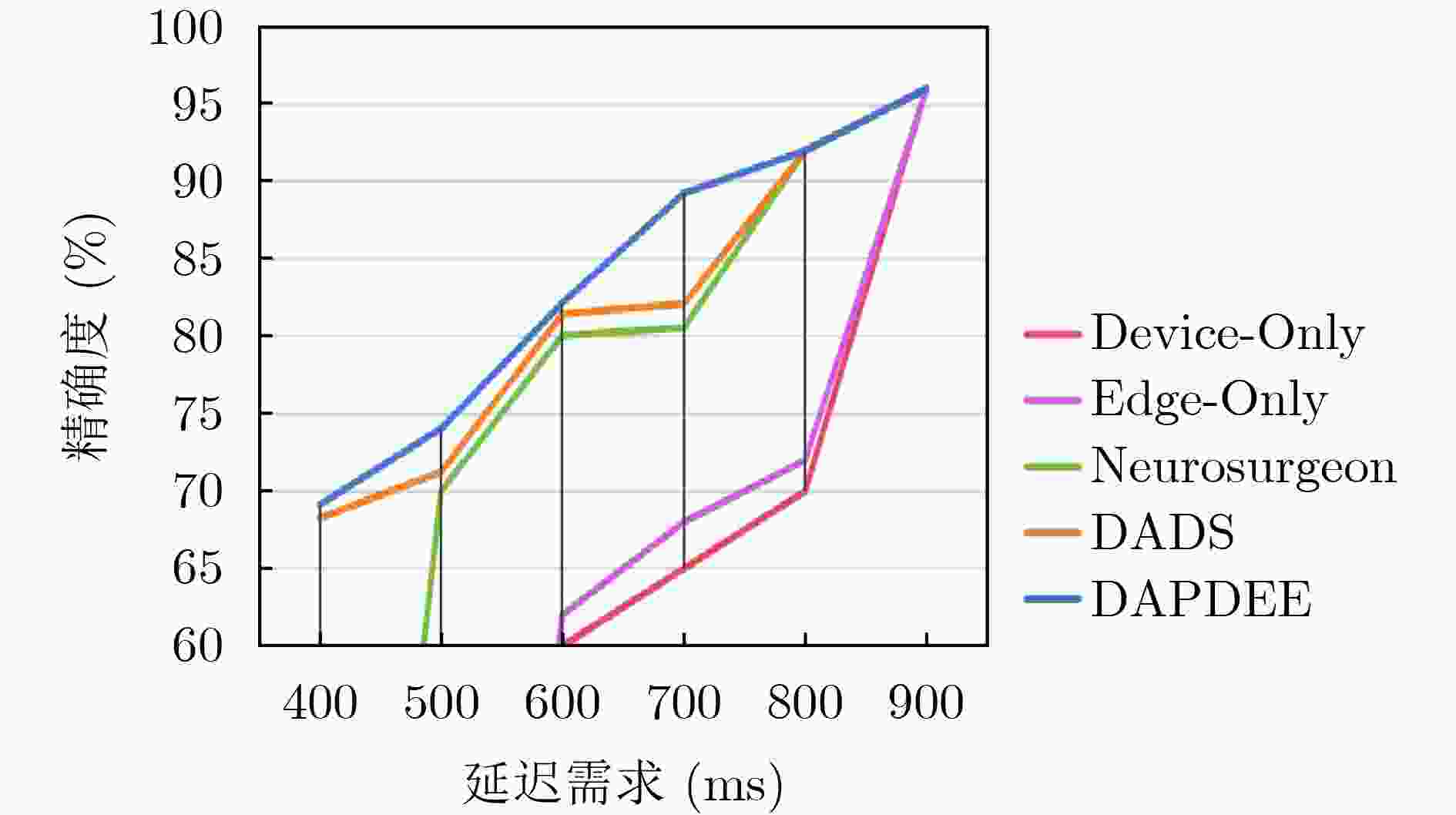
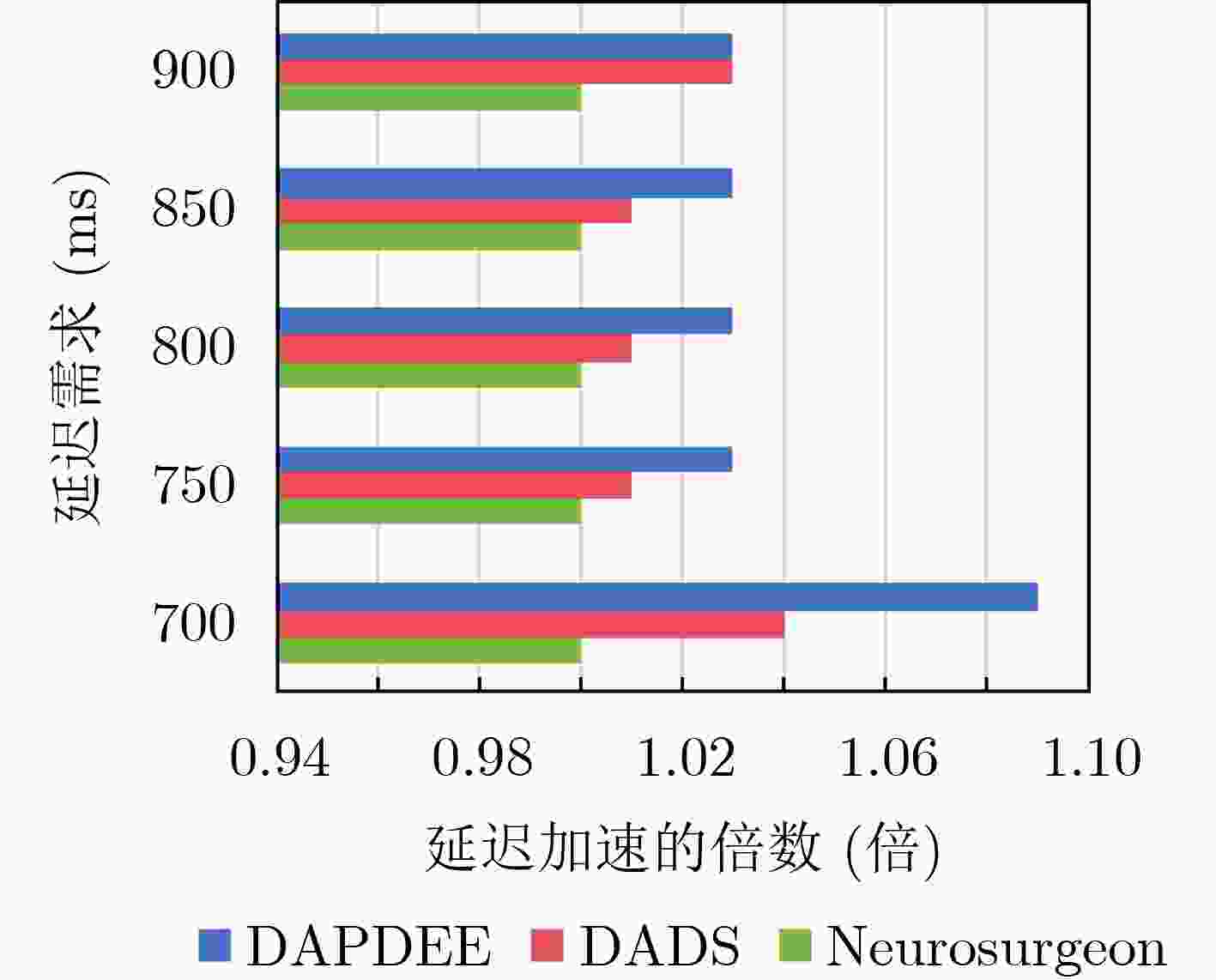
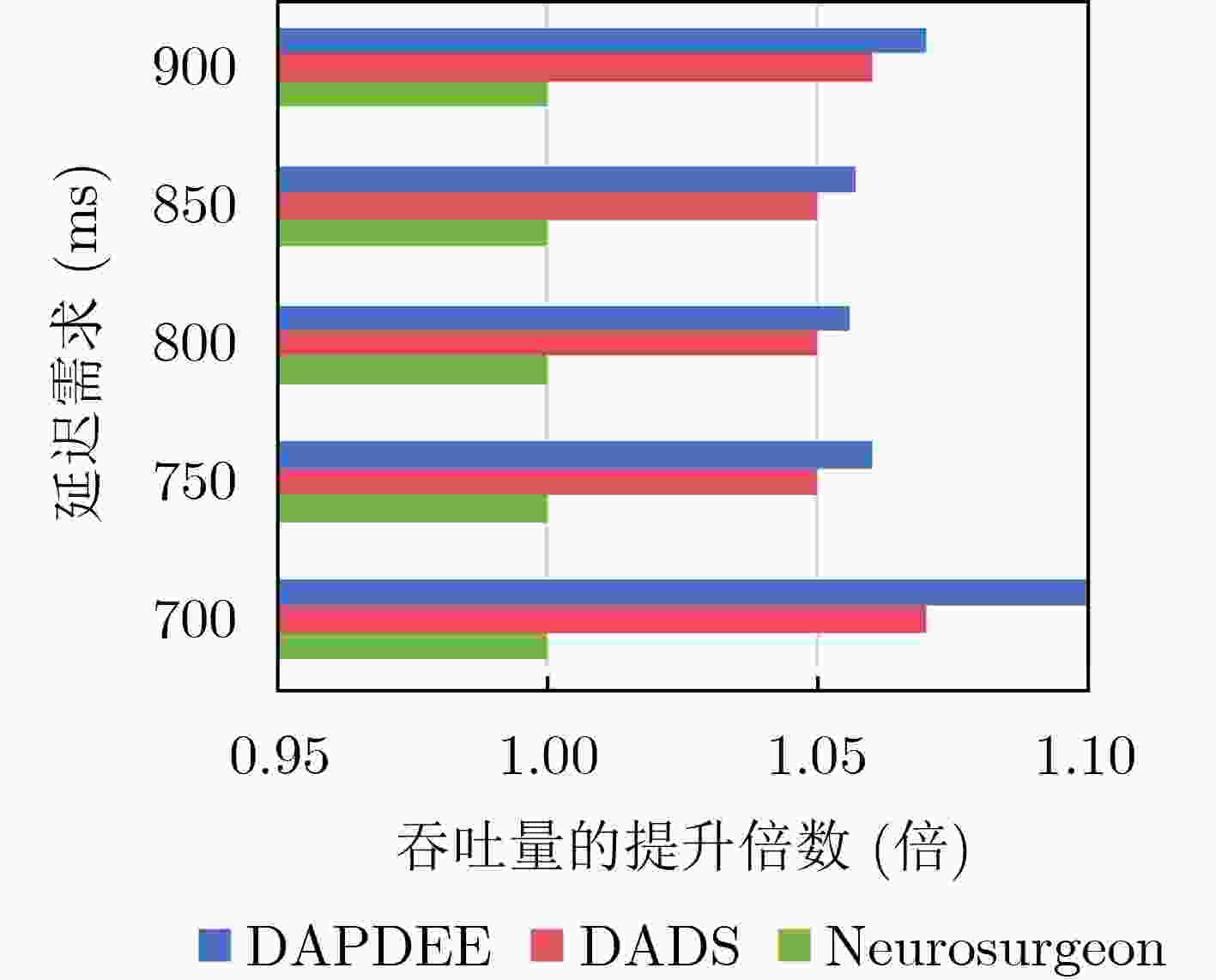
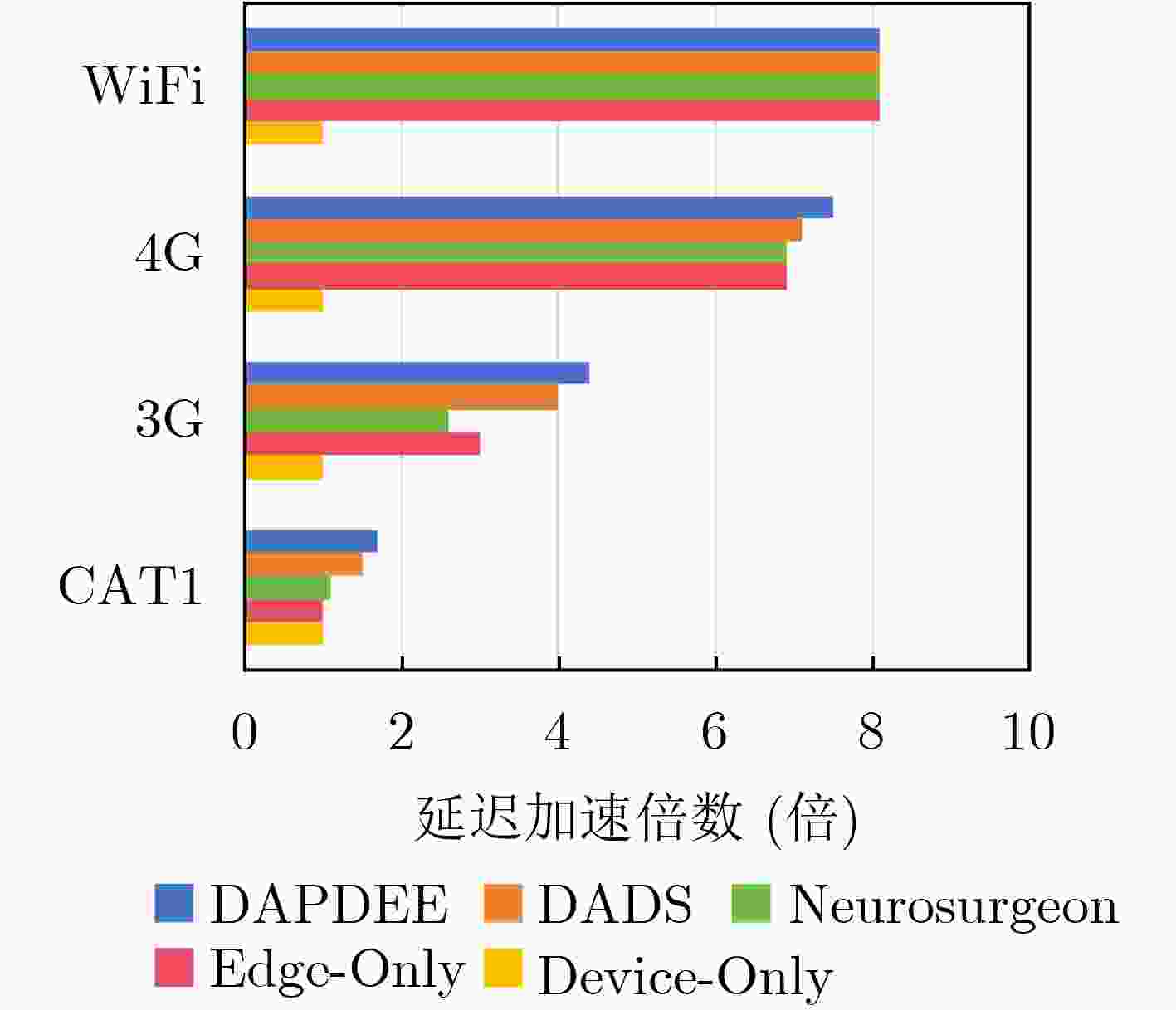
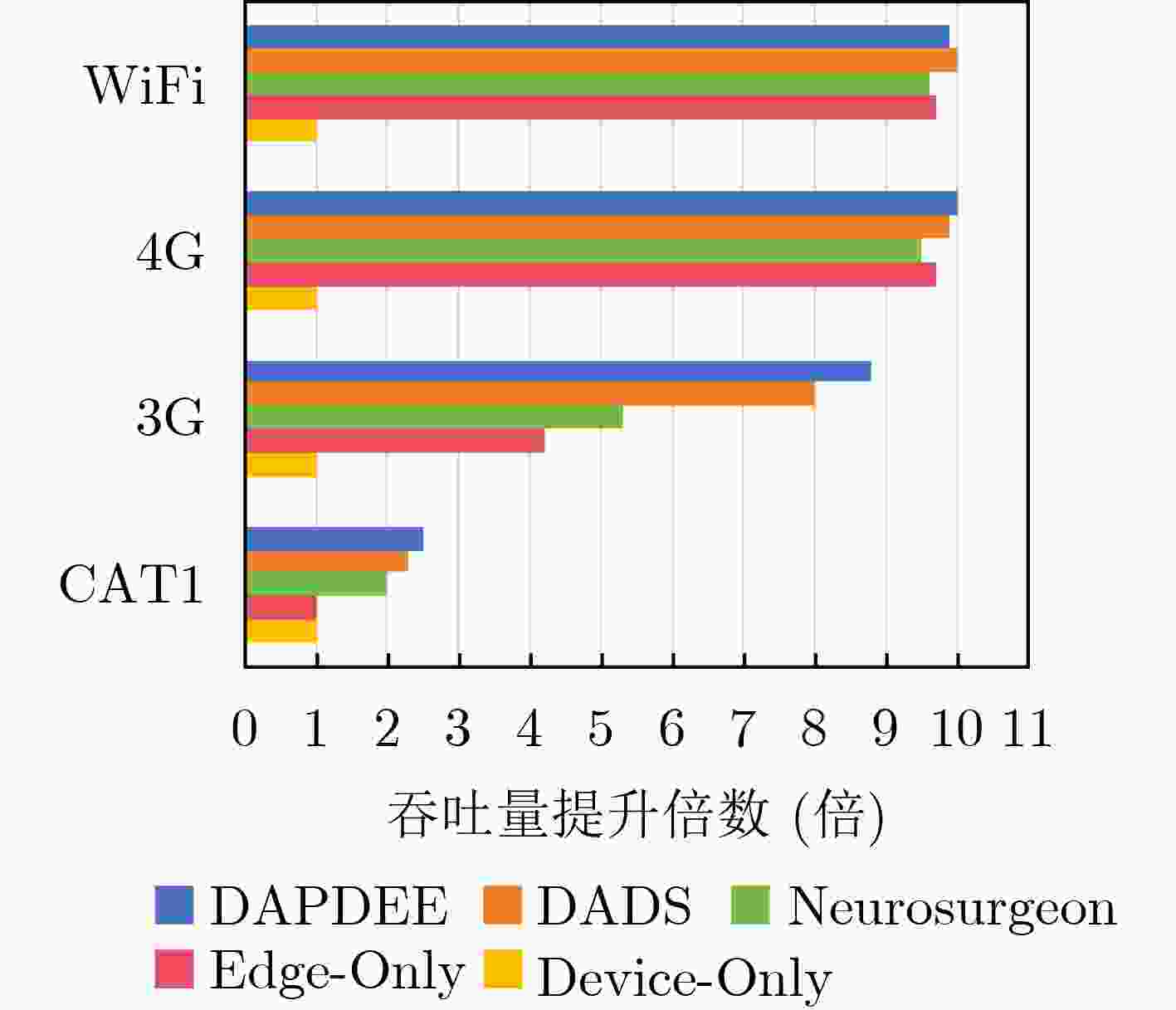
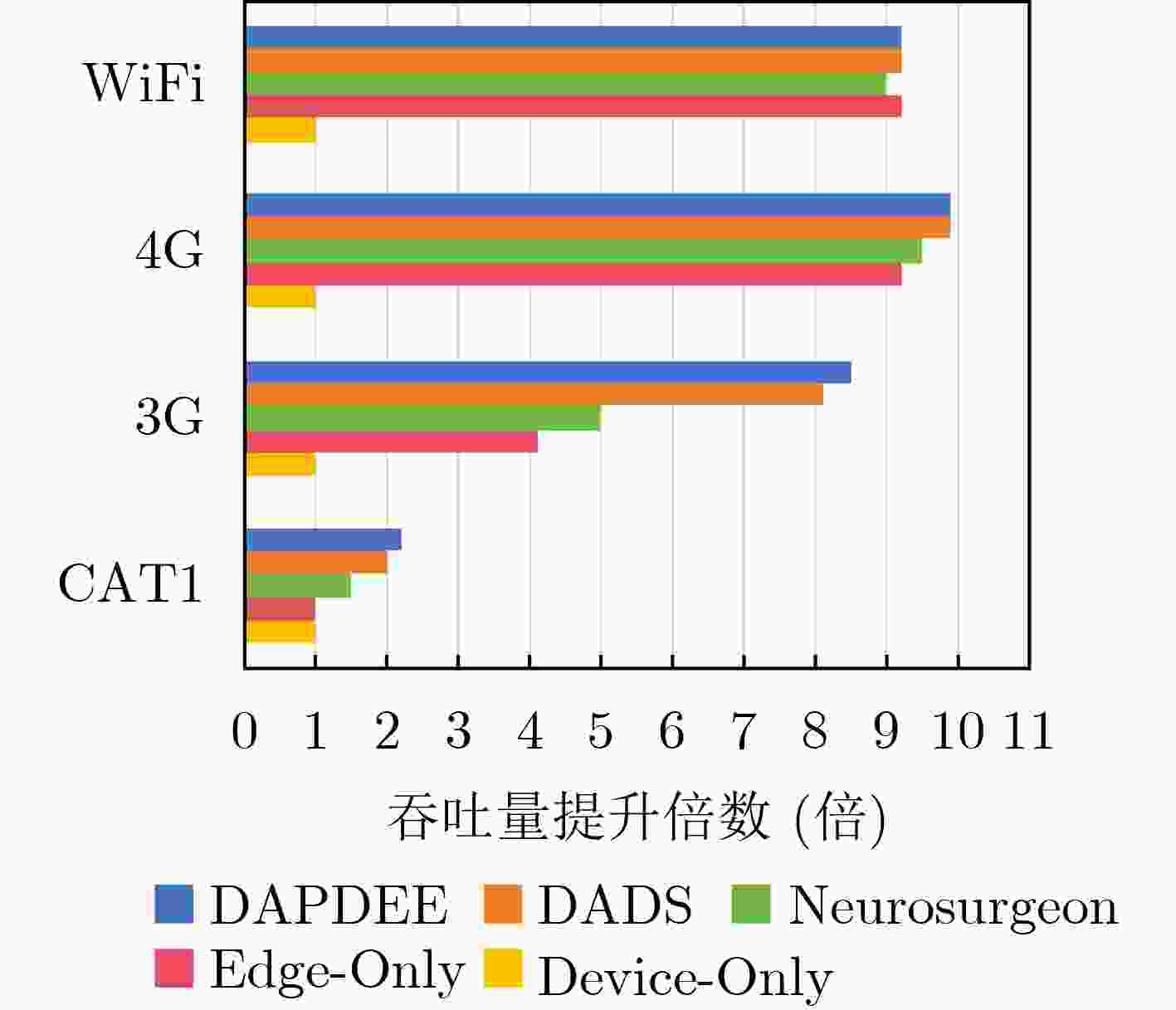
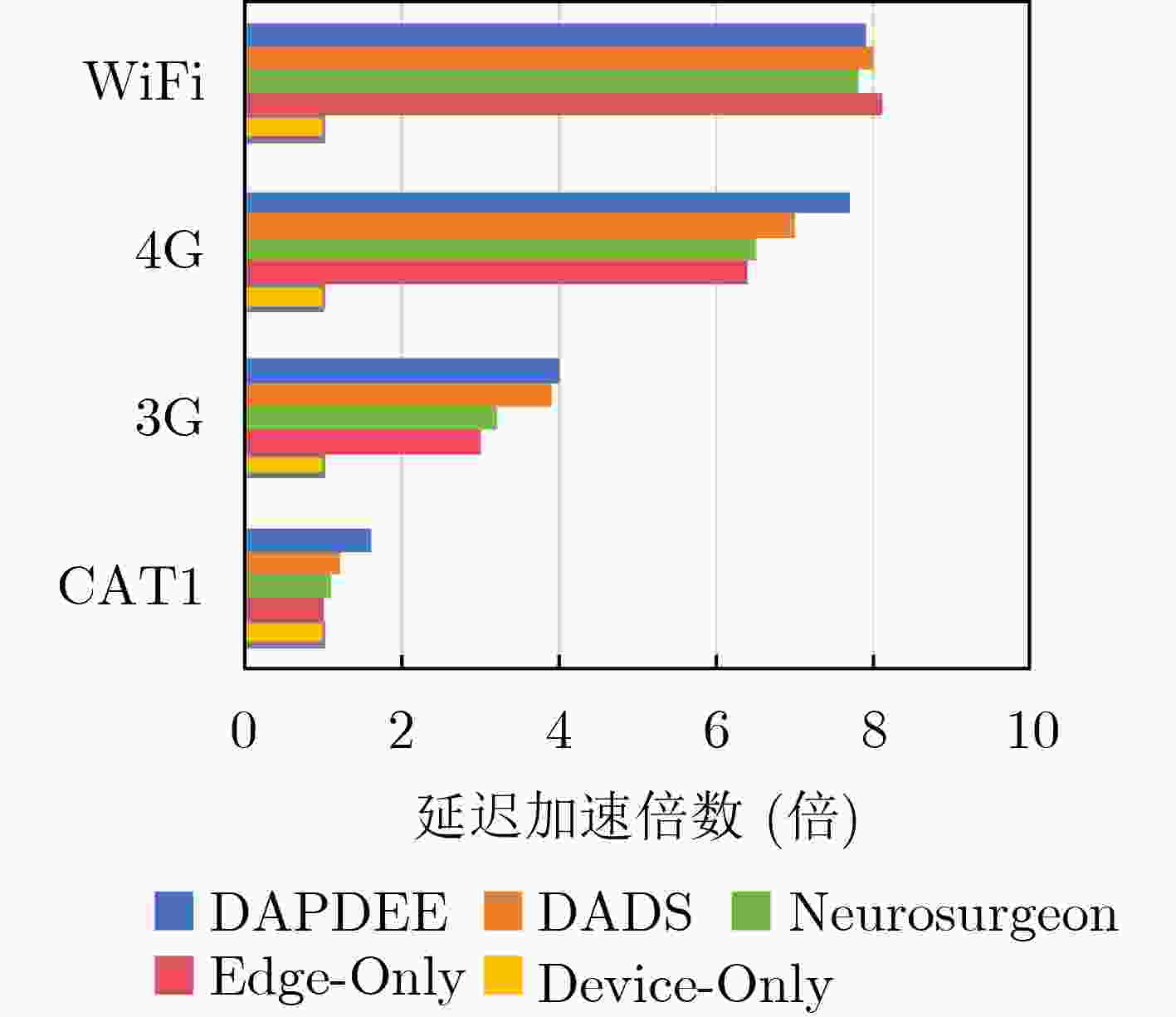
Objective The deployment of Deep Neural Networks (DNNs) for inference tasks in industrial intelligence applications is constrained by the complexity of Directed Acyclic Graph (DAG) structures and dynamic resource limitations, making it challenging to simultaneously optimize both latency and accuracy. Existing methods are generally restricted to chain-structured DNNs and lack adaptive mechanisms to accommodate network variability and heterogeneous computational resources. To address these limitations, this paper proposes a Dynamic Adaptive Partitioning framework based on a Deep Early Exit mechanism (DAPDEE), designed to achieve low-latency, high-accuracy inference through edge-end collaborative computing. The significance of this work lies in its potential to provide a generalizable solution suitable for diverse network conditions and computing environments. Methods The proposed DAPDEE framework incorporates several technical innovations: First, it abstracts both chain and complex DNN architectures into a unified DAG representation, establishing a general topological foundation for partition optimization. Second, it employs offline optimization of early exit classifiers using a multi-task learning approach, requiring only the loading of pre-trained model parameters during deployment. Combined with real-time indicators, such as network bandwidth and terminal computational load, this enables dynamic selection of optimal exit points and partitioning strategies. Finally, an inverse search mechanism is applied to jointly optimize latency and accuracy, aiming to minimize single-frame end-to-end delay under light workloads and to maximize system throughput under heavy workloads. Through these strategies, the framework enables efficient inference suitable for time-sensitive scenarios, including smart manufacturing and autonomous driving. Results and Discussions Experimental results demonstrate that the DAPDEE framework substantially improves performance compared to conventional Device-Only methods under varying network conditions. Specifically, under CAT1, 3G, and 4G networks, DAPDEE achieves latency reductions of up to 7.7% under heavy loads and 7.5% under light loads, with throughput improvements reaching up to 9.9 times. Notably, the accuracy loss remains consistently below 1.2% ( Fig. 6 ,Fig. 7 ), confirming the framework’s ability to maintain reliable inference performance. These results verify the effectiveness of DAPDEE in adapting to dynamic network environments and heterogeneous computational loads. For instance, when the bandwidth is fixed at 1.1 Mbps (3G), the optimal partition strategy adjusts in response to varying latency constraints, revealing a positive correlation between relaxed latency requirements and deeper exit points (Fig. 6 ). Conversely, with fixed latency constraints and increasing bandwidth, the partition point progressively shifts toward the terminal device, reflecting enhanced resource utilization on the end side (Fig. 7 ). Furthermore, practical deployments on a PC and a Raspberry Pi-based intelligent vehicle validate the theoretical performance gains, as demonstrated by the applied partitioning strategies (Algorithm 1, Algorithm 2).Conclusions In summary, the proposed DAPDEE framework effectively addresses the challenge of balancing inference efficiency and accuracy in edge-end collaborative scenarios involving complex DAG-structured DNNs. By integrating early exit mechanisms with dynamic partitioning strategies and multidimensional load evaluation, DAPDEE exhibits strong adaptability and robustness under diverse network conditions and resource constraints. These findings advance the current state of DNN partitioning methodologies and offer practical insights for optimizing cloud-edge-terminal architectures and reinforcement learning-based adaptive mechanisms. Nonetheless, areas for further improvement remain. These include incorporating multi-task concurrency, refining the energy consumption model, and enhancing real-time partitioning efficiency for complex DAG topologies. Future research will focus on extending the framework to support multi-task collaborative optimization and reducing the computational complexity of online partitioning algorithms for DAG-structured DNNs. -
1 DAPDEE轻负载分区算法
输入:$ G,{F}_{\mathrm{d}},{F}_{\mathrm{e}},D,B $ 输出:$ {V}_{\mathrm{d}},{V}_{\mathrm{s}},{V}_{\mathrm{e}},{T}_{\mathrm{d}},{T}_{\mathrm{t}},{T}_{\mathrm{e}} $ (1)计算网络特征:$ {F}_{\mathrm{t}}=\mathrm{n}\mathrm{e}\mathrm{t}(D,B) $ (2)构建扩展图$ {{G}}^{{{'}}} $:$ {G}^{{{'}}}=\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{h}(G,{F}_{\mathrm{d}},{F}_{\mathrm{e}},{F}_{\mathrm{t}}) $ (3)执行最小切割:$ \left[{V}_{\mathrm{d}},{V}_{\mathrm{s}},{V}_{\mathrm{e}},{T}_{\mathrm{d}},{T}_{\mathrm{t}},{T}_{\mathrm{e}}\right]=\mathrm{c}\mathrm{u}\mathrm{t}\left(G{{'}}\right) $ (4)返回结果:$ {V}_{\mathrm{d}},{V}_{\mathrm{s}},{V}_{\mathrm{e}},{T}_{\mathrm{d}},{T}_{\mathrm{t}},{T}_{\mathrm{e}} $ 2 DAPDEE重负载分区算法
输入:$ G,{F}_{\mathrm{d}},{F}_{\mathrm{e}},{D}_{\mathrm{t}},B,\varepsilon ,K $ 输出:$ {V}_{\mathrm{d}},{V}_{\mathrm{s}},{V}_{\mathrm{e}},{T}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ (1)计算网络特征:$ {F}_{\mathrm{t}}=\mathrm{n}\mathrm{e}\mathrm{t}({D}_{\mathrm{t}},B) $ (2)当$ \left|{T}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{{{'}}}-{T}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right|\ge \varepsilon $时循环: (3)更新$ {T}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{{{'}}} $:$ {T}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{{{'}}}={T}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ (4)执行搜索:$ \left[\alpha ,\gamma ,{V}_{\mathrm{d}},{V}_{\mathrm{s}},{V}_{\mathrm{e}},{T}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right]=\mathrm{S}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{h}\left(\right) $算法 (5)返回结果:返回 $ {V}_{\mathrm{d}},{V}_{\mathrm{s}},{V}_{\mathrm{e}},{T}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 3 search()算法
(1)初始化参数:$ {T}_{\mathrm{m}\mathrm{a}\mathrm{x}}=+\infty $ (2)遍历$ \alpha $的范围:对于每个$ \alpha $从$ {\alpha }_{x} $~$ {\alpha }_{y} $,步长为$ \delta $: (3)遍历$ \gamma $的范围: 对于每个$ \gamma $从$ {\gamma }_{x} $~$ {\gamma }_{y} $,步长为$ \delta $: (4)执行算法1: $ \left[{V}_{\mathrm{d}},{V}_{\mathrm{s}},{V}_{\mathrm{e}},{T}_{\mathrm{d}},{T}_{\mathrm{t}},{T}_{\mathrm{e}}\right]=\mathrm{算}\mathrm{法}1 $ (5)计算最大时间: $ {T}_{\mathrm{m}\mathrm{a}\mathrm{x}}=\mathrm{m}\mathrm{a}\mathrm{x}({T}_{\mathrm{d}},{T}_{\mathrm{t}},{T}_{\mathrm{e}}) $ (6)更新最优解: 如果$ {T}_{\mathrm{m}\mathrm{a}\mathrm{x}}\le {T}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{*}} $,
$ {\alpha }^{*}=\alpha ;{\gamma }^{*}=\gamma ;{T}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{*}={T}_{\mathrm{m}\mathrm{a}\mathrm{x}} $(7)返回结果: 返回 $ {\alpha }^{*},{\gamma }^{*},{V}_{\mathrm{d}},{V}_{\mathrm{s}},{V}_{\mathrm{e}},{T}_{\mathrm{d}},{T}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{*} $ 4 优化算法
输入:$ \mathrm{E}\mathrm{x}\mathrm{i}\mathrm{t}=\left\{\mathrm{1,2},\cdots ,N-1\right\},A=\left\{{\alpha }_{1},{\alpha }_{2},\cdots ,{\alpha }_{N-1}\right\},G,{F}_{\mathrm{d}} $,
${F}_{\mathrm{e}},{D}_{\mathrm{t}},B,T $, ${C}_{\mathrm{u}\mathrm{s}\mathrm{a}\mathrm{g}\mathrm{e}},{M}_{\mathrm{u}\mathrm{s}\mathrm{a}\mathrm{g}\mathrm{e}} $, ${B}_{\mathrm{u}\mathrm{p}},{D}_{\mathrm{n}\mathrm{e}\mathrm{t}},{E}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{y}},{P}_{\mathrm{t}\mathrm{a}\mathrm{s}\mathrm{k}},{T}_{\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{d}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}} $输出:退出点$ n $和分区策略$ {S}_{n} $ (1) 初始化:实时采集系统指标 (2) 对于每个$ n $从$ N-1 $~1: (3) 选择退出点$ n $,构建的$ {G}_{n} $扩展图$ {G}_{n}{{'}} $ (4) 归一化各维度指标 (5) 动态分配权重 (6) 计算综合负载评分$ {L}_{\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}=\displaystyle\sum\nolimits_{i=1}^{k}{\omega }_{i}\cdot {\hat{X}}_{i} $ (7) 如果任一指标变化超过阈值$ \Delta X={\mu }_{X}+2{\sigma }_{X} $: (8) 触发权重更新并重新计算$ {L}_{\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}} $ (9) 如果当前任务优先级$ {P}_{\mathrm{t}\mathrm{a}\mathrm{s}\mathrm{k}} $为高(=1.0): (10) 立即调用轻负载算法(算法1) (11) 如果$ {0\le L}_{\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}} < 0.4 $: (12) 调用轻负载分区算法(算法1) (13) 如果$ {0.4\le L}_{\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}e}\le 1 $: (14) 调用重负载分区算法(算法2) (15) 计算总时间:$ {T}_{n}=\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}T\left({T}_{\mathrm{d}}+{T}_{\mathrm{t}}+{T}_{\mathrm{e}}\right) $ (16) 如果 $ {T}_{n}\le {T}_{\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{d}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}} $: (17) 返回退出点$ n $和分区策略$ {S}_{n} $ (18) 否则: (19) 继续循环 (20) 根据实际推理延迟和精度数据,更新权重$ {\omega }_{i} $与动态阈值$ \Delta X $ (21) 返回退出点$ n $和分区策略$ {S}_{n} $ -
[1] BASHA S H S, FARAZUDDIN M, PULABAIGARI V, et al. Deep model compression based on the training history[J]. Neurocomputing, 2024, 573: 127257. doi: 10.1016/j.neucom.2024.127257. [2] CHENG Hongrong, ZHANG Miao, and SHI J Q. A survey on deep neural network pruning: Taxonomy, comparison, analysis, and recommendations[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2024, 46(12): 10558–10578. doi: 10.1109/TPAMI.2024.3447085. [3] HUANG Mingzhong, LIU Yan, ZHAO Lijie, et al. A lightweight deep neural network model and its applications based on channel pruning and group vector quantization[J]. Neural Computing and Applications, 2024, 36(10): 5333–5346. doi: 10.1007/s00521-023-09332-z. [4] SAPKAL A, HEISNAM L, and KUSI S S. Evolution of cloud computing: Milestones, innovations, and adoption trends[J]. International Research Journal of Engineering and Technology (IRJET), 2024, 11(3): 548–563. [5] FU Ziyan, ZHOU Yuezhi, WU Chao, et al. Joint optimization of data transfer and co-execution for DNN in edge computing[C]. ICC 2021-IEEE International Conference on Communications, Montreal, Canada, 2021: 1–6. doi: 10.1109/ICC42927.2021.9500513. [6] 曹绍华, 陈辉, 陈舒, 等. AccFed: 物联网中基于模型分割的联邦学习加速[J]. 电子与信息学报, 2023, 45(5): 1678–1687. doi: 10.11999/JEIT220240.CAO Shaohua, CHEN Hui, CHEN Shu, et al. AccFed: Federated learning acceleration based on model partitioning in internet of things[J]. Journal of Electronics & Information Technology, 2023, 45(5): 1678–1687. doi: 10.11999/JEIT220240. [7] WANG Yingchao, YANG Chen, LAN Shulin, et al. End-edge-cloud collaborative computing for deep learning: A comprehensive survey[J]. IEEE Communications Surveys & Tutorials, 2024, 26(4): 2647–2683. doi: 10.1109/COMST.2024.3393230. [8] LIANG Huanghuang, SANG Qianlong, HU Chuang, et al. DNN surgery: Accelerating DNN inference on the edge through layer partitioning[J]. IEEE Transactions on Cloud Computing, 2023, 11(3): 3111–3125. doi: 10.1109/TCC.2023.3258982. [9] 李峰, 毕冉, 马野, 等. 带优先级DAG实时任务图模型的响应时间分析[J]. 计算机学报, 2024, 47(12): 2909–2924. doi: 10.11897/SP.J.1016.2024.02909.LI Feng, BI Ran, MA Ye, et al. Response time analysis for prioritized DAG task[J]. Chinese Journal of Computers, 2024, 47(12): 2909–2924. doi: 10.11897/SP.J.1016.2024.02909. [10] RAHMATH P H, SRIVASTAVA V, CHAURASIA K, et al. Early-exit deep neural network - A comprehensive survey[J]. ACM Computing Surveys, 2024, 57(3): 75. doi: 10.1145/3698767. [11] KANG, Yiping, HAUSWALD J, GAO Cao, et al. Neurosurgeon: Collaborative intelligence between the cloud and mobile edge[C]. The Twenty-Second International Conference on Architectural Support for Programming Languages and Operating Systems, Xi’an, China, 2017: 615–629. doi: 10.1145/3037697.3037698. [12] HU Chuang, BAO Wei, WANG Dan, et al. Dynamic adaptive DNN surgery for inference acceleration on the edge[C]. IEEE INFOCOM 2019 - IEEE Conference on Computer Communications, Paris, France, 2019: 1423–1431. doi: 10.1109/INFOCOM.2019.8737614. [13] WANG Huitian, CAI Guangxing, HUANG Zhaowu, et al. ADDA: Adaptive distributed DNN inference acceleration in edge computing environment[C]. 2019 IEEE 25th International Conference on Parallel and Distributed Systems (ICPADS), Tianjin, China, 2019: 438–445. doi: 10.1109/ICPADS47876.2019.00069. [14] 施建锋, 陈忻阳, 李宝龙. 面向物联网的云边端协同计算中任务卸载与资源分配算法研究[J]. 电子与信息学报, 2025, 47(2): 458–469. doi: 10.11999/JEIT240659.SHI Jianfeng, CHEN Xinyang, and LI Baolong. Research on task offloading and resource allocation algorithms in cloud-edge-end collaborative computing for the internet of things[J]. Journal of Electronics & Information Technology, 2025, 47(2): 458–469. doi: 10.11999/JEIT240659. [15] TEERAPITTAYANON S, MCDANEL B, and KUNG H T. BranchyNet: Fast inference via early exiting from deep neural networks[C]. 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 2016: 2464–2469. doi: 10.1109/ICPR.2016.7900006. [16] TEERAPITTAYANON S, MCDANEL B, and KUNG H T. Distributed deep neural networks over the cloud, the edge and end devices[C]. 2017 IEEE 37th International Conference on Distributed Computing Systems (ICDCS), Atlanta, USA, 2017: 328–339. doi: 10.1109/ICDCS.2017.226. [17] LANE N, BHATTACHARYA S, MATHUR A, et al. DXTK: Enabling resource-efficient deep learning on mobile and embedded devices with the DeepX toolkit[C]. The 8th EAI International Conference on Mobile Computing, Applications and Services, Cambridge, UK, 2016: 98–107. doi: 10.4108/eai.30-11-2016.2267463. -





 下载:
下载:



 下载:
下载:
