可重构铁电数据选择器设计及在映射中的应用

吴乾火; 王伦耀; 查晓婧; 储著飞; 夏银水

doi:10.11999/JEIT250263

可重构铁电数据选择器设计及在映射中的应用

doi: 10.11999/JEIT250263 cstr: 32379.14.JEIT250263

宁波大学信息科学与工程学院宁波 315211

基金项目: 国家自然科学基金(U23A20351, 62304115)，浙江省自然科学基金创新群体项目(LDT23F04021F04)，宁波市重点研发计划(2023Z233, 2023Z071)，浙江省教育厅一般项目(Y202248965)

详细信息

作者简介:
吴乾火：男，硕士生，研究方向为铁电存算一体电路设计和逻辑综合

王伦耀：男，教授，研究方向为存算一体逻辑电路设计与综合

查晓婧：女，讲师，研究方向为存算一体逻辑综合

储著飞：男，教授，研究方向为集成电路设计自动化

夏银水：男，教授，研究方向为低功耗集成电路设计

通讯作者:
王伦耀　wanglunyao@nbu.edu.cn

中图分类号: TP331.1
计量
- 文章访问数: 154
- HTML全文浏览量: 55
- PDF下载量: 34
- 被引次数: 0
出版历程
- 收稿日期: 2025-04-14
- 修回日期: 2025-07-21
- 网络出版日期: 2025-08-07

Design of Reconfigurable FeFET-MUX and Its Application in Mapping

Faculty of Electrical Engineering and Computer Science, Ningbo university, Ningbo 315211, China

Funds: The National Natural Science Foundation of China (U23A20351, 62304115), The Natural Science Foundation of Zhejiang Province (LDT23F04021F04), Ningbo Key Research and Development Program (2023Z233, 2023Z071), General Project of Zhejiang Provincial Education Department (Y202248965)

摘要

摘要: 目前以铁电晶体管(FeFET)为基础的存算一体逻辑电路的映射以阵列为主，该文提出一种以铁电晶体管-数据选择器(FeFET-MUX)为基本电路单元存算一体逻辑电路的实现方法。该方法主要包含两方面内容：(1) 提出一种可重构的FeFET-MUX电路，该电路具有结构共享、数据输入端可扩展的特点。(2) 提出适合该FeFET-MUX映射的逻辑函数分割方法，通过将待实现的逻辑函数表示成二元决策图(BDD)，然后将BDD分割成适合FeFET-MUX映射的子BDD集合，最后完成逻辑函数用FeFET-MUX的映射。该文所提FeFET-MUX电路的逻辑功能用已有的FeFET模型进行仿真验证，用于映射的BDD分割算法用C++实现。实验结果表明，相比于传统的非结构共享二选一FeFET-MUX电路的映射结果，采用所提结构共享FeFET-MUX电路结合BDD分割算法，FeFET的使用数量平均可以减少79.9%。
- 逻辑电路映射 /
- 存算一体 /
- 铁电晶体管电路 /
- 数据选择器 /
- 二元决策图分割
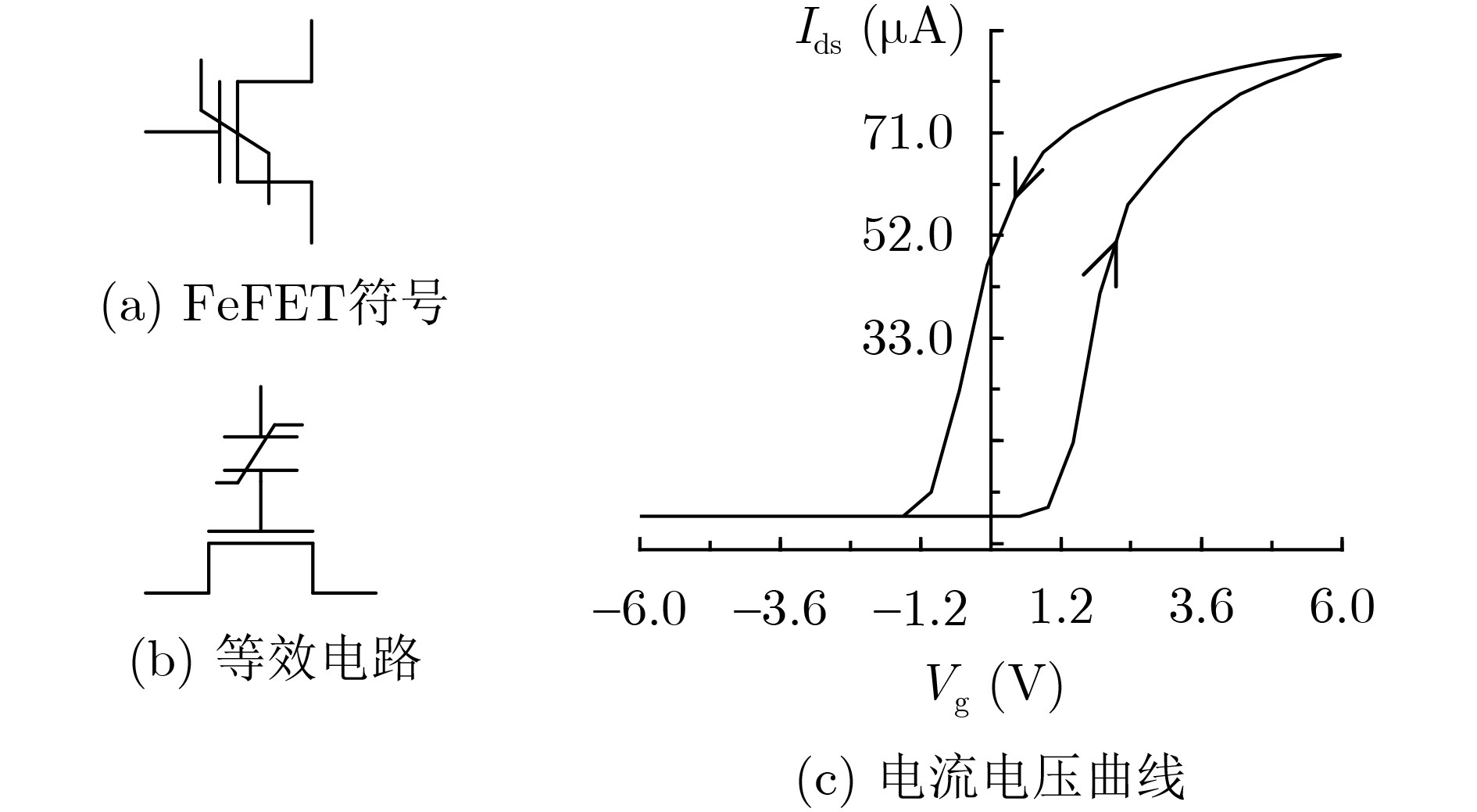
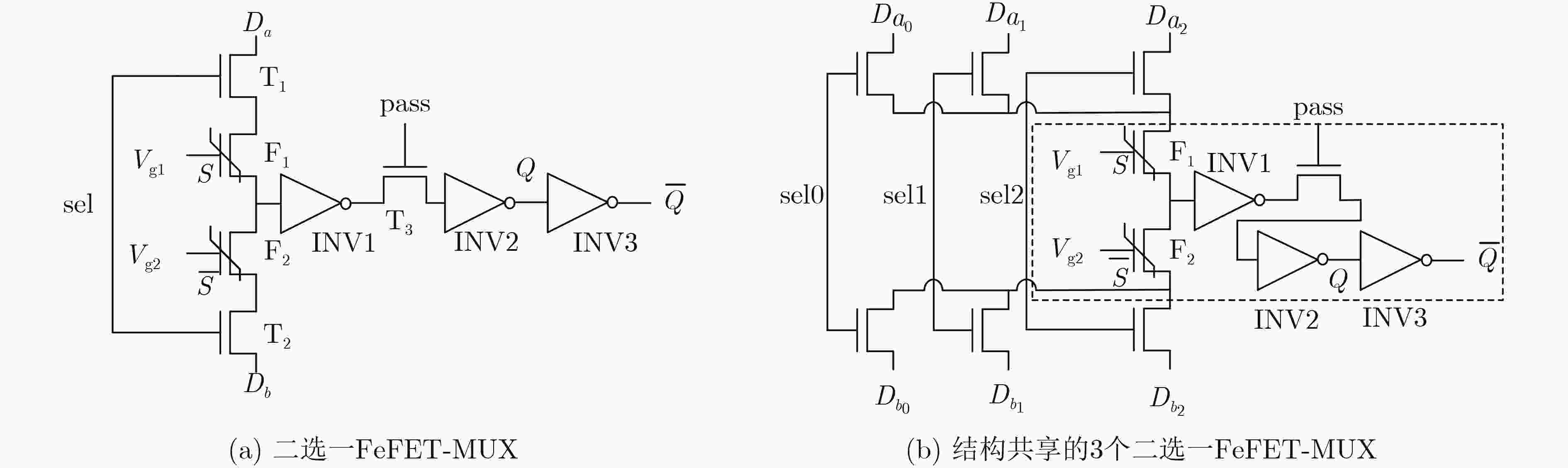
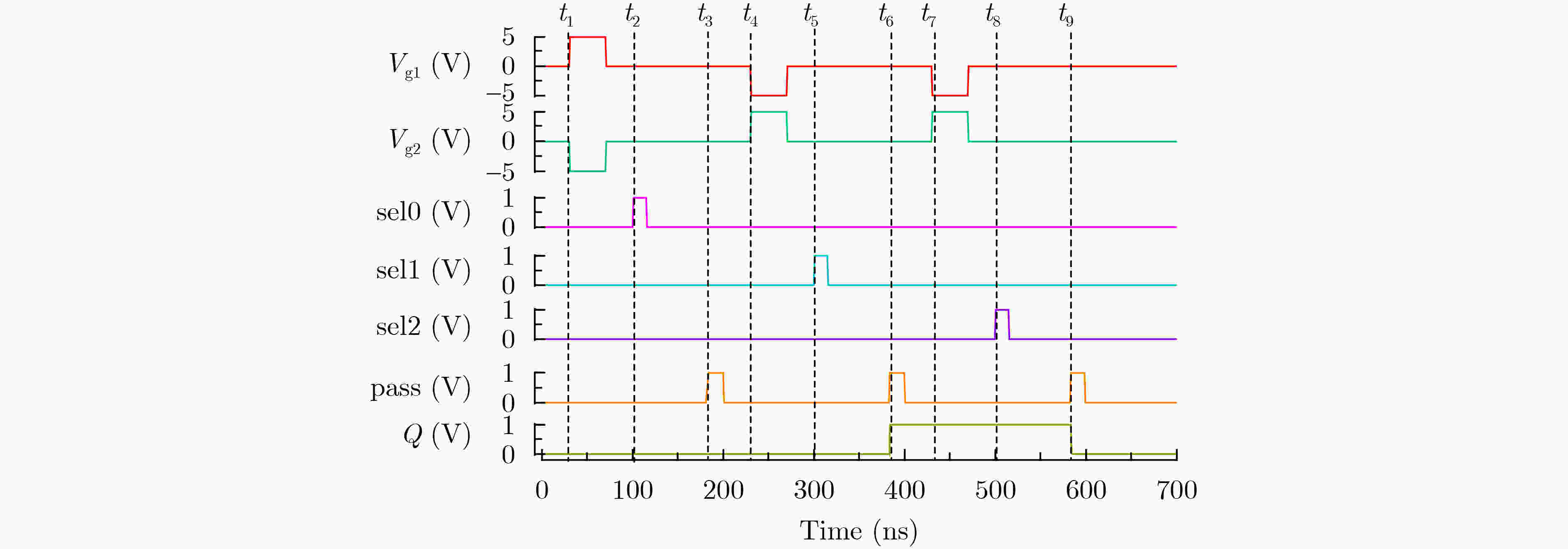
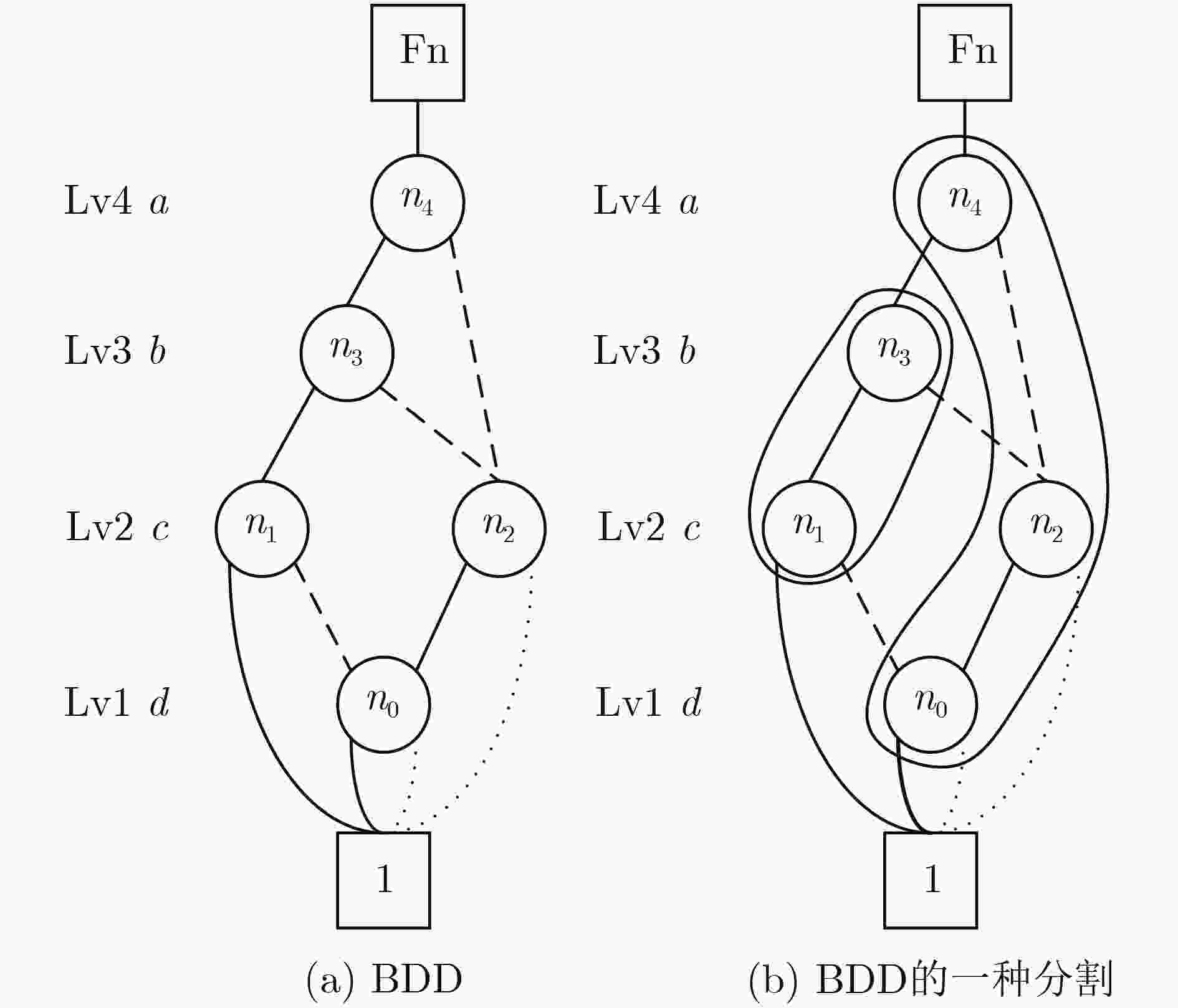
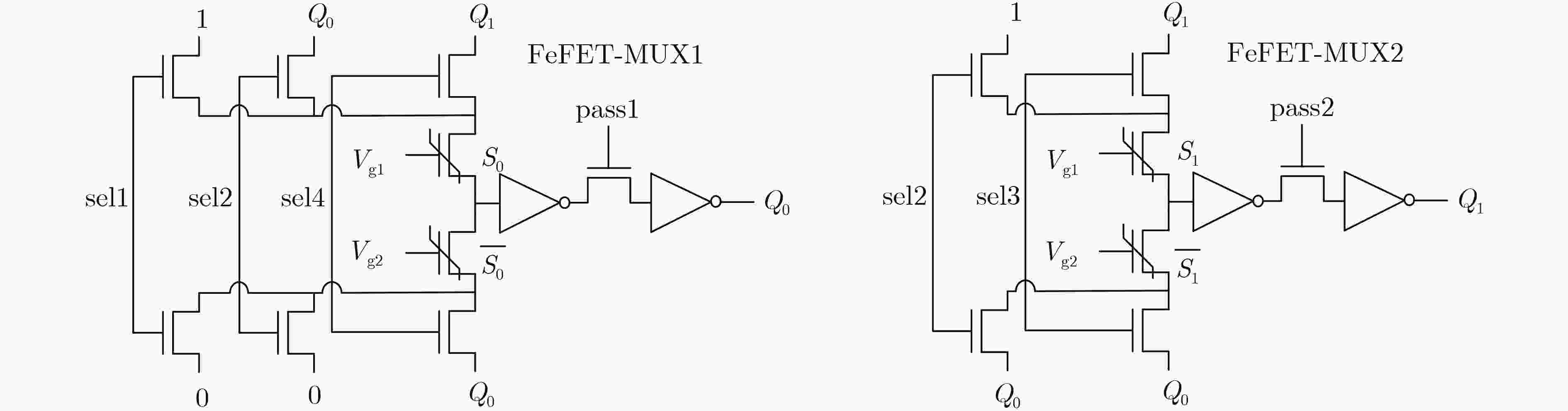
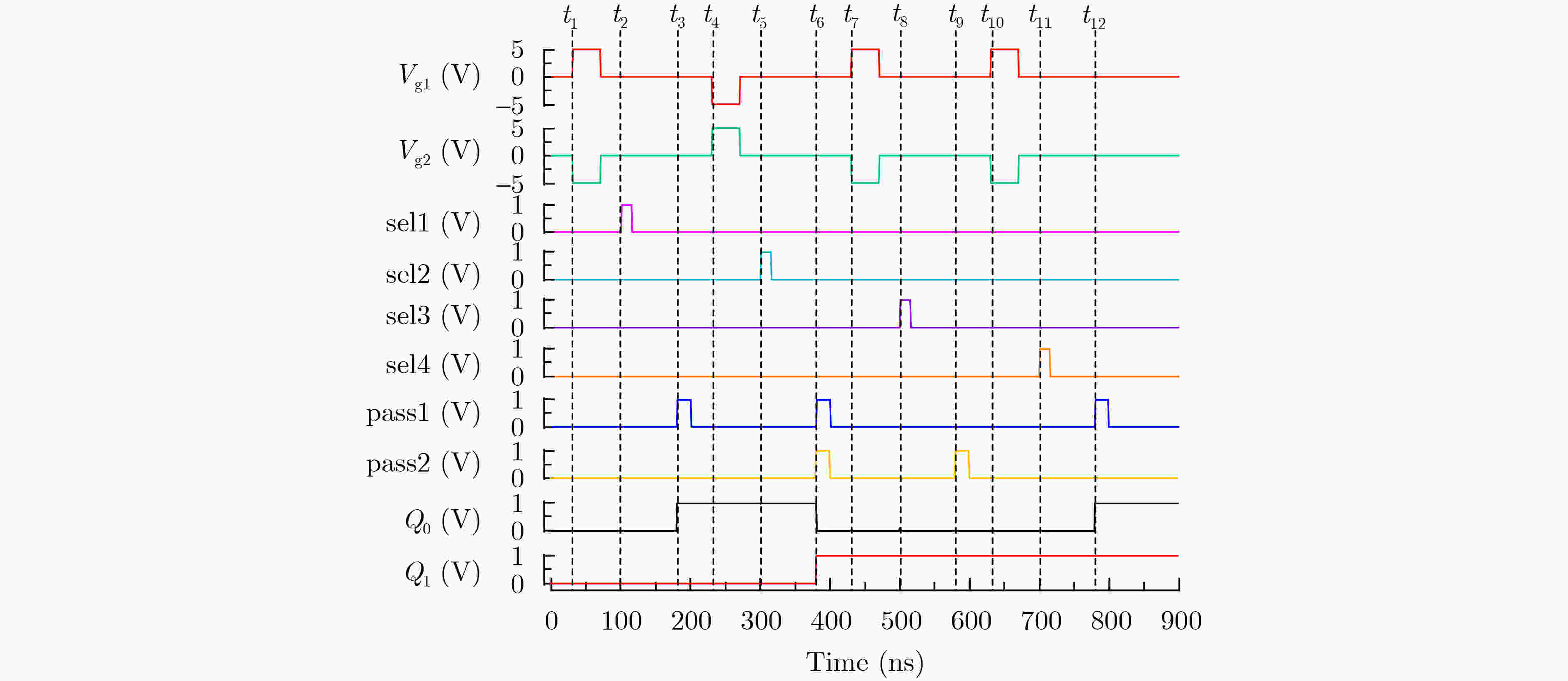
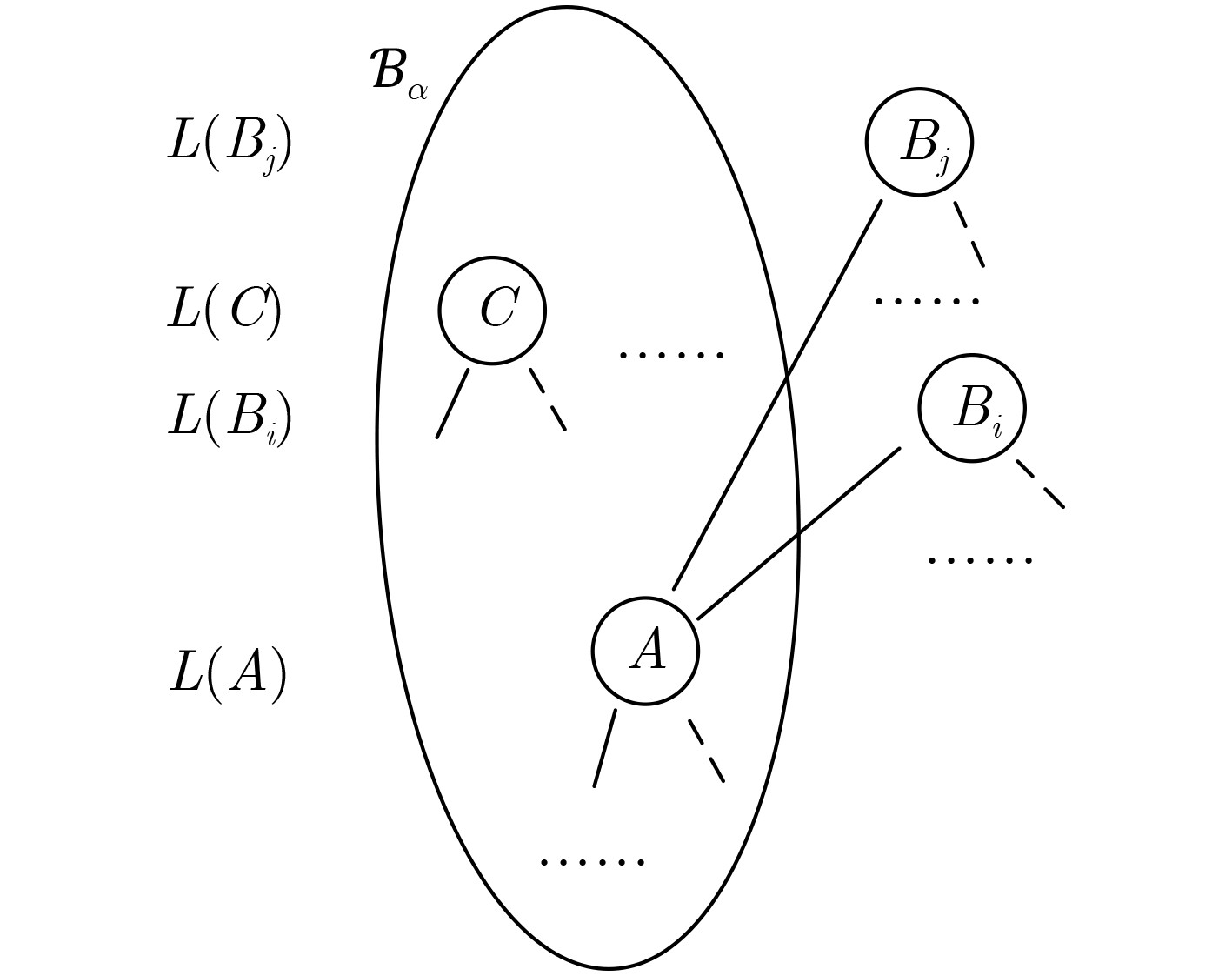
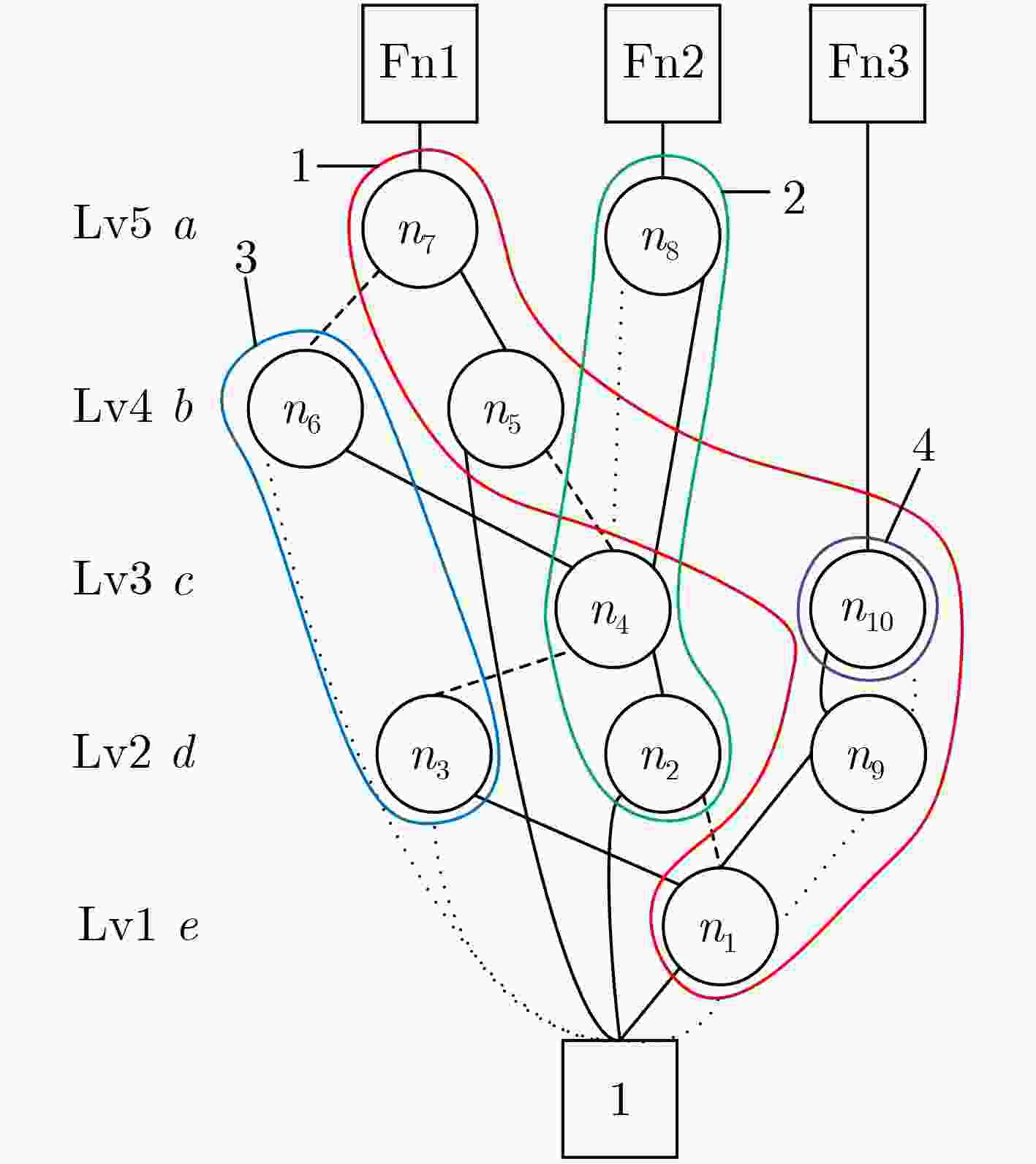
Abstract: Objective The growing demand for massive computing power and big data processing has exposed bottlenecks in conventional Von Neumann architectures, known as the “storage wall” and the “power wall”. Computing-in-Memory (CiM) offers a promising solution by integrating storage and computation, thereby reducing delays and energy consumption caused by data transfer. Emerging non-volatile memories used in CiM circuit design include Spin Transfer Torque Magnetic Random Access Memory (STT-MRAM), Phase Change Memory (PCM), Resistive Random Access Memory (ReRAM), and Ferroelectric Field-Effect Transistors (FeFETs). FeFETs have become key components in CiM designs due to their non-volatile storage capability, low power consumption, high on–off ratio, compatibility with Complementary Metal-Oxide-Semiconductor (CMOS) processes, and voltage-driven writing mechanism. Various FeFET-based CiM circuit designs have been proposed, with most focusing on array-based structures. However, the potential of FeFET-based CiM logic circuits remains underexplored. This study proposes a methodology for mapping Boolean functions onto FeFET-based CiM logic circuits by designing a reconfigurable FeFET Multiplexer (FeFET-MUX) and developing corresponding Boolean function partitioning algorithms. Methods The reconfigurable FeFET-MUX consists of an elementary 2-to-1 MUX, as shown in Fig. 2(a), with multiple data inputs and selection inputs, illustrated in Fig. 2(b). The sub-circuit enclosed within the dashed box in Fig. 2(b) functions as the storage element of the FeFET-MUX and is time-shared by the data pathways. To ensure correct logical function execution, at any given time, no more than one address input is permitted to write to the FeFETs, and no more than one data input is selected simultaneously. Logical functions can be expressed using Binary Decision Diagrams (BDDs). By replacing each node in the BDD with a 2-to-1 MUX, the corresponding functions can be implemented using 2-to-1 MUX circuits. This technique is also applicable to mapping with 2-to-1 FeFET-MUXs; however, its major limitation is the relatively high area overhead. In this work, instead of replacing each individual BDD node with a 2-to-1 MUX, a sub-BDD is mapped onto the proposed FeFET-MUX, reducing area consumption. To prevent logic errors caused by incorrect rewriting of stored data due to the shared structure, a BDD partitioning approach is proposed. After applying specific partitioning rules, each sub-BDD can be independently implemented using the proposed FeFET-MUX, ensuring that stored data is preserved until it is no longer needed, thereby maintaining the logical function’s correctness.The operation of the proposed FeFET-MUX follows a three-phase cycle: (1) The polarization states of the two FeFETs are programmed by applying complementary gate pulses V_g1 and V_g2; (2) During each computation cycle, the selection gate pulses are temporally modulated to select distinct input data, which are routed to the FeFET drains; (3) Finally, the output enable pulses control the transmission of the computed result to the inverter’s output for storage. The proposed BDD partitioning algorithms are presented in Algorithm 1 and Algorithm 2. The methodology proceeds as follows: First, the target BDD, constructed using the Colorado University Decision Diagram (CUDD) library, is traversed through a breadth-first search. Next, upon identifying the starting node of a sub-BDD via the subroutine “find_node_start”, the subroutine “Extend_node” iteratively evaluates candidate nodes for inclusion in the current sub-BDD. After the traversal is complete, Algorithm 1 invokes the subroutine “Out_node_check” to determine whether additional sub-BDDs need to be created. Results and Discussions The proposed algorithms are implemented in C++ and executed on an Ubuntu 24.04 platform with an Intel Ultra 7 processor and 32 GB of memory. The compiler used is g++, version 13.3.0. Test benchmarks are selected from open-source designs described in Verilog. Prior to mapping, the benchmarks are converted into Reduced Ordered Binary Decision Diagrams (ROBDDs) using the CUDD library. Node information is extracted and stored in data structures, and ROBDD partitioning is performed using the proposed algorithms. The experimental results show that the number of sub-BDDs is not directly determined by the number of circuit inputs or outputs but is associated with the maximum number of nodes present at the same level within the BDD. This relationship results from the constraint that each sub-BDD cannot contain multiple nodes at the same level. For example, ROBDDs such as “parity,” which contain only one sub-BDD, exhibit a maximum of one node per level. However, the reverse does not always apply. For example, the circuit “i3” has a maximum of one node per level but still requires multiple sub-BDDs due to the presence of nodes with level differences greater than one, which violate the partitioning constraint and necessitate additional sub-BDDs to ensure correct function mapping. By integrating the reconfigurable FeFET-MUX with the proposed partitioning algorithms, the number of FeFET devices required decreases by an average of 79.9% compared with conventional mapping approaches (Table 2). In addition, the methodology successfully processes large-scale benchmarks, such as “i10,” which contains over 30,000 BDD nodes, demonstrating its scalability. Conclusion This work presents a novel methodology for mapping Boolean functions to FeFET-based CiM logic circuits. The approach consists of two core contributions: (1) A reconfigurable FeFET-MUX circuit is designed, featuring shared FeFET components and a common output drive stage. This configuration consolidates multiple 2-to-1 MUX functions into a single circuit, significantly improving resource utilization. (2) A BDD partitioning strategy is proposed, in which the Boolean logic circuit is partitioned into sub-BDDs, each implemented by a corresponding FeFET-MUX. Experimental results based on open-source logic synthesis benchmarks demonstrate an average reduction of 79.9% in FeFET usage (Table 2) compared to conventional mapping techniques. This is particularly important because FeFET devices occupy considerably more area than conventional Metal-Oxide-Semiconductor (MOS) transistors. Reducing FeFET usage leads to substantial area savings at the circuit level. Moreover, the proposed algorithms effectively process large and complex designs, including circuits exceeding 30,000 BDD nodes, confirming their applicability to large-scale CiM logic implementations.
- Logic circuit mapping /
- Computing-in-Memory (CiM) /
- Ferroelectric field-effect Transistor circuits /
- Multiplexer /
- Binary Decision Diagram (BDD) partitioning

HTML全文

图 1 n型FeFET

下载: 全尺寸图片幻灯片

图 2 本文提出的FeFET-MUX电路

下载: 全尺寸图片幻灯片

图 3 对图2(b)所示电路的逻辑功能仿真的结果

下载: 全尺寸图片幻灯片

图 4 逻辑函数的BDD表示形式以及BDD的分割

下载: 全尺寸图片幻灯片

图 5 与图4(b)分割对应的用FeFET-MUX实现的电路图

下载: 全尺寸图片幻灯片

图 6 对图5电路的逻辑功能仿真的结果

下载: 全尺寸图片幻灯片

图 7 一个BDD的分割

下载: 全尺寸图片幻灯片

图 8 多输出BDD的分割示例

下载: 全尺寸图片幻灯片

表 1 单个二选一FeFET-MUX的功耗和延迟

S	D_a	D_b	平均功耗(nW)	延迟(ns)
0	0	0	29.4	1.1
0	0	1	76.0	1.2
0	1	0	29.6	1.1
0	1	1	76.5	1.3
1	0	0	29.4	1.1
1	0	1	29.6	1.1
1	1	0	76.0	1.3
1	1	1	76.5	1.3
avg			52.9	1.2

下载: 导出CSV

1 BDD_Partitioning

输入：ROBDD ${\mathcal{B}} $
输出：${\mathcal{B}} $ with sub_bdds marks
1. i=0;
2. N_st=find_start_node(${\mathcal{B}} $);
3. WHILE(N_st!=Null_node) {
4. 　Extend_node(${\mathcal{B}} $, N_st, i);
5. 　i++;
6. 　N_st=find_start_node(${\mathcal{B}} $); }
7. Out_node_check(${\mathcal{B}} $, sub_bdds);

下载: 导出CSV

2 Extend_node(${\mathcal{B}} $, N_st, i)

输入：ROBDD bdd ${\mathcal{B}} $, N_st, i
输出：${\mathcal{B}} $ with sub_bdds marks
1. WHILE(N_st!=const_node) {
2. 　IF Select(N_st.T) && Select(N_st.E) THEN
3. 　　N_st=Add_nLv_node(${\mathcal{B}} $, L(N_st), i);
4. 　ELSE {
5. 　　selT=0; selE=0;
6. 　　ΔL₁=L(N_st)–L(N_st.T);
7. 　　selT=Mul_sel(${\mathcal{B}} $, N_st.T, ΔL₁);
8. 　　ΔL₂=L(N_st)-L(N_st.E);
9. 　　selE=Mul_sel(${\mathcal{B}} $, N_st.E, ΔL₂);
10. 　 IF(selT \|\| selE) THEN
11. 　 N_st =Node_sel(${\mathcal{B}} $, N_st, ΔL₁, ΔL₂, selT, selE, i);
12. ELSE N_st=Add_other_node(${\mathcal{B}} $, L(N_st), i); } }

下载: 导出CSV

表 2 基准电路的算法测试结果

电路	I/O	ROBDD 节点数(N_bdd)	ROBDD 单层最大节点数	子BDD数 (N_{sub_bdd})	子BDD 最大节点数	FeTRd(%)	时间(s)
5xp1	7/10	55	11	18	6	67.2	1.010E-4
alu4	14/8	733	123	132	13	82.0	2.701E-3
apex1	45/45	1423	247	257	21	81.9	1.100E-2
apex4	9/19	903	348	358	7	60.4	8.434E-3
b9	41/21	126	19	36	13	71.4	3.820E-4
clip	9/5	146	41	47	8	67.8	3.440E-4
cm163a	16/5	33	7	8	9	75.8	1.160E-4
cordic	23/2	95	6	8	20	91.6	1.360E-4
dalu	75/16	803	142	142	24	82.3	5.169E-3
e64	65/65	368	30	65	60	82.3	9.750E-4
ex4p	12828	710	34	115	27	83.8	4.199E-3
frg2	143/139	1274	74	217	36	83.0	1.100E-2
misex3	14/14	782	141	168	12	78.5	4.326E-3
parity	16/1	17	1	1	16	94.1	6.100E-5
pair	173/173	3872	170	580	52	85.0	8.200E-2
seq	41/35	2025	276	405	19	80.0	2.700E-2
squar5	5/8	39	12	15	4	61.5	1.050E-4
table5	17/15	693	105	120	15	82.7	2.758E-3
too_large	38/3	777	73	90	23	88.4	2.726E-3
vda	17/39	506	124	127	11	74.9	2.074E-3
x3	135/99	697	79	148	40	78.8	6.481E-3
x4	94/71	544	55	124	21	77.2	2.753E-3
i2	201/1	584	24	36	116	93.8	2.028E-3
i3	132/6	133	1	10	37	92.5	2.250E-4
i9	88/63	925	32	264	19	71.5	1.400E-2
i10	257/224	33995	1831	3455	68	89.8	5.402
avg						79.9

下载: 导出CSV

参考文献(19)

[1]	LI Yueting, BAI Tianshuo, XU Xinyi, et al. A survey of MRAM-centric computing: From near memory to in memory[J]. IEEE Transactions on Emerging Topics in Computing, 2023, 11(2): 318–330. doi: 10.1109/TETC.2022.3214833.
[2]	ANTOLINI A, LICO A, SCARSELLI E F, et al. An embedded PCM peripheral unit adding analog MAC in-memory computing feature addressing non-linearity and time drift compensation[C]. ESSCIRC 2022-IEEE 48th European Solid State Circuits Conference (ESSCIRC), Milan, Italy, 2022: 109–112. doi: 10.1109/ESSCIRC55480.2022.9911447.
[3]	DING Zhetao, LI Xueyang, JIN Chengji, et al. Experimental demonstration of non-volatile Boolean logic with field configurable 1FeFET-1RRAM technology[J]. IEEE Electron Device Letters, 2024, 45(6): 1084–1087. doi: 10.1109/LED.2024.3390403.
[4]	BEYER S, DÜNKEL S, TRENTZSCH M, et al. FeFET: A versatile CMOS compatible device with game-changing potential[C]. 2020 IEEE International Memory Workshop (IMW), Dresden, Germany, 2020: 1–4. doi: 10.1109/IMW48823.2020.9108150.
[5]	MARCHAND C, NICOLAS A, MATRANGOLO P A, et al. FeFET based Logic-in-Memory design methodologies, tools and open challenges[C]. 2023 IFIP/IEEE 31st International Conference on Very Large Scale Integration (VLSI-SoC), Dubai, United Arab Emirates, 2023: 1–6. doi: 10.1109/VLSI-SoC57769.2023.10321901.
[6]	JIANG Yuxiao, NI Kai, KÄMPFE T, et al. CSA-CiM: Enhancing multifunctional computing-in-memory with configurable sense amplifiers[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2025, 44(5): 1869–1873. doi: 10.1109/TCAD.2024.3506864.
[7]	LIU Rui, ZHANG Xiaoyu, XIE Zhiwen, et al. FeCrypto: Instruction set architecture for cryptographic algorithms based on FeFET-based in-memory computing[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2023, 42(9): 2889–2902. doi: 10.1109/TCAD.2022.3233736.
[8]	YAN Aibin, CHEN Yu, GAO Zhongyu, et al. FeMPIM: A FeFET-based multifunctional processing-in-memory cell[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2024, 71(4): 2299–2303. doi: 10.1109/TCSII.2023.3331267.
[9]	LALENI N, MÜLLER F, CUÑARRO G, et al. A high-efficiency charge-domain compute-in-memory 1F1C macro using 2-bit FeFET cells for DNN processing[J]. IEEE Journal on Exploratory Solid-State Computational Devices and Circuits, 2024, 10: 153–160. doi: 10.1109/JXCDC.2024.3495612.
[10]	HUANG Yuanyu, HUANG P T, LEE P Y, et al. A new approach for reconfigurable multifunction logic-in-memory using complementary ferroelectric-FET (CFeFET)[J]. IEEE Transactions on Electron Devices, 2023, 70(8): 4497–4500. doi: 10.1109/TED.2023.3287941.
[11]	BREYER E T, MULAOSMANOVIC H, TROMMER J, et al. Compact FeFET circuit building blocks for fast and efficient nonvolatile logic-in-memory[J]. IEEE Journal of the Electron Devices Society, 2020, 8: 748–756. doi: 10.1109/JEDS.2020.2987084.
[12]	RAMANUJAM S and BURLESON W. Reconfiguring the mux-based arbiter PUF using FeFETs[C]. 2021 22nd International Symposium on Quality Electronic Design (ISQED), Santa Clara, USA, 2021: 257–262. doi: 10.1109/ISQED51717.2021.9424328.
[13]	DÜNKEL S, TRENTZSCH M, RICHTER R, et al. A FeFET based super-low-power ultra-fast embedded NVM technology for 22nm FDSOI and beyond[C]. 2017 IEEE International Electron Devices Meeting (IEDM), San Francisco, USA, 2017: 19.7. 1–19.7. 4. doi: 10.1109/IEDM.2017.8268425.
[14]	AZIZ A, GHOSH S, DATTA S, et al. Physics-based circuit-compatible SPICE model for ferroelectric transistors[J]. IEEE Electron Device Letters, 2016, 37(6): 805–808. doi: 10.1109/LED.2016.2558149.
[15]	NI Kai, JERRY M, SMITH J A, et al. A circuit compatible accurate compact model for ferroelectric-FETs[C]. 2018 IEEE Symposium on VLSI Technology, Honolulu, USA, 2018: 131–132. doi: 10.1109/VLSIT.2018.8510622.
[16]	DENG Shan, YIN Guodong, CHAKRABORTY W, et al. A comprehensive model for ferroelectric FET capturing the key behaviors: Scalability, variation, stochasticity, and accumulation[C]. 2020 IEEE Symposium on VLSI Technology, Honolulu, USA, 2020: 1–2. doi: 10.1109/VLSITechnology18217.2020.9265014.
[17]	YIN Xunzhao, CHEN Xiaoming, NIEMIER M, et al. Ferroelectric FETs-based nonvolatile logic-in-memory circuits[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2019, 27(1): 159–172. doi: 10.1109/TVLSI.2018.2871119.
[18]	CHAKRABORTI S, CHOWDHARY P V, DATTA K, et al. BDD based synthesis of Boolean functions using memristors[C]. 2014 9th International Design and Test Symposium (IDT), Algeries, Algeria, 2014: 136–141. doi: 10.1109/IDT.2014.7038601.
[19]	CHAKRABORTY A, GUPTA P S, SINGH R, et al. BDD-based synthesis approach for in-memory logic realization utilizing Memristor Aided loGIC (MAGIC)[J]. Integration, 2021, 81: 254–267. doi: 10.1016/j.vlsi.2021.08.002.