SR-FDN: A Frequency-Domain Diffusion Network for Image Detail Restoration in Super-Resolution
-
摘要: 现有的一些利用频域信息的图像超分辨率重建方法在处理高频细节时仍存在一定的改进空间,在某些场景下难以避免模糊或失真的现象。为了解决这一问题,该文提出一种基于频域扩散模型的超分辨率重建网络SR-FDN。具体来说,SR-FDN引入双分支频域注意力机制,在频域与空间域进行特征融合,能够有效地捕捉频域特征并恢复高频信息,进一步提升细节恢复效果。SR-FDN还使用了小波下采样代替传统U-Net噪声预测器中的卷积下采样,在降低图像尺寸的同时保留更多的细节信息。此外,SR-FDN通过频域损失函数的约束和条件图像的引导,使得生成的高分辨率图像在细节和纹理方面具有更高的精确度。在多个基准数据集上的实验表明,所提的SR-FDN可以重建出质量更好、细节更丰富的图像,并且在定性和定量比较中均有明显优势。Abstract:
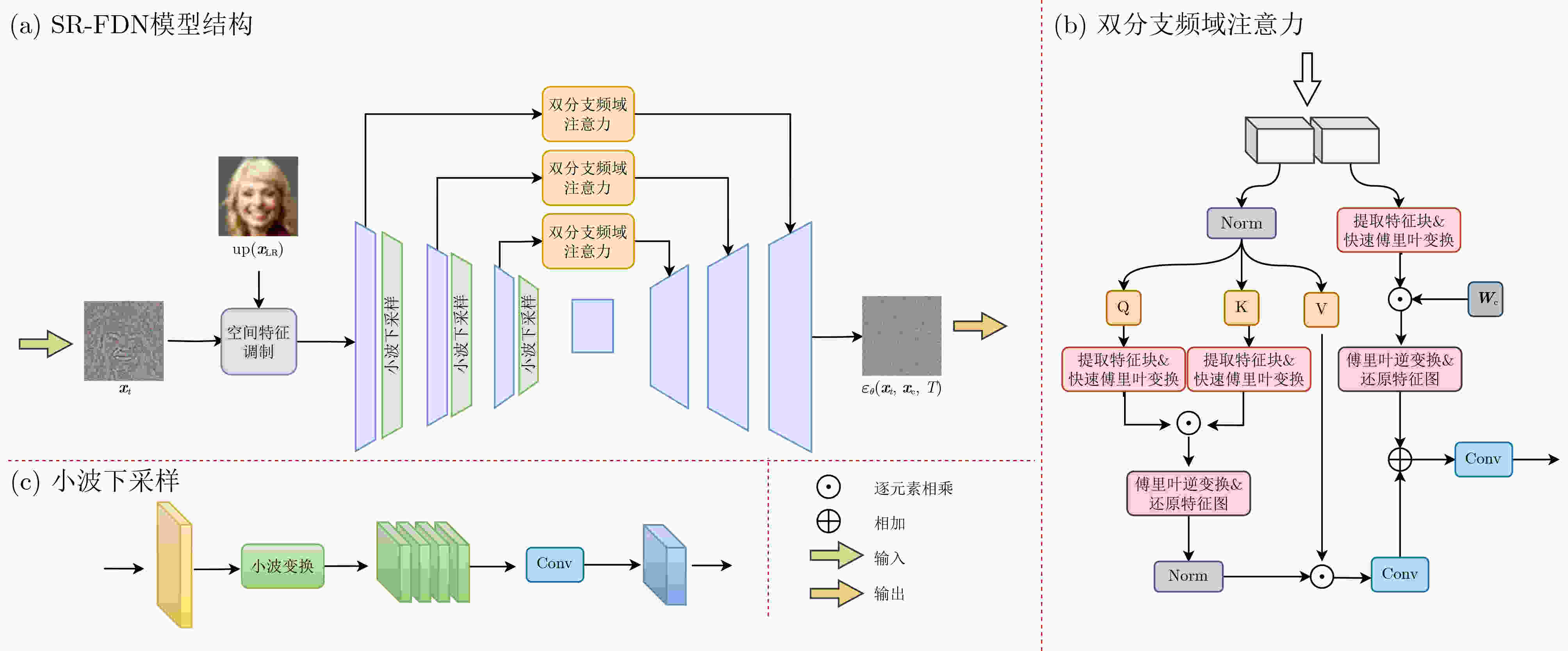
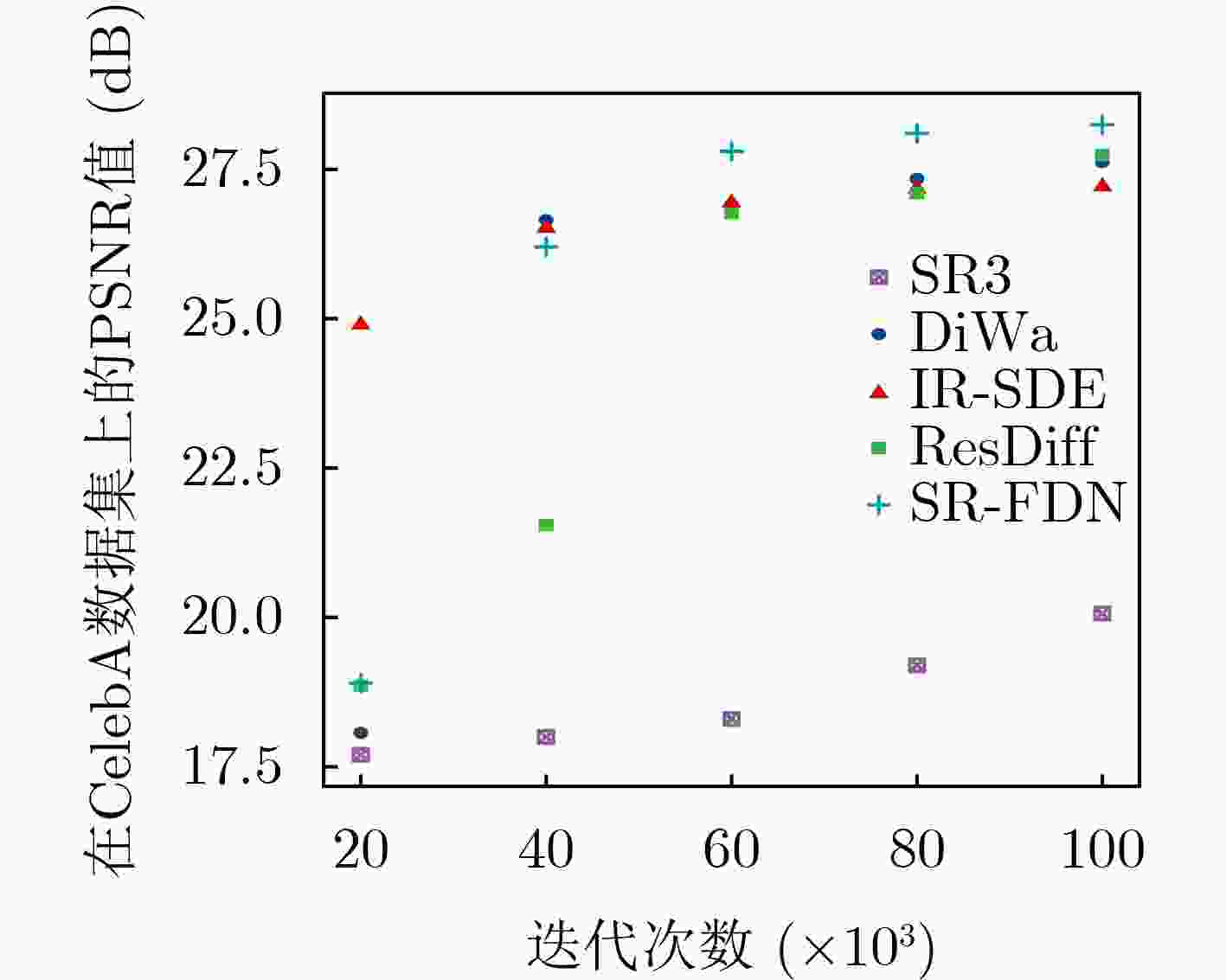
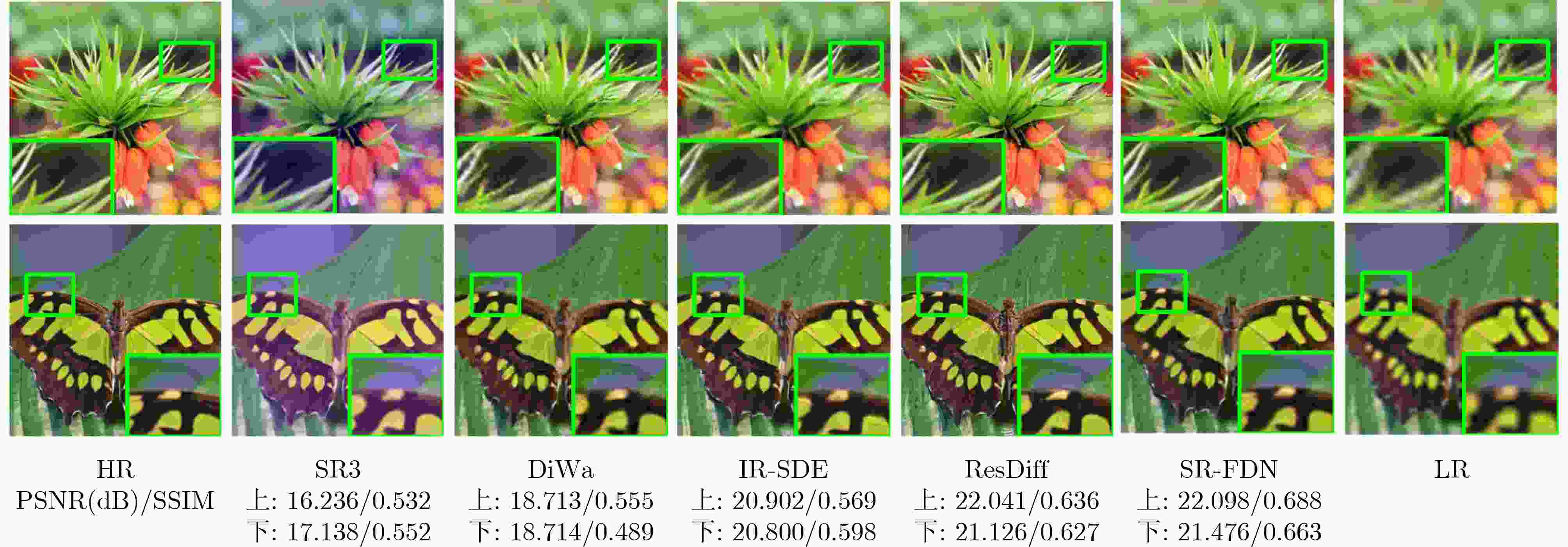
Objective Image Super-Resolution (SR) is a critical computer vision task aimed at reconstructing High-Resolution (HR) images from Low-Resolution (LR) inputs, with broad applications in fields such as medical imaging and satellite imaging. Recently, diffusion-based SR methods have attracted significant attention due to their generative capability and strong performance in restoring fine image details. Existing diffusion model-based SR approaches have demonstrated potential in recovering textures and structures, with some methods focusing on spatial domain features and others utilizing frequency domain information. Spatial domain features aid in reconstructing overall structural information, whereas frequency domain decomposition separates images into amplitude and phase components across frequencies. High-frequency components capture details, textures, and edges, whereas low-frequency components describe smooth structures. Compared to purely spatial modeling, frequency domain features improve the aggregation of dispersed high-frequency information, enhancing the representation of image textures and details. However, current frequency domain SR methods still show limitations in restoring high-frequency details, with blurring or distortion persisting in some scenarios. To address these challenges, this study proposes SR-FDN, an SR reconstruction network based on a frequency-domain diffusion model. Methods SR-FDN leverages the distribution mapping capability of diffusion models to improve image reconstruction. The proposed network integrates spatial and frequency domain features to enhance high-frequency detail restoration. Two constraints guide the model design: (1) The network must generate plausible HR images conditioned solely on LR inputs, which serve as the primary source of structural information, ensuring high-fidelity reconstruction. (2) The model should balance structural reconstruction with enhanced detail restoration. To achieve this, a dual-branch frequency domain attention mechanism is introduced. A portion of the features undergoes Fourier transform for frequency domain processing, where high-frequency information is emphasized through self-attention. The remaining features adjust frequency domain weights before being combined with spatial domain representations. Skip connections in the U-Net architecture preserve LR structural information while enhancing frequency domain details, improving both structural and textural reconstruction. Wavelet downsampling replaces conventional convolutional downsampling within the U-Net noise predictor, reducing spatial resolution while retaining more detailed information. In addition, a Fourier frequency domain loss function constrains amplitude and phase components of the reconstructed image, further enhancing high-frequency detail recovery. To guide the generative process, additional image priors are incorporated, enabling the diffusion model to restore textures consistent with semantic category features. Results and Discussions The results of SR-FDN on face datasets and general datasets for 4× and 8× SR ( Table 1 ,Table 2 ,Table 3 ) demonstrate that the proposed method achieves strong performance across objective evaluation metrics. These results indicate that SR-FDN can effectively restore image detail information while better preserving structural and textural features. A comparison of iteration counts between SR-FDN and other diffusion-based methods (Fig. 2 ) shows that SR-FDN can reconstruct higher-quality images with fewer iterations. Despite the reduced number of iterations, SR-FDN maintains high-fidelity reconstruction, reflecting its ability to lower computational overhead without compromising image quality. To further verify the effectiveness of the proposed SR-FDN, visual comparisons on the FFHQ dataset (Fig. 3 ) and the DIV2K dataset (Fig. 4 ) are presented. The results show that SR-FDN offers clearer and more detailed image reconstruction, particularly in high-frequency regions such as facial features and hair textures. Ablation experiments (Table 5 ) and feature visualization results (Fig. 5 ) are also provided. These results confirm that the proposed dual-branch frequency domain design and the Fourier domain loss function significantly contribute to improved restoration of fine details.Conclusions This study proposes SR-FDN, a diffusion-based SR reconstruction model that integrates frequency domain information to enhance detail restoration. The SR-FDN model incorporates a dual-branch frequency domain attention mechanism, which adaptively reinforces high-frequency components, effectively addressing the limitations of conventional methods in recovering edge structures and texture details. In addition, SR-FDN employs wavelet downsampling to preserve informative features while reducing spatial resolution, and introduces a frequency domain loss function that constrains amplitude and phase information, enabling more effective fusion of frequency and spatial domain features. This design substantially enhances the model’s ability to recover high-frequency details. Extensive experiments on benchmark datasets demonstrate that SR-FDN reconstructs images with superior quality and richer details, exhibiting clear advantages in both qualitative and quantitative evaluations. -
1 训练阶段
1: repeat 2: $ ({{\boldsymbol{x}}_{{\mathrm{LR}}}},{{\boldsymbol{x}}_{{\mathrm{HR}}}}){\text{~}}({{\boldsymbol{x}}}_{{\mathrm{LR}}}^i,{{\boldsymbol{x}}}_{{\mathrm{HR}}}^i)_{i = 1}^N $ 3: $ \varepsilon\text{~}\mathcal{N}(0,\boldsymbol{I}) $ 4: $ t{\text{~}}U(\{ 1, 2,\cdots ,T\} ) $ 5: 梯度下降优化损失函数$ {\mathcal{L}_\theta } $ 6: until 收敛 2 采样阶段
1:$ \boldsymbol{x}_T\text{~}\mathcal{N}(0,\boldsymbol{\boldsymbol{I}}) $ 2: for $ t = T, \cdots ,2,1 $ do 3: $ {\boldsymbol{z}} = \mathcal{N}(0,{\boldsymbol{I}}) $ if $ t > 1 $, else $ {\boldsymbol{z}} = {{\textit{0}}} $ 4: $ \boldsymbol{x}_{t-1}=\dfrac{1}{\sqrt{\alpha_t}}\left(\boldsymbol{x}_t-\dfrac{1-\alpha_t}{\sqrt{1-\overline{\alpha_t}}}{\boldsymbol{\varepsilon}}_{\theta}({\boldsymbol{x}}_t,t)\right)+\sigma_t{\boldsymbol{z}} $ 5: end for 6: return $ {{\boldsymbol{x}}}_0+\mathrm{up}({{\boldsymbol{x}}}_{\mathrm{LR}}) $ 表 1 在两个人脸数据集进行4倍图像超分辨率重建的定量比较
32×32↓
128×128FFHQ CelebA PSNR(dB) SSIM LPIPS PSNR(dB) SSIM LPIPS 基准值 ﹢∞ 1.000 0 ﹢∞ 1.000 0 SRCNN 24.360 0.658 0.296 25.760 0.682 0.312 SRGAN 24.865 0.751 0.141 26.299 0.788 0.104 ESRGAN 25.348 0.765 0.117 26.457 0.799 0.099 SR3 19.285 0.511 0.143 20.066 0.532 0.120 DiWa 24.958 0.738 0.081 27.620 0.813 0.050 IR-SDE 25.830 0.770 0.023 27.212 0.809 0.046 ResDiff 25.679 0.767 0.113 27.741 0.822 0.045 SR-FDN 26.156 0.787 0.142 28.246 0.835 0.088 注:最好的结果用粗体突出显示,次好的结果用下划线突出显示。 表 2 基于扩散的图像超分辨率重建模型进行4倍超分的定量比较
64×64↓
256×256DIV2K Urban100 Set5 Set14 BSD100 PSNR SSIM LPIPS PSNR SSIM LPIPS PSNR SSIM LPIPS PSNR SSIM LPIPS PSNR SSIM LPIPS 基准值 ﹢∞ 1.000 0 ﹢∞ 1.000 0 ﹢∞ 1.000 0 ﹢∞ 1.000 0 ﹢∞ 1.000 0 SR3 17.010 0.541 0.387 16.512 0.498 0.305 16.158 0.584 0.148 17.202 0.546 0.189 17.357 0.544 0.256 DiWa 20.238 0.523 0.172 18.212 0.461 0.262 24.176 0.637 0.090 20.414 0.588 0.163 22.336 0.566 0.190 IR-SDE 19.721 0.451 0.253 17.786 0.385 0.254 21.999 0.604 0.177 19.282 0.422 0.271 20.817 0.436 0.283 ResDiff 20.975 0.588 0.140 18.411 0.504 0.170 25.682 0.766 0.082 20.973 0.571 0.135 22.544 0.570 0.163 SR-FDN 20.967 0.593 0.250 18.645 0.499 0.251 24.941 0.748 0.144 21.179 0.592 0.241 22.887 0.597 0.292 注:最好的结果用粗体突出显示,次好的结果用下划线突出显示。 表 3 在两个人脸数据集进行8倍图像超分辨率重建的定量比较
32×32↓
256×256FFHQ CelebA PSNR(dB) SSIM LPIPS PSNR(dB) SSIM LPIPS 基准值 ﹢∞ 1.000 0 ﹢∞ 1.000 0 SRCNN 23.390 0.507 0.628 22.81 0.535 0.625 SRResNet 23.883 0.564 0.587 23.307 0.601 0.129 SR3 17.773 0.593 0.221 18.346 0.621 0.196 DiWa 22.179 0.516 0.216 23.240 0.563 0.190 IR-SDE 24.146 0.628 0.187 25.438 0.685 0.143 ResDiff 24.220 0.660 0.161 23.846 0.686 0.153 SR-FDN 25.441 0.664 0.198 25.577 0.583 0.287 注:最好的结果用粗体突出显示,次好的结果用下划线突出显示。 表 4 基于扩散的图像超分辨率重建方法在CelebA数据集中采样时间的比较
方法 采样时间(s) SR3 17 DiWa 7 ResDiff 24 IR-SDE 4 SR-FDN 23 表 5 消融实验
模型 模型组成 评价指标 FDL-SFT HWDB DFDA PSNR(dB) SSIM 模型1 × × × 27.509 0.803 模型2 √ × × 27.843 0.833 模型3 √ √ × 28.061 0.806 模型4
(SR-FDN)√ √ √ 28.246 0.835 -
[1] LIANG Jie, ZENG Hui, and ZHANG Lei. Details or artifacts: A locally discriminative learning approach to realistic image super-resolution[C]. 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, USA, 2022: 5647–5656. doi: 10.1109/CVPR52688.2022.00557. [2] DONG Chao, LOY C C, HE Kaiming, et al. Image super-resolution using deep convolutional networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(2): 295–307. doi: 10.1109/TPAMI.2015.2439281. [3] MOSER B B, RAUE F, FROLOV S, et al. Hitchhiker's guide to super-resolution: Introduction and recent advances[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2023, 45(8): 9862–9882. doi: 10.1109/TPAMI.2023.3243794. [4] YANG Qi, ZHANG Yanzhu, ZHAO Tiebiao, et al. Single image super-resolution using self-optimizing mask via fractional-order gradient interpolation and reconstruction[J]. ISA Transactions, 2018, 82: 163–171. doi: 10.1016/j.isatra.2017.03.001. [5] SUN Long, PAN Jinshan, and TANG Jinhui. ShuffleMixer: An efficient ConvNet for image super-resolution[C]. The 36th International Conference on Neural Information Processing Systems, New Orleans, USA, 2022: 1259. [6] ZHANG Yulun, LI Kunpeng, LI Kai, et al. Image super-resolution using very deep residual channel attention networks[C]. The 15th European Conference on Computer Vision, Munich, Germany, 2018: 294–310. doi: 10.1007/978-3-030-01234-2_18. [7] 程德强, 袁航, 钱建生, 等. 基于深层特征差异性网络的图像超分辨率算法[J]. 电子与信息学报, 2024, 46(3): 1033–1042. doi: 10.11999/JEIT230179.CHENG Deqiang, YUAN Hang, QIAN Jiansheng, et al. Image super-resolution algorithms based on deep feature differentiation network[J]. Journal of Electronics & Information Technology, 2024, 46(3): 1033–1042. doi: 10.11999/JEIT230179. [8] HUANG Huaibo, HE Ran, SUN Zhenan, et al. Wavelet-SRNet: A wavelet-based CNN for multi-scale face super resolution[C]. 2017 IEEE International Conference on Computer Vision, Venice, Italy, 2017: 1698–1706. doi: 10.1109/ICCV.2017.187. [9] LIANG Jingyun, CAO Jiezhang, SUN Guolei, et al. SwinIR: Image restoration using swin transformer[C]. 2021 IEEE/CVF International Conference on Computer Vision, Montreal, Canada, 2021: 1833–1844. doi: 10.1109/ICCVW54120.2021.00210. [10] LEDIG C, THEIS L, HUSZAR F, et al. Photo-realistic single image super-resolution using a generative adversarial network[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, USA, 2017: 105–114. doi: 10.1109/CVPR.2017.19. [11] WANG Xintao, YU Ke, WU Shixiang, et al. ESRGAN: Enhanced super-resolution generative adversarial networks[C]. The 15th European Conference on Computer Vision Workshops, Munich, Germany, 2019: 63–79. doi: 10.1007/978-3-030-11021-5_5. [12] 韩玉兰, 崔玉杰, 罗轶宏, 等. 基于密集残差和质量评估引导的频率分离生成对抗超分辨率重构网络[J]. 电子与信息学报, 2024, 46(12): 4563–4574. doi: 10.11999/JEIT240388.HAN Yulan, CUI Yujie, LUO Yihong, et al. Frequency separation generative adversarial super-resolution reconstruction network based on dense residual and quality assessment[J]. Journal of Electronics & Information Technology, 2024, 46(12): 4563–4574. doi: 10.11999/JEIT240388. [13] 任坤, 李峥瑱, 桂源泽, 等. 低分辨率随机遮挡人脸图像的超分辨率修复[J]. 电子与信息学报, 2024, 46(8): 3343–3352. doi: 10.11999/JEIT231262.REN Kun, LI Zhengzhen, GUI Yuanze, et al. Super-resolution inpainting of low-resolution randomly occluded face images[J]. Journal of Electronics & Information Technology, 2024, 46(8): 3343–3352. doi: 10.11999/JEIT231262. [14] WOLF V, LUGMAYR A, DANELLJAN M, et al. DeFlow: Learning complex image degradations from unpaired data with conditional flows[C]. 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, USA, 2021: 94–103. doi: 10.1109/CVPR46437.2021.00016. [15] HO J, JAIN A, and ABBEEL P. Denoising diffusion probabilistic models[C]. The 34th International Conference on Neural Information Processing Systems, Vancouver, Canada, 2020: 574. [16] SONG Jiaming, MENG Chenlin, and ERMON S. Denoising diffusion implicit models[C]. The 9th International Conference on Learning Representations, Vienna, Austria, 2021. [17] LI Haoying, YANG Yifan, CHANG Meng, et al. SRDiff: Single image super-resolution with diffusion probabilistic models[J]. Neurocomputing, 2022, 479: 47–59. doi: 10.1016/j.neucom.2022.01.029. [18] SAHARIA C, HO J, CHAN W, et al. Image super-resolution via iterative refinement[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2023, 45(4): 4713–4726. doi: 10.1109/TPAMI.2022.3204461. [19] MOSER B B, FROLOV S, RAUE F, et al. Waving goodbye to low-res: A diffusion-wavelet approach for image super-resolution[C]. The International Joint Conference on Neural Networks, Yokohama, Japan, 2024: 1–8. doi: 10.1109/IJCNN60899.2024.10651227. [20] LUO Ziwei, GUSTAFSSON F, ZHAO Zheng, et al. Image restoration with mean-reverting stochastic differential equations[C]. The 40th International Conference on Machine Learning, Honolulu, USA, 2023: 957. [21] ROMBACH R, BLATTMANN A, LORENZ D, et al. High-resolution image synthesis with latent diffusion models[C]. 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, USA, 2022: 10674–10685. doi: 10.1109/CVPR52688.2022.01042. [22] SHANG Shuyao, SHAN Zhengyang, LIU Guangxing, et al. ResDiff: Combining CNN and diffusion model for image super-resolution[C]. The 38th AAAI Conference on Artificial Intelligence, Vancouver, Canada, 2024: 8975–8983. doi: 10.1609/aaai.v38i8.28746. [23] XU Guoping, LIAO Wentao, ZHANG Xuan, et al. Haar wavelet downsampling: A simple but effective downsampling module for semantic segmentation[J]. Pattern Recognition, 2023, 143: 109819. doi: 10.1016/j.patcog.2023.109819. [24] ZHANG Yutian, LI Xiaohua, and ZHOU Jiliu. SFTGAN: A generative adversarial network for pan-sharpening equipped with spatial feature transform layers[J]. Journal of Applied Remote Sensing, 2019, 13(2): 026507. doi: 10.1117/1.jrs.13.026507. -





 下载:
下载:




 下载:
下载:
