Spatial Self-Attention Incorporated Imputation Algorithm for Severely Missing Multivariate Time Series
-
摘要: 多元时间序列应用广泛,但极易发生缺失,影响相关规律的有效挖掘。已有插补方法大多面向低缺失率场景设计,应用至高缺失率场景通常面临梯度消失、时空依赖关系建模不足、复杂非线性特征表征困难等难题。该文提出一种融合空间自注意力感知的严重缺失多元时间序列插补算法(SSAImpute)。该算法采用双分支孪生结构,分别设计了空间自注意力感知和时域自注意力编码模块。其中,空间自注意力感知模块通过融合数据源位置等空间信息增强序列的相关性建模能力;时域自注意力编码模块设计了掩码自适应自注意力机制有效捕获时间层面的时间前后依赖性和特征相关性,避免了梯度消失现象。孪生分支之间通过动态加权融合,优化最终的插补输出。实现结果表明,与7个现有时间序列插补模型对比,该文所提方法在Inter-Sensor的4个子数据集均能有效提升严重缺失场景下的多元时间序列插补精度,在PeMS 3个子数据集的插补结果RMSE比次优方法分别提升4.1%, 6.7%和4.7%。该算法有望为严重缺失场景下的多元时间序列提供更准确的解决方案,进而为下游基于数据驱动的分析和决策任务提供更可靠的数据基础。Abstract:
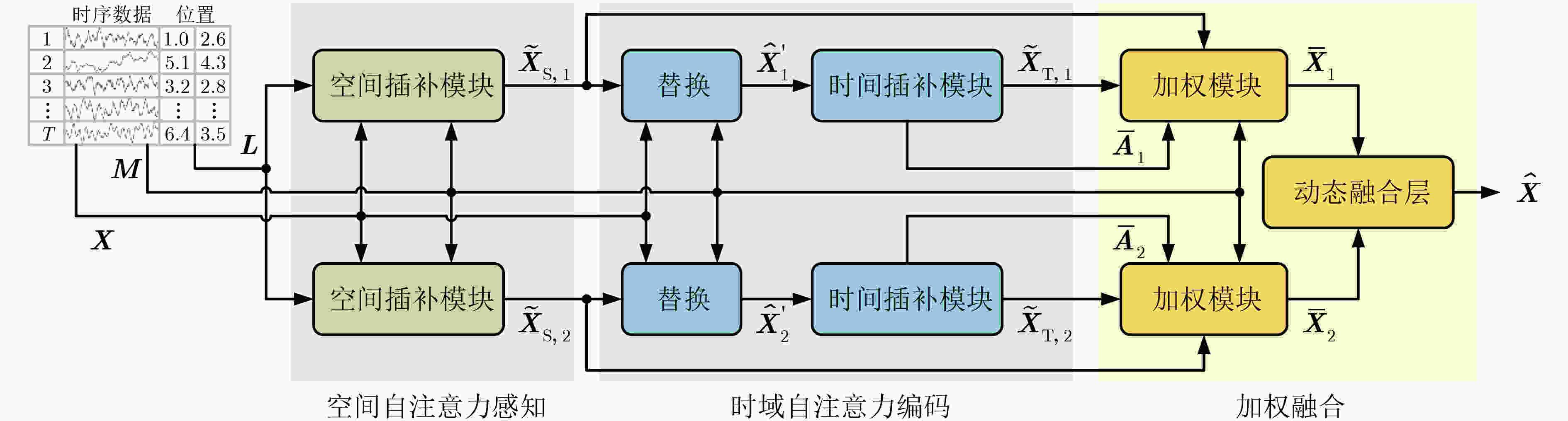
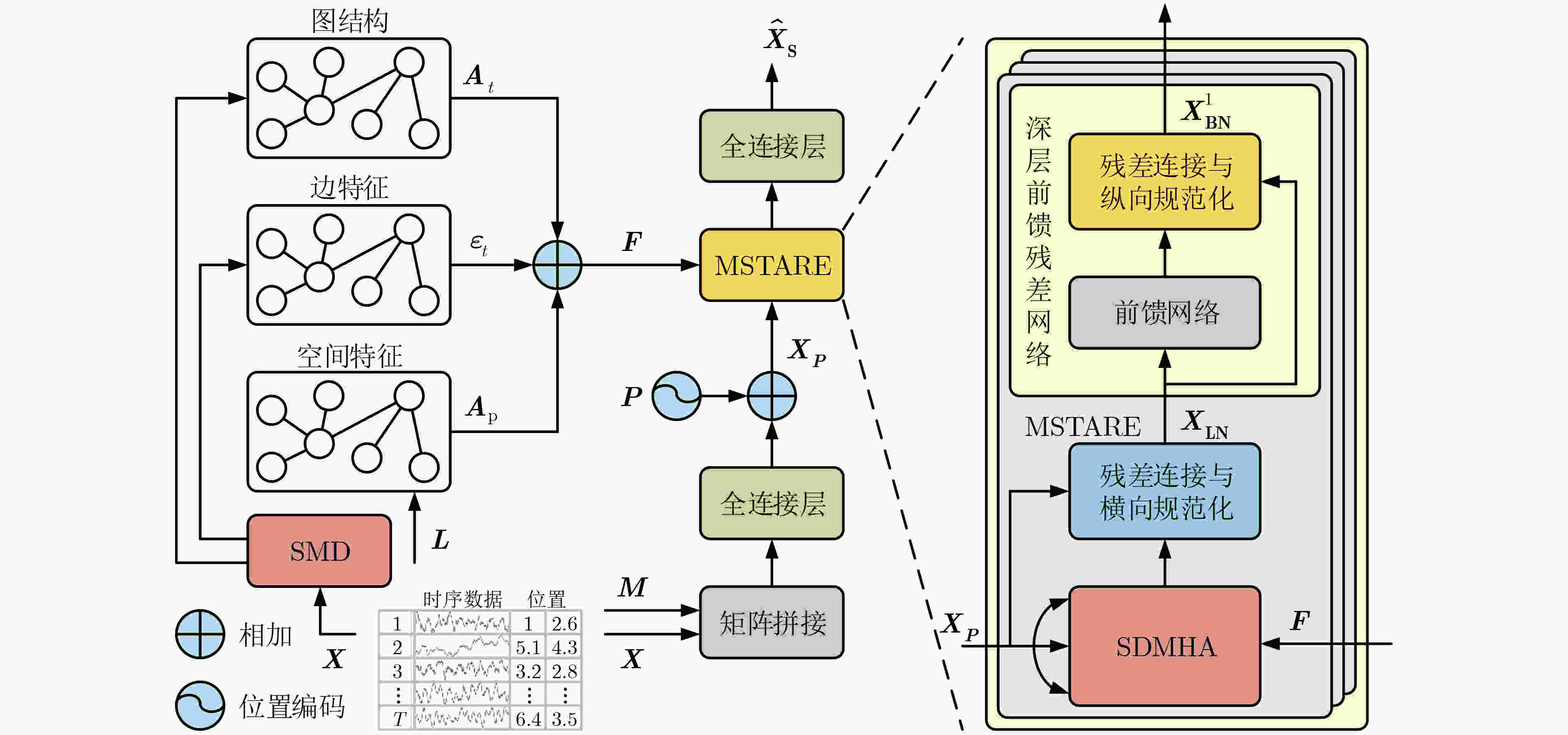
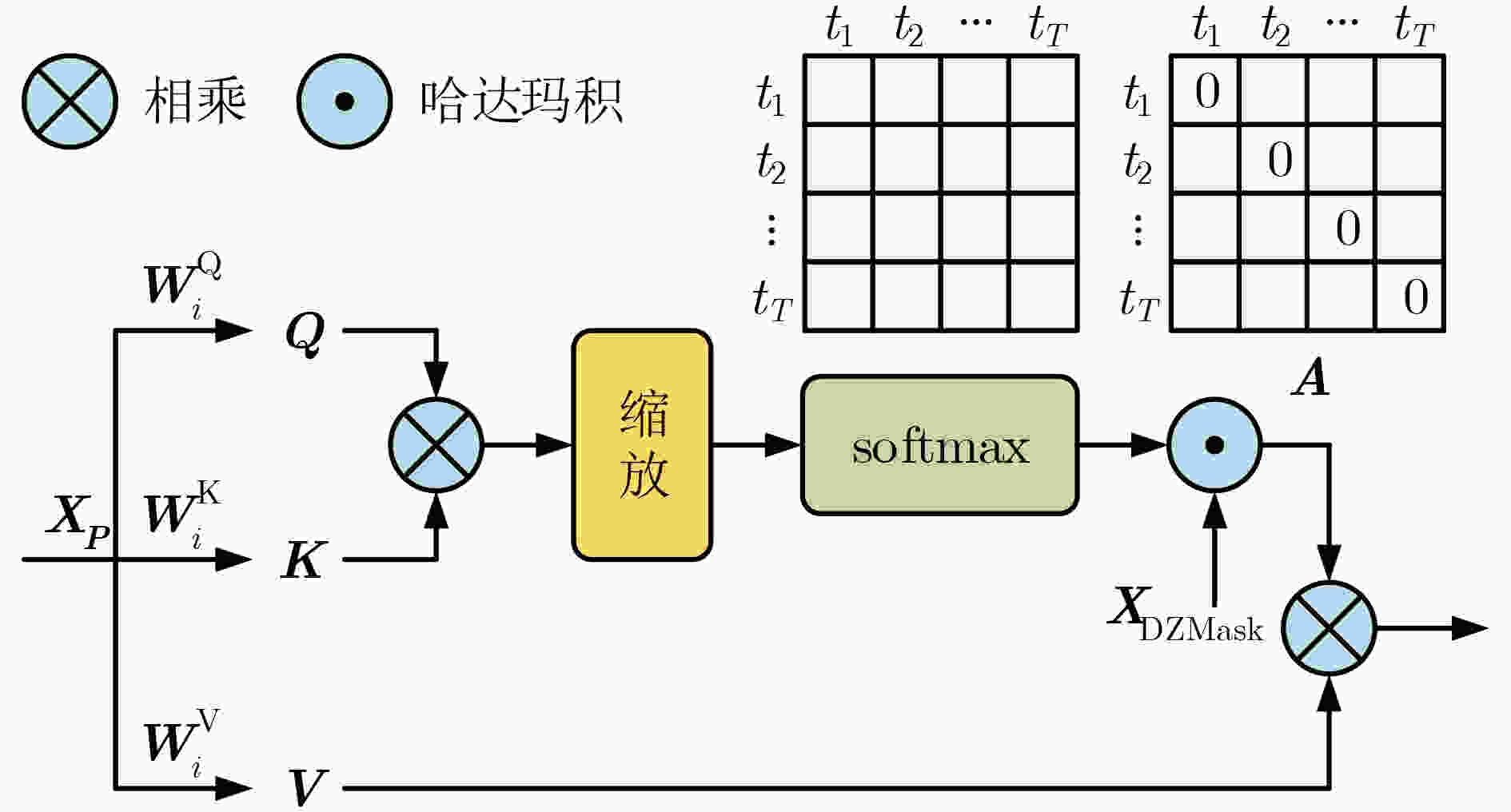
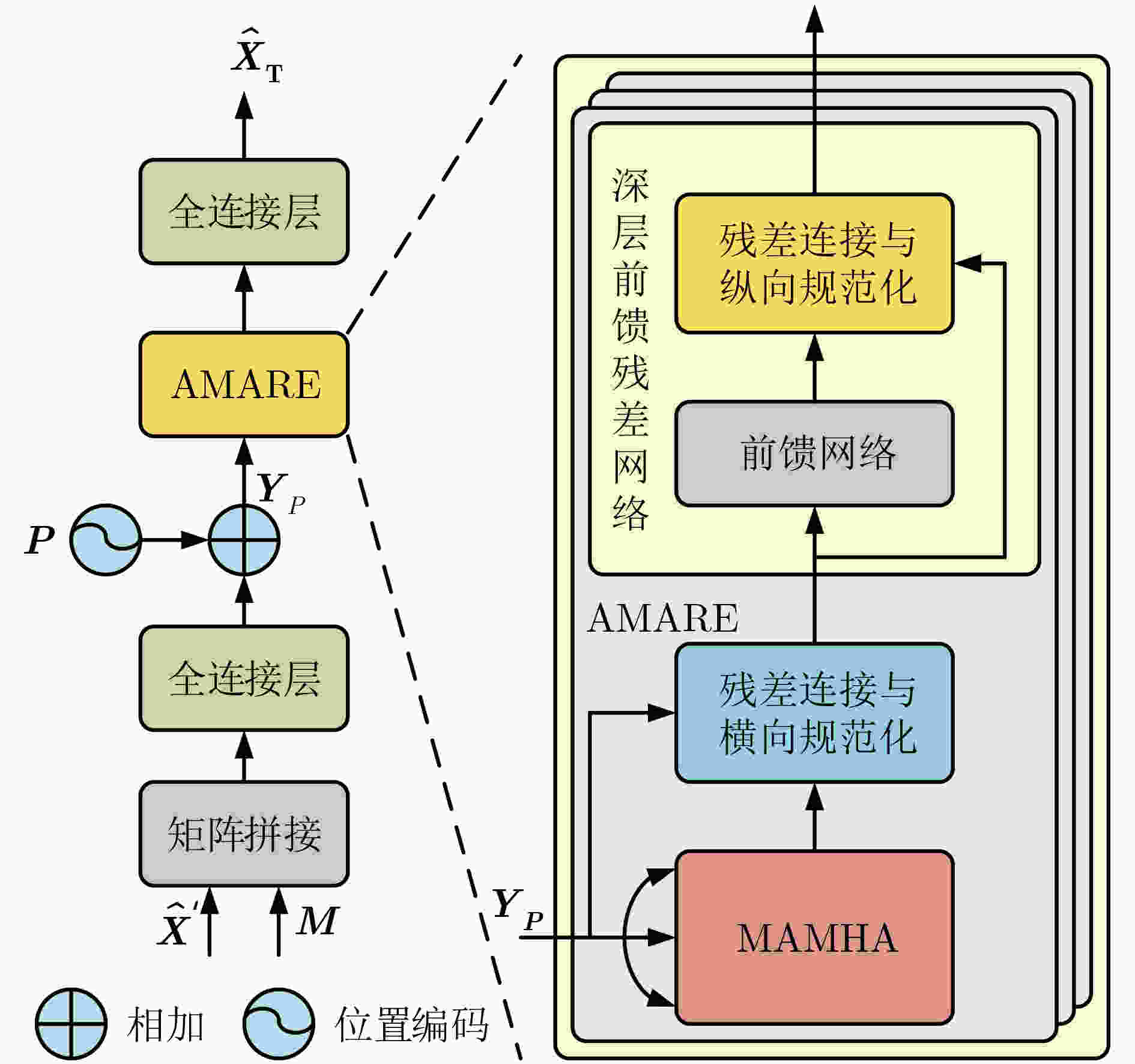
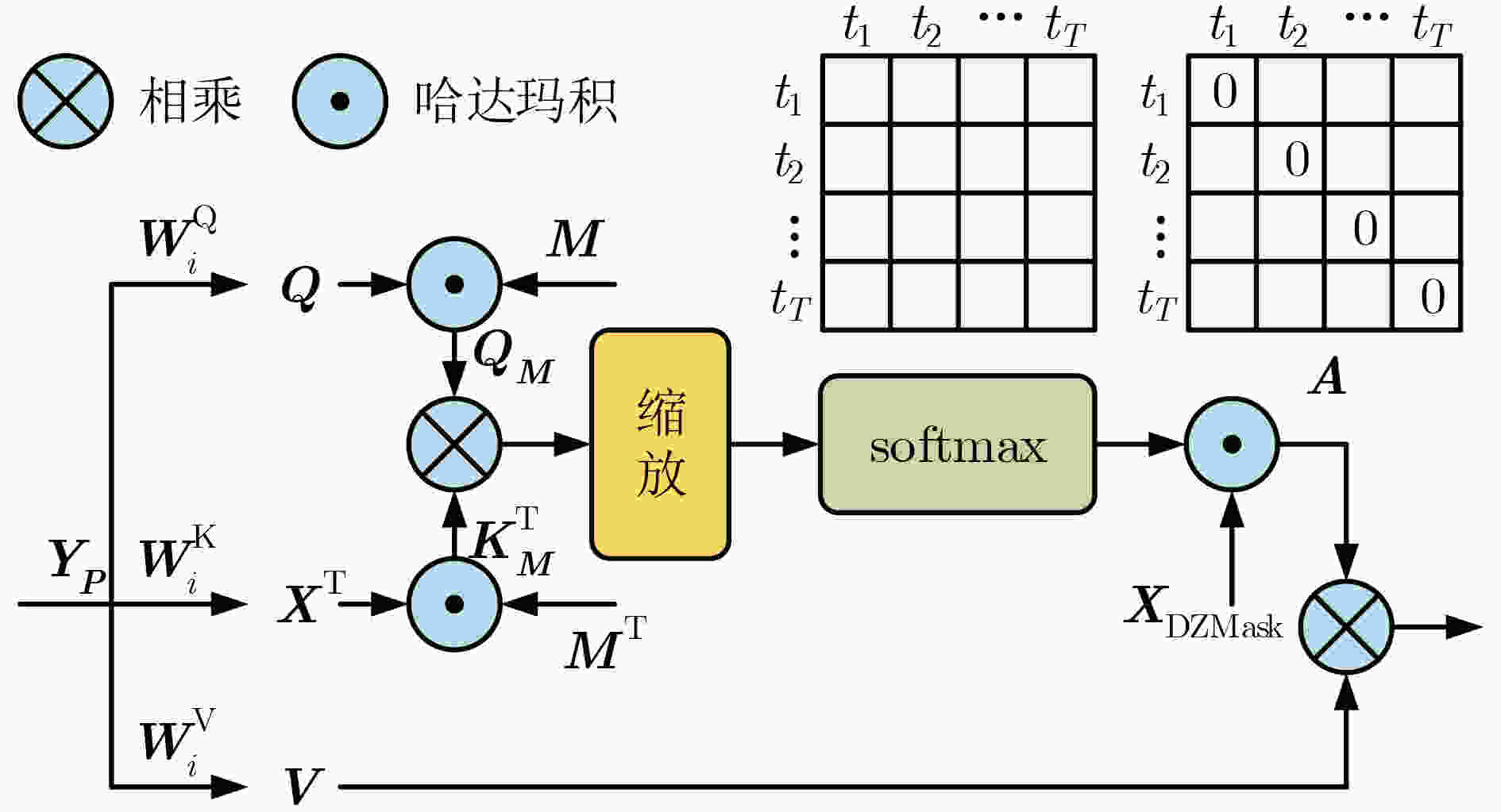
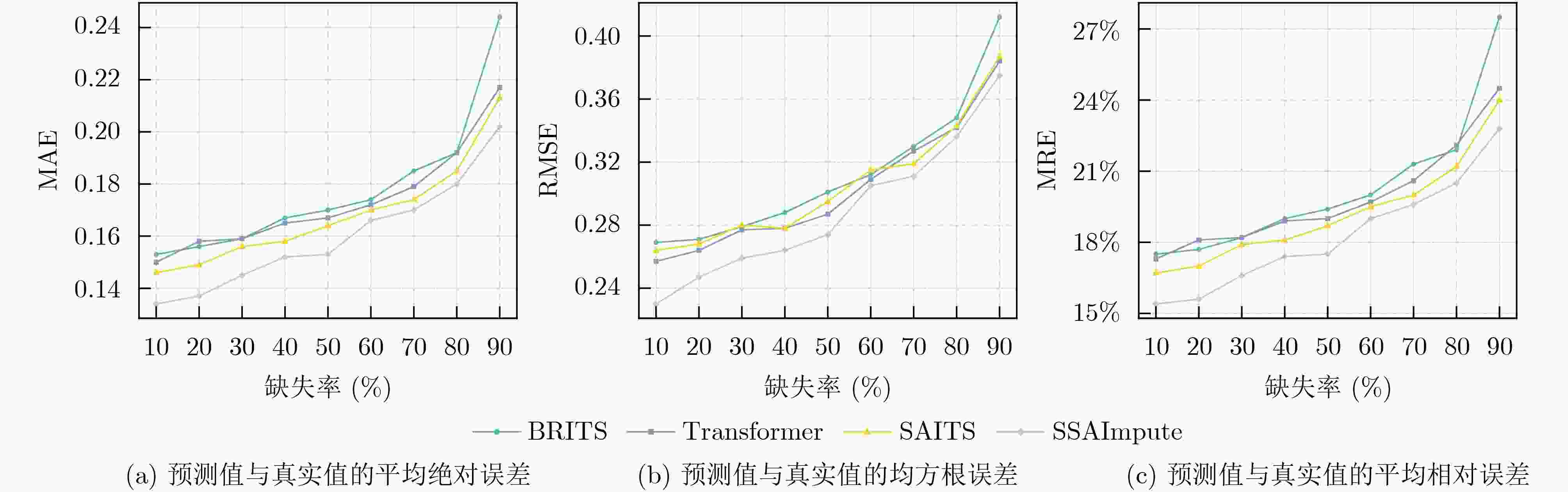
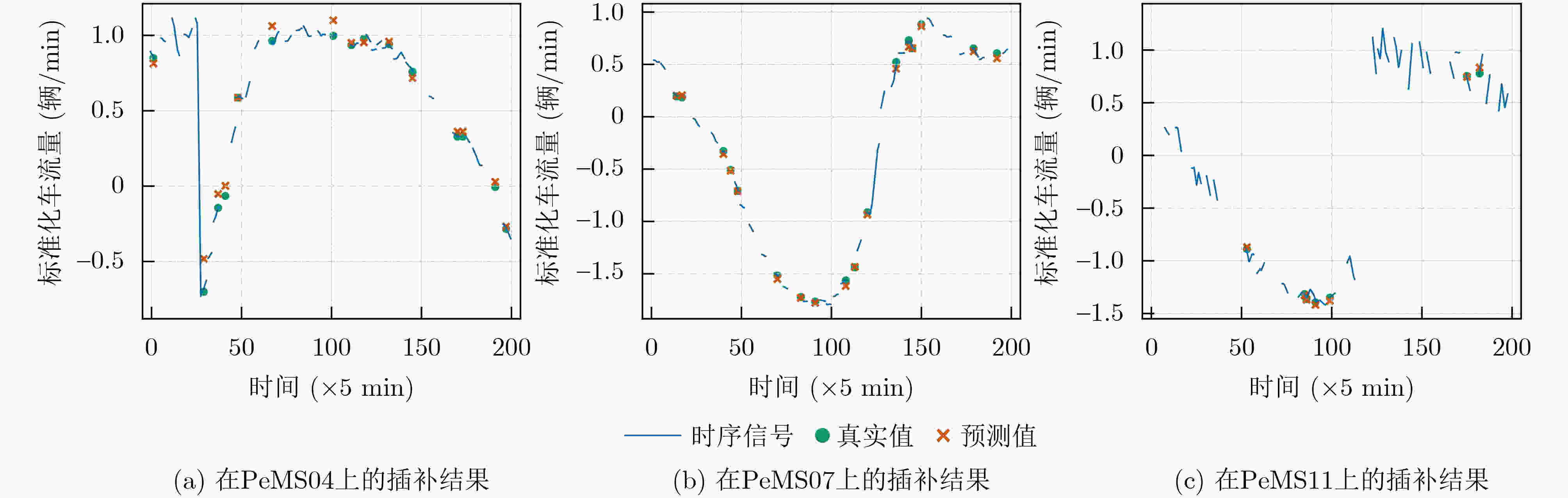
Objective Multivariate time series data, characterized by their high dimensionality and temporal dynamics, are widely generated across diverse application domains, including healthcare monitoring, industrial sensor networks, and autonomous systems. However, these data are often subject to severe missingness caused by sensor malfunctions, transmission errors, or environmental disturbances, which obscures critical spatiotemporal patterns and hinders downstream analytical tasks such as anomaly detection, predictive maintenance, and decision support. Existing imputation methods, ranging from statistical approaches to machine learning models, are primarily tailored to low missing-rate scenarios. When applied to high missing-rate conditions, they face challenges such as gradient vanishing during model training, insufficient capture of spatiotemporal dependencies, and limited ability to represent complex nonlinear features, with performance deteriorating sharply as the missing rate increases. To address these limitations, this study proposes the Spatial Self-Attention Incorporated Imputation algorithm (SSAImpute), designed to enhance imputation performance specifically under severely missing conditions. Methods The proposed SSAImpute algorithm adopts a dual-branch Siamese architecture with adversarial fusion. Each branch comprises two core modules: a spatial self-attention-aware module and a subsequent temporal self-attention encoding module. The spatial self-attention-aware module constructs a dynamic adjacency matrix from the geolocations of data sources to explicitly quantify inter-variable spatial relationships. These spatial dependencies are then integrated with temporal features to strengthen sequence correlation modeling and enrich feature representations with embedded spatial information. The temporal self-attention encoding module employs a multi-dimensional residual attention mechanism with bidirectional temporal dependency learning. A missing-aware positional encoding scheme and a mask-adaptive self-attention mechanism are incorporated to effectively capture temporal dependencies and feature correlations, thereby mitigating severe missingness and alleviating the vanishing gradient problem. The two Siamese branches are fused through adversarial learning and dynamic weighting, which jointly refine the final imputation results. To evaluate the performance of SSAImpute against competing methods, three conventional metrics are used: Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Mean Relative Error (MRE). Results and Discussions Extensive experiments are conducted on four public datasets—Inter-Sensor, PeMS04, PeMS07, and PeMS11, in comparison with seven state-of-the-art time series imputation models: Mean, Median, K-Nearest Neighbor (KNN), Multi-directional Recurrent Neural Network (M-RNN), Bidirectional Recurrent Imputation for Time Series (BRITS), Transformer, and Self-Attention-based Imputation for Time Series (SAITS). The results show that the proposed method consistently improves imputation accuracy across all datasets, even under severe missingness. On the Inter-Sensor dataset, SSAImpute demonstrates superior performance compared with all competing methods. For all four time series, SSAImpute outperforms the others across all evaluation metrics, with improvements over the best-performing baseline (SAITS) of 15.9% in MAE, 0.19% in RMSE, and 16.6% in MRE for temperature; 11.1% in MAE, 1.04% in RMSE, and 13.2% in MRE for humidity; 9.8% in MAE, 10.2% in RMSE, and 24.3% in MRE for light; and 8.8% in MAE, 0.4% in RMSE, and 8.8% in MRE for voltage. On the PeMS datasets, SSAImpute also exceeds all competing methods across PeMS04, PeMS07, and PeMS11. The achieved MAE, RMSE, and MRE are 0.203, 0.328, and 22.4% for PeMS04; 0.153, 0.274, and 17.5% for PeMS07; and 0.180, 0.282, and 19.3% for PeMS11, respectively. The performance under different missing-ratio scenarios is further investigated. Although accuracy decreases exponentially with higher missingness, SSAImpute consistently outperforms the three strongest baselines ( Fig. 6 ). Visualization of the imputed time series further verifies its effectiveness, with reconstructed values closely aligned with the ground truth (Fig. 7 ). These findings confirm the contributions of the spatial self-attention-aware module, the temporal self-attention encoding module, and the adversarial learning with dynamic weighting mechanism.Conclusions This study proposes a spatial self-attention-incorporated imputation method for severely missing multivariate time series data, built on a dual-branch Siamese framework. Each branch integrates a spatial self-attention-aware module, which incorporates geolocation information of the data source, followed by a temporal self-attention encoding mechanism to capture contextual dependencies. These modules jointly strengthen feature extraction of spatiotemporal dependencies, enabling more accurate reconstruction under high missingness. The proposed method provides a robust data foundation for downstream data-driven analysis and decision-making tasks in real-world applications. -
Key words:
- Deep learning /
- Multivariate time series /
- Self-attention /
- Imputation /
- Severe missing data
-
表 1 SSAImpute模型参数设置
参数 PeMS04 PeMS07 PeMS11 Inter-Sensor 输入序列长度 240 240 240 240 自注意力头数 4 4 4 4 堆叠层数 1 1 1 1 隐藏层维度 512 512 256 128 前馈网络隐藏单元数 128 32 32 512 表 2 SSAImpute在PeMS数据集上的消融实验结果
方法 PeMS04 PeMS07 PeMS11 MAE RMSE MRE(%) MAE RMSE MRE(%) MAE RMSE MRE(%) SSAImpute-SMD 0.206 0.334 22.7 0.161 0.275 18.4 0.181 0.285 19.7 SSAImpute-S 0.208 0.333 22.9 0.159 0.282 18.1 0.180 0.284 19.7 SSAImpute-TSAE 0.209 0.330 23.1 0.157 0.276 17.9 0.180 0.290 19.6 SSAImpute-Pos 0.209 0.336 23.0 0.160 0.284 18.2 0.182 0.286 19.8 SSAImpute-Fixed 0.207 0.332 22.8 0.159 0.283 18.2 0.181 0.288 19.8 SSAImpute 0.203 0.328 22.4 0.153 0.274 17.5 0.177 0.282 19.3 注:SSAImpute-SMD:去除SMD模块;SSAImpute-S:其中S代表Single,为单分支结构;SSAImpute-TSAE:去除时域自注意力编码模块;SSAImpute-Pos:去除位置信息;SSAImpute-Fixed:使用固定权重进行双分支融合。 表 3 模型在Inter-Sensor数据集上的消融实验结果
方法 Temperature Humidity Light Voltage MAE RMSE MRE(%) MAE RMSE MRE(%) MAE RMSE MRE(%) MAE RMSE MRE(%) SSAImpute-SMD 0.118 0.517 24.2 0.113 0.480 23.6 0.141 0.269 18.6 0.130 0.829 36.8 SSAImpute-S 0.120 0.515 24.6 0.116 0.486 24.1 0.143 0.271 18.9 0.129 0.830 36.6 SSAImpute-TSAE 0.119 0.520 24.5 0.118 0.483 24.6 0.150 0.285 19.8 0.137 0.829 39.0 SSAImpute-Pos 0.121 0.514 24.8 0.115 0.481 24.1 0.145 0.279 19.3 0.129 0.833 36.7 SSAImpute-Fixed 0.117 0.515 23.9 0.117 0.480 24.4 0.142 0.274 18.8 0.132 0.826 37.7 SSAImpute 0.111 0.513 22.6 0.110 0.477 22.9 0.138 0.265 15.3 0.124 0.827 35.2 表 4 模型在PeMS数据集上的插补性能
方法 PeMS04 PeMS07 PeMS11 MAE RMSE MRE(%) MAE RMSE MRE(%) MAE RMSE MRE(%) Mean[14] 0.893 1.014 98.5 0.861 0.992 98.1 0.906 1.040 98.7 Median[14] 0.907 1.029 99.9 0.876 1.001 99.9 0.918 1.055 99.9 KNN[36] 0.646 0.754 71.3 0.618 0.73 70.6 0.653 0.767 71.2 M-RNN[25] 0.270 0.407 29.8 0.241 0.375 27.5 0.233 0.352 25.3 BRITS[26] 0.212 0.347 23.4 0.170 0.301 19.4 0.192 0.303 20.9 Transformer[37] 0.208 0.342 22.9 0.167 0.287 19.0 0.188 0.296 20.5 SAITS[30] 0.209 0.348 23.0 0.164 0.296 18.7 0.186 0.299 20.2 SSAImpute 0.203 0.328 22.4 0.153 0.274 17.5 0.177 0.282 19.3 表 5 模型在Inter-Sensor数据集上的插补性能
方法 Temperature Humidity Light Voltage MAE RMSE MRE
(%)MAE RMSE MRE
(%)MAE RMSE MRE
(%)MAE RMSE MRE
(%)Mean[14] 0.475 0.739 97.0 0.463 0.698 96.7 0.761 0.928 100 0.245 0.829 69.7 Median[14] 0.489 0.772 100.0 0.478 0.733 99.9 0.755 0.939 99.9 0.201 0.829 69.7 KNN[36] 0.302 0.624 61.6 0.291 0.581 60.7 0.375 0.572 49.6 0.222 0.823 63.2 M-RNN[25] 0.300 0.582 61.2 0.290 0.539 60.6 0.305 0.460 40.4 0.317 0.836 89.9 BRITS[26] 0.194 0.538 39.8 0.187 0.499 39.0 0.184 0.329 24.4 0.136 0.824 38.7 Transformer[37] 0.191 0.524 39.0 0.186 0.494 39.0 0.163 0.304 21.6 0.143 0.824 40.7 SAITS[30] 0.132 0.514 27.1 0.126 0.482 26.4 0.153 0.295 20.2 0.136 0.830 38.7 SSAImpute 0.111 0.513 22.6 0.112 0.477 22.9 0.138 0.265 15.3 0.124 0.827 35.2 -
[1] LUO Yonghong, CAI Xiangrui, ZHANG Ying, et al. Multivariate time series imputation with generative adversarial networks[C]. The 32nd International Conference on Neural Information Processing Systems, Montréal, Canada, 2018: 1603–1614. [2] UCHIHARA M, TANABE A, and KAJIO H. Clinical issues and suggestions: Dashboard visualization of the trajectory of patients with malignant hormone-producing tumors for precision medicine[C]. 2023 Workshop on Visual Analytics in Healthcare (VAHC), Melbourne, Australia, 2023: 47–49. doi: 10.1109/VAHC60858.2023.00015. [3] PAL R, ADHIKARI D, HEYAT M B B, et al. Yoga meets intelligent internet of things: Recent challenges and future directions[J]. Bioengineering, 2023, 10(4): 459. doi: 10.3390/bioengineering10040459. [4] 骆阳, 张旗. 基于模糊关联规则的海量气象数据动态挖掘[J]. 电子设计工程, 2023, 31(22): 149–152. doi: 10.14022/j.issn1674-6236.2023.22.031.LUO Yang and ZHANG Qi. Dynamic mining of massive meteorological data based on fuzzy association rules[J]. Electronic Design Engineering, 2023, 31(22): 149–152. doi: 10.14022/j.issn1674-6236.2023.22.031. [5] WANG Yunsheng, XU Xinghan, HU Lei, et al. A time series continuous missing values imputation method based on generative adversarial networks[J]. Knowledge-Based Systems, 2024, 283: 111215. doi: 10.1016/j.knosys.2023.111215. [6] XU Longfei, XU Lingyu, and YU Jie. A multi-task learning-based generative adversarial network for red tide multivariate time series imputation[J]. Complex & Intelligent Systems, 2023, 9(2): 1363–1376. doi: 10.1007/s40747-022-00856-w. [7] MIAO Xiaoye, WU Yangyang, CHEN Lu, et al. An experimental survey of missing data imputation algorithms[J]. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(7): 6630–6650. doi: 10.1109/TKDE.2022.3186498. [8] LIN Weichao, TSAI C F, and ZHONG Jiarong. Deep learning for missing value imputation of continuous data and the effect of data discretization[J]. Knowledge-Based Systems, 2022, 239: 108079. doi: 10.1016/j.knosys.2021.108079. [9] 郭艳, 宋晓祥, 李宁, 等. 多变量时间序列中基于克罗内克压缩感知的缺失数据预测算法[J]. 电子与信息学报, 2019, 41(4): 858–864. doi: 10.11999/JEIT180541.GUO Yan, SONG Xiaoxiang, LI Ning, et al. Missing data prediction based on Kronecker compressing sensing in multivariable time series[J]. Journal of Electronics & Information Technology, 2019, 41(4): 858–864. doi: 10.11999/JEIT180541. [10] LIU Hui, YU Jian, CHEN Xiangzhi, et al. NeuMF: Predicting anti-cancer drug response through a neural matrix factorization model[J]. Current Bioinformatics, 2022, 17(9): 835–847. doi: 10.2174/1574893617666220609114052. [11] 朱宇航, 刘树新, 吉立新, 等. 一种融合局部拓扑影响力的时序链路预测算法[J]. 电子与信息学报, 2022, 44(4): 1440–1452. doi: 10.11999/JEIT210019.ZHU Yuhang, LIU Shuxin, JI Lixin, et al. A temporal link predict algorithm based on fusion local structure influence[J]. Journal of Electronics & Information Technology, 2022, 44(4): 1440–1452. doi: 10.11999/JEIT210019. [12] XU Meng, DI Yining, DING Hongxing, et al. AGNP: Network-wide short-term probabilistic traffic speed prediction and imputation[J]. Communications in Transportation Research, 2023, 3: 100099. doi: 10.1016/j.commtr.2023.100099. [13] LIU Hui, WANG Feng, YU Jian, et al. DBDNMF: A dual branch deep neural matrix factorization method for drug response prediction[J]. PLoS Computational Biology, 2024, 20(4): e1012012. doi: 10.1371/journal.pcbi.1012012. [14] SAMAD M D, ABRAR S, and DIAWARA N. Missing value estimation using clustering and deep learning within multiple imputation framework[J]. Knowledge-Based Systems, 2022, 249: 108968. doi: 10.1016/j.knosys.2022.108968. [15] ZHANG Weibin, ZHANG Pulin, YU Yinghao, et al. Missing data repairs for traffic flow with self-attention generative adversarial imputation net[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(7): 7919–7930. doi: 10.1109/TITS.2021.3074564. [16] THOMAS T and RAJABI E. A systematic review of machine learning-based missing value imputation techniques[J]. Data Technologies and Applications, 2021, 55(4): 558–585. doi: 10.1108/DTA-12-2020-0298. [17] XUE Yu, TANG Yihang, XU Xin, et al. Multi-objective feature selection with missing data in classification[J]. IEEE Transactions on Emerging Topics in Computational Intelligence, 2022, 6(2): 355–364. doi: 10.1109/TETCI.2021.3074147. [18] KIM H, GOLUB G H, and PARK H. Missing value estimation for DNA microarray gene expression data: Local least squares imputation[J]. Bioinformatics, 2005, 21(2): 187–198. doi: 10.1093/bioinformatics/bth499. [19] CAMASTRA F, CAPONE V, CIARAMELLA A, et al. Prediction of environmental missing data time series by support vector machine regression and correlation dimension estimation[J]. Environmental Modelling & Software, 2022, 150: 105343. doi: 10.1016/j.envsoft.2022.105343. [20] LIN Weichao and TSAI C F. Missing value imputation: A review and analysis of the literature (2006–2017)[J]. Artificial Intelligence Review, 2020, 53(2): 1487–1509. doi: 10.1007/s10462-019-09709-4. [21] DABERDAKU S, TAVAZZI E, and DI CAMILLO B. A combined interpolation and weighted K-Nearest Neighbours approach for the imputation of longitudinal ICU laboratory data[J]. Journal of Healthcare Informatics Research, 2020, 4(2): 174–188. doi: 10.1007/s41666-020-00069-1. [22] FANG Le, XIANG Wei, ZHOU Yuan, et al. Dual-branch cross-dimensional self-attention-based imputation model for multivariate time series[J]. Knowledge-Based Systems, 2023, 279: 110896. doi: 10.1016/j.knosys.2023.110896. [23] QIN Rui and WANG Yong. ImputeGAN: Generative adversarial network for multivariate time series imputation[J]. Entropy, 2023, 25(1): 137. doi: 10.3390/e25010137. [24] CHE Zhengping, PURUSHOTHAM S, CHO K, et al. Recurrent neural networks for multivariate time series with missing values[J]. Scientific Reports, 2018, 8(1): 6085. doi: 10.1038/s41598-018-24271-9. [25] YOON J, ZAME W R, and VAN DER SCHAAR M. Estimating missing data in temporal data streams using multi-directional recurrent neural networks[J]. IEEE Transactions on Biomedical Engineering, 2019, 66(5): 1477–1490. doi: 10.1109/TBME.2018.2874712. [26] CAO Wei, WANG Dong, LI Jian, et al. BRITS: Bidirectional recurrent imputation for time series[C]. The 32nd International Conference on Neural Information Processing Systems, Montréal, Canada, 2018: 6776–6786. [27] SUO Qiuling, ZHONG Weida, XUN Guangxu, et al. GLIMA: Global and local time series imputation with multi-directional attention learning[C]. 2020 IEEE International Conference on Big Data (Big Data), Atlanta, USA, 2020: 798–807. doi: 10.1109/BigData50022.2020.9378408. [28] MA Jiawei, SHOU Zheng, ZAREIAN A, et al. CDSA: Cross-dimensional self-attention for multivariate, geo-tagged time series imputation[EB/OL]. https://arxiv.org/abs/1905.09904, 2019. [29] SHAN Siyuan, LI Yang, and OLIVA J B. NRTSI: Non-recurrent time series imputation[C]. ICASSP 2023 - 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 2023: 1–5. doi: 10.1109/ICASSP49357.2023.10095054. [30] DU Wenjie, CÔTÉ D, and LIU Yan. SAITS: Self-attention-based imputation for time series[J]. Expert Systems with Applications, 2023, 219: 119619. doi: 10.1016/j.eswa.2023.119619. [31] CHUI C K, MHASKAR H N, and VAN DER WALT M D. Data-driven atomic decomposition via frequency extraction of intrinsic mode functions[J]. GEM - International Journal on Geomathematics, 2016, 7(1): 117–146. doi: 10.1007/s13137-015-0079-3. [32] VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[C]. The 31st International Conference on Neural Information Processing Systems, Long Beach, USA, 2017: 6000–6010. [33] PAN Zhuofu, WANG Yalin, WANG Kai, et al. Intel lab data[EB/OL]. https://db.csail.mit.edu/labdata/labdata.html, 2023. [34] 潘立强, 李建中, 骆吉洲. 传感器网络中一种基于时-空相关性的缺失值估计算法[J]. 计算机学报, 2010, 33(1): 1–11. doi: 10.3724/SP.J.1016.2010.00001.PAN Liqiang, LI Jianzhong, and LUO Jizhou. A temporal and spatial correlation based missing values imputation algorithm in wireless sensor networks[J]. Chinese Journal of Computers, 2010, 33(1): 1–11. doi: 10.3724/SP.J.1016.2010.00001. [35] BOX G E P, JENKINS G M, REINSEL G C, et al. Time Series Analysis: Forecasting and Control[M]. 5th ed. Hoboken: Wiley, 2015. [36] ZHANG Shichao. Nearest neighbor selection for iteratively kNN imputation[J]. Journal of Systems and Software, 2012, 85(11): 2541–2552. doi: 10.1016/j.jss.2012.05.073. [37] NIE Tong, QIN Guoyang, MA Wei, et al. ImputeFormer: Low rankness-induced transformers for generalizable spatiotemporal imputation[C]. The 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Barcelona, Spain, 2024: 2260–2271. doi: 10.1145/3637528.3671751. -





 下载:
下载:


 下载:
下载:
