Dynamic Analysis and Synchronization Control of Extremely Simple Cyclic Memristive Chaotic Neural Network
-
摘要: 忆阻器可作为突触引入人工神经网络,提升神经元间连接的合理性,并丰富网络的类脑化动力学行为。该文基于忆阻器提出了一种仅含单向突触连接的极简环形神经网络的混沌化方法,以三节点神经网络为例构造了一类动力学行为丰富且结构简单的忆阻环形神经网络。基于单参数和双参数分岔图以及Lyapunov指数谱,研究了这类网络关于忆阻器耦合强度与内部参数的丰富动力学演化过程,如倍周期分岔与反倍周期分岔。借助相平面图和吸引盆刻画了网络的丰富多稳态行为,如点吸引子与点吸引子、点吸引子与周期吸引子、点吸引子与混沌吸引子。依赖于忆阻器耦合强度的多变量调幅控制行为也被发现和研究。通过电子电路实验检验了所提出网络的物理存在性。此外,针对所提出网络潜在的应用需求,设计了一种新型多幂次趋近律,用于在固定时间内实现混沌同步。数值仿真结果表明了同步策略的可行性与有效性。Abstract:
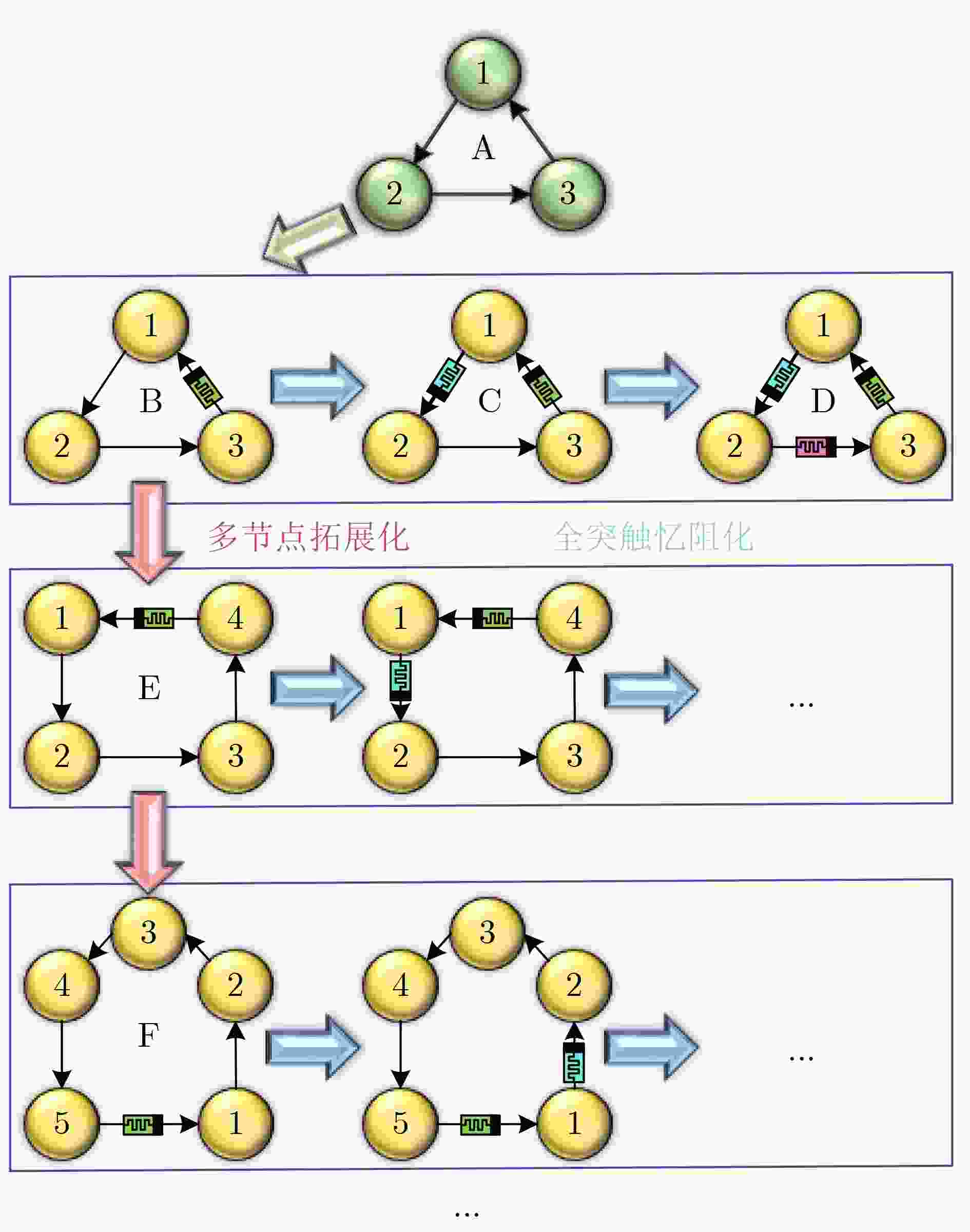
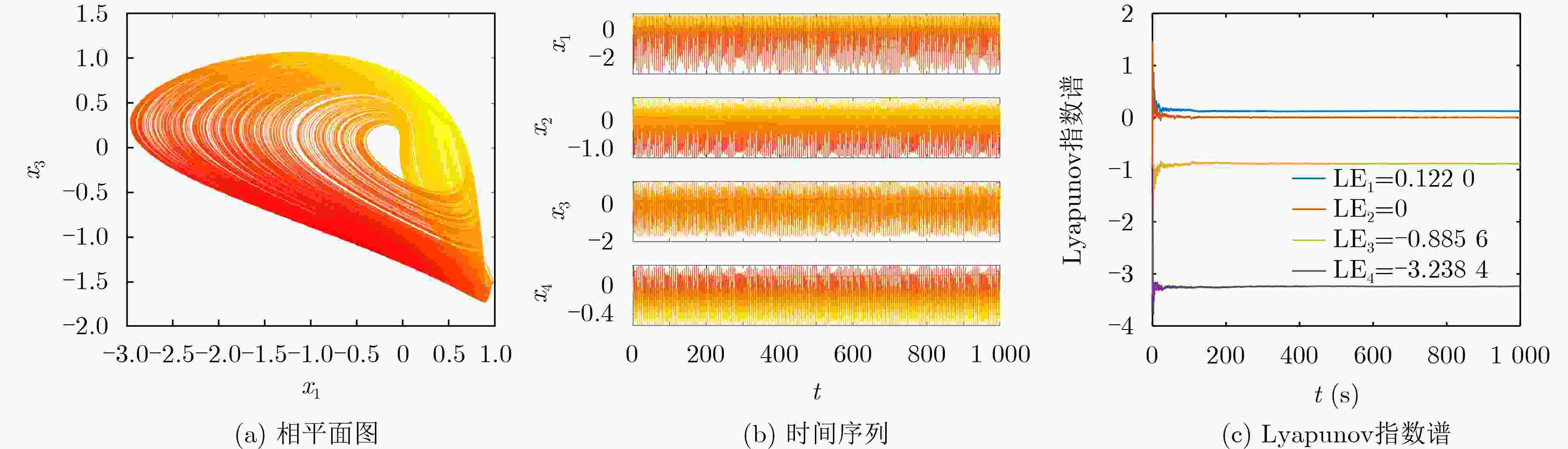
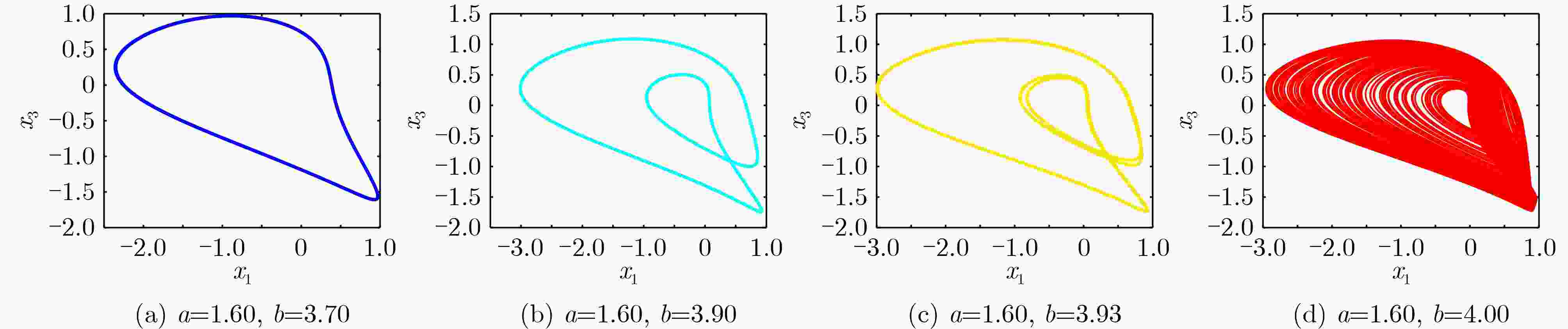
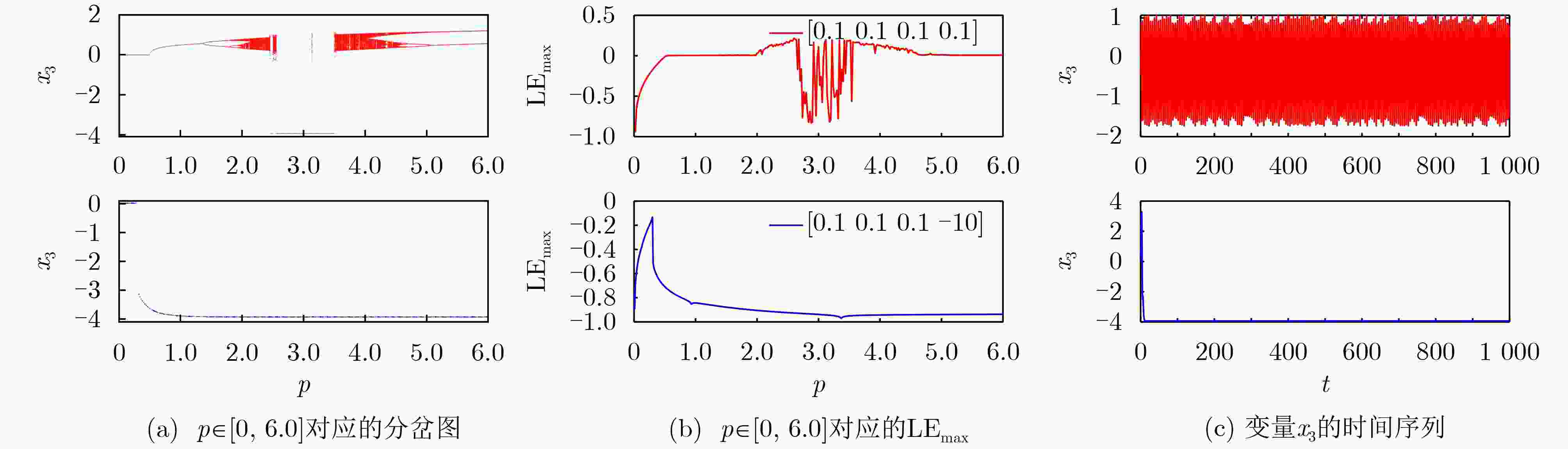
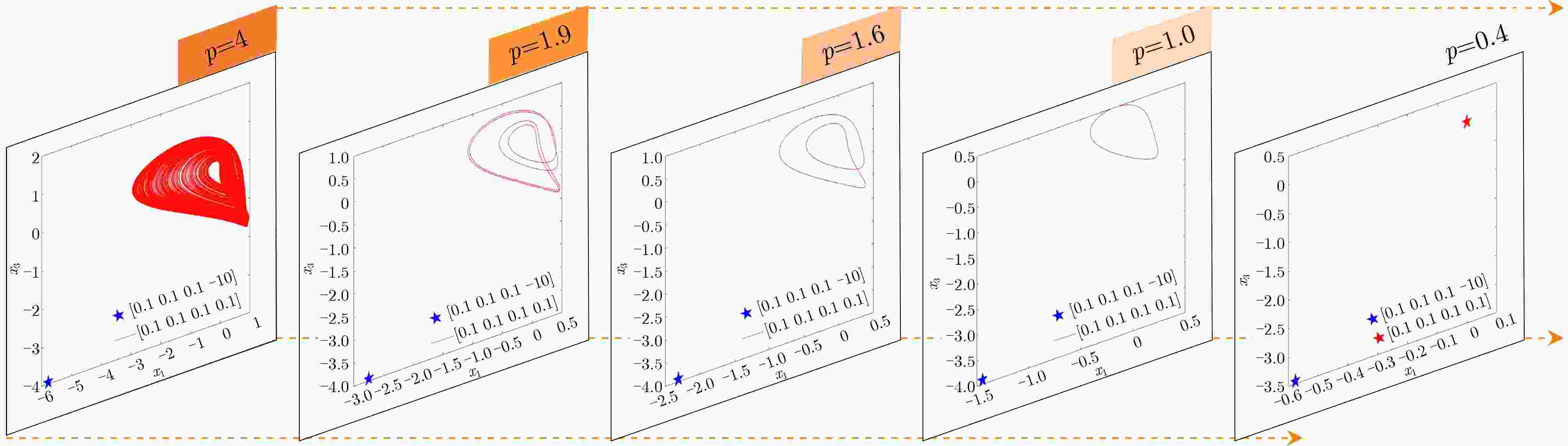
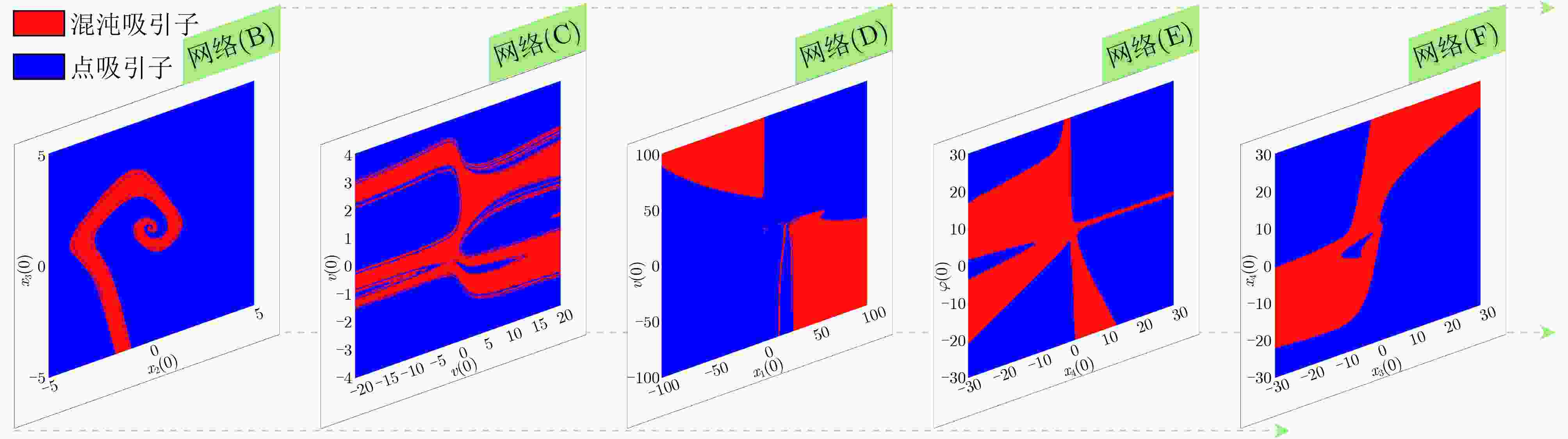
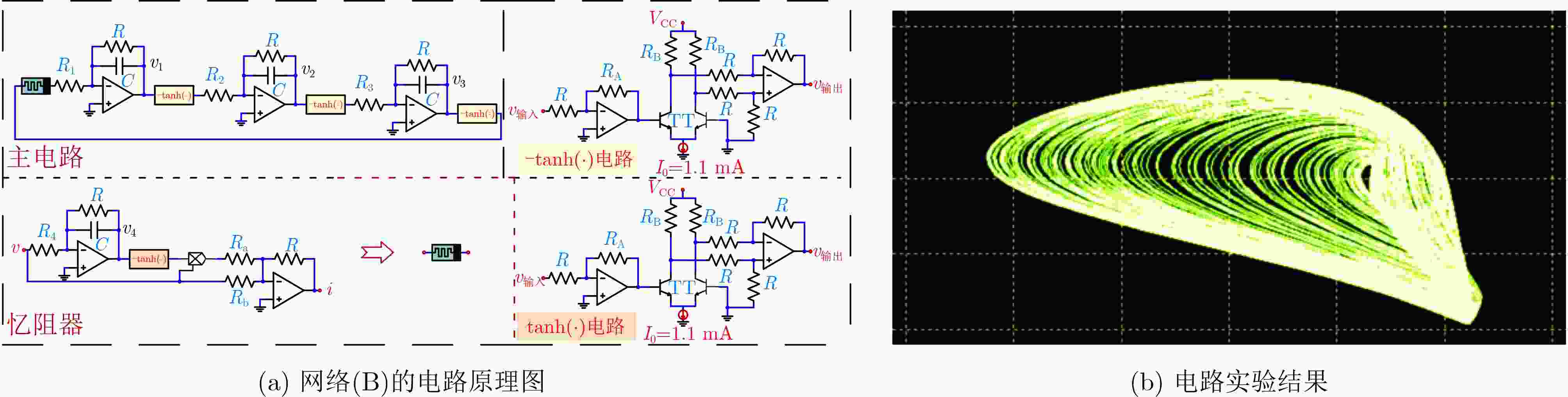
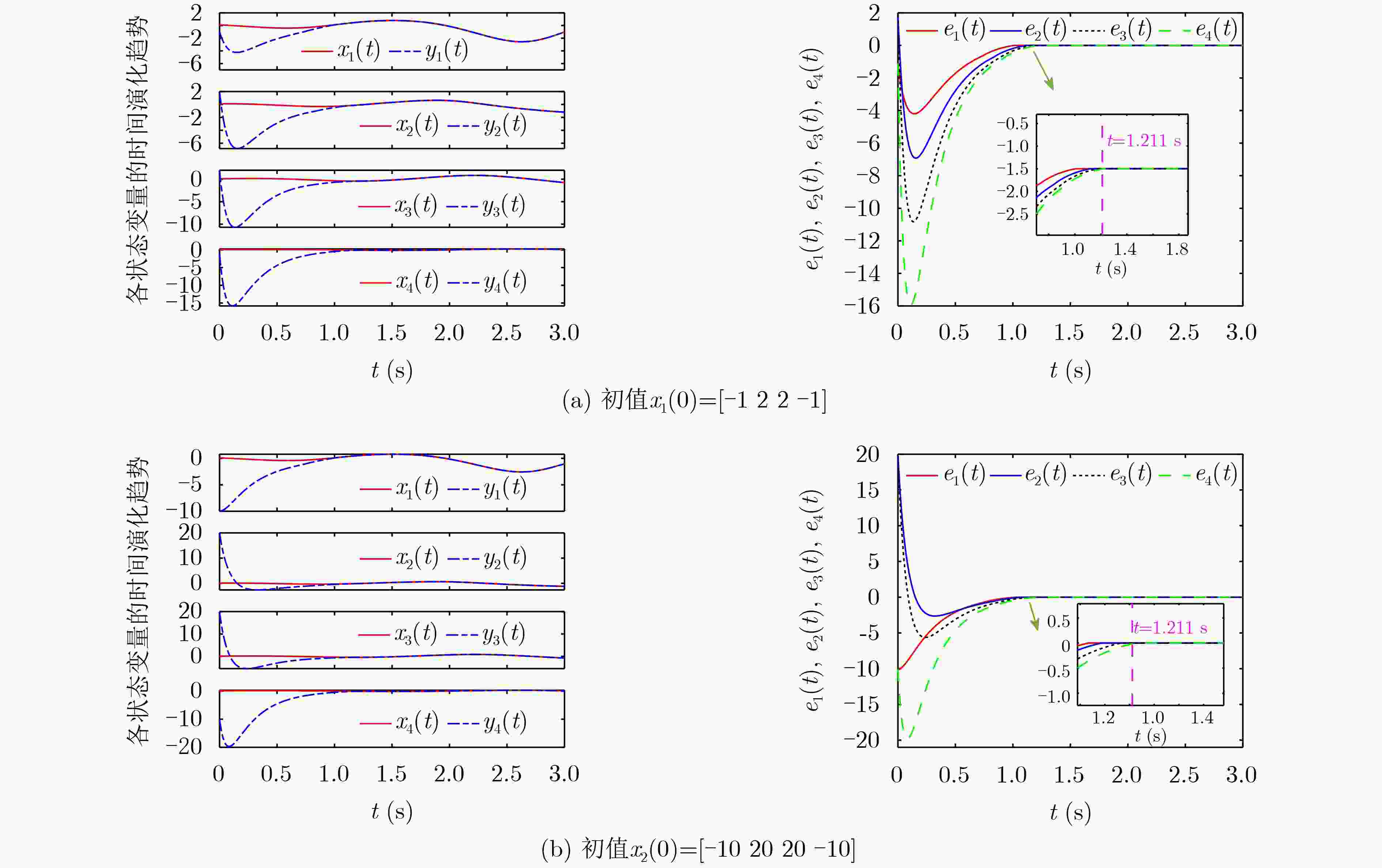
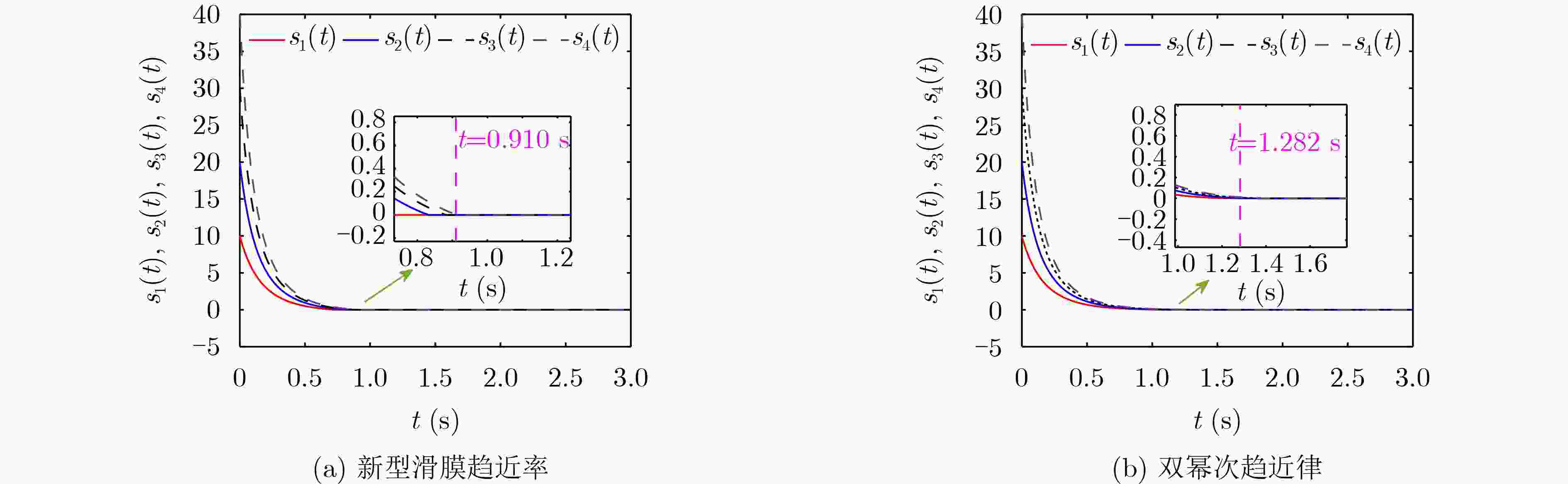
Objective Memristors are considered promising devices for the construction of artificial synapses because their unique nonlinear and non-volatile properties effectively mimic the functions and mechanisms of biological synapses. These features have made memristors a research focus in brain-inspired science. Memristive neural networks, composed of memristive neurons or memristive synapses, constitute a class of biomimetic artificial neural networks that exhibit dynamic behaviors more closely aligned with those of biological neural systems and provide more plausible biological interpretations. Since the concept of the memristive neural network was proposed, extensive pioneering research has been conducted, revealing several critical issues that require further exploration. Although current memristive neural networks can generate complex dynamic behaviors such as chaos and multistability, these effects are often achieved at the cost of increased network complexity or the requirement for specialized memristive characteristics. Therefore, the systematic exploration of simple memristive neural networks that can produce diverse dynamic behaviors, the proposal of practical design strategies, and the development of efficient, precise control schemes remain of considerable research value. Methods This paper proposes a chaoticization method for an Extremely Simple Cyclic Memristive Convolutional Neural Network (ESCMCNN) that contains only unidirectional synaptic connections based on memristors. Using a three-node neural network as an example, a class of memristive cyclic neural networks with simple structures and rich dynamic behaviors is constructed. Numerical analysis tools, including bifurcation diagrams, basins of attraction, phase plane diagrams, and Lyapunov exponents, are employed to investigate the networks’ diverse bifurcation processes, multiple types of multistability, and multi-variable signal amplitude control. Electronic circuit experiments are used to validate the feasibility of the proposed networks. Finally, a novel multi-power reaching law is developed to achieve chaotic synchronization within fixed time. Results and Discussions For a three-node cyclic neural network initially in a periodic state, two network chaotification methods—full-synaptic memristivation and multi-node extension—are proposed using magnetically controlled memristors ( Fig. 1 ). Phase plane diagrams illustrate the chaotic attractors generated by these networks (Fig. 2 ), confirming the feasibility of the proposed methods. Using network (B) as an example, numerical analysis tools are utilized to study its diverse dynamic evolution processes (Fig. 5 ,Fig. 6 ,Fig. 7 ), various forms of multistability (Fig. 8 ,Fig. 9 ), and multi-variable amplitude control (Fig. 10 ). The physical realization of network (B) is further demonstrated through circuit experiments (Fig. 11 ,Fig. 12 ). Additionally, the effectiveness of the fixed-time synchronization control strategy for network (B) is verified through numerical simulations (Fig. 13 ,Fig. 14 ).Conclusions This paper proposes a construction method for the ESCMCNN capable of generating rich dynamic behaviors. A series of ESCMCNNs is successfully designed based on a three-node neural network in a periodic state. The dynamic evolution of the ESCMCNN as a function of memristive parameters is investigated using numerical tools, including single- and dual-parameter bifurcation diagrams and Lyapunov exponents. Under different initial conditions, the ESCMCNN exhibits various forms of multistability, including the coexistence of point attractors with periodic attractors, and point attractors with chaotic attractors. The study further demonstrates that the oscillation amplitudes of multiple variables in the ESCMCNN are strongly dependent on the memristive coupling strength. The reliability of these numerical results is confirmed through electronic circuit experiments. In addition, a novel multi-power reaching law is proposed to achieve fixed-time synchronization of the network, and its feasibility and effectiveness are validated through simulation tests. -
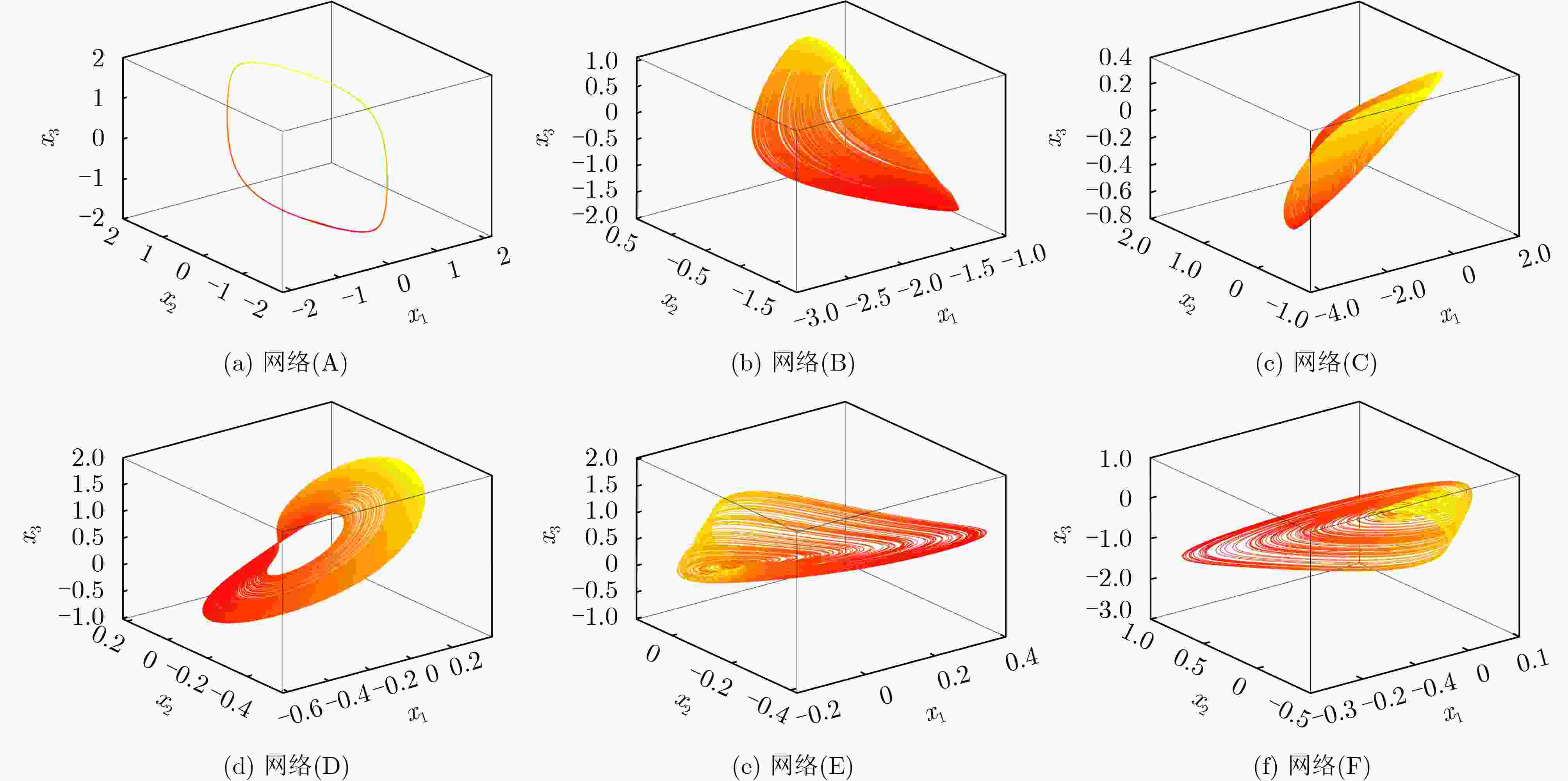
图 3 表1中各环形神经网络的${x_1} {\text{-}} {x_2} {\text{-}} {x_3}$相平面图
表 1 图1中各环形神经网络的模型、参数和初值
编号 模型 参数 初值 图像 A $ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = - {x_1} - 4\tanh ({x_3})} \\ {{{\dot x}_2} = - {x_2} + 2.5\tanh ({x_1})} \\ {{{\dot x}_3} = - {x_3} + 4\tanh ({x_2})} \end{array}} \right. $ - [0.1 0.1 0.1] 图3(a) B $ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = - {x_1} + p( - a - b\tanh (\varphi ))\tanh ({x_3})} \\ {{{\dot x}_2} = - {x_2} + 2.5\tanh ({x_1})} \\ {{{\dot x}_3} = - {x_3} + 4\tanh ({x_2})} \\ {\dot \varphi = - \varphi + \tanh ({x_3})} \end{array}} \right. $ a = 1.6, b = 4,
p = 4[0.1 0.1 0.1 0.1] 图3(b) C $ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = - {x_1} + p(a + b\tanh (u))\tanh ({x_3})} \\ {{{\dot x}_2} = - {x_2} + q(c + d\tanh (v))\tanh ({x_1})} \\ {{{\dot x}_3} = - {x_3} - 1.6\tanh ({x_2})} \\ {\dot u = - u + \tanh ({x_3})} \\ {\dot v = - v + \tanh ({x_1})} \end{array}} \right. $ a = 8, b = –4.5,
c = 1.25, d = 2.6
p = 2, q = 2.5[0.1 0.1 0.1 0.1 0.1] 图3(c) D $ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = - {x_1} + p(a + b\tanh (u))\tanh ({x_3})} \\ {{{\dot x}_2} = - {x_2} + q(c + d\tanh (v))\tanh ({x_1})} \\ {{{\dot x}_3} = - {x_3} + k(e + f\tanh (w))\tanh ({x_2})} \\ {\dot u = - u + \tanh ({x_3})} \\ {\dot v = - v + \tanh ({x_1})} \\ {\dot w = - w + \tanh ({x_2})} \end{array}} \right. $ a = 2.4, b = –6,
c = 2, d = –5,
e = 6, f = –9,
p = 1, q = 1,
k = –1[0.1 0.1 0.1 0.1 0.1 0.1] 图3(d) E $ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = - {x_1} + p(a + b\tanh (\varphi ))\tanh ({x_4})} \\ {{{\dot x}_2} = - {x_2} - 1.8\tanh ({x_1})} \\ {{{\dot x}_3} = - {x_3} - 8\tanh ({x_2})} \\ {{{\dot x}_4} = - {x_4} + 5\tanh ({x_3})} \\ {\dot \varphi = - \varphi + \tanh ({x_4})} \end{array}} \right. $ a = –2, b = 3,
p = 0.2[0.1 0.1 0.1 0.1 0.1] 图3(e) F $ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = - {x_1} + p(a + b\tanh (\varphi ))\tanh ({x_5})} \\ {{{\dot x}_2} = - {x_2} - 5\tanh ({x_1})} \\ {{{\dot x}_3} = - {x_3} - 4\tanh ({x_2})} \\ {{{\dot x}_4} = - {x_4} - 2.4\tanh ({x_3})} \\ {{{\dot x}_5} = - {x_5} + 0.25\tanh ({x_4})} \\ {\dot \varphi = - \varphi + \tanh ({x_5})} \end{array}} \right. $ a = 0.5, b = –3.2,
p = 2.5[0.1 0.1 0.1 0.1 0.1 0.1] 图3(f) 表 2 网络(B)的平衡点类型与对应的特征值
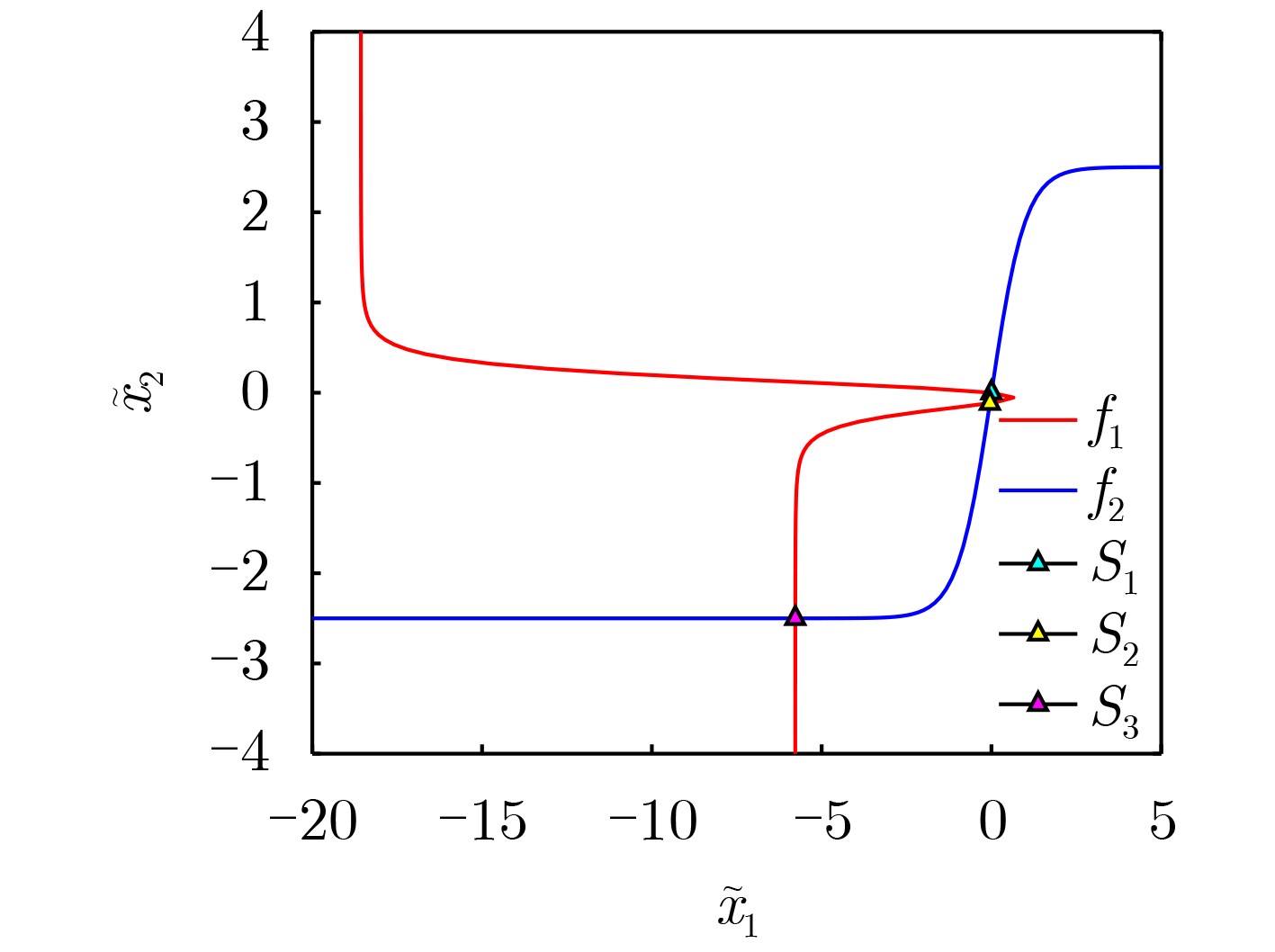
平衡点 特征值 类型 $ {O_1}(0,0,{\text{0,0}}) $ $ - 1.000, - 5.000,1.000 \pm 3.464{\mathrm{i}} $ Index-2不稳定鞍点 $ {O_2}( - 0.046, - 0.116,{{ - 0}}{{.462, - 0}}{\text{.432}}) $ $ 1.639, - 3.573, - 1.033 \pm 2.607{\mathrm{i}} $ Index-1不稳定鞍点 $ {O_3}( - 5.776, - 2.500, - 3.946, - 0.999) $ $ - 0.982, - 1.018, - 1.000 \pm 0.018{\mathrm{i}} $ 稳定焦点 -
[1] KROGH A. What are artificial neural networks?[J]. Nature Biotechnology, 2008, 26(2): 195–197. doi: 10.1038/nbt1386. [2] 王春华, 蔺海荣, 孙晶如, 等. 基于忆阻器的混沌、存储器及神经网络电路研究进展[J]. 电子与信息学报, 2020, 42(4): 795–810. doi: 10.11999/JEIT190821.WANG Chunhua, LIN Hairong, SUN Jingru, et al. Research progress on chaos, memory and neural network circuits based on memristor[J]. Journal of Electronics & Information Technology, 2020, 42(4): 795–810. doi: 10.11999/JEIT190821. [3] 王璇, 杜健嵘, 李志军, 等. 串扰忆阻突触异质离散神经网络的共存放电与同步行为[J]. 物理学报, 2024, 73(11): 110503. doi: 10.7498/aps.73.20231972.WANG Xuan, DU Jianrong, LI Zhijun, et al. Coexisting discharge and synchronization of heterogeneous discrete neural network with crosstalk memristor synapses[J]. Acta Physica Sinica, 2024, 73(11): 110503. doi: 10.7498/aps.73.20231972. [4] LI Fangyuan, QIN Wangsheng, XI Minqi, et al. Plane coexistence behaviors for Hopfield neural network with two-memristor-interconnected neurons[J]. Neural Networks, 2025, 183: 107049. doi: 10.1016/j.neunet.2024.107049. [5] 温新宇, 王亚赛, 何毓辉, 等. 忆阻类脑计算[J]. 物理学报, 2022, 71(14): 140501. doi: 10.7498/aps.71.20220666.WEN Xinyu, WANG Yasai, HE Yuhui, et al. Memristive brain-like computing[J]. Acta Physica Sinica, 2022, 71(14): 140501. doi: 10.7498/aps.71.20220666. [6] 赖强, 秦铭宏. 基于忆阻电磁辐射的极简环形HNN动力学行为增强研究[J]. 贵州师范大学学报: 自然科学版, 2025, 43(3): 1–11. doi: 10.16614/j.gznuj.zrb.2025.03.001.LAI Qiang and QIN Minghong. Enhanced dynamics of an extremely simple cyclic HNN based on memristive electromagnetic radiation[J]. Journal of Guizhou Normal University: Natural Sciences, 2025, 43(3): 1–11. doi: 10.16614/j.gznuj.zrb.2025.03.001. [7] JIN Peipei, WANG Guangyi, LIANG Yan, et al. Neuromorphic dynamics of Chua corsage memristor[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2021, 68(11): 4419–4432. doi: 10.1109/TCSI.2021.3121676. [8] LAI Qiang, LIU Yijin, and FORTUNA L. Dynamical analysis and fixed-time synchronization for secure communication of hidden multiscroll memristive chaotic system[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2024, 71(10): 4665–4675. doi: 10.1109/TCSI.2024.3434551. [9] 王梦蛟, 杨琛, 贺少波, 等. 一种新型复合指数型局部有源忆阻器耦合的Hopfield神经网络[J]. 物理学报, 2024, 73(13): 130501. doi: 10.7498/aps.73.20231888.WANG Mengjiao, YANG Chen, HE Shaobo, et al. A novel compound exponential locally active memristor coupled Hopfield neural network[J]. Acta Physica Sinica, 2024, 73(13): 130501. doi: 10.7498/aps.73.20231888. [10] DING Dawei, XIAO Heng, YANG Zongli, et al. Coexisting multi-stability of Hopfield neural network based on coupled fractional-order locally active memristor and its application in image encryption[J]. Nonlinear Dynamics, 2022, 108(4): 4433–4458. doi: 10.1007/s11071-022-07371-0. [11] BAO Han, CHEN Zhuguan, MA Jun, et al. Planar homogeneous coexisting hyperchaos in Bi-Memristor cyclic Hopfield neural network[J]. IEEE Transactions on Industrial Electronics, 2024, 71(12): 16398–16408. doi: 10.1109/TIE.2024.3387058. [12] LAI Qiang and YANG Liang. Discrete memristor applied to construct neural networks with homogeneous and heterogeneous coexisting attractors[J]. Chaos, Solitons & Fractals, 2023, 174: 113807. doi: 10.1016/j.chaos.2023.113807. [13] WAN Qiuzhen, CHEN Simiao, LIU Tieqiao, et al. A novel locally active memristive autapse-coupled Hopfield neural network under electromagnetic radiation[J]. Integration, 2025, 103: 102410. doi: 10.1016/j.vlsi.2025.102410. [14] LI Yongxin, LI Chunbiao, ZHANG Sen, et al. Offset boosting-oriented construction of multi-Scroll attractor via a memristor model[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2025, 72(2): 918–931. doi: 10.1109/TCSI.2024.3455350. [15] 武花干, 边逸轩, 陈墨, 等. 忆阻耦合异构忆阻细胞神经网络的多稳态与相位同步研究[J]. 电子与信息学报, 2024, 46(9): 3818–3826. doi: 10.11999/JEIT240010.WU Huagan, BIAN Yixuan, CHEN Mo, et al. Multistable state and phase synchronization of memristor-coupled heterogeneous memristive cellular neural network[J]. Journal of Electronics & Information Technology, 2024, 46(9): 3818–3826. doi: 10.11999/JEIT240010. [16] PARASTESH F, JAFARI S, AZARNOUSH H, et al. Chimera in a network of memristor-based Hopfield neural network[J]. The European Physical Journal Special Topics, 2019, 228(10): 2023–2033. doi: 10.1140/epjst/e2019-800240-5. [17] 贾美美, 曹佳伟, 白明明. 新型忆阻耦合异质神经元的放电模式和预定义时间混沌同步[J]. 物理学报, 2024, 73(17): 170502. doi: 10.7498/aps.73.20240872.JIA Meimei, CAO Jiawei, and BAI Mingming. Firing modes and predefined-time chaos synchronization of novel memristor-coupled heterogeneous neuron[J]. Acta Physica Sinica, 2024, 73(17): 170502. doi: 10.7498/aps.73.20240872. [18] ZHANG Yuman and LI Yuxia. Nonlinear dynamics and sliding mode control for global fixed-time synchronization of a novel 2×2 memristor-based cellular neural network[J]. Chaos, Solitons & Fractals, 2024, 189: 115611. doi: 10.1016/j.chaos.2024.115611. [19] YU Fei, KONG Xinxin, YAO Wei, et al. Dynamics analysis, synchronization and FPGA implementation of multiscroll Hopfield neural networks with non-polynomial memristor[J]. Chaos, Solitons & Fractals, 2024, 179: 114440. doi: 10.1016/j.chaos.2023.114440. [20] HOPFIELD J J. Neural networks and physical systems with emergent collective computational abilities[J]. Proceedings of the National Academy of Sciences of the United States of America, 1982, 79(8): 2554–2558. doi: 10.1073/pnas.79.8.2554. [21] YANG Xiaosong. 3-D cellular neural networks with cyclic connections cannot exhibit chaos[J]. International Journal of Bifurcation and Chaos, 2008, 18(4): 1227–1230. doi: 10.1142/S0218127408020951. -





 下载:
下载:





 下载:
下载:
