Research on Station Centrality and Cascade Failure Invulnerability of Urban Rail Transit Networks
-
摘要: 轨道交通网络站点中心性研究对轨道交通系统安全至关重要。识别轨道交通网络的关键节点有助于提前设置预案,降低站点故障影响,确保运行安全。根据现有研究分析,静态拓扑和动态客流是影响站点中心性的两大关键因素。鉴于此,该文提出一种融合静态拓扑和动态客流的轨道交通站点中心性指标。该指标基于PageRank与改进K核评估轨道交通网络的静态拓扑中心性,并充分考虑进站人数和出站人数评估动态客流中心性。此外,该文还提出了一种动态客流对于静态拓扑重要性的增强方法,确保二者的有机融合。基于上海市轨道交通网络真实数据的级联失效实验表明该文方法能够有效、稳定地识别轨道交通网络的关键站点。对这些站点进行重点保护,可以增强轨道交通网络对级联失效的抗毁性,提升整体系统安全。Abstract:
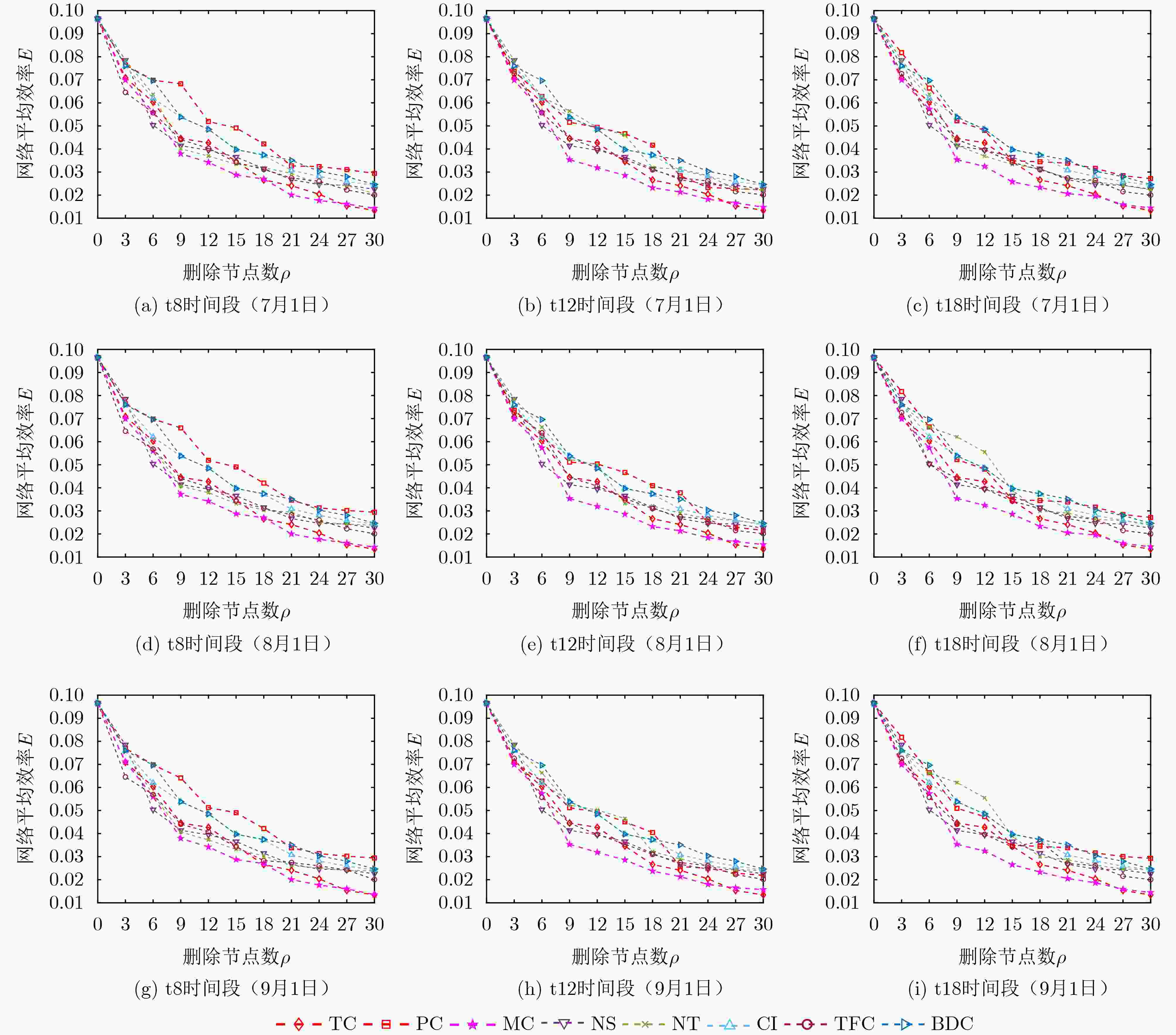
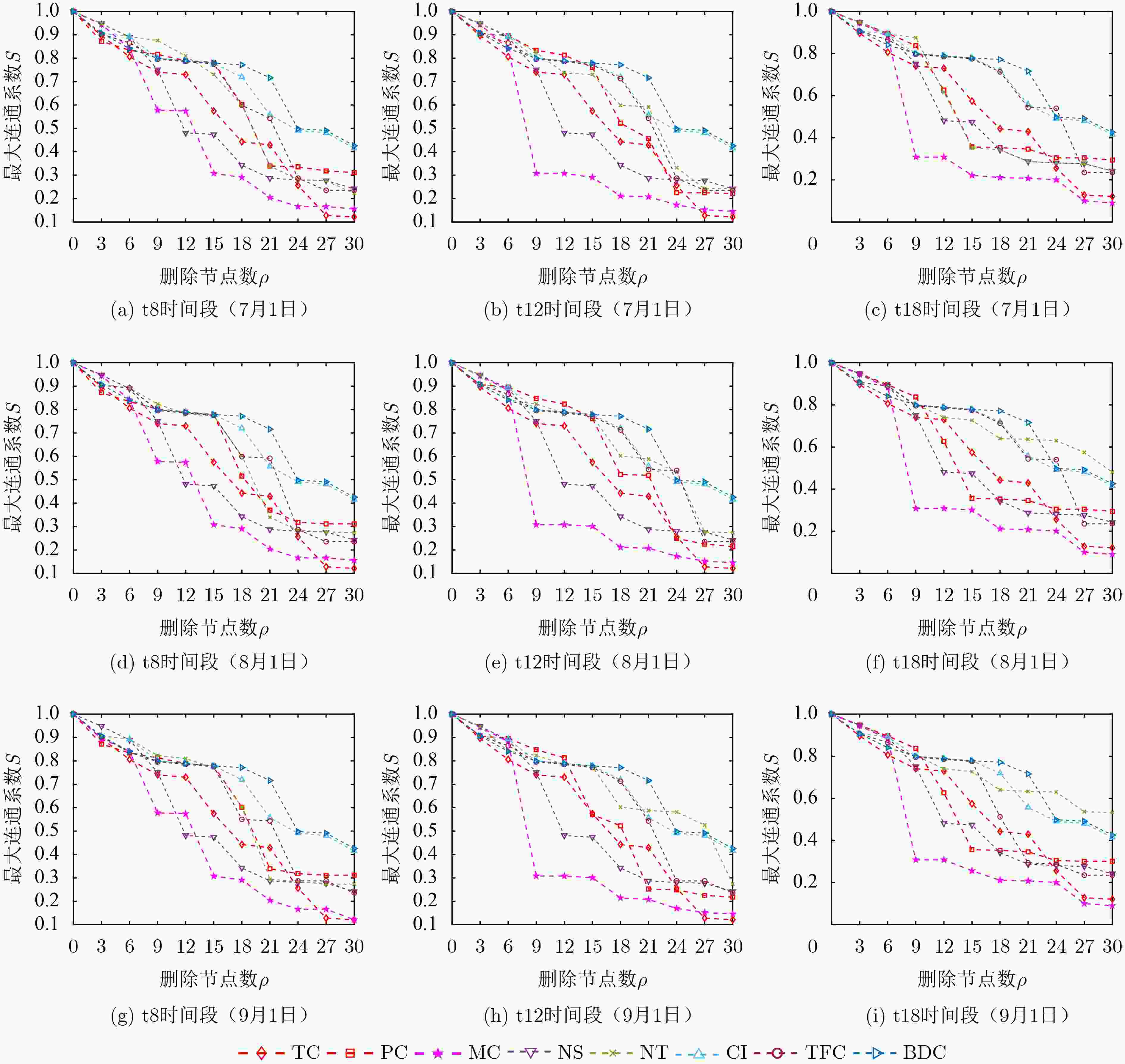
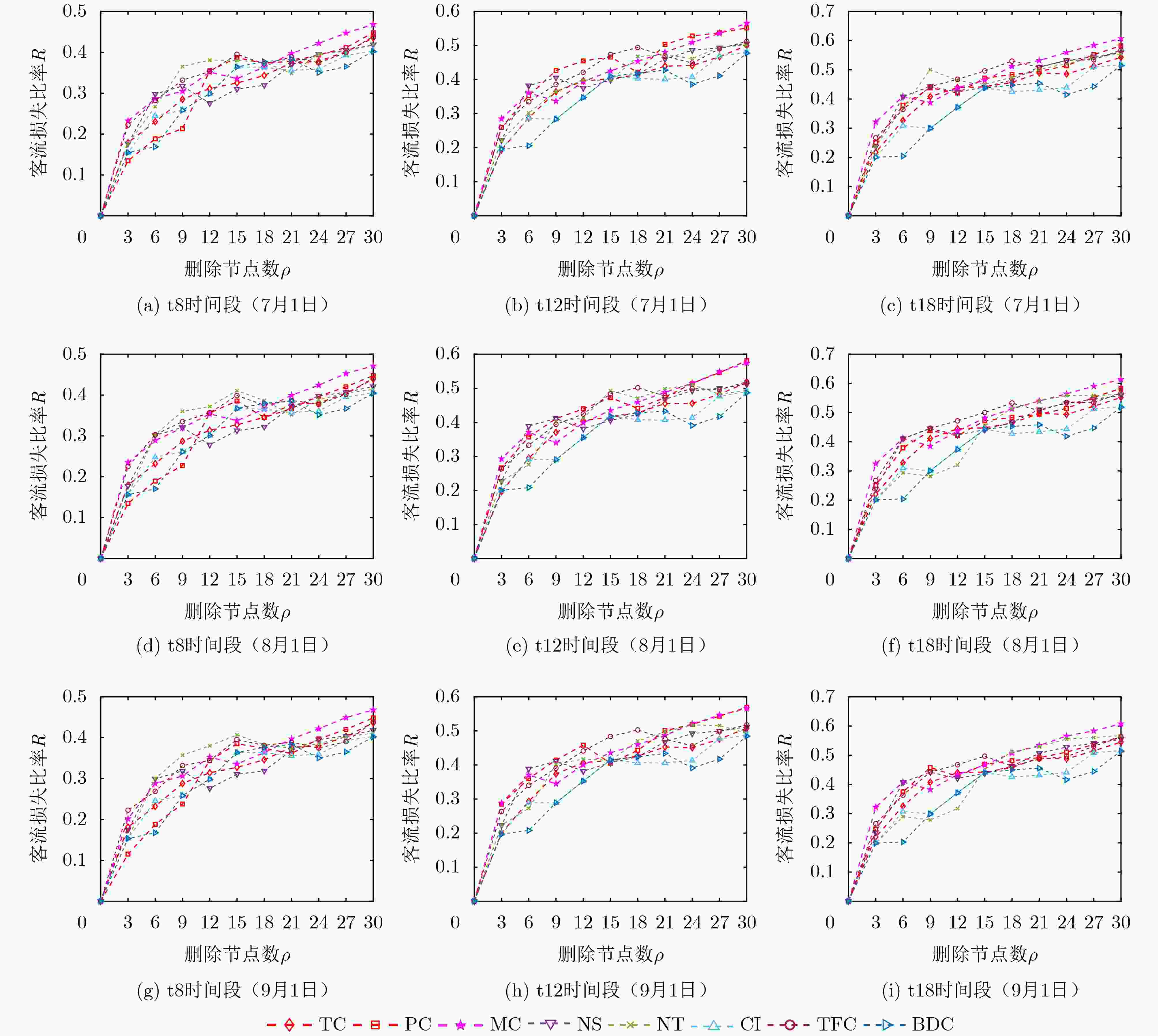
Objective Research on node centrality in rail transit networks is essential for ensuring operational safety. Identifying critical stations enables the development of preventive strategies and mitigates the effects of station failures. Existing studies highlight two key determinants of station importance: static topology and dynamic passenger flow. However, most current approaches treat these factors separately, leading to biased estimations of node importance. To address this limitation, this study proposes a novel node centrality measure that integrates static topology and dynamic passenger flow. The method combines topology-based centrality—derived from PageRank and a modified K-shell algorithm—with passenger centrality, which is based on station inflow and outflow volumes. A reinforcement mechanism ensures that passenger centrality consistently amplifies topology-based centrality, balancing the influence of both components. Using cascade failure simulations and real-world data from the Shanghai Metro, the proposed method reliably identifies key stations. These findings offer practical guidance for the design and maintenance of robust metro systems, enhancing their resilience to cascading failures and improving overall safety and stability. Methods The proposed method integrates static topology and dynamic passenger flow to evaluate the centrality of urban rail transit stations, addressing the limitations of existing approaches in identifying key stations. It consists of three components: static topology centrality, dynamic passenger flow centrality, and an integration strategy. (1) Static topology centrality is computed using a combination of PageRank and an improved K-core method. This hybrid approach captures both connectivity and node importance based on iterative removal order, mitigating the loss of resolution caused by the long-tail degree distribution typical in transit networks. (2) Dynamic passenger flow centrality assigns separate weights to inbound and outbound flows to account for congestion effects and directional asymmetry—factors often overlooked in previous models. The weights are derived from average boarding and alighting times and adjusted for flow variations across morning peak, evening peak, and off-peak periods. (3) Integration strategy: An exponential function combines the two centrality measures, ensuring that passenger flow consistently amplifies topology-derived importance. This design improves sensitivity to dynamic changes while preserving structural significance. The integrated centrality metric enhances network resilience by supporting targeted protection of critical stations, based on both static and dynamic characteristics. Results and Discussions This study investigates the vulnerability of Shanghai’s urban rail transit network by simulating cascading failures and identifying key stations. Using dynamic passenger flow data from three representative weekdays across 14 subway lines—comprising 289 stations and 335 edges—a load-capacity model is applied to assess node importance based on each station’s effect on network stability during cascading failure events. The results ( Fig. 1 ,Fig. 2 ,Fig. 3 ) demonstrate that the proposed method consistently and effectively identifies key stations, outperforming five benchmark approaches. When assessing passenger flow loss, passenger flow centrality alone proves more informative than static topology centrality alone (Fig. 3 ). Moreover, the influence of passenger flow centrality is more pronounced during morning and evening peak periods, highlighting the role of temporal dynamics in station vulnerability. These findings highlight the importance of incorporating dynamic passenger flow data into vulnerability assessments to better capture real-world operational risks. The ablation study (Table 1 ) confirms that the integrated centrality—combining static topology and dynamic flow—offers superior performance over single-factor methods. Prioritizing the protection of stations identified by this approach can substantially improve the network’s resilience to cascading failures and enhance overall system safety.Conclusions This study investigates station centrality in urban rail transit networks and analyzes the cascading failure effects triggered by key node disruptions using a load-capacity model. The proposed method enhances the ranking of station importance by jointly capturing network structure and usage patterns, offering practical value for the design and maintenance of safe and resilient metro systems. Experiments on the Shanghai Metro network show that the method effectively identifies critical stations, with improvements observed in network average efficiency, connectivity, and reduced passenger flow loss. The results indicate the following: (1) Accurate identification of key stations requires the integration of both static topology and dynamic passenger flow; relying on either alone limits precision. (2) Failures at key stations can induce substantial cascading failures, highlighting the need to prioritize their protection to improve system resilience. (3) Future research should focus on developing more effective strategies for integrating static and dynamic centrality measures to extend applicability across different urban transit networks. -
Key words:
- Rail transit network /
- Topology centrality /
- Dynamic passenger flow /
- Cascade failure
-
表 1 融合方式对比实验结果
评价指标 日期 TC PC 指数融合 线性融合 1+PC 2+PC(MC) 3+PC TC+PC 网络平均效率E 7月1日 0.037 35 0.046 09 0.034 60 0.033 85 0.034 09 0.037 21 8月1日 0.037 35 0.046 09 0.035 08 0.034 04 0.034 05 0.038 07 9月1日 0.037 35 0.046 68 0.034 84 0.033 79 0.033 97 0.038 08 最大连通系数S 7月1日 0.544 06 0.555 82 0.404 96 0.383 39 0.404 27 0.461 82 8月1日 0.544 06 0.555 82 0.412 57 0.387 77 0.405 54 0.471 28 9月1日 0.544 06 0.563 44 0.406 23 0.384 43 0.403 69 0.471 63 客流损失比率R 7月1日 0.420 18 0.446 26 0.472 81 0.467 65 0.465 21 0.486 92 8月1日 0.425 87 0.446 26 0.474 32 0.471 09 0.470 17 0.487 02 9月1日 0.421 46 0.442 64 0.470 50 0.467 10 0.465 75 0.483 46 平均差距 / 21.488% 29.973% 3.805% 1.179% 3.096% 11.014% -
[1] 鞠艳妮, 李宗平, 陈宇帆, 等. 区域轨道交通系统节点重要度及故障恢复研究[J]. 中国安全科学学报, 2021, 31(2): 112–119. doi: 10.16265/j.cnki.issn1003-3033.2021.02.016.JU Yanni, LI Zongping, CHEN Yufan, et al. Study on node importance and failure recovery of regional rail transit system[J]. China Safety Science Journal, 2021, 31(2): 112–119. doi: 10.16265/j.cnki.issn1003-3033.2021.02.016. [2] 谌微微, 张富贵, 赵晓波. 轨道交通线网拓扑结构模型及节点重要度分析[J]. 重庆交通大学学报: 自然科学版, 2019, 38(7): 107–113. doi: 10.3969/j.issn.1674-0696.2019.07.18.CHEN Weiwei, ZHANG Fugui, and ZHAO Xiaobo. Topological structure model and node importance analysis of rail transit network[J]. Journal of Chongqing Jiaotong University: Natural Science, 2019, 38(7): 107–113. doi: 10.3969/j.issn.1674-0696.2019.07.18. [3] SHEN Yi, YANG Huang, REN Gang, et al. Model cascading overload failure and dynamic vulnerability analysis of facility network of metro station[J]. Reliability Engineering & System Safety, 2024, 242: 109711. doi: 10.1016/j.ress.2023.109711. [4] LIU Guangyi, AMINI A, PANDEY V, et al. Data-driven distributionally robust mitigation of risk of cascading failures[C]. 2024 American Control Conference (ACC), Toronto, Canada, 2024: 3264–3269. doi: 10.23919/ACC60939.2024.10644661. [5] GENG Jiawei, ZHANG Chuntian, YANG Lixing, et al. Integrated scheduling of metro trains and shuttle buses with passenger flow control strategy on an oversaturated metro line[J]. Computers & Industrial Engineering, 2024, 189: 109980. doi: 10.1016/j.cie.2024.109980. [6] 张震, 刘迪洋, 张进, 等. 基于节点冗余容量动态控制的复杂网络鲁棒性研究[J]. 电子与信息学报, 2021, 43(5): 1349–1356. doi: 10.11999/JEIT200185.ZHANG Zhen, LIU Diyang, ZHANG Jin, et al. Research on the robustness of complex networks based on dynamic control of node redundancy capacity[J]. Journal of Electronics & Information Technology, 2021, 43(5): 1349–1356. doi: 10.11999/JEIT200185. [7] 刘凤增, 肖兵, 陈施思, 等. 负载作用下相依网络择优恢复方法研究[J]. 电子与信息学报, 2020, 42(7): 1694–1701. doi: 10.11999/JEIT190486.LIU Fengzeng, XIAO Bing, CHEN Shisi, et al. A preferential recovery method of interdependent networks under load[J]. Journal of Electronics & Information Technology, 2020, 42(7): 1694–1701. doi: 10.11999/JEIT190486. [8] 冯佳, 许奇, 李夏苗, 等. 城市轨道交通系统网络复杂性研究[J]. 交通运输系统工程与信息, 2017, 17(6): 242–247. doi: 10.16097/j.cnki.1009-6744.2017.06.035.FENG Jia, XU Qi, LI Xiamiao, et al. Complex network study on urban rail transit systems[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(6): 242–247. doi: 10.16097/j.cnki.1009-6744.2017.06.035. [9] 梁青槐, 柴树山, 钟思敏, 等. 城市轨道交通站点网络结构综合重要度识别[J]. 铁道工程学报, 2019, 36(9): 66–71. doi: 10.3969/j.issn.1006-2106.2019.09.012.LIANG Qinghuai, CHAI Shushan, ZHONG Simin, et al. Identification of comprehensive importance of urban rail transit stations in network structure[J]. Journal of Railway Engineering Society, 2019, 36(9): 66–71. doi: 10.3969/j.issn.1006-2106.2019.09.012. [10] 李晓璐, 于昕明, 雷方舒, 等. 城市轨道交通系统灾害链网络模型构建与评价[J]. 中国安全科学学报, 2018, 28(6): 179–184. doi: 10.16265/j.cnki.issn1003-3033.2018.06.030.LI Xiaolu, YU Xinming, LEI Fangshu, et al. Construction of disaster chain network model and evaluation of network index for urban rail transit system[J]. China Safety Science Journal, 2018, 28(6): 179–184. doi: 10.16265/j.cnki.issn1003-3033.2018.06.030. [11] 左忠义, 刘泽宇, 杨广川. 基于引力影响模型的轨道交通网络关键节点识别研究[J]. 交通运输系统工程与信息, 2025, 25(1): 102–112. doi: 10.16097/j.cnki.1009-6744.2025.01.011.ZUO Zhongyi, LIU Zeyu, and YANG Guangchuan. Key node identification of rail transit network based on gravity influence model[J]. Journal of Transportation Systems Engineering and Information Technology, 2025, 25(1): 102–112. doi: 10.16097/j.cnki.1009-6744.2025.01.011. [12] LI Jing, LU Qingchang, XU Pengcheng, et al. Cascading failures on multimodal public transportation networks: The role of station coupling strength[J]. IEEE Transactions on Intelligent Transportation Systems, 2024, 25(11): 17187–17199. doi: 10.1109/TITS.2024.3450019. [13] 朱广宇, 孙歆霓, 杨荣正, 等. 变时间尺度城轨客流的本征模量分解及组合深度学习预测[J]. 电子与信息学报, 2023, 45(12): 4421–4430. doi: 10.11999/JEIT221300.ZHU Guangyu, SUN Xinni, YANG Rongzheng, et al. Intrinsic mode decomposition and combined deep learning prediction of urban rail transit passenger flow at variable time scales[J]. Journal of Electronics & Information Technology, 2023, 45(12): 4421–4430. doi: 10.11999/JEIT221300. [14] 胡映月, 陈峰, 陈培文, 等. 基于网络客流传播的轨道交通关键站点识别[J]. 西南交通大学学报, 2017, 52(6): 1193–1200, 1215. doi: 10.3969/j.issn.0258-2724.2017.06.021.HU Yingyue, CHEN Feng, CHEN Peiwen, et al. Critical station identification based on passenger propagation in urban mass transit network[J]. Journal of Southwest Jiaotong University, 2017, 52(6): 1193–1200, 1215. doi: 10.3969/j.issn.0258-2724.2017.06.021. [15] LI Jing, LU Qingchang, XU Pengcheng, et al. Critical station identification for cascading failure mitigation considering the Lyapunov-stability of metro stations[J]. Reliability Engineering & System Safety, 2025, 256: 110772. doi: 10.1016/j.ress.2024.110772. [16] 刘诗序, 关宏志, 严海. 网络交通流动态演化的混沌现象及其控制[J]. 物理学报, 2012, 61(9): 090506. doi: 10.7498/aps.61.090506.LIU Shixu, GUAN Hongzhi, and YAN Hai. Chaotic behavior in the dynamical evolution of network traffic flow and its control[J]. Acta Physica Sinica, 2012, 61(9): 090506. doi: 10.7498/aps.61.090506. [17] 李宗平, 陈宇帆, 鞠艳妮, 等. 多制式区域轨道交通网络关键节点识别[J]. 安全与环境学报, 2022, 22(6): 3217–3226. doi: 10.13637/j.issn.1009-6094.2021.1013.LI Zongping, CHEN Yufan, JU Yanni, et al. Identification of key nodes in multi-mode regional rail transit networks[J]. Journal of Safety and Environment, 2022, 22(6): 3217–3226. doi: 10.13637/j.issn.1009-6094.2021.1013. [18] 高超, 蒋世洪, 王震, 等. 基于动态客流的城市轨道交通关键站点识别[J]. 中国科学: 信息科学, 2021, 51(9): 1490–1506. doi: 10.1360/SSI-2020-0303.GAO Chao, JIANG Shihong, WANG Zhen, et al. A novel method to identify influential stations based on dynamic passenger flows[J]. Scientia Sinica Informationis, 2021, 51(9): 1490–1506. doi: 10.1360/SSI-2020-0303. [19] 刘星雨, 刘杰, 王喆, 等. 基于K-shell的城际轨道网络关键节点识别研究[J]. 北京交通大学学报, 2024, 48(4): 181–190. doi: 10.11860/j.issn.1673-0291.20230077.LIU Xingyu, LIU Jie, WANG Zhe, et al. Research on identification of key nodes in intercity rail networks based on K-shell[J]. Journal of Beijing Jiaotong University, 2024, 48(4): 181–190. doi: 10.11860/j.issn.1673-0291.20230077. [20] 翟志鹏, 曹阳, 沈琴琴, 等. 基于多时空图融合与动态注意力的交通流预测[J/OL]. 计算机工程, 1–9. https://doi.org/10.19678/j.issn.1000-3428.0069439.ZHAI Zhipeng, CAO Yang, SHEN Qinqin, et al. Traffic flow prediction model based on multiple spatio-temporal graph fusion and dynamic attention[J/OL]. Computer Engineering, 1–9. https://doi.org/10.19678/j.issn.1000-3428.0069439. [21] WANG Zhixiao, DU Changjiang, FAN Jianping, et al. Ranking influential nodes in social networks based on node position and neighborhood[J]. Neurocomputing, 2017, 260: 466–477. doi: 10.1016/j.neucom.2017.04.064. [22] SUN Li, ZHAO Juanjuan, ZHANG Fan, et al. FMSYS: Fine-grained passenger flow monitoring in a large-scale metro system based on AFC smart card data[C]. 28th Pacific-Asia Conference on Knowledge Discovery and Data Mining, Taipei, China, 2024: 336–349. doi: 10.1007/978-981-97-2262-4_27. [23] 杨安安, 陈艳艳, 黄建玲, 等. 基于短时客流预测的地铁动态限流预警模型研究[J]. 城市轨道交通研究, 2018, 21(10): 29–33. doi: 10.16037/j.1007-869x.2018.10.007.YANG Anan, CHEN Yanyan, HUANG Jianling, et al. Early warning model of metro dynamic flow limitation based on short-term passenger flow forecasting[J]. Urban Mass Transit, 2018, 21(10): 29–33. doi: 10.16037/j.1007-869x.2018.10.007. [24] 杨景峰, 朱大鹏, 赵瑞琳. 城市轨道交通网络特性与级联失效鲁棒性分析[J]. 计算机工程与应用, 2022, 58(7): 250–258. doi: 10.3778/j.issn.1002-8331.2105-0157.YANG Jingfeng, ZHU Dapeng, and ZHAO Ruilin. Analysis on characteristics of urban rail transit network and robustness of cascading failure[J]. Computer Engineering and Applications, 2022, 58(7): 250–258. doi: 10.3778/j.issn.1002-8331.2105-0157. [25] LATORA V and MARCHIORI M. Efficient behavior of small-world networks[J]. Physical Review Letters, 2001, 87(19): 198701. doi: 10.1103/PhysRevLett.87.198701. [26] YANG Xiaofan, MEGSON G M, TANG Yuanyan, et al. Largest connected component of a star graph with faulty vertices[J]. International Journal of Computer Mathematics, 2008, 85(12): 1771–1778. doi: 10.1080/00207160701619200. [27] 陈培文, 陈峰, 胡映月, 等. 基于复杂网络的城市轨道交通网络中心性研究[J]. 复杂系统与复杂性科学, 2017, 14(2): 97–102,109. doi: 10.13306/j.1672-3813.2017.02.014.CHEN Peiwen, CHEN Feng, HU Yingyue, et al. On urban rail transit network centrality using complex network theory[J]. Complex Systems and Complexity Science, 2017, 14(2): 97–102,109. doi: 10.13306/j.1672-3813.2017.02.014. -





 下载:
下载:


 下载:
下载:
