Application of WAM Data Set and Classification Method of Electromagnetic Wave Absorbing Materials
-
摘要: 电磁辐射防护吸波材料的性能主要由厚度、最大反射损耗和有效吸收带宽决定。研究集中在金属有机框架、碳基和陶瓷吸波材料上,利用弱人工智能分析(Wave Absorption Materials, WAM)数据集。划分训练集和测试集后进行数据增强以及相关性和主成分分析。采用决策树算法制定分类指标,发现MOFs(Metal Organic Frameworks)类材料的反射损耗优于碳基材料类,MOFs类材料容易满足最大反射损耗值小于–45 dB。多次训练后,随机森林算法泛化性能比决策树算法好,ROC-AUC值更高。运用神经网络进行分类研究,结果表明自组织映射神经网络在分类上表现更佳,而概率神经网络效果较差。将二分类问题扩展到三分类问题后,使用非线性分类、聚类算法和Boosting类算法,发现最大反射损耗是关键指标。进一步分析表明,WAM数据集非线性可分,模糊聚类效果较好。人工智能有助于揭示材料特性与吸波性能的关系,加速新材料研发,支持吸波材料知识图谱和知识库的建设。Abstract:
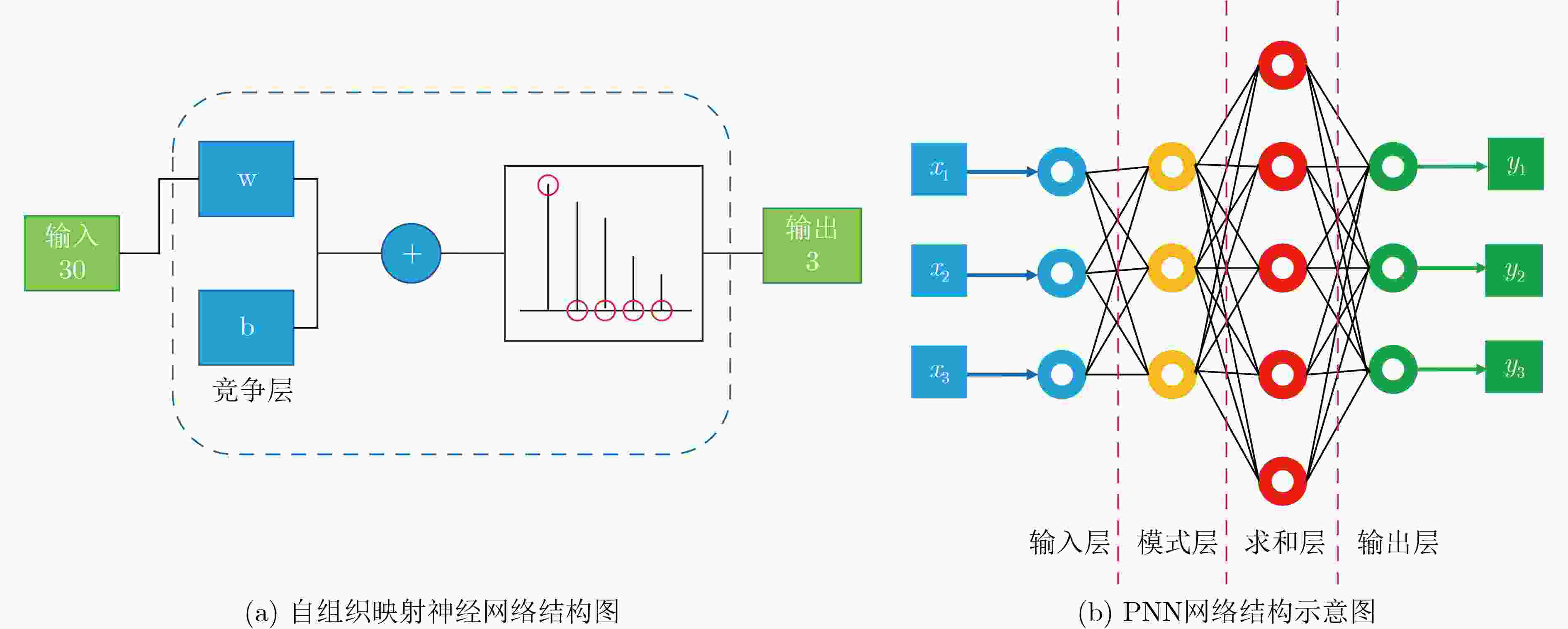
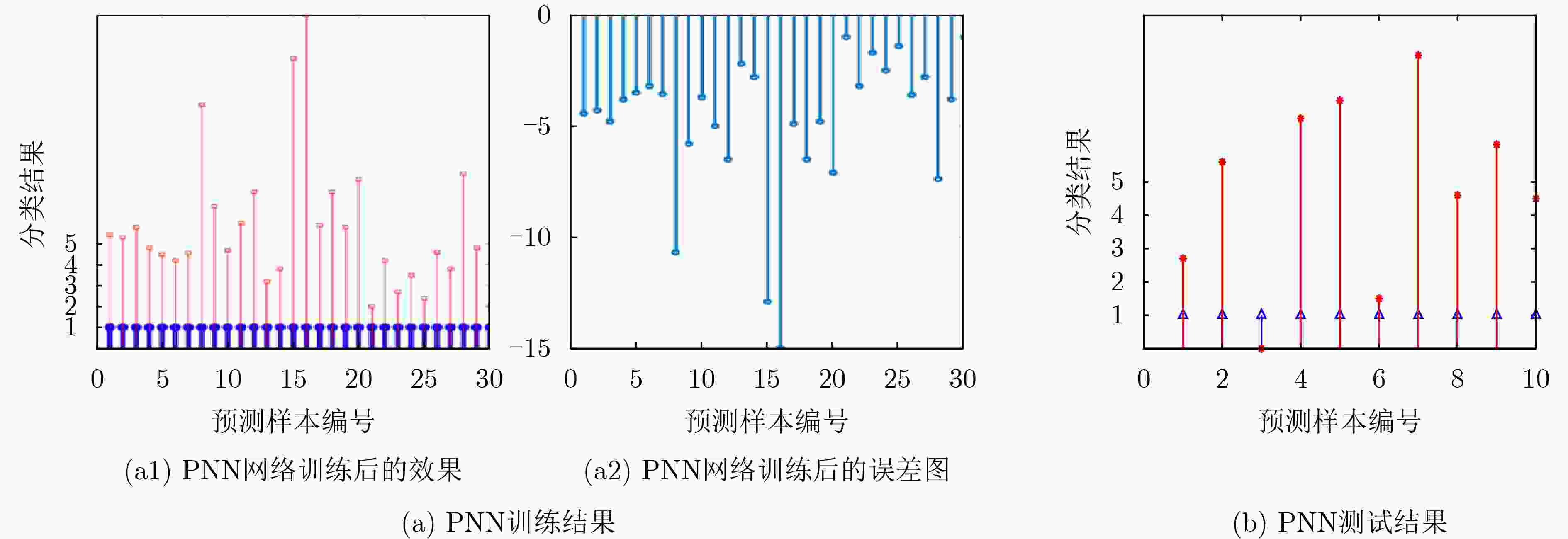
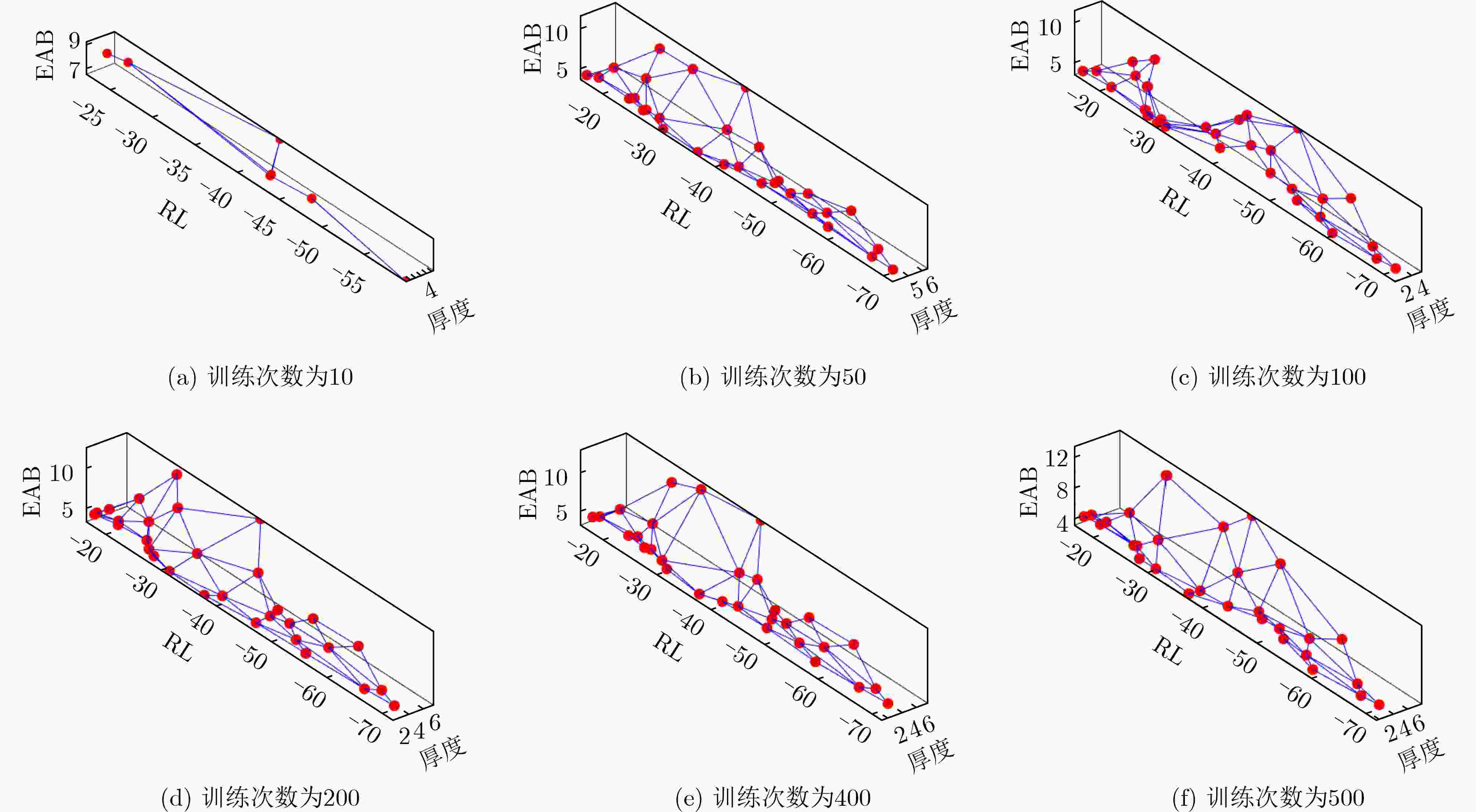
The performance of electromagnetic radiation shielding and absorbing materials depends primarily on thickness, maximum reflection loss, and effective absorption bandwidth. Current research focuses on Metal Organic Frameworks (MOFs), carbon-based, and ceramic absorbing materials, analyzed using weak artificial intelligence techniques applied to the Wave-Absorbing Materials (WAM) dataset. After dividing the dataset into training and testing subsets, data augmentation, correlation analysis, and principal component analysis are performed. A decision tree algorithm is then applied to establish classification indicators, revealing that the reflection loss of MOF materials exceeds that of carbon-based materials. MOFs are more likely to achieve a maximum reflection loss below –45 dB. The random forest algorithm demonstrates stronger generalization ability than the decision tree algorithm, with a higher ROC–AUC value. Neural network classification shows that the self-organizing map neural network yields superior classification performance, whereas the probabilistic neural network performs poorly. When the binary classification problem is extended to a three-class problem, nonlinear classification, clustering, and Boosting algorithms indicate that maximum reflection loss serves as a key discriminative feature. Further analysis confirms that the WAM dataset is nonlinearly separable and that fuzzy clustering achieves better results. Artificial intelligence facilitates the identification of relationships between material properties and absorption performance, accelerates the development of new Wave-Absorbing Materials (WAM), and supports the construction of a knowledge graph and database for absorbing materials. Objective Computational materials science, high-throughput experimentation, and the Materials Genome Initiative (MGI) have emerged as key frontiers in modern materials research. The MGI provides a strategic framework and developmental roadmap for advancing materials discovery through artificial intelligence. Analogous to gene sequencing in bioinformatics, its central objective is to accelerate the identification of novel material compositions and structures. Extracting valuable information from large-scale datasets substantially reduces costs, enhances efficiency, fosters interdisciplinary integration, and promotes transformative progress in materials development. Big data analytics, high-performance computing, and advanced algorithms form the core pillars of this initiative, supplying essential support for new materials research and development. Nevertheless, the discovery of new compositions and structures depends on the effective screening of candidate materials to identify those exhibiting superior properties suitable for engineering applications. Achieving this goal requires the establishment of comprehensive datasets, the development of reliable classification algorithms, the improvement of model generalization performance, and the advancement of application-oriented software tools. Methods Pattern recognition techniques are employed in this study. A self-developed WAM dataset is first constructed, comprising a test set and a validation set. Data preprocessing is performed initially, including data augmentation, data integration, and principal component analysis. Decision tree and random forest algorithms are applied to establish classification indicators and define classification criteria. Self-Organizing Map (SOM) and Probabilistic Neural Network (PNN) models are subsequently utilized for material classification. Finally, the accuracy of various clustering algorithms is evaluated, and the fuzzy clustering algorithm is found to achieve relatively superior performance and satisfactory classification results. Results and Discussions It is found that the reflection loss of MOF materials is superior to that of carbon-based materials. Semantic segmentation algorithms are identified as unsuitable for classifying the WAM dataset. Among the neural network approaches, the SOM achieves higher classification accuracy than the PNN. The WAM dataset is determined to be nonlinearly separable, indicating that classification performance depends strongly on the intrinsic data distribution characteristics. The maximum reflection loss is identified as the key indicator for effective classification. Conclusions A self-developed WAM dataset is constructed to address the lack of publicly available datasets for applying pattern recognition methods to electromagnetic WAM. The performance of multiple algorithms is evaluated, and the optimal algorithm is identified according to the dataset characteristics. The conventional binary classification problem is extended to a three-class framework, providing the foundation for further research on multi-class classification. The application of artificial intelligence algorithms is found to enhance the credibility and reliability of the research, reduce time and labor costs, and facilitate the exploration of relationships between material properties and absorption performance. This approach shortens the research and development cycle, supports the screening of new materials, and contributes to the establishment of a knowledge base for absorbing materials. However, the knowledge extracted from the WAM dataset remains limited by data sparsity, which constrains the effectiveness of artificial intelligence methods. -
名称 厚度(mm) 损耗(dB) 带宽(GHz) Co@C 2 –49.76 5.44 Co@C@NRGO 2 –73.4 5.3 MPC@Ni/C 2.2 –73.8 5.8 Ni@C-700 1.8 –73.2 4.8 Fe3O4@NPC 3 –65.5 4.5 C-MIL-88/GNP 0.12 –28.0 4.2 Fe7S8/C 1.45 –68.8 4.56 MCC/rGO 3.6 –62.5 11.68 Cu/C 2.3 –52.0 6.8 CuO/C 1.55 –57.5 4.7 表 2 Carbon类材料吸波性能数据集[22]
名称 厚度(mm) 损耗(dB) 带宽(GHz) Ni/纳米石墨 1.5 –17.5 6 NiFeCo/纳米石墨 0.3 –28 7.5 洋葱碳/水性丙烯酸 5 –17.2 3.2 洋葱碳/水性丙烯酸 3 –14.3 3.8 石墨烯 10 –26 13.9 石墨烯/碳管 10 –39.5 16 石墨烯/PPy 3 –27 5.9 石墨烯/PVA 3.5 –44.5 7.5 石墨烯/Fe3O4 3 –23 5.8 氮掺杂石墨烯 3.3 –53.2 8.1 表 3 Ceramics类材料吸波性能数据集[23]
名称 厚度(mm) 损耗(dB) 带宽(GHz) Graphene nanosheets/MgO 1.5 –36.5 2 Edge-Rich Graphene/Si3N4 3.75 –26.7 4.2 SiC-Si3N4 2.5 –27.1 2.7 SiC/SiO2-Si3N4 3.8 –30 3.5 Ti3SiC2/cordierte 1.5 –14.1 2.4 Ni/ZnO 2 –45.4 4.6 FeCo/ZnO 1.9 –53.81 3.8 CuFe2O4/MgO 2 –25.35 8.38 Fe3Si/CNTs/SiC 3 –40 4.8 C/AlN 2 –30 2 表 4 WAM数据集的验证集[24]
名称 厚度(mm) 损耗(dB) 带宽(GHz) CNT/CFs 2.5 –42 2.7 CNT/PANI/CFs 2 –45.7 5.6 CNTs/Fe3O4/CFs 1.5 –59.9 0 CNTs/Fe3O4/PANI/CFs 2 –22.4 6.9 CNT/CFs 3 –44.6 7.44 CNTs/SiCf 3.35 –37.6 1.5 CNT/SiCf 4 –62.5 8.8 SiOC/CFs 2.3 –47.9 4.6 WMCNT/PPy/CFs 3.5 –17 6.12 MWCNTs/PDEOT/CFs 2 –39 4.5 表 5 特征变量的随机森林算法与决策树算法重要性评分对比
特征变量 决策树算法
重要性得分随机森林算法
重要性得分厚度(mm) 0.298 0.475 有效吸收带宽(GHz) 0.702 0.524 表 6 不同分类算法归纳总结
分类算法 分类结果及分类误差 近邻法 近邻法不论按照“厚度/损耗”、“厚度/带宽”还是“带宽/损耗”进行组合,均能将数据准确地分为3类 二次判别法 分界线是曲线,二次判别法不论按照“碳基/陶瓷”“有机/碳基”“有机/陶瓷”进行组合,发生误报、
漏报的概率很小,均有1~2个样品被误分类,会有样品出现在分界线上Boosting类算法 产生两个弱分类错误样本或者产生两个组合分类错误样本 聚类算法 不论二维还是三维空间,均将数据准确地分为3类 GMM模型 高斯成分个数k=3时最能刻画数据分布;根据标签确定初始值的方法最能刻画数据分布 最优聚类数 最优聚类数的数量为3或者6 排序算法 反射损耗是3个数据标签里最重要的标签。 备注:以上内容的代码引用自文献[26,27]。 -
[1] 汪洪, 向勇, 项晓东, 等. 材料基因组——材料研发新模式[J]. 科技导报, 2015, 33(10): 13–19. doi: 10.3981/j.issn.1000-7857.2015.10.001.WANG Hong, XIANG Yong, XIANG Xiaodong, et al. Materials genome enables research and development revolution[J]. Science & Technology Review, 2015, 33(10): 13–19. doi: 10.3981/j.issn.1000-7857.2015.10.001. [2] 施思齐, 徐积维, 崔艳华, 等. 多尺度材料计算方法[J]. 科技导报, 2015, 33(10): 20–30. doi: 10.3981/j.issn.1000-7857.2015.10.002.SHI Siqi, XU Jiwei, CUI Yanhua, et al. Multiscale materials computational methods[J]. Science & Technology Review, 2015, 33(10): 20–30. doi: 10.3981/j.issn.1000-7857.2015.10.002. [3] 王海舟, 汪洪, 丁洪, 等. 材料的高通量制备与表征技术[J]. 科技导报, 2015, 33(10): 31–49. doi: 10.3981/j.issn.1000-7857.2015.10.003.WANG Haizhou, WANG Hong, DING Hong, et al. Progress in high-throughput materials synthesis and characterization[J]. Science & Technology Review, 2015, 33(10): 31–49. doi: 10.3981/j.issn.1000-7857.2015.10.003. [4] 都仕, 张宋奇, 王立权, 等. 高分子材料基因组——高分子研发的新方法[J]. 高分子学报, 2022, 53(6): 592–607. doi: 10.11777/j.issn1000-3304.2021.21404.DU Shi, ZHANG Songqi, WANG Liquan, et al. Polymer genome approach: A new method for research and development of polymers[J]. Acta Polymerica Sinica, 2022, 53(6): 592–607. doi: 10.11777/j.issn1000-3304.2021.21404. [5] 宫祥瑞, 蒋滢. 机器学习在高分子材料基因组研究中的进展与挑战[J]. 高分子学报, 2022, 53(11): 1287–1300. doi: 10.11777/j.issn1000-3304.2022.22094.GONG Xiangrui and JIANG Ying. Advances and challenges of machine learning in polymer material genomes[J]. Acta Polymerica Sinica, 2022, 53(11): 1287–1300. doi: 10.11777/j.issn1000-3304.2022.22094. [6] 刘伦洋, 丁芳, 李云琦. 高分子材料大数据研究: 共性基础、进展及挑战[J]. 高分子学报, 2022, 53(6): 564–580. doi: 10.11777/j.issn1000-3304.2021.21360.LIU Lunyang, DING Fang, and LI Yunqi. Big data approach on polymer materials: Fundamental, progress and challenge[J]. Acta Polymerica Sinica, 2022, 53(6): 564–580. doi: 10.11777/j.issn1000-3304.2021.21360. [7] 李云琦, 刘伦洋, 陈文多, 等. 材料基因组学的发展现状、研究思路与建议[J]. 中国科学: 化学, 2018, 48(3): 243–255. doi: 10.1360/N032017-00182.LI Yunqi, LIU Lunyang, CHEN Wenduo, et al. Materials genome: Research progress, challenges and outlook[J]. Scientia Sinica (Chimica), 2018, 48(3): 243–255. doi: 10.1360/N032017-00182. [8] 宿彦京, 付华栋, 白洋, 等. 中国材料基因工程研究进展[J]. 金属学报, 2020, 56(10): 1313–1323. doi: 10.11900/0412.1961.2020.00199.SU Yanjing, FU Huadong, BAI Yang, et al. Progress in materials genome engineering in China[J]. Acta Metallurgica Sinica, 2020, 56(10): 1313–1323. doi: 10.11900/0412.1961.2020.00199. [9] 戚兴怡, 胡耀峰, 王若愚, 等. 机器学习在新材料筛选方面的应用进展[J]. 化学学报, 2023, 81(2): 158–174. doi: 10.6023/A22110446.QI Xingyi, HU Yaofeng, WANG Ruoyu, et al. Recent advance of machine learning in selecting new materials[J]. Acta Chimica Sinica, 2023, 81(2): 158–174. doi: 10.6023/A22110446. [10] 谢建新, 宿彦京, 薛德祯, 等. 机器学习在材料研发中的应用[J]. 金属学报, 2021, 57(11): 1343–1361. doi: 10.11900/0412.1961.2021.00357.XIE Jianxin, SU Yanjing, XUE Dezhen, et al. Machine learning for materials research and development[J]. Acta Metallurgica Sinica, 2021, 57(11): 1343–1361. doi: 10.11900/0412.1961.2021.00357. [11] 仲陆祎, 权斌, 车仁超, 等. 基于机器学习的羰基铁/四氧化三铁复合吸波材料的优化设计[J]. 中国材料进展, 2024, 43(7): 652–657. doi: 10.7502/j.issn.1674-3962.202209040.ZHONG Luyi, QUAN Bin, CHE Renchao, et al. Optimal design of microwave absorbing material of carbonyl iron/ferroferric oxide composite via machine learning[J]. Materials China, 2024, 43(7): 652–657. doi: 10.7502/j.issn.1674-3962.202209040. [12] 蔡长旭. 基于机器学习的吸波材料优化研究[D]. [硕士论文], 电子科技大学, 2023. doi: 10.27005/d.cnki.gdzku.2023.001834.CAI Changxu. Research on optimization of absorbing materials basedon machine learning[D]. [Master dissertation], University of Electronic Science and Technology of China, 2023. doi: 10.27005/d.cnki.gdzku.2023.001834. [13] 韩玲艳. 基于机器学习的吸波材料优化设计方法[D]. [硕士论文], 华东师范大学, 2020. doi: 10.27149/d.cnki.ghdsu.2020.000740.HAN Lingyan. Machine learning – based optimal design methods of absorbing materials[D]. [Master dissertation], East China Normal University, 2020. doi: 10.27149/d.cnki.ghdsu.2020.000740. [14] 张引, 陈敏, 廖小飞. 大数据应用的现状与展望[J]. 计算机研究与发展, 2013, 50(S2): 216–233.ZHANG Yin, CHEN Min, and LIAO Xiaofei. Big data applications: A survey[J]. Journal of Computer Research and Development, 2013, 50(S2): 216–233. [15] 丁兆云, 贾焰, 周斌. 微博数据挖掘研究综述[J]. 计算机研究与发展, 2014, 51(4): 691–706. doi: 10.7544/issn1000-1239.2014.20130079.DING Zhaoyun, JIA Yan, and ZHOU Bin. Survey of data mining for microblogs[J]. Journal of Computer Research and Development, 2014, 51(4): 691–706. doi: 10.7544/issn1000-1239.2014.20130079. [16] 贺玲, 吴玲达, 蔡益朝. 数据挖掘中的聚类算法综述[J]. 计算机应用研究, 2007, 24(1): 10–13. doi: 10.3969/j.issn.1001-3695.2007.01.003.HE Ling, WU Lingda, and CAI Yichao. Survey of clustering algorithms in data mining[J]. Application Research of Computers, 2007, 24(1): 10–13. doi: 10.3969/j.issn.1001-3695.2007.01.003. [17] QU Ning, SUN Hanxu, SUN Yuyao, et al. 2D/2D coupled MOF/Fe composite metamaterials enable robust ultra–broadband microwave absorption[J]. Nature Communications, 2024, 15(1): 5642. doi: 10.1038/s41467-024-49762-4. [18] WANG Yanli, YANG Shuhao, WANG Huiya, et al. Hollow porous CoNi/C composite nanomaterials derived from MOFs for efficient and lightweight electromagnetic wave absorber[J]. Carbon, 2020, 167: 485–494. doi: 10.1016/j.carbon.2020.06.014. [19] CHEN Congjie, SHAN Zhen, TAO Shifei, et al. Atomic tuning in electrically conducting bimetallic organic frameworks for controllable electromagnetic wave absorption[J]. Advanced Functional Materials, 2023, 33(45): 2305082. doi: 10.1002/adfm.202305082. [20] 韩国栋, 孙勇, 周俊祥, 等. 多金属MOF衍生多孔碳微波吸收性能研究进展[J]. 空军工程大学学报, 2024, 25(1): 1–10. doi: 10.3969/j.issn.2097-1915.2024.01.001.HAN Guodong, SUN Yong, ZHOU Junxiang, et al. Research progress on microwave absorption performance of multi-metal MOF-derived porous carbon[J]. Journal of Air Force Engineering University, 2024, 25(1): 1–10. doi: 10.3969/j.issn.2097-1915.2024.01.001. [21] 韩国栋, 孙勇, 周俊祥, 等. 单金属MOF衍生多孔碳微波吸收性能研究进展[J]. 空军工程大学学报, 2023, 24(6): 2–14. doi: 10.3969/j.issn.2097-1915.2023.06.001.HAN Guodong, SUN Yong, ZHOU Junxiang, et al. Research progress on microwave absorption performance of monometallic MOF-derived porous carbon[J]. Journal of Air Force Engineering University, 2023, 24(6): 2–14. doi: 10.3969/j.issn.2097-1915.2023.06.001. [22] 席嘉彬. 高性能碳基电磁屏蔽及吸波材料的研究[D]. [博士论文], 浙江大学, 2018.XI Jiabin. Carbon-based materials for high-performance electromagnetic interference shielding and microwave absorption[D]. [Ph. D. dissertation], Zhejiang University, 2018. [23] 谭俊杰, 赵国梁, 徐晨. 陶瓷基吸波复合材料研究进展[J]. 陶瓷学报, 2023, 44(5): 849–863. doi: 10.13957/j.cnki.tcxb.2023.05.002.TAN Junjie, ZHAO Guoliang, and XU Chen. Progress of ceramic-based composites for microwave absorption[J]. Journal of Ceramics, 2023, 44(5): 849–863. doi: 10.13957/j.cnki.tcxb.2023.05.002. [24] DU Yuzhang, LIU Yichen, WANG Aoao, et al. Research progress and future perspectives on electromagnetic wave absorption of fibrous materials[J]. iScience, 2023, 26(10): 107873. doi: 10.1016/j.isci.2023.107873. [25] 侯冠一, 刘军, 张立群. 计算材料学在高分子材料领域的研究进展与发展趋势[J]. 高分子学报, 2023, 54(2): 166–185. doi: 10.11777/j.issn1000-3304.2022.22181.HOU Guanyi, LIU Jun, and ZHANG Liqun. Research progress and development of computational materials science for the polymeric materials[J]. Acta Polymerica Sinica, 2023, 54(2): 166–185. doi: 10.11777/j.issn1000-3304.2022.22181. [26] 蔡利梅. 模式识别: 使用MATLAB分析与实现[M]. 北京: 清华大学出版社, 2022: 3.CAI Limei. Pattern Recognition: Analyzing and Implementing with MATLAB[M]. Beijing: Tsinghua University Press, 2022: 3. [27] 温正, 孙华克. MATLAB智能算法[M]. 北京: 清华大学出版社, 2017.WEN Zheng and SUN Huake. MATLAB Intelligent Algorithm[M]. Beijing: Tsinghua University Press, 2017. -





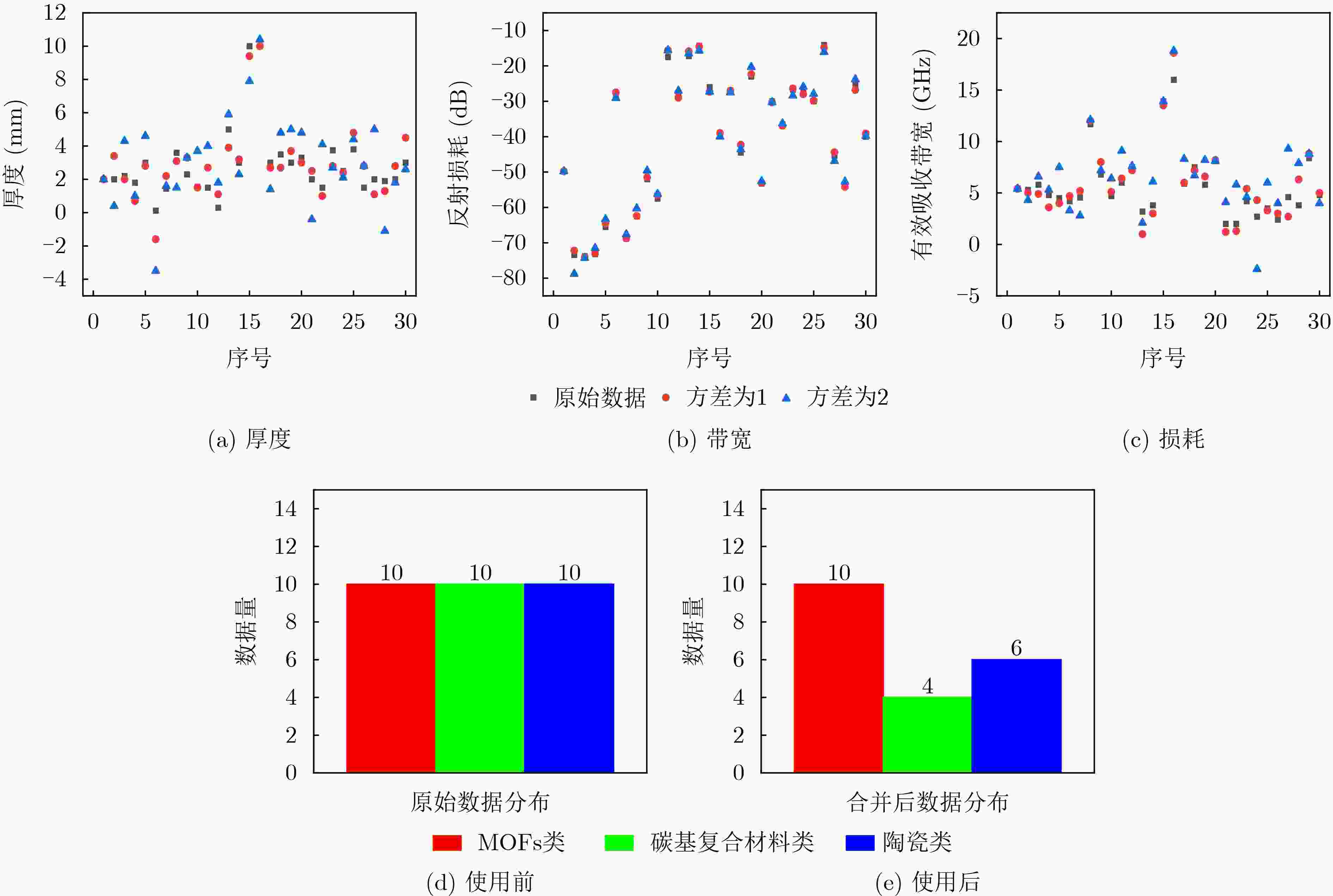
 下载:
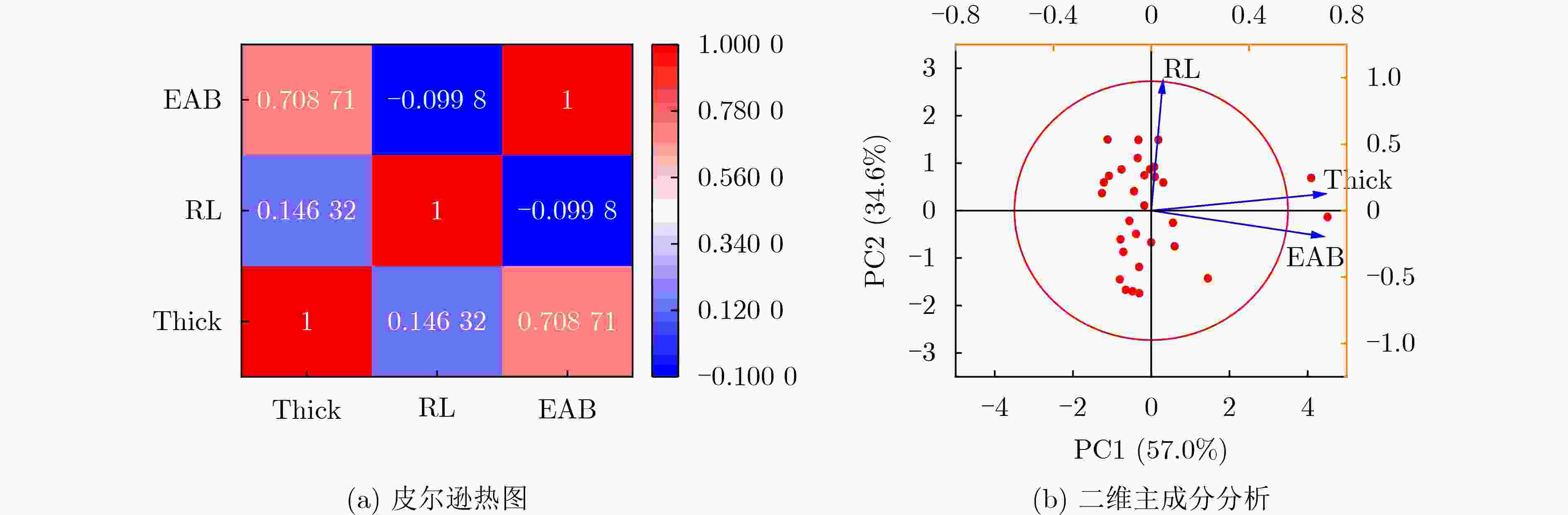
下载:
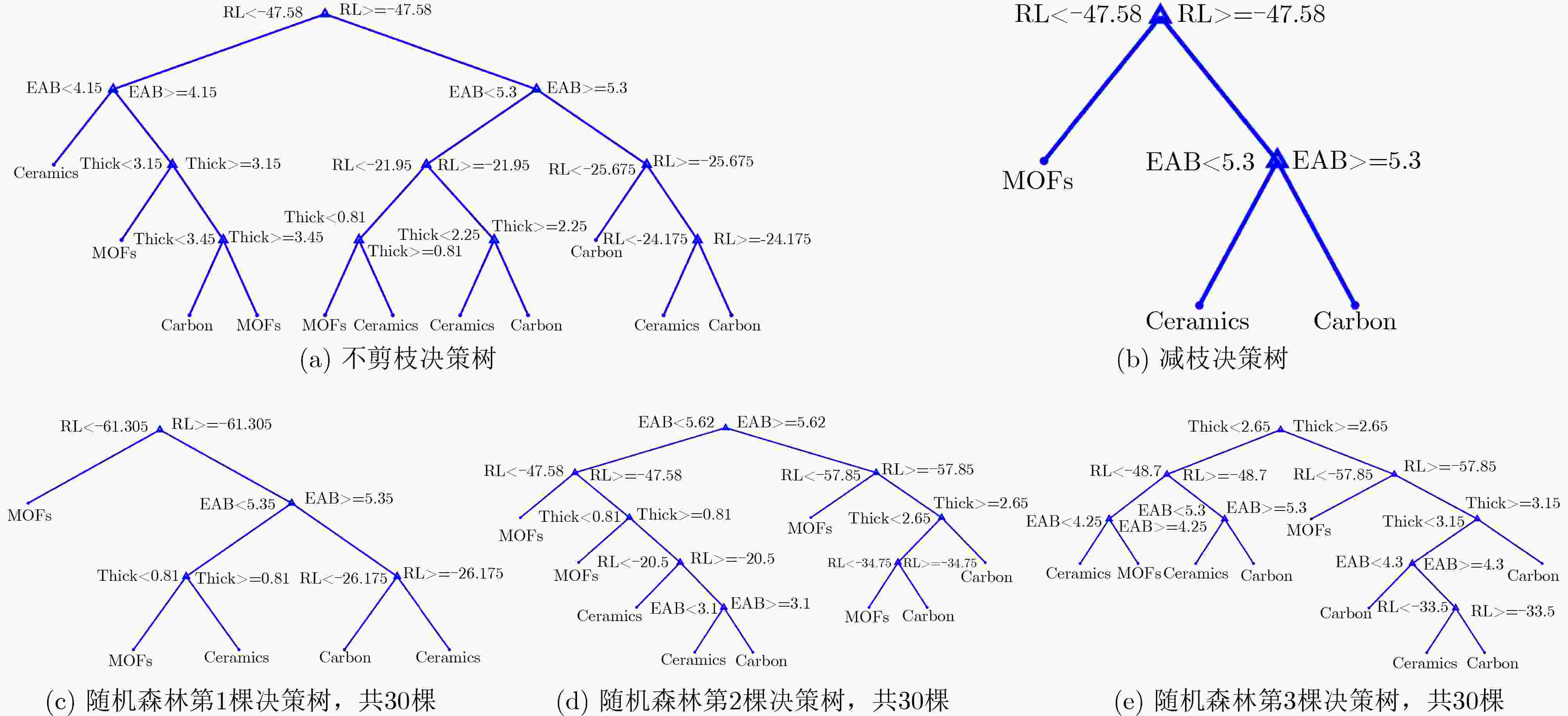


 下载:
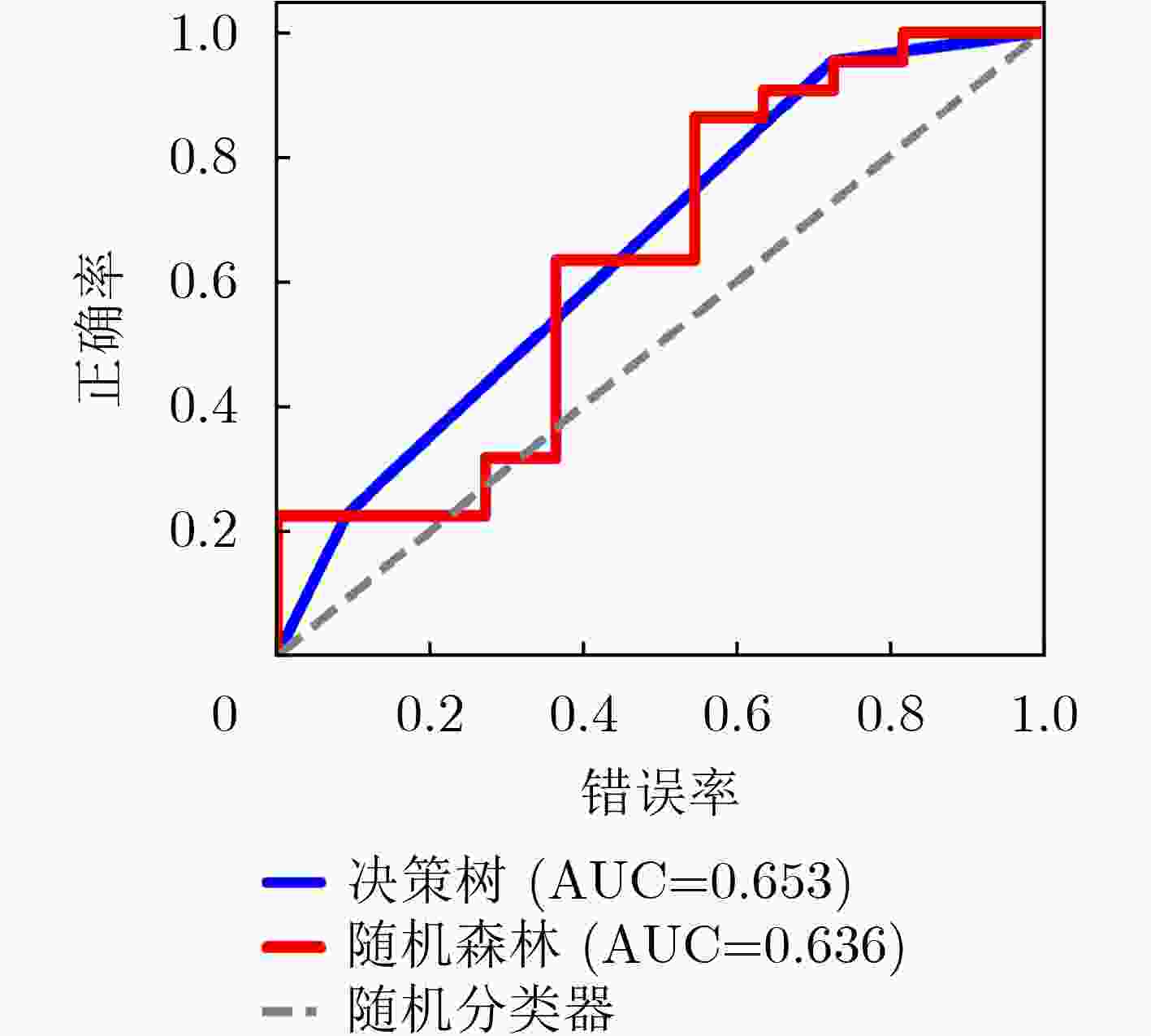
下载:
